- Учителю
- Урок математики в 6 классе Тема: Пропорция
Урок математики в 6 классе Тема: Пропорция
Тема урока: Пропорция
Цели урока:
Дидактические: введение понятия пропорции и ее членов, формулировка основного свойства пропорции;
Развивающие: развитие воображения, математической интуиции, памяти, мышления; формирование правильной математической речи;
Воспитательные: активизация познавательной и творческой активности учащихся.
Оборудование: демонстрационные карточки, таблицы, схемы.
Тип урока: урок сообщения новых знаний.
Ход урока
-
Организационный момент
-
Устные упражнения по карточкам
Фронтальная работа. Числа изображены на карточках, которые демонстрируются учащимся поочередно. На обратных сторонах карточек записаны ответы.
1. Выразите в процентах числа:
0,2 [20%] 0,15 [15%]
![]() [50%]
[50%] ![]() [60%]
[60%]
![]() [75%]
[75%] ![]() [5%]
[5%]
1 [100%] 3 [300%]
2. Сколько процентов составляет:
4 от 5 (80%) 12 от 8 (150%)
100 от 50 (200%) 72 от 24 (300%)
39 от 195 (20%) ![]() от
от ![]() (200%)
(200%)
3. Найдите отношение:
6 к 20 (![]() ) 8 к 40 (
) 8 к 40 (![]() )
)
![]() (
(![]() )
) ![]() (
(![]() )
)
![]() (
(![]() )
) ![]() (
(![]() )
)
( По материалу каждой карточки задаются дополнительные вопросы; проверяется глубина знаний учащихся по теме «Отношения».)
Вопросы:
-
Что называется отношением двух чисел?
-
Что показывает отношение двух чисел?
-
Какую часть первое число составляет от второго?
-
Сколько процентов одно число составляет от другого?
-
Объяснение нового материала
Вопросы:
Даны два отношения: 1,4 к 0,7 и 50 к 25. Найдите эти отношения. (![]() ,
,![]() )
)
Сравните данные отношения. (отношения равны, так как значения частных равны 2.)
Следовательно, мы можем записать равенство![]() или 1,4 : 0,7 = 50 : 25.
или 1,4 : 0,7 = 50 : 25.
Равенство двух отношений называют пропорцией.
(Формулировка определения понятия «пропорция» записывается учащимися в тетрадь.)
Общий вид пропорции:
a : b = c : d или ![]() .
.
Чтение записи a : b = c : d следующее:
«Отношение a к b равно отношению c к d»;
чтение записи ![]() :
:
«a так относится к b, как c относится к d»;
Название членов пропорции
a : b = c : d или ![]()
следующее: а и d - крайние члены, b 0, d 0;
b и c - средние члены.
(Используется схема, изображенная на плакате.)
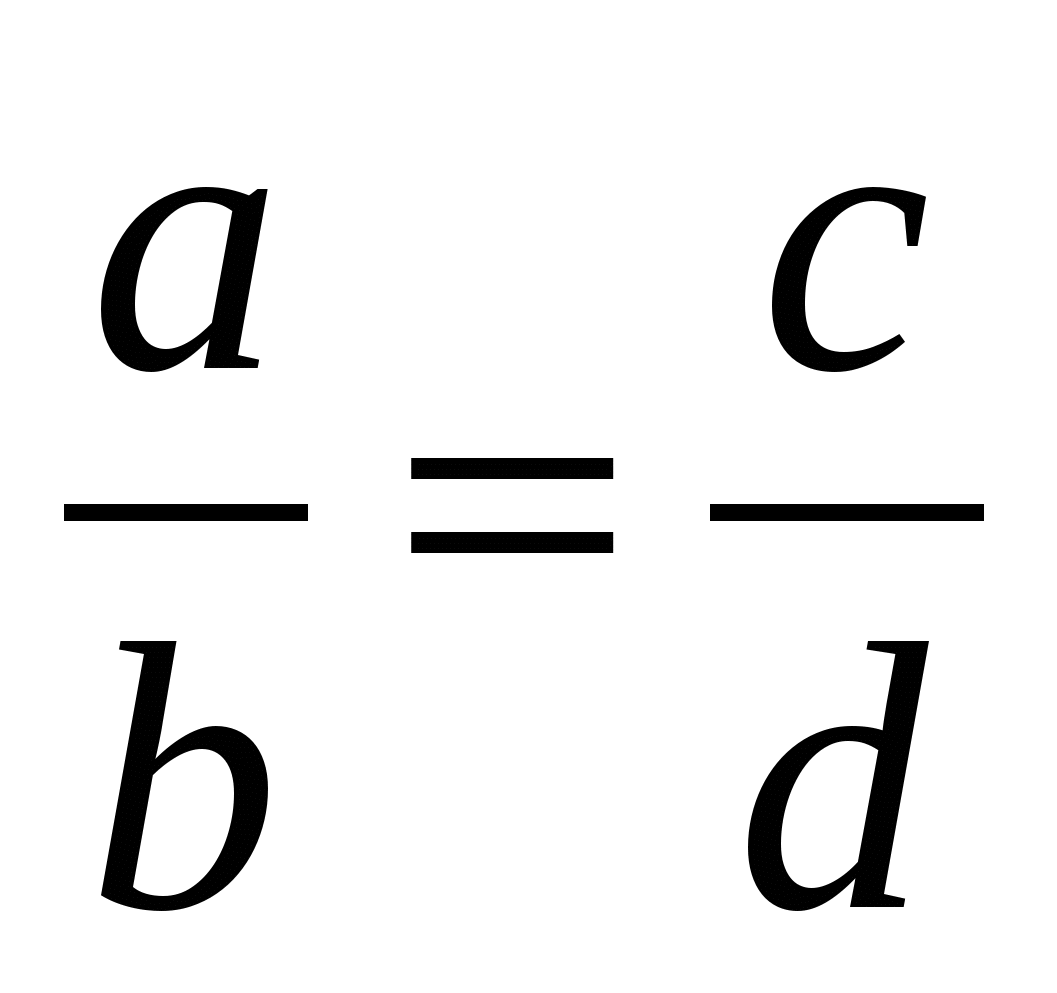
средние
a : b = c : d
крайние
Задание 1. (задание записано на доске, выполняется учениками устно.)
Установите, является ли пропорцией равенство (1-2).
1. ![]() (пропорция, так как 0,3=0,3)
(пропорция, так как 0,3=0,3)
2. ![]() (равенство не является пропорцией, так как
(равенство не является пропорцией, так как ![]() )
)
Задание 2. (Выполняется устно.)
В пропорции 2,4 : 0,6 = 8 : 2найдите произведение ее крайних и произведение ее средних членов, то есть
2,4 2 = 4,8 и 0,6 8 = 4,8
Получим, что 2,4 2 = 0,6 8.
Задание 3.
Найдите произведение крайних членов пропорции 1-2 и произведение средних членов.
1. ![]() (6 9 = 3 18, 54 = 54.)
(6 9 = 3 18, 54 = 54.)
2. ![]() (
(![]() )
)
Вывод: (вывод делают сами ученики.) Произведение крайних членов пропорции равно произведению ее средних членов.
Итак, мы сформулировали основное свойство пропорции: в верной пропорции произведение крайних членов равно произведению средних.
Вопросы:
Верно ли обратное утверждение?
Сформулируйте его. Приведите пример.
(Если произведение крайних членов равно произведению средних членов пропорции, то пропорция верна.)
Запишем основное свойство пропорции ![]() :
:
a d = b c или a : b = c : d, a d = b c.
И обратно:
Если a d = b c, то ![]() .
.
(Далее создается проблемная ситуация.)
Можно ли из данной пропорции составить новые пропорции? Сколько?
(На размышление учащимся дается две минуты, затем верное решение демонстрируется на доске с помощью следующей таблицы. Таблица не убирается до конца урока.)
![]()

a : b = c : d
a d = b c
![]()
![]()
![]()
![]()
Задание 4. (у доски выполняет сильный ученик.)
Используя верное равенство 5 1,2 = 2 3, составьте четыре верные пропорции:
(Учащиеся записывают в тетрадях.)
![]() - верная пропорция, так как 5 1,2 = 2 3; 6 = 6.
- верная пропорция, так как 5 1,2 = 2 3; 6 = 6.
![]() - верная пропорция.
- верная пропорция.
![]() - верная пропорция.
- верная пропорция.
![]() - верная пропорция.
- верная пропорция.
IV. Закрепление нового материала
(На доске одновременно решают двое учащихся. Остальные учащиеся записывают в тетрадях.)
№ 746(в, д) - устно, (а, е) - письменно. Прочитайте пропорции и проверьте, верны ли они, используя основное свойство пропорции:
а) ![]()
в) ![]()
д) ![]()
е) ![]()
Ответы и решения. а) ![]()
![]()
![]() 117 = 117.
117 = 117. ![]() - верная пропорция.
- верная пропорция.
в) Неверная пропорция.
д) Верная пропорция.
е) ![]()
15 0,09 = 1,8 2,7, 1350 4860.
![]() - неверная пропорция.
- неверная пропорция.
V. Домашнее задание
§ 4, п. 21, № 760, 761, 749, 763, 765 (а), составить пропорцию и новые, получающиеся из данной.
Пояснения: а) определение пропорции; б) основное свойство пропорции.
VI. Подведение итогов урока
Вопросы:
-
Что такое пропорция?
-
Сформулируйте основное свойство пропорции.
-
Сколько можно составить новых пропорций из данной?
Сообщаются оценки учащимся.