- Учителю
- Конспект урока по математике для 11 класса «Логарифмические уравнения и методы их решения»
Конспект урока по математике для 11 класса «Логарифмические уравнения и методы их решения»
Пилишкина Нина Николаевна
учитель математики высшей категории
ГУ лицей город Аксу
Павлодарская область г.Аксу ул.Энтузиастов 16 кв 28
телефон 68141
11 класс
Тема: Логарифмические уравнения и методы их решения.
Задача: 1. Сформировать умения и навыки решения логарифмических
уравнений.
2. Развитие продуктивного мышления и навыков самоконтроля в
процессе выполнения упражнений.
3. Развитие умений логически мыслить и аргументировано отстаивать
свои убеждения
Основные знания и умения:
Знать: определение логарифмического уравнения; основные методы решения логарифмических уравнений.
Умения: уметь решать логарифмические уравнения.
Ход урока
Ι. Организация урока.
Подготовка необходимых письменных принадлежностей, тетрадей, учебников.
ΙΙ. Актуализация опорных знаний.
Повторить: 1) Определение и свойства логарифмической функции;
2) Формулы логарифмирования и формулу перехода от одного
основания логарифма к другому;
3) Понятие о равносильности уравнений.
Устно: Используя основные свойства логарифмической функции и правила логарифмирования, установите закономерность заполнения таблицы и найдите х.
1 группа
1
2
8
3
х=5 log 2=2 ![]() х=2
х=2
5
Х
log![]() 2
2
2
3
2
9
хlg3=3 ![]() х=10
х=10
Х
lg3
3
3
64
4
3
2log 7=7 ![]() х=2
х=2
7
2
log![]() 7
7
2группа
1
5
Х
log![]() 6
6
х=5log 6![]() х=36
х=36
3
81
4
2
lg5
Х
lg7
х=lg5+lg7=lg35 ![]() х=lg35
х=lg35
7
12
5
3
log![]() 27
27
log![]() 3
3
X
х=![]() =3
=3 ![]() х=3
х=3
6
3
2
3 группа
1
![]()
Х
2log![]() 5
5
х=![]() =
=![]()
![]() х=5
х=5
2
32
5
2
7
2
5
х=log324-3log32 = log3![]() =log 33 =1
=log 33 =1 ![]() х =1
х =1
log![]() 24
24
3log![]() 2
2
x
3
3
5
125
3 log 5 =5 ![]() х=3
х=3
logх 5
3
5
ΙΙΙ. Изучение нового материала.
Учащиеся работают в группах. Каждая группа должна определить метод решения и решить предложенные уравнения.
Решить уравнения:
1группа
1
log3(1-2x)=1
ОДЗ: 1-2х![]() 0
0 ![]() х
х![]() 0,5
0,5
1-2х=31![]() х=-1
х=-1
Ответ: х= -1
2
log2(x-12)=2
ОДЗ: х![]() 12
12
х-12=2![]()
![]() х=16
х=16
Ответ: х=16
3
logx( ![]() )=-1,5
)=-1,5
ОДЗ:![]()
х-1,5=5-1,5![]() х=5
х=5
Ответ: х= 5
4
logx![]() =-0,4
=-0,4
ОДЗ:![]()
х-0,4=6-0,4![]() х=6
х=6
Ответ: х= 6
Вывод: Уравнения, решаемые с помощью определения логарифма.
2 группа
1
log2x-log211=log219-log2(30-x)
ОДЗ: 0![]()
![]()
![]()
х(30-х)=11*19
х 2 -30х+209=0 ![]()
х1=11, х2=19
Ответ: ![]()
2
log5x-log5(2x-5)=![]() log58-2log5
log58-2log5![]()
ОДЗ:
![]()
![]()
![]()
![]()
![]() х2-3х=4х-10
х2-3х=4х-10![]()
х2-7х+10=0
х1=2![]()
х2=5![]()
Ответ: х=5
3
lg(x+1)+lgx=lg6
ОДЗ: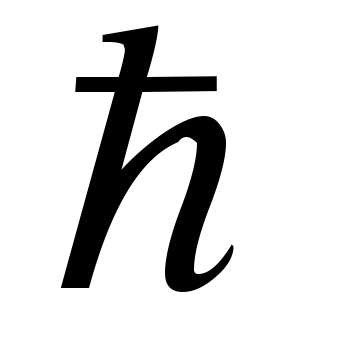
![]() х
х![]()
х(х+1)=6![]()
х2+х-6=0
х1=-3![]()
х2=2![]()
Ответ: х=2
4
log3(x-6)-![]() log32=1+
log32=1+![]() log3(x-10)
log3(x-10)
ОДЗ: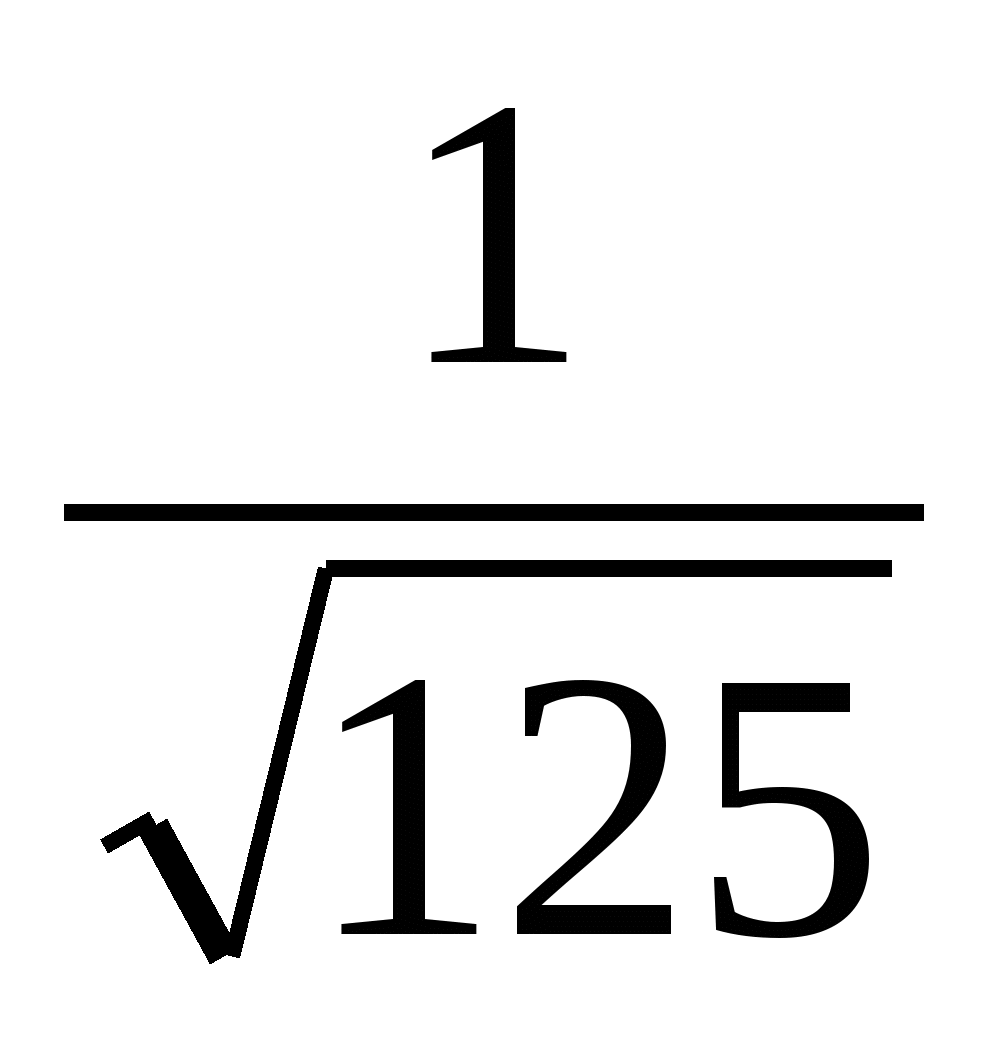
![]() х
х![]() 10
10
2log3(x-6)-log32=2+log3(x-10)
![]()
![]()
х2-30х+216=0
х1=12, х2=18 ![]()
Ответ:
х1=12,
х2=18
Вывод: Уравнения, решаемые потенцированием.
3 группа
1
log32(x+2)=5log3(x+2)
ОДЗ: х+2![]() 0, х
0, х![]()
log3(x+2)(log3(x+2)-5)=0
-
log3(x+2)=0
 x+2=30
x+2=30
![]() x=-1
x=-1![]()
-
log3(x+2)=5
 x+2=35
x+2=35
![]() x=241
x=241![]()
Ответ: х1=-1
х2=241
2
log2x lg(x+1)-2log2x=0
ОДЗ: 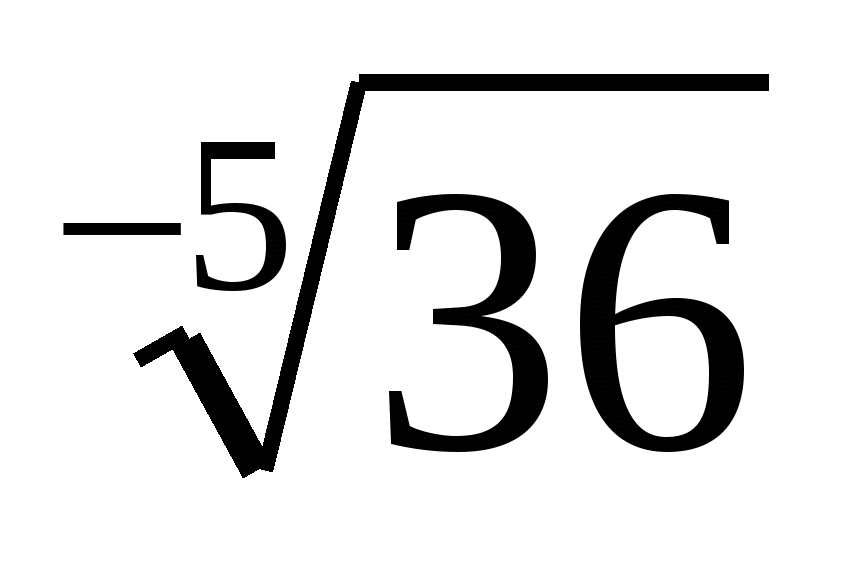
![]() х
х![]() 0
0
log2x(lg(x+1)-2)=0
-
log2x=0
 x1=20=1
x1=20=1 -
lg(x+1)=2
 102=x+1
102=x+1
![]() x2=99
x2=99
Ответ:
х1=1
х2=99
3
2log3x log2![]() -
- ![]()
ОДЗ: 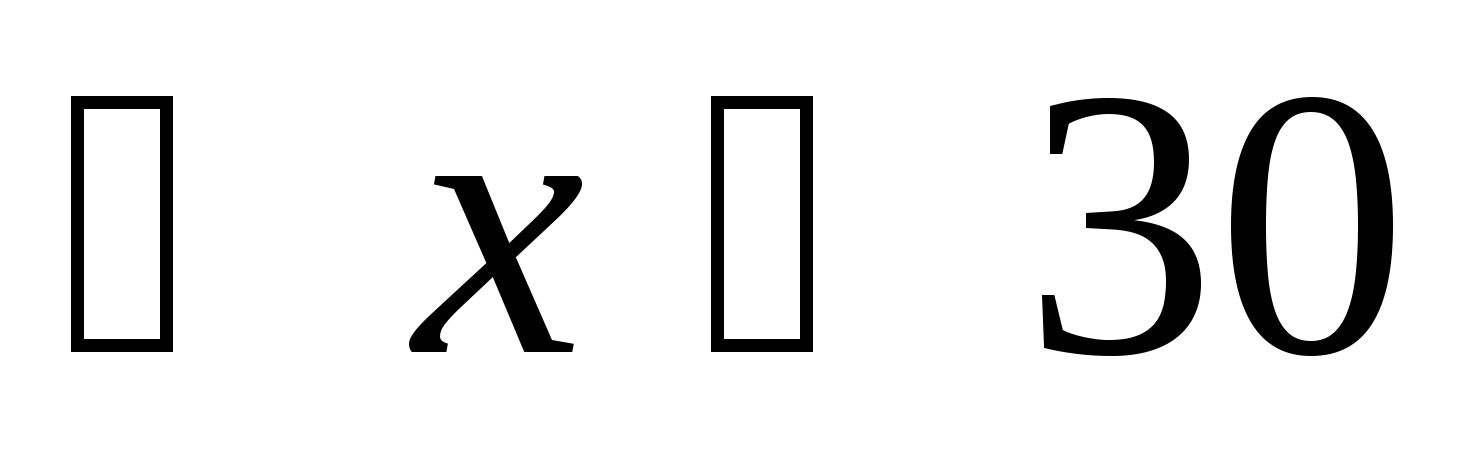
2log3x log2![]() -5log3x=0
-5log3x=0
log3x(log2(x-5)-5)=0
-
log3x=0
 x1=30=1
x1=30=1
-
log2(x-5)=5
 x=25+5
x=25+5
т.е. х=37
Ответ: х=37
4
log42x=6log4![]()
ОДЗ: х![]() 0
0
log4x(log4x-3)=0
-
log4x=0
 x1=40=1
x1=40=1 -
log4x-3=0
 log4x=3
log4x=3
![]() x=43=64
x=43=64
Ответ:
х1=1,х2=64
Вывод: Уравнения, решаемые путем разложения на множители.
4 группа
1
log32x-3log3x+2=0
ОДЗ: х![]() 0
0
Пусть у= log3x, тогда получим уравнение
у2-3у+2=0 ![]() у1=1 у2=2
у1=1 у2=2
-
log3x=1
 х1=3
х1=3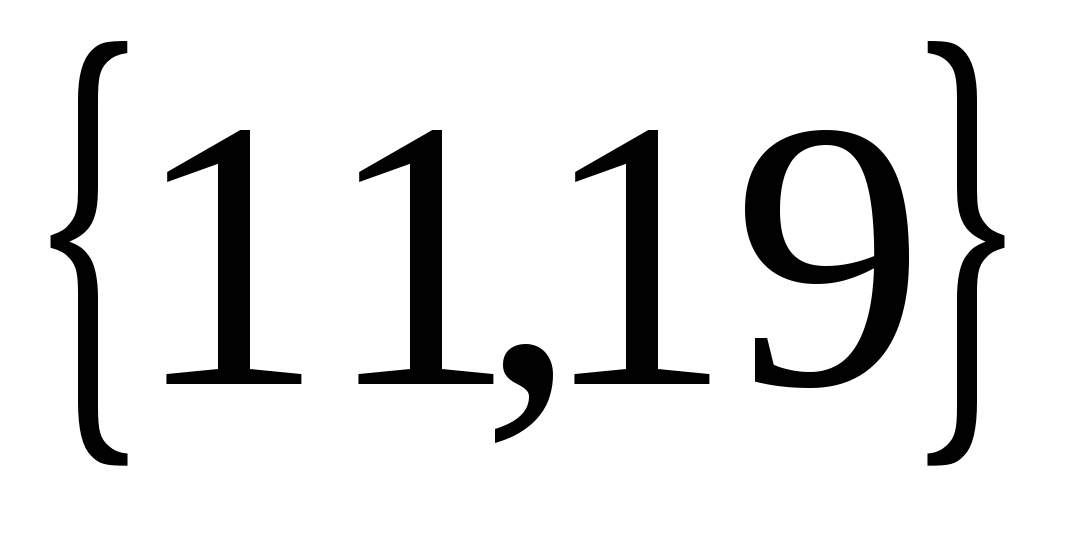
-
log3x=2
 х2=32=9
х2=32=9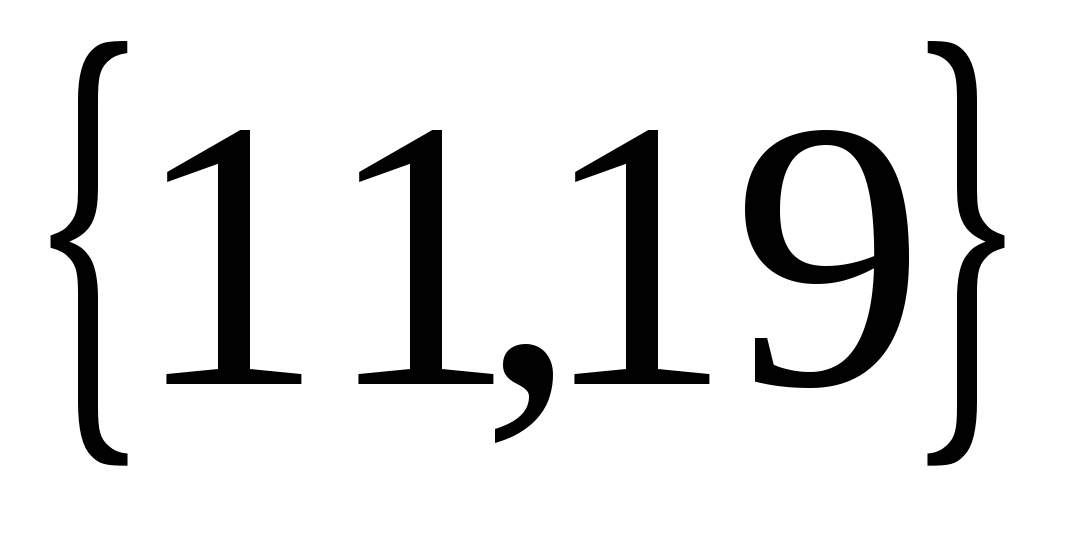
Ответ: х1=3 х2=9
2
logx2![]() -logx3
-logx3![]() +
+![]() =0
=0
ОДЗ: ![]()
![]() logx23-
logx23-![]() logx3+
logx3+![]() =0
=0
Пусть у= logx3, тогда получим уравнение
у2-6у+5=0![]() у1=1;у2=5
у1=1;у2=5
-
logx3=1 т.е. х=3
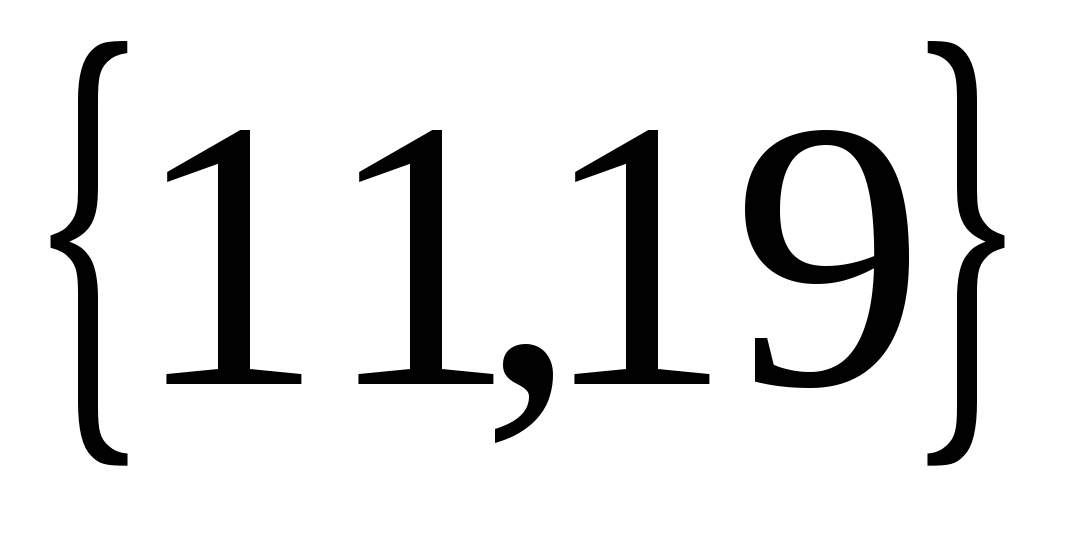
-
logx3=5 т.е.х5=3
 х=
х=
Ответ: ![]()
3
![]()
ОДЗ:
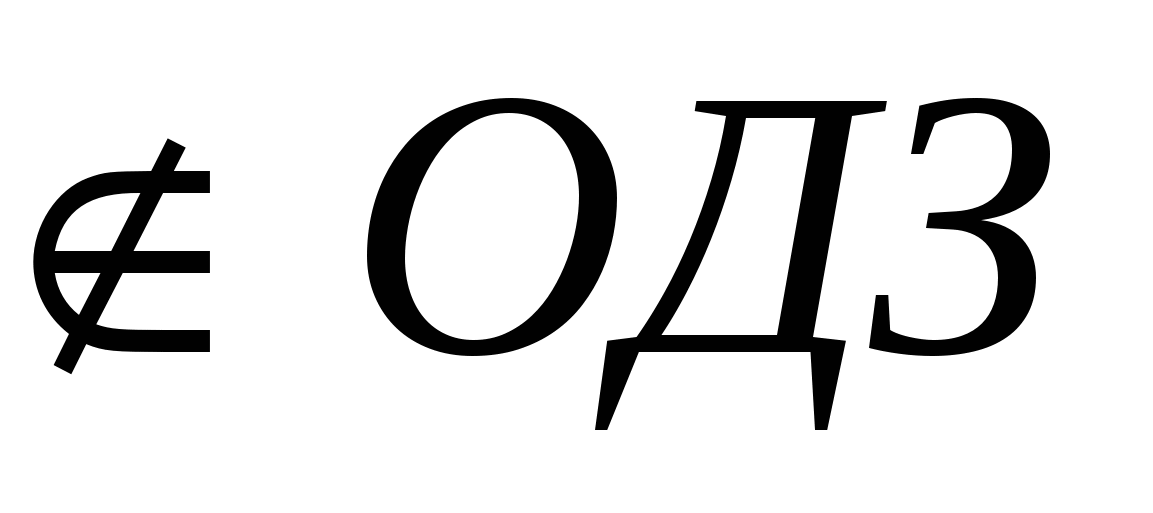
2(lgx+2)+3(lgx+1)=2(lg2x+3lgx+2)
2lg2x+lgx-3=0
-
lgx=-

 x1=10-3/2
x1=10-3/2 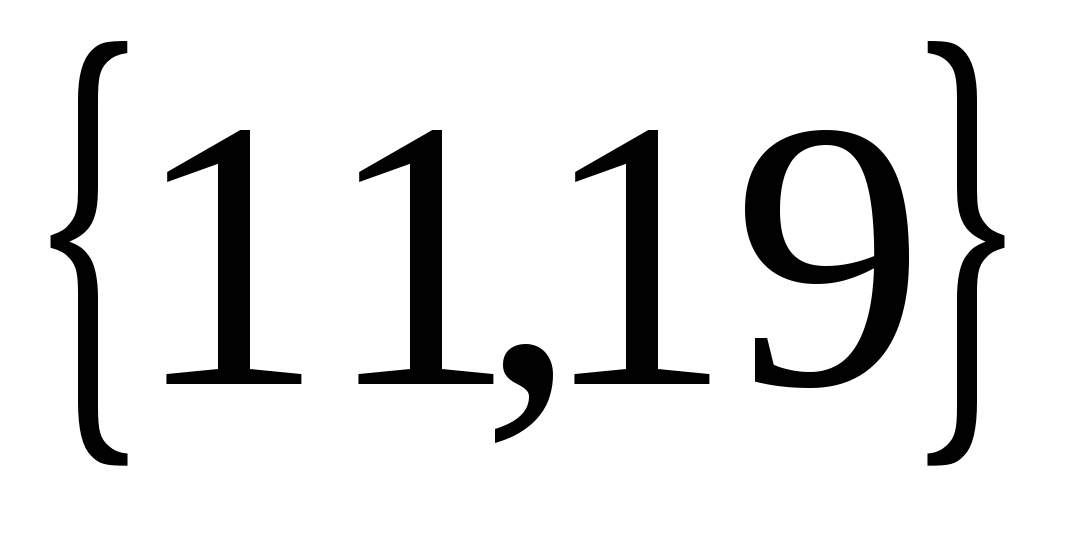
-
lgx=1
 x2=10
x2=10 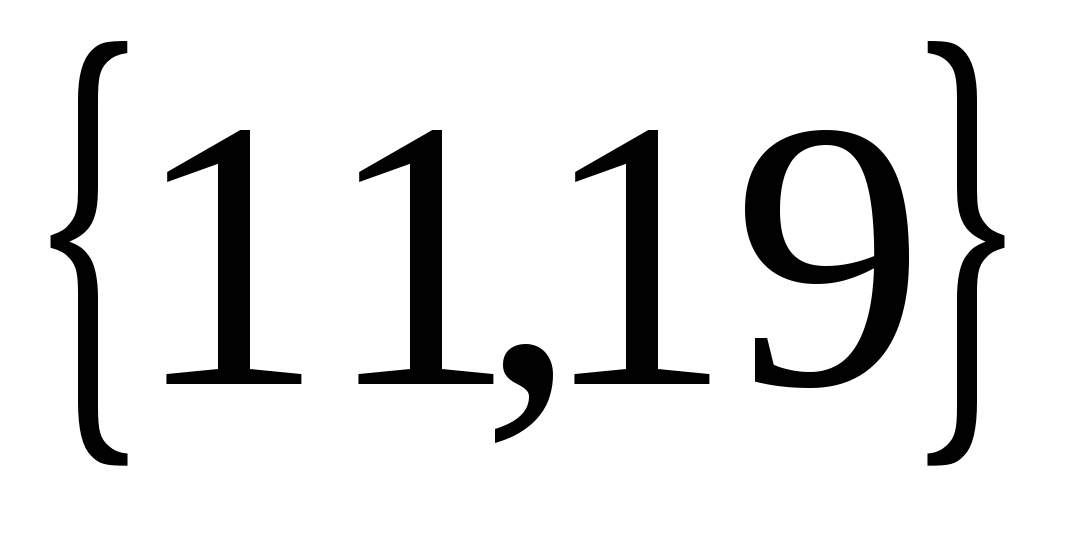
Ответ:
![]()
4
log3x+logx3=2
ОДЗ:![]()
log3x+ ![]()
log32x-2log3x+1=0
log3x=1 ![]() x=3
x=3![]()
Ответ: х=3
Выод: Уравнения, решаемые введением вспомогательной переменной
Общий вывод: Определение: Логарифмическими уравнениями называются уравнения, в которых неизвестная содержится только под знаком логарифма (в частности в основании логарифма)
Например: lg(x-3)=2, logx5=3log5(2x), log5x log2(x-3)=2log5x.
Методы решения:
-
Уравнения, решаемые с помощью определения логарифма;
-
Уравнения, решаемые потенцированием;
-
Уравнения, решаемые разложением на множители;
-
Уравнения, решаемые введением вспомогательной переменной.
ΙΥ. Как решить следующие уравнения?
-
хlg x+lg x -12=102lgx
Данные уравнения называются показательно - логарифмическими.
ОДЗ: х![]() 0
0
Способ решения: Прологарифмируем обе части уравнения по основанию 10.
(lg2x+5lgx-12)lgx=2lgx
lgx(lg2x+5lgx-14)=0
а) lgx=0 ![]() x=100=1
x=100=1 ![]()
б) lg2x+5lgx-14=0 ![]() lgx=-7 , т.е. х1=10-7
lgx=-7 , т.е. х1=10-7![]()
lgx=2, x2=102=100 ![]()
Ответ: ![]()
-
Решите уравнение: log2(x-3)+x=9 (*)
Данные уравнения называются трансцендентные уравнения
Способ решения: Графический способ решения.
Преобразуем данное уравнение, к виду log2(x-2)=9-x
На одном чертеже построим графики функций у=log2(x-3) и у=9-х
Графики пересекаются в точке А(7;2).
Следовательно, х=7 - корень уравнения.
Ответ: х=7
ΥΙ. Подведение итогов урока.
-
Ответить на вопросы учащихся.
-
Что нового узнали на уроке? Сформулируйте определение логарифмического уравнения и перечислите методы их решения.
-
Объявить оценки за урок.
ΥΙΙ. Задание на дом:
Решить уравнение (*)
А.Абылкасымов глава ΙΙΙ, §17, №278(1), №279(3), №281(1)