Многоуровневые задачи по теме Арифметическая и геометрическая прогрессия

Матричная модель многоуровневых задач по теме «Арифметическая и геометрическая прогрессия»

Базовая задача 1.

Задачи, приводимые под понятие арифметической прогрессии

Из предложенных последовательностей выберите ту, которая является арифметической прогрессией:

1) 2; 5; 8; 11;14; 17;…

2) 3; 9; 27; 81; 243;…

3) 1; 6; 11; 20; 25;…

4) -4; -8; -16; -32;…

5) 5; 25; 35; 45; 55;…

6)-2; -4; - 6; - 8; - 10;…

Выпишите первые восемь членов арифметической прогрессии (а_n), если:

а) а₁ = 1,7, d = -0,2;

Дано: (а _n ), а₁ = - 3, а₂ = 4.

Найти: а₁₆ - ?

Базовая задача 2.

Задачи, при решении которых используется характеристическое свойство арифметической прогрессии

Найдите среднее арифметическое чисел 4 и 10. Запишите в порядке возрастания найденное число с данными. Образует ли данная тройка чисел арифметическую прогрессию?

Найдите четвертый, пятый и шестой члены этой последовательности:

4;…;20;…;…;…

Найдите члены арифметической прогрессии (а_n), обозначенные буквами а₁; -8; а₂; - 2; а₅; 4

Базовая задача 3.

Задачи, по нахождению одних параметров арифметической прогрессии a_n, a_1, d, n, S _n по известным двум.

1. (а_n ) - арифметическая прогрессия, а₁ =10; d = - 0,1. Найди а₄.

1) 9,7; 2) 97; 3) -97;

4) 10,3; 5) -10,3.

Ответ: 1

П р и м е р . Найти сумму первых ста нечётных чисел.

Ответ: 10000

1. Найти первый член а₁ и разность d арифметической прогрессии в котором

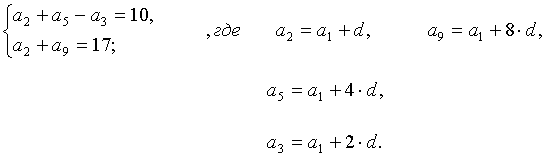
Ответ: а₁=13, d=-1.

Базовая задача 4.

Задачи, приводимые под понятие геометрической прогрессии

Найдите первые пять членов геометрической прогрессии (b_n), если: b₁ = 6, q =2

Ответ: 6,12,24,48,96

Найдите первые пять членов геометрической прогрессии (b_n), если: b₁ = 0,4, q = ½;

Ответ: 0,4; 0,2; 0,1; 0,05; 0,025

В геометрической прогрессии b₁; b₂; 4; 8;…. Найди b₁.

1) - 4; 2) 1; 3) 1/4; 4) 1/8; 5) - 1.

Ответ: 3

Базовая задача 5.

Задачи, при решении которых используется характеристическое свойство геометрической прогрессии

Найдите среднее геометрическое чисел 2 и . (средним геометрическим чисел a и b называется число ). Запишите в порядке убывания найденное число с данными. Образует ли данная тройка чисел геометрическую прогрессию?

Ответ: 1

Найдите четвертый, пятый и шестой члены этой последовательности:

2,…; ;…;…;…

1/4, 1/8,1/16

Найдите члены геометрической прогрессии (b_n), обозначенные буквами b₁; -8; b₃; - 2; b₅; -. Все члены отрицательны.

Ответ: -16,-8,-4,-2,-1,…

Базовая задача 6.

Задачи, по нахождению одних параметров геометрической прогрессии b_n, b_1, q, n, S _n по известным двум.

(b_n) - геометрическая прогрессия. Найди b₆ , если b₁ = 4; q = 1/2

1)- 1/8; 2) 1,25; 3) 1/8; 4)12,5; 5) - 1,25.

Ответ: 3

Последовательность (с_n) геометрическая прогрессия, первый член которой равен с₁, а знаменатель равен q. Выразите через c₁ и q: c_k+3;

Ответ: c_k+3= c_{1 ∙} q^k+2

1. Сумма первого и четвертого членов геометрической прогрессии равна 40, а сумма второго и пятого равна 10. Найти знаменатель прогрессии.

Ответ: 0,25.

Базовая задача 7.

Задачи по теме «Бесконечно убывающая геометрическая прогрессия.»

Найти сумму членов бесконечно убывающей геометрической прогрессии:

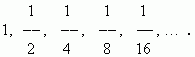
Ответ:

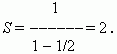
5. Найти знаменатель бесконечно убывающей геометрической прогрессии, сумма которой равна 1,6, если второй член равен (-0,5).

Ответ: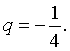

7. Сумма бесконечно убывающей геометрической прогрессии равна 4, а сумма кубов её членов равна 192. Найти первый член и знаменатель прогрессии.

Ответ: ,

Базовая задача 8.

Задачи смешанного характера на арифметическую и геометрическую прогрессию.

Сумма трех чисел, составляющих арифметическую прогрессию, равна 30. Если от

первого числа отнять 5, от второго отнять 4, а третье число оставить без

изменения, то полученные числа составят геометрическую прогрессию. Найти эти

числа .

Ответ: 8 ,10 ,12 или 17 ,10 ,3 .

1. Три числа a, b, 12 в указанном порядке составляют возрастающую геометрическую прогрессию, а числа a, b, 9 - арифметическую прогрессию. Найти a+b.

Ответ: 9.

Числа x, y и z образуют геометрическую прогрессию, а числа x+y, y+ z, x+ z образуют арифметическую прогрессию.

Найти z, если x+y+z=15 и z<x.

Ответ: z=20

Базовая задача 9.

Задачи по применению арифметической и геометрической прогрессии к решению текстовых задач.

Курс воздушных ванн начинают с 15 мин. в первый день и увеличивают время этой процедуры в каждый следующий день на 10 минут. Сколько дней следует принимать ванны в указанном режиме, чтобы достичь их максимальной продолжительности 1 час 45 минут?

Ответ: 10 дней следует принимать ванны.

Через три года в банке оказалось 880 руб., положенных под 40% (простые) годовых. Каков первоначальный вклад?

Ответ: первоначальный вклад 400 руб.

Если положить на вклад «Накопительный» некоторую сумму денег, то ежегодно она увеличивается на 10% от имеющейся на вкладе суммы. Вкладчик положил на вклад «Накопительный» 30000 рублей и три года подряд пополнял свой вклад и не снимал

с него денег. Определите, на сколько рублей увеличился его вклад за эти три года.

Ответ: 9930.

Базовая задача 10.

Задачи на комбинирование прогрессий и элементарных функций.

Пусть x₁, x₂ корни уравнения 12·x-x²=A, а x₃, x₄ корни уравнения 108·x-x²=В. Найти А, если известно, что последовательность x₁, x₂, x₃, x₄ - геометрическая прогрессия, все члены которой положительны.

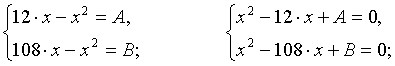
x₁, x₂, x₃, x₄ - геометрическая прогрессия.

x₁, x₁·q, x₁·q², x₁·q³;

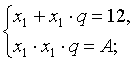
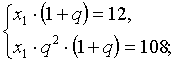
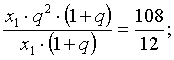
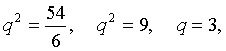
Ответ: .

Решить уравнение

Решение. Последовательность образует геометрическую прогрессию со знаменателем q = . По условию q ≠1 => х ≠1. Переформулируем задачу: сумма членов геометрической прогрессии равна 0. Найти х.

- не удовлетворяет условию задачи.

Ответ: -1.

Решите неравенство:

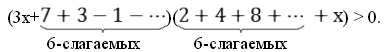
Двое учащихся упрощают скобки в данном неравенстве. Сумма 6-ти слагаемых арифметической прогрессии равна (-18) . Сумма 6-ти слагаемых геометрической прогрессии равна 126.

Неравенство перепишется в виде : (3х-18)(х+126)>0.

Третий ученик решает его методом интервалов.

Ответ: (- ; -126) U (6; + ).