Урок алгебры в 8 классе по теме «Уравнения, приводимые к квадратным уравнениям».

Магперова Р.К.

Урок алгебры в 8 классе по теме « Уравнения, приводимые к квадратным уравнениям».

Тип урока: изучение и первичное закрепление новых знаний.

Аннотация:

Урок изучения нового материала, основанный на деятельностном подходе, с использованием активных методов обучения. В ходе выполнения практической работы в группе, учащиеся самостоятельно знакомятся с определением биквадратного уравнения и составляют алгоритм решения таких уравнений, рассматривают решения уравнений методом введения новой переменной. Фронтальная работа с классом осуществляется в форме интерактивной беседы.

Цельурока:

• Развитие способностей анализировать, проводить сопоставления, обобщать, выдвигать гипотезы, строить доказательства, проводить наблюдения, планировать деятельность;

• Воспитание культуры речи; построение плана ответа; формирование умений осуществлять взаимосотрудничество, взаимоконтроль;

• Введение определения биквадратного уравнения, формирование умения решать биквадратные уравнения, исследовать число корней биквадратного уравнения.

1.Орг. момент.

Объявление темы урока, запись в тетрадях даты и темы урока.

Попробуйте сформулировать задачи нашего урока (заслушиваем несколько ответов учащихся).

+ Ввести понятие биквадратного уравнения, познакомиться с алгоритмом решения уравнений методом введения новой переменной, рассмотреть различные типы уравнений, приводящихся к квадратным.

2.Фронтальная и индивидуальная проверка и коррекция знаний и умений учащихся

А сейчас я предлагаю немного повторить:

• 3 ученика проходят к доске и решают предложенные квадратные уравнения по карточкам:

7х²-3х-4=0 3х²-9√2х+12=0 х²-(√3-2)х-2√3=0

Д=9+112=121 Д=162-144=18 Д=3+4√3+4=(√3+2)²

Х_1,2= 1; -4/7. Х_1,2=2√2; √2. Х_1,2=2; -√3.

• Класс:

сформулируйте и задайте вопросы по предыдущему материалу, который, по-вашему мнению, необходим для изучения новой темы. Отвечаем при необходимости с приведением примеров.

Что значит решить уравнение?Какое название имеет уравнение второй степени?Как называется квадратное уравнение, у которого первый коэффициент равен 1?От чего зависит количество корней квадратного уравнения?По какой формуле рассчитывается дискриминант?Сколько корней имеет квадратное уравнение, если D больше 0?Сколько корней имеет квадратное уравнение, если D меньше 0?Сколько корней имеет квадратное уравнение, если Dравен 0? Общая формула корней квадратного уравнения?

Проверка решенных уравнений.

3.Этап формирования новых знаний

Изучите предложенный материал по учебнику (стр.62), сформулируйте и запишите вопросы по теме в лист оценивания.

Итог самостоятельной работы.

- Итак, что же вы узнали?

+ Биквадратным называется уравнение вида ах⁴ + вх² + с = 0, где а ≠ 0.

- Существенно ли замечание, что а ≠ 0?

+ Да, т.к. еслиа будет равно 0, то уравнение будет квадратным (неполным).

- Приведите пример биквадратного уравнения.

+ Например, 10х⁴ + 5х² + 3 = 0 (Дети приводят примеры биквадратных уравнений).

-Как называется метод приведения уравнения четвертой степени к квадратному?

+ Метод введения новых переменных.

-Каков алгоритм решения биквадратных уравнений?

+Алгоритм следующий:

1) Ввести замену переменной.

2) Составить квадратное уравнение с новой переменной: at² + bt + c=0.

3) Решить новое квадратное уравнение.

4) Вернуться к замене переменной.

5) Решить получившиеся уравнения.

4.Проверка первичного понимания.

№ 189(1) решает один из учеников по алгоритму с комментариями у доски.

Затем решаем по группам. 1-я группа продолжает работу, решая задания из предложенной карточки.

2-я, 3-я, 4-я группы переходят к исследованию

5. Исследование.

- Сейчас мы проведём исследование: сколько корней имеет биквадратное уравнение. Каждая пара получит своё уравнение и решит его.

(Учитель раздаёт уравнения: х⁴-10х²+9=0, 2х⁴ -х²-1=0, х⁴+5х²+4=0, 2х⁴+5х²+4=0,

х⁴-8х²+16=0, х⁴+8х²+16=0.)

А потом мы сделаем выводы о том, сколько корней имеют биквадратные уравнения.

+ Дети решают уравнения

- Итак, что получилось? Рассказывает 1 пара.

+ х⁴-10х²+9=0. У нас получился дискриминант положительный, значит, квадратное уравнение имеет 2 корня, корни тоже положительные, значит всего 4 корня.

-Хорошо. Вторая пара.

+ 2х⁴ -х²-1=0. Дискриминант положительный, один корень положительный, а другой отрицательный, значит, биквадратное уравнение имеет 2 корня.

- Третья пара.

+ х⁴+5х²+4=0. Дискриминант квадратного уравнения положительный, но корни отрицательные, значит, биквадратное уравнение не имеет корней.

- Четвёртая пара.

+ 2х⁴+5х²+4=0. А у нас дискриминант отрицательный, поэтому уравнение не имеет корней.

- Молодцы! Следующая пара.

+ Уравнение х⁴-8х²+16=0 имеет 2 корня, т.к. квадратное уравнение имеет 1 корень (Д=0).

- И последняя пара.

+ Уравнение х⁴+8х²+16=0 не имеет корней, т.к. хотя и Д=0, но корень-то отрицательный.

Итог исследования.

Итоги исследования мы поместим в таблицу.

Посмотрите и прокомментируйте.

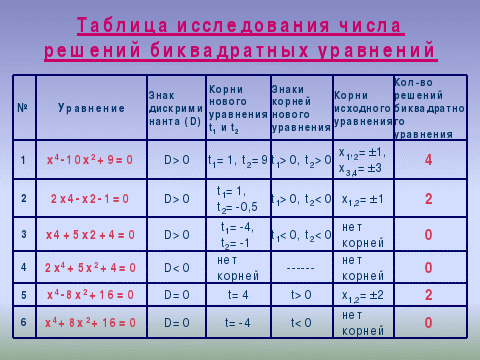
+ Ученики комментируют по цепочке.

Группа № 1 проверяют решения и сверяются с предложенными ответами.

6. Группы1,2,3,4 выполняют задание № 191(1) с комментариями у доски. Затем

№ 5.68 из нового учебника.

7. Итог урока.

- Подведём итог урока. Продолжите фразу:

СЕГОДНЯ НА УРОКЕ Я ПОВТОРИЛ…

СЕГОДНЯ НА УРОКЕ Я УЗНАЛ…

СЕГОДНЯ НА УРОКЕ Я НАУЧИЛСЯ…

НА СЛЕДУЮЩИХ УРОКАХ МНЕ НЕОБХОДИМО…

8. Задание на дом (дифференцированное):

1-й уровень № 189(2-4), № 191(2-4)

2-й уровень № 194, № 195

9. Оценки.

Алгоритм решения уравнений, приводимых к квадратным

1) Ввести замену переменной.

2) Составить квадратное уравнение с новой переменной: at² + bt + c=0.

3) Решить новое квадратное уравнение.

4) Вернуться к замене переменной.

5) Решить получившиеся уравнения.

Образец:

х⁴-25х²+144=0

Введем новую переменную х²=у, тогда получаем уравнение:

у²-25у+144=0

а=1 в=-25 с=144

D=b²-4ac=(-25)²-4*1*144=625-576=49>0, два корня

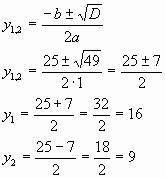
Подставляем в замену х²=у

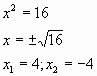
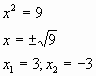
Ответ: 4; -4; 3; -3

4. "Программируемый тест"

На оценку "4-5"

1. Определить вид уравнения: а⁴-4а²+3=0а) линейное;
б) биквадратное;
в) неполное;
г) квадратное.2. Приведите уравнение к квадратному: (х²-4х)²+9(х²-4х)+20=0а) а²-а+28=0;
б) а²+9а+20=0;
в) а²+11х+28=0;
г) а²-9а+20=0.3. Найдите дискриминант: 3х²+11х-34=0а) 196;
б) 225;
в) 529;
г) 14. Решите уравнение: 4х⁴-5х²+1=0.а)

б)

в)

г) .

На оценку "3"1. Определить вид уравнения: 5а⁴-3а²-3=0а) линейное;
б) биквадратное;
в) неполное;
г) квадратное.2. Приведите уравнение к квадратному: с⁴-6с²+8=0а) х²-х+8=0;
б) х²-6х+8=0;
в) а²+6х+8=0;
г) а²+6+8а=0.3. Найдите дискриминант: 4у²+7у+3=0а) 169;
б) 16;
в) 1;
г) 814. Решите уравнение: х⁴-25х²+144=0.а) 4; -4; -3; 3;
б) -4; -4; 3; 3
в) -4; 4; 1/3; -1/3
г) -3; -3; 4.

Ответы вносятся в карточку и быстро проверяются с помощью ключа:

А

Б

В

Г

1

2

3

4

Лист оценивания

№

Знаю,

умею

Иногда

Допускаю ошибки

Часто

Допускаю ошибки,

не знаю

1

Решение неполных квадратных уравнений

2

Формулы дискриминанта и корней квадратного уравнения ( Д, Д/4)

3

Вычисление дискриминанта и корней квадратного уравнения ( Д, Д/4)

4

5

6

7

8

9

10

.