Урок 'Площадь круга' (9 класс)

Урок математики в 9-м классе по теме "Площадь круга"
Бутакова Светлана Андриановна, учитель математики
Цели урока:

Изучить формулу площади круга, применять ее при решении задач.
Рассмотреть различные способы определения центра окружности (круга), если он не указан, учить аккуратно и точно пользоваться измерительными приборами.
Развивать познавательный интерес учащихся, математическую речь, познакомить их с историческим материалом.
Воспитывать сотрудничество, внимание и уважение друг к другу.

Оборудование:

циркуль, линейка, модель круга;
проектор, компьютер;
задания для работы в группах;
маркеры, листы бумаги А4.
Класс разбивается на группы, в каждой группе выбирается ответственный, который отвечает за дисциплину, порядок и работоспособность группы. Он же на перемене перед уроком проверяет домашнее задание. Ответы на вопросы пишутся маркером на листах А4 и показываются учителю.

I. Организационный момент.

В книге П.Л. Треверс «Мери Поппинс» в одном из эпизодов Кошка задает вопрос Королю.

Ученик: «Первый вопрос: «Высоко ли до неба?»

Король удовлетворенно хмыкнул. Этот вопрос был как раз в его вкусе, и он улыбнулся с видом превосходства.

Ученик: - Ну, конечно,- начал он,- это понятие относительное, если мы будем измерять высоту от уровня моря - результат будет один. Если с вершины горы - другой. И приняв все это в расчет, а также определив широту и долготу, учитывая данные метеорологии, психологии, геологии, топологии и болтологии, а также астрономии и физиологии, статистики, лингвистики, беллетристики и мистики, мы можем…»

К сожалению, мы вынуждены прервать цитату. Желающие могут прочесть книгу и узнать, чем закончился этот разговор. Как ни странно, но Король прав. Задача измерения весьма трудная, и одной изобретательности недостаточно. Надо многое знать - законы природы, свойства фигур, математические формулы.

Тема сегодняшнего урока «Площадь круга». Вы выведете формулу для вычисления площади круга, познакомитесь с историей развития числа π.

Вам сегодня предстоит выполнить лабораторно-практическую работу. В этой работе вы сами определите центр окружности там, где он не обозначен, измерите ее радиус и вычислите площадь заданных фигур. Чтобы успешно справиться с поставленной задачей необходимо, ответить на следующие вопросы.
II. Устная работа.

Фронтальная работа с классом.

Вопрос:

Какая формула используется для вычисления длины окружности?

Чему равно отношение длины окружности к диаметру?

Радиус окружности увеличили в 2 (3, 4, n)раз. Как изменилась длина окружности?

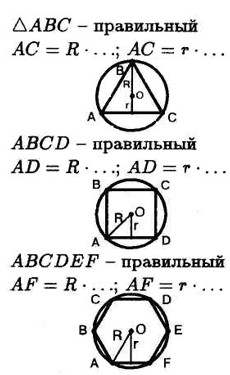
Если треугольник ABC правильный, то AC=R·…, AC=r·…

ABCD - правильный. AD=R·…, AD=r·…
ABCDEF - правильный. AF=R·…, AF=r·…

III. Работа по готовым чертежам.

(Письменная работа на листах А4. На доске заранее сделаны чертежи. Готовые решения крепятся на доске рядом с задачей.)

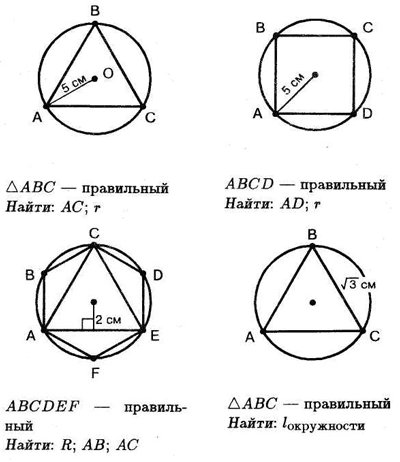
Сейчас за 5 минут вы должны решить и показать решение 4 задач.

IV. Проверка задания на дом.

Вам были предложены для решения дома 4 задачи. Ответственные проверили решения задач в своих группах? Есть ли вопросы по домашней работе? (Если есть вопросы по домашней работе, то решение таких задач объясняют ученики, которые их решили.)
Вопрос: Какую геометрическую фигуру называют окружностью? (Окружность - это множество точек плоскости, равноудаленных от данной точки.)

Ученик: Окружность - удивительно гармоничная фигура, древние греки считали ее самой совершенной. Совершенство окружности - в расположении всех ее точек на одинаковом расстоянии от центра. Именно поэтому окружность - единственная кривая. «которая может скользить сама по себе», вращаясь вокруг центра. Основное свойство окружности дает ответ на вопросы, почему для ее вычерчивания используют циркуль и почему колеса делают круглыми, а не квадратными.

Кстати, о колесе. Это одно из самых великих изобретений человечества. Оказывается, додуматься до колеса было не так просто, как это может показаться. Ведь даже ацтеки, жившие в Мексике, почти до XVI в. не знали колеса.

Одной из задач в домашней работе была теоретическая: Почему канализационные люки делают круглыми, а не квадратными? (Сравните сторону квадрата с его диагональю. Квадратная крышка может провалиться в люк, чего никогда не случится с круглой крышкой.)

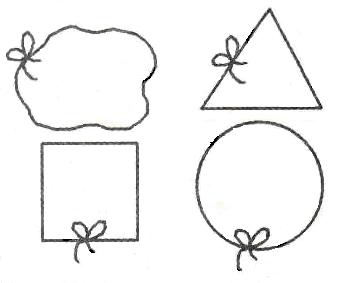
Ученик: Окружность обладает еще одним интересным свойством. Возьмем веревочку и свяжем ее в кольцо. Положив полученное кольцо на плоскость, сделаем из него разные фигуры: квадрат, треугольник, окружность и т.д. Площадь, ограниченная окружностью (т.е. площадь круга) - наибольшая среди полученных таким образом площадей.

IV. Объяснение новой темы.

Вопрос: Какую геометрическую фигуру называют кругом? (Кругом называют часть плоскости, ограниченную окружностью)

Вопрос: Какая формула используется для вычисления площади круга? (S = πR2)

Выведем формулу для вычисления площади круга.

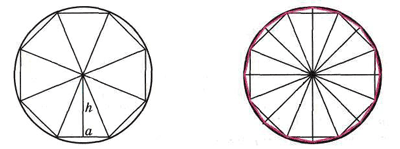
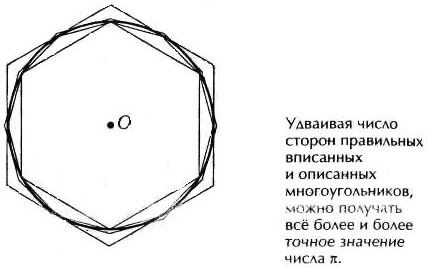
Рассмотрим правильный многоугольник, вписанный в окружность. Его площадь равна произведению площади одного треугольника на их количество: . Если же увеличивать число сторон многоугольника бесконечно, то он практически сольется с окружностью. И тогда a · h → 2π · R, h→ R. Площадь такого многоугольника очень незначительно отличается от площади соответствующего круга: . Итак, площадь круга вычисляется по формуле S = πR2.

Вопрос:
Пропорциональность каких величин указана в формуле?
Как относятся площади двух кругов ?
Как изменится площадь круга, если его радиус увеличить в 3 раза?
Как изменится радиус круга, если его площадь уменьшили в 25 раз?
V. Создание проблемной ситуации. Лабораторно-практическая работа.

Сейчас вам предстоит выполнить лабораторно-практическую работу. Каждая команда решает только одно задание. На решение этих задач вам дается 4 минуты. (Ответственные выбирают задания. Решения №1 и №2 оформляются на листах А4.)

Задания:

1. Найдите центр круга удобным для вас способом и вычислите его площадь. Постройте круг, площадь которого в 4 раза больше площади данного круга. Во сколько раз длина окружности, ограничивающая первый круг, меньше длины окружности, ограничивающей второй круг?

2. Выполните необходимые измерения и найдите площадь закрашенной части фигуры.

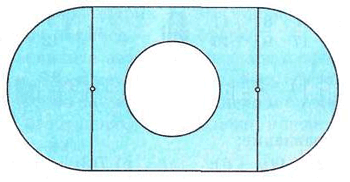
3. Окружности с общим центром называются концентрическими, а разность их радиусов называется шириной ограниченного ими кольца. В кольце, образованном двумя концентрическими окружностями, хорда большей окружности, касающаяся меньшей, равна a. Определите площадь кольца.

4. Вычислите площадь круга, если она меньше площади описанного квадрата на 4,3м3. (π = 3,14)

5. Из жести в форме круга радиусом 4см вырезали правильный шестиугольник наибольшей площади. Сколько процентов жести ушло в отходы?

Вычислите площадь круг радиусом 4см вырезали правильный шестиугольник наибольшей площади. Сколько процентов жести ушло в отходы?

(Через отведенное время обсуждаются решения задач 1 и 2, решения остальных задач записаны на листах А4, а чертежи, если необходимо, выполняются на доске.)

Вопрос: Какие геометрические свойства используются для нахождения центра окружности, если он не обозначен?
Возможные ответы:

а) вписанный угол, опирающийся на диаметр;
б) свойство точек серединного перпендикуляра;
в) взаимно перпендикулярные диаметры.

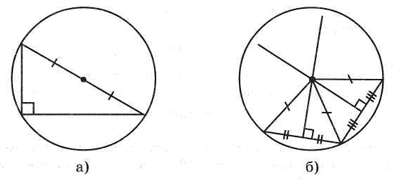
Заслушиваются ответы учащихся у доски.

VI. Итоги урока. Отметки за работу на уроке.

Подведем итоги урока вашими ответами на устный тест.

Вопрос: Установите, истинны или ложны следующие высказывания:

Длину окружности можно вычислить по формуле C = πD, где D -диаметр окружности. (истинно)

Площадь круга равна произведению квадрата его радиуса на π. (истинно)

Длина полуокружности диаметра 10 равна 5π. (истинно)

Площадь круга можно вычислить по формуле , где D - диаметр круга. (ложно)

Площадь круга радиуса 10 равна 10π. (ложно)
VII. Сообщения учащихся о числе π.

3,14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 59230 78164 06286 20899 86280 34825 34211 70679…

Ученик: π - первая буква греческого слова окружность, периферия. Впервые такое обозначение ввел в 1706 году английский математик Джонс. Общепринятым это обозначение стало в 1736 году, после одной из работ Эйлера, великого математика, физика, астронома. Письменная история числа π начинается с египетского папируса, датируемого примерно 2000 годом до н.э., где оно принимается равным …. Архимед для оценки числа π вычислял периметры вписанных и описанных многоугольников до 96-угольника. Ему принадлежит приближенное значение

Для закрепления в памяти числа Архимеда может оказаться полезной шутка из учебника Магницкого:

Двадцать две совы скучали
На больших сухих суках.
Двадцать две совы мечтали
О семи больших мышах,
О мышах довольно юрких
В аккуратных серых шкурках.
Слюнки капали с усов
У огромных серых сов.
Ученик: Индусы в V-VI веках пользовались числом китайцы - числом , а также числом

Три первые цифры числа π запомнить совсем несложно. А для большего числа знаков существуют забавные поговорки и стихи. Например, такие:

Нужно только постараться
И запомнить все как есть:
Три, четырнадцать, пятнадцать,
Девяноста два и шесть.