- Учителю
- «Дробно-линейная функция» - 9 класс
«Дробно-линейная функция» - 9 класс
"СУБАШСКАЯ ОСНОВНАЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА" БАЛТАСИНСКОГО МУНИЦИПАЛЬНОГО РАЙОНА
РЕСПУБЛИКИ ТАТАРСТАН
Разработка урока - 9 класса
Тема: Дробно - линейная функция
Автор: учитель математики высшей
квалификационной категории
Гарифуллина Раиля Рифкатовна
2014
Тема урока: Дробно - линейная функция.
Цель урока:
- образовательная: Познакомить учащихся с понятиями дробно - линейная функция и уравнение асимптот;
- развивающая: Формирование приемов логического мышления, развитие интереса к предмету; развить нахождение области определеиия, области значения дробно - линейной функции и формирование навыков построения её графика;
- мотивационная цель: воспитание математической культуры учащихся, внимательности, сохранение и развитие интереса к изучению предмета через применение различных форм овладения знаниями.
Оборудование и литература: Ноутбук, проектор, интерактивная доска, координатная полскость и график функции у= 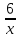 , карта рефлексии, мультимедийная презентация, Алгебра : учебник для 9 класса основной общеобразовательной школы/ Ю.Н. Макарычев, Н.Г.Мендюк, К.И.Нешков, С.Б.Суворова; под редакции С.А.Теляковского / М: "Просвещение", 2004 с дополнениями .
, карта рефлексии, мультимедийная презентация, Алгебра : учебник для 9 класса основной общеобразовательной школы/ Ю.Н. Макарычев, Н.Г.Мендюк, К.И.Нешков, С.Б.Суворова; под редакции С.А.Теляковского / М: "Просвещение", 2004 с дополнениями .
Тип урока:
-
урок совершенствования знаний, умений, навыков.
Ход урока.
I организационный момент:
Цель: - развитие устных вычислительных навыков;
-
повторение теоретических материалов и определений необходимых для изучения новой темы.
Добрый день! Начинаем урок с проверки домашнего задания:
Внимание на экран (слайд 1-4):
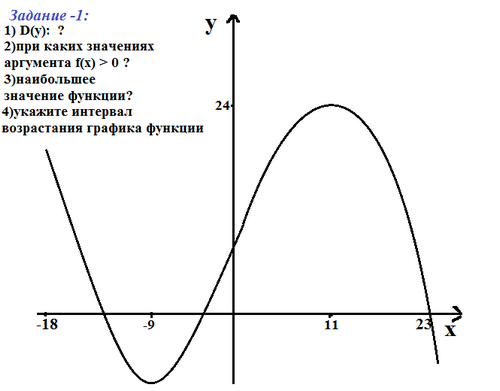
Задание - 1.
Отвечайте, пожалуйста, по графику данной функции на 3 вопрос (найти наибольшее значение функции, ...)
(24)
Задание -2. Вычислите значение выражения:
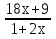 -
- 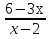 =
= 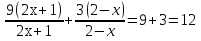
Задание -3: Найдите утроенную сумму корней квадратного уравнения:
Х 2-671∙Х + 670= 0.
Сумма коэффициентов квадратного уравнения равна нулю:
1+(-671)+670 = 0. Значит, х1=1 и х2=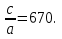 Следовательно,
Следовательно,
3∙(х 1+х 2 )=3∙671=2013
А теперь запишем последовательно ответы на все 3 задания через точки. (24.12.2013.)
-
с целью подготовки к ГИА вычислим устно и набираем буквы соответсвующие числам: (слайд -5)
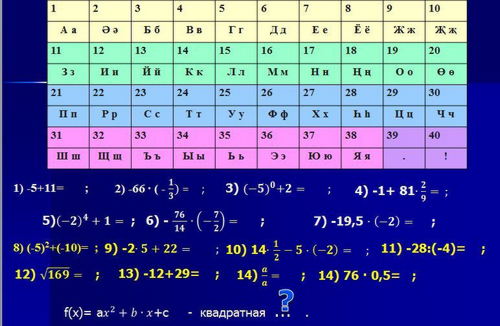
Результат: Да, все верно! И так, тема сегоднешнего урока:
Дробно - линейная функция.
Прежде чем выезжать на дорогу, водитель должен знать правила дорожного движения: запрещающие и разрешающие знаки. Нам с вами сегодня тоже нужно вспомнить некоторые запрещающие и разрешающие знаки. Внимание на экран! (Слайд-6) 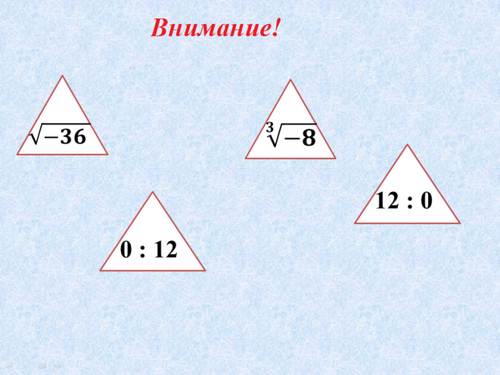
Вывод:
- выражение не имеет смысла;
- верное выражение, ответ : -2;
-
верное выражение, ответ : -0;
-
нельзя разделить на ноль 0!
Обратите внимание, все ли верно записано? (слайд - 7)
1) 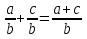 ; 2)
; 2) 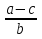 =
= 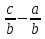 ; 3)
; 3) 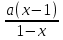 = a .
= a .
( 1) верное равенство, 2) 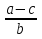 = -
= -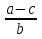 ; 3)
; 3) 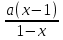 = - a )
= - a )
II. Изучение новой темы: (cлайд - 8).
Цель: Научить навыкам нахождения области определеиия и области значения дробно - линейной функции, построение её графика с использованием параллельного переноса графика функции по оси абсцисс и ординат.
Определите, график какой функции задан на координатной плоскости?
Задан график функции на координатной плоскости.
-
Запишите формулу для данной функции;
-
Да, верно! Вам было задано график функции, у=
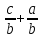 Вам известно все свойства данной функции:
Вам известно все свойства данной функции:
-
Вопрос
Ожидаемый ответ
Найти область определения функции, (D(y)=?)
Х ≠0, или (-∞;0]U[0;+∞)
Найти область значений функции, (Е(y)=?)
у ≠0, или (-∞;0]U[0;+∞)
Определить интервал возрастания функции
Не имеет
Определить интервал убывания функции
(-∞;0]U[0;+∞)
Указать интервал, который функция имеет положительные значения
[0;+∞)
Указать интервал, который функция имеет отрицательные значения
(-∞;0]
Дальше, следуем по инструкции
-
Перемещаем график функции с использованием параллельного переноса по оси Ох (абцисс) на 1 единицу направо;
График какой функции построили?
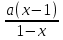
-
Перемещаем график функции с использованием параллельного переноса по оси Оу (ординат) на 2 единицы вверх;
А теперь, график какой функции построили?
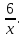
-
Проводим прямые х=1 и у=2
Как вы думаете? Какие прямые мы с вами получили?
Это те прямые, к которой приближаются точки кривой графика функции по мере их удаления в бесконечность.
И они называются - асимптотами.
То есть одна асимптота гиперболы проходит параллельно оси y на расстоянии 2 единиц справа от нее, а вторая асимптота проходит параллельно оси x на расстоянии 1 единицы выше ее.
-
Молодцы! А теперь сделаем вывод:
Графиком дробно-линейной функции является гипербола, которую можно получить из гиперболы y =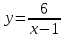 с помощью параллельных переносов вдоль координатных осей. Для этого формулу дробно-линейной функции надо представить в следующем виде: у=
с помощью параллельных переносов вдоль координатных осей. Для этого формулу дробно-линейной функции надо представить в следующем виде: у=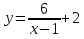
где n - количество единиц, на которое гипербола смещается вправо или влево, m - количество единиц, на которое гипербола смещается вверх или вниз. При этом асимптоты гиперболы сдвигаются в прямые x = m, y = n.
Приведём примеры дробно - линейной функции:
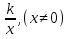
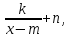 ;
; 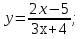 .
.
Дробно-линейная функция - это функция вида y = 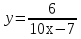 , где x - переменная, a, b, c, d - некоторые числа, причем c ≠ 0, ad - bc ≠ 0.
, где x - переменная, a, b, c, d - некоторые числа, причем c ≠ 0, ad - bc ≠ 0.
с≠0 и ad-bc≠0, так как при с=0 функция превращается в линейную функцию.
Если ad-bc=0, получается сократимая дробь значение, которое приравняется 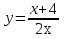 ( т.е. константа).
( т.е. константа).
Свойства дробно-линейной функции:
1. При возрастании положительных значений аргумента значения функции убывают и стремятся к нулю, но остаются положительными.
2. При возрастании положительных значений функции значения аргумента убывают и стремятся к нулю, но остаются положительными.
III - закрепление пройденного материала.
Цель: - развивать навыки и умения представления формул дробно-линейной функции к виду: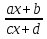
-
Закрепить умений составления уравнений асимптота и построения графика дробно - линейной функции.
Пример -1:
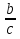 .
.
Решение: Используя преобразования данную функцию представляем в виде 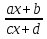 .
.
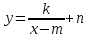 =
=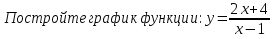 (слайд-10)
(слайд-10)
Физкультминутка:
(разминку ведет - дежурный )
Цель: - снятие умственной нагрузки и укрепление состояние здоровья учащихся.
Работа с учебником: №184.
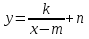 .
.
Решение: Используя преобразования данную функцию представляем в виде у=k/(х-m)+n .
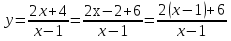 =
=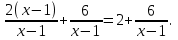 де х≠0.
де х≠0.
Запишем уравнение асимптота: х=2 и у=3.
Значит, график функции 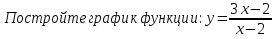 перемещается по оси Ох на расстоянии 2 единиц справа от нее и по оси Оу на расстоянии 3 единицы выше ее.
перемещается по оси Ох на расстоянии 2 единиц справа от нее и по оси Оу на расстоянии 3 единицы выше ее.
Групповая работа:
Цель: - формирование умений выслушать других и в то же время конкретно высказать свое мнение;
-
воспитание личности, способной лидерству;
-
воспитание у учащихся культуры математичекой речи.
Вариант № 1
Дана функция: ![]()
1. Приведите дробно-линейную функцию к стандартному виду и запишите уравнение асимптот.
2. Найдите область определения функции .
3. Найдите множество значений функции .
Вариант № 2
Дана функция ![]()
1. Приведите дробно-линейную функцию к стандартному виду и запишите уравнение асимптот.
2. Найдите область определения функции
3. Найдите множество значений функции
Вариант № 3
Дана функция: ![]()
1. Приведите дробно-линейную функцию к стандартному виду и запишите уравнение асимптот.
2. Найдите область определения функции.
3. Найдите множество значений функции .
Вариант № 4
Дана функция: ![]()
1. Приведите дробно-линейную функцию к стандартному виду и запишите уравнение асимптот.
2. Найдите область определения функции.
3. Найдите множество значений функции.
(Та группа, которая закончила работу первым, готовится для защиты групповой работы у доски. Проводится анализ работ.)
IV. Подведение итогов урока.
Цель: - анализ теоретической и практической деятельности на уроке;
- формирование навыков самооценки у учащихся;
- Рефлексия, самооценка активности и сознательности учащихся.
И так, дорогие мои ученики! Урок подходит к концу. Вам предстоит заполнить карту рефлекции. Аккуратно и разборчиво пишите свои мнения
Фамилия и имя ________________________________________
Этапы урока
Определение уровня слож-ности этапов урока
Ваше нас-троение
Оценка вашей деятельности на уроке, 1-5 балл
легкий
ср.тяж.
трудный
Организационный этап
Изучение нового материала
Формирование навы-ков умения построе-ния графика дробно - линейной функции
Работа в группах
Общее мнение об уроке
Домашнее задание:
Цель: - поверка уровня освоения данной темы.
[п.10* , №180(а), 181(б).]
Подготовка к ГИА : (Работа на "Виртуальном факультативе")
Задание из серии ГИА (№23 -максимальный балл ):
Постройте график функции У=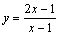 и определите, при каких значениях с прямая у=с имеет с графиком ровно одну общую точку.
и определите, при каких значениях с прямая у=с имеет с графиком ровно одну общую точку.
Вопросы и задания опубликуется с 14.00 до 14.30 ч.
Время опубликования ваших ответов с 19.00 до 20.00 ч.и видеосвязь по решению заданий ГИА по Skype начинается 20.10 ч.