- Учителю
- Рабочая программа и календарно-тематическое планирование по математике 6 класс по учебнику Виленкина Н. Я.
Рабочая программа и календарно-тематическое планирование по математике 6 класс по учебнику Виленкина Н. Я.
Рабочая программа
к учебнику «Математика», 6 класс, авт. Н.Я.Виленкин, В.И.Жохов, А.С.Чесноков, С.И.Шварцбурд, 31 издание, стереотипное, Мнемозина,2014.
Составитель: Давыдова Г.В., Зазулина Н.Б. - учителя математики.
Пояснительная записка
Рабочая программа составлена на основе Федерального государственного образовательного стандарта основного общего образования, примерной программы основного общего образования по математике, федерального перечня учебников, рекомендованных или допущенных к использованию в образовательном процессе в образовательных учреждениях, базисного учебного плана, авторского тематического планирования с учетом преемственности с примерными программами для начального общего образования.
Сознательное овладение учащимися системой арифметических знаний и умений необходимо в повседневной жизни, для изучения смежных дисциплин и продолжения образования. Практическая значимость школьного курса математики 6 класса обусловлена тем, что объектом изучения служат количественные отношения действительного мира. Математическая подготовка необходима для понимания принципов устройства и использования современной техники, восприятия научных и технических понятий и идей. Математика - язык науки и техники. С её помощью моделируются и изучаются явления и процессы, происходящие в природе.
Арифметика является одним из опорных предметов основной школы: она обеспечивает изучение других дисциплин. В первую очередь это относится к предметам естественно-научного цикла, в частности к физике. Развитие логического мышления учащихся при обучении математике в 5-6 классах способствует усвоению предметов гуманитарного цикла. Практические умения и навыки арифметического характера необходимы для трудовой и профессиональной подготовки школьников.
Развитие у учащихся правильных представлений о сущности и происхождении арифметических абстракций, о соотношении реального и идеального, о характере отражения математической наукой явлений и процессов реального мира, о месте арифметики в системе наук и роли математического моделирования в научном познании и в практике способствует формированию научного мировоззрения учащихся, а также формированию качеств мышления, необходимых для адаптации в современном информационном обществе.
Требуя от учащихся умственных и волевых усилий, концентрации внимания, активности воображения, арифметика развивает нравственные черты личности (настойчивость, целеустремленность, творческую активность, самостоятельность, ответственность, трудолюбие, дисциплину и критичность мышления) и умение аргументированно отстаивать свои взгляды и убеждения, а также способность принимать самостоятельные решения. Активное использование и решение текстовых задач на всех этапах учебного процесса развивают творческие способности школьников.
Изучение математики в 5-6классах позволяет формировать умения и навыки умственного труда: планирование своей работы, поиск рациональных путей её выполнения, критическую оценку результатов. В процессе изучения математики школьники учатся излагать свои мысли ясно и исчерпывающе, лаконично и ёмко, приобретают навыки чёткого, аккуратного и грамотного выполнения математических записей.
Важнейшей задачей школьного курса арифметики является развитие логического мышления учащихся. Сами объекты математических умозаключений и принятые в арифметике правила их конструирования способствуют формированию умений обосновывать и доказывать суждения, приводить чёткие определения, развивают логическую интуицию, кратко и наглядно раскрывают механизм логических построений и учат их применению. Показывая внутреннюю гармонию математики, формируя понимание красоты и изящества математических рассуждений, арифметика вносит значительный вклад в эстетическое воспитание учащихся.
Сознательное овладение учащимися системой арифметических знаний и умений необходимо в повседневной жизни, для изучения смежных дисциплин и продолжения образования. Практическая значимость школьного курса математики 6 класса обусловлена тем, что её объектом являются количественные отношения действительного мира.
Курс строится на индуктивной основе с привлечением элементов дедуктивных рассуждений. Теоретический материал курса излагается на наглядно - индуктивном уровне, математические методы и законы формулируются в виде правил.
Курс математики 6-го класса - важное звено математического образования и развития школьников. На этом этапе заканчивается в основном обучение счету на множестве рациональных чисел, формируется понятие переменной и даются первые знания о приемах решения линейных уравнений, продолжается обучение решению текстовых задач, совершенствуются и обогащаются умения геометрических построений и измерений. Серьезное внимание уделяется формированию умений рассуждать, делать простые доказательства, давать обоснования выполняемых действий. При этом учащиеся постепенно осознают правила выполнения основных логических операций. Параллельно закладываются основы для изучения систематических курсов стереометрии, физики, химии и других смежных предметов.
Статус документа.
Настоящая рабочая программа написана на основании следующих нормативных документов:
- Федеральный Закон от 29.12.2012 г. №273-ФЗ «Об образовании » в Российской Федерации
- Федеральный государственный образовательный стандарт основного общего образования (утвержден приказом Министерства образования и науки РФ от 17.12.2010 г № 1897.)
- Учебный план Университетского лицея - муниципального бюджетного общеобразовательного учреждения города Димитровграда Ульяновской области на 2014-2015 учебный год
- Государственная программа - примерная программа, созданная на основе федерального компонента государственного образовательного стандарта, по математике 5-6 (автор составитель: В.И. Жохов). - 2-е изд., стер. - М.: Мнемозина, 2010. - 31 с.
- Федеральный перечень учебников, рекомендованных (допущенных) Министерством образования и науки РФ к использованию в образовательном процессе в общеобразовательных учреждениях, реализующих программы общего образования на 2014-2015 учебный год
-Распоряжение Министерства образования Ульяновской области от 31.01.2012 года № 320-Р «О введении Федерального образовательного стандарта основного общего образования в общеобразовательных учреждениях Ульяновской области»
- Примерные программы по учебным предметам. Математика. 5-9 классы [Текст].- 3-е изд., перераб. - М.: Просвещение, 2011. - 64с. - (Стандарты второго поколения).
Рабочая программа выполняет две основные функции.
Информационно-методическая функция позволяет всем участникам образовательного процесса получить представление о целях, содержании, общей стратегии обучения, воспитания и развития учащихся средствами данного учебного предмета.
Организационно-планирующая функция предусматривает выделение этапов обучения, структурирование учебного материала, определение его количественных и качественных характеристик на каждом из этапов, в том числе для содержательного наполнения промежуточной аттестации учащихся.
Структура документа
Рабочая программа включает три раздела: пояснительную записку; основное содержание с примерным распределением учебных часов по данному разделу курса; требования к уровню подготовки выпускников.
Цели изучения.
Изучение математики на ступени основного общего образования направлено на достижение следующих целей:
-
овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
-
интеллектуальное развитие учащихся, формирование качеств мышления, характерных для математической деятельности и необходимых для продуктивной жизни в обществе, ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей;
-
формирование представлений о математических идеях и методах математики
-
формирование представлений о математике как форме описания и методе познания деятельности
воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, играющей особую роль в общественном развитии, формирование понимания значимости математики для научно-технического прогресса.
Задачи обучения:
-
Приобретение математических знаний и умений;
-
Овладение обобщенными способами мыслительной, творческой деятельности;
-
Освоение компетенций (учебно-познавательной, коммуникативной, рефлексивной, личностного саморазвития, информационно-технологической, личностно-смысловой).
Место предмета в федеральном базисном учебном плане Согласно федеральному базисному учебному плану для образовательных учреждений Российской Федерации на изучение математики в 6 классе отводится не менее 170 часов из расчета 5 ч в неделю. Из школьного компонента выделено еще 2 часа в неделю, итого 7 недельных часов или 238 часов.
Контрольных работ - 15 (включая итоговую контрольную работу).
Уровень обучения - повышенный.
Срок реализации - один учебный год.
Отличительные особенности рабочей программы по сравнению с примерной.
В программу внесены изменения: увеличено количество часов на изучение некоторых тем.
Дополнительные недельные часы, выделенные из школьного компонента, будут использованы на усиление изучения программного материала:
-на решение дополнительных развивающих задач;
-на развитие логического мышления, умения действовать в нестандартной ситуации;
-на широкое использование личностно-ориентированного обучения;
-для формирования навыков самостоятельной работы: умению читать математический текст, умению задавать вопросы по тексту; составлять план к пункту;
-для формирования грамотной математической речи учащихся, умению правильно объяснить свои действия и доказывать верность используемых шагов.
ЛИЧНОСТНЫЕ, МЕТАПРЕДМЕТНЫЕ И ПРЕДМЕТНЫЕ РЕЗУЛЬТАТЫ ОСВОЕНИЯ СОДЕРЖАНИЯ КУРСА
Программа позволяет добиваться следующих результатов освоения образовательной программы основного общего образования:
личностные:
-
ответственного отношения к учению, готовности и способности обучающихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию;
-
формирования коммуникативной компетентности в общении и сотрудничестве со сверстниками, старшими и младшими в образовательной, учебно-исследовательской, творческой и других видах деятельности;
-
умения ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры;
-
первоначального представления о математической науке как сфере человеческой деятельности, об этапах её развития, о её значимости для развития цивилизации;
-
критичности мышления, умения распознавать логически некорректные высказывания, отличать гипотезу от факта;
-
креативности мышления, инициативы, находчивости, активности при решении арифметических задач;
-
умения контролировать процесс и результат учебной математической деятельности;
-
формирования способности к эмоциональному восприятию математических объектов, задач, решений, рассуждений;
метапредметные:
-
способности самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач;
-
умения осуществлять контроль по образцу и вносить необходимые коррективы;
-
способности адекватно оценивать правильность или ошибочность выполнения учебной задачи, её объективную трудность и собственные возможности её решения;
-
умения устанавливать причинно-следственные связи; строить логические рассуждения, умозаключения (индуктивные, дедуктивные и по аналогии) и выводы;
-
умения создавать, применять и преобразовывать знаково-символические средства, модели и схемы для решения учебных и познавательных задач;
-
развития способности организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками: определять цели, распределять функции и роли участников, взаимодействовать и находить общие способы работы; умения работать в группе: находить общее решение и разрешать конфликты на основе согласования позиций и учёта интересов; слушать партнёра; формулировать, аргументировать и отстаивать своё мнение;
-
формирования учебной и общепользовательской компетентности в области использования информационно-коммуникационных технологий (ИКТ-компетентности);
-
первоначального представления об идеях и о методах математики как об универсальном языке науки и техники;
-
развития способности видеть математическую задачу в других дисциплинах, в окружающей жизни;
-
умения находить в различных источниках информацию, необходимую для решения математических проблем, и представлять её в понятной форме; принимать решение в условиях неполной и избыточной, точной и вероятностной информации;
-
умения понимать и использовать математические средства наглядности (рисунки, чертежи, схемы и др.) для иллюстрации, интерпретации, аргументации;
-
умения выдвигать гипотезы при решении учебных задач и понимания необходимости их проверки;
-
понимания сущности алгоритмических предписаний и умения действовать в соответствии с предложенным алгоритмом;
-
умения самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем;
-
способности планировать и осуществлять деятельность, направленную на решение задач исследовательского характера;
-
предметные:
-
умения работать с математическим текстом (структурирование, извлечение необходимой информации), точно и грамотно выражать свои мысли в устной и письменной речи, применяя математическую терминологию и символику, использовать различные языки математики (словесный, символический, графический), развития способности обосновывать суждения, проводить классификацию;
-
владения базовым понятийным аппаратом: иметь представление о числе, дроби, процентах, об основных геометрических объектах (точка, прямая, ломаная, угол, многоугольник, многогранник, круг, окружность, шар, сфера и пр.), формирования представлений о статистических закономерностях в реальном мире и различных способах их изучения;
-
умения выполнять арифметические преобразования рациональных выражений, применять их для решения учебных математических задач и задач, возникающих в смежных учебных предметах;
-
умения пользоваться изученными математическими формулами;
-
знания основных способов представления и анализа статистических данных; умения решать задачи с помощью перебора всех возможных вариантов;
-
умения применять изученные понятия, результаты и методы при решении задач из различных разделов курса, в том числе задач, не сводящихся к непосредственному применению известных алгоритмов.
Личностным результатом изучения предмета является формирование следующих умений и качеств:
- Независимость и критичностью мышления;
- Воля и настойчивость в достижении цели.
Метапредметным результатом изучения курса является формирование универсальных учебных действий (УДД):
Регулятивные УДД:
Самостоятельно обнаруживать и формулировать учебную проблему, определять цель УД;
Выдвигать версии решения проблемы, осознавать (и интерпретировать в случае необходимости) конечный результат, выбирать средства достижения цели из предложенных, а также искать их самостоятельно;
Составлять (индивидуально или в группе) план решения проблемы (выполнения проекта);
Работая по плану, сверять свои действия с целью и при необходимости исправлять ошибки самостоятельно (в том числе и корректировать план);
В диалоге с учителем совершенствовать самостоятельно выбранные критерии оценки.
Познавательные УДД:
Проводить наблюдение и эксперимент под руководством учителя;
Осуществлять расширенный поиск информации с использованием ресурсов библиотек и Интернета;
Осуществлять выбор наиболее эффективных способов решения задач в зависимости от конкретных условий;
Анализировать, сравнивать, классифицировать и обобщать факты и явления;
Давать определения понятиям.
Коммуникативные УДД:
Самостоятельно организовывать учебное взаимодействие в группе (определять общие цели, договариваться друг с другом и т.д.);
В дискуссии уметь выдвинуть аргументы и контраргументы;
Учиться критично относиться к своему мнению, с достоинством признавать ошибочность своего мнения и корректировать его;
Понимая позицию другого, различать в его речи: мнение (точку зрения), доказательство (аргументы), факты (гипотезы, аксиомы, теории).
Способы контроля и оценивания образовательных достижений учащихся
Формы промежуточной и итоговой аттестации. Промежуточная аттестация проводится в форме тестов, контрольных, самостоятельных работ. Итоговая аттестация предусмотрена в виде административной контрольной работы.
Критерии и нормы оценки учебной деятельности
В основу критериев оценки учебной деятельности учащихся положены объективность и единый подход. При 5 - балльной оценке для всех установлены общедидактические критерии.
Оценка "5" ставится в случае:
1. Знания, понимания, глубины усвоения обучающимся всего объёма программного материала.
2. Умения выделять главные положения в изученном материале, на основании фактов и примеров обобщать, делать выводы, устанавливать межпредметные и внутрипредметные связи, творчески применяет полученные знания в незнакомой ситуации.
3. Отсутствие ошибок и недочётов при воспроизведении изученного материала, при устных ответах устранение отдельных неточностей с помощью дополнительных вопросов учителя, соблюдение культуры письменной и устной речи, правил оформления письменных работ.
Оценка "4" ставится в случае:
1. Знания всего изученного программного материала.
2. Умений выделять главные положения в изученном материале, на основании фактов и примеров обобщать, делать выводы, устанавливать внутрипредметные связи, применять полученные знания на практике.
3. Незначительные (негрубые) ошибки и недочёты при воспроизведении изученного материала, соблюдение основных правил культуры письменной и устной речи, правил оформления письменных работ.
Оценка "3" (уровень представлений, сочетающихся с элементами научных понятий):
1. Знание и усвоение материала на уровне минимальных требований программы, затруднение при самостоятельном воспроизведении, необходимость незначительной помощи преподавателя.
2. Умение работать на уровне воспроизведения, затруднения при ответах на видоизменённые вопросы.
3. Наличие грубой ошибки, нескольких негрубых при воспроизведении изученного материала, незначительное несоблюдение основных правил культуры письменной и устной речи, правил оформления письменных работ.
Оценка "2" ставится в случае:
1. Знание и усвоение материала на уровне ниже минимальных требований программы, отдельные представления об изученном материале.
2. Отсутствие умений работать на уровне воспроизведения, затруднения при ответах на стандартные вопросы.
3. Наличие нескольких грубых ошибок, большого числа негрубых при воспроизведении изученного материала, значительное несоблюдение основных правил культуры письменной и устной речи, правил оформления письменных работ.
Оценка "1" ставится в случае:
полного незнания изученного материала, отсутствия элементарных умений и навыков.
Устный ответ
Оценка "5" ставится, если ученик:
1) Показывает глубокое и полное знание и понимание всего объёма программного материала; полное понимание сущности рассматриваемых понятий, явлений и закономерностей, теорий, взаимосвязей;
2) Умеет составить полный и правильный ответ на основе изученного материала; выделять главные положения, самостоятельно подтверждать ответ конкретными примерами, фактами; самостоятельно и аргументировано делать анализ, обобщения, выводы. Устанавливать межпредметные (на основе ранее приобретенных знаний) и внутрипредметные связи, творчески применять полученные знания в незнакомой ситуации. Последовательно, чётко, связно, обоснованно и безошибочно излагать учебный материал; давать ответ в логической последовательности с использованием принятой терминологии; делать собственные выводы; формулировать точное определение и истолкование основных понятий, законов, теорий; при ответе не повторять дословно текст учебника; излагать материал литературным языком; правильно и обстоятельно отвечать на дополнительные вопросы учителя. Самостоятельно и рационально использовать наглядные пособия, справочные материалы, учебник, дополнительную литературу, первоисточники; применять систему условных обозначений при ведении записей, сопровождающих ответ; использование для доказательства выводов из наблюдений и опытов;
3) Самостоятельно, уверенно и безошибочно применяет полученные знания в решении проблем на творческом уровне; допускает не более одного недочёта, который легко исправляет по требованию учителя; имеет необходимые навыки работы с приборами, чертежами, схемами и графиками, сопутствующими ответу; записи, сопровождающие ответ, соответствуют требованиям.
Оценка "4" ставится, если ученик:
1) Показывает знания всего изученного программного материала. Даёт полный и правильный ответ на основе изученных теорий; незначительные ошибки и недочёты при воспроизведении изученного материала, определения понятий дал неполные, небольшие неточности при использовании научных терминов или в выводах и обобщениях из наблюдений и опытов; материал излагает в определенной логической последовательности, при этом допускает одну негрубую ошибку или не более двух недочетов и может их исправить самостоятельно при требовании или при небольшой помощи преподавателя; в основном усвоил учебный материал; подтверждает ответ конкретными примерами; правильно отвечает на дополнительные вопросы учителя.
2) Умеет самостоятельно выделять главные положения в изученном материале; на основании фактов и примеров обобщать, делать выводы, устанавливать внутрипредметные связи. Применять полученные знания на практике в видоизменённой ситуации, соблюдать основные правила культуры устной речи и сопровождающей письменной, использовать научные термины;
3) Не обладает достаточным навыком работы со справочной литературой, учебником, первоисточниками (правильно ориентируется, но работает медленно). Допускает негрубые нарушения правил оформления письменных работ.
Оценка "3" ставится, если ученик:
1) усвоил основное содержание учебного материала, имеет пробелы в усвоении материала, не препятствующие дальнейшему усвоению программного материала;
2) материал излагает несистематизированно, фрагментарно, не всегда последовательно;
3) показывает недостаточную сформированность отдельных знаний и умений; выводы и обобщения аргументирует слабо, допускает в них ошибки;
4) допустил ошибки и неточности в использовании научной терминологии, определения понятий дал недостаточно четкие;
5) не использовал в качестве доказательства выводы и обобщения из наблюдений, фактов, опытов или допустил ошибки при их изложении;
6) испытывает затруднения в применении знаний, необходимых для решения задач различных типов, при объяснении конкретных явлений на основе теорий и законов, или в подтверждении конкретных примеров практического применения теорий;
7) отвечает неполно на вопросы учителя (упуская и основное), или воспроизводит содержание текста учебника, но недостаточно понимает отдельные положения, имеющие важное значение в этом тексте;
8) обнаруживает недостаточное понимание отдельных положений при воспроизведении текста учебника (записей, первоисточников) или отвечает неполно на вопросы учителя, допуская одну-две грубые ошибки.
Оценка "2" ставится, если ученик:
1) не усвоил и не раскрыл основное содержание материала;
2) не делает выводов и обобщений.
3) не знает и не понимает значительную или основную часть программного материала в пределах поставленных вопросов;
4) или имеет слабо сформированные и неполные знания и не умеет применять их к решению конкретных вопросов и задач по образцу;
5) или при ответе (на один вопрос) допускает более двух грубых ошибок, которые не может исправить даже при помощи учителя.
Оценка "1" ставится, если ученик:
1) не может ответить ни на один из поставленных вопросов;
2) полностью не усвоил материал.
Примечание.
По окончанию устного ответа учащегося педагогом даётся краткий анализ ответа, объявляется мотивированная оценка. Возможно привлечение других учащихся для анализа ответа, самоанализ, предложение оценок
Оценка самостоятельных письменных и контрольных работ
Оценка "5" ставится, если ученик:
1) выполнил работу без ошибок и недочетов;
2) допустил не более одного недочета.
Оценка "4" ставится, если ученик:
1) выполнил работу полностью, но допустил в ней не более одной негрубой ошибки и одного недочета;
2) или не более двух недочетов.
Оценка "3" ставится, если ученик:
1) правильно выполнил не менее половины работы или допустил не более двух грубых ошибок;
или не более одной грубой и одной негрубой ошибки и одного недочета;
или не более двух-трех негрубых ошибок;
или одной негрубой ошибки и трех недочетов;
2) или при отсутствии ошибок, но при наличии четырех-пяти недочетов.
Оценка "2" ставится, если ученик:
1) допустил число ошибок и недочетов превосходящее норму, при которой может быть выставлена оценка "3";
2) правильно выполнил менее половины работы.
Оценка "1" ставится, если ученик:
1) не приступал к выполнению работы;
2) или правильно выполнил не более 10 % всех заданий.
Примечание.
1) Учитель имеет право поставить ученику оценку выше той, которая предусмотрена нормами, если учеником оригинально выполнена работа.
2) Оценки с анализом доводятся до сведения учащихся, как правило, на последующем уроке, предусматривается работа над ошибками, устранение пробелов.
Общая классификация ошибок
При оценке знаний, умений и навыков учащихся следует учитывать все ошибки (грубые и негрубые) и недочеты.
Грубыми считаются следующие ошибки:
1) незнание определения основных понятий, законов, правил, основных положений теории, незнание формул, общепринятых символов обозначений величин, единиц их измерения;
2) незнание наименований единиц измерения (физика, химия, математика, биология, география, черчение, трудовое обучение, ОБЖ);
3) неумение выделить в ответе главное;
4) неумение применять знания для решения задач и объяснения явлений;
5) неумение делать выводы и обобщения;
6) неумение читать и строить графики и принципиальные схемы;
7) неумение подготовить установку или лабораторное оборудование, провести опыт, наблюдения, необходимые расчеты или использовать полученные данные для выводов;
8) неумение пользоваться первоисточниками, учебником и справочниками;
9) нарушение техники безопасности;
10) небрежное отношение к оборудованию, приборам, материалам.
К негрубым ошибкам следует отнести:
1) неточность формулировок, определений, понятий, законов, теорий, вызванная неполнотой охвата основных признаков определяемого понятия или заменой одного-двух из этих признаков второстепенными;
2) ошибки при снятии показаний с измерительных приборов, не связанные с определением цены деления шкалы (например, зависящие от расположения измерительных приборов, оптические и др.);
3) ошибки, вызванные несоблюдением условий проведения опыта, наблюдения, условий работы прибора, оборудования;
4) ошибки в условных обозначениях на принципиальных схемах, неточность графика (например, изменение угла наклона) и др.;
5) нерациональный метод решения задачи или недостаточно продуманный план устного ответа (нарушение логики, подмена отдельных основных вопросов второстепенными);
6) нерациональные методы работы со справочной и другой литературой;
7) неумение решать задачи, выполнять задания в общем виде.
Недочетами являются:
1) нерациональные приемы вычислений и преобразований, выполнения опытов, наблюдений, заданий;
2) ошибки в вычислениях (арифметические - кроме математики);
3) небрежное выполнение записей, чертежей, схем, графиков;
4) орфографические и пунктуационные ошибки (кроме русского языка)
Содержание учебного предмета
Предметным результатом изучения курса является сформированность следующих умений:
Предметная область «Арифметика»:
Выполнять устно арифметические действия: сложение и вычитание двузначных чисел и десятичных дробей с двумя знаками, умножение однозначных чисел, арифметические операции с обыкновенными дробями с однозначным знаменателем и числителем;
Переходить от одной формы записи чисел к другой, представлять десятичную запись в виде обыкновенной и в простейших случаях обыкновенную в виде десятичной, проценты - в виде дроби и дробь - в виде процентов;
Выполнять арифметические действия с рациональными числами, находить значения числовых выражений (целых и дробных);
Округлять целые числа и десятичные дроби, выполнять оценку числовых выражений;
Пользоваться основными единицами длины, массы, времени, скорости, площади, объема; переводить одни единицы измерения в другие;
Решать текстовые задачи, в том числе связанные с отношениями и с пропорциональностью величин, дробями и процентами.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
Решения несложных практических расчетных задач, в том числе с использованием при необходимости справочных материалов, калькулятора;
Устной прикидки и оценки результата вычислений;
Интерпретации результатов решения задач с учетом ограничений, связанных с реальными свойствами рассматриваемых процессов и явлений.
Предметная область «Алгебра»:
Переводить условия задачи на математический язык; использовать методы работы с математическими моделями;
Осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления;
Определять координаты точки и изображать числа точками на координатной прямой;
Составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления;
Решать текстовые задачи алгебраическим методом.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
Выполнение расчетов по формулам, составления формул, выражающих зависимости меду реальными величинами.
Предметная область «Геометрия»:
Пользоваться геометрическим языком для описания предметов окружающего мира;
Распознать геометрические фигуры, различать их взаимное расположение;
Изображать геометрические фигуры, распознавать на чертежах, моделях и в окружающей обстановке основные пространственные тела;
В простейших случаях строить развертки пространственных тел;
Вычислить площади, периметры, объемы простейших геометрических фигур (тел) по формулам.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
Решения несложных геометрических задач, связанных с нахождением изученных геометрических величин (используя при необходимости справочники и технические средства);
Построений геометрическими инструментами (линейка, угольник, циркуль, транспортир).
Планирование учебного материала к учебнику «Математика 6»
Тематическое планирование реализует один из возможных подходов к распределению изучаемого материала по учебно-методическим комплектам по математике, выпускаемым издательством «Просвещение», а также УМК Н. Я. Виленкина, В. И. Жохова и др.
В примерном тематическом планировании разделы основного содержания по математике разбиты на темы в хронологии их изучения, по соответствующим учебникам. Особенностью примерного тематического планирования является то, что в нём содержится описание возможных видов деятельности учащихся в процессе усвоения соответствующего содержания, направленных на достижение поставленных целей обучения. Это ориентирует учителя на усиление деятельностного подхода в обучении, на организацию разнообразной учебной деятельности, отвечающей современным психолого-педагогическим воззрениям, на использование современных технологий.
Тематическое планирование составлено из расчёта часов, указанных в проекте Базисного учебного (образовательного) плана (БУП) образовательных учреждений общего образования (не менее 5 часов в неделю, 170 часов в год) и учебно-методический комплект по наглядной геометрии составляет 45 часов.
I вариант: 5 часов математики в неделю в течение всего учебного года, итого 170 часа.
II вариант:7 часов математики в неделю в течение всего учебного года, итого 238 часов.
СТРУКТУРА КУРСА
Тема
Базис
Школь-ный компонент
(повы-шенный уровень)
Итого
Коли-чество контрольных работ
Делимость чисел
20
7
27
1
Сложение и вычитание дробей с разными знаменателями
22
8
30
2
Умножение и деление обыкновенных дробей
32
8
40
3
Отношения и пропорции
20
8
28
2
Положительные и отрицательные числа
12
6
18
1
Сложение и вычитание положительных и отрицательных чисел
12
6
18
1
Умножение и деление положительных и отрицательных чисел
13
6
19
1
Решение уравнений
15
4
19
2
Координаты на плоскости
12
6
18
1
Итого итоговое повторение курса математики 5-6 классов
12
9
21
1
Общее количество часов
170
68
238
15
2. Содержание учебного предмета
Наименование разделов учебной программы и характеристика основных содержательных линий;
№
Наименование разделов учебной программы
Характеристика основных содержательных линий
1
Делимость чисел
Делимость натуральных чисел. Делители и кратные числа. Признаки делимости на 2, 3, 5, 9, 10. Простые и составные числа. Разложение натурального числа на простые множители. Наибольший общий делитель и наименьшее общее кратное. Деление с остатком.
Основная цель - завершить изучение натуральных чисел, подготовить основу для освоения действий с обыкновенными дробями.
В данной теме завершается изучение вопросов, связанных с натуральными числами. Основное внимание должно быть уделено знакомству с понятиями «делитель» и «кратное», которые находят применение при сокращении обыкновенных дробей и при их приведении к общему знаменателю. Упражнения полезно выполнять с опорой на таблицу умножения - прямым подбором.
Определенное внимание уделяется знакомству с признаками делимости, понятием простого и составного чисел. При их изучении целесообразно формировать умения проводить простейшие умозаключения, обосновывая свои действия ссылками на определение, правила.
Учащиеся должны уметь разложить число на множители. Например, они должны понимать, что 36=6∙6=4∙9=2∙18 и т.п. добиваться от всех учащихся.
2
Сложение и вычитание дробей с разными знаменателями
Основное свойство дроби. Сокращение дробей. Приведение дробей к общему знаменателю. Понятие о наименьшем общем знаменателе нескольких дробей. Сравнение дробей. Решение текстовых задач.
Основная цель - выработать прочные навыки преобразования дробей, сложения и вычитания дробей.
Одним из важнейших результатов обучения является усвоение основного свойства дроби, применяемого для преобразования дробей: сокращения, приведение к новому знаменателю. Умение приводить дроби к общему знаменателю используется для сравнения дробей.
При рассмотрении действий с дробями используются правила сложения и вычитания дробей с одинаковыми знаменателями, понятие смешанного числа. Важно обратить внимание на случай вычитания дроби из целого числа.
3
Умножение и деление обыкновенных дробей
Умножение и деление обыкновенных дробей. Основные задачи на дроби.
Основная цель - выработать прочные навыки арифметических действий с обыкновенными дробями и решения основных задач на дроби.
В этой теме завершается работа над формированием навыков арифметических действий с обыкновенными дробями. Навыки должны быть достаточно прочными, чтобы учащиеся не испытывали затруднений в вычислениях с рациональными числами, чтобы алгоритмы действий с обыкновенными дробями могли стать в дальнейшем опорой для формирования умений выполнять действия с алгебраическими дробями.
Расширение аппарата действий с дробями позволяет решать текстовые задачи, в которых требуется найти дробь от числа или число по данному значению его дроби.
4
Отношения и пропорции
Пропорция. Основное свойство пропорции. Решение задач с помощью пропорции. Понятие о прямой и обратной пропорциональности величин. Задачи на пропорции. Масштаб. Формулы длины окружности и площади круга. Шар.
Основная цель - сформировать понятия пропорции, прямой и обратной пропорциональности величин.
Необходимо, чтобы учащиеся усвоили основное свойство пропорции, так как оно находит применение на уроках математики, химии, физики. В частности, достаточное внимание должно быть уделено решению с помощью пропорции задач на проценты.
Понятие о прямой и обратной пропорциональности величин можно сформировать как обобщение нескольких конкретных примеров, подчеркнув при этом практическую значимость этих понятий, возможность их применения для упрощения решения соответствующих задач.
В данной теме даются представления о длине окружности и площади круга. Соответствующие формулы к обязательному материалу не относятся. Рассмотрение геометрических фигур завершается знакомством с шаром.
5
Положительные и отрицательные числа
Положительные и отрицательные числа. Противоположные числа. Модуль числа и его геометрический смысл. Сравнение чисел. Целые числа. Изображение чисел на координатной прямой. Координата точки.
Основная цель - расширить представления учащихся о числе путем введения отрицательных чисел.
Целесообразность введения отрицательных чисел показывается на содержательных примерах. Учащиеся должны научиться изображать положительные и отрицательные числа на координатной прямой. В дальнейшем она будет служить наглядной основой для правил сравнения чисел, сложения и вычитания чисел.
Специальное внимание должно быть уделено усвоению вводимого здесь понятия модуля числа, прочное значение которого необходимо для формирования умения сравнивать отрицательные числа, а в дальнейшем и для овладения алгоритмами арифметических действий с положительными и отрицательными числами.
6
Сложение и вычитание положительных и отрицательных чисел
Сложение и вычитание положительных и отрицательных чисел.
Основная цель - выработать прочные навыки сложения и вычитания положительных и отрицательных чисел.
Действия с отрицательными и положительными числами вводятся на основе представлений об изменении величин: сложение и вычитание чисел иллюстрируется соответствующими перемещениями точек координатной прямой. При изучении данной темы отрабатываются алгоритмы сложения и вычитания при выполнении действий с целыми и дробными числами.
7
Умножение и деление положительных и отрицательных чисел
Умножение и деление положительных и отрицательных чисел. Понятие о рациональном числе. Десятичное приближение обыкновенной дроби. Применение знаков арифметических действий для рационализации вычислений.
Основная цель - выработать прочные навыки арифметических действий с положительными и отрицательными числами.
Навыки умножения и деления положительных и отрицательных чисел отрабатываются сначала при выполнении отдельных действий, а затем в сочетании с навыками сложения и вычитания при вычислении значений числовых выражений.
При изучении данной темы учащиеся должны усвоить, что для обращения обыкновенной дроби в десятичную достаточно разделить (если это возможно) числитель на знаменатель. В каждом конкретном случае они должны знать, в какую дробь обращается данная обыкновенная дробь - в десятичную или периодическую. Учащиеся должны знать представление в виде десятичной дроби таких дробей, как ![]() и т.д.
и т.д.
8
Решение уравнений
Простейшие преобразования выражений: раскрытие скобок, приведение подобных слагаемых. Решение линейных уравнений. Примеры решения текстовых задач с помощью линейных уравнений.
Основная цель - подготовить учащихся к выполнению преобразований выражений, решению уравнений.
Преобразования буквенных выражений путем раскрытия скобок и приведения подобных слагаемых отрабатывается в той степени, в которой они необходимы для решения несложных уравнений.
Введение арифметических действий над отрицательными числами позволяет ознакомить учащихся с общими приемами решения линейных уравнений с одной переменной.
9
Координаты на плоскости
Построение перпендикуляра к прямой и параллельных прямых с помощью чертежного треугольника и линейки. Прямоугольная система координат на плоскости, абсцисса и ордината точки. Примеры графиков, диаграмм.
Основная цель - познакомить учащихся с прямоугольной системой координат на плоскости.
Учащиеся должны научиться распознавать и изображать перпендикулярные и параллельные прямые. Основное внимание следует уделить отработке навыков их построения с помощью линейки и чертежного треугольника, не требуя воспроизведения точных определений.
Основным результатом знакомства учащихся с координатной плоскостью должны стать знания порядка записи координат точек плоскости и их названий, умения построить координатные оси, отметить точку по заданным координатам, определить координаты точки, отмеченной на координатной плоскости.
Формированию вычислительных и графических умений способствует построение столбчатых диаграмм. При выполнении соответствующих упражнений найдут применение изученные ранее сведения о масштабе и округлении чисел.
10
Повторение. Решение задач
Примерный календарно-тематический план
I вариант: 5 ч в неделю, всего 170 ч;
II вариант: 7 ч в неделю, всего 238 ч.
№
урока
Содержание обучения
Базис
Школьный компонент
(повышен-ный уровень)
Итого
§1. Делимость чисел
20
7
27
1-2
Повторение.
2
2
3-5
Делители и кратные
3
-
3
6-8
Признаки делимости на 10, на 5 и на 2
3
-
3
9-11
Признаки делимости на 9 и на 3
2
1
3
12-14
Простые и составные числа
2
1
3
15-17
Разложение на простые множители
2
1
3
18
Решение старинных задач с помощью уравнений.
-
1
1
19-21
Наибольший общий делитель
3
-
3
22-25
Наименьшее общее кратное
4
-
4
26
Контрольная работа №1 по теме «НОД и НОК чисел»
1
-
1
27
Резерв. Решение задач по теме «НОД и НОК чисел»
1
1
§2. Сложение и вычитание дробей с разными знаменателями
22
8
30
28-30
Основное свойство дроби
2
1
3
31-33
Сокращение дробей
3
-
3
34-37
Приведение дробей к общему знаменателю
3
1
4
38-43
Сравнение, сложение и вычитание дробей с разными знаменателями.
6
-
6
44
«Многоэтажные» дроби.
-
1
1
45
Контрольная работа № 2 по теме «Сокращение, сложение и вычитание обыкновенных дробей»
1
-
1
46
Резерв. Решение задач по теме «Сокращение, сложение и вычитание обыкновенных дробей»
1
1
47-53
Сложение и вычитание смешанных чисел
6
1
7
54-55
Решение задач на движение и совместную работу.
-
2
2
56
Контрольная работа № 3 по теме «Сложение и вычитание смешанных чисел»
1
-
1
57
Резерв. Решение задач по теме «Сложение и вычитание смешанных чисел»
1
1
§3.Умножение и деление обыкновенных дробей
32
8
40
58-63
Умножение дробей
4
1
5
64-67
Нахождение дроби от числа..
4
-
4
68-72
Применение распределительного свойства умножения.
5
-
5
73
Контрольная работа № 4 по теме «Умножение обыкновенных дробей»
1
-
1
74
Резерв. Решение задач по теме «Умножение обыкновенных дробей»
1
1
75-77
Взаимно обратные числа
2
1
3
78-82
Деление
5
-
5
83
Контрольная работа № 5 по теме «Деление»
1
-
1
84
Резерв. Решение задач по теме «Деление»
1
1
85-89
Нахождение числа по его дроби.
5
-
5
90
Аликвотные дроби.
-
1
1
91-94
Дробные выражения.
4
-
4
95
Контрольная работа № 6 по теме «Дробные выражения»
1
-
1
96
Резерв. Решение задач по теме «Дробные выражения»
97
Задачи на уравнивание.
-
1
1
§4. Отношения и пропорции
19
9
28
98-102
Отношения.
5
-
5
103-105
Пропорции.
3
-
3
106
Практическая работа по сбору и представлению данных в виде таблиц и диаграмм; анализ данных
-
1
1
107-110
Прямая и обратная пропорциональные зависимости
3
1
4
111
Пропорциональное деление.
-
1
1
112
Контрольная работа № 7 по теме «Отношения и пропорции»
1
-
1
113
Резерв. Решение задач по теме «Отношения и пропорции»
-
1
1
114-116
Масштаб.
2
1
3
117-118
Задачи на сложные пропорции.
-
2
2
119-121
Длина окружности и площадь круга.
2
1
3
122-123
Шар
2
-
2
124
Контрольная работа № 8 по теме «Окружность и круг»
1
-
1
125
Резерв. Решение задач по теме «Окружность и круг»
1
1
§5. Положительные и отрицательные числа
13
5
18
126-129
Координаты на прямой.
3
1
4
130-132
Противоположные числа
2
1
3
133-135
Модуль числа.
2
1
3
136
Решение уравнений с модулем.
-
1
1
137-139
Сравнение чисел
3
-
3
140-141
Измерение величин.
2
-
2
142
Контрольная работа № 9 по теме «Противоположные числа и модуль»
1
-
1
143
Резерв. Решение задач по теме «Противоположные числа и модуль»
§6. Сложение и вычитание положительных и отрицательных чисел.
11
7
18
144-145
Сложение чисел с помощью координатной прямой
2
-
2
146-147
Задачи, решаемые в целых числах.
-
2
2
148-150
Сложение отрицательных чисел.
2
1
3
151-153
Сложение чисел с разными знаками
3
-
3
154
Решение простейших уравнений с параметром
-
1
1
155-159
Вычитание
3
2
5
160
Контрольная работа № 10 по теме «Сложение и вычитание положительных и отрицательных чисел»
1
-
1
161
Резерв. Решение задач по теме «Сложение и вычитание положительных и отрицательных чисел»
§7. Умножение и деление положительных и отрицательных чисел
12
7
19
162-164
Умножение
3
-
3
165-168
Деление.
3
1
4
169
Множества
-
1
1
170-172
Рациональные числа.
2
1
3
173-174
Решение задач на «обратный ход»
-
2
2
175-178
Свойства действий с рациональными числами.
3
1
4
179
Контрольная работа № 11 по теме «Умножение и деление рациональных чисел»
1
-
1
180
Резерв. Решение задач по теме «Умножение и деление рациональных чисел»
1
1
§8. Решение уравнений
15
4
19
181-183
Раскрытие скобок
3
-
3
184-186
Коэффициент
2
1
3
187-190
Подобные слагаемые.
3
1
4
191
Контрольная работа № 12 по теме «Раскрытие скобок»
1
-
1
192-196
Решение уравнений
4
1
5
197
Контрольная работа № 13 по теме «Решение уравнений»
1
-
1
198
Резерв. Решение задач по теме «Решение уравнений»
199
Треугольные числа.
-
1
1
§9. Координаты на плоскости
13
5
18
200-201
Перпендикулярные прямые
2
-
2
202-204
Параллельные прямые
2
1
3
205
Старинные задачи на дроби.
-
1
1
206-209
Координатная плоскость
3
1
4
210-211
Столбчатые диаграммы.
2
-
2
212
Полигон частот
-
1
1
213-216
Графики.
3
1
4
217
Контрольная работа № 14 по теме «Координатная плоскость»
1
-
1
Повторение
13
8
21
218-219
Признаки делимости
1
1
2
220-221
НОД и НОК
1
1
2
222-223
Арифметические действия с обыкновенными дробями
1
1
2
224-225
Отношения и пропорции
1
1
2
226-227
Сравнение, сложение и вычитание рациональных чисел
1
1
2
228-229
Умножение и деление рациональных чисел
1
1
2
230-231
Решение уравнений
1
1
2
232-234
Решение задач с помощью уравнения
2
1
3
235
Координатная плоскость
1
-
1
236
Итоговая контрольная работа.
1
-
1
237
Анализ контрольной работы
1
-
1
238
Обобщающий урок
1
-
1
Итого.
170
68
238
Планируемые результаты изучения учебного предмета
Основные требования к уровню подготовки по математике обучающихся,
оканчивающих 6 класс.
В результате изучения математики ученик должен
знать / понимать
• существо понятия алгоритма; приводить примеры алгоритмов;
• как используются математические формулы, уравнения; примеры их применения для решения математических и практических задач;
• как потребности практики привели математическую науку к необходимости расширения понятия числа;
• вероятностный характер многих закономерностей окружающего мира;
уметь
• выполнять арифметические операции с обыкновенными дробями;
• переходить от одной формы записи чисел к другой, представлять проценты - в виде дроби и дробь - в виде процентов;
• выполнять арифметические действия с рациональными числами;
• решать текстовые задачи, включая задачи, связанные с отношением
и пропорциональностью величин, дробями и процентами;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
• решения несложных практических задач
• устной прикидки и оценки результатов вычислений;
• интерпретации результатов решения задач с учетом ограничений, связанных с реальными свойствами рассматриваемых процессов и явлений.
Планируемые результаты на базовом и повышенном уровнях к каждому разделу учебной программы.
Тема 1 «Делимость чисел»
Раздел математики. Сквозная линия
-
Числа и вычисления
Обязательный минимум содержания образовательной области математика:
Делимость натуральных чисел. Делимость произведения. Делимость суммы и разности
Признаки делимости на 2, 3, 5, 9, 10, 4, 25.
Простые и составные числа.
Разложение натурального числа на простые множители.
Наибольший общий делитель и наименьшее общее кратное.
Требования к математической подготовке
Уровень обязательной подготовки обучающихся:
Усвоить понятия "делитель" и "кратное".
Познакомиться с понятиями "наибольший общий делитель" и "наименьшее общее кратное".
Познакомиться с признаками делимости.
-
Уметь разлагать число на множители
Уровень продвинутой подготовки обучающихся:
Уметь применять алгоритмы нахождения наибольшего общего делителя и наименьшего общего кратного.
Знать признаки делимости чисел.
Уметь разлагать число на простые множители.
Тема 2 «Сложение и вычитание дробей с разными знаменателями»
Раздел математики. Сквозная линия
Числа и вычисления
Обязательный минимум содержания образовательной области математика:
Обыкновенная дробь.
Основное свойство дроби.
Сравнение дробей.
Сложение и вычитание дробей с разными знаменателями.
Требования к математической подготовке
Уровень обязательной подготовки обучающихся:
Усвоить основное свойство дроби.
Уметь сокращать дроби.
Уметь приводить дроби к наименьшему общему знаменателю.
-
Уметь сравнивать дроби.
-
Уметь выполнять сложение и вычитание дробей с разными знаменателями.
-
Уметь выполнять сложение и вычитание смешанных чисел.
Уровень продвинутой подготовки обучающихся:
Уметь выполнять сложение и вычитание дробей с разными знаменателями и смешанных чисел.
При выполнении арифметических действий с дробями и смешанными числами сочетать устные и письменные приемы вычислений.
-
Уметь сравнивать дроби и упорядочивать наборы дробных чисел.
Тема 3 «Умножение и деление обыкновенных дробей»
Раздел математики. Сквозная линия
Числа и вычисления
Обязательный минимум содержания образовательной области математика:
Умножение и деление обыкновенных дробей.
-
Нахождение части от целого и целого по его части.
Требования к математической подготовке
Уровень обязательной подготовки обучающихся:
Уметь выполнять умножение и деление дробей.
Уметь находить часть от целого и целое по его части.
-
Уметь вычислять несложные дробные выражения.
Уровень продвинутой подготовки обучающихся:
Уметь применять распределительный закон умножения при действиях с дробями.
Уметь решать текстовые задачи на нахождение дроби от числа и числа по его дроби.
-
Уметь выполнять совместные действия с обыкновенными и десятичными дробями.
Тема 4 «Отношения и пропорции»
Раздел математики. Сквозная линия
Вычисления и числа.
Обязательный минимум содержания образовательной области математика:
Отношение, выражение отношения в процентах.
-
Пропорция.
-
Пропорциональная и обратно пропорциональная зависимости.
Требования к математической подготовке
Уровень обязательной подготовки обучающихся:
Усвоить основное свойство пропорции.
Уметь решать несложные задачи с помощью пропорций.
Познакомиться с понятиями и формулами длины окружности и площади круга.
Уровень продвинутой подготовки обучающихся:
Уметь решать задачи с помощью пропорций и задачи на проценты.
Уметь решать практические задачи на прямую и обратную пропорциональную
зависимости.
Распознавать геометрические тела: сфера и шар, виды симметрии
Тема 5 «Положительные и отрицательные числа»
Раздел математики. Сквозная линия
Вычисления и числа.
Обязательный минимум содержания образовательной области математика:
Целые числа: положительные, отрицательные и нуль.
-
Модуль (абсолютная величина) числа.
-
Сравнение рациональных чисел.
Требования к математической подготовке
Уровень обязательной подготовки обучающихся:
Уметь изображать положительные и отрицательные числа на координатной прямой.
Уяснить понятие модуля числа.
Уметь сравнивать числа.
Уровень продвинутой подготовки обучающихся:
Уметь изображать положительные и отрицательные числа на координатной прямой.
Уяснить понятие модуля числа и его геометрический смысл. Уметь находить модуль любого числа
Уметь сравнивать числа.
Тема 6 «Сложение и вычитание положительных и отрицательных чисел»
Раздел математики. Сквозная линия
Вычисления и числа.
Обязательный минимум содержания образовательной области математика:
Сложение и вычитание положительных и отрицательных чисел.
Требования к математической подготовке
Уровень обязательной подготовки обучающегося:
Уметь выполнять сложение и вычитание положительных и отрицательных чисел.
Уровень продвинутой подготовки обучающегося:
Уметь выполнять сложение и вычитание положительных и отрицательных чисел.
Уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни для устной прикидки и оценки результата вычислений; проверки результата вычисления с использованием различных приемов.
Тема 7 «Умножение и деление положительных и отрицательных чисел»
Раздел математики. Сквозная линия
Вычисления и числа.
Обязательный минимум содержания образовательной области математика:
Умножение и деление положительных и отрицательных чисел.
Числовые выражения, порядок действий в них, использование скобок.
Законы арифметических действий: переместительный, сочетательный,
распределительный.
Требования к математической подготовке
Уровень обязательной подготовки обучающихся:
Уметь выполнять умножение и деление положительных и отрицательных чисел.
Уметь выполнять арифметические действия с рациональными числами.
Уровень продвинутой подготовки обучающихся:
Уметь выполнять умножение и деление положительных и отрицательных чисел.
Уметь выполнять арифметические действия с рациональными числами.
Уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни для устной прикидки и оценки результата вычислений; проверки результата вычисления с использованием различных приемов.
Тема 8 «Решение уравнений»
Раздел математики. Сквозная линия
Уравнения и неравенства.
Выражения и их преобразования.
Обязательный минимум содержания образовательной области математика:
Уравнение с одной переменной.
Корень уравнения.
Линейное уравнение.
Простейшие преобразования выражений: раскрытие скобок, приведение подобных
слагаемых.
Требования к математической подготовке
Уровень обязательной подготовки обучающихся:
Уметь решать линейные уравнений и уравнения, сводящиеся к ним.
Уметь выполнять простейшие преобразования выражений при решении уравнений.
Уровень продвинутой подготовки обучающихся:
Уметь выполнять преобразования выражений при решении уравнений.
Уметь выполнять арифметические действия с рациональными числами.
Понимать, как используются уравнения; уметь применять их для решения математических и практических задач;
Тема 9 «Координаты на плоскости»
Раздел математики. Сквозная линия
Геометрические фигуры и их свойства.
Обязательный минимум содержания образовательной области математика:
Параллельные и перпендикулярные прямые (знакомство).
Декартовы координаты на плоскости.
Координаты точки.
Требования к математической подготовке
Уровень обязательной подготовки обучающегося:
Уметь распознавать параллельные и перпендикулярные прямые, различать их взаимное
расположение.
Уметь определять координаты точки плоскости.
Уметь строить точки с заданными координатами.
Уровень продвинутой подготовки обучающегося:
Уметь строить фигуры по точкам.
Тема «Повторение. Решение задач»
Раздел математики. Сквозная линия
Числа и вычисления.
-
Выражения и преобразования.
-
Уравнения и неравенства.
Обязательный минимум содержания образовательной области математика
Арифметические действия с рациональными числами.
-
Простейшие преобразования выражений.
-
Линейное уравнение с одной переменной.
Требования к математической подготовке
Уровень обязательной подготовки обучающихся:
Уметь выполнять арифметические действия с рациональными числами.
Уметь решать линейные уравнений и уравнения, сводящиеся к ним.
Уметь решать текстовые задачи с помощью пропорций и процентов.
Уметь решать несложные текстовые задачи с помощью уравнений.
Уметь определять координаты точки плоскости.
Уметь строить точки с заданными координатами.
Уровень продвинутой подготовки обучающихся:
Уметь решать текстовые задачи с помощью уравнений.
Уметь решать практические задачи на прямую и обратную пропорциональную
зависимости.
Уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни для устной прикидки и оценки результата вычислений; проверки результата вычисления с использованием различных приемов.
Понимать, как используются уравнения; уметь применять их для решения математических и практических задач.
Описание учебно-методического, материально-технического и информационного обеспечения образовательного процесса
Печатные пособия
№
Авторы
Название
Год издания
Издательство
Виленкин Н. Я., Жохов В. И. и др.
Математика, учебник для 6 класса общеобразовательных учреждений.
2013
«Мнемозина»
Виленкин Н. Я., Жохов В. И.
Рабочая тетрадь по математике для 6 класс
2013
«Мнемозина»
Выговская В.В.
Поурочные разработки по математике 6 класс к учебному комплекту Н.Я. Виленкина
2012
М.: «Вако»
Чесноков А.С., Нешков К.И.
Дидактические материалы по математике 6 класс
2011
Классик
Стиль
И.Ф.Шарыгин
Л.Н.Ерганжиева
Наглядная геометрия. 5-6 классы
2007
Дрофа
Жохов В. И..
Математический тренажер: 6 класс
2010
Мнемозина
Жохов В. И..
Преподавание математики в 5/6 классах" - методические рекомендации для учителей к учебнику Н. Я. Виленкина
2008
Вербум-М
В.И.Жохов,
Л.Б. Крайнова
Математика. 6класс. Контрольные работы для учащихся образовательных учреждений.
2013
М.: Мнемозина
Глазков Ю.А.
Математика. 6класс: контрольные измерительные материалы.
2014
М.: Издательство «Экзамен»
В.И.Ахременкова
Рабочая программа по математике. 6 класс
2013
ВАКО
В.И.Жохов
Математические диктанты
2011
М.: Мнемозина
В.В.Выговская
Сборник практических задач по математике.
2014
М.: «Вако»
Минаева С.С.
Дроби и проценты.5-7 классы.
2014
М.: Издательство «Экзамен»
А.С.Конте
Математические диктанты. 5-6 классы
2014
Волгоград: Учитель.
Список электронных ресурсов:
-
- cетевое объединение методистов (огромный набор методических материалов по предметам)
-
- каталог всевозможных учебных и методических материалов по всем аспектам преподавания в школе
-
- школьный мир (каталог образовательных ресурсов)
-
- Ярославский институт развития образования (много методических материалов, ссылки)
-
- Федеральный портал Российское образование
-
- Российский общеобразовательный портал
-
- «Учительская газета»
-
- все приложения к газете «1сентября»
-
- «Вестник образования»
-
-школьный сектор дистанционного образования
-
- единая коллекция цифровых образовательных ресурсов
-
- коллекция анимированных картинок
-
- коллекция анимированных картинок
-
- портал для детей и любящих их взрослых
-
- Пиканал. Некоторый предметный справочник
-
- виртуальная школа Кирилла и Мефодия
-
- открытый колледж
-
- математическая гимнастика
-
- математическая гостиная
-
- математические олимпиады и олимпиадные задачи
-
- математический калейдоскоп
-
- московский центр непрерывного математического образования
-
- Кенгуру
-
- открытый Колледж. Математика
-
- головоломки для умных людей
-
- домашний компьютер и школа
-
- сайт и для учителей математики
- ребусы и кроссворды по геометрии -
- сеть творческих учителей/сообщество учителей математики
-
- для учителя математики, алгебры и геометрии
-
- математика на 5! Сайт для учителей математики
-
- методические рекомендации учителям математики
-
- к уроку математики
-
- досье школьного учителя математики
-
- интернет портал PROШколу.ru
-
- единая коллекция цифровых образовательных ресурсов
Приложения к рабочей программе «Математика 6»
Контроль реализации программы
Стартовый контроль:
№1. Вычислите: 16,44 + 7,583.
№2. Выполните умножение: 22,7 ∙ 3,5
№3. Решите уравнение: 1,7 ∙ у = 1,53
№4. Найдите значение выражения:
2∙а + 1,5∙с, если а=1,4 и с=0,8
№5. Найдите 35% от 900.
№6. Площадь прямоугольника равна 14,5см2, длина одной из его сторон равна 2,5см. Чему равна длина другой стороны?
№7. Скорость течения 3,7 км/ч. Найдите скорость катера по течению и его скорость против течения, если собственная скорость катера 12 км/ч.
Часть 2.
№7. Решите уравнение: 4,2 ∙ (0,25 + х) = 1,47
№8. Найдите значение выражения:
0,351 : 2,7 + 3,05 ∙ (13,1 - 1,72)
№10. В саду 120 фруктовых деревьев. Из них 50%- яблони, 20%- груши, остальные- вишни. Сколько вишен в саду?
Вариант - 2.
Часть 1.
№1. Вычислите: 4,39+ 23,7
№2. Выполните умножение: 4,15∙ 8,6
№3. Решите уравнение: 5,4 ∙ х= 3,78
№4. Найдите значение выражения:
3∙р +2,5∙у, если р =2,4 и у = 0,6
№5. Найдите 45% от 600.
№6. Одна сторона прямоугольника равна 3,5см, площадь прямоугольника равна 7,84см2. Найдите другую сторону прямоугольника.
№7. Собственная скорость теплохода 30,5 км/ч. Скорость течения 2,8 км/ч. Найдите скорость теплохода против течения и его скорость по течению.
Часть2.
№7. Решите уравнение: (4,5 - у) ∙ 5,8 = 8,7
№8. Найдите значение выражения:
(12,3 + 1,68) ∙ 2,05 - 0,348 : 2,9
№10. В книге 240 страниц. Первый рассказ занимает 20% книги, второй-40%, остальное - третий рассказ. Сколько страниц занимает третий рассказ?
Ответы:
№ задания
1
2
3
4
5
6
7
8
9
10
1 вариант
24,023
79,45
0,9
14,8
315
5,8
8,3 км/ч
15,7 км/ч
0,1
34,839
36
2 вариант
28,09
35,69
0,7
8,7
270
2,24
27,7 км/ч
33,3 км/ч
3
28,539
96
Или можно провести такой входной контроль
1вариант
Входной контроль 6класс
1.Найдите значение выражения
8-0,026:0,4 +0,16*4,5.
2. Решить уравнение
3,9+5,2х - 1,6х=18,48.
3.Решить задачу
Длина дороги 60км. Покрыто асфальтом 80% этой дороги. Сколько километров дороги покрыто асфальтом?
4. Упростить выражение 2,3х - 0,03х +0,82х и найти его значение при х=10; 0,01.
5. Решить задачу
Витя три дня собирал яблоки в саду. В первый день он собрал 29кг, что на 4кг больше, чем во второй день. А в третий день он собрал в 2раза меньше, чем за два первых дня. Сколько кг яблок собрал Витя за три дня?
2вариант
Входной контроль 6класс
1.Найдите значение выражения
6 - 0,037 : 0,5 + 0,28 * 6,5.
2. Решить уравнение
1,2 +4,1х - 1,3х =9,74.
3.Решить задачу
Собрали 1540кг яблок и груш. Груши составляют 25% этого количества. Сколько собрали груш?
4.Упростить выражение 4,7х - 0,07х +0,48х и найти его значение при х=100; 0,1.
5. Решить задачу
Нильс с дикими гусями был в полете три дня.
В первый день они пролетели 46км, что на 8км больше, чем во второй день, а в третий день они пролетели в 3раза меньше, чем за два первых дня вместе. Сколько километров пролетел Нильс с дикими гусями за три дня?
1вариант
Входной контроль 6класс
1.Найдите значение выражения
8-0,026:0,4 +0,16*4,5.
2. Решить уравнение
3,9+5,2х - 1,6х=18,48.
3.Решить задачу
Длина дороги 60км. Покрыто асфальтом 80% этой дороги. Сколько километров дороги покрыто асфальтом?
4. Упростить выражение 2,3х - 0,03х +0,82х и найти его значение при х=10; 0,01.
5. Решить задачу
Витя три дня собирал яблоки в саду. В первый день он собрал 29кг, что на 4кг больше, чем во второй день. А в третий день он собрал в 2раза меньше, чем за два первых дня. Сколько кг яблок собрал Витя за три дня?
2вариант
Входной контроль 6класс
1.Найдите значение выражения
6 - 0,037 : 0,5 + 0,28 * 6,5.
2. Решить уравнение
1,2 +4,1х - 1,3х =9,74.
3.Решить задачу
Собрали 1540кг яблок и груш. Груши составляют 25% этого количества. Сколько собрали груш?
4.Упростить выражение 4,7х - 0,07х +0,48х и найти его значение при х=100; 0,1.
5. Решить задачу
Нильс с дикими гусями был в полете три дня.
В первый день они пролетели 46км, что на 8км больше, чем во второй день, а в третий день они пролетели в 3раза меньше, чем за два первых дня вместе. Сколько километров
Промежуточный контроль
Промежуточный контроль по математике
в 6 классе
I вариант
1.Найти неизвестный член пропорции:
![]()
2.Решить задачу:
У Сережи и Пети 69 марок. У Пети в ![]() раза больше, чем у Сережи. Сколько марок у каждого мальчика?
раза больше, чем у Сережи. Сколько марок у каждого мальчика?
3.Решить задачу
Первоначально футболка стоила 320 рублей. На распродаже ее цена снизилась на 15%. Сколько рублей стала стоить футболка после скидки?
4.Найти значение выражения
![]()
5.Масштаб карты 1 : 10 000 000. Чему равно расстояние между городами А и В (в км), если на карте оно составляет 6 см.
Промежуточный контроль по математике в 6 классе
II вариант
1.Найти неизвестный член пропорции
![]()
2.Решить задачу
В двух загонах 88 овец. Во втором загоне овец в ![]() раза больше, чем в первом. Сколько овец в каждом загоне?
раза больше, чем в первом. Сколько овец в каждом загоне?
3.Решить задачу
На первую смену в летний лагерь было выделено 196 путевок. На вторую смену - на 25% больше. Сколько путевок выделено на вторую смену?
4.Найти значение выражения
![]()
5.Масштаб карты 1 : 1 000 000. Чему равно расстояние между городами А и В (в км), если на карте оно составляет 8,5 см.
Промежуточный контроль по математике
в 6 классе
I вариант
1.Найти неизвестный член пропорции:
![]()
2.Решить задачу:
У Сережи и Пети 69 марок. У Пети в ![]() раза больше, чем у Сережи. Сколько марок у каждого мальчика?
раза больше, чем у Сережи. Сколько марок у каждого мальчика?
3.Решить задачу
Первоначально футболка стоила 320 рублей. На распродаже ее цена снизилась на 15%. Сколько рублей стала стоить футболка после скидки?
4.Найти значение выражения
![]()
5.Масштаб карты 1 : 10 000 000. Чему равно расстояние между городами А и В (в км), если на карте оно составляет 6 см.
Промежуточный контроль по математике в 6 классе
II вариант
1.Найти неизвестный член пропорции
![]()
2.Решить задачу
В двух загонах 88 овец. Во втором загоне овец в ![]() раза больше, чем в первом. Сколько овец в каждом загоне?
раза больше, чем в первом. Сколько овец в каждом загоне?
3.Решить задачу
На первую смену в летний лагерь было выделено 196 путевок. На вторую смену - на 25% больше. Сколько путевок выделено на вторую смену?
4.Найти значение выражения
![]()
5.Масштаб карты 1 : 1 000 000. Чему равно расстояние между городами А и В (в км), если на карте оно составляет 8,5 см.
Итоговый контроль
Пояснительная записка
Итоговая работа по структуре и содержанию приближена к новой форме итоговой аттестации в 9 классе.
Работа состоит из 2 частей:
I часть - содержит 14 заданий;
II часть - содержит 2 задания;
При выполнении первой части нужно указать только ответы.
При этом:
-
если к заданию приводятся варианты ответов (четыре ответа), то надо выбрать ответ, соответствующий верному;
-
если ответы не приводятся, то полученный ответ надо записать в отведенном для этого месте.
Ответы на задание теста I части оцениваются одним баллом. Ответы на задания II части оцениваются двумя баллами. За правильно выполненную I часть можно получить 14 баллов, за правильно выполненную II часть можно получить 4 балла.
Максимальный балл за всю работу- 18
Вариант № 1
Часть 1
-
Какое неравенство неверное?
1) 5 > -3 2) -1,7 > -1,5 3) -![]() < 0 4) -9 < -6
< 0 4) -9 < -6
-
Координаты точек A(8; 2), B(-4; -1). В какой точке отрезок AB пересекает ось ординат?
1) (0; 0); 2) (1; 0); 3) (0; 1); 4) (0; -1)
-
Решите уравнение 8 х + 5 (6 - 7х) = - 7х + 10
-
Найдите значение выражения: -
1) 12,2; 2) - 37; 3) -12,2; 4) 37
-
Сколько понадобится времени 9 бульдозерам, чтобы расчистить площадку, которую 7 бульдозеров расчищают за 6,3 ч?
-
Какую цифру следует поставить вместо * в число 9*425*, чтобы полученное число делилось на 12?
1) 2; 2) 6; 3) 8; 4) 5
-
Упростите выражение: 7· (2а - 4,2) - (4 + а)
-
Найдите число, 12% которого равны 240.
-
Указать верную пропорцию:
1) 2 : 3 = 5 : 10 2) 2 : 3 = 10 : 15 3) 5 : 10 = 8 : 4 4) 12 : 18 = 3 : 2
-
Найдите сумму всех целых чисел, кратных 7, лежащих в промежутке (-14; 22)
-
Сократите дробь
-
Найдите значение выражения:
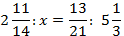 :
: 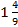 .
.
Часть 2
-
Вычислите: (1,8 · 0,4 -
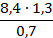 ) : ( - 0,8).
) : ( - 0,8). -
Решите задачу, составив уравнение.
Расстояние между городами автомобиль преодолевает за 3 ч. Если бы его скорость была на 15 км/ч больше, то на этот путь ему потребовалось бы 2,4 ч. Определите скорость автомобиля и расстояние между городами.
Вариант № 2
Часть 1
-
Какое неравенство неверное?
1) 5,2 > -3,1 2) -5 < -1 3) 0 > -![]() 4) -4,5 < -4,6
4) -4,5 < -4,6

-
Координаты точек A(-1; 4), B(3; -4). В какой точке отрезок AB пересекает ось абсцисс?
1) (0; 0); 2) (1; 0); 3) (0; 1,5); 4) (0; -1)
-
Решите уравнение 6 (- 2 - х) + 8 х = 9
-
Найдите значение выражения: -
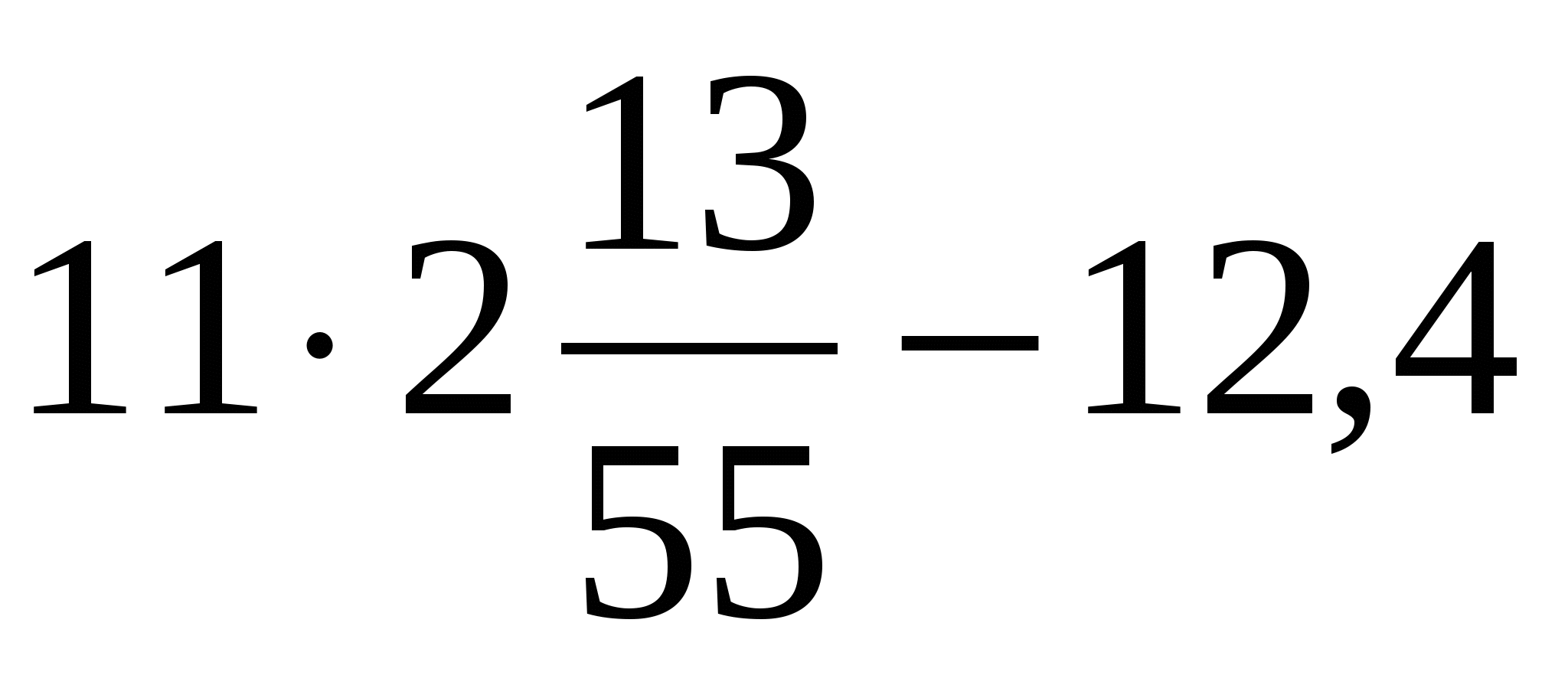
1) -2,5 2) 2,5 3) -2,50 4) 0
-
4 каменщика могут выполнить кладку за 15 дней. За сколько дней выполнят эту же кладку 3 каменщика?
-
Какую цифру следует поставить вместо * в число 555*1*, чтобы полученное число делилось на 6?
1) 2; 2) 3; 3) 4; 4) 6
-
Упростите выражение: 6 · (х + 8,5) - 4 · (6,4 + х)
-
Найдите число, 37% которого равны 518.
-
Указать верную пропорцию:
1)3 : 5 = 10 : 122) 3 : 8 = 5 : 6 3) 3 : 8 = 6 : 164) 5 : 3 = 10 : 8
-
Найдите сумму всех целых чисел кратных 8, лежащих в промежутке (-16; 25)
-
Сократите дробь
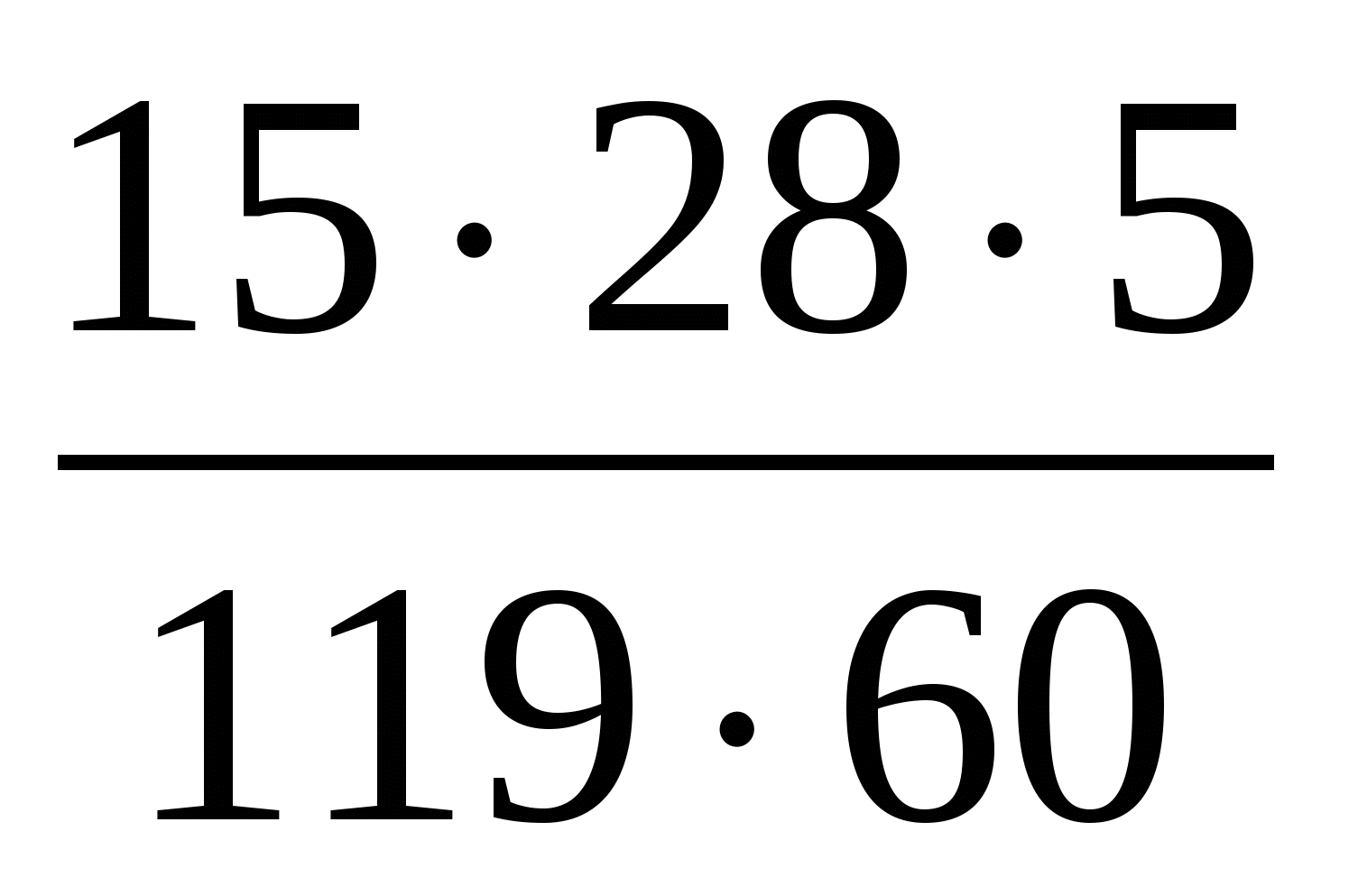
-
Найдите значение выражения:
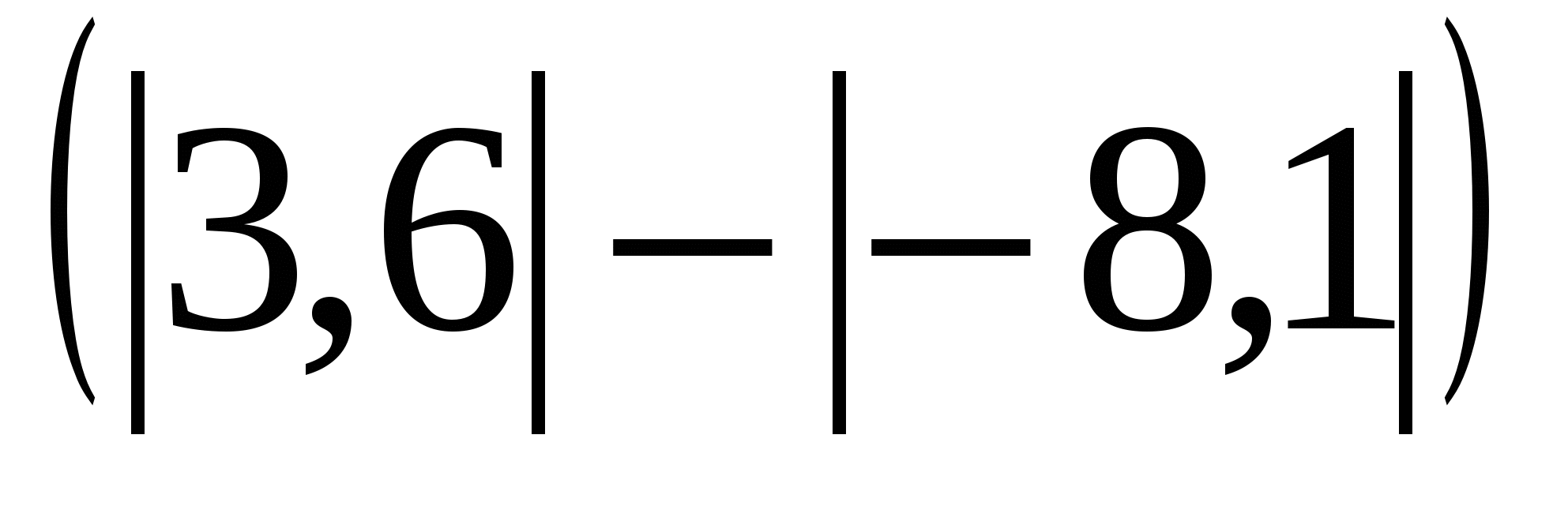 :
:  .
.
Часть 2
-
Вычислите: (2,6 · 0,3 -
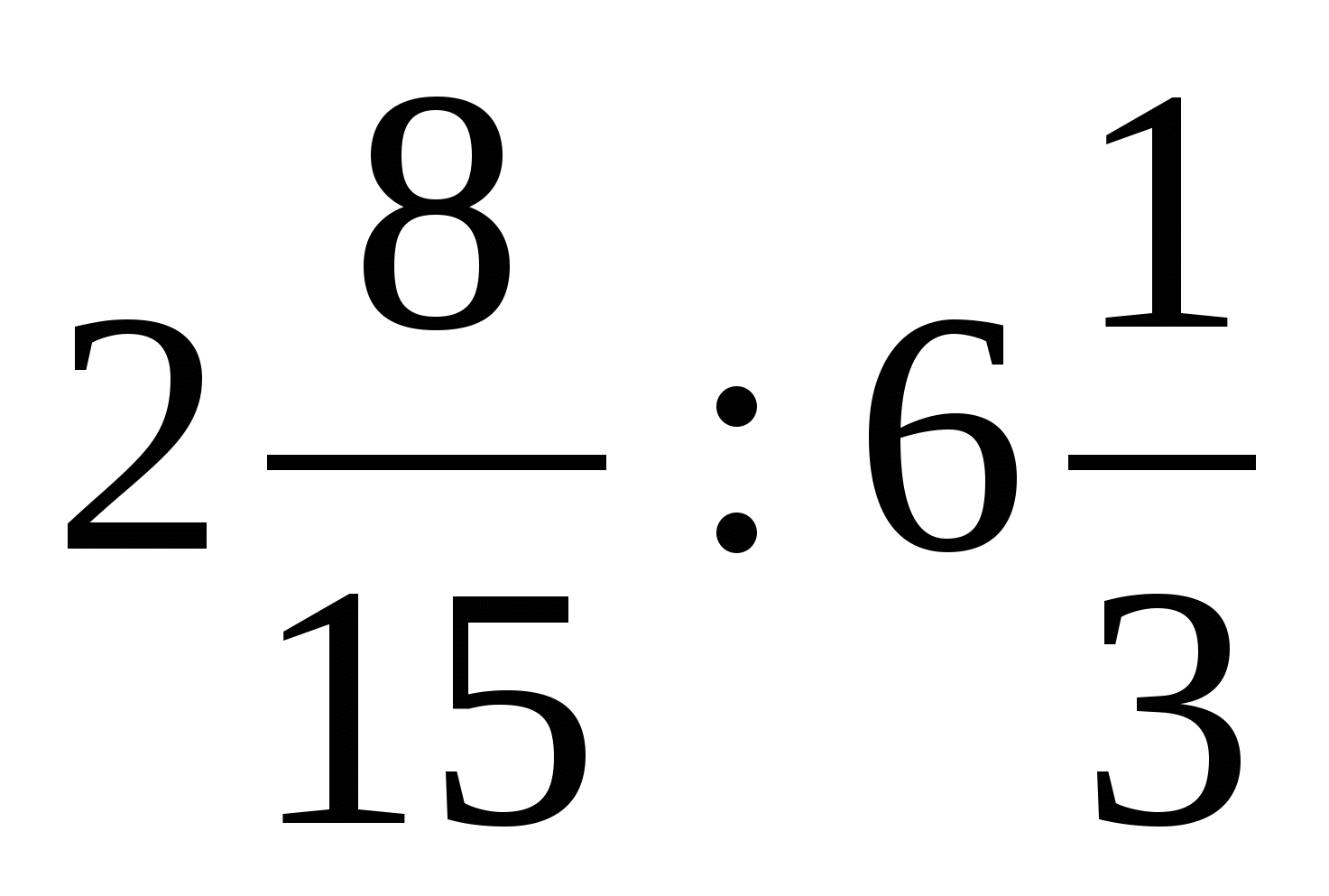 ) : ( - 1,9).
) : ( - 1,9).
-
Решите задачу, составив уравнение.
На одном складе было в 2,5 раза меньше овощей, чем на втором. После того как на первый склад завезли 180 т овощей, а на второй - 60 т, овощей на обоих складах стало поровну. Сколько тонн овощей было на каждом складе первоначально?
Ответы на задание теста I части оцениваются одним баллом. Ответы на задания II части оцениваются двумя баллами. За правильно выполненную I часть можно получить 14 баллов, за правильно выполненную II часть можно получить 4 балла.
Максимальный балл за всю работу- 18
Шкала перевода в пятибалльную систему
«2»
«3»
«4»
«5»
0 - 5 баллов
6 - 10 баллов
11 - 14 баллов
15 - 18 баллов
Комплект теоретических вопросов на конец года
Какое число называется делителем (кратным) данного числа?
Какое число является делителем любого натурального числа?
равен самый маленький (большой) делитель числа а?
Чему равно самое маленькое кратное числа а?
Существует ли самое большое кратное числа а?
Что такое парные делители?
Как найти все делители числа а?
Как по записи числа определить, делится ли оно на 2, 5, 10 без остатка?
Что такое четное (нечетное) число?
Как применять признаки делимости на 2, 5, 10 для решения задач, проверки вычислений?
Как по записи числа определить, делится ли оно на 3, 9?
Как по записи числа определить, делится ли оно на 6, 18, 15?
Как применять признаки делимости при решении задач, проверке вычислений?
Как можно классифицировать натуральные числа в зависимости от количества их делителей?
Является ли число 1 простым (составным)?
Какие числа называются простыми (составными)?
Может ли простое число быть четным (нечетным)?
Какие существуют методы для отыскания простых чисел?
Существует ли составное число, которое нельзя разложить на простые множители? Чем могут отличаться два разложения одного и того же числа на простые множители?
Какие способы разложения на простые множители изучили?
Какое число называется наибольшим общим делителем (НОД) двух натуральных чисел? Всегда ли он существует?
Какие числа называются взаимно простыми?
Как найти НОД двух (трех) натуральных чисел?
Чему равен НОД чисел а и b, если а делится на b, если а и b взаимно простые?
Какими числами являются числа а и 1?
Какое число называется наименьшим общим кратным (НОК) двух натуральных чисел а и b?
Всегда ли оно существует?
Как найти НОК двух (трех) чисел?
Чему равно НОК чисел а и b, если а делится на b, если а и b взаимно простые?
Как применяются НОД и НОК при решении задач?
В чем состоит основное свойство дроби?
Изменится ли дробь, если числитель и знаменатель этой дроби умножить на 5 (разделить на 23)?
Что значит сократить дробь?
Какая дробь называется несократимой?
Как применяется сокращение дробей для решения задач?
Какое число может служить общим знаменателем двух дробей?
Какое число называется дополнительным множителем?
Как найти дополнительный множитель?
Как привести дроби к наименьшему общему знаменателю?
Какие правила сравнения дробей мы изучили?
Как сравнить две дроби с разными знаменателями?
Как применяется сравнение дробей для решения практических задач?
Как сложить (вычесть) дроби с разными знаменателями?
Как сложить (вычесть) обыкновенную и десятичную дроби?
Как применяется сложение (вычитание) обыкновенных дробей при решении уравнений и задач?
Как сложить два смешанных числа?
На каких свойствах сложения основан алгоритм сложения смешанных чисел?
Как выполнить вычитание смешанных чисел?
На каких свойствах вычитания основано вычитание смешанных чисел?
Как сложить (вычесть) десятичную дробь и смешанное число?
Как умножить дробь на натуральное число?
Как умножить дробь на дробь?
В чем состоит алгоритм умножения смешанных чисел?
Как возвести в квадрат (куб) обыкновенную дробь, смешанное число?
Как применяется умножение дробей и смешанных чисел для решения уравнений и задач?
Как найти дробь от числа?
Как найти несколько процентов от числа?
Как применяется нахождение дроби от числа для решения задач?
Как с помощью микрокалькулятора найти несколько процентов от числа?
Как умножить смешанное число на натурально? Какое свойство умножения при этом используется?
Как применяется распределительное свойство умножения для рационализации вычислений с обыкновенными дробями и смешанными числами?
Как применяется распределительное свойство умножения для упрощения выражений, содержащих смешанные числа и обыкновенные дроби, и при решении задач?
Какие числа называются взаимно обратными? Какое число является обратным самому себе?
Как записать число, обратное дроби, натуральному числу, смешанному числу?
Как применять взаимно обратные числа при нахождении значений выражений, решении уравнений вида ах=1?
Как разделить дробь на натуральное число? дробь на дробь?
Как выполняется деление смешанных чисел?
Как применяется деление обыкновенных дробей при нахождении значения выражений, решении уравнений и задач?
Как применять свойство деления дробей для упрощения вычислений?
Как найти число по заданному значению его дроби?
Как найти число по заданному значению его процентов?
Как применять нахождение числа по его дроби при решении задач?
Какое выражение называется дробным?
Что называется числителем, знаменателем дробного выражения?
Как найти значение дробного выражения?
Какие свойства действий с дробями при этом используются?
Что называется отношением двух чисел?
Что показывает отношение двух чисел?
Как найти, какую часть число а составляет от числа b?
Как выразить отношение в процентах?
Как находить отношения именованных величин?
Как применяется понятие «отношение» при решении задач?
Что называется пропорцией? Какие члены пропорции называются средними, а какие крайними?
Как составить верную пропорцию?
В чем заключается основное свойство пропорции?
Как проверить, верная ли пропорция?
Как найти неизвестный крайний (средний) член пропорции?
Какие величины называются прямо пропорциональными (обратно пропорциональными)?
Что можно сказать об отношениях соответствующих значений прямо пропорциональных (обратно пропорциональных) величин?
Что называется масштабом карты, плана, чертежа? Какие виды масштабов бывают?
Как применяется понятие «масштаб» для решения задач?
Что называется окружностью, радиусом, диаметром окружности?
Как найти длину окружности, зная ее радиус?
Как найти площадь круга, зная радиус ограничивающей его окружности?
Являются ли длина окружности и ее диаметр (площадь круга и его диаметр) прямо пропорциональными величинами?
Что называется радиусом шара, его диаметром? Что называется сферой?
Какие числа называются положительными, отрицательными? Является ли нуль положительным, отрицательным числом? Какая прямая называется координатной прямой? Что называется координатой точки на прямой? Где в повседневной жизни применяются координаты?
Какие числа называются противоположными? Какое число противоположно самому себе? Сколько противоположных чисел есть у каждого числа? Каким числом является число, противоположное отрицательному (положительному, натуральному) числу? Какие числа называются целыми?
Что называется модулем числа? Как обозначается модуль числа? Может ли модуль числа быть больше (меньше, равен) самого числа?
Как сравнить два числа с разными (одинаковыми) знаками? Какие правила сравнения чисел с нулем вы знаете? Как сравнить число и его модуль? При каком условии модуль числа больше самого числа? Равен ему?
Что означает положительное (отрицательное) перемещение точки на координатной прямой? Где в реальной жизни мы сталкиваемся с изменением величин?
Что значит прибавить к числу а число b? Как изменится число а, если b положительное (отрицательное) число? Что можно сказать о сумме противоположных чисел? Как записать это свойство с помощью буквенного выражения?
Как сложить два отрицательных числа? Какое число получается при сложении двух отрицательных чисел? Что общего между сложением двух отрицательных и двух положительных чисел?
Как сложить два числа с разными знаками? Может ли сумма двух чисел с разными знаками быть положительным (отрицательным) числом или нулем?
Что означает вычесть из числа а число b? Может ли разность двух чисел быть числом положительным, нулем, отрицательным?
Как найти длину отрезка на числовой прямой?
Как перемножить два числа с разными знаками? Как перемножить два отрицательных числа? Как возвести в квадрат положительное, отрицательное число? Какое число получается в результате? Как связаны квадраты противоположных чисел?
Как разделить отрицательное число на отрицательное? Как разделить числа с разными знаками?
Какие числа называются рациональными? Являются ли натуральные (целые, дробные, нуль, десятичные дроби) рациональными числами? Существуют ли числа, не являющиеся рациональными?
Как раскрыть скобки, перед которыми стоит знак «+» , «-«? Как записать сумма (разность) двух выражений и упростить ее? Как применяется раскрытие скобок для решения уравнений?
Что называется коэффициентом выражения? Как определить знак коэффициента в уравнении? Какие слагаемые называются подобными? Чем могут отличаться подобные слагаемые? Что значит привести подобные слагаемые? Какие свойства действий применяются при приведении подобных слагаемых?
Изменятся ли корни уравнения, если обе части уравнения умножить на ненулевое число? на нуль? Как перенести слагаемое из одной части уравнения в другую? Какие уравнения называются линейными? Как применяется раскрытие скобок и приведение подобных слагаемых для решения уравнений?
Как применяются уравнения при решении задач? Какие основные типы задач решаются с помощью уравнений?
Какие прямые называются перпендикулярными? Какие отрезки, лучи называются перпендикулярными? Как построить перпендикулярные прямые?
Какие прямые называются параллельными? Какие отрезки, лучи называются параллельными? Как построить параллельные прямые? Как расположены на плоскости две прямые, перпендикулярные третьей прямой?
Как называют пару чисел, определяющих положение точки на координатной плоскости? Как называется первая (вторая) координата точки? Как построить точку с заданными координатами в прямоугольной системе координат? Как определить координаты точки в прямоугольной системе координат? Какие особенностями обладают координаты точек, лежащих на оси абсцисс (ординат)? Построение фигур в координатной плоскости по координатам их вершин.
В чем отличие столбчатой диаграммы от круговой? Как построить столбчатую диаграмму по данным задачи? Как по графику зависимости величин определять соответствующие значения этих величин? Как построить график зависимости величин по данным задачи?
Перечень самостоятельных работ
№ темы
Наименование темы
НОД И НОК чисел
Сокращение, сложение и вычитание обыкновенных дробей
Сложение и вычитание смешанных чисел
Умножение обыкновенных дробей
Деление дробей
Дробные выражения
Отношения и пропорции
Окружность и круг
Противоположные числа и модуль
Сложение и вычитание положительных и отрицательных чисел
Умножение и деление рациональных чисел
Раскрытие скобок
Решение уравнений
Координатная плоскость
Итоговая контрольная работа за курс математики 6 класса
№
Тема
Масштаб.
Параллельные и перпендикулярные прямые
Столбчатые диаграммы
Перечень практических работ
№
Тема
Признаки делимости на 10, на 5, на 2
Длина окружности и площадь круга
Перечень лабораторных работКонтрольные работы
К - 1 «НОД и НОК чисел»
К - 2 «Сокращение, сложение и вычитание обыкновенных дробей»
К - -3 «Сложение и вычитание смешанных чисел»
К - 4 «Умножение обыкновенных дробей»
К - -5 «Деление»
К - -6 «Дробные выражения»
К - 7 «Отношения и пропорции»
К - 8 «Окружность и круг»
К - 9 «Противоположные числа и модуль»
К - 10 «Сложение и вычитание положительных и отрицательных чисел»
К - 11 «Умножение и деление рациональных чисел»
К - 12 «Раскрытие скобок»
К-13 «Решение уравнений»
К-14 «Координатная плоскость»
К-15 « Итоговая контрольная работа»
Экранно-звуковые пособия (могут быть в цифровом виде)
№
Название
Год изготовления
Изготовитель
CD-диск Электронное издание «Математика: 5-11 класс. Практикум»
2005
«НФПК»
CD-диск «Математика» из серии «Большая детская энциклопедия»
2009
ООО
«Издательство»
Видеофильм по истории развития математики «Первая наука человечества. Из прошлого в настоящее математики»
-
ООО «Видеостудия «КВАРТ»
4.3. Технические средства обучения (средства ИКТ)
Наименование технического средства обучения
-
1.
Мультимедийный компьютер
-
2.
Мультимедиапроектор
-
3.
Интерактивная доска «SmartBoard»
4.4. Цифровые образовательные ресурсы
№
Название
Год изготовления
Изготовитель
4.5. Учебно-практическое и учебно-лабораторное оборудование
№
Название
Год изготовления
Изготовитель
Комплект чертежных инструментов (классных и раздаточных): линейка, транспортир, угольник, циркуль
2011
-
Комплект для моделирования (цветная бумага, картон, калька, копировальная бумага, клей, ножницы, пластилин)
2014-2015
4.6. Натуральные объекты
№
Название
Год изготовления
Изготовитель
4.7. Демонстрационные пособия
№
Название
Год изготовления
Изготовитель
4.8. Музыкальные инструменты
№
Название
Год изготовления
Изготовитель
4.9. Натуральный фонд
№
Название
Год изготовления
Изготовитель
39