Исследовательская работа Применение интеграла для рсчета водоизмещения судна

Исследовательская работа

Применения интеграла для расчета водоизмещения судна.

Цель: познакомиться с методом вычисления интеграла с помощью формулы трапеций и показать применение данного способа для решения практических задач.

Вводная информация.

Рассмотрим определенный интеграл, 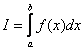где - функция, непрерывная на отрезке . Проведём разбиение отрезка на равных отрезков:

. При этом, очевидно: (нижний предел интегрирования) и (верхний предел интегрирования). Точки также называют узлами.

Тогда определенный интеграл можно вычислить приближенно по формуле трапеций:

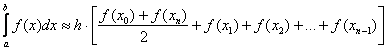, где:

- длина каждого из маленьких отрезков или шаг;

- значения подынтегральной функции в точках .

Задания.

1. Обвод ватерлинии задан уравнением . Изобразить его на участке изменения x от 0 до 30м. Вычислить площадь ватерлинии по правилу трапеций при n = 10 и сравнить этот результат с точным значением площади (вычисленное по криволинейной трапеции).

2. Обвод шпангоута задан уравнением изобразить его в пределах изменения z от 0 до 6 м. Вычислить площадь погруженной чсти шпангоута для осадки T = 5,0 м точно (вычисленное по криволинейной трапеции) и приближенно по правилу трапеций при n = 5.