10класс.

Тема урока: Методы решения тригонометрических уравнений.

« Правильному применению методов можно научиться только применяя их на разнообразных примерах.»

Г. Цейтен

Цели :

Образовательные- Повторение, обобщение и систематизация материала темы; сформировать умение применять при решении уравнений нужный способ.

Развивающие -способствовать формированию умений применять приемы: сравнения, обобщения, выделения главного, переноса знаний в новую ситуацию; развитию математического кругозора, мышления и речи, внимания и памяти.

Воспитательные- Содействовать воспитанию интереса к математике, воспитание настойчивости в приобретении знаний и умений, умения принимать самостоятельные решения.

Оборудование: интерактивная доска.

Тип урока: урок обобщения и систематизации знаний.

Ход урока: I Организационный момент. Вступительное слово учителя:

Сегодня ребята мы поговорим с вами о различных методах решения тригонометрических уравнений, научимся проводить анализ заданий и способов их выполнения, будем находить наиболее рациональные способы решения уравнений и попытаемся самостоятельно оценить свои знания. Прежде чем перейти непосредственно к нашей работе, мы сформируем экспертную группу (3 человека), участники которой на каждом этапе нашего урока помогут мне оценить ваши знания, проверят домашние задания и решения примеров классной работы, подведут итоги предстоящей работы.

II. Устная работа. На интерактивной доске появляется слайд.

Учитель: «Исправьте ошибки на доске и подумайте об их причинах».

Уравнение

Ответ с ошибкой

Правильный ответ

Нет корней

III Групповая работа. Игра-Домино. (раздаю карточки)

Начальная карточка.

-1

1

5/6

arccos(-/2)

/4

arccos(-/2)

cos0

arccos (1/2)

0

arcsin1

3/4

0

ctg x = -1

sin 0

1

+2n

cosx=1

/6

/2+n

arctg 1

cos x = -1

3/4

cos

/2

arccos(-1)

2n

sinx=1

/2+2n

cosx=0

cos

arcsin0

IV. Тестирование . (групповая работа)

На интерактивной доске появляется слайд со следующим тестом.

Классификация тригонометрических уравнений по методам решения.

уравнения

Уравнения

методы

ответ

1

4sin²x - cos 2x = 1

А) Метод замены переменной

Е

2

4 tg x - 12ctg x + 13 = 0

Б) Метод разложения на множители

А

3

3sin²x - 4sinxcosx + cos²x = 0

В) Метод преобразования разности в произведение

Г

4

3sin²x - 5sinx - 2 = 0

Г) Метод однородных уравнений

А

5

sin 5x - sin x = 0

Д) Другой способ

В

6

sin x - cos x = 1

Е) Метод понижение степени

Д

7

14cos² x - 2cos 2x = 9sin 2x - 2

Ж) Уравнения ,приводимые к квадратным уравнениям

Г

8

Б

9

3cos²x - sinx - 1 =0

Ж

1группа - описывает алгоритм метода Ж и решает уравнение №9, 2группа -метод Г и решает уравнение№5, 3группа -метод Б и уравнение№8.

1группа рассказывает о методе решения уравнений ,приводимых к квадратным.

3cos²x - sinx - 1 =0

3 (1 - sin²x) - sinx -1 = 0

3 - 3 sin²x - sinx -1 = 0

- 3 sin²x - sinx + 2 = 0

3 sin²x + sinx - 2 = 0

Пусть sinx = y

3y² + y - 2 = 0 D = b² - 4ac = 1 - 4∙3∙(-2) = 25

y_1,2 = (- 1 ± 5)/6 = 2/3; - 1

sinx = 2/3 или sinx = - 1

x = (- 1)ⁿ arcsin(2/3) + πn, n € Z x = - π/2+ 2πk, k € Z

Ответ: x₁= (- 1)ⁿ arcsin(2/3) + πn; x ₂= - π/2+ 2πk, n, k € Z

2группа о решении однородных уравнений. (Решение однородных уравнений (уравнения, в которых у всех слагаемых сумма показателей одинакова) и приводимых к ним сводится к решению алгебраических относительно tgx путём деления обеих частей уравнения на cosx≠0 и cos2 x≠0 соответственно.)

3tg²x - 4tgx + 1 = 0

Учитель предлагает учащимся по желанию выйти к доске и решить полученное уравнение. Желающие выходят к доске, на местах решают в тетрадях.

Решение: пусть tgx = y

3y² - 4y + 1 = 0

D = 16 - 4·3·1 = 4

Y_1,2 = (4 ± 2)/6 = 1; 1/3

tgx = 1 или tgx = 1/3

x = π/4 + πn, n € Z x = arctg(1/3) + πk, k € Z

Ответ: x ₁= π/4 + πn, n € Z , x₂ = arctg(1/3) + πk, k € Z

3гр.Рассказывает о методе разложения на множители.( Решение с помощью разложения на множители сводится к решению двух элементарных уравнений.)

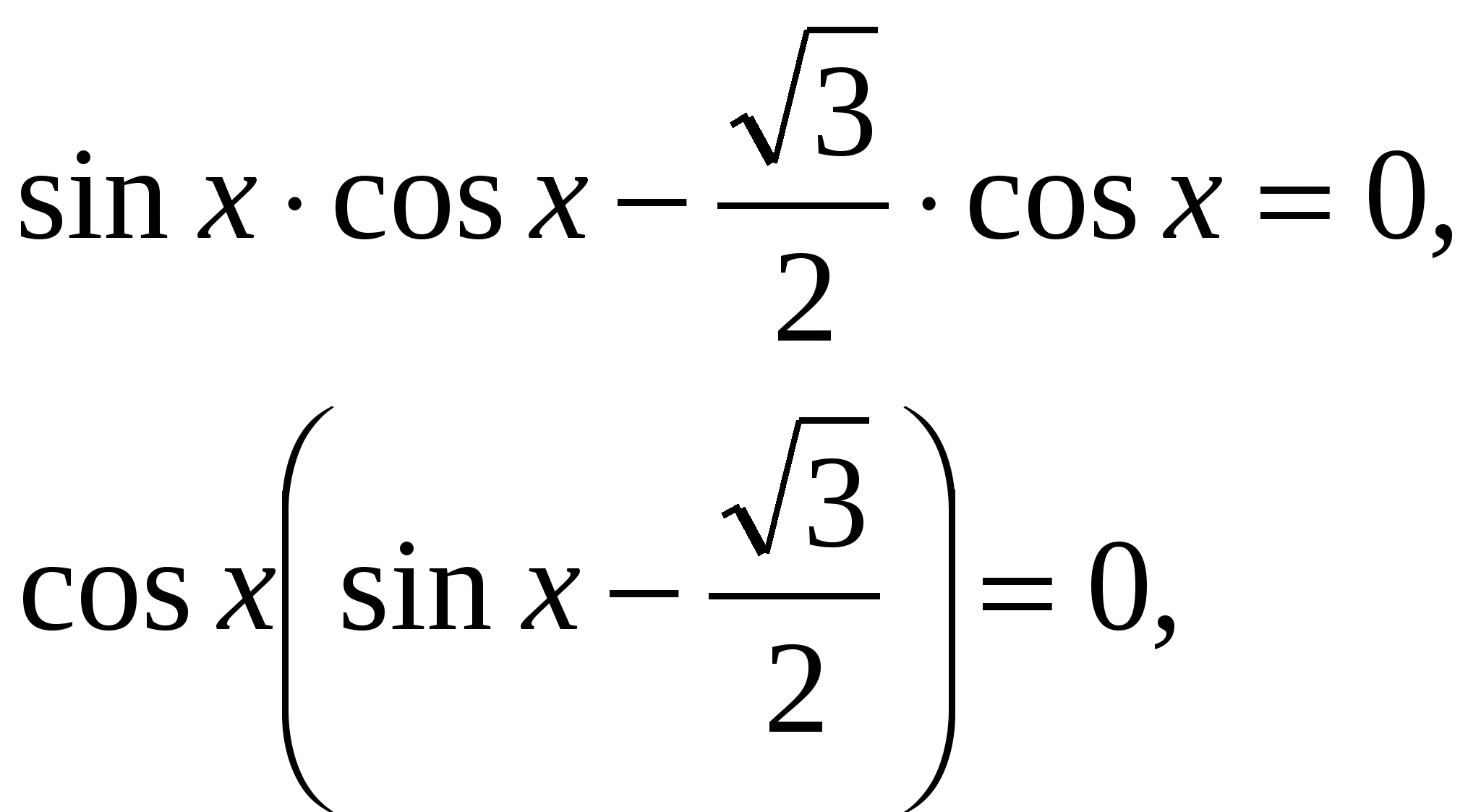
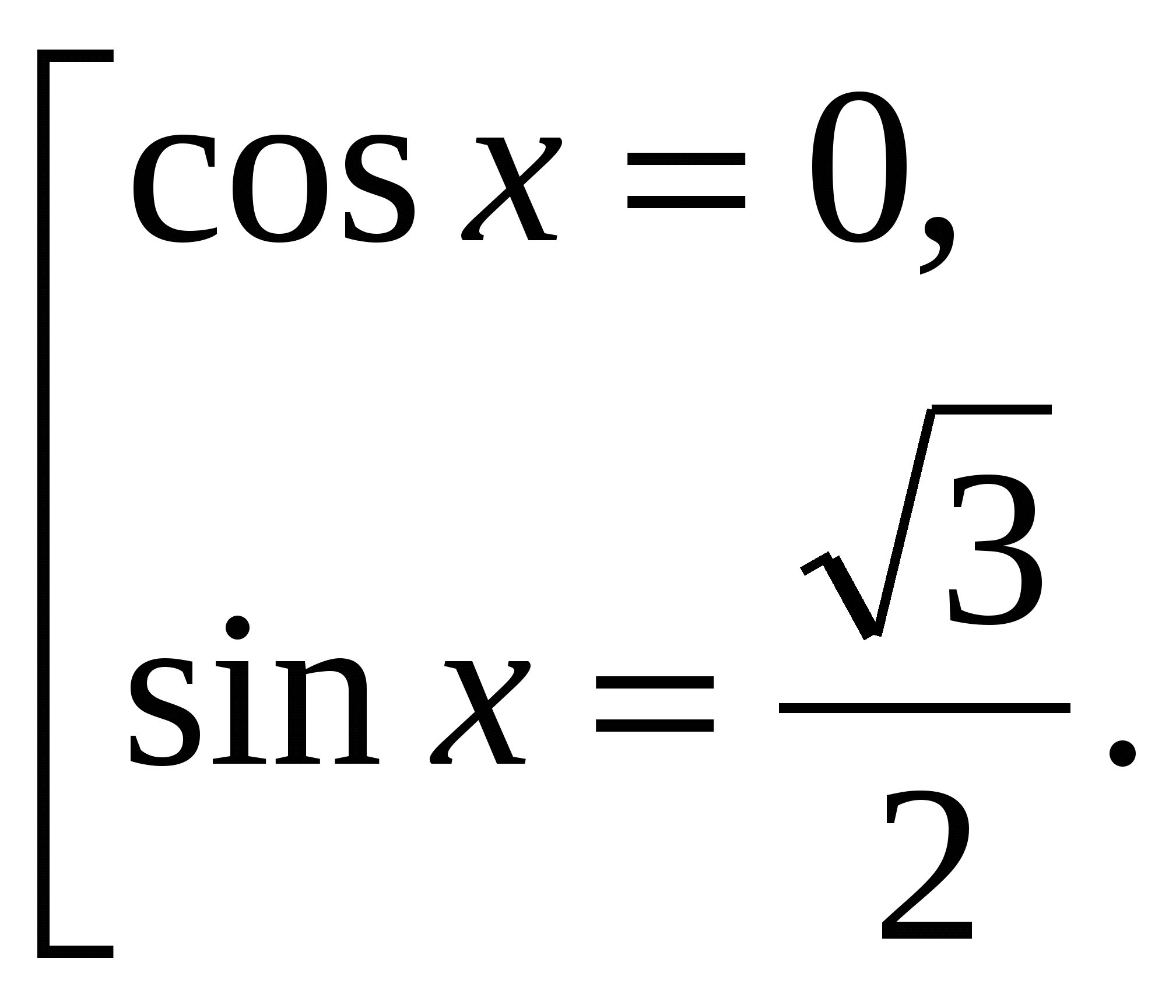
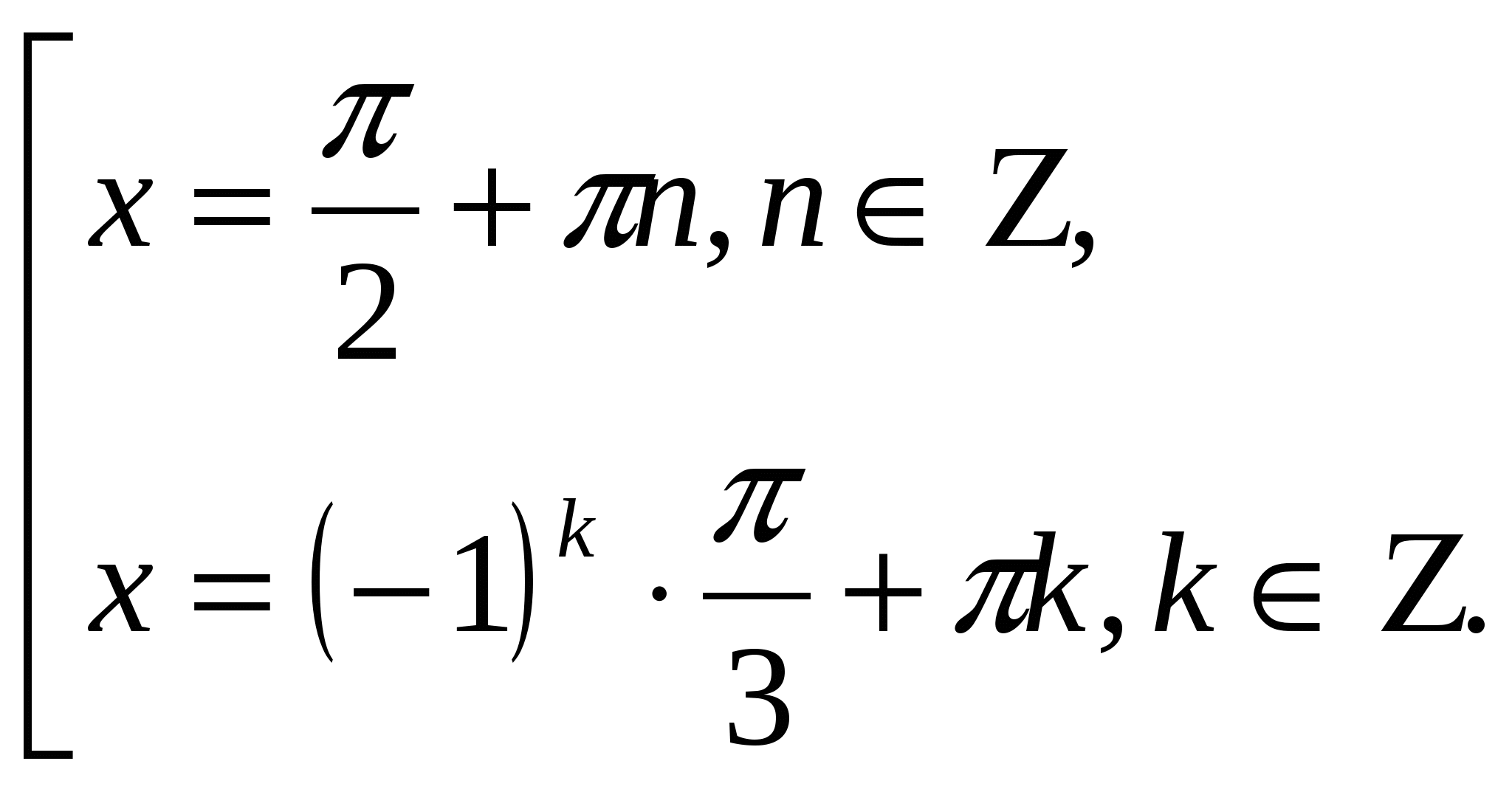Ответ: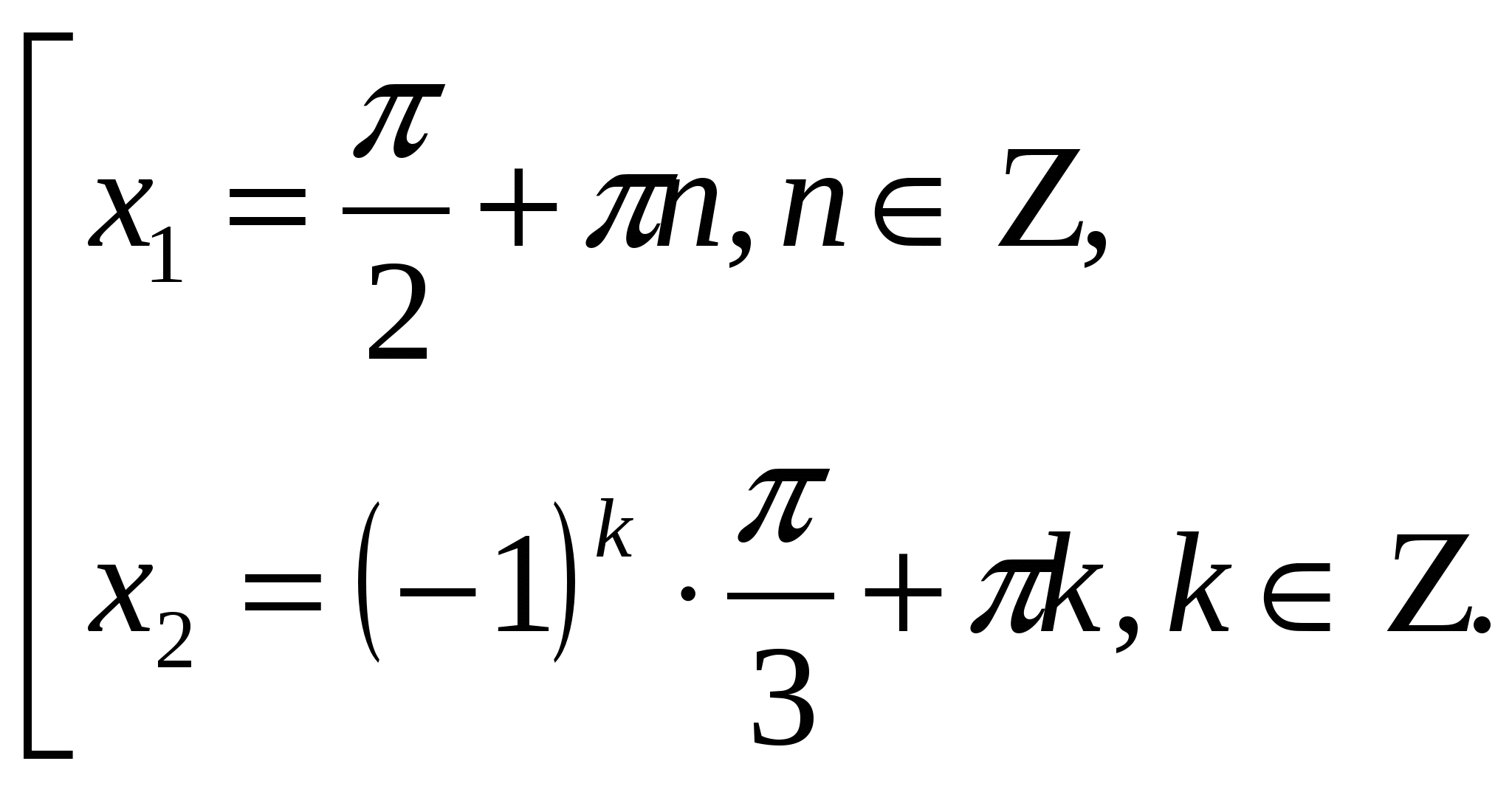

IV.Гимнастика для глаз.Учитель показывает уравнение из второго столбца, решениями которых являются выражения из первого столбца. Если учитель показал верный ответ , учащиеся смотрят вверх, если неправильно ,то учащиеся опускают глаза.

На интерактивной доске появляется слайд.

.

V .Новая тема: Решение тригонометрических уравнений. Учитель называет вид уравнения, оставшегося ся на доске: sin x - cos x = 1. Какими методами еще можно решать данное уравнение?

Предлагает учащимся уравнение, которое можно решить несколькими способами, и вместе разбирает эти способы. Дети, предложившие тот или иной способ, решают задания у доски.

Поиск способов решения. В результате наблюдения и обсуждения могут быть выявлены следующие способы решения.

1 способ. ( Сведением к однородному уравнению, выразив sin x, cos x и 1 через функции половинного аргумента)

Приведение к однородному уравнению.

cos x - sin x=1,

cos²- sin²-2sin cos=sin² + cos² ,

2sin²+2sin cos=0.

sin( sin+ cos)=0.

1) sin=0, 2) sin+ cos=0,

=πk, k€Z. tg= -1,

x=2 πk, k€Z. = - + πn, n€Z,

x= - +2 πn, n€Z.

Ответ: x₁=2 πk, k€Z. X₂= - +2 πn, n€Z.

2 способ.. 3 способ.

Разложение Введение

на множители вспомогательного угла

cos x - sin x=1, cos x - sin x=1,

(cos x - 1) - sin x = 0, (cos x- sin x)=1,

(1- cos x) + sin x = 0, sin cos x - cos sin x=

2sin² + 2sin cos = 0, sin( - x)= .

sin( sin+ cos) = 0. sin(x-)= -.

1) sin=0, 2) sin+ cos=0, х=(-1)^к+1 + + πk, k€Z

=πk, k€Z. tg= -1, Ответ: х=(-1)^к+1+ + πk, k€Z

x=2 πk, k€Z. = - + πn, n€Z,

x= - +2 πn, n€Z.

Ответ: x₁=2 πk, k€Z. X₂= - +2 πn, n€Z.

VI. Домашнее задание: Учащиеся выбирают уровень А или В, и решают уравнения, которые можно решить несколькими способами..

УРОВЕНЬ А.

Решите уравнение:

а) 1 + sin x = 0;

б) 3cos x - 2sin2 x = 0.

в) ;

г) sin 4x + sin 2x = 0.

УРОВЕНЬ В

Решите уравнение:

а) ;

б) sin 4x - sin 2x = 0.

в) 2sin xcos x = cos 2x - 2sin2 x;

г) 2sin² x - 3sin 2x - 4cos 2x = 4

д) sin x + 4 cos x = 1,

VII. Итог урока: Итак, подведем итоги. Сегодня мы повторили способы решения тригонометрических уравнений, вспомнили формулы , решали тригонометрические уравнения разными способами и поняли, что при решении разными способами необязательно получаются одинаковые ответы.

Далее учитель отмечает хорошую работу одних учащихся, недостаточную активность других. Выставляются оценки.

В конце урока можно дать ребятам небольшую анкету, которая позволяет осуществить самоанализ, дать качественную и количественную оценку уроку. Некоторые пункты можно варьировать, дополнять, это зависит от того, на какие элементы урока обращается особое внимание. Можно попросить учащихся аргументировать свой ответ.

1.На уроке я работал
2.Своей работой на уроке я
3.Урок для меня показался
4. Материал урока мне был
5.Домашнее задание мне кажется

активно / пассивно
доволен / не доволен
коротким / длинным
понятен / не понятен
интересен / скучен
легким / трудным

Северо-Казахстанская область

Акжарский район

С..Ленинградское

Ул. Сейфуллина №18 кв.2

Охрименко Нина Михайловна

Учитель математики 1 категории Ленинградской средней школы №1

Педстаж - 32 года

87154631168 номер телефона