Практические работы по математике ЕН.01.

Министерство образования и науки Республики Татарстан

ГБПОУ «Спасский техникум отраслевых технологий»

Задания для проведения

практических занятий

по математике

2 курс СПО

для специальностей:

Составитель:Субботкина И.П.

Сборник заданий по организации самостоятельной работы студентов преподавателями дисциплины математика в учреждениях среднего профессионального образования.

Содержание1. ПЗ№1.Операции над матрицами. Вычисление определителей.

4

2. ПЗ№2.Транспонирование матриц. Нахождение обратной матрицы

6

3. ПЗ№3.Решение систем линейных уравнений с помощью метода Крамера

7

4. ПЗ№4.Решение систем линейных уравнений методом Гаусса

8

5. ПЗ№5. Пределы. Раскрытие неопределенностей, вычисление пределов с помощью замечательных

9

6. ПЗ№6.Вычисление производных

11

7. ПЗ№7.Неопределенный и определенный интегралы. Площадь криволинейной трапеции

10

8. ПЗ№8.Арифметические действия с комплексными числами

11

9. ПЗ№9.Размещения, перестановки, сочетания. Бином Ньютона

13

10. ПЗ№10.Вычисление вероятностей

14

11. ПЗ№11.Множества, их виды. Операции над множествами. Графическое представление множеств.

21

12. ПЗ№12.Решение дифференциальных уравнений

25

13. ПЗ№13.Графы

27

12. Список литературы

30

13.Интернет ресурсы

30

Практическое занятие №1

Тема: Операции над матрицами. Вычисление определителей.

Цель занятия: научиться вычислять действия над матрицами, вычислять определители

Задания для решения на занятии

Определите тип матриц: 2)

3) 4) 5)

Найти 3А+2В, если А=, В=

Найти 2А+3В-С, если А=, В=, С=

Найти А²- 3А+5Е, если А=,

Найти произведение матриц:

1) А= и В=

2) А= и В=

3) А= и В=

Убедитесь, что АВ ≠ ВА, если:

1) А= В=

2) А=, В=

3) А=, В=

Вычислить определители:

1) 2) 3) 4)

5) 6) 7) 8) 9)

Домашнее задание

Найти произведение матриц: и В=

Вычислить определитель:

Практическое занятие №2

Тема: Транспонирование матриц. Нахождение обратной матрицы

Цель занятия: научиться транспонировать матрицы, вычислять обратную матрицу

Задания для решения на занятии

Транспонировать матрицы:

А= 2) В=

Вычислить обратную матрицу, выполнить проверку:

1. А= 2) В= 3) C=

4) D= 5) F=

Домашнее задание

Вычислить обратную матрицу, выполнить проверку:

1. А= 2) В=

Практическое занятие №3

Тема: Решение систем линейных уравнений с помощью метода Крамера

Цель занятия: научиться решать системы уравнений методом Крамера

Задания для решения на занятии

Решить систему линейных уравнений методом Крамера:

1) 2)

3) 4)

4)

Домашнее задание

Решить систему линейных уравнений методом Крамера:

Практическое занятие №4

Тема: Решение систем линейных уравнений методом Гаусса

Цель занятия: научиться решать системы уравнений методом Гаусса

Задания для решения на занятии

Решить систему линейных уравнений методом Гаусса:

1) 2)

3) 4)

5)

Домашнее задание

Решить систему линейных уравнений методом Гаусса:

Практическое занятие №5

Тема: Пределы. Раскрытие неопределенностей, вычисление пределов с помощью замечательных

Цель занятия: научиться вычислять пределы различными методами

Задания для решения на занятии1

9

17

(1+x)^0,5x

2

10

18

(1+)

3

11

2∙

19

(1+)

4

12

20

(1+)^3х

5

13

21

5+ -

6

14

22

7

15

23

(1-4х)^5/x

8

16

(1+)

24

Домашнее задание1

8∙

3

5

(1+5х)^1/x

2

7∙

4

6

Практическое занятие №6

Тема: Вычисление производных

Цель занятия: Научиться вычислять производные сложных функций

Задачи для решения на занятии

1. Точка движется прямолинейно по закону . Найти ее скорость в момент времени .

2. Дана кривая . Провести к ней касательную в точке, абсцисса которой х=-1.

3. Найти производные функций:

1) 3) 4)

4. Найти производные сложных функций.

Домашнее задание

Применяя формулы и правила дифференцирования, найти производные следующих функций:

1). 2) 3)

4) 5) 6)

7) 8) 9)

10) 11)

Практическое занятие №7

Тема: Неопределенный и определенный интегралы. Площадь криволинейной трапеции

Цель занятия: закрепить и обобщить навыки вычисления неопределенного и определенного интегралов, площади криволинейной трапеции

Задания для решения на занятии

Вычислить неопределенные интегралы:1.

4.

2.

5.

3.

6.+

Вычислить определенные интегралы:

а)

б) dx

г)

д)

е)

ж)

з)

и)

к)

л)

м)

Вычислить площади криволинейных трапеций, ограниченных линиями:1

у=1-х², у=-х-1

7

у=2х-х², х+у=0

2

у=х²-3х+2, у=х-1

8

у=-х²+6х-5, у=-х-0,5

3

у=х²-1, у=2х+2

9

у=, у=х, х=7

4

у=-х²+2х+3, у=3-х

10

у=, у=-х²+4х-2

5

у=х²-4х, у=-(х-4)²

11

у=, у=-log₂х+1, у=0

6

у=х²+2х-3, у=-х²+2х+5

12

у=, у=х-3, у=-х+4

Домашнее задание

Вычислить площади криволинейных трапеций, ограниченных линиями: а) у=2х²-1, у=х² б) у=, у=х-2, у=-х+4

Практическое занятие №8

Тема: Арифметические действия с комплексными числами

Цель занятия: научиться применять арифметические действия с комплексными числами к преобразованию выражений

Задания для решения на занятии

Вычислить:

а)

в)

б)

г)

Вычислить квадратные корни: а) б)

Решить квадратные уравнения:

а) х² + (5 - 2i) x + 5(1- i) = 0

б) z² − (2 + 4 i)z − (7 − 4i) = 0

в) х² + (1 - 2i) х - 2i = 0

г) (2 +i) x² - (5 - i) x + 2 - 2i = 0

Решите уравнения относительно действительных переменных х и у:

а) 2 + 5xi - 3yi = 14i + 3х - 5у

б)

в) (4 + 3i)² х + (4 − 3i)² у = − 7 + 120 i

Преобразовать:

Домашнее задание

Вычислить: а)

Практическое занятие №9

Тема: Размещения, перестановки, сочетания. Бином Ньютона

Цель занятия: научиться вычислять количество комбинаций элементов множества в соответствии с заданными правилами.

Задания для решения на занятии

Вычислить: 1) - 2) 3) 4)

Упростить: 1) 2) (-)п!

Найти значения выражения: +

Решить уравнение:

4. =79

5. =156

6. =

7. =

Задачи: 1. Сколькими способами можно составить график очередности ухода в отпуск 8 сотрудников лаборатории?

2. Сколькими способами можно выбрать для подарка 3 предмета из 9 различных предметов?

3. Доказать, что число трехбуквенных слов, которые можно образовать из букв, составляющих слово «гипотенуза», равно числу всех возможных перестановок букв, составляющих слово «призма».

Представить в виде многочлена, используя формулу бинома Ньютона:

А) (3а-1)⁵ Б) (2+t)⁶

Домашнее задание

Найти значения выражения: (-)

Решить уравнение: =18

Решить задачу: Сколькими разными способами можно рассадить троих учащихся, пришедших на факультативные занятия, на сорока имеющихся в классе стульях?

Представить в виде многочлена, используя формулу бинома Ньютона:

(к+2)⁴

Практическое занятие №10

Тема: Вычисление вероятностей

Цель занятия: научиться вычислять вероятности, применяя классическое определение вероятности и вероятности сложных событий

Задания для решения на занятии

1. Определите, какие из следующих событий невозможные, какие-достоверные, какие-случайные:

А={футбольный матч «Спартак»-«Динамо» закончился вничью};

В={вы выиграете, участвуя в беспроигрышной лотерее};

С={в полночь выпадет снег, а через 2 часа будет светить солнце};

D={завтра будет контрольная по математике};

E={30 февраля будет дождь};

F={вас изберут президентом США};

G={вас изберут президентом России}.

2. Вы купили в магазине телевизор, на который фирма-производитель дает 2 года гарантии. Какие из следующих событий невозможные, какие-достоверные, какие-случайные:

А={телевизор не сломается в течение года};

В={телевизор не сломается в течение двух лет};

С={в течение двух лет вам не придется платить за ремонт телевизора};

D={телевизор сломается на третий год}?

3. В коробке лежит 10 красных, 1 зеленая и 2 синие ручки. Из коробки наугад вынимают 2 предмета. Какие из следующих событий невозможные, какие-достоверные, какие-случайные:

А={ вынуты 2 красные ручки };

В={ вынуты 2 зеленые ручки };

С={ вынуты 2 синие ручки };

D={ вынуты ручки двух разных цветов };

E={вынуты 2 ручки };

F={ вынуты 2 карандаша }?

4. Три господина, придя в ресторан, сдали в гардероб свои шляпы. Расходились по домам они уже в темноте и разобрали шляпы наугад. Какие из следующих событий невозможные, какие-достоверные, какие-случайные:

А={ каждый надел свою шляпу };

В={ все надели чужие шляпы };

С={ двое надели чужие шляпы, а один-свою };

D={ двое надели свои шляпы, а один-чужую }?

5. В игре «Любовь с первого взгляда» участвуют трое юношей и три девушки. Каждый юноша выбирает одну девушку, а каждая девушка-одного из юношей.Если юноша и девушка выбирают друг друга, то образуется пара. Какие из следующих событий невозможные, какие-достоверные, какие-случайные:

А={ не образовалось ни одной пары };

В={ образовалась одна пара};

С={ образовалось 2 пары };

D={ образовалось 3 пары }?

6. Винни-Пух, Пятачок и все-все-все садятся за круглый стол праздновать день рождения. При каком количестве всех-всех-всех событие А={ Винни-Пух и Пятачок будут сидеть рядом } является достоверным, а при каком-случайным?

7. В школе учится N учеников. При каких значениях N событие А={ в школе есть ученики с совпадающими днями рождениями } является достоверным, а при каком-случайным?

8. Среди 100 билетов школьной благотворительной лотереи 20 выигрышных. Сколько билетов вам надо купить, чтобы событие А={ вы ничего не выиграете } было невозможным?

9. В шкафу 10 пар ботинок с 36-го по 45-й размер - по одной паре каждого. Ботинки достают из шкафа наугад. Какое наименьшее количество ботинок надо вынуть из шкафа, чтобы событие А={ из вынутых ботинок можно составить хотя бы одну пару} было достоверным?

10. В классе учится 10 мальчиков и 20 девочек. Какие из следующих событий являются для такого класса невозможным, какие-достоверные, какие-случайные:

А={в классе есть 2 человека, родившихся в разные месяцы};

В={ в классе есть 2 человека, родившихся в одном месяце };

С={ в классе есть 2 мальчика, родившихся в одном месяце };

D={ в классе есть 2 девочки, родившихся в одном месяце };

E={все мальчики родились в разные месяцы};

F={все девочки родились в разные месяцы };

G={есть мальчик и девочка, родившиеся в одном месяце};

Н={есть мальчик и девочка, родившиеся в разные месяцы}?

11. Автобусу, в котором едет 15 пассажиров, предстоит сделать 10 остановок. Какие из следующих событий невозможные, какие-достоверные, какие-случайные:

А={ все пассажиры выйдут из автобуса на разных остановках };

В={ все пассажиры выйдут на одной остановке};

С={ на каждой остановке хоть кто-то выйдет };

D={ найдется остановка, на которой никто не выйдет };

E={ на всех остановках выйдет четное число пассажиров };

F={ на всех остановках выйдет нечетное число пассажиров}?

12а. В коробке 3 красных, 3 желтых, 3 зеленых шара. Вытаскиваем наугад N шаров. Рассмотрим событие А={ среди вынутых шаров окажутся шары ровно трех цветов }. Для каждого N от 1 до 9 определите, какое это событие- невозможное, достоверное или случайное.

12б. В коробке снова 3 красных, 3 желтых, 3 зеленых шара. Вытаскиваем наугад 4 шара. Рассмотрим событие В={среди вынутых шаров окажутся шары ровно М цветов }. Для каждого М от 1 до 4 определите, какое это событие- невозможное, достоверное или случайное.

Решить задачи:

1. Игральный кубик подбросили 1 раз. Какова вероятность появления шестерки?

2. В урне 3 белых и 7 черных шаров. Случайным образом вынули 1 шар. Какова вероятность того, что он белый?

3. Бросили один раз 2 игральных кубика. Какова вероятность того, что на обеих гранях в сумме выпадет 7 очков?

4. Бросили один раз 2 игральных кубика. Какова вероятность того, что произведение выпавших очков делится на 3?

5. Какова вероятность того, что наудачу выбранное число от 40 до 70 является кратным 6?

6. Набирая номер телефона, абонент забыл последние 2 цифры и, помня, что эти цифры различны, набрал их наудачу. Какова вероятность того, что набраны нужные цифры?

7. Из колоды в 36 карт наугад вынимают одну карту. Какова вероятность того, что это будет карта бубновой масти?

8. Из букв слова «Вероятность» наугад выбирается одна буква. Какова вероятность того, что выбранная буква будет: а) гласной; б) согласной; в) буква «О»?

9. Все натуральные числа от 1 до 30 написаны на одинаковых карточках и положены в урну. После тщательного перемешивания карточек из урны извлекается одна карточка. Какова вероятность, что число на взятой карточке окажется кратным 5?

10. В урне 6 белых и 4 черных шара. Из урны вынимают шар и откладывают в сторону. Этот шар оказался белым. После этого из урны вынимают еще один шар. Найти вероятность того, что этот шар тоже будет белым.

11. В первом ящике находятся шары с номерами от 1 до 5, а во втором - с номерами от 6 до 10. Из каждого ящика вынули по одному шару. Найти вероятность следующих событий: а) сумма номеров вынутых шаров меньше 7; б) сумма номеров вынутых шаров равна 11; в) сумма номеров вынутых шаров не больше 11.

12. Бросают два одинаковых игральных кубика. Какова вероятность того, что модуль разности выпавших очков равен 2?

13. Произвольным образом выбирается двузначное число. Какова вероятность того, что это число окажется: а) кратным 3; б)кратным 6; в) кратным 50?

14. Студенту предложили написать на доске любое натуральное число от 100 до 200. Найти вероятность того, что: а) это число нечетное; б)среди цифр этого числа есть 3; в)это число не является кубом целого числа; г) сумма его цифр больше 3.

15. Куб, все грани которого окрашены, распилен на 1000 кубиков одинакового размера, которые затем тщательно перемешаны. Найти вероятность того, что наудачу извлеченный кубик имеет: а) одну окрашенную грань; б) две окрашенные грани; в) три окрашенные грани.

Домашнее задание

1. Имеется корзина с 10 черными и 12 белыми шарами. Найдите вероятность вытаскивания с закрытыми глазами черного шара.

2. Представьте, что вы стоите на 4 этаже 9-этажного дома. Вам необходимо спуститься вниз. Известно, что лифт начал своё движение вверх с 1 этажа. Какова вероятность того. Что лифт приедет именно на 4 этаж?

3. Какова вероятность того, что Андрей из мешка с бочонками для лото вытащит бочонок с четной цифрой, если в лото участвуют бочонки от 1 до 99?

4. Допустим, что вы забыли последнюю цифру номера телефона друга и набрали ее наугад. Какова вероятность того, что вы набрали ее верно?

5. Возьмем всем известный кубик с шестью гранями с нанесенными на него цифрами от 1 до 6.

а) Какова вероятность того, что при подбрасываний выпадет цифра 3?

б) …выпадет четная цифра? в) …число, кратное трем? г) …число 0?

Практическое занятие №11

Тема: Множества, их виды. Операции над множествами. Графическое представление множеств.

Цель занятия: Научиться определять виды множеств, выполнять операции над ними.

Задания для решения на занятии

1. М-множество четырехугольников. Принадлежит ли этому множеству:

1) ромб; 2) трапеция; 3) окружность; 4) прямоугольник;

5) диагональ квадрата; 6)призма?

2. Указать, какие из данных множеств являются конечными, бесконечными, пустыми:

а)М-множество действительных корней квадратного уравнения х²+1=0;

б)К множество всех четных чисел;

в) В-множество всех студентов КТК;

г) С-множество прямоугольных треугольников, у которых сумма

квадратов катетов не равна квадрату гипотенузы?

д) Т-множество целых корней уравнения х²-9=0.

3. Задать характеристическим свойством множество:

1) всех параллелограммов;

2)всех квадратов;

3)всех прямоугольников;

4)всех ромбов;

5)всех равнобедренных треугольников;

6)всех прямоугольных треугольников.

4. Дано множество К={21;54;153;171;234}. Составить подмножество Р из чисел, которые: 1) делятся на 7; 2) делятся на 9; 3) не делятся на 5.

5. Доказать, что А=В, если

а)А-множество букв слова «Весна», В-множество букв слова «Навес».

б)А-множество корней уравнения 4х-8=16, В-множество корней уравнения 5^х-3=125.

6. Известно, что С I, DI, CD=. Отметить области, изображающие множества: , , CD, , С, C, .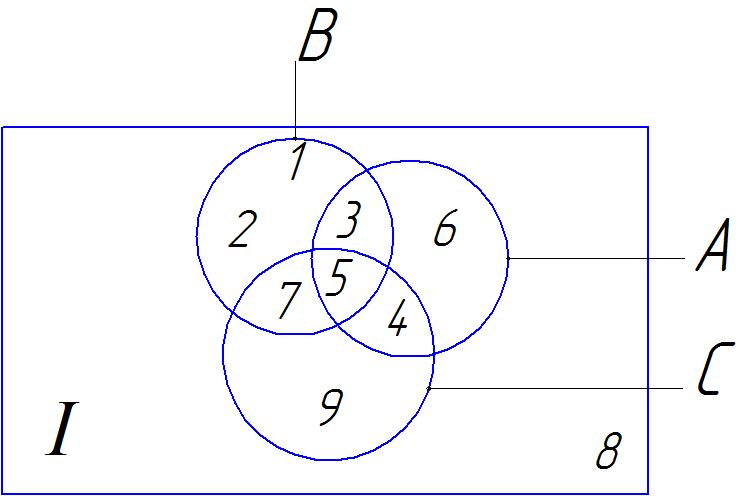

7. На рисунке приведена диаграмма Эйлера-Венна для трех множеств. Найти элементы множеств: : , , ,, , В\С, С\А, А\В\С.

8. А={ё;к;л;м;н}, В={к;о;з;ё;л}, С={б;ы;ч;о;к}, I={ ё;к;л;м;н;о;з;б;ы;ч;а;в;г}. Найти и изобразить кругами Эйлера:

а) в)) д) D=U\(

б) г) е) D=U\(

9. Доказать, используя круги Эйлера: а)=А

б)=А

10.Даны отрезки А=[-4;5], В=(2;6], С=(5;10].Найти множества и изобразить их кругами Эйлера:

а) в) д) (С\();

б) г) е) (

13. В группе имеется 22 студента; 10 из них умеют играть в шахматы, 8 - в шашки; и в шахматы, и в шашки играют 3 студента. Сколько студентов не умеет играть ни в шахматы, ни в шашки?

2. В одной известной спортивной семье семеро детей увлекались легкой атлетикой, шестеро - лыжными гонками, пятеро - велоспортом. Четверо занимались легкой атлетикой и лыжами, трое - легкой атлетикой и велоспортом, двое - лыжными гонками и велоспортом, а один увлекался легкой атлетикой, лыжами и велоспортом.

Сколько детей было в семье?

Сколько из них увлекалось только одним видом спорта?

3. Среди 150 школьников марки собирают только мальчики. Марки СССР собирают 67 человек, марки Африки - 48, марки Америки - 34, только марки СССР - 11, только Африки - 7, только Америки - 2. Лишь один школьник собирает марки СССР, Америки и Африки.

Сколько девочек среди 150 школьников?

Домашнее задание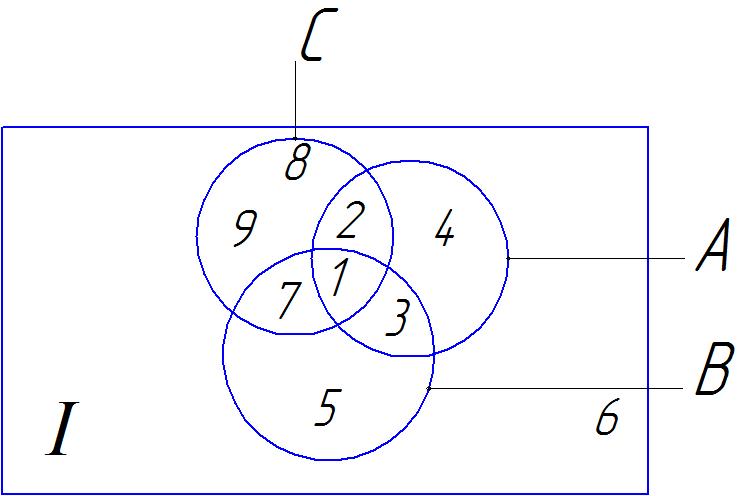

1. На рисунке приведена диаграмма Эйлера-Венна для трех множеств. Найдите элементы множеств: , , ,, , В\С,

2. В спортивной делегации 100 человек. Среди них 70 человек владеют английским языком, а 27 - французским. Сколько человек владеет обоими этими языками, если известно, что 15 человек не знают ни английского, ни французского?

Практическое занятие № 12

Тема: Решение дифференциальных уравнений

Цель занятия: научиться определять вид дифференциального уравнения, решать дифференциального уравнения 1-го порядка.

Задачи для решения на занятии

1. Найти общие решения дифференциальных уравнений с разделяющимися переменными.1.

   2.

   3.

   4.

   5.

   6.

   7.

   8.

2. Найти частные решения дифференциальных уравнений.

10. , если у=1 при х=2.

11. , если у=0,5 при

III. Найти общее решение однородных дифференциальных уравнений.

12. ; 13. ; 14.

IV. Найти общее решение линейных дифференциальных уравнений15.

16.

17.

18.

19.

20.

21.

22.

V. Найти частные решения уравнений, удовлетворяющие указанным начальным условиям:23. , если у=0 при х=0

24. , если у=1 при х=0

25. , при у=0

26. , если у=0,5 при х=1

Домашнее задание

Решите уравнения1.

4.

2.

5.

3.

6.

Практическое занятие № 13

Тема: Графы

Цель занятия: научиться определять вид графа, решать дифференциального решать элементарные задачи на применение графов.

Задачи для решения на занятии

1. Определить вид графа:

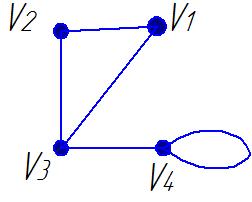
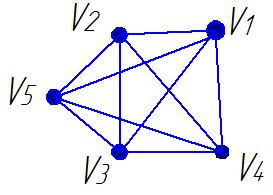
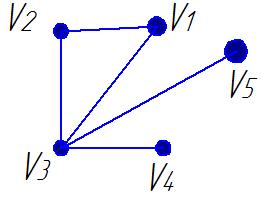
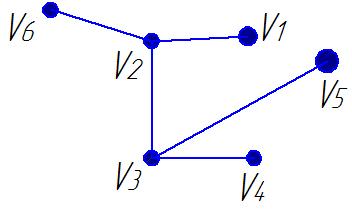
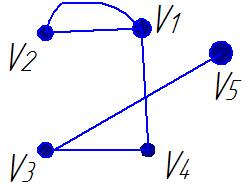
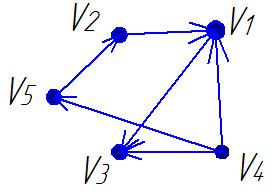
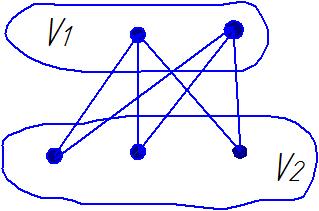
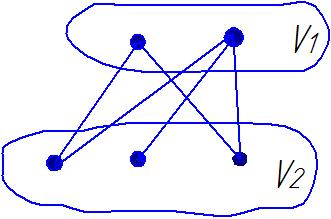
2

А) Составить матрицу смежности для графа.

б) Выписать вершины, смежные с вершиной 1. в) Указать четные вершины графа.

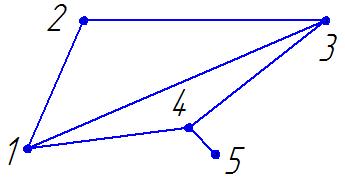
3

а)Составить матрицу инцидентности для графа.

б) Список ребер.

в) Указать ребра, инцидентные вершине 2. г)Определить степень вершины 3.

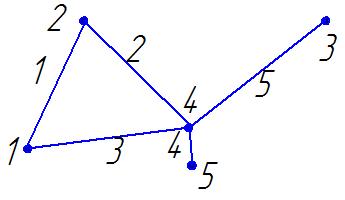
4

Нарисовать остовы графа:

5

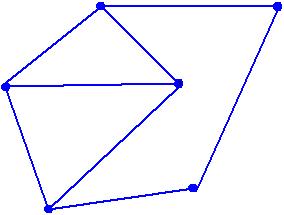
Найти:

а)объединение графов,

б)пересечение,

в)кольцевую сумму,

г)граф, который получится при удалении вершины 1 из графа G,

д)граф, который получится при удалении ребра 4 из графа G.

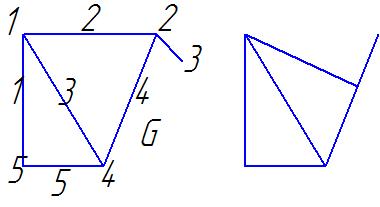
Домашнее задание

А) Составить матрицу смежности для графа.

б) Выписать вершины, смежные с вершиной 1.

в) Указать четные вершины графа

г) Составить матрицу инцидентности для графа.

д) Список ребер.

е) Указать ребра, инцидентные вершине 2.

ж) Определить степень вершины 3.

Список литературы

1. Баврин И. Высшая математика. - М.: Академия, 2009г.

2. Гурман В.Е. Руководство к решению задач по теории вероятностей - М.: Высшая школа, 2011 г.

3. Данко П.В. и др. Высшая математика в упражнениях и задачах. Часть 1 и 2.-М.: Высшая школа, 2010 г.

4. Пехлецкий И.Д. Математика.- М.Академия,2010 г

5. Соловейчик И.Л., Лисичкин В.Т. Сборник задач по математике для техникумов. М. ОНИКС 21 век, Мир и образование, 2008 г

Интернет ресурсы

1. Видеоуроки по математике. Алгебра 10-11кл. [Электронный ресурс]. / Режим доступа: mirurokov.ru/videouroki-po-matematike-algebra-10-11-klass.html . Дата обращения: 01.10.2013.

2.Примеры уроков. Российский общеобразовательный портал. [Электронный ресурс]. / Режим доступа:edu.of.ru/profil/default.asp?ob_no=16819</<font color="#000000"> . Дата обращения: 07.10.2013.

3.Фестиваль педагогических идей «Открытый урок». [Электронный ресурс]. / Режим доступа:festival.1september.ru/articles/subjects/1?page=76. Дата обращения: 07.12.2012.