- Учителю
- конспект урока по теме «Методы решения уравнений' (11 класс)
конспект урока по теме «Методы решения уравнений' (11 класс)
Разработчик: Рабцун Лидия Васильевна, учитель математики
Урок повторения в XI классе по теме «Методы решения уравнений»
Разработка урока
-
Предмет: алгебра
-
Класс: 10
-
Тема: Методы решения уравнений
-
Тип урока: урок обобщения и систематизации знаний по теме «Методы решения уравнений»
-
Цель урока: закрепление основных приёмов и методов решения уравнений.
-
Задачи:
-
Образовательная:
-
1. Проверить и обобщить знания и умения учащихся по теме «Методы решения уравнений»
-
2. Проверить умение выполнять арифметические действия с целыми и дробными числами, проверить умение выполнять преобразование тригонометрических выражений, выражений, содержащих модуль и корни.
-
Развивающая:
1. Развивать логическое мышление. -
2. Активизировать мыслительную деятельность, познавательную активность.
-
3.Формировать навыки самоконтроля, адекватной самооценки и саморегуляции собственной деятельности.
-
Воспитательная:
1. Воспитывать аккуратность, трудолюбие. -
2. Развивать общую культуру личности.
-
3. Способствовать толерантному воспитанию учащихся.
-
Формы организации учебной деятельности: индивидуальная, фронтальная, парная.
-
Средства: компьютер, интерактивная доска, набор индивидуальных карточек, презентация к уроку, наглядные пособия,
Ход урока:
-
Организационный момент.
Сегодня мы поговорим об общих целях, общих методах, которые пронизывают всю школьную линию уравнений с VII по XI класс. При решении уравнений эти методы нужно постоянно держать в поле своего внимания (вопрос о проверке корней следует рассмотреть отдельно, на других уроках).
Мы рассмотрим два метода: метод разложения на множители и метод введения новых переменных.
Метод разложения на множители
Суть этого метода заключается в следующем: пусть надо решить уравнение ![]() и пусть
и пусть ![]()
![]()
Тогда уравнение ![]() можно заменить совокупностью более простых уравнений:
можно заменить совокупностью более простых уравнений:![]()
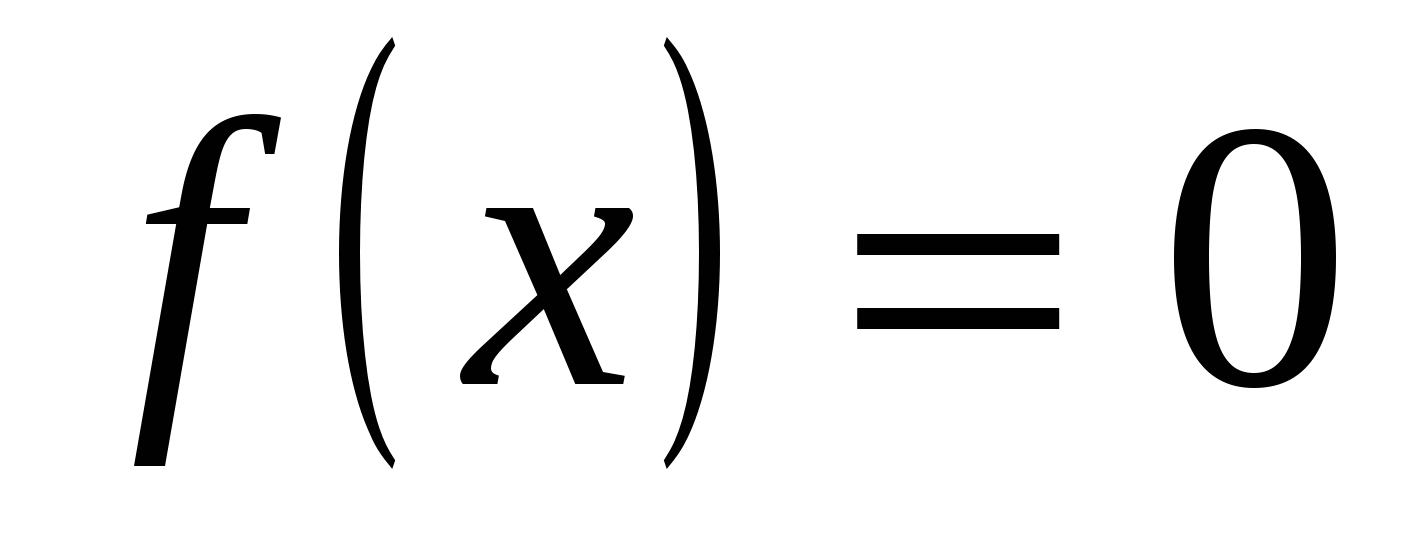
Найдя корни уравнений этой совокупности и отобрав из них те корни, которые принадлежат области определения уравнения ![]() , мы получим корни исходного уравнения.
, мы получим корни исходного уравнения.
-
Актуализация знаний учащихся
Решить уравнение:
1. ![]()
Решение.
![]()
![]()
![]() или
или ![]()
![]()
![]()
Ответ: -3; ![]() ;
; ![]()
2. ![]()
Решение:
![]()
![]() или
или ![]()
D=25
![]()
Ответ: -1; ![]() ;
; ![]() .
.
3. ![]()
Решение:
![]()
![]()
![]()
![]() или
или ![]()
![]()
![]()
![]()
![]()
Ответ: ![]() ;
; ![]() ; 1; 3.
; 1; 3.
4. ![]()
Решение:
![]()
![]() или
или ![]()
![]()
![]()
![]()
![]()
а) ![]() б)
б) ![]()
![]()
![]()
Ответ: -2; ![]() ; 0;
; 0; ![]() ; 2.
; 2.
5. ![]() О.Д.З.
О.Д.З. ![]()
Решение:
![]() или
или ![]() или
или ![]()
![]()
![]()
![]()
Ответ: 0; 1; 7.
6. ![]()
Решение:
![]()
![]()
![]()
![]() или
или ![]()
![]()
![]()
Ответ: -3; 1; 2.
7. ![]()
Решение:
Прибавим и отнимем ![]() . Число 63 представим как 63=64-1.
. Число 63 представим как 63=64-1.
![]()
![]()
![]()
![]()
![]()
![]() или
или ![]()
D<0. D<0
Ответ: нет действительных корней.
8. ![]()
Решение:
![]()
![]()
![]()
![]()
![]() или
или ![]()
D=121, ![]()
9. ![]()
Решение:
![]() - корень уравнения
- корень уравнения ![]() :
: ![]()
![]()
![]() или
или ![]()
![]()
![]()
Ответ: ![]() .
.
10. ![]()
Решение:
![]()
![]()
![]()
![]()
![]()
![]() или
или ![]()
![]()
![]()
![]() или
или ![]()
![]()
![]()
![]()
![]()
![]()
Ответ: ![]()
![]() .
.
11. ![]()
Решение:
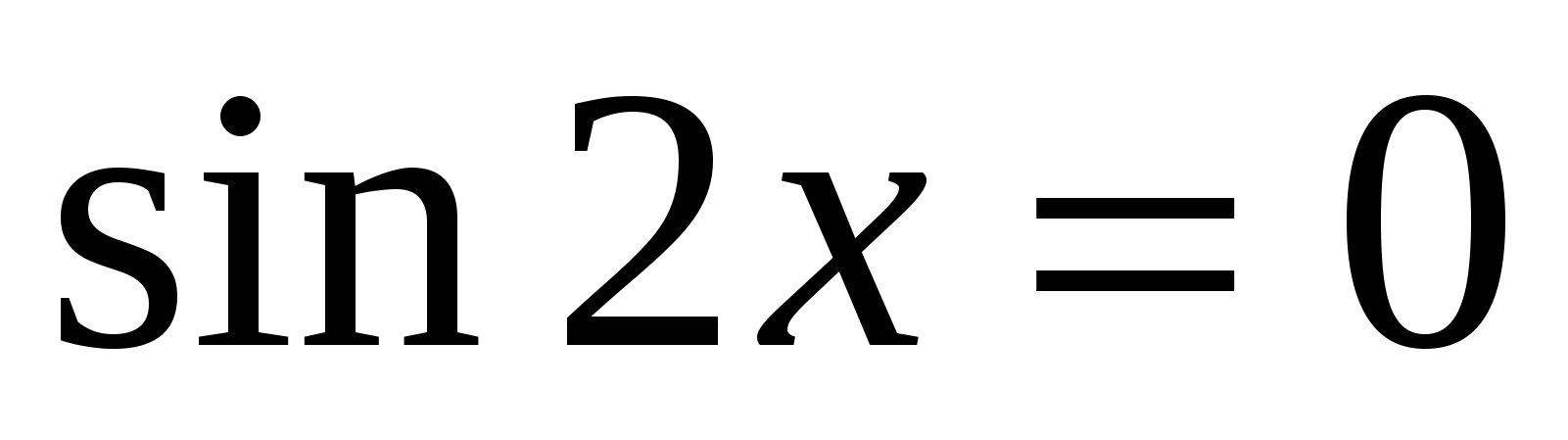
![]()
![]()
![]()
![]() или
или ![]()
![]()
![]()
![]()
![]()
Ответ: ![]()
12. ![]()
![]()
Решение:
![]()
![]()
![]() или
или ![]()
![]()
![]()
![]()
![]()
Ответ: -4 и 4.
13. Решить систему уравнений 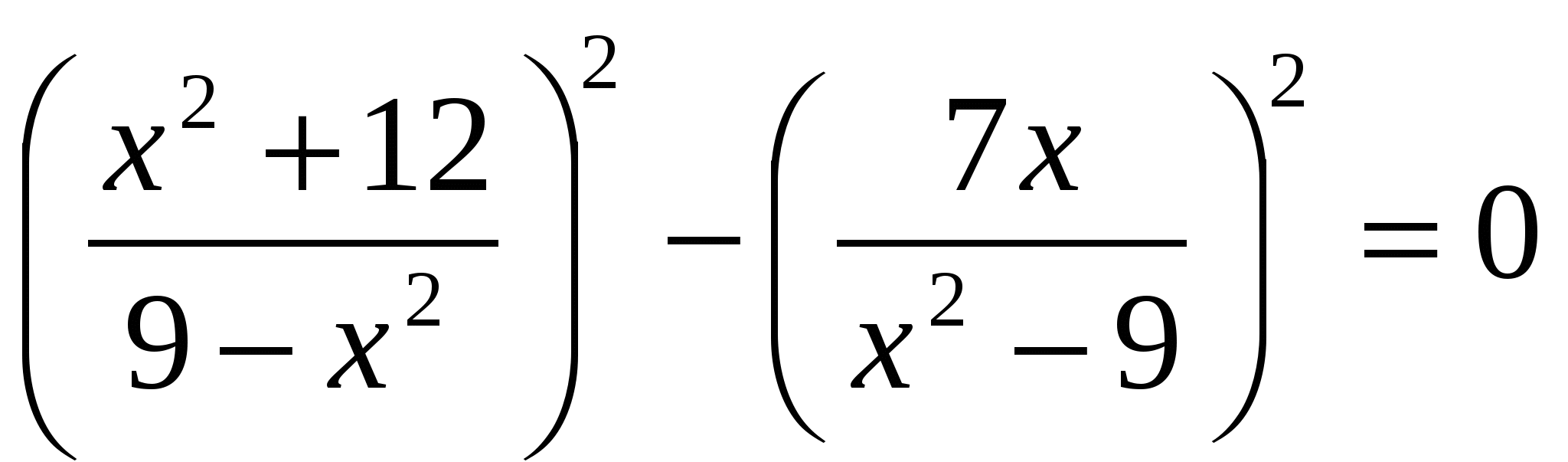
Решение:
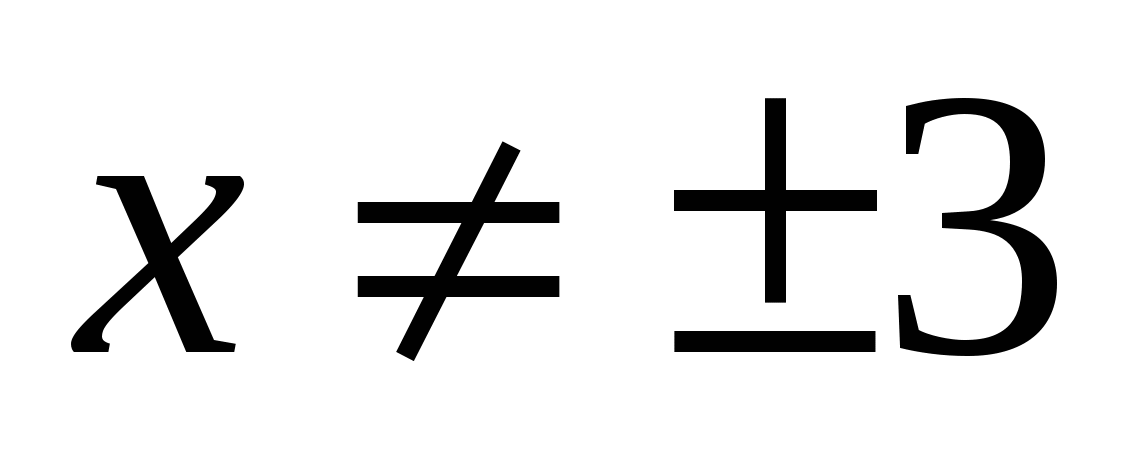
Пусть ![]() и учитывая, что
и учитывая, что
![]() запишем исходную систему иначе:
запишем исходную систему иначе:
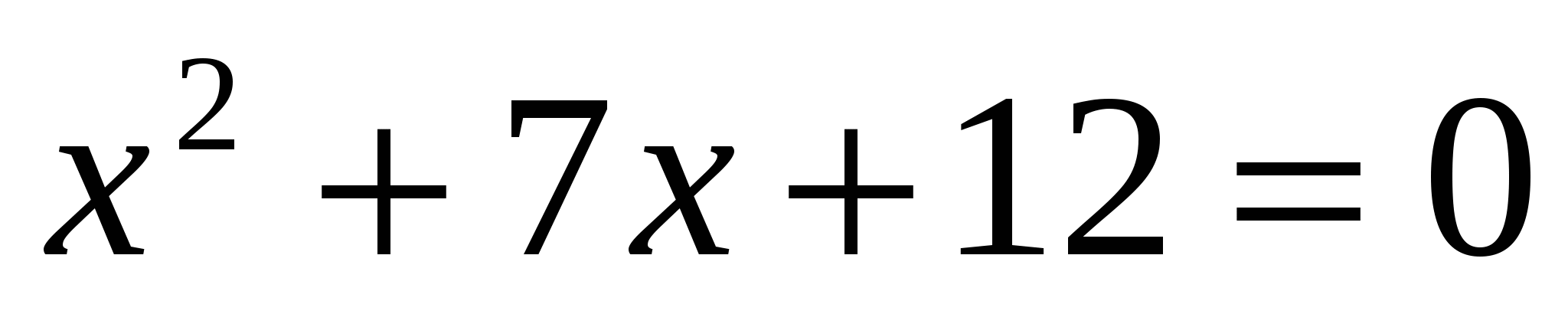
Отсюда ![]() и тогда
и тогда ![]()
Таким образом, исходная система равносильна системе 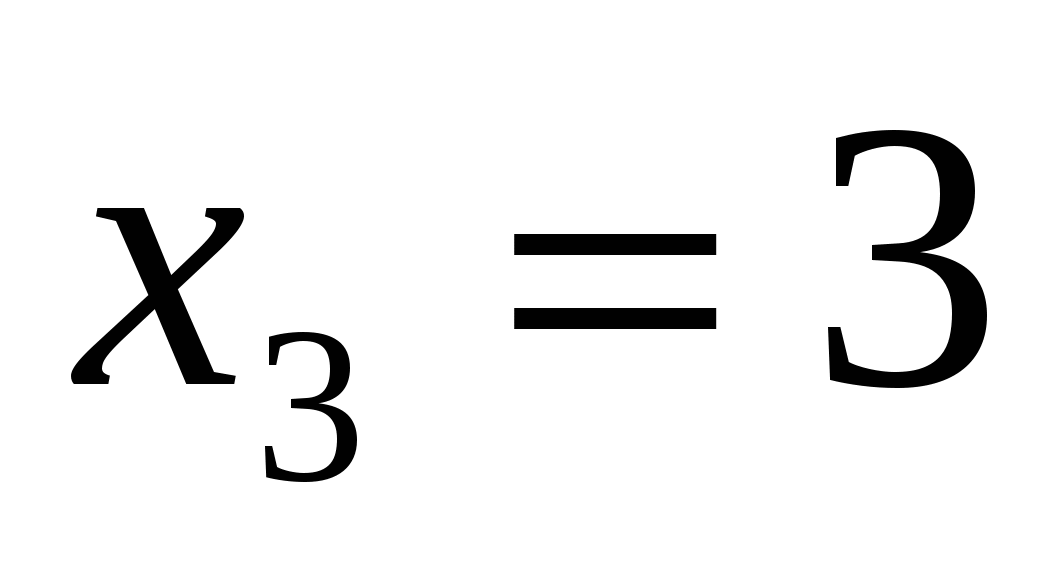
Эта система распадается на две:
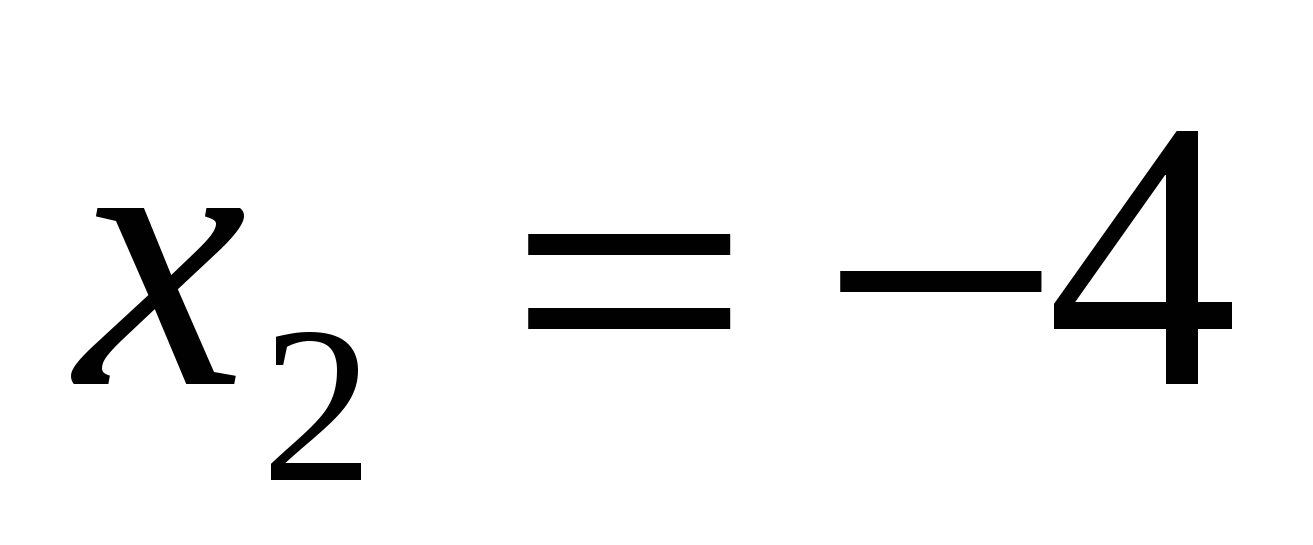 и
и 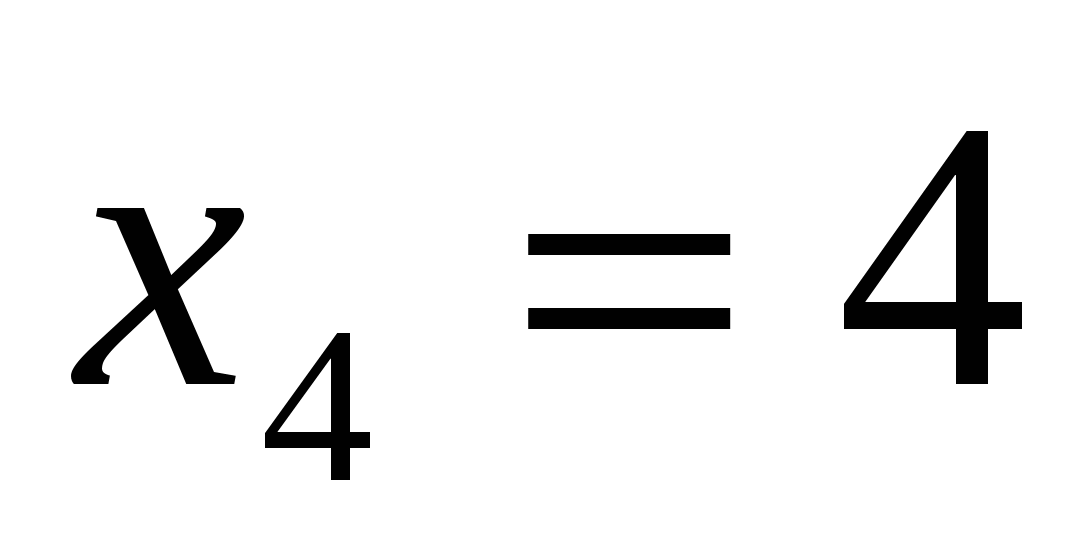
Ответ: (4;3); (3;4).
Метод введения новых переменных
Суть метода очень проста: если уравнение ![]() удалось преобразовать к виду
удалось преобразовать к виду ![]() , то нужно ввести новую переменную
, то нужно ввести новую переменную ![]() , решить уравнение
, решить уравнение ![]() , а затем рассмотреть совокупность уравнений:
, а затем рассмотреть совокупность уравнений:
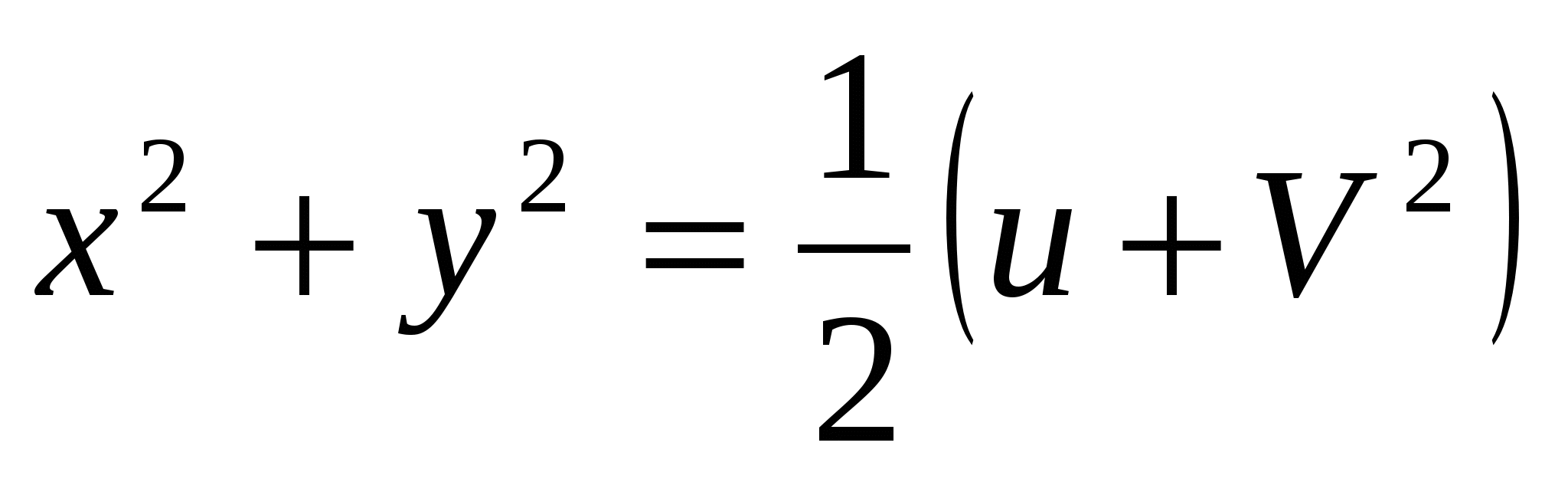 , где
, где ![]() - корни уравнения
- корни уравнения ![]()
Умение удачно ввести новую переменную - важный элемент математической культуры. Новая переменная в уравнениях иногда действительно очевидна, но иногда ее трудно увидеть, а можно выявить лишь в процессе каких-либо преобразований.
Бывает полезно так же ввести не одну, а две переменные.
Решить уравнение:
1. ![]()
Решение:
![]() при
при ![]()
Ответ: нет корней.
2. ![]()
Решение:
![]()
![]()
![]()
1) ![]() 2)
2) ![]()
![]()
![]()
Ответ: -4;-1;1;4.
3. ![]()
Решение::
Пусть ![]() , тогда уравнение примет вид:
, тогда уравнение примет вид:
![]()
![]()
4. ![]()
Решение:
![]()
![]()
Пусть ![]()
![]()
D=9, ![]() - посторонний корень
- посторонний корень
1) ![]() ,
,
![]()
Ответ: ![]()
5. ![]()
Решение:
Пусть ![]() , тогда уравнение примет вид:
, тогда уравнение примет вид: ![]()
![]()
![]()
![]()
![]()
![]() -9 - посторонний корень
-9 - посторонний корень
1) ![]()
![]()
![]()
Ответ: -1 и 2.
Рассмотрим несколько уравнений, где применение метода введения новых переменных не так очевидна.
6. ![]()
Решение:
Данное уравнение - симметричное, оно является уравнением четвертой степени. Разделим обе части уравнения на ![]() . Получим
. Получим
![]()
![]()
![]()
Пусть ![]() , тогда уравнение примет вид:
, тогда уравнение примет вид:
![]()
![]()
1) ![]()
![]() 2)
2) ![]()
![]()
![]()
D=5 D<0
![]()
Ответ: ![]()
7. ![]()
Решение:
Пусть ![]()
Уравнение примет вид: ![]()
Значит, ![]()
![]()
![]()
![]()
Ответ: ![]()
8. ![]()
![]()
![]()
Пусть ![]() , тогда уравнение примет вид:
, тогда уравнение примет вид:
![]()
![]()
1) ![]() 2)
2) ![]()
![]()
![]()
D<0 ![]()
![]() или
или ![]()
Ответ: -5;0
9. ![]()
Решение:
![]() :
: ![]()
![]()
![]()
Пусть ![]() , тогда уравнение примет вид:
, тогда уравнение примет вид:
![]()
![]()
![]()
1) ![]() 2)
2) ![]()
![]()
![]()
![]()
![]()
Ответ: ![]()
10. ![]()
Решение:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() - посторонний корень
- посторонний корень
![]()
1) ![]()
![]()
![]() или
или ![]()
![]()
![]()
Ответ: 6; 8.
11. Решить уравнение
![]() :
: ![]()
![]()
![]()
Пусть ![]() , тогда уравнение примет вид:
, тогда уравнение примет вид:
![]()
![]()
![]() 1)
1) ![]() . 2)
. 2) ![]()
![]()
![]()
D=9
![]()
![]()
Ответ: 0,5; 2.
12. ![]()
![]()
![]()
Решение:
![]()
![]()
![]()
Пусть ![]() , тогда уравнение примет вид:
, тогда уравнение примет вид:
![]()
![]()
![]()
1) ![]()
![]()
D=76
![]()
2) ![]()
![]()
D=400-720<0
Ответ: ![]()
13. ![]()
Решение:
Пусть ![]()
![]() , тогда уравнение примет вид:
, тогда уравнение примет вид:
![]()
![]() (разложим на множители)
(разложим на множители)
![]()
![]()
![]()
![]()
![]() или
или ![]()
1) ![]() 2)
2) ![]()
![]()
![]()
![]()
![]()
D=1 ![]()
![]()
![]()
![]()
![]()
Ответ: -1; 0,5; 2; 4.
Можно решить иначе: разделить обе части уравнения на ![]()
Получим: ![]()
Пусть ![]() , тогда уравнение примет вид:
, тогда уравнение примет вид:
![]()
![]()
![]() и т.д. (дальнейшее очевидно)
и т.д. (дальнейшее очевидно)
14. ![]()
![]()
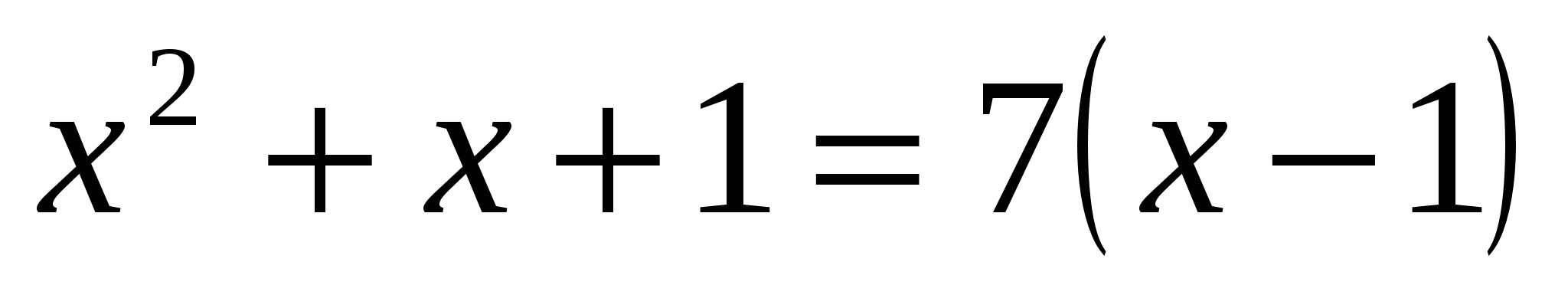
![]()
Решение:
Заметим, что ![]()
Пусть ![]()
![]()
Тогда ![]()
![]() и
и
![]()
![]() , но
, но ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
, ![]()
![]()
![]()
![]()
![]()
![]()
Уравнение не имеет корней
![]()
![]()
![]()
![]()
![]()
![]()
![]()
D/4=![]()
![]()
Ответ: 3; 143.
15. ![]()
Решение:
![]() . Тогда уравнение примет вид:
. Тогда уравнение примет вид:
![]()
![]()
![]()
![]()
![]()
Итак, исходное равенство будет верным, если выполняется система
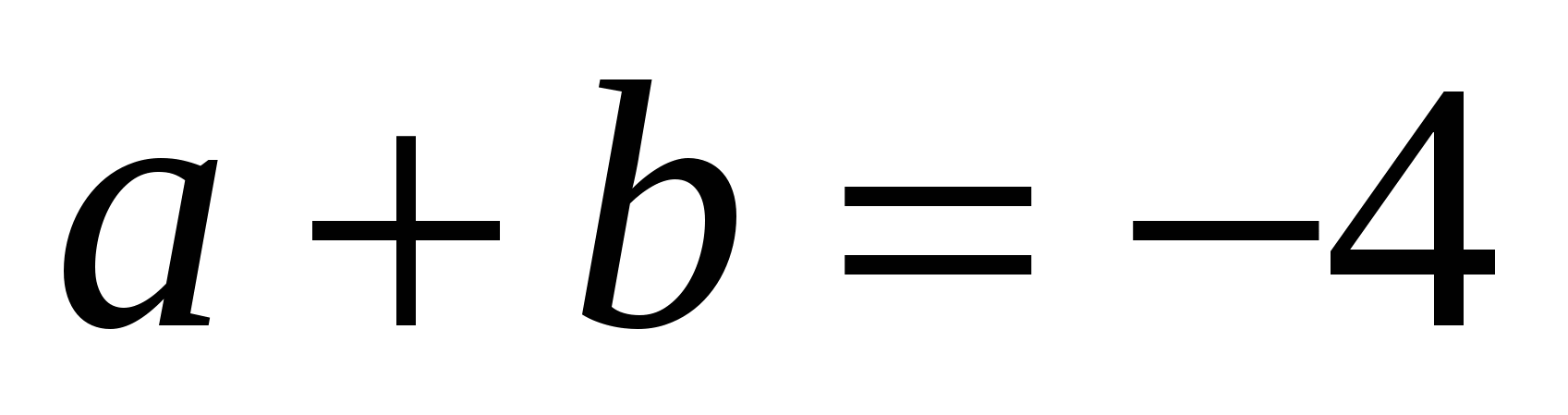
![]()
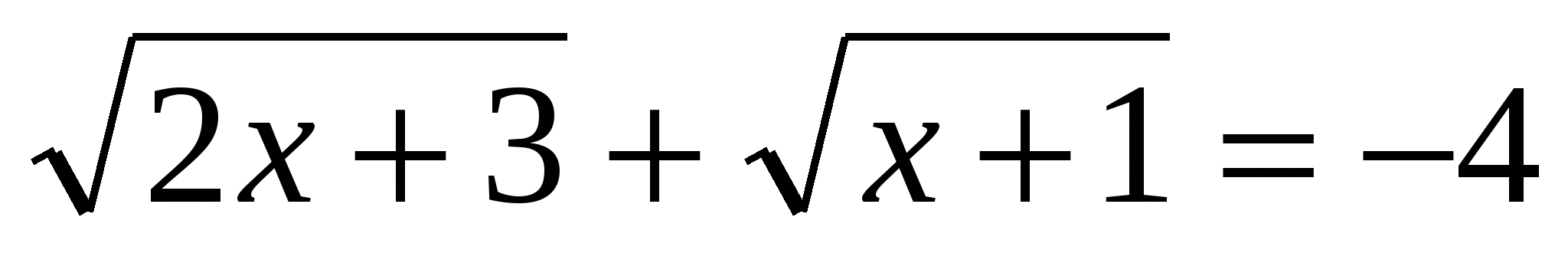
1) ![]()
2) ![]()
![]()
![]()
D=4
![]()
Если ![]() , то
, то ![]()
Если ![]() , то
, то ![]()
1) ![]() ;
; ![]()
2) ![]() и
и ![]()
Ответ: 2; 28.
Решение иррациональных уравнений также можно упростить с помощью удачно выбранной тригонометрической подстановки, т.е. переменные уравнения заменяются на значения каких-либо тригонометрических функций.
16. ![]()
Решение:
Пусть ![]() . Замена возможна, т.к.
. Замена возможна, т.к. ![]() . Тогда
. Тогда ![]()
![]()
![]()
![]()
Значит, ![]()
![]()
![]()
![]()
1) ![]() 2)
2) ![]()
![]()
![]()
![]()
![]()
![]()
Тогда корни: ![]()
Откуда имеем: 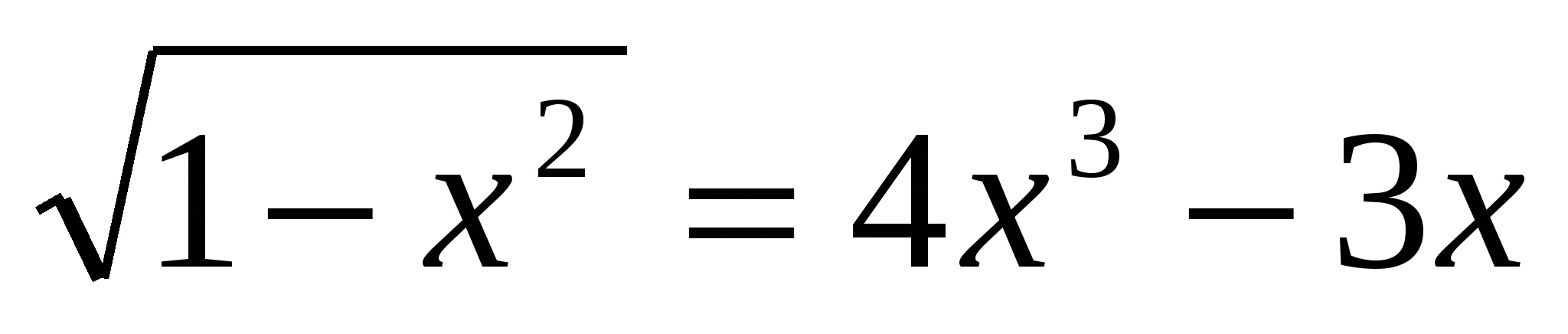
![]()
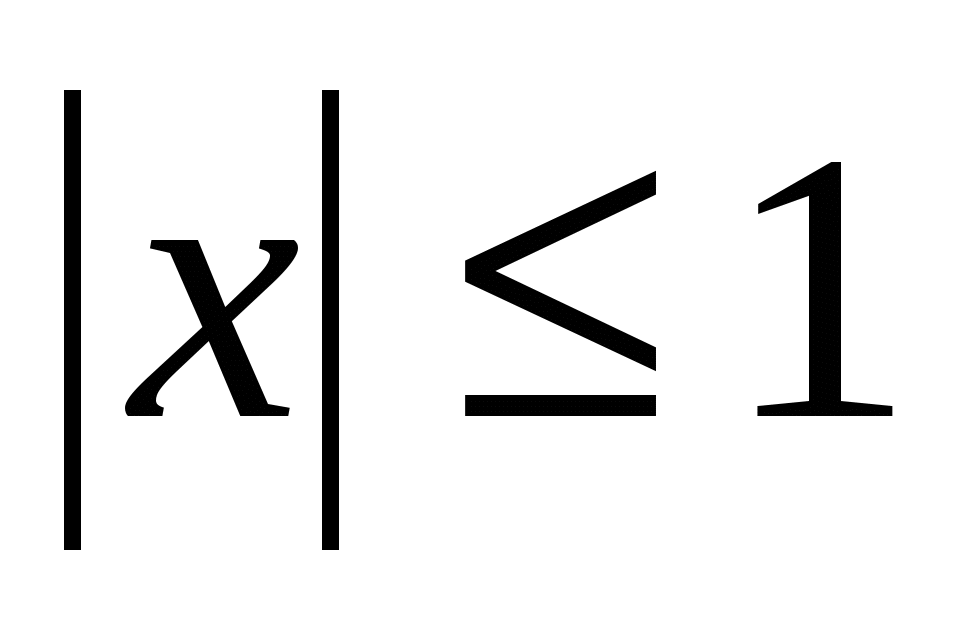
Ответ: ![]()
17. 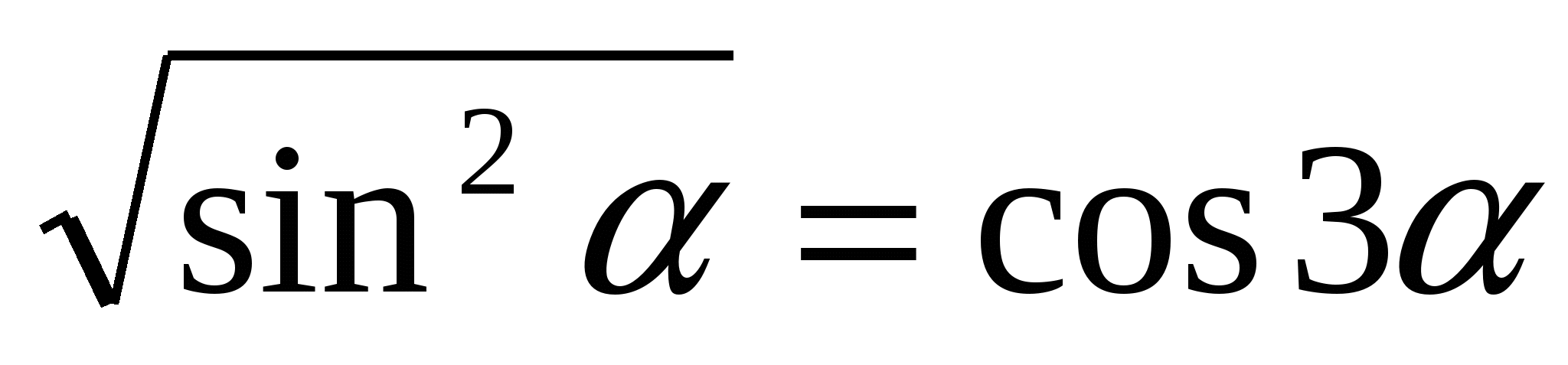 (1)
(1)
Решение:
Полагая ![]() , преобразуем систему (1) к виду
, преобразуем систему (1) к виду
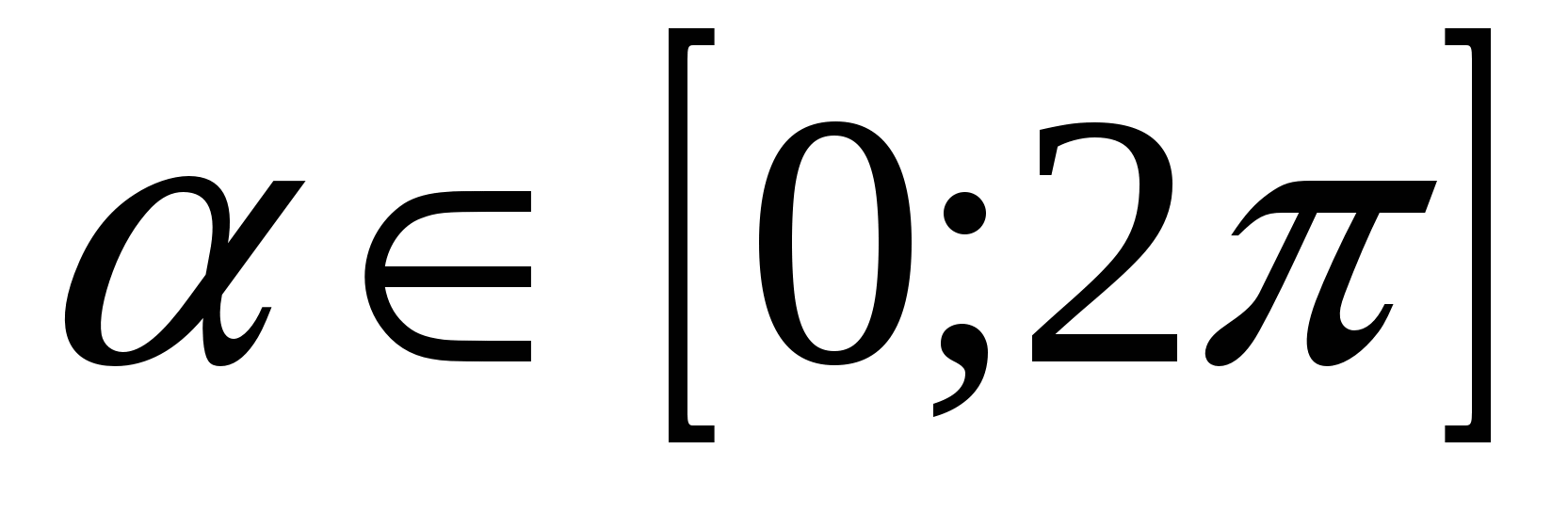 (2)
(2)
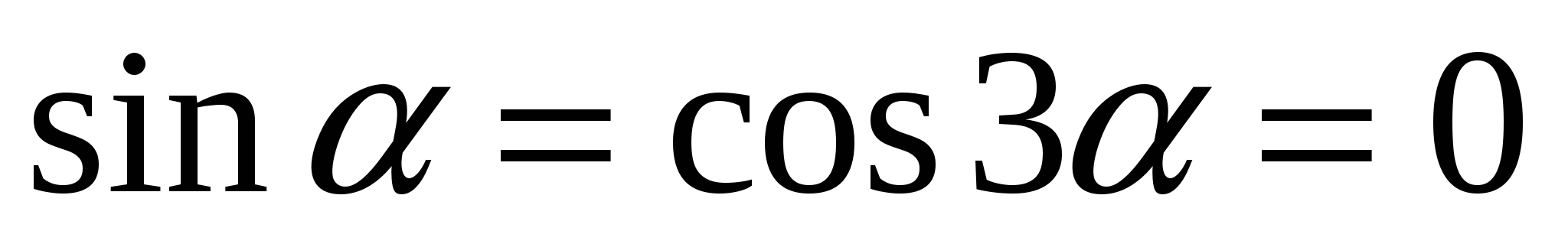
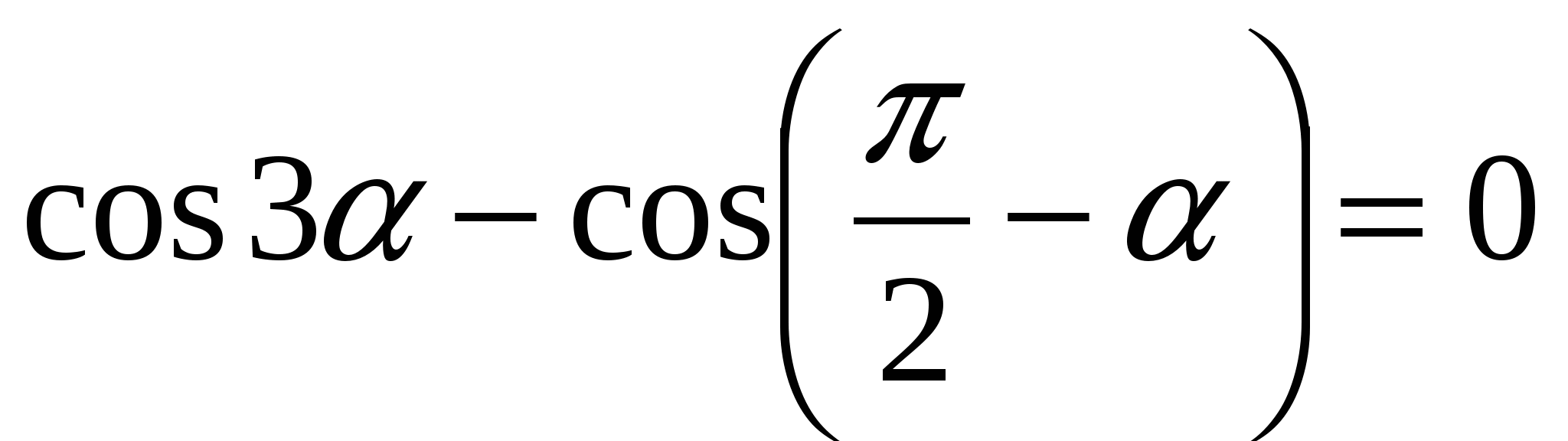
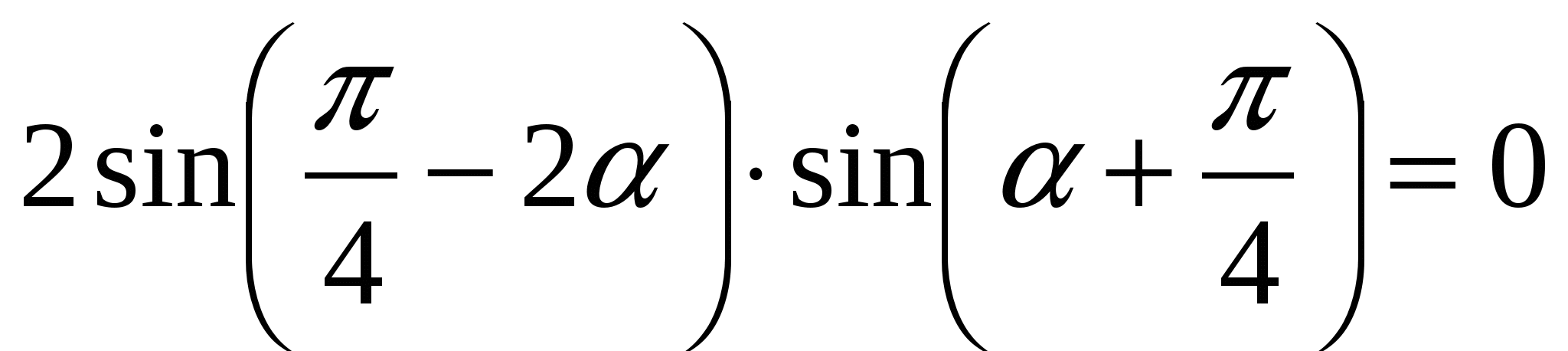
1) ![]()
![]() , тогда
, тогда
![]()
Значит, 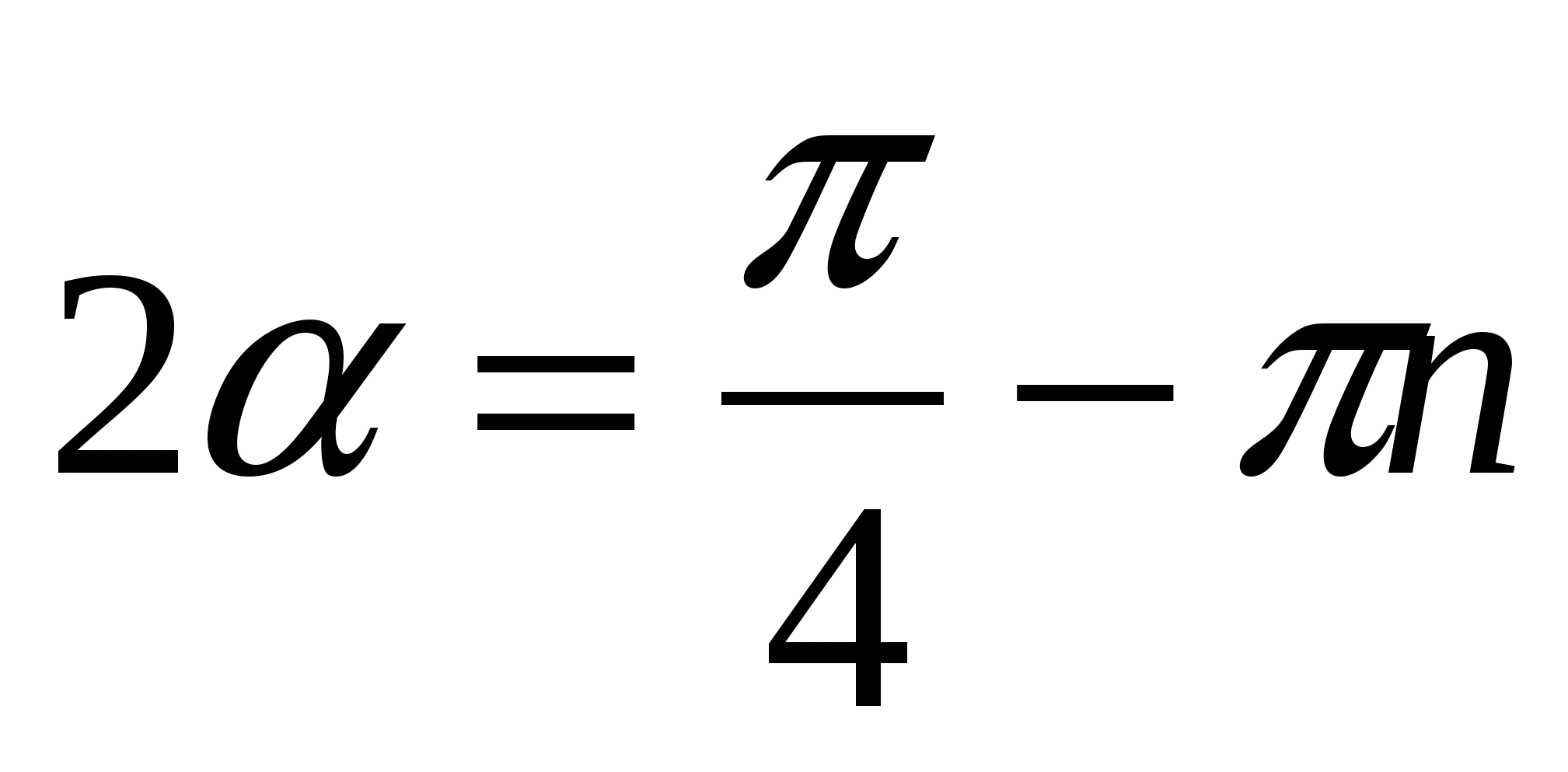
![]()
И 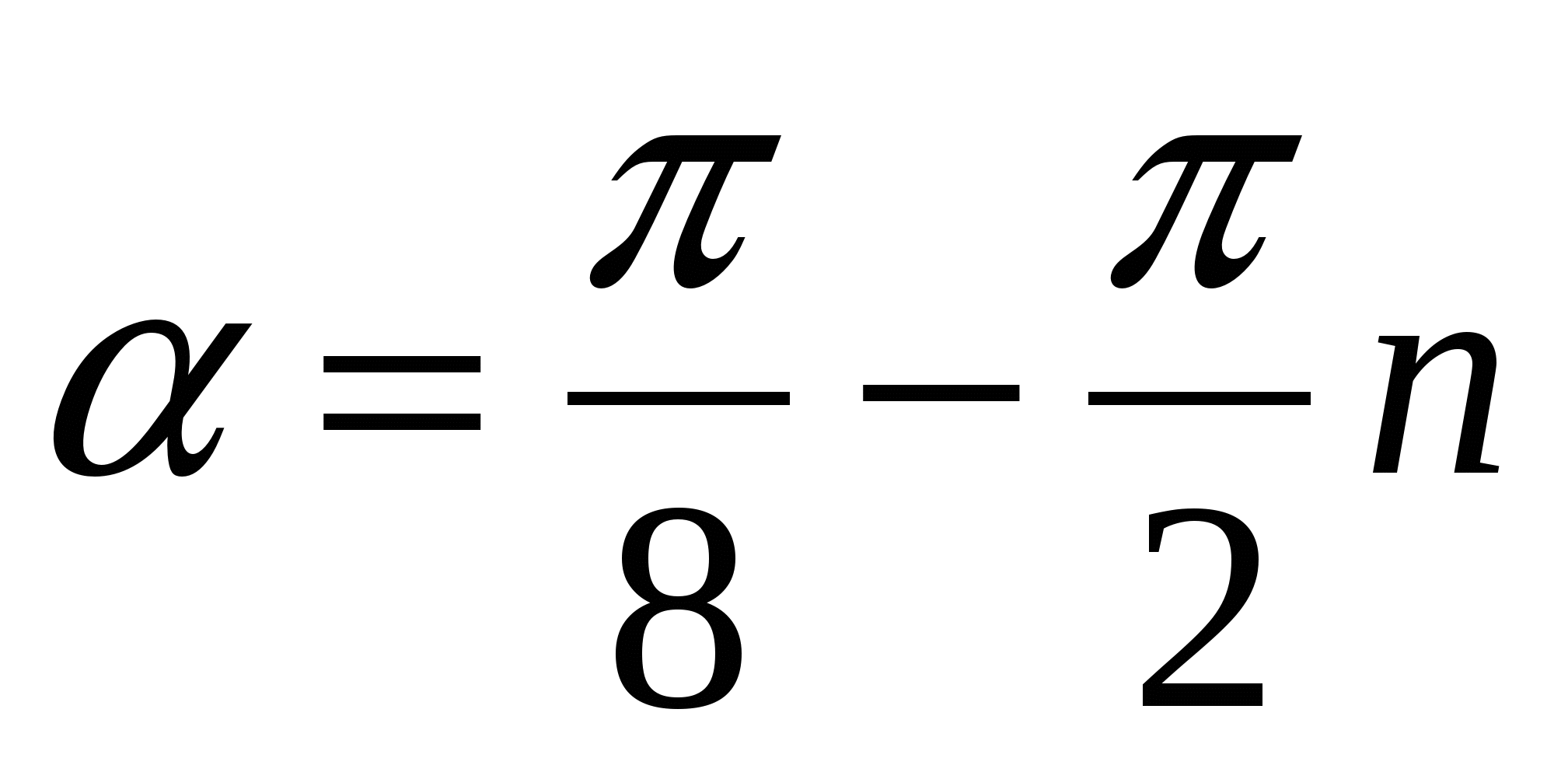
![]()
Ответ: (2;3), (3;2).
Задания для самостоятельной работы. Домашнее задание
Решить уравнение:
1. ![]()
2. ![]()
3. ![]()
4. ![]()
5. ![]()
6. ![]()
7. ![]()
8. ![]()
9. ![]()
10. ![]()
11. ![]()
12. ![]()
13. ![]()
14. ![]()
15. ![]()
16. ![]()
17. ![]()
III. Итог урока
За два часа работы учащиеся углубили свои знания и умения по решению уравнений двумя способами: способом разложения на множители и способом замены переменных, что способствует формированию умений решать уравнения различного типа высокого уровня сложности.
Предложенные задания как устные, так и письменные способствовали развитию логического мышления и познавательной деятельности.
Выполнение заданий формировали ответственность, глубину мысли, самостоятельность, аккуратность, требовательность в работе.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()