Разработка урока по алгебре на тему Применение производной

Класс: 10

Предмет: алгебра

Тема урока: Применение производной к исследованию функции.

Цель урока: повторение и систематизация знаний и умений по применению производной к исследованию функции.

Задачи:

1. повторить понятие критические точки функции, экстремумы функции, наибольшее и наименьшее значение функции; проверить умения и навыки применения производной к исследованию функции;

2. развивать грамотную математическую речь, умение наблюдать, сравнивать, обобщать, анализировать; содействовать формированию умений самооценки и взаимооценки.

3. воспитывать культуры общения, умения работать в группе

Тип урока: повторение и систематизация знаний.

Оборудование: интерактивная доска, компьютер, листы для оценивания, карточки с заданиями, стикеры для обратной связи, маркеры.

Методы обучения: критическое мышление, ИКТ, оценивание для обучения и оценивание обучения.

Виды деятельности: индивидуальная работа, групповая работа, фронтальная работа.

Ход урока:

I. Организационный момент.

Психологический настрой « Мы все такие разные».

Каждый учащийся должен не просто назвать свое имя, а на первую букву своего имени подобрать прилагательное, определяющее его характер ( Анастасия - амбициозная, Владимир - всезнающий и т.д.)

Тема нашего занятия - исследование функции с помощью производной. Давайте запишем дату и тему урока в тетрадь. Как вы думаете, ребята, какова цель нашего урока? (Дети формулируют цель.) Цель урока - закрепить и систематизировать знания учащихся по исследованию функций с помощью производной.

Итак, на сегодняшнем уроке мы повторим применение производной к исследованию функции, будем учиться друг у друга, отвечать на вопросы. Будьте внимательны, уважайте своих одноклассников, активно работайте, высказывайте свое мнение. Прежде чем начать работать, давайте создадим новые группы. (на листочках написаны положительные и отрицательные числа, с помощью жеребьевки ребята делятся на две группы).

2. Актуализация знаний: прием «Корзина» идей, понятий, имен…

На доске висит нарисованная корзина, в которой условно будет собрано все то, что все ученики вместе знают о применении производной к исследованию функции.

Обмен информацией проводится по следующей процедуре:

1. Что вы знаете о применении производной к исследованию функции.

2. Сначала каждый ученик вспоминает и записывает в тетради все, что знает по этому вопросу (строго индивидуальная работа, продолжительность 1-2 минуты).

3. Затем происходит обмен информацией в парах или группах. Ученики делятся друг с другом известным знанием (групповая работа). Время на обсуждение не более 3 минут. Это обсуждение должно быть организованным, например, ученики должны выяснить, в чем совпали имеющиеся представления, по поводу чего возникли разногласия.

4. Далее каждая группа по кругу называет какое-то одно сведение или факт, при этом, не повторяя ранее сказанного (составляется список идей).

5. Все сведения кратко в виде тезисов записываются учителем в «корзинке» идей (без комментариев), даже если они ошибочны. В корзину идей можно «сбрасывать» факты, мнения, имена, проблемы, понятия, имеющие отношение к теме урока. Далее в ходе урока эти разрозненные в сознании ребенка факты или мнения, проблемы или понятия могут быть связаны в логические цепи.

III. Работа со справочным материалом: поработав с текстом сформулировать ответы на вопросы (повторение теоретического материала)

Вопросы раздаются каждой группе.

1) Какая функция называется возрастающей?

2) Какая функция называется убывающей?

3) Как связан "знак" производной с возрастанием и убыванием функции?

4) Что называется точкой максимума?

5) Что называется точкой минимума?

6) Какие точки называются стационарными?

7) Какие точки называются критическими?

8) Каков алгоритм нахождения наибольшего и наименьшего значений непрерывной на заданном отрезке функции?

IV. Задание «Найди ошибки»

Каждой группе раздаются задания, группа решает, кто будет отвечать.

</ 1. Изображён график производной. Точки х=-1, х=1, х=2 являются точками максимума.

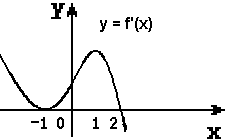
2. Производная функции в точке хо равна 0, значит хо - критическая точка. Верно ли?

3. Производная функции не существует в точке хо, значит хо - критическая точка. Верно ли?

4. Критическая точка является точкой экстремума. Верно ли?

5. Точка экстремума является критической точкой. Верно ли?

V. Эстафета «Бег с препятствиями»

Повторим, как же нужно вычислять производные функций?

«Бег с препятствиями» - это эстафета, учащиеся идут поочерёдно к доске, на столе берут карточку с заданием, и выполняют его. Зарабатывают баллы по количеству верных заданий.

1 группа: ; ; ; ;

2 группа: ; ; ; ;

VI. Задание группе « Найти экстремумы функции»

1 группа y = x³ + 6x² - 15x - 3

2 группа y = x³ - 6x² - 15x + 7

VII. Литературная страница « Графики функции в пословицах»

Первая женщина математик С. В. Ковалевская сказала:

« Математик должен быть поэтом в душе». И, следуя ее словам, мы на нашем уроке откроем литературную страничку «Графики функций - пословицы». Подберите к графикам функций, изображенных на слайдах, пословицы, которые раскрывают суть процессов функции:

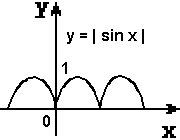
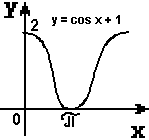
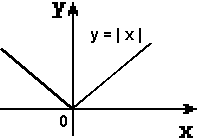
1 2 3

"Как аукнется, так и откликнется".

"Повторение - мать учения".

"Любишь с горы кататься, люби и саночки возить»

IX. Домашнее задание: повторить применение производной к построению графика функции

X. Заполнение оценочных листов: члены группы выставляют в свои оценочные листы баллы по выполненым заданиям.

X. Рефлексия: Продолжите фразу:

Сегодня на уроке я повторил…

Сегодня на уроке я закрепил…

Мне предстоит повторить…