- Учителю
- Методическая разработка по теме «Вектор» в 10 классе (геометрия)
Методическая разработка по теме «Вектор» в 10 классе (геометрия)
Методическая разработка
по теме «Вектор»
в 10 классе (геометрия)
Повторение
Из опыта работы
учителя СШ №24
Косоноговой Р.М.
Харцызск
2014
Цель: Сформулировать умения и навыки использования теории векторов к решению задач
Знать: Определение вектора, формулировку скалярного произведения векторов, координаты векторов
Уметь: Решать задачи, используя координатный и координатно-векторный методы
Нормировать: выработать алгоритм решения задач на координатной плоскости
Ценить: стремление решать задачи нетрадиционным способами;
умение рационально использовать рабочее время;
умение преодолевать трудности
I у-м
Геометрия- это интуиция ….
любой человек в здравом уме не сомневаетсяв том, чтогеометрические утверждения должны представлять практическое применение в окружающей действительности: в землемерии, архитектуре, в машиностроительном искусстве.
Г.гельмгольц
Структурно - часовая модель
Этапы
У-М
С-П
О-С
А-П
С-О
К-Р
Кол-во модулей
1
2
3
3
3
3
I У-М
Цель: Формирование внутренней мотивации содержания.
Из истории векторов:
Под векторной величиной или вектором понимают величину, обладающую направлением, например силой скорость, ускорение.
Интерес к векторами векторному исчислению появился в XIX веке в связи с потребностями математики и физики.
Однако, истоки исчисления с направленными отрезками возникли в далеком прошлом. В Древней Греции Пифагорийцы, открыв иррациональные числа, которые нельзявыразить дробями, не решились ввести более широкое толкование числа. Математики того времени пытались свести вопросы арифметики и алгебры к решению задач геометрическим путем. Таким образом было положено начало геометрической алгебре.
В труде Эвкалида «начала» сложение и вычитание сводилось к сложению и вычитанию отрезков, а умножение - к построению прямоугольников на отрезках, соответствующих по длине множителям.
В 1587г.был опубликован на голландском языке трактат фламандского ученого С.Стевина «Начала статистики». В нем автор, рассматривая сложения сил, действующих под углом 90 ˚, необходимо воспользоваться параллелограммом сил. При этом для обозначения сил ввели стрелки. Так впервые ввели сложение векторов., перпендикулярных друг другу. Позже французский математик Луи Пуансо (1777-1859) в книге «элементы статики»1803г. Разработал теорию векторов, которой пользуются при рассмотрении сил, действующих в разных направлениях.
Термин «вектор» происходит от латинского слова vektor, что означает несущий или ведущий, влекущий., переносящий.
Долгое время вектор рассматривали как направленный отрезок, но с разработкой теории преобразований вектор рассматривают как параллельный перенос.
В современной математике, раздел, изучающий действия с векторами, называют векторной алгеброй.
С-П этап
Цель: развитие поисковой познавательной активности и самостоятельности
учащихся
…. В математических науках есть очень удачные изобретения, способное приобрести большую пользу, удовлетворяя любовь к знаниям, облегчая все ремесло и сокращая труд человека.
Р.Декарт
Векторы
I Повторение
-
Дать определение вектора.
Вектором называют направленный отрезок(определены начало и конец).
 B
B ![]()
![]()
A
-
Какие векторы называются противоположными
Два вектора, имеющие одинаковые длины и противоположные направления
B B
![]()
A A
-
Что называется модулем вектора
Модулем вектора называется его длина
![]()
-
Какие векторы называются коллинеарными
Векторы, лежащие на одной или
параллельных прямых
 B D E
B D E
A M P
K![]()
![]()
C
5.Как можно сложить два вектора
Правило треугольника
![]()
![]()
![]()
![]()
![]()
![]()
Правило параллелограмма
![]()
![]()
![]()
![]()
![]()
6. Как найти разность двух векторов ![]() и
и ![]() ?
?
Правило треугольника
![]()
![]()
![]()
![]()
![]()
![]()
Правило параллелограмма
![]()
![]()
![]()
![]()
7. Разложение вектора по двум неколлинеарным векторам.
Любой вектор можно
разложить по двум не
коллинеарным векторам
![]()
![]()
![]()
где ![]() - ед. пара чисел
- ед. пара чисел
![]()
![]()
![]()
![]()
![]()
![]()
![]()
О - С Этап
Цель: проверить первичный уровень усвоения и понимания изученного
материала.
«… принципы геометрии являются
всей математики»
О. Хайям
II Применение векторов к решению задач.
Задача 1. Точка ![]() - середина отрезка
- середина отрезка![]() , а
, а ![]() - произвольная точка плоскости. Доказать, что
- произвольная точка плоскости. Доказать, что ![]()
Решение.
![]()
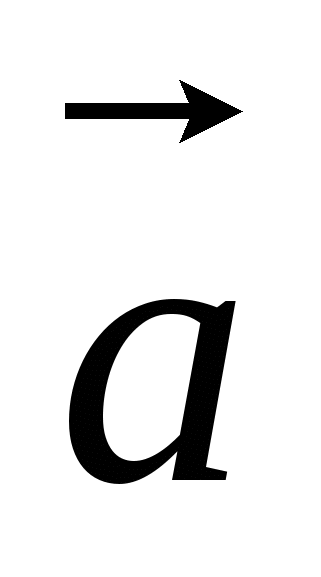
![]()
![]()
![]()
-
По правилу треугольника
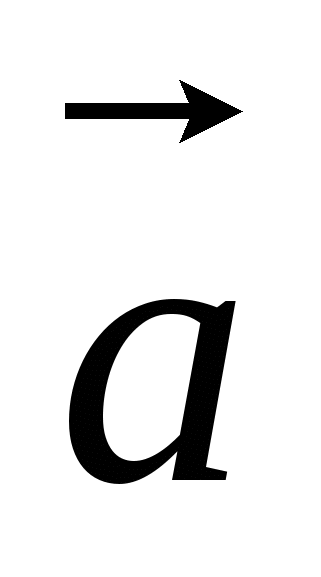 ;
; 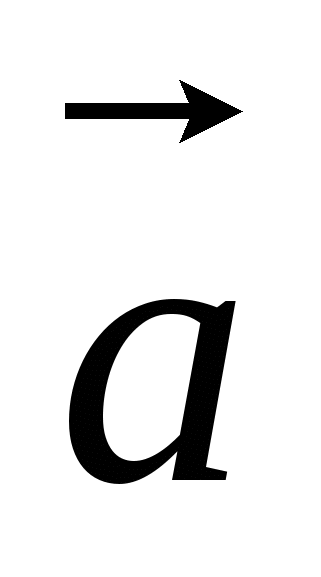
-
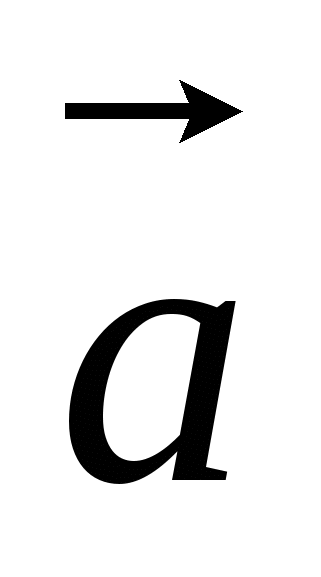 , т.к. точка
, т.к. точка 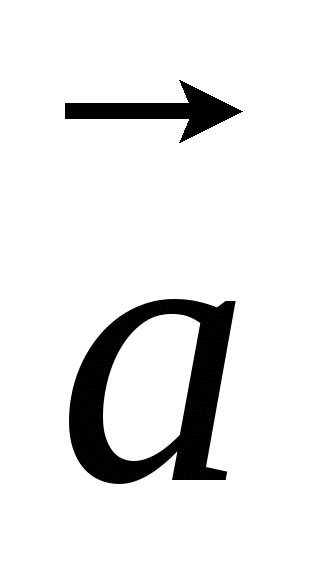 - середина отрезка
- середина отрезка 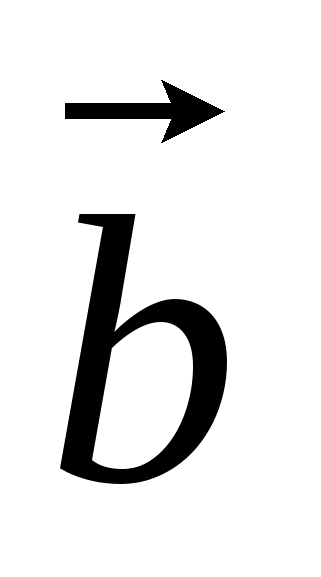 , то
, то 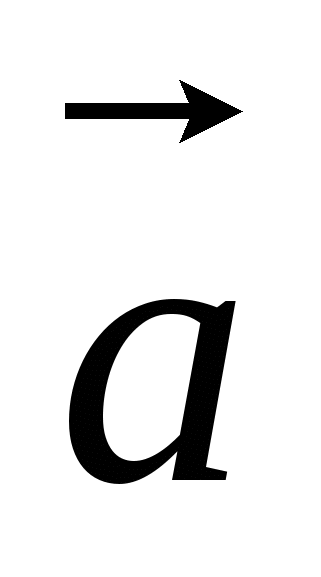
-
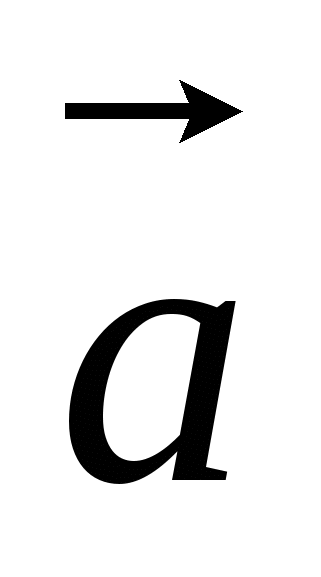
Задача 2. Доказать векторную формулу средней линии четырехугольника.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() и
и ![]() середины сторон
середины сторон ![]() и
и ![]()
Решение.
1. ![]()
![]()
2. ![]() и
и ![]()
3. ![]()
![]()
![]()
Задача 3. Доказать, что прямая проведенная через середины оснований трапеции проходит через точку пересечения продолжений боковых сторон.
Решение.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
1. ![]() - данная трапеция
- данная трапеция ![]() и
и ![]() середины сторон
середины сторон ![]() и
и ![]() .
. ![]() - точка пересечения прямых
- точка пересечения прямых ![]() и
и ![]() .
.
2. ![]() , тогда
, тогда ![]()
3. ![]() ,
, ![]() , поэтому
, поэтому ![]() ;
; ![]()
4. т.к. ![]() - середина
- середина ![]() , то
, то ![]() , аналогично
, аналогично ![]()
5. ![]() ;
; ![]() , т.е. векторы
, т.е. векторы ![]() и
и ![]() коллинеарны, т.е. точка
коллинеарны, т.е. точка ![]() лежит на прямой
лежит на прямой ![]()
III Применение векторов к доказательству теорем
Теорема 1. Средняя линия треугольника параллельна его третьей стороне и равна половине ее.
Доказательство.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
1. ![]() ;
; ![]() ;
; ![]()
2. ![]()
3. Пусть ![]() и
и ![]() - середины сторон
- середины сторон ![]() , и
, и ![]()
4. ![]() ;
;
![]() ;
; ![]()
5. ![]() , тогда
, тогда ![]() , т.е.
, т.е. ![]()
Теорема 2. Средняя линия трапеции параллельна основаниям и равна их полусумм.
Доказательство.
![]()
![]()
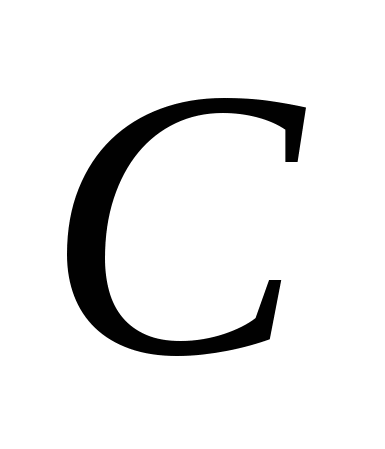
![]()
![]()
![]()
![]()
1. ![]() - средняя линия
- средняя линия
2. ![]()
3. ![]()
4. ![]() и
и ![]() , тогда
, тогда ![]() ;
; ![]()
5. ![]()
![]() , тогда
, тогда ![]()
IV Самостоятельно решить.
1. Доказать, что если ![]() - точка пересечения медиан треугольника
- точка пересечения медиан треугольника ![]()
![]() - произвольная точка пространства, то выполняется равенство
- произвольная точка пространства, то выполняется равенство
![]()
Замечание. Использовать свойство медиан треугольника и формулы разности и суммы векторов.
2. Дан правильный шестиугольник ![]() . Доказать, что
. Доказать, что ![]() .
.
Замечание. Использовать равенство векторов и на рисунке и правило сложения.
А - П Этап.
Цель: формирование умений навыков, норм деятельности, применение знаний в нестандартных ситуациях
Геометрия - это искусство правильно измерять.
П. Раме.
Пусть вектор ![]() имеет началом точку
имеет началом точку ![]() , а концом точку
, а концом точку ![]() , тогда
, тогда ![]() и вектор
и вектор ![]() имеет координаты
имеет координаты ![]()
При этом:
-
Равные векторы имеют равные координаты
-
Если координаты двух векторов равны, то эти векторы равны
-
Нулевые вектора имеют нулевые координаты
-
Модуль вектора
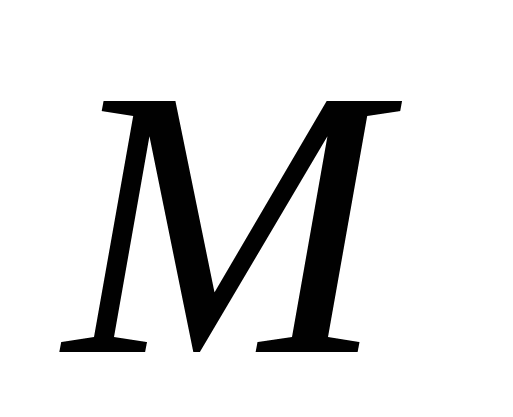
-
Если
 и
и 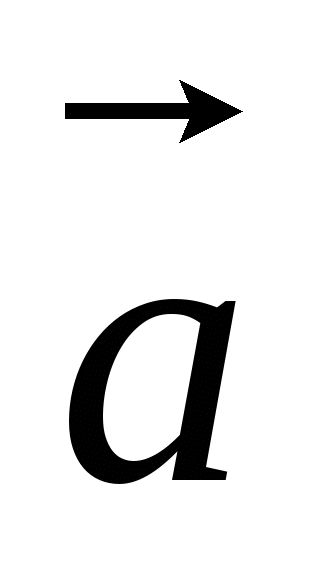 - середина отрезка
- середина отрезка 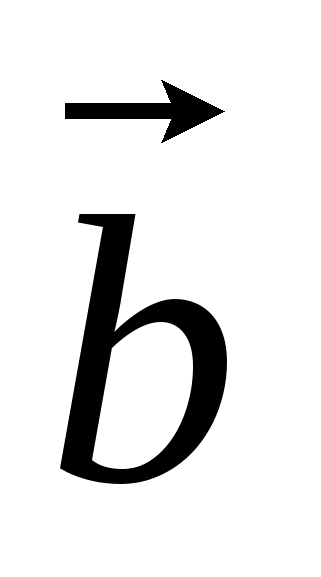 , то
, то 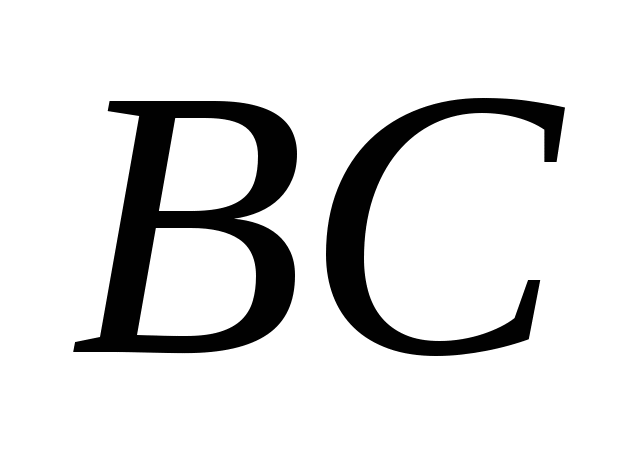
VII Решение задач с использованием координат вектора.
Задача 1.
Докажите, что середина гипотенузы прямоугольного треугольника равноудалена от всех его вершин.
Решение.

![]()
![]()
![]()
![]()
![]()
![]()
-
Пусть дан прямоугольный треугольник
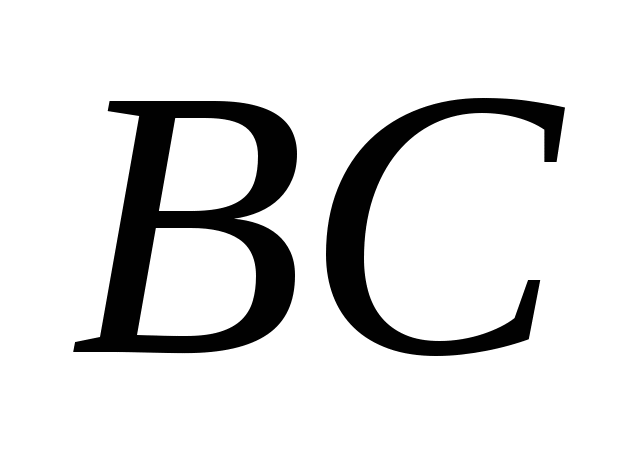 с прямым углом
с прямым углом 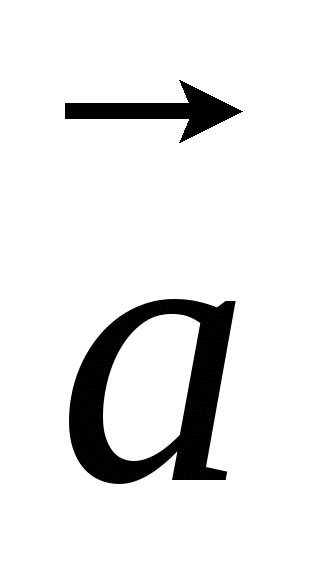 .
. 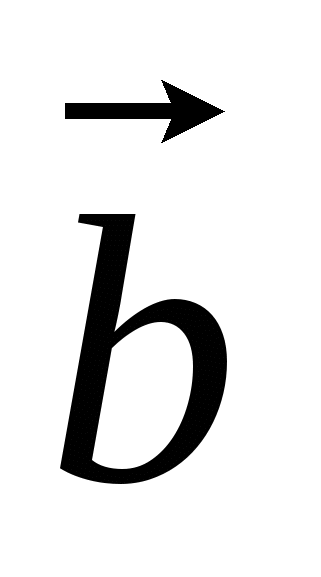 - середина
- середина 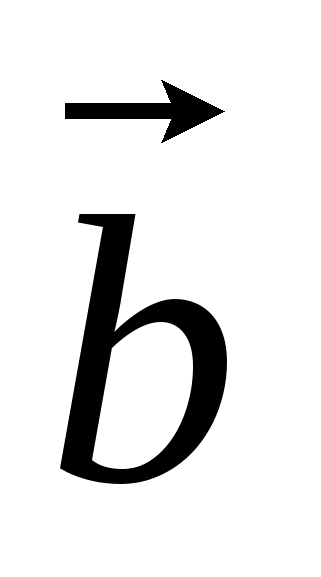
-
Введем прямоугольную систему координат так, чтобы
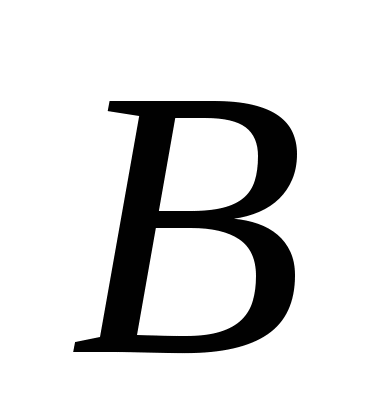
-
Пусть
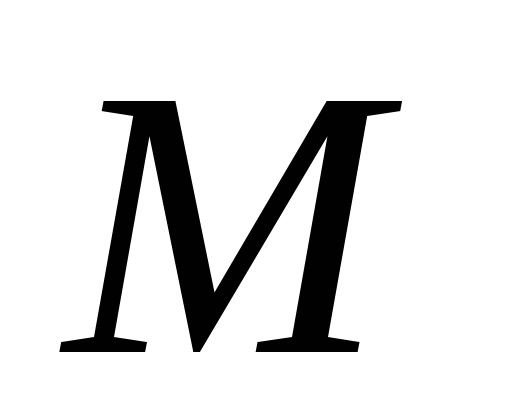 и
и 
-
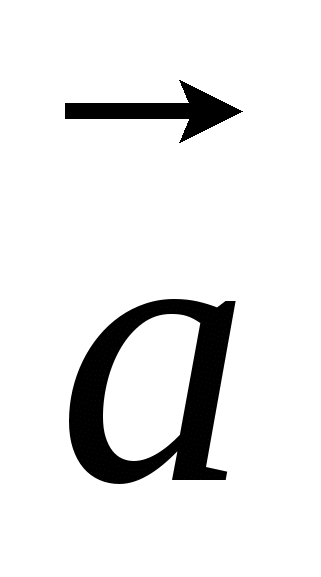
Следовательно, ![]()
Задача 2.
Докажите, что сумма квадратов всех сторон параллелограмма равна сумме квадратов всех его диагоналей.
Решение.
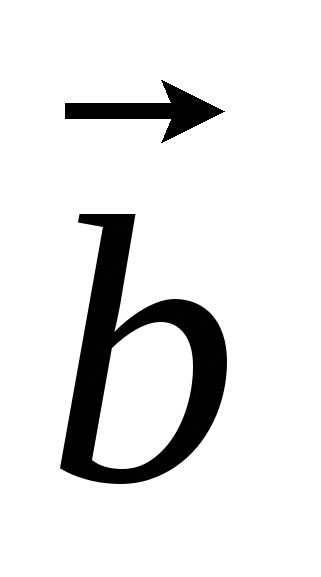
![]()
![]()
![]()
![]()
![]()
![]()
![]()
-
Введем прямоугольную систему координат так, чтобы
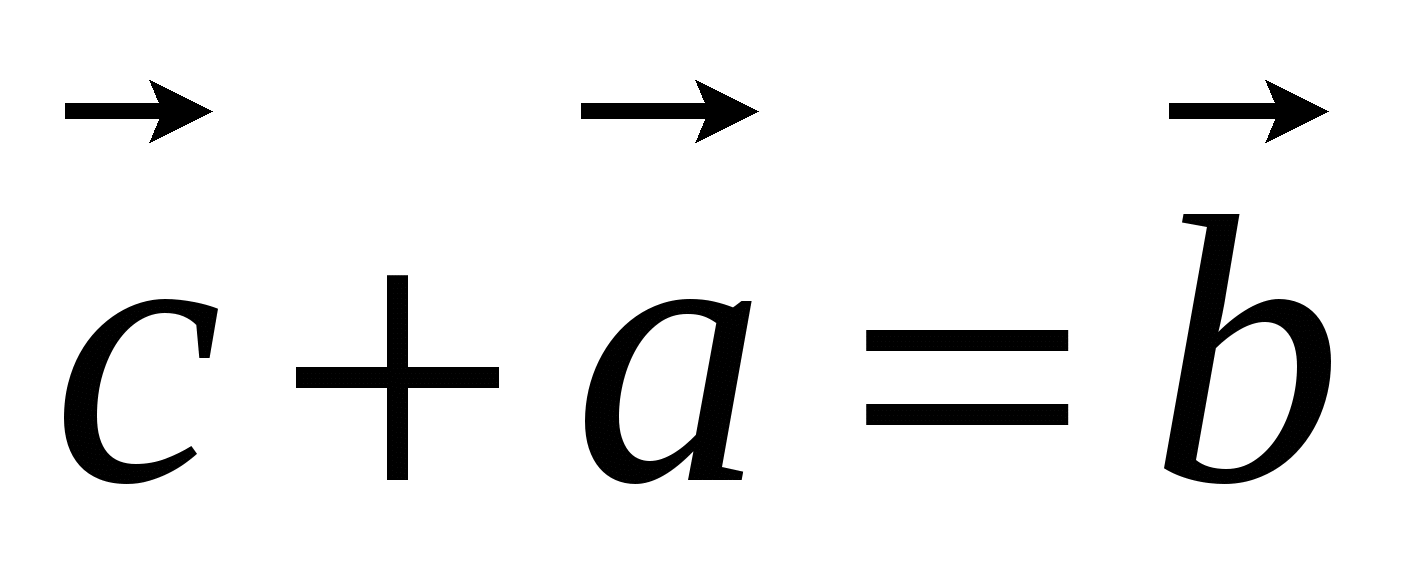
-
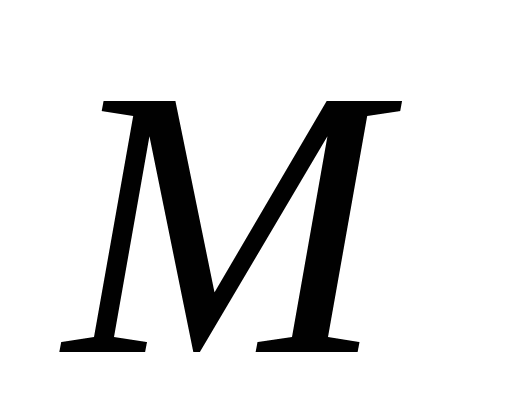

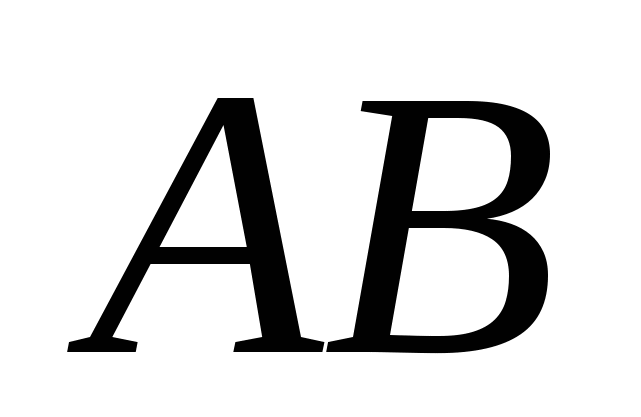
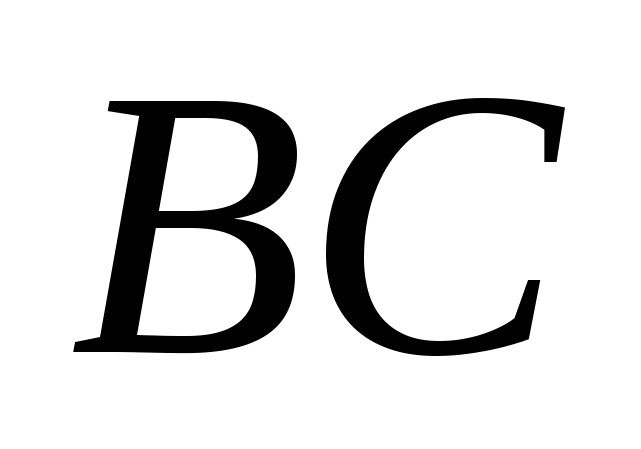
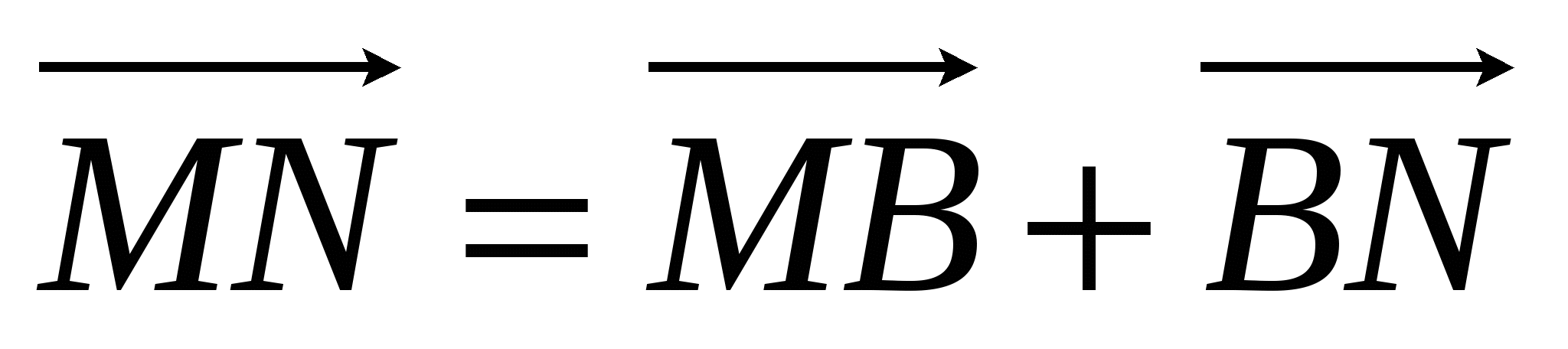
-
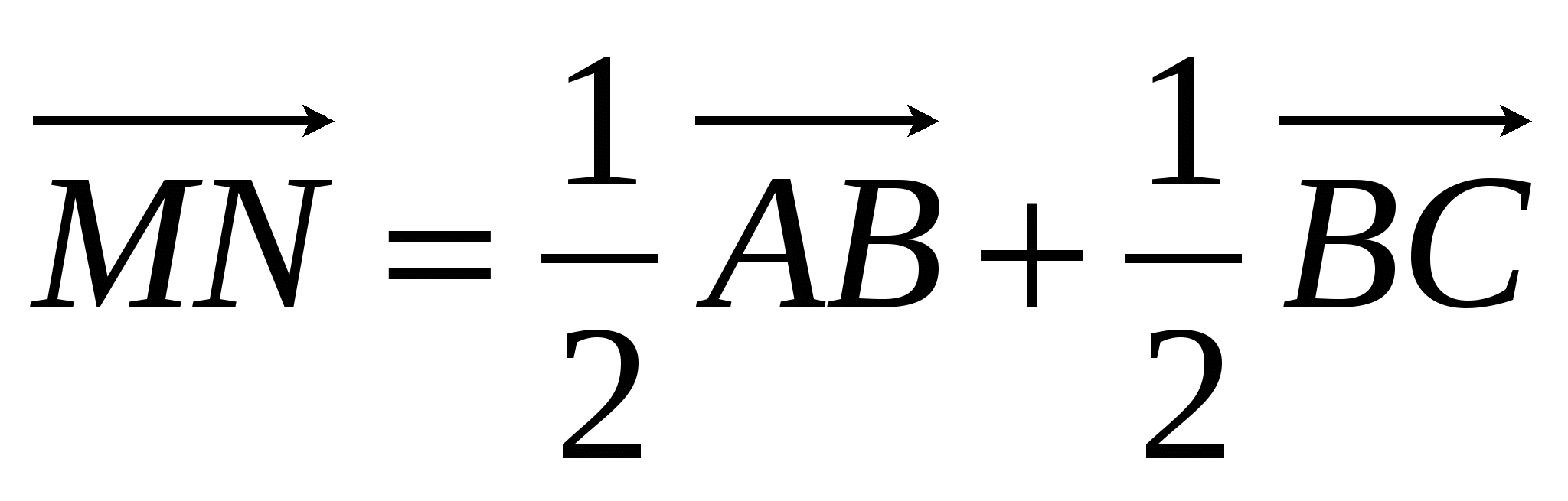
-
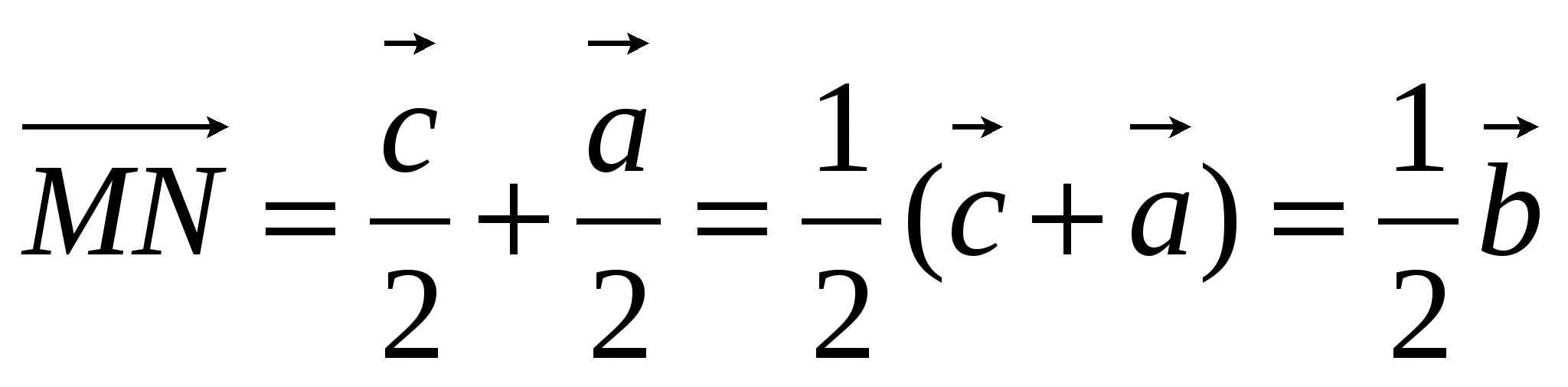
VIII Самостоятельно решить
1. Точки ![]() и
и ![]() имеют координаты
имеют координаты ![]()
Найти координаты и модуль вектора ![]()
Ответ: ![]() .
.
2. Найти координаты вершины ![]() параллелограмма
параллелограмма ![]() , если заданы координаты трех его вершин
, если заданы координаты трех его вершин ![]()
Ответ: ![]()
Дополнительно.
Используя формулу уравнения окружности в прямоугольной системе координат ![]() , где
, где ![]() - центр окружности,
- центр окружности, ![]() - координаты произвольной точки, решить задачу:
- координаты произвольной точки, решить задачу:
Найти уравнение окружности с центром в точке ![]() , проходящей через начало координат.
, проходящей через начало координат.
Ответ: ![]()
С - О Этап
Цель: нормирование целостной системы личностных знаний.
Геометрия является познанием всего существующего.
Платон
Скалярным произведением двух векторов ![]() и
и ![]() , называется число
, называется число ![]() , т.е.
, т.е. ![]()
Если ![]()
Скалярный квадрат вектора, равен квадрату модуля этого вектора ![]()
Теорема. Скалярное произведение двух ненулевых векторов равно произведению их модулей на косинус угла между ними.
![]() .
.
Если ненулевые векторы взаимно перпендикулярно, то их скалярное произведение равно нулю.
X Решение задач с использованием скалярного произведения векторов.
Задача 1.
Найти косинус угла между медианами равнобедренного прямоугольного треугольника, проведенными к его катетам.
Решение.
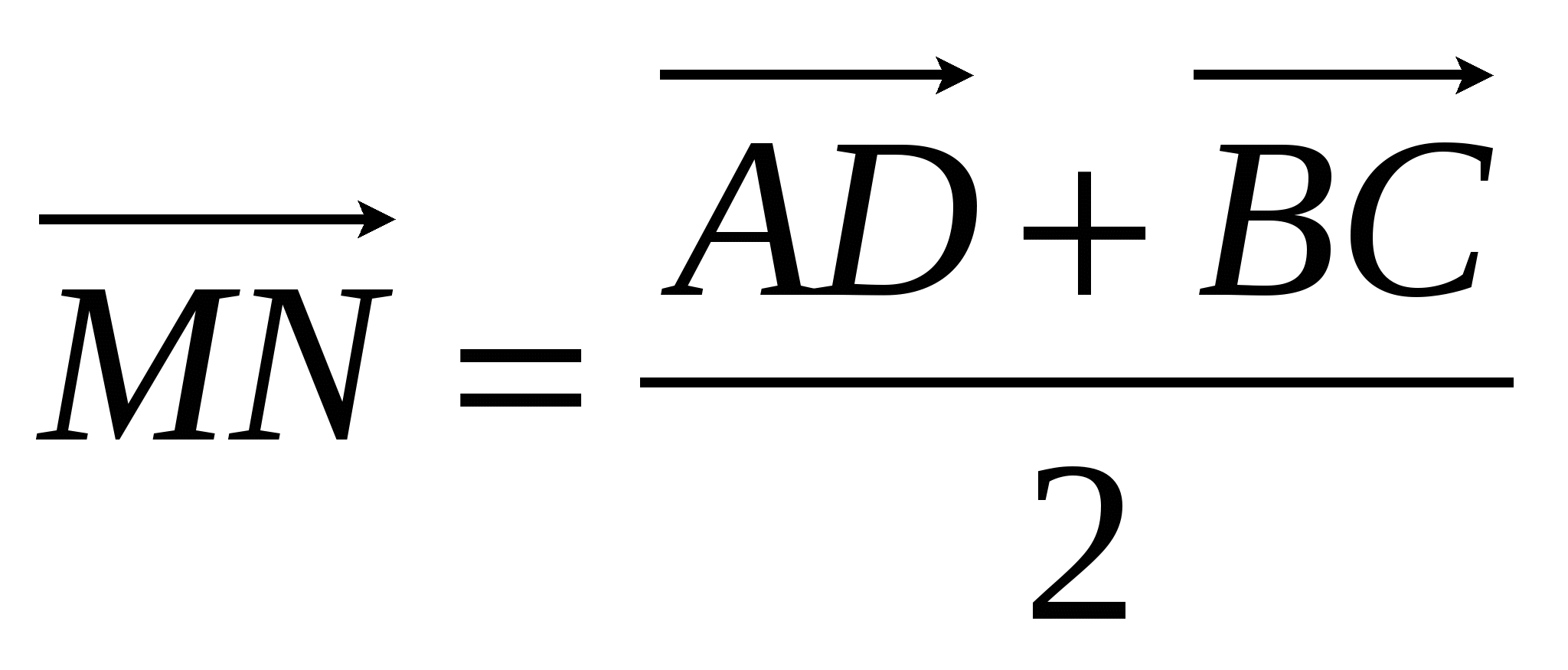
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
-
Направим оси
 и
и 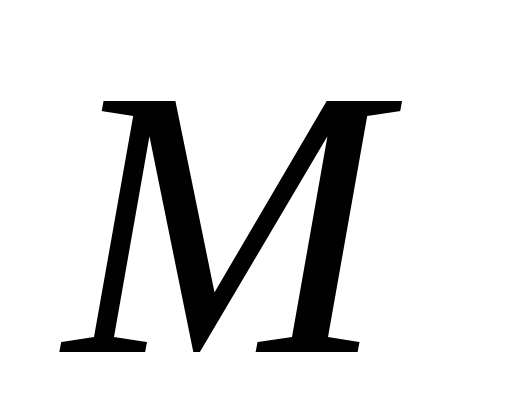 вдоль катетов треугольника и обозначим длины его катетов через
вдоль катетов треугольника и обозначим длины его катетов через 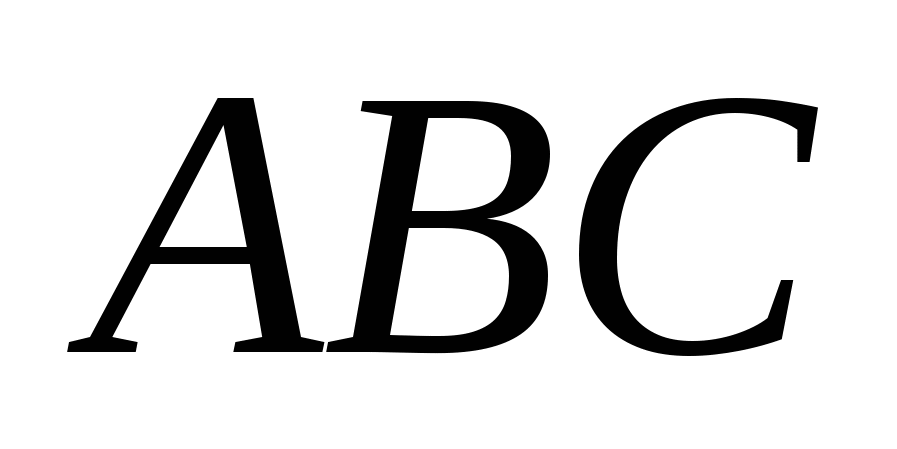
-

-
Координаты середин катетов
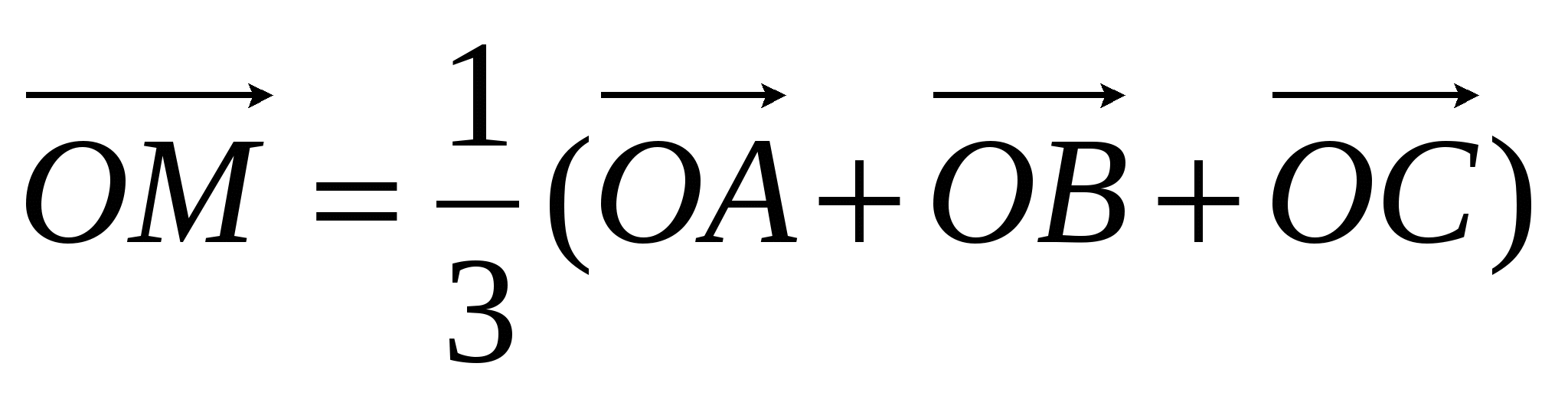
-

-
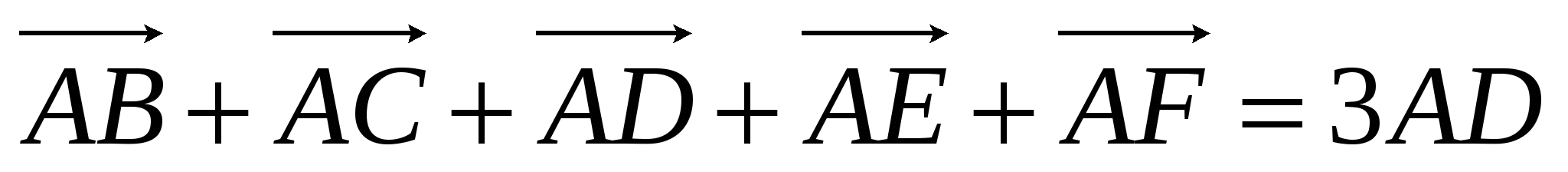
т.к. искомый угол является углом между прямыми и не может быть тупым.
Ответ: ![]()
Задача 2.
Даны вершины трапеции ![]() Найти величину угла между большей диагональю и меньшей стороной.
Найти величину угла между большей диагональю и меньшей стороной.
Решение.
![]()
![]()
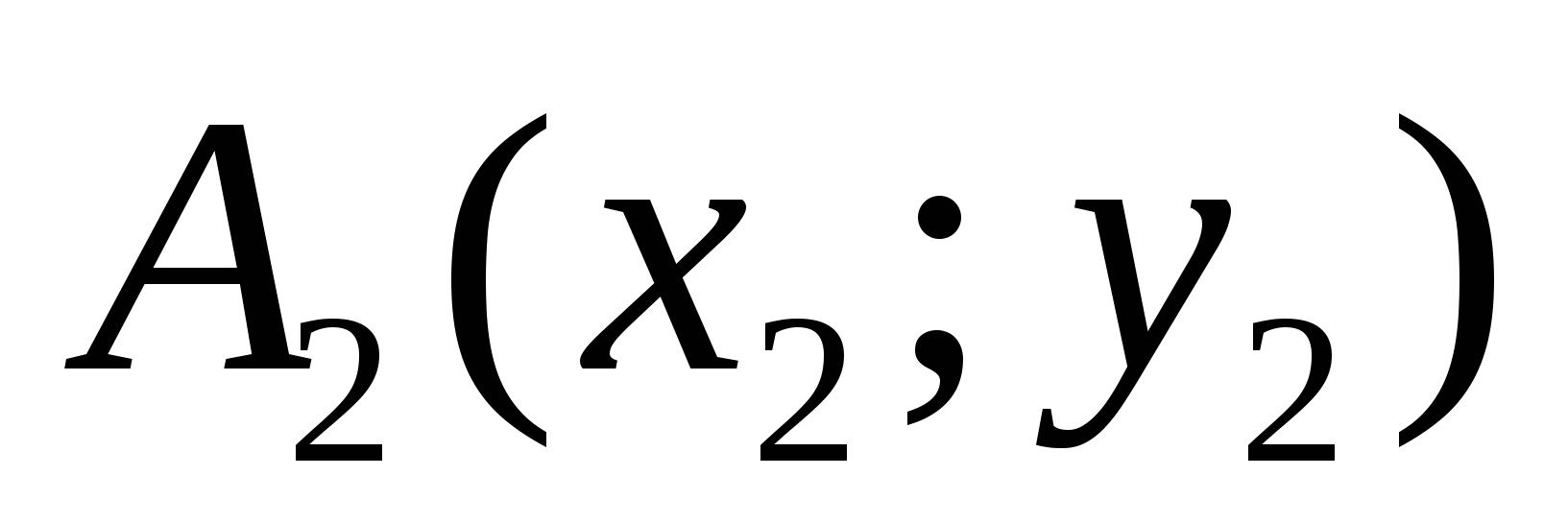
![]()
![]()
![]()
1. ![]()
2. ![]()
![]() - большая диагональ
- большая диагональ
3. ![]()
![]()
![]()
![]()
4. ![]() - меньшая сторона. Требуется найти угол
- меньшая сторона. Требуется найти угол ![]()
Пусть ![]() , тогда
, тогда
![]()
![]()
![]()
![]()
Задача 3.
Найти угол лежащий против основания равнобедренного треугольника, если медианы, проведенные к боковым сторонам, взаимно перпендикулярны.
Решение.
![]()
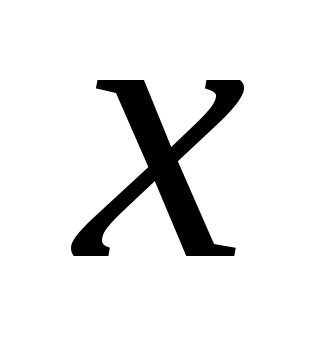
![]()
![]()
![]()
![]()
![]()
![]()
-
Пусть
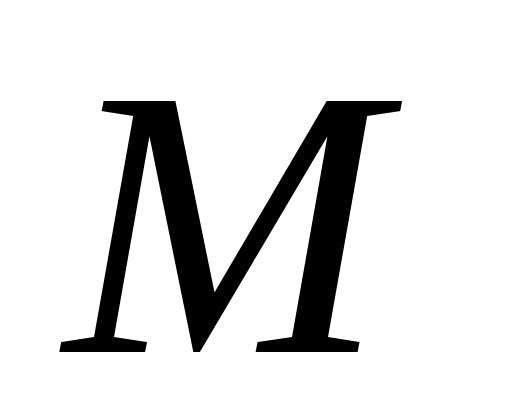 равнобедренный с основанием
равнобедренный с основанием 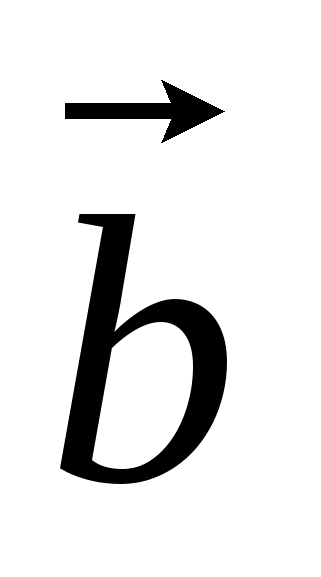 .
. 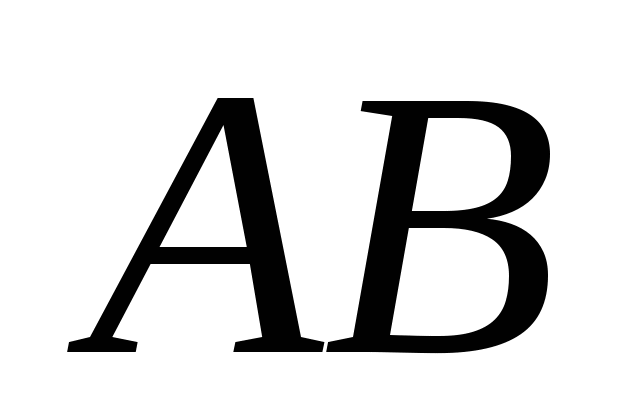 и
и 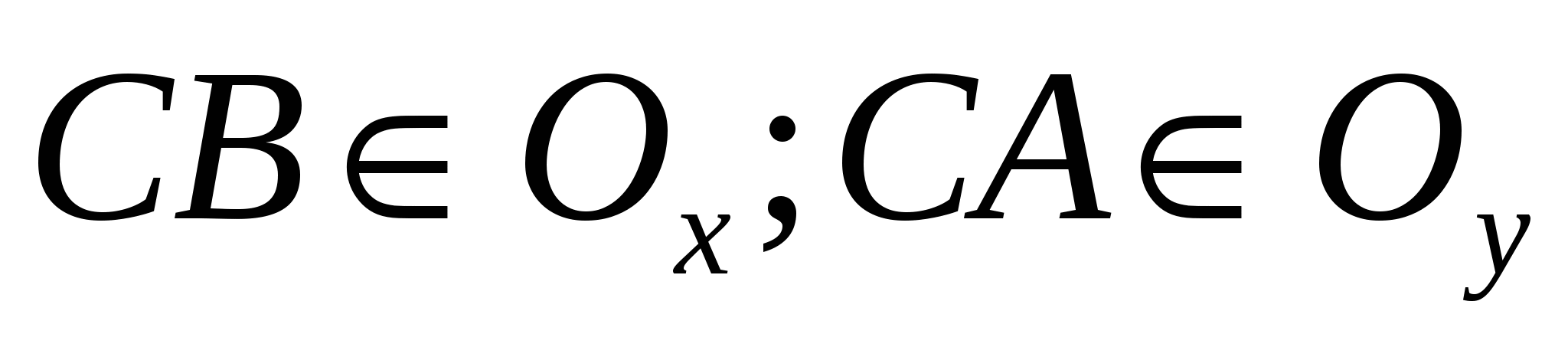 - медианы
- медианы -
Пусть
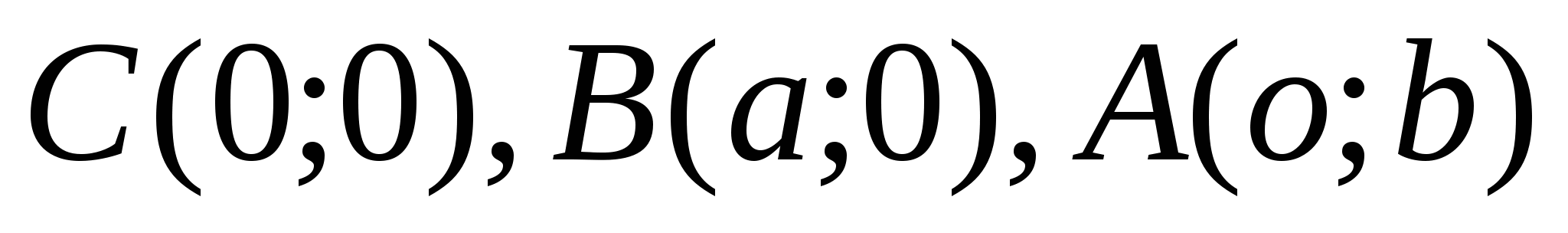
-
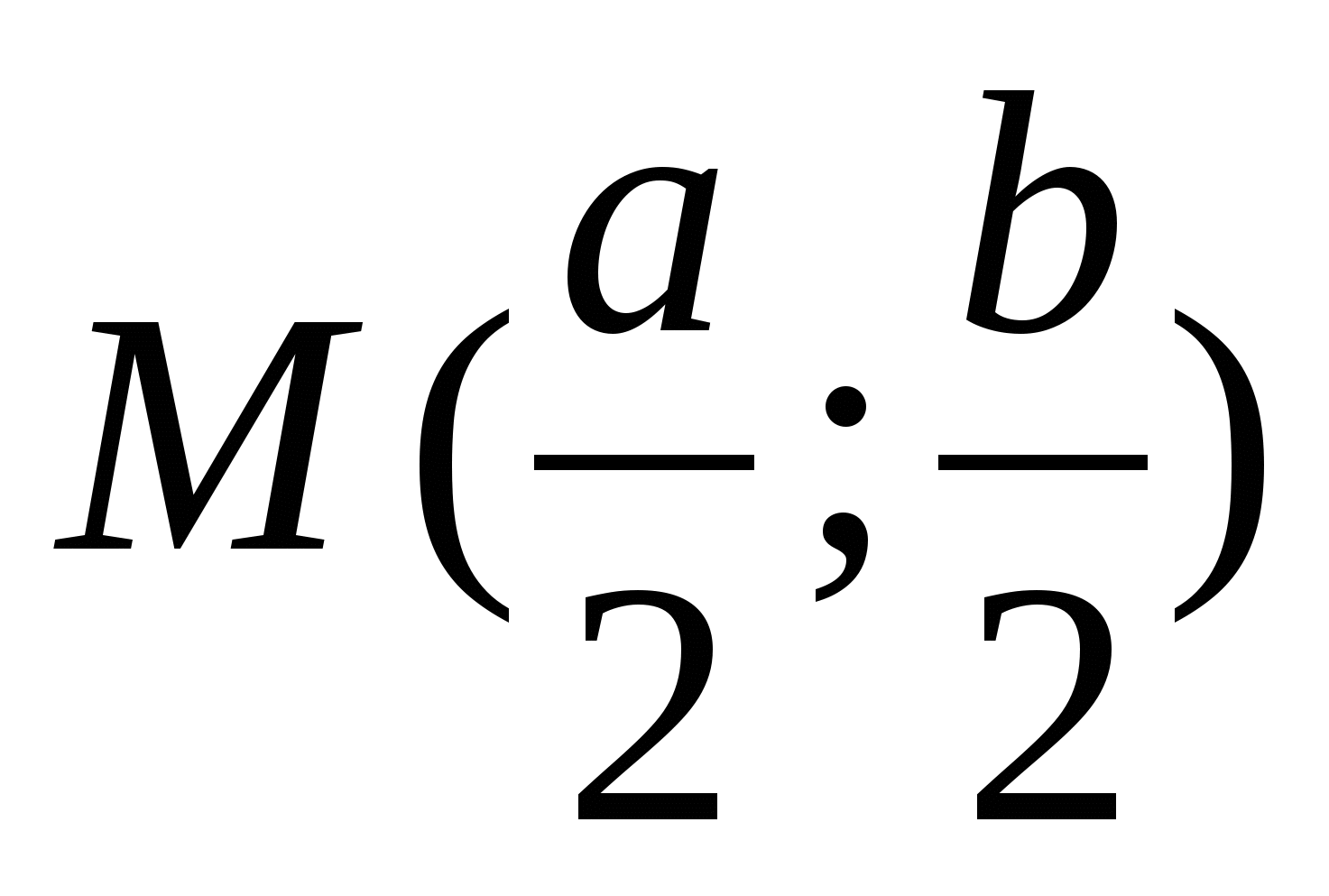
-
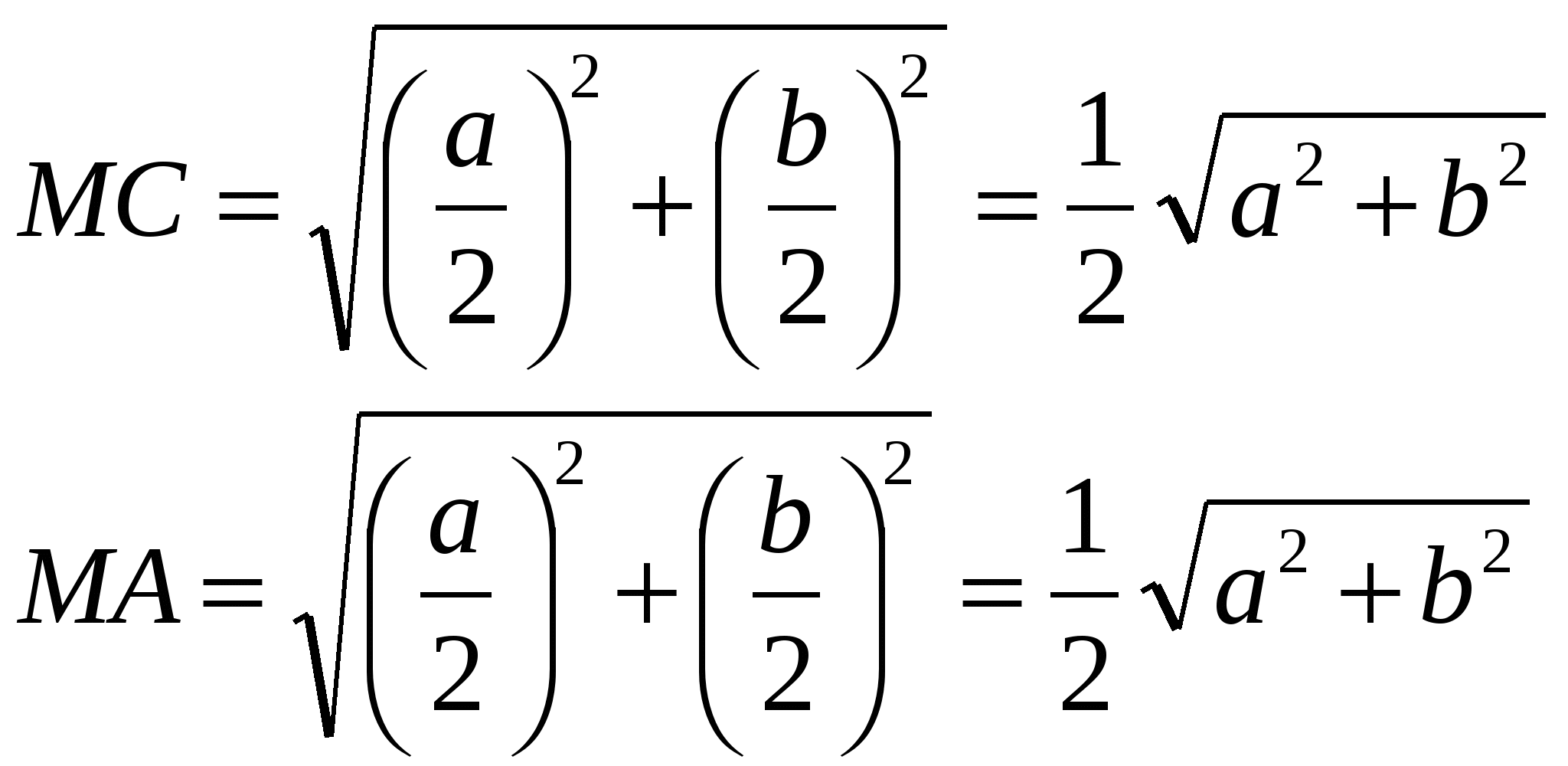
т.к. ![]() , то
, то ![]()
![]() т.к.
т.к. ![]()
![]()
![]() , тогда
, тогда
![]()
![]()
![]()
Ответ: ![]()
К - Р Этап.
Цель: Развитие творческой рефлексии.
То, что не может геометрия, не можем и мы.
Б. Паскаль
XI Самостоятельно решить
1. Являются ли треугольник ![]() прямоугольным, если
прямоугольным, если ![]()
Ответ: ![]()
2. Найти ![]() , при котором два вектора
, при котором два вектора ![]() и
и ![]() имеет одинаковую длину.
имеет одинаковую длину.
Ответ: ![]() ,
, ![]()
Примечание.
а) Использовать формулу длины вектора
б) Повторить решение тригонометрических уравнений вида ![]()
3. Доказать, что в ромбе диагонали взаимно перпендикулярны.
Замечание.
-
Ввести базисные векторы, лежащие на одной сторонах параллелограмма.
-
Использовать свойство скалярного произведения двух векторов.
XII Контрольная работа по теме «Вектор на плоскости».
I - В.
1. Докажите, что если ![]() - медиана треугольника
- медиана треугольника ![]() , то
, то ![]()
2. Доказать, что медианы равнобедренного треугольника проведенные к боковым сторонам равны между собой.
II - В.
-
Вычислить
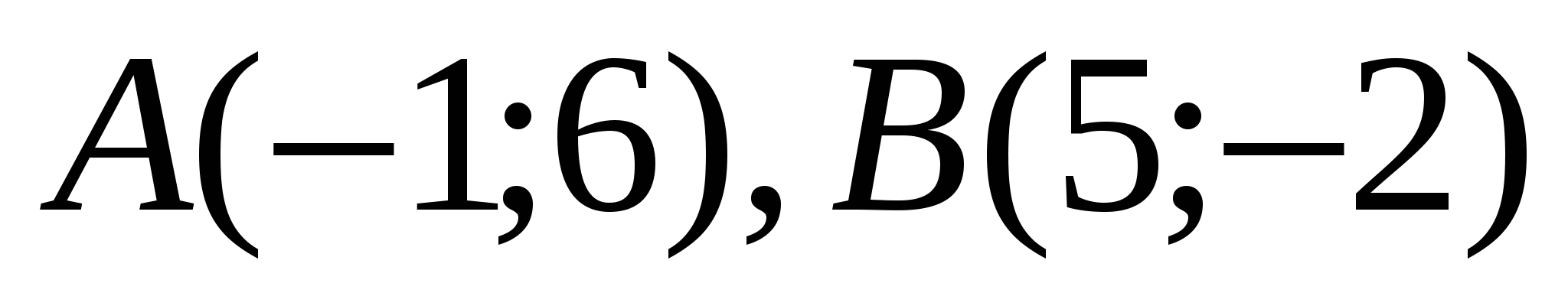 , где
, где  - угол между векторами
- угол между векторами 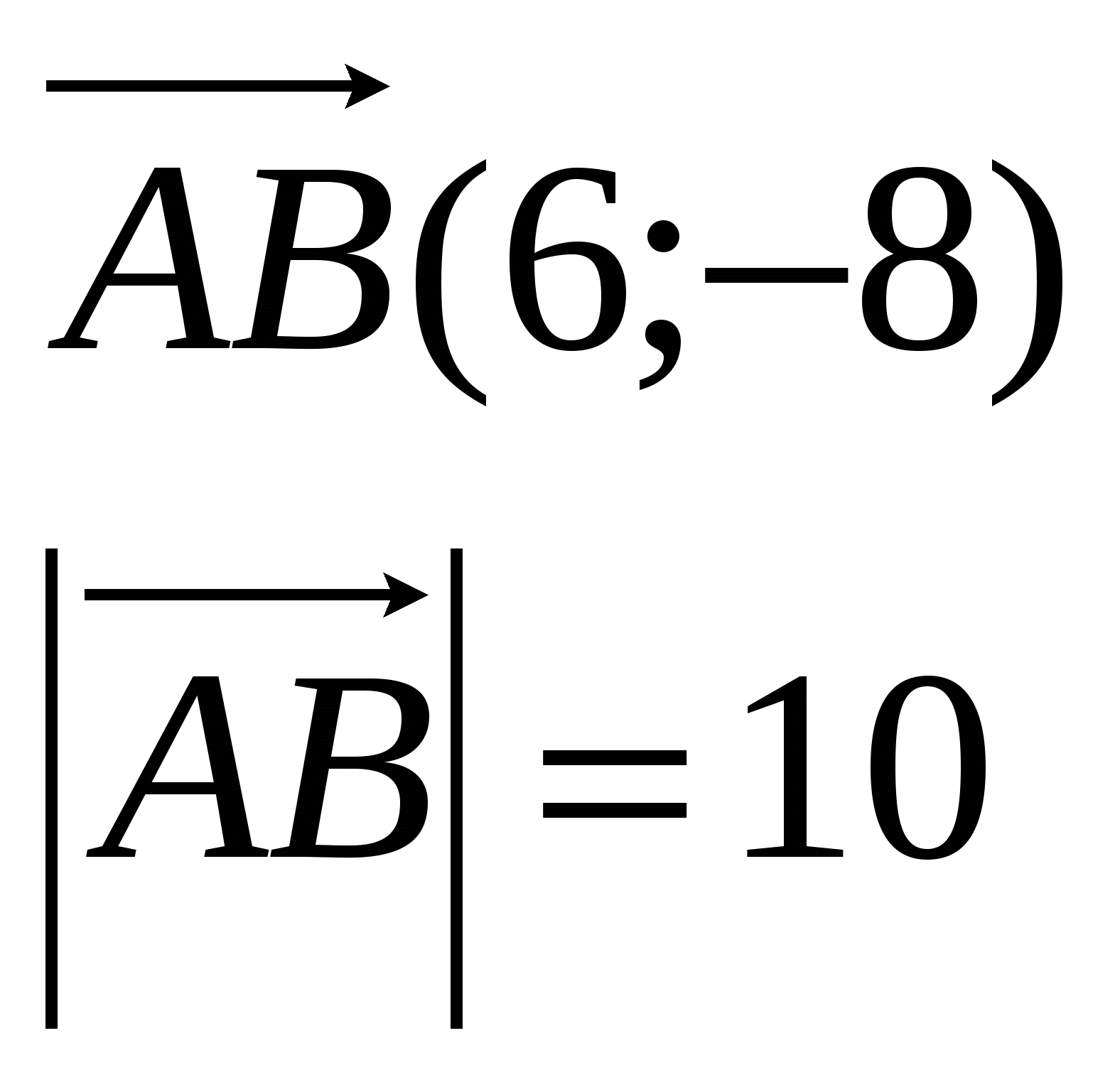
-
На координатной плоскости заданы точки
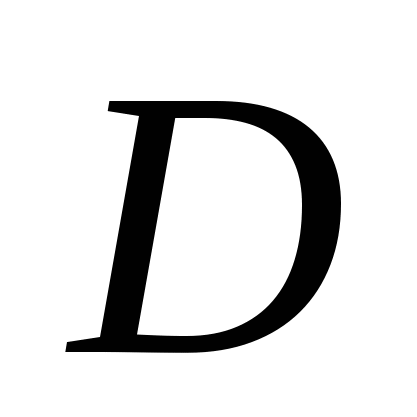 . Найти площадь треугольника
. Найти площадь треугольника 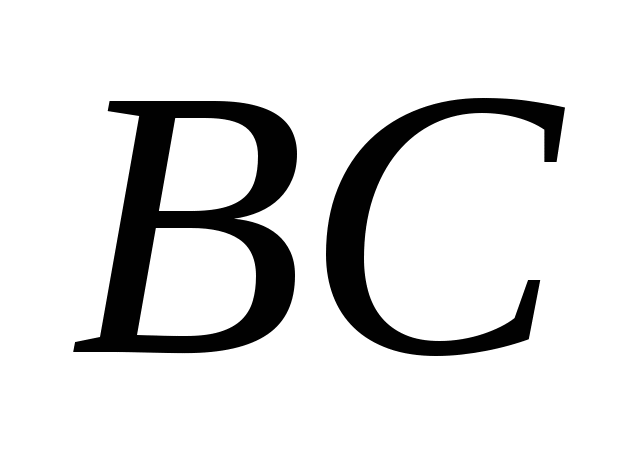
Решение.
В - 1
1.
![]()
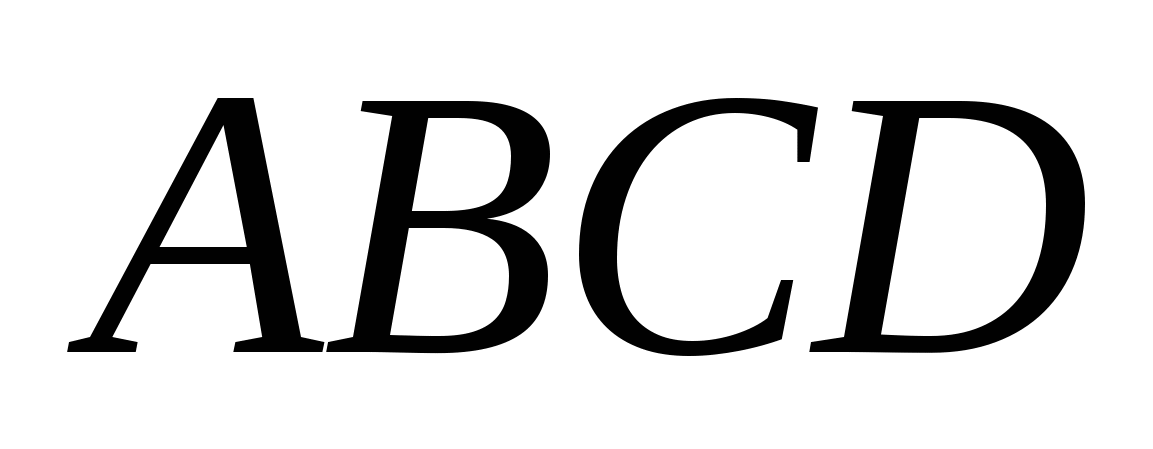
![]()
![]()
![]()
1. ![]() - середина отрезка
- середина отрезка ![]()
2. 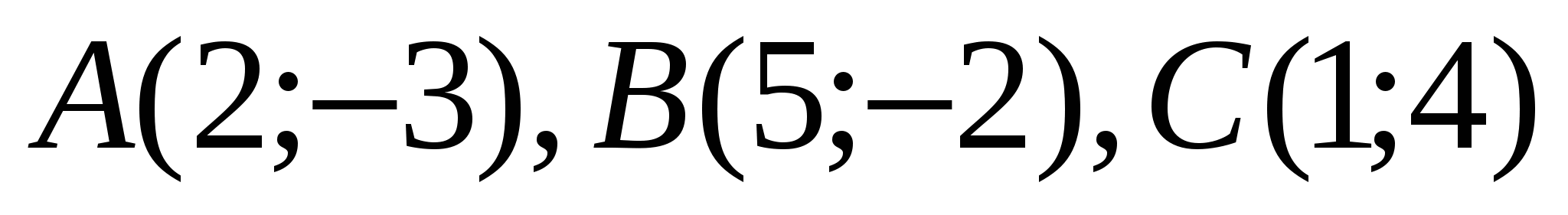
3. ![]()
2.
![]()
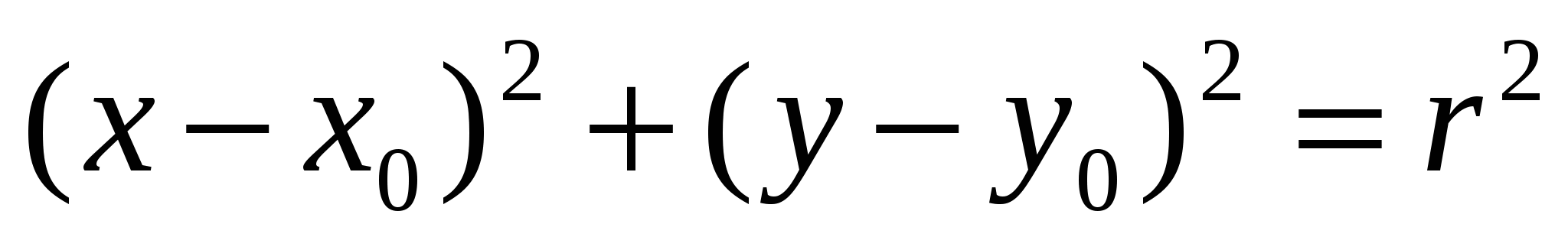
![]()
![]()
![]()
![]()
1. ![]()
2. ![]() и
и ![]() , значит
, значит ![]()
![]()
![]() Значит
Значит ![]() , т.е.
, т.е. ![]()
Решение
В - 2
1. 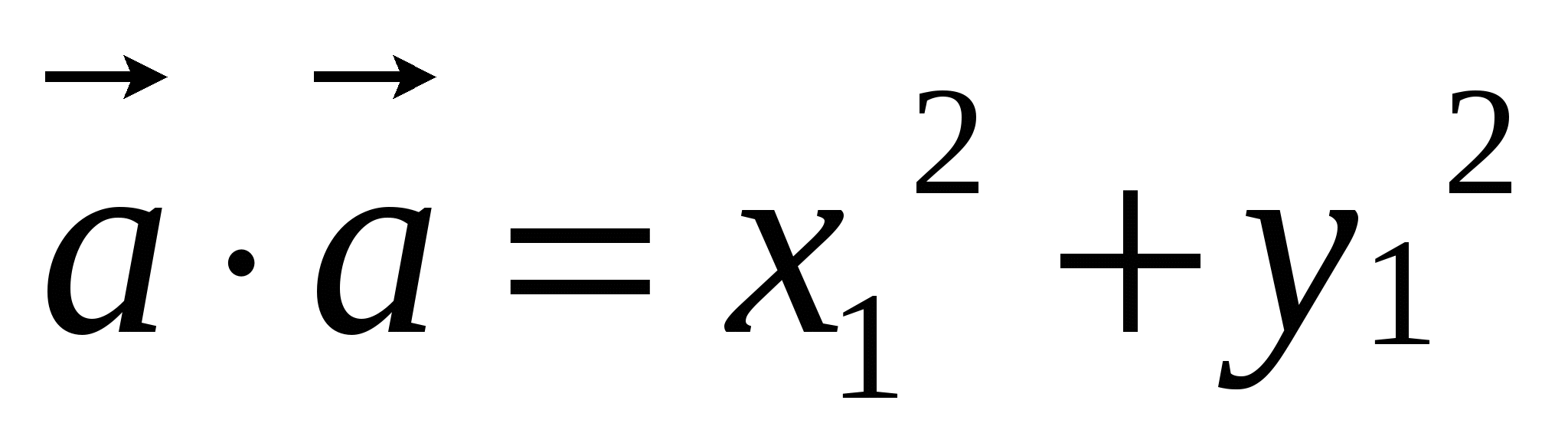 ,
,
т.к. по определению угла между векторами ![]() , то
, то ![]()
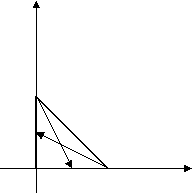
2.
![]()
![]()
![]()
-
Пусть
 - искомая площадь
- искомая площадь -
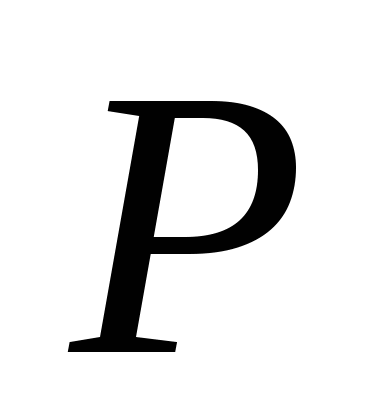
-
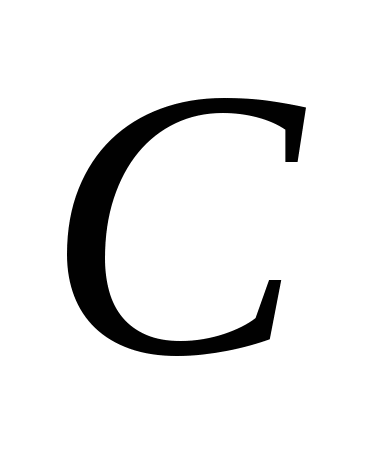
-

-
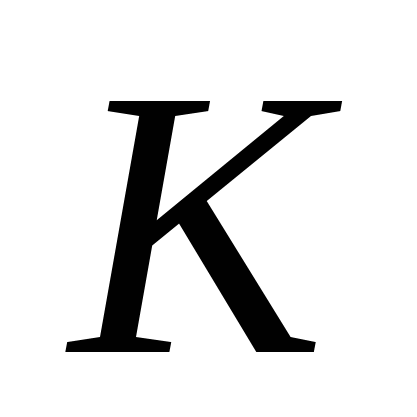
-
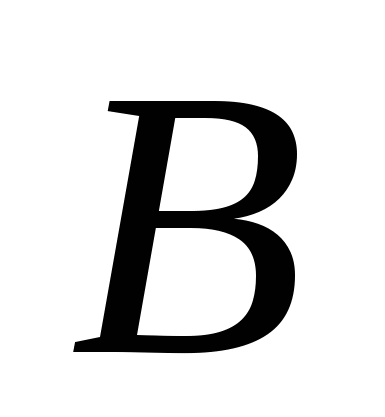
Ответ: ![]()
Литература
-
Г.В. Апостолова «Геометрия 8» Киев «Генеза» 2008.
-
Г.В. Апостолова «Геометрия 9» Киев «Генеза» 2009.
-
А.В. Погорелов «Геометрия 7 - 11 » Москва «Просвещение» 1989.
-
А.С. Атанасян «Геометрия 7 - 9 » Москва «Просвещение» 1990.