- Учителю
- Урок по алгебре и началам анализа в 11 классе 'Бенефис одной задачи'
Урок по алгебре и началам анализа в 11 классе 'Бенефис одной задачи'
Урок «Бенефис одной задачи»
11 класс
Учитель математики высшей категории
МОУ «СОШ № 12» г. Щекино Тульской области
ТИМОФЕЕВА Галина Александровна
Цели: - рассмотреть различные способы решения одной задачи;
- развитие творчества, логического мышления, речи, вычислительных навыков и навыков самостоятельной работы;
- воспитание интереса к математике, расширение кругозора.
Ход занятия.
-
Организационный момент.
-
Решение задачи.
-
Подведение итогов занятия. Задание на дом.
Оборудование.
-
мультимедийный проектор, компьютер;
-
плакат с высказываниями о математике;
-
экран.
Организационный момент.
- Здравствуйте, садитесь!
- Сегодня у нас не совсем обычный урок, а урок - бенефис - бенефис одной задачи. Одним из требований к уроку бенефису является возможность увидеть несколько способов решения задачи.
Урок -бенефис - это урок - отчет о самостоятельных домашних исследованиях.
И сегодня мы рассмотрим 6 способов решения одной задачи, которая была вам представлена для обдумывания неделю назад.
Решение задачи.
Познакомит нас с «героиней» сегодняшнего занятия -
ЗАДАЧА. На графике функции у = |3х - 2| найдите точку, ближайшую к точке А(3;0).
Решение.
ООФ: х
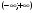
ОЗФ: у

Зададим данную функцию в виде двух аналитических выражений:
у = |3х - 2| = 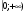
Построим график данной функции.
х
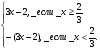
2
у
0
4
у = 3х - 2, х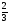
х
0
-2
у
2
8
у = 2 - 3х, х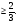
Наша задача сводится к нахождению расстояния АК, где АК 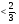 l1.
l1.
Это можно сделать несколькими способами, а именно:
1. используя подобие треугольников;
2. теорему Пифагора;
3. через угловые коэффициенты и взаимное расположение прямых на плоскости;
4. координатный способ;
5. с помощью производной;
6. используя формулу нахождения расстояния от точки до прямой.
1 способ. (на доске)
По графику функции видно, что 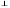
Рассмотрим треугольник АКС. По теореме Пифагора имеем: АС2 = СК2 + АК2.
Выразим через х и у СК и АК.
СК = 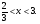 ; АК =
; АК = 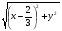 .
.
Заметим, что АС = АО - ОС = 3 - 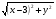
Поэтому имеет место система 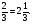
Воспользовавшись подстановкой у = 3х - 2, составляем уравнение 30х2 - 47х + 18 = 0.
Решив его, получаем: х1 =0,9 и х2 = 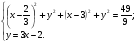
х2 - не удовлетворяет области допустимых значений. Поэтому у = 3 ·0,9 - 2 = 0,7.
Ответ: К(0,9; 0,7).
2 способ. (через проектор)
Проведем АЕ 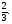 ОА, точка Е(3; 7). Получим ∆ САЕ ~ ∆ АКС.
ОА, точка Е(3; 7). Получим ∆ САЕ ~ ∆ АКС.
Из ∆ САЕ получим: СЕ = 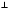 .
.
Отсюда S∆ САЕ =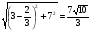 АС· АЕ =
АС· АЕ =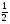 .
.
Но S∆ САЕ =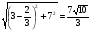 АК· СЕ, значит, АК =
АК· СЕ, значит, АК = 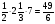 .
.
А теперь выразим расстояние между двумя точками А и К через их координаты:
АК = 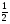 .
.
Составим и решим систему уравнений: 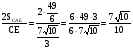
Получим: х=0,9; у=0,7.
Ответ: К(0,9; 0,7).
3 способ (на доске)
При х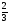 функция у = |3х - 2| имеет вид: у = 3х - 2, а ее графиком является прямая l1.
функция у = |3х - 2| имеет вид: у = 3х - 2, а ее графиком является прямая l1.
Угловой коэффициент k прямой l1 равен 3. так как АК 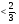 l1, то угловой коэффициент k1 прямой АК связан с коэффициентом k соотношением k1 = -
l1, то угловой коэффициент k1 прямой АК связан с коэффициентом k соотношением k1 = - 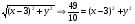 , т.е. k1 = -
, т.е. k1 = -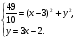 .
.
Тогда уравнение прямой АК имеет вид: у = - 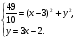 (х - 3).
(х - 3).
Точка пересечения прямых АК и l1 определяется системой: 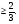
Решение этой системы дает точку К(0,9; 0,7).
Ответ: К(0,9; 0,7).
4 способ (через проектор)
Выразим длину отрезка АК через х и у.
АК = 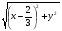 .
.
По условию у = 3х - 2, поэтому имеем равенство: АК = 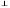 .
.
По условию задачи расстояние АК - кратчайшее. Оно достигается когда (х-0,9)2=0, т.е. при х = 0,9. тогда у=3·0,9 - 2 = 0,7.
Ответ: К(0,9; 0,7).
5 способ (на доске)
В этом способе воспользуемся формулой для нахождения расстояния от точки до прямой: от А(хо; уо) до прямой ах+bу +с=0 по формуле d = 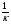 .
.
Найдем расстояние от точки А(3,0) до прямой у= 3х -2 или 3х -у -2 =0.
d = 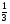 .
.
АК = 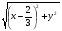 и у= 3х -2.
и у= 3х -2.
Тогда 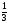 ;
;
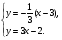 ;
;
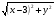 ;
;
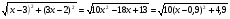 ;
;
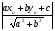 ;
;
(10х -9) = 0;
10х-9 =0;
х = 0,9;
у = 0,7.
Ответ: К(0,9; 0,7).
6 способ (через проектор)
Выразим через х расстояние от точки А до точки К.
АК = 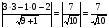 ,где
,где 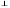
Обозначим f(x)= 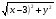 и найдем f'(x)=20x -18.
и найдем f'(x)=20x -18.
f '(x)= 0 20x - 18 = 0;
20x =18;
x =0,9, заметим, что 0,9 (
(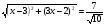 .
.
Кроме того f '(0,7)<0 и f '(1)>0,следовательно, функция f(x) достигает минимума в точке х=0,9.
Найдем значение функции f(x) на границах интервала (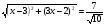 и при х = 0,9.
и при х = 0,9.
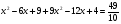 ; f(3)=49; f(0,9)=4,9.
; f(3)=49; f(0,9)=4,9.
Сравнив эти значения, мы убедились, что f(x) принимает наименьшее значение при х=0,9.
Тогда у= 0,7.
Ответ: К(0,9; 0,7).
Подведение итогов.
Итак, сегодня на уроке мы рассмотрели шесть способов решения одной задачи, а именно:
1. используя подобие треугольников;
2. теорему Пифагора;
3. через угловые коэффициенты и взаимное расположение прямых на плоскости;
4. координатный способ;
5. с помощью производной;
6. используя формулу нахождения расстояния от точки до прямой.
Какой способ решения вам понравился? Почему?
Домашнее задание: найдите задачу с несколькими способами решения.