Методическая разработка на тему:

Решение показательных уравнений и неравенств.

Функцию вида y = a^x, где a > 0 и a ≠ 1, называют показательной функцией.

Основные свойства показательной функции y = a^x:График показательной функции

Графиком показательной функции является экспонента:

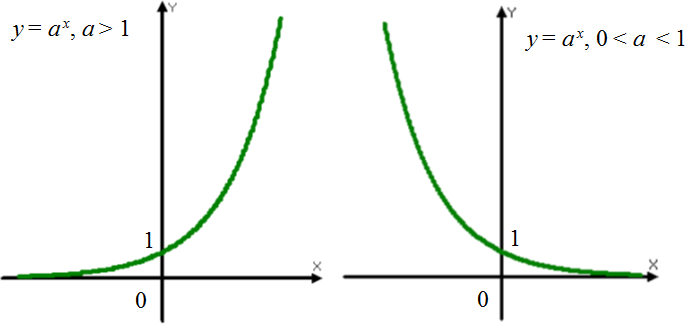
Графики показательных функций (экспоненты)

Решение показательных уравнений

Показательными называются уравнения, в которых неизвестная переменная находится только в показателях каких-либо степеней.

Для решения показательных уравнений требуется знать и уметь использовать следующую несложную теорему:

Теорема 1. Показательное уравнение a^f(x) = a^g(x) (где a > 0, a ≠ 1) равносильно уравнению f(x) = g(x).

Помимо этого, полезно помнить об основных формулах и действиях со степенями:

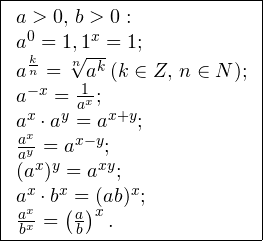
Пример 1. Решите уравнение:

Решение: используем приведенные выше формулы и подстановку:

Уравнение тогда принимает вид:

Дискриминант полученного квадратного уравнения положителен:

Это означает, что данное уравнение имеет два корня. Находим их:

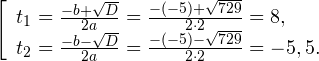
Переходя к обратной подстановке, получаем:

Второе уравнение корней не имеет, поскольку показательная функция строго положительна на всей области определения. Решаем второе:

С учетом сказанного в теореме 1 переходим к эквивалентному уравнению: x = 3. Это и будет являться ответом к заданию.

Ответ: x = 3.

Пример 2. Решите уравнение:

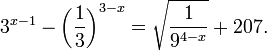
Решение: ограничений на область допустимых значений у уравнения нет, так как подкоренное выражение имеет смысл при любом значении x (показательная функция y = 9^4-x положительна и не равна нулю).

Решаем уравнение путем равносильных преобразований с использованием правил умножения и деления степеней:

Последний переход был осуществлен в соответствии с теоремой 1.

Ответ: x = 6.

Пример 3. Решите уравнение:

Решение: обе части исходного уравнения можно поделить на 0,2^x. Данный переход будет являться равносильным, поскольку это выражение больше нуля при любом значении x (показательная функция строго положительна на своей области определения). Тогда уравнение принимает вид:

Ответ: x = 0.

Пример 4. Решите уравнение:

Решение: упрощаем уравнение до элементарного путем равносильных преобразований с использованием приведенных в начале статьи правил деления и умножения степеней:

Деление обеих частей уравнения на 4^x, как и в предыдущем примере, является равносильным преобразованием, поскольку данное выражение не равно нулю ни при каких значениях x.

Ответ: x = 0.

Пример 5. Решите уравнение:

Решение: функция y = 3^x, стоящая в левой части уравнения, является возрастающей. Функция y = -x-2/3, стоящая в правой части уравнения, является убывающей. Это означает, что если графики этих функций пересекаются, то не более чем в одной точке. В данном случае нетрудно догадаться, что графики пересекаются в точке x = -1. Других корней не будет.

Ответ: x = -1.

Пример 6. Решите уравнение:

Решение: упрощаем уравнение путем равносильных преобразований, имея в виду везде, что показательная функция строго больше нуля при любом значении x и используя правила вычисления произведения и частного степеней, приведенные в начале статьи:

Ответ: x = 2.

Решение показательных неравенств

Показательными называются неравенства, в которых неизвестная переменная содержится только в показателях каких-либо степеней.

Для решения показательных неравенств требуется знание следующей теоремы:

Теорема 2. Если a > 1, то неравенство a^f(x) > a^g(x) равносильно неравенству того же смысла: f(x) > g(x). Если 0 < a < 1, то показательное неравенство a^f(x) > a^g(x) равносильно неравенству противоположного смысла: f(x) < g(x).

Пример 7. Решите неравенство:

Решение: представим исходное неравенство в виде:

Разделим обе части этого неравенства на 3^2x, при этом (в силу положительности функции y = 3^2x) знак неравенства не изменится:

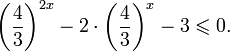
Воспользуемся подстановкой:

Тогда неравенство примет вид:

Итак, решением неравенства является промежуток:

переходя к обратной подстановке, получаем:

Левое неравенства в силу положительности показательной функции выполняется автоматически. Воспользовавшись известным свойством логарифма, переходим к эквивалентному неравенству:

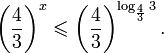
Поскольку в основании степени стоит число, большее единицы, эквивалентным (по теореме 2) будет переход к следующему неравенству:

Итак, окончательно получаем ответ:

Пример 8. Решите неравенство:

Решение: используя свойства умножения и деления степеней, перепишем неравенство в виде:

Введем новую переменную:

С учетом этой подстановки неравенство принимает вид:

Умножим числитель и знаменатель дроби на 7, получаем следующее равносильное неравенство:

Итак, неравенству удовлетворяют следующие значения переменной t:

Тогда, переходя к обратной подстановке, получаем:

Поскольку основание степени здесь больше единицы, равносильным (по теореме 2) будет переход к неравенству:

Окончательно получаем ответ:

Пример 9. Решите неравенство:

Решение:

Делим обе части неравенства на выражение:

Оно всегда больше нуля (из-за положительности показательной функции), поэтому знак неравенства изменять не нужно. Получаем:

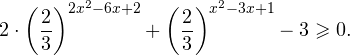
Воспользуемся заменой переменной:

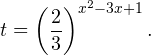
Исходное уравнение тогда принимает вид:

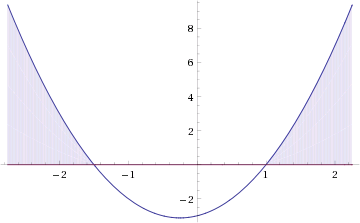
Итак, неравенству удовлетворяют значения t, находящиеся в промежутке:

Переходя к обратной подстановке получаем, что исходное неравенство распадается на два случая:

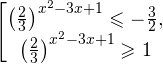
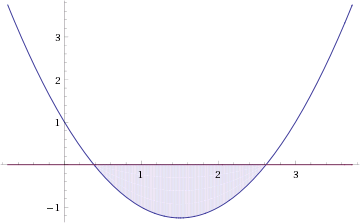
Первое неравенство решений не имеет в силу положительности показательной функции. Решаем второе:

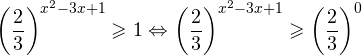
Поскольку основание степени в данном случае оказалось меньше единицы, но больше нуля, равносильным (по теореме 2) будет переход к следующему неравенству:

</</font>

Итак, окончательный ответ:

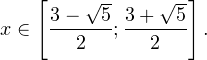
Пример 10. Решите неравенство:

Решение:

Ветви параболы y = 2x+2-x² направлены вниз, следовательно она ограничена сверху значением, которое она достигает в своей вершине:

Ветви параболы y = x²-2x+2, стоящей в показателе, направлены вверх, значит она ограничена снизу значением, которое она достигает в своей вершине:

Вместе с этим ограниченной снизу оказывается и функция y = 3^x2-2x+2, стоящая в правой части уравнения. Она достигает своего наименьшего значения в той же точке, что и парабола, стоящая в показателе, и это значение равно 3¹ = 3. Итак, исходное неравенство может оказаться верным только в том случае, если функция слева и функция справа принимают в одной точке значение, равное 3 (пересечением областей значений этих функций является только это число). Это условие выполняется в единственной точке x = 1.

Ответ: x = 1.