Конспект урока-повторения в 8 классе по теме «Четырехугольники»

Тема урока: « Четырехугольники», 8 класс

Учитель математики МБОУ СОШ № 25 г. Воронеж

Жукова Елена Витальевна

Цели урока

Обучающая цель: обеспечить усвоение учащимися определений и свойств четырехугольников, обобщить и систематизировать знания о четырехугольниках; отработать навыки решения базовых типов задач по данной теме.

Воспитательная цель: воспитание мотивов учения, положительного отношения к получению знаний; воспитание дисциплинированности, воспитание эстетических представлений.

Развивающая цель: развитие умения устанавливать общие свойства фигур; умения классифицировать; умений применять знания на практике; умения работать в нужном темпе; умения действовать самостоятельно.

Задачи урока

1. Учебно-познавательные задачи, направленные на фор­мирование умений и навыков по осво­ению систематических знаний: отработка понятий, выявление связей между четырехугольниками;

2. Учебно-познавательные задачи, направленные на фор­мирование навыка самостоятельного приобретения и интеграции знаний: обобщить знания, умения и навыки по теме; проанализировать информацию о новом четырехугольнике дельтоиде.

3. Учебно-практические и учебно-познавательные задачи, направленные на формирование ИКТ-компетентности обучающихся: формирование навыков обучающихся выполнения тестов за компьютером.

4. Учебно-практические задачи, направленные на формиро­вание навыка сотрудничества: формирование навыков групповой работы по исследованию свойств дельтоида.

5. Учебно-практические и учебно-познавательные зада­чи, направленные на формирование навыка само­организации и саморегуляции: отработка навыков самостоятельной работы.

6. Учебно-практические и учебно-познавательные задачи, направленные на формирование навыка рефлексии: формирование навыков самооценки знаний и умений.

Тип урока: урок обобщения, систематизации знаний, умений и навыков.

Методы обучения: метод программированных заданий, исследовательский, алгоритмический методы.

Оборудование: презентация, раздаточный материал (схемы, задачи разного уровня, фигуры), компьютерный тест.

Эпиграф: «Сравнение математических фигур и величин служит материалом для игр и обучения мудрости». И. Песталоцци.

Ход урока.

1. Организационный момент.

Гениальный математик и физик Максвелл учился плохо, особенно по арифметике, пока не начал изучать этот предмет. Он быстро стал лучшим учеником в школе.

• О каком разделе математики идет речь? ( О геометрии)

2. Актуализация знаний.

« Я думаю, что никогда до настоящего времени мы не жили в такой геометрический период. Все вокруг - геометрия». Эти слова, сказанные великим французским архитектором Ле Корбюзье в начале XX века, очень точно характеризуют и наше время. Мир, в котором мы живем, наполнен геометрией домов и улиц, гор и полей, творениями природы и человека. Так же, как самое большое здание складывается из маленьких кирпичей, так и сложные геометрические фигуры составляются из простейших геометрических фигур.

• Какие геометрические фигуры изучаются в курсе геометрии 8 класса? (Четырехугольники)

Итак, тема нашего урока «Четырехугольники». На уроке мы обобщим знания, умения и навыки по этой теме. Для этого необходимо повторить теоретические сведения, проверить ваше творческое домашнее задание. А также проведем компьютерное тестирование ваших знаний о четырехугольниках, решим основные типы задач, проведем небольшое исследование.

Сегодня на уроке вам предстоит оценить себя самим.

Перед вами на партах лежит таблица, которую вы в конце урока заполните плюсами и минусами за каждый вид вашей деятельности .

Вспомним с вами основные понятия по теме «Четырехугольники». Для этого я буду задавать вопрос, а вы по цепочке будете на них отвечать.

• Что называется четырехугольником?

• Перечислите основные виды четырехугольников?

• Сформулируйте определение параллелограмма.

• Назовите основные свойства параллелограмма.

• Что называется прямоугольником?

• Какое новое свойство у прямоугольника?

• Что такое ромб?

• Сформулируйте особое свойство ромба.

• Что называется квадратом?

• Перечислите свойства квадрата.

• Что такое трапеция?

• Назовите виды трапеции .

3. Учебно-познавательная деятельность

• Проверка домашнего задания.

Вашим домашним заданием было найти сведения из истории четырехугольников. Сейчас мы заслушаем только 2 учеников, остальные сдадут доклады на проверку.

• Тестирование.

Мы повторили основные теоретические сведения о четырехугольниках.

Пришло время проверить ваши знания теории. Для этого вам необходимо пройти тестирование.

1 уровень - заполняет схему и таблицу на своих местах (раздаточный материал на парте). Можно пользоваться учебником. Потом проверим вашу работу.

2 уровень - проходит компьютерное тестирование. Для этого вам нужно пройти к компьютерам.

(Вопросы к тестам в приложении).

№

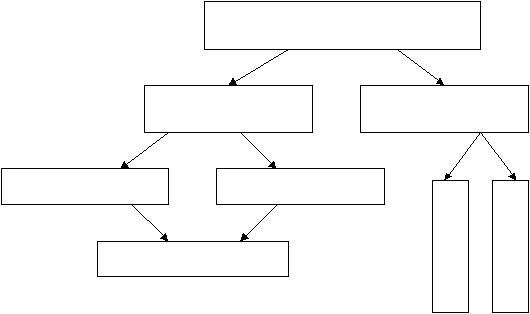
СВОЙСТВА ЧЕТЫРЕХУГОЛЬНИКОВ

параллело-грамм

ромб

прямоуголь-ник

Квад-рат

1

Противолежащие стороны параллельны и равны

2

Все стороны равны

3

Противолежащие углы равны

4

Все углы прямые

5

Диагонали пересекаются и точкой пересечения делятся пополам

6

Диагонали равны

7

Диагонали взаимно перпендикулярны и являются биссектрисами углов

4. Интеллектуально-преобразовательная деятельность.

1.Практическая работа исследовательского характера.

В школьном курсе геометрии изучаются только 5 видов четырехугольников. Сегодня на уроке предлагаю выйти за рамки школьной программы и познакомиться с еще одним четырехугольником. Для этого мы проведем небольшое исследование.

Перед вами четырехугольник, который называется ромбоид или дельтоид. Ваша задача: изучить свойства данного четырехугольника ( 1 ряд изучает стороны, 2 ряд - меньшую диагональ, 3 ряд - большую диагональ).

Давайте обсудим ваши предположения и запишем его определение и свойства в тетрадь.

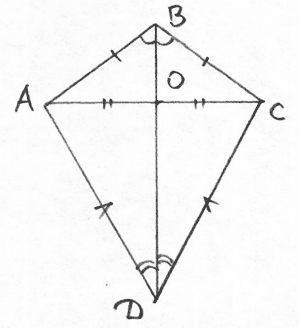
Ромбоид ( дельтоид )- это четырехугольник, у которого две стороны, прилежащие к одной вершине, попарно равны.

Свойства:

• Меньшая диагональ точкой пересечения делится пополам.

• Диагонали перпендикулярны.

• Большая диагональ является биссектрисой углов.

• Меньшая диагональ делит его на два равнобедренных треугольника.

2. Решение задач.

(У доски 2 ученика одновременно решают разные задачи с оформлением, остальные по уровням в тетради. Проверка решения задач всем классом.)

Задача №1(1 уровень)

Найдите углы ромба, если один из его углов равен 20°.

Ответ: 160°, 20°, 160°.

Задача № 2(2 уровень)

Стороны параллелограмма относятся как 1:2, а его периметр равен

30 см. Найдите стороны параллелограмма.

Ответ: 5 см, 10 см.

5. Рефлексивная деятельность.

1. Домашнее задание.

• Составить таблицу свойств и признаков четырехугольников.

(Для этого давайте обсудим, как лучше составить эту таблицу: что будем писать в строках, что в столбцах. Я предлагаю следующие таблицы. А вы как думаете?)

Четырехугольник

параллелограмм

прямоугольник

ромб

квадрат

Свойства

Признаки

Четырехугольник

Свойства

Признаки

параллелограмм

прямоугольник

ромб

квадрат

• Придумать сказку о четырехугольниках с использованием свойств и признаков.

2. Итог урока

Подведем итоги урока.

На парте лежит таблица самооценки ваших знаний, о которой я говорила в начале урока. Там же записаны критерии самооценки.

«+» - активное участие или правильное решение;

«+ -» - частичное участие или неполное решение;

«-» - не принял участие или неверное решение.

Фамилия

Имя

Домашнее задание

Тестирова-ние

Задача

Практическая работа

Работа на уроке

Заполните эту таблицу и сдайте мне, чтобы я поставила окончательную оценку вам за урок. В журнал пойдут только хорошие оценки.

На следующих уроках мы продолжим изучать четырехугольники. Повторим их признаки, рассмотрим задачи, предлагающиеся на контрольной работе, на ГИА, на ЕГЭ.

Дополнительные задачи:

Задача № 1. (2 уровень)

Один из углов параллелограмма в пять раз больше другого. Найти углы параллелограмма.

Задача № 2. (2 уровень)

Диагонали прямоугольника АВСD пересекаются в точке О,

АВО = 36°. Найдите АОD.

Задача № 3. (1 уровень)

Найдите углы прямоугольной трапеции, если один из ее углов равен 20°.

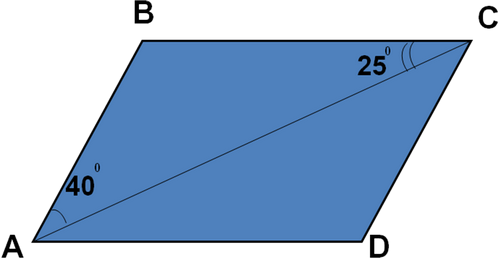
Задача № 4. (1 уровень)

Найдите углы параллелограмма ABCD.

Приложение №1

Тест по теме: «Четырехугольники».

Четырёхугольник, у которого только две стороны параллельны

1. ромб

2. трапеция

3. квадрат

4. прямоугольник

Трапеция, у которой один из углов равен 90 градусов, называется

1. равнобедренной

2. остоугольной

3. тупоугольной

4. прямоугольной

Любой ромб является:

1. квадратом

2. прямоугольником

3. параллелограммом

4. трапецией

Если в параллелограмме диагонали перпендикулярны, то этот параллелограмм:

1. ромб

2. квадрат

3. прямоугольник

4. нет правильного ответа

Любой прямоугольник является:

1. ромбом

2. квадратом

3. параллелограммом

4. нет правильного ответа

Найдите неверное утверждение.

1. квадрат - одновременно параллелограмм и прямоугольник

2. угол между стороной и диагональю квадрата равен 45 град.

3. диагонали квадрата взаимно перпендикулярны

4. существует квадрат, который не является ромбом

Если в четырёхугольнике диагонали перпендикулярны, то этот четырёхугольник:

1. ромб

2. квадрат

3. прямоугольник

4. нет правильного ответа

Квадрат - это…

1. параллелограмм с равными сторонами

2. параллелограмм с равными углами

3. прямоугольник, у которого все стороны равны

4. нет правильного ответа

У этого четырёхугольника диагонали всегда равны?

1. трапеция

2. прямоугольник

3. ромб

4. параллелограмм

Найдите неверное утверждение.

1. У прямоугольника углы - прямые

2. у ромба все стороны равны

3. у квадрата диагонали взаимно перпендикулярны

4. у трапеции стороны попарно параллельны

Приложение №2

История четырехугольников

В древних египетских и вавилонских документах встречаются следующие виды четырехугольников: квадраты, прямоугольники, равнобедренные и прямоугольные трапеции. В частности, в клинописных математических табличках встречаются прямоугольные треугольники, рассеченные параллелями к одному из катетов на прямоугольной трапеции.

Четырёхугольник, у которого противоположные стороны попарно параллельны, называется параллелограммом

Термин «параллелограмм» греческого происхождения, который был введен Евклидом. Он называл параллелограмм "параллельно-линейной площадью". Слово parallhlogrammou составлено из parallhloz и grammh-- "линия" это слово дало основу для термина "параллелограмм".

Понятие параллелограмма и некоторые его свойства были известны пифагорейцам.

В «Началах» Евклида доказывается следующая теорема: в параллелограмме противоположные стороны равны и противоположные углы равны, а диагональ разделяет его пополам. Евклид не упоминает о том, что точка пересечения диагоналей параллелограмма делит их пополам. Он не рассматривает ни прямоугольника, ни ромба. Полная версия параллелограммов была разработана к концу средних веков и появилась в учебниках лишь с 17 века. Все теоремы о параллелограммах основываются непосредственно или косвенно на аксиоме параллельности Евклида.

Первые геометры, в том числе и Евклид, мыслили прямоугольник, вписанный в круг.

Ромб - это параллелограмм, у которого все стороны равны.

Слово «ромб» тоже греческого происхождения, оно означало в древности вращающееся тело, веретено, юлу. Образ ромба был связан первоначально с сечением, проведенным в обмотанном веретене.

Есть и другое значение.Термин «ромб» образован от греч. ρομβος - «бубен». Если сейчас бубны в основном делают круглой формы, то раньше их делали как раз в форме квадрата или ромба. Кстати, название карточной масти бубны, знаки которой имеют ромбическую форму, происходит ещё с тех времён, когда бубны не были круглыми.

Слово «ромб» впервые употребляется у Герона и Паппа Александрийского.

Квадрат - это прямоугольник, у которого все стороны равны.

Термин «квадрат» происходит от латинского quadratum (quadrare- сделать четырехугольным), перевод с греческого -четырехугольник.

Трапеция - это четырёхугольник, где две стороны параллельны, а две другие не параллельны.

Трапеция - слово греческое, означавшее в древности «столик». В «Началах» термин «трапеция» применяется не в современном, а в другом смысле: любой четырехугольник (не параллелограмм). «Трапеция» в нашем смысле встречается впервые у древнегреческого математика Посидония (1век). В средние века трапецией называли, по Евклиду, любой четырехугольник (не параллелограмм); лишь в 18 веке это слово приобретает современный смысл.