Карта темы (ФГОС)_Сложение и вычитание дробей с разными знаменателями _6 кл

Город_Лобня_Пухова Любовь Кимовна

ТЕМАТИЧЕСКОЕ И ПОУРОЧНОЕ ПЛАНИРОВАНИЕ СОДЕРЖАНИЯ КУРСА МАТЕМАТИКИ С УЧЁТОМ ИСПОЛЬЗОВАНИЯ СРЕДСТВ ЦОР

И ЗДОРОВЬЕСБЕРЕГАЮЩИХ ТЕХНОЛОГИЙ

ПРИ ОБУЧЕНИИ ТЕМЕ ШКОЛЬНОГО КУРСА МАТЕМАТИКИ

КАРТА ТЕМЫ

«СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ С РАЗНЫМИ ЗНАМЕНАТЕЛЯМИ», 6 КЛАСС,

учебник «МАТЕМАТИКА 6, авторы: Н.Я. Виленкин. В.И. Жохов. А.С. Чесноков, С.И.Шварцбурд»

Тематическое планирование темы «Сложение и вычитание дробей с разными знаменателями » составлено на основе авторской программы к УМК «Математика» для 5-6 классов, авторы Н.Я.Виленкин и др. (М.: Мнемозина). При планировании на изучение темы отводится 25 часов по 6 часов в неделю, дана характеристика основных видов деятельности учащихся (Таблица 1).

Учитывая цели обучения по теме «Сложение и вычитание дробей с разными знаменателями» (сам. раб.2) и основываясь на тематическом планировании темы (Таблица 1) составлена карта изучения темы (Таблица 2).

Таблица 1.

Тематическое планирование темы «Сложение и вычитание дробей с разными знаменателями»,

6 часов в неделюСодержание

материала

Кол-во

часов

Характеристика основных видов деятельности ученика

(на уровне учебных действий)

ГЛАВА 1. Обыкновенные дроби.

§ 2. Сложение и вычитание дробей с разными знаменателями (25 часов)

2.8

Основное свойство дроби

3

Формулируют основное свойство обыкновенной дроби, записывают его с помощью букв.

С помощью координатного луча объясняют равенство дробей с разными знаменателями.

Записывают дробь, равную данной, используя основное свойство дроби; находят значение выражения. Решают задачи на применение основного свойства дроби, исследуют ситуации, требующие оценки действия в соответствии с поставленной задачей. Приводят свои примеры на равенство дробей с разными знаменателями. сопоставляя и отбирая информацию. Формулируют объяснение, какое натуральное число надо записать вместо буквы в числителе или знаменателе, чтобы выполнялось верное равенство дробей

2.9

Сокращение дробей

3

Выполняют умножение и деление числителя и знаменателя обыкновенной дроби на заданное число.

Сокращают дроби, применяют распределительный закон умножения при нахождении значения выражения, а затем сокращают дробь; решают задачи на нахождение части килограмма, которую составляют граммы и приводят примеры, какую часть часа или развернутого угла составляет данное число минут или градусов. Обнаруживают и устраняют ошибки логического (в ходе решения) и арифметического (в вычислении) характера. Объясняют выбор действия в соответствии с поставленной задачей и условиями ее реализации, самостоятельно оценивают результат.

2.10

Приведение дробей к общему знаменателю

3

Формулируют алгоритм приведения дроби к наименьшему общему знаменателю, алгоритм сравнения дробей с разными знаменателями. Объясняют, как привести дроби к новому знаменателю; выводят понятие дополнительный множитель, формулируют правило: как привести дробь к наименьшему общему знаменателю.

Приводят примеры дробей с разными знаменателями и объясняют, как их привести к наименьшему общему знаменателю; выполняют устные вычисления. Используют различные приемы проверки правильности выполняемых заданий.

2.11

Сравнение, сложение и вычитание дробей с разными знаменателями

8

Объясняют правило: как сравнить две дроби с разными знаменателями; сравнивают дроби с разными знаменателями; исследуют и объясняют преобразование обыкновенных дробей, объясняют ситуации, требующие сравнения чисел и их упорядочения.

Складывают и вычитают дроби с разными знаменателями; изображают результат на координатном луче.

Приводят примеры с указанием компонентов сложения и вычитания дробей с разными знаменателями. Объясняют решение уравнений, содержащих дроби с разными знаменателями.

Приводят примеры на сравнение, сложение и вычитание дробей с разными знаменателями.

2.12

Сложение и вычитание смешанных чисел

8

Складывают и вычитают смешанные числа, прогнозируют результат вычислений, находят значение выражения, моделируют ситуацию, иллюстрирующую арифметическое действие и ход его выполнения.

Объясняют, как иллюстрировать сложение и вычитание дробей с разными знаменателями в буквенных обозначениях на координатном луче. Объясняют, какая дробь из предложенных дробей с разными знаменателями будет расположена левее (правее) на координатном луче.

Таблица 2.

Карта изучения темы «Сложение и вычитание дробей с разными знаменателями»Ц2

Ц3

Ц1

Ц2

Ц3

Ц1

Ц2

Ц3

Ц1

Ц2

Ц2

Ц3

Ц4

Ц5

Ц2

Ц5

пункт

2.8

пункт

2.8

пункт

2.8

пункт

2.9

пункт

2.9

пункт

2.9

пункт

2.10

пункт

2.10

пункт

2.10

пункт

2.11

пункт

2.11

пункт

2.11

пункт

2.11

пункт

2.11

пункт

2.11

контрольная

работа

анализ контрольной работы

18

19

20

21

22

23

24

25

Ц1

Ц2

Ц2

Ц3

Ц4

Ц5

Ц2

Ц5

пункт

2.12

пункт

2.12

пункт

2.12

пункт

2.12

пункт

2.12

пункт

2.12

контрольная

работа

анализ контрольной работы

2. Блок актуализации знаний учащихся

Знают: обыкновенные дроби, правильные и неправильные дроби, смешанные числа, любое натуральное число можно записать в виде дроби с любым натуральным знаменателем, свойство деления суммы на число

Умеют: сравнивать дроби с одинаковыми знаменателями, складывать и вычитать дроби с одинаковыми знаменателями, производить сложение и вычитание смешанных чисел, записывать дробь в виде частного

3. Предметные результаты

Выпускник научится (1 уровень - базовый)

Знать: 1) что две равные дроби являются различными записями одного и того же числа;

2) какая дробь является несократимой;

3) какое число называют дополнительным множителем, наименьшим общим знаменателем;

4) как сложить смешанные числа;

5) определение правильного многоугольника.

Уметь: 1) анализировать по рисунку дроби с разными знаменателями;

2) формулировать основное свойство дроби;

3) составлять для данной дроби равную ей дробь, используя новый знаменатель;

4) приводить данную дробь к новому знаменателю;

5) находить дополнительный множитель;

6) составлять для данной дроби несократимую дробь;

7) приводить дроби к наименьшему общему знаменателю;

8) отмечать на координатном луче дроби с разными знаменателями;

9) выполнять действия по нахождению значения выражения, содержащего дроби с разными знаменателями;

10) сравнивать две дроби с разными знаменателями и упорядочивать такие дроби;

11) решать уравнения с дробями;

12) решать текстовые задачи на сложение и вычитание дробей с разными знаменателями;

13) делать проверку сложения вычитанием при сложении дробей с разными знаменателями;

14) приводить примеры правильных многоугольников;

15) выделять целую и дробную части смешанной дроби.

Выпускник получит возможность научиться (2 уровень - углублённый)

Знать: 1) какое число может служить общим знаменателем двух дробей;

2) приемы сокращения дробей;

3) формулировать правило сравнения двух дробей с одинаковыми числителями и разными знаменателями;

4) на каких свойствах сложения основано сложение смешанных чисел.

Уметь:1) приводить дроби к наименьшему общему знаменателю, используя наименьшее общее кратное;

2) заменять десятичную дробь обыкновенной дробью и выполнять действия сложения и вычитания;

3) сравнивать и упорядочивать дроби с разными знаменателями, у которых числитель выражается в буквенном виде;

4) находить значение выражения с использованием свойства вычитания числа из суммы и суммы из числа и дробями с разными знаменателями;

5) отмечать на координатном луче дроби с разными знаменателями, числители и знаменатели которых выражены в буквенном виде;

6) выполнять действия по нахождению периметра правильного многоугольника, стороны которого выражены дробями с разными знаменателями;

7) упорядочивать смешанные числа с разными знаменателями;

8) решать текстовые задачи на движение с использованием дробей с разными знаменателями;

9) находить натуральные значение букв, входящих в дроби с разными знаменателями, при которых выполняется верное равенство.

IV. Образцы заданий итоговой контрольной работы

I уровень (базовый)

Баллы

II уровень (углубленный)

Баллы

1. Найдите значение выражения:

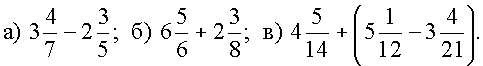
1

1. Найдите значение выражения:

1

2. На автомашину положили сначала т груза, а потом еще т . Сколько всего тонн груза положили на автомашину?

1

2. Путник в первый час прошел км, что на км меньше, чем во второй час, и на км больше, чем в третий час. Сколько километров прошел путник за эти три часа?

1

3 Ученица рассчитывала за ч приготовить уроки и ч потратить на уборку квартиры. Однако на все это у нее ушло на ч больше. Сколько времени потратила ученица на всю эту работу?

1

3. Хозяйка рассчитывала за ч приготовить обед и ч потратить на стирку белья. Однако на стирку у нее ушло на ч больше. Сколько времени хозяйка потратила на всю домашнюю работу?

1

4. Решите уравнение

1

4. Решите уравнение:

2

5^*.

Найдите две дроби, каждая из которых меньше , но больше

1

5^*. Разложите число 84 на два взаимно простых множителя четырьмя различными способами (разложения, отличающиеся только порядком множителей, считать за один способ).

2

V. Средства обучения

1) схема сложения чисел с разными знаменателями

2) блок-схема алгоритма приведения дроби к наименьшему общему знаменателю;

3) рисунок окружности и прямоугольника для равных дробей с разными знаменателями

4) рисунок координатного луча с изображением равных дробей с разными знаменателями;

5) схема сложения смешанных чисел с разными знаменателями

VI. Задания для внеаудиторной самостоятельной работы

I уровень

(базовый)

№ 237,238,268,239,271,297,299,300(а-д),308,328(а,в),341,335,339,359(а-д), 360, 367, 368, 385,390,391,392, 396,414,415,416,417,421

II уровень

(углубленный)

№ 240,269,270,256,257,262,290,294,298,300(е-ж),309,311,320,328(б,г),342,359(ж,з),364,3655,369,388,389,393,394,395,418,420

VII. Темы индивидуальных заданий

1) Изображение дробей на Руси

2) Использование дробей в Древнем Риме

3) Дружественные числа.

VIII. Метапредметные результаты: перечень учебных действий (умений) для освоения темы

Познавательные УУД

Регулятивные УУД

Коммуникативные УУД

Ученик научится:

• осуществлять поиск нужной информации, используя материал учебника и сведения, полученные от взрослых;

• использовать рисуночные и символические варианты математической записи;

• строить несложные модели математических понятий, задачных ситуаций;

• строить небольшие математические сообщения в устной форме;

• проводить сравнение (по одному или нескольким основаниям, наглядное и по представлению, сопоставление и противопоставление), понимать выводы, сделанные на основе сравнения;

• выделять в явлениях существенные и несущественные, необходимые и достаточные признаки;

• проводить аналогию и на ее основе строить выводы.

Ученик получит возможность научиться:

• под руководством учителя осуществлять поиск необходимой и дополнительной информации;

• работать с дополнительными текстами и заданиями;

• соотносить содержание схематических изображений с математической записью;

• моделировать задачи на основе анализа жизненных сюжетов;

• устанавливать аналогии; формулировать выводы на основе аналогии, сравнения, обобщения;

• строить рассуждения о математических явлениях;

• пользоваться эвристическими приемами для нахождения решения математических задач.

Ученик научится:

• принимать учебную задачу и следовать инструкции учителя;

• планировать свои действия в соответствии с учебными задачами и инструкцией учителя;

• выполнять действия в устной форме;

• учитывать выделенные учителем ориентиры действия в учебном материале;

• в сотрудничестве с учителем находить несколько вариантов решения учебной задачи, представленной на наглядно-образном уровне;

• вносить необходимые коррективы в действия на основе принятых правил;

• выполнять учебные действия в устной и письменной речи;

• осуществлять пошаговый контроль под руководством учителя в доступных видах учебно-познавательной деятельности.

Ученик получит возможность научиться:

• выполнять действия в опоре на заданный ориентир;

• в сотрудничестве с учителем, классом находить несколько вариантов решения учебной задачи;

• на основе вариантов решения практических задач под руководством учителя делать выводы о свойствах изучаемых объектов;

• выполнять учебные действия в устной, письменной речи и во внутреннем плане;

• самостоятельно оценивать правильность выполнения действия и вносить необходимые коррективы в действия с наглядно-образным материалом.

Ученик научится:

• принимать активное участие в работе парами и группами, используя речевые коммуникативные средства;

• допускать существование различных точек зрения;

• стремиться к координации различных мнений о математических явлениях в сотрудничестве; договариваться, приходить к общему решению;

• использовать в общении правила вежливости;

• использовать простые речевые средства для передачи своего мнения;

• контролировать свои действия в коллективной работе;

• понимать содержание вопросов и воспроизводить вопросы;

• следить за действиями других участников в процессе коллективной познавательной деятельности.

Ученик получит возможность научиться:

• строить понятные для партнера высказывания и аргументировать свою позицию;

• использовать средства устного общения для решения коммуникативных задач.

• корректно формулировать свою точку зрения;

• проявлять инициативу в учебно-познавательной деятельности;

• контролировать свои действия в коллективной работе; осуществлять взаимный контроль.