- Учителю
- Конспект занятия Обратные тригонометрические функции
Конспект занятия Обратные тригонометрические функции
Тема: Обратные тригонометрические функции. Примеры использования обратных тригонометрических функций.
Цель: формирование алгоритма вычислений значений тригонометрических выражений, в которых участвуют обратные тригонометрические функции и применение алгоритма для решения более сложных задач.
Задачи:
-
Научить применять определения арксинуса, арккосинуса, арктангенса и арккотангенса для нахождения значений выражений, содержащих аркфункции.
-
Составить алгоритм вычисления синуса, косинуса, косинуса, тангенса и котангенса то арксинуса, арккосинуса, арктангенса и арккотангенса.
-
Формировать способность оценивать поставленную задачу и по результатам анализа научить составлять алгоритм действий по решению новой задачи.
Ход занятия:
I. Актуализация знаний.
1. На уроках мы с вами занимались изучением обратных тригонометрических функций.
-
Какие обратные тригонометрические функции вы знаете?
(y=arcsin x, x ![]() [-1;1]; y=,
x
[-1;1]; y=,
x ![]() [-1;1];
y=arctg x, x
[-1;1];
y=arctg x, x ![]() [-
[-![]() ;+
;+![]() ];
y=arcctg x, x
];
y=arcctg x, x ![]() [-
[-![]() ;+
;+![]() ])
])
-
Дайте определение арксинуса, арккосинуса, арктангенса и арккотангенса числа a.
(arcsin a=?, где a![]() [-1;1], а ?
[-1;1], а ?
![]() [-
[-![]() /2;
/2;
![]() /2]; arccos
a= ?, где a
/2]; arccos
a= ?, где a![]() [-1;1], а
[-1;1], а
![]() [0;
[0;
![]() ]; arctg a=
]; arctg a=
![]() , где
a
, где
a![]() [-
[-![]() ;+
;+![]() ], а
], а
![]()
![]() [-
[-![]() /2;
/2;
![]()
![]() /2];
arcctg a =
/2];
arcctg a = ![]() , где
a
, где
a![]() [-
[-![]() ;+
;+![]() ], а
], а
![]()
![]() [0;
[0;
![]() ])
])
-
Перечислите формулы для арксинуса, арккосинуса, арктангенса и арккотангенса по группам.
-
(sin (arcsin a)=a, a
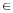 [-1;1]; cos(arccos a)=a, a
[-1;1]; cos(arccos a)=a, a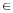 [-1;1]; tg(arctg a)=a, a
[-1;1]; tg(arctg a)=a, a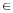 [-
[-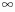 ;+
;+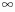 ];
ctg(arcctga)=a, a
];
ctg(arcctga)=a, a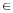 [-
[-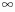 ;+
;+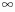 ]).
]).
-
arcsin(sin
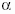 )=
)=
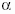 ,
,
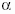
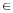 [-/2;
[-/2; 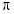 /2];arccos(cos
/2];arccos(cos
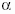 )=
)=
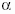 ,
,
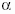
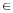 [0;
[0;
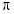 ];
arctg(tg
];
arctg(tg 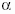 )=
)=
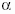 ,
,
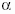
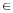 [-
[-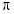 /2;
/2;
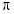 /2];
arcctg(ctg
/2];
arcctg(ctg 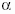 )=
)=
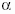 ,
,
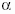
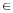 [0;
[0;
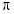 ].
].
-
2. Распределите данные выражения на 2 группы, при решении которых может быть использована та или иная группа формул.

Значения каких выражений могли бы найти устно? Каких нет? Почему? Какова же цель нашего урока? (Цель: нахождение способа решений выражений синуса, косинуса, тангенса и котангенса, аргументами, которых являются арксинус, арккосинус, арктангенс и арккотангенс.)
II. Формирование алгоритма по решению задач нового типа:
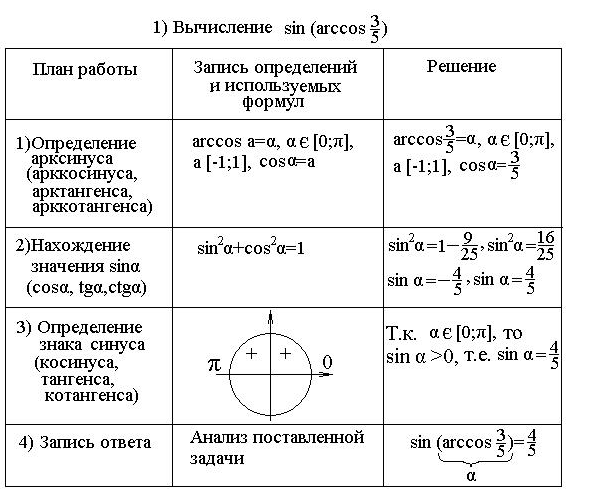
III. Решение задач повышенной сложности
Обратные тригонометрические функции имеют широкое применение в математическом анализе. Однако у большинства старшеклассников задачи, связанные с данным видом функций, вызывают значительные затруднения. В основном это связано с тем, что во многих учебниках и учебных пособиях задачам такого вида уделяется слишком мало внимания. И если с задачами на вычисление значений обратных тригонометрических функций учащиеся хоть как-то справляются, то уравнения и неравенства, содержащие такие функции, в большинстве своем ставят ребят в тупик. На самом деле, в этом нет ничего удивительного, ведь практически ни в одном учебнике не объясняется методика решения даже самых простейших уравнений и неравенств, содержащих обратные тригонометрические функции.
Рассмотрим несколько уравнений и неравенств, содержащих обратные тригонометрические функции, и решим их с подробным объяснением.
Пример 1.
Решить уравнение: 3arccos (2x + 3) = 5π/2.
Решение.
Выразим из уравнения обратную тригонометрическую функцию, получим:
arccos (2x + 3) = 5π/6. Теперь воспользуемся определением арккосинуса.
Арккосинусом некоторого числа a, принадлежащего отрезку от -1 до 1, является такой угол y из отрезка от 0 до π, что его косинус и равен числу x. Поэтому можно записать так:
2x + 3 = cos 5π/6.
Распишем правую часть полученного уравнения по формуле приведения:
2x + 3 = cos (π - π/6).
Имеем:
2x + 3 = -cos π/6;
2x + 3 = -√3/2;
2x = -3 - √3/2.
Приведем правую часть к общему знаменателю.
2x = -(6 + √3) / 2;
x = -(6 + √3) / 4.
Ответ: -(6 + √3) / 4.
Пример 2.
Решить уравнение: cos (arccos (4x - 9)) = x2 - 5x + 5.
Решение.
Так как cos (arcсos x) = x при x принадлежащем [-1; 1], то данное уравнение равносильно системе:
{4x - 9 = x2 - 5x + 5,
{-1 ≤ 4x - 9 ≤ 1.
Решим уравнение, входящее в систему.
4x - 9 = x2 - 5x + 5.
Оно квадратное, поэтому получим, что
x2 - 9x + 14 = 0;
D = 81 - 4 · 14 = 25;
x1 = (9 + 5) / 2 = 7;
x2 = (9 - 5) / 2 = 2.
Решим двойное неравенство, входящее в систему.
-1 ≤ 4x - 9 ≤ 1. Прибавим ко всем частям 9, будем иметь:
8 ≤ 4x ≤ 10. Разделим каждое число на 4, получим:
2 ≤ x ≤ 2,5.
Теперь объединим полученные ответы. Легко видеть, что корень x = 7 не удовлетворяет ответу неравенства. Поэтому единственным решением уравнения будет x = 2.
Ответ: 2.
Пример 3.
Решить уравнение: tg (arctg (0,5 - x)) = x2 - 4x + 2,5.
Решение.
Так как tg (arctg x) = x при всех действительных числах, то данное уравнение равносильно уравнению:
0,5 - x = x2 - 4x + 2,5.
Решим полученное квадратное уравнение с помощью дискриминанта, предварительно приведя его в стандартный вид.
x2 - 3x + 2 = 0;
D = 9 - 4 · 2 = 1;
x1 = (3 + 1) / 2 = 2;
x2 = (3 - 1) / 2 = 1.
Ответ: 1; 2.
Пример 4.
Решить уравнение: arcctg (2x - 1) = arcctg (x2/2 + x/2).
Решение.
Так как arcctg f(x) = arcctg g(x) тогда и только тогда, когда f(x) = g(x), то
2x - 1 = x2/2 + x/2. Решим полученное квадратное уравнение:
4x - 2 = x2 + x;
x2 - 3x + 2 = 0.
По теореме Виета получим, что
x = 1 или x = 2.
Ответ: 1; 2.
Пример 5.
Решить уравнение: arcsin (2x - 15) = arcsin (x2 - 6x - 8).
Решение.
Так как уравнение вида arcsin f(x) = arcsin g(x) равносильно системе
{f(x) = g(x),
{f(x) € [-1; 1],
то исходное уравнение равносильно системе:
{2x - 15 = x2 - 6x + 8,
{-1 ≤ 2x - 15 ≤ 1.
Решим полученную систему:
{x2 - 8x + 7 = 0,
{14 ≤ 2x ≤ 16.
Из первого уравнения по теореме Виета имеем, что x = 1 или x = 7. Решая второе неравенство системы, получаем, что 7 ≤ x ≤ 8. Поэтому в окончательный ответ подходит только корень x = 7.
Ответ: 7.
Пример 6.
Решить уравнение: (arccos x)2 - 6 arccos x + 8 = 0.
Решение.
Пусть arccos x = t, тогда t принадлежит отрезку [0; π] и уравнение принимает вид:
t2 - 6t + 8 = 0. Решим полученное квадратное уравнение по теореме Виета, получим, что t = 2 или t = 4.
Так как t = 4 не принадлежит отрезку [0; π], то получим, что t = 2, т.е. arccos x = 2, а значит x = cos 2.
Ответ: cos 2.
Пример 7.
Решить уравнение: (arcsin x)2 + (arccos x)2 = 5π2/36.
Решение.
Воспользуемся равенством arcsin x + arccos x = π/2 и запишем уравнение в виде
(arcsin x)2 + (π/2 - arcsin x)2 = 5π2/36.
Пусть arcsin x = t, тогда t принадлежит отрезку [-π/2; π/2] и уравнение принимает вид:
t2 + (π/2 - t)2 = 5π2/36.
Решим полученное уравнение:
t2 + π2/4 - πt + t2 = 5π2/36;
2t2 - πt + 9π2/36 - 5π2/36 = 0;
2t2 - πt + 4π2/36 = 0;
2t2 - πt + π2/9 = 0. Умножим каждое слагаемое на 9, чтобы избавиться от дробей в уравнении, получим:
18t2 - 9πt + π2 = 0.
Найдем дискриминант и решим полученное уравнение:
D = (-9π)2 - 4 · 18 · π2 = 9π2.
t = (9π - 3π) / 2 · 18 или t = (9π + 3π) / 2 · 18;
t = 6π/36 или t = 12π/36.
После сокращения имеем:
t = π/6 или t = π/3. Тогда
arcsin x = π/6 или arcsin x = π/3.
Таким образом, x = sin π/6 или x = sin π/3. То есть x = 1/2 или x =√3/2.
Ответ: 1/2; √3/2.
Пример 8.
Найти значение выражения 5nx0, где n - количество корней, а x0 - отрицательный корень уравнения 2 arcsin x = - π - (x + 1)2.
Решение.
Так как -π/2 ≤ arcsin x ≤ π/2, то -π ≤ 2 arcsin x ≤ π. Кроме
того, (x + 1)2 ≥ 0 при всех действительных x,
тогда -(x + 1)2 ≤ 0 и -π - (x + 1)2 ≤ -π.
Таким образом, уравнение может иметь решение, если обе его части одновременно равны -π , т.е. уравнение равносильно системе:
{2 arcsin x = -π,
{-π - (x + 1)2 = -π.
Решим полученную систему уравнений:
{arcsin x = -π/2,
{(x + 1)2 = 0.
Из второго уравнения имеем, что x = -1, соответственно n = 1, тогда 5nx0 = 5 · 1 · (-1) = -5.
IV. Итог занятия