Разработка открытого урока по алгебре Тригонометрические уравнения

Тема урока: «Решение тригонометрических уравнений».

Цели урока:

1. Образовательные - обеспечить повторение и систематизацию материала темы. Создать условия контроля усвоения знаний и умений. Научить применять при решении уравнений метод мажоранта.

2. Развивающие - способствовать формированию умений применять приемы: сравнения, обобщения, выявления главного, переноса знаний в новую ситуацию, развитию математического кругозора, мышления и речи, внимания и памяти.

3. Воспитательные - содействовать воспитанию интереса к математике (стимулировать мотивацию и интерес) и ее приложениям, активности, мобильности, умения общаться, общей культуры, развитие творческой самостоятельности и инициативы.

Тип урока: комбинированный.

Формируемые УУД (универсальные учебные действия):

• Личностные: способствовать формированию самооценки на основе критерия успешности учебной деятельности; готовности преодолевать школьные трудности; учебно-познавательный интерес к учебному материалу.

• Регулятивные: способствовать формированию умения ставить перед собой цель и планировать свои действия; способствовать формированию умения учеников оценивать правильность выполнения действия на уровне адекватной оценки; вносить необходимые коррективы в действие после его завершения на основе его оценки и учёта характера сделанных ошибок.

• Познавательные: создавать всевозможные условия для осуществления исследовательской деятельности; учить высказывать предположения, обсуждать проблемные вопросы, находить ошибки в предложенных решениях, выявлять известное и неизвестное; ориентироваться в своей системе знаний, строить математические высказывания.

• Коммуникативные: работать в паре, формулировать собственное мнение и позицию; способствовать развитию монологической и диалогической речи.

Методы обучения: частично - поисковый, аналитический, репродуктивный. Проверка уровня знаний, решение познавательных обобщающих задач, системные обобщения, самопроверка, восприятие нового материала, взаимопроверка.

Формы организации урока: индивидуальная, фронтальная, парная.

Оборудование и источники информации: Интерактивная доска; мультимедийный проектор; компьютер. У учащихся на партах ноутбук, листы учета знаний; системно - обобщающая схема; по два подписанных листочка и два бланка для записи ответов.

Планируемые результаты:

• Личностные: формировать способности к самооценке на основе критерия успешности учебной деятельности; требовательное отношение к себе и своей работе;

• Метапредметные: уметь учащимися принимать и сохранять учебную задачу, планировать своё действие в соответствии с её постановкой; оценивать правильность выполнения действия на уровне адекватной оценки;

• Предметные: повторить и систематизировать материала темы, сформировать понимание важности её для сдачи ЕГЭ.

ХОД УРОКА:

1. Организационный момент. ( Слайды 1 - 2. )

Учитель: Эпиграфом к нашему уроку я взяла слова Конфуция:

«Три пути ведут к знанию:

путь РАЗМЫШЛЕНИЯ - это путь самый благородный,

путь ПОДРАЖАНИЯ - это путь самый легкий

и путь ОПЫТА - это путь самый горький».

Прежде чем приступить к работе, определим тему к которой нас поведут эти пути.

Собрать пазл. Устная фронтальная работа.

Каждый из вас должен поставить перед собой цель сегодняшнего урока. Перед вами лежат оценочные листы, подпишите их, в левом столбце которых написаны цели, выберите те из них, которые соответствуют вашим, и поставьте напротив знак «+» или допишите свою цель. В течение урока мы с вами будем выполнять различные задания. По окончанию решения каждой задачи, вы должны оценить свою работу:

"+" - справился с задачей без затруднений,

"±" - справился с задачей, но возникали сложности,

"-" - не справился с задачей.

Микро вывод: Повторим, обобщим, приведём в систему и пополним изученные виды, типы, методы и приемы решений тригонометрических уравнений.

Перед нами стоит задача - показать свои знания и умения по решению тригонометрических уравнений.

2. Проверочная работа. (Презентация. Слайды 3, 4, 5.)

Т е м а: «Решение простейших тригонометрических уравнений»( индивидуальная работа с взаимопроверкой).

Ц е л ь : контроль знаний и приведение в систему знаний по простейшим тригонометрическим уравнениям.

1. Каково будет решение уравнения при ?

2. При каком значении а уравнение имеет решение?

3. Какой формулой выражается это решение?

4. На какой оси откладывается значение а при решении уравнения ?

5. В каком промежутке находится ?

6. В каком промежутке находится значение а?

7. Чему равняется ?

8. В каком промежутке находится ?

9. Какой формулой выражается решение уравнения ?

1. Каково будет решение уравнения при ?

2. При каком значении а уравнение имеет решение?

3. Какой формулой выражается это решение?

4. На какой оси откладывается значение а при решении уравнения ?

5. В каком промежутке находится ?

6. В каком промежутке находится значение а?

7. Чему равняется ?

8. В каком промежутке находится ?

9. Какой формулой выражается решение уравнения ?

Работа окончена, собираются бланки с ответами. Учащиеся отмечают на листочках неправильные шаги и количество правильных ответов, заносят в лист учета знаний.

На экране - слайд 6. (Ответы)

3. Систематизация теоретического материала.

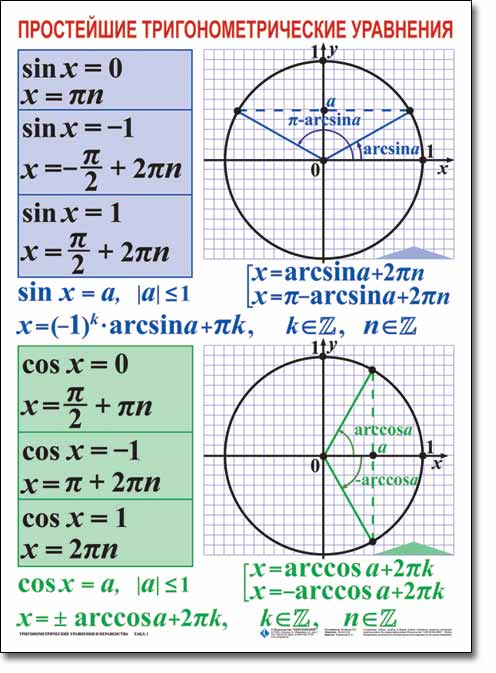
1. Устные задания на определение вида простейших тригонометрических уравнений. Слайды 8 и 9.

Цель: обобщение знаний по видам простейших тригонометрических уравнений.

На слайдах вы видите схемы решений тригонометрических уравнений. Как вы думаете, какая из схем представленной группы является лишней? Что объединяет остальные схемы?

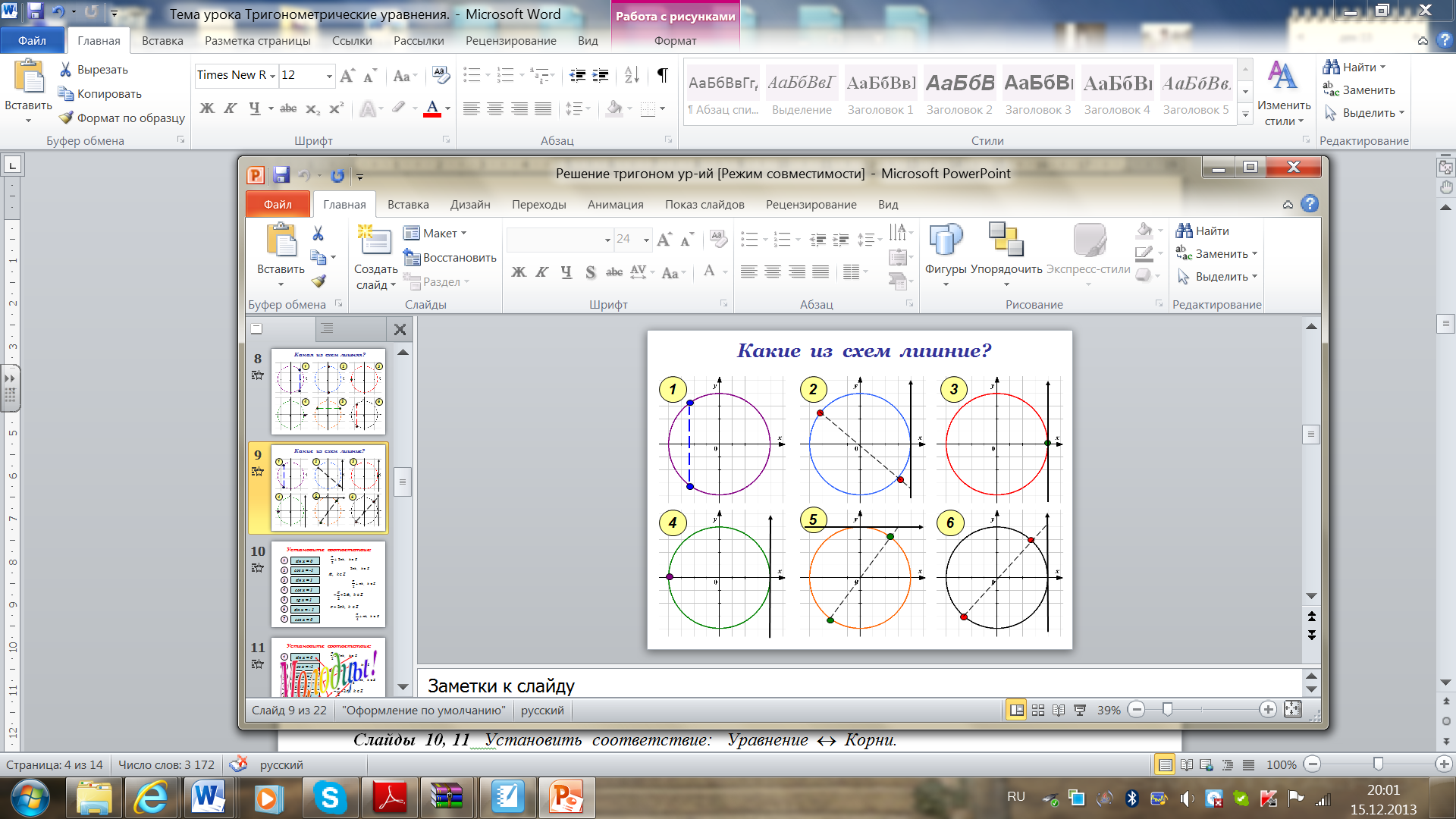
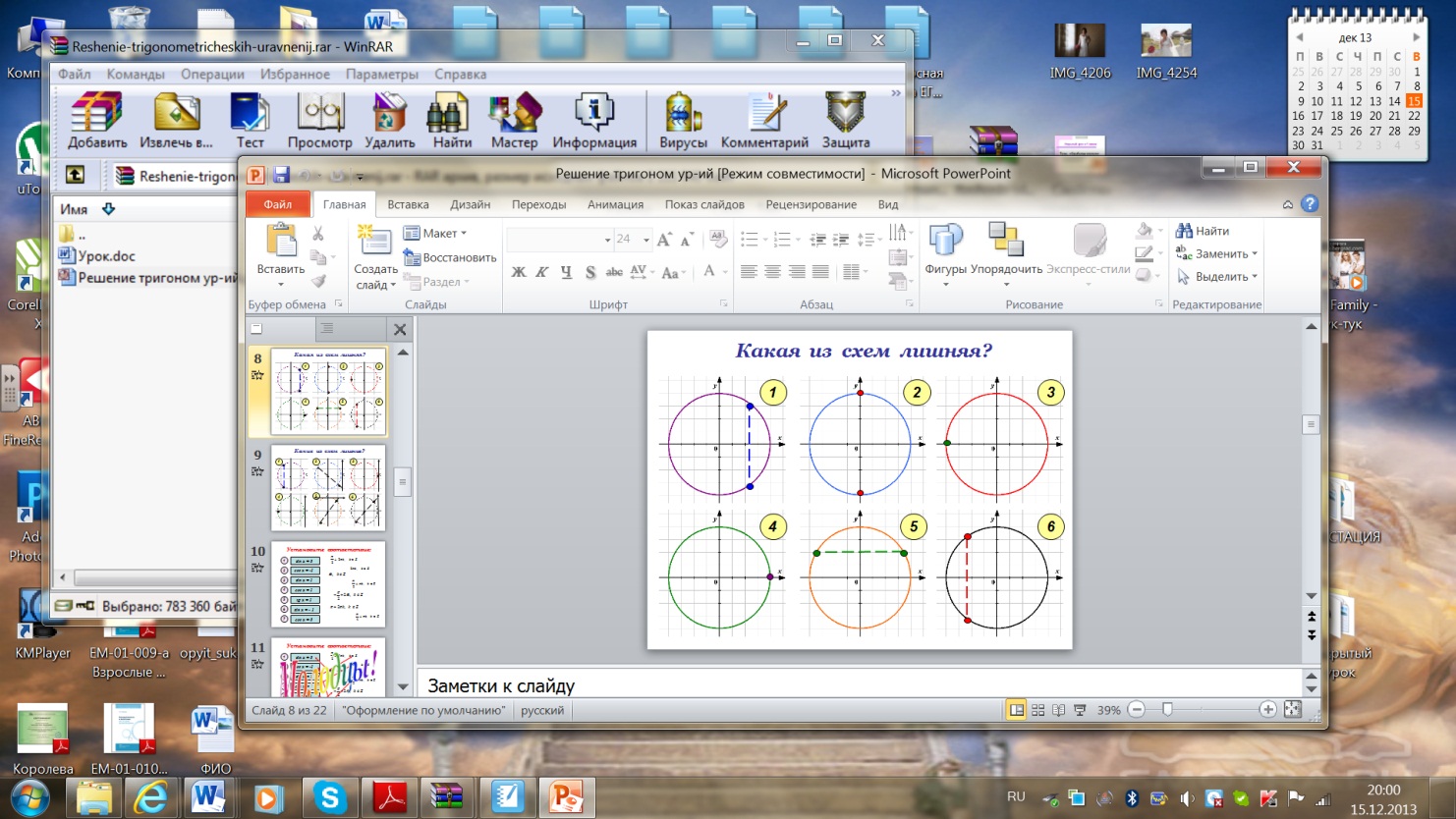
О т в е т ы :

Слайд 8. 5 - я схема лишняя, так как эта схема изображает решение уравнения вида ; 1, 2, 3, 4, 6 - изображают решение уравнений вида .

Слайд 9. 1 - я схема лишняя, так как она изображает решение уравнения вида ;

5 - я схема лишняя, так как эта схема изображает решение уравнения вида ;

2, 3, 4, 6 - изображают решение уравнений вида .

2. Экспресс - опрос ( Слайды 12, 13, 14, 15)

Учащимся предлагается определить, решение какого тригонометрического уравнения показано на тригонометрической окружности. Записать его корни1.

Слайд 12

2.

Слайд 13

3.

Слайд 14

3. Найди ошибку. (Слайд 7)

В каждом из приведенных примеров сделаны ошибки. Назовите верный ответ и подумайте о причине ошибки.

Цель: повторение решения простейших тригонометрических уравнений ( создавать всевозможные условия для осуществления исследовательской деятельности; находить ошибки в предложенных решениях; ориентироваться в своей системе знаний, строить математические высказывания).cos x=1/2 , х = ± π/6 + 2πк, к Z

Верно : х = ± π/3 + 2πк, к Z

Ошибка в вычислении значений тригонометрической функции

2) sin x =√ 3/2 , x = π/3 + πк, к Z

Верно : x = (-1)^к π/3 + πк, к Z

Ошибка в формуле нахождения решения уравнения sin x =a

3) cos x = -1/2, x = ±(-π/3) + 2πm, m Z

Верно : x = ±2π/3 + 2πm, m Z

По определению арккосинуса

(-π/3) [0;π]

4) sin x =√10/3, x = (-1)^к arcsin√10/3 + πn, n Z

x- не существует, так как √10/3 не удовлетворяет условию | sin x | ≤ 1

5) tg x =-1, x =- π/4 + 2πn, n Z

Верно : x = -π/4 + πn, n Z

Ошибка в периоде

6) ctg x =-√3/3, x= -π/3+πm, m Z

Верно : x= 2π/3+πm, m Z

По определению arcctg (-π/3) [0;π]

4. Классификация тригонометрических уравнений.

Цель: привести в систему знания по типам и методам решения тригонометрических уравнений (работа в парах).

Распределите уравнения по 5 группам, определив методы, применяемые для их решения (работа в парах).

cos (x +π/3)=1

sin 2x =-√3/2 ,

tg (2x -π/4)= √3/3

Это простейшие тригонометрические уравнения типа, которые решаются сначала по известным формулам относительно f(x), а затем полученные уравнения решаются относительно х.

2 cos ²3x+ sin 3x-1=0

сtg x-√3tg x+1=√3

cos ⁴x/4- sin⁴ x/4=-1

Эти уравнения приводятся к алгебраическим путем введения новой переменной и сведению его к квадратному уравнению.

sin² x- sin x=0

cos ²x+ sin x cos x=1

Данные уравнения решаются разложением на множители. При решении таких уравнений нужно пользоваться правилом: произведение нескольких множителей равно нулю, если хотя бы один из них равен нулю, а остальные при этом имеют смысл.

2sin x-3 cos x=0

4 sin² x+2 sin x cos x=3

3cos ²x-4 sin x cos x+ sin² x=0

Однородные уравнения первой (второй) степени. Они решаются делением обеих частей уравнения на cos x (sin x), cos ²x (sin² x)

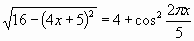
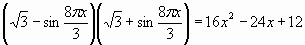
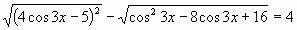
Проблема!!!

4.Объяснение нового материала.

Цель: Познакомить учащихся с еще одним методом решения тригонометрических уравнений - методом мажоранта.

Можете ли вы сейчас предложить метод его решения? В чем заключается проблема его решения?

- Такие уравнения решаются особым методом - "Методом мажорант", с которым вас познакомит ваш одноклассник.

Выступление ученика по теме "Метод мажорант".

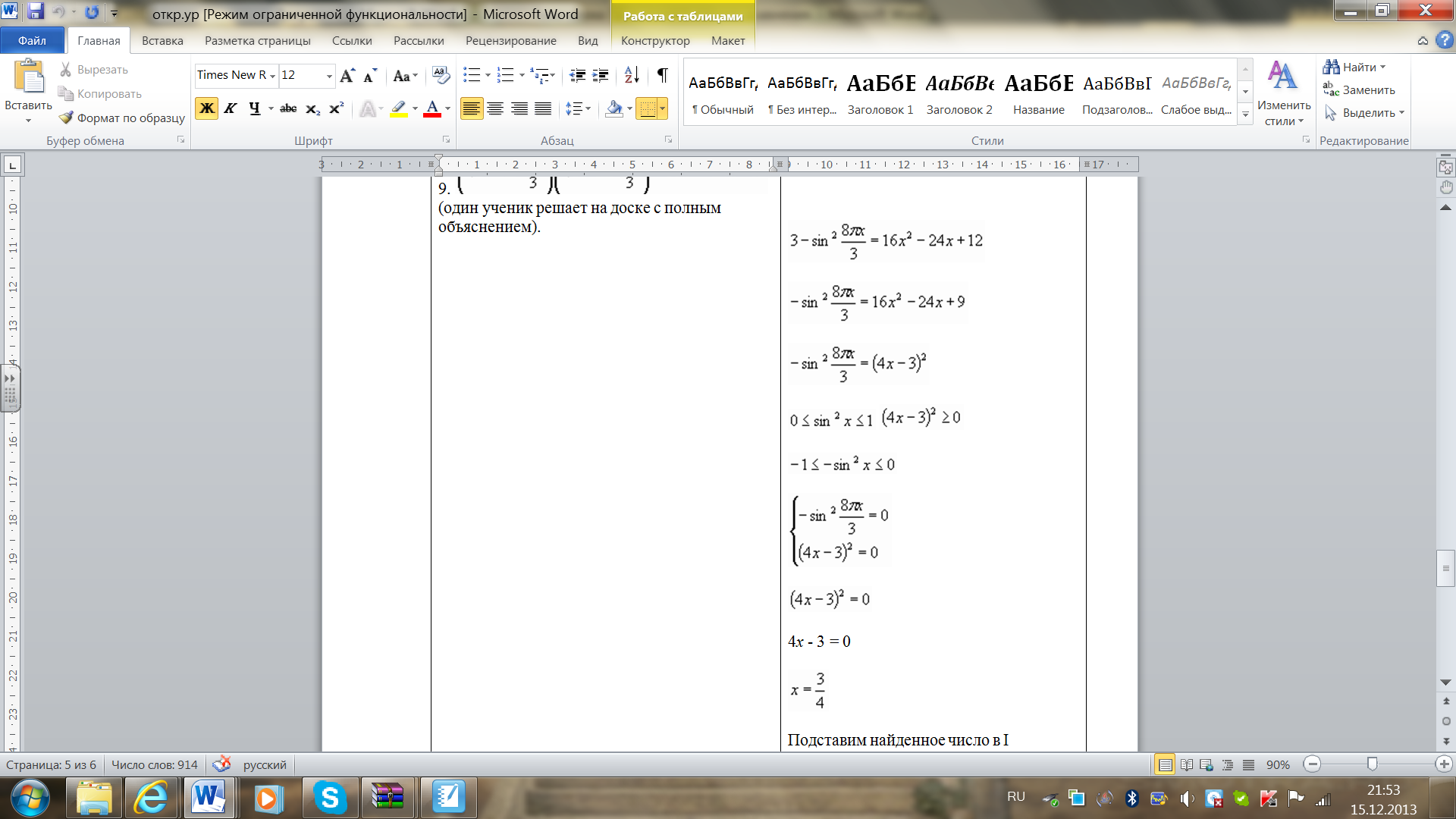
Подставим найденное число в I уравнение.

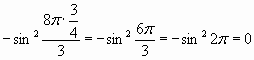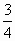=> - корень уравнения.

5. Самостоятельная работа (обучающего характера).

Решить уравнение, применяя метод мажоранта.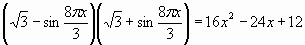

</ Решить уравнение, применяя метод мажоранта.

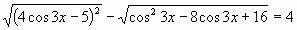
5. Домашнее задание:

Правильному применению методов можно научиться, только применяя их на разнообразных примерах (Г. Цейтен)

Какими путями мы сегодня шли к кладези знаний?

Домашние зачетные работы по уровням вместе с аннотацией.

Домашняя работа разбита по группам (3 уровня сложности: легкий уровень, средний уровень и усложненный уровень). Задания оцениваются самими учащимися по системе:

«5»- задание выполнено верно и самостоятельно

«4»- задание выполнено верно и полностью, но часть задания выполнена с помощью одноклассников

«3»-интересовался решением и все решил с помощью одноклассников.

5. Подведение итогов урока.

Оценка содержания урока:

занимательно

интересно

познавательно

полезно

продуктивно

Оценка деятельности на уроке:

задумался

удивился

загорелся

убедился

принял решение

сделал для себя открытие

Оценка внутреннего состояния на уроке:

взволнованное

удовлетворенное

позитивное

отличное

Памятка 1.

1. Метод приведения к простейшим тригонометрическим уравнениям.

1. Выразить тригонометрическую функцию через известные компоненты.

2. Найти аргумент функции по формулам:

3. Найти неизвестную переменную.

2. Метод введения новой переменной.

1. Привести уравнение к алгебраическому виду относительно одной из тригонометрических функций.

2. Обозначить полученную функцию переменной t .

3. Записать и решить полученное алгебраическое уравнение.

4. Сделать обратную замену.

5. Решить простейшее тригонометрическое уравнение.

3. Приведение уравнения к виду tg x =a

1. Привести данное уравнение к виду

a) a sin x + b cos x = 0 (однородное уравнение первой степени)

б) a sin² x + b sin x · cos x + c cos² x = 0 (однородное уравнение второй степени).

2. Разделить обе части уравнения на: а) cos x ≠ 0; б) cos² x ≠ 0;

и получить уравнение относительно tg x: а) a tg x + b = 0; б) a tg² x + b tg x + c = 0.

3. Решить уравнение известными способами.

4. Разложение на множители.

Алгоритм решения:

1. Используя всевозможные тригонометрические формулы, привести данное уравнение к уравнению, решаемому методами I, II, III, IV.

2. Решить полученное уравнение известными методами.
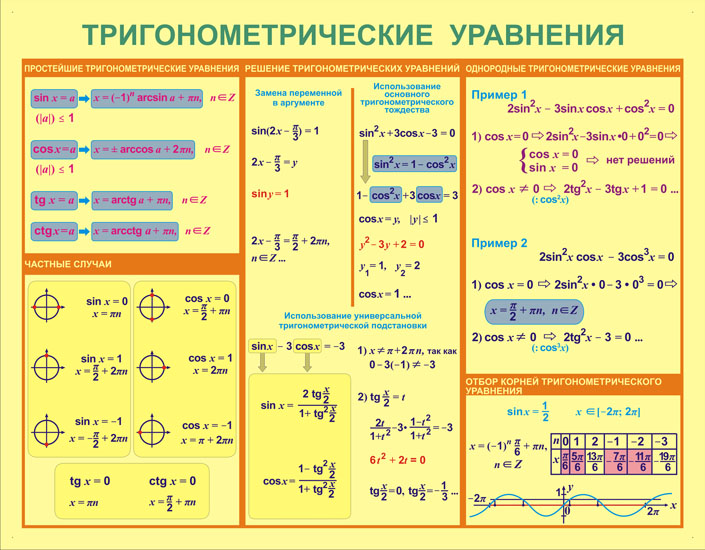
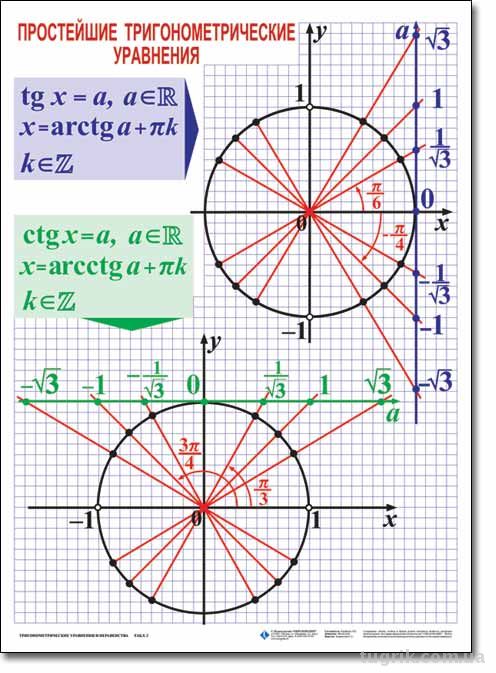