- Учителю
- Урок на тему Решение комбинаторных задач
Урок на тему Решение комбинаторных задач
В данной статье рассмотрим один из уроков в курсе математики 5 класса, посвященного знакомству с комбинаторикой.
Цели урока.
Образовательные:
- познакомить учащихся с новым типом задач (комбинаторные задачи), приемами их решения - перебор возможных вариантов, построение дерева возможных вариантов, применение правила умножения;
- ввести новое понятие - факториал, закрепить его при решении задач, примеров, уравнений.
Воспитательные:
- формирование уважения к товарищам, умения слушать и слышать собеседника
- формирование отношения к дружбе как одной из важнейших человеческих ценностей.
Развивающие:
- формирование интереса к предмету;
- формирование вычислительных навыков;
- развитие логического мышления;
- формирование умения доказывать, обосновывать свое мнение.
Ход урока
1. Организационный момент
Учитель: Сегодня у нас с вами необычный урок. Мы будем решать задачи, связанные с одним из интереснейших разделов математики - комбинаторикой. В науке и в реальной жизни очень часто приходится решать задачи, главным вопросом которых является вопрос "Сколькими способами это можно сделать?". Например:
- Сколькими способами можно поставить ученику оценку на уроке?
- Сколькими способами можно назначить дежурного в классе?
- Сколькими способами можно назначить двух дежурных в классе?
Решая такие задачи, приходится составлять различные комбинации из конечного числа элементов и подсчитывать число комбинаций. Такие задачи получили название комбинаторных задач, а раздел математики, в котором рассматриваются подобные задачи, называют комбинаторикой. А какой еще теме будет посвящен урок, вы узнаете, когда мы проверим, как вы справились с выполнением домашнего задания.
2. Проверка выполнения домашнего задания
(На предыдущем уроке домашнее задание составляется таким образом, чтобы заданий было ровно 6. Например, в учебнике Виленкина Н.Я. и др. это могут быть № 693(а, в), 735(1), 765(а,б,в) )
На доске - таблица и закрепленные магнитами карточки. На карточках с одной стороны - ответ к заданию из домашней работы, с другой стороны - буква.
Учитель: Проверим домашнюю работу. Откройте тетради, возьмите карандаши. Найдите ответы к номерам домашней работы.
Учащиеся выходят к доске по одному, выбирают карточку с ответом и прикрепляют ее в ячейку таблицы под номером задания. Сначала карточки закрепляют в клетках таблицы вверх стороной, на которой записан ответ, чтобы учащиеся могли проверить правильность выполнения домашней работы. Остальные проверяют свои ответы в тетрадях.
"5" - если все верно
"4" - если одна ошибка
"3" - 2-3 ошибки
"2" - больше 3 ошибок
Учитель: Перевернем карточки, какое слово получили? (ДРУЖБА). Действительно, сегодня на уроке мы будем не только решать математические задачи, совершенствовать навыки вычислений, но и говорить о дружбе.
3. Новый материал.
Учитель: Итак, мы уже сказали, что будем сегодня учиться решать задачи, главным вопросом которых является вопрос "Сколькими способами..".
Задача 1.
Имеются три слова "ДРУЖБА", "ДЕЛО", "ЛЮБИТ" (нарезать листочки с этими словами - по 7 карточек на каждое слово). Сколькими способами из этих слов можно составить фразу?
Учащиеся предлагают варианты, эти варианты составляют на доске.
Ответ: 6 способов.
Учитель: Как вы думаете, какой вариант является верным с точки зрения русского языка? (Дружба любит дело). Как вы понимаете это высказывание?
Учитель: Здесь был приведен полный перебор всех возможных вариантов, или, как обычно говорят, всех возможных комбинаций. Поэтому это комбинаторная задача. Давайте подумаем, как можно записать, оформить решение этой задачи.
1 способ. Обозначим предложенные слова заглавными буквами:
ДРУЖБА - Д
ЛЮБИТ - Л
ДЕЛО - Е (возьмем вторую букву этого слова)
Тогда все названные вами способы можно просто перечислить: ДЛЕ, ДЕЛ, ЛДЕ, ЛЕД, ЕДЛ, ЕЛД.
2 способ.
Оказывается, решение можно оформить в виде модели, которую называют деревом возможных вариантов. Она, во-первых, наглядна, как всякая картинка, и, во-вторых, позволяет все учесть, ничего не пропустив,
Учащиеся под руководством учителя составляют схему:
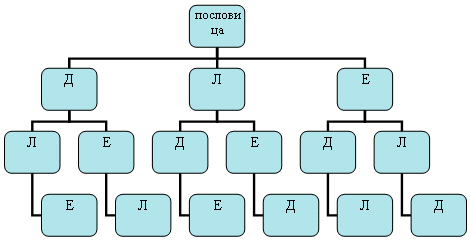
Способ 3 (рассуждение)
На первом месте может стоять одно из трех слов: ДРУЖБА,
ЛЮБИТ, ДЕЛО. Если первое слово выбрано, то на втором месте
может стоять одно из двух оставшихся слов, а на третьем месте -
только одно оставшееся слово. Значит, всего вариантов:
![]() .
.
Заметим, что последний прием называется правилом умножения.
У каждого из этих трех способов есть свои преимущества и свои недостатки (обсудить) Выбор решения - за вами! Отметим все же, что правило умножения позволяет в один шаг решать самые разнообразные задачи.
Задача 2.
У Ани 3 подруги, и она каждой из них купила по шоколадке и хочет подарить их к празднику. Сколькими способами она может это сделать?
Решение: Решение выполняют на доске ученики (решение выполняется 3 способами)
Задача 3.
В компании друзей - 6 человек: Андрей, Борис, Витя, Гриша, Дима, Егор. В школьной столовой за столом 6 стульев. Друзья решили каждый день, завтракая, рассаживаться на эти 6 стульев по-разному. Сколько раз они смогут это сделать без повторений?
Решение:
Учитель: Какой способ мы выберем? (Учащиеся под руководством учителя должны придти к выводу, что это третий способ - правило умножения).
Решение оформляет на доске ученик.
Для удобства рассуждений будем считать, что друзья усаживаются за стол поочередно. Будем считать, что первой усаживается за стол Андрей. У него 6 вариантов выбора стула. Вторым усаживается Борис, и независимо выбирает стул из 5 оставшихся. Витя делает свой выбор третьим и на выбор у него будет 4 стула. У Гриши будет уже 3 варианта, у Димы - 2, у Егора - 1. По правилу умножения получаем:
![]() .
.
Ответ - 720 дней или почти 2 года.
Учитель: Как мы видим, условия задач разные, а решения, по сути дела, одинаковы. Удобно, поэтому ввести и одинаковые обозначения для этих ответов.
Определение: произведение всех натуральных чисел от 1 до п включительно называется п - факториал и обозначается символом п!
п! = ![]()
Знак п! читается "Эн факториал", что в дословном переводе с английского языка обозначает "состоящий из пмножителей". Отметим важную особенность этой величины - ее быстрый рост.
Задача 4.
Вычислите:
а) 1!; б) 2!; в) 3!; г) 4!; д) 5!; е)10!
Считают, что 0! =1 (записать)
Задача 5.
Учитель: ДРУЖБА - одно из важнейших богатств, которое может быть у человека. Недаром о дружбе слагаются стихи и песни, сочиняют пословицы и поговорки. Какие пословицы и поговорки о дружбе вы знаете?
Друзья познаются в беде.
Не имей сто рублей, а имей сто друзей.
Один в поле не воин.
Сам погибай, а товарища выручай.
Старый друг лучше новых двух.
Без друга в жизни туго.
- Молодцы! Для каждого человека очень важно, чтобы у него были хорошие, настоящие друзья. Давайте решим несколько примеров с применением нового понятия - факториал, и узнаем новую пословицу о дружбе.
6! - 5!
![]()
![]()
п -?
Карточки с ответами выполняют с запасом (есть карточки с числами, не являющимися ответами).
6! - 5!
![]()
![]()
п -?
5048
40256
600
24
7
Нет
друга -
ищи,
а нашел -
береги
Задание 6.
К Васе в гости пришли 4 друзей, и они собираются смотреть новый фильм. У Васи в комнате есть кресло и еще он принес 4 стула из кухни. Кресло он, несомненно, займет сам, а на стульях рассадит своих друзей. Вася подсчитал, что рассадить друзей он сможет 24 способами.
Учитель: Правильно ли рассчитал Вася? (Да, с точки зрения математики)
- Хорошо ли он поступил? (Обсуждается моральный аспект проблемы)
4. Физкультурная минутка.
Учитель: А теперь давайте немного отдохнем, а для этого проведем физкультурную минутку. Если я правильно прочитаю выражение, то вы встаете и поднимаете руки вверх, а если неправильно - садитесь, руки в бок.
Встали. Начинаем, будьте внимательны.
Частное 4х и 2!
+
5! + 7! + 3!
Сумма 5!, 7! и 3!
+
20! - 19!
Частное 20! и 19!
-
6. Самостоятельная работа.
Учитель: Ну, а теперь, когда мы хорошо отдохнули, давайте проверим, что мы научились делать сегодня на уроке. Для этого выполним самостоятельную работу.
1. Шесть разных писем раскладывают в 6 разных конвертов. Сколько существует способов такого раскладывания?
2. Вычислите:
а) 6! - 2![]() ; б) 4! +
(2+3)2
; б) 4! +
(2+3)2
2. Вычислите:
а) 32 + 5! б) (9-4)2 + 4!
3. Сколькими способами 5 мальчиков могут занять очередь к билетной кассе, если первым все равно будет Толя?
3. Сколькими способами Даша может съесть обед, состоящий из первого, второго, третьего и пирожного, если первым она наверняка съест пирожное?
7. Домашнее задание.
- Придумать, записать условия и решения 2 комбинаторных задач на тему "Семья". Оформить на листах А4, можно выполнить рисунки к задачам.
8. Итог урока.
Давайте подведем итоги урока.
- Что нового узнали? (Получили правило умножения, рассмотрели его геометрическую модель - дерево вариантов, ввели новое понятие - факториал)
- Что понравилось?
- Что запомнилось?
- Оценки за урок.