- Учителю
- Вне классное мероприятие по математике для 7 класса
Вне классное мероприятие по математике для 7 класса
Внеклассное занятие по математике
7 класс
Тема: « За страницами учебника математики »
Основные цели:
-
формирование интереса к математике;
-
привитие интереса к решению нестандартных математических задач;
-
повышение активной творческой деятельности учащихся;
-
знакомство с терминологией;
-
развитие навыков общения.
Задачи:
1. Воспитательная - развитие познавательного интереса обучающихся, повысить уровень их математической культуры.
2. Учебная - развитие креативных навыков и формирование системы геометрических образов.
3. Развивающая - развитие памяти, внимательности, логического мышления, находчивости обучающихся, навыков самостоятельной деятельности, способностей к анализу и синтезу, к абстрагированию.
4. Познавательная - знакомство с историческим данными, расширение кругозора обучающихся.
Форма занятия:
с применением игровых технологий и ИКТ.
Оборудование:
Урок проводится в классе, где имеется компьютер, экран и проектор, т. к. основным дидактическим обеспечением урока является презентация, специально разработанная для этого урока.
Ход урока:
Приветственное слово учителя
Мой юный друг!
Сегодня ты пришел вот в этот класс,
Чтоб посидеть, подумать, отдохнуть,
Умом своим на все взглянуть.
Сегодня у нас с вами необычное занятие по математике, мы будем говорить и выполнять то, с чем на уроках сталкиваемся нечасто, поэтому называется наш урок «За страницами учебника…»
"Крупное научное открытие даёт решение крупной проблемы,
но и в решении любой задачи присутствует крупица открытия"
Сегодня перед нами будет много проблем, с которыми, я надеюсь мы справимся. Вы узнаете много нового из области математики и не только.
А для начала давайте проведём конкурс эрудитов.
1. Какое число кратно всем числам? 0
2. В каком городе состоялась I Всесоюзная математическая олимпиада?
Тбилиси
3. В какой стране впервые появились отрицательные числа?
Древний Китай
4. Как называется единица со ста нулями? Гугол
5. Какой знаменитый человек, своеобразный «титан» эпохи Возрождения, ввел в математику знаки + и - ?
Леонардо да Винчи
6. Кто из русских писателей занимался составлением арифметических задач? В. Толстой
7. Этим геометрическим телом играли дети в Древней Греции в «футбол». Как они называли его тогда? Сфера
Подведение итогов, признание (Ф.И. обучающихся) эрудитами .
Продолжаем наши открытия. И сейчас успех ждет того, кто умеет хорошо считать. Вы думаете это проще простого? Давайте проверим…
1. Сколько четырехугольников вы видите? 8
2. Сколько треугольников на чертеже? 12
3. . Сколько треугольников на чертеже? 28
Подведение итогов, признание (Ф.И. обучающихся) лучшими счетоводами.
А сколько кубов вы здесь видете? ( 6 или 7 или 13)
Такие картинки называются зрительными иллюзиями или оптическими обманами.
Как вы думаете возможно ли выполнить такую композицию из кубиков?
И следующий блок нашего урока называется « Возможное и невозможное»
Эффекты вращения.
Параллельные линии.
Окружность.
Равные отрезки.
Яркость рисунка.
Мерцание, пульсация.
Физминутка
Возможное
Julian Beever - британский художник, известный своими рисунками, которые он делает мелом на английских, французских, немецких, американских, австралийских и бельгийских тротуарах. И известен он тем, что создает трехмерные изображения, некоторые из которых вы можете посмотреть.
Невозможное
Деревянный кубик
Двое на лестнице
Рама
Фигуры
Лестница
Трезубец
Устали от невозможного? А теперь давайте вернемся к нашим возможностям и разгадаем ребусы, которые для нас подобрали ребята из 7а класса.
Последний ребус с ответом поверхность.
Об одной удивительной поверхности я вам предлагаю поговорить более подробно.
Таинственный и знаменитый лист Мебиуса (иногда говорят: "лента Мёбиуса") придумал в 1858 г. немецкий геометр Август Фердинанд Мёбиус (1790-1868), ученик "короля математиков" Гаусса. Мёбиус был первоначально астрономом, как Гаусс и многие другие из тех, кому математика была обязана своим развитием. В те времена занятия математикой не встречали поддержки, а астрономия давала достаточно денег, чтобы не думать о них, и оставляла время для собственных размышлений. И Мёбиус стал одним из крупнейших геометров XIX в. В возрасте 68 лет ему удалось сделать открытие поразительной красоты. Это открытие односторонних поверхностей, одна из которых - лист Мёбиуса.
Давайте проведем несколько опытов.
-
Опыт N 1
Склейте два кольца- одно простое и лист Мёбиуса. Разрежьте каждое из них пополам вдоль. Что у Вас получилось?
-
Опыт N 2
Чтобы получить ленту Мёбиуса, мы поворачиваем полоску бумаги на пол оборота. А интересно что у вас получится, если вы склеите ленту, сделав полный оборот , и получившееся кольцо разрежете пополам вдоль?
-
Опыт N 3
Приготовьте второй лист Мебиуса из достаточно широкой полоски и разрезайте его ножницами так, чтобы линия разреза все время шла вдвое ближе к левому краю полоски, чем к правому (линия разреза обойдет лист Мебиуса дважды). Что получится на этот раз?
Число перекручиваний
Результат разрезания
Свойства
0
2 кольца
Длина окружности та же, но кольцо в два раза уже
1
1 кольцо
Кольцо перекручено дважды, оно вдвое длиннее, но уже
2
2 кольца
Кольцо перекручено дважды, оно вдвое длиннее, но уже
3
1 кольцо
Кольцо перекручено 6 раз и оно вдвое уже
Эксперимент на дом.
а) На обеих сторонах ленты на равном расстоянии от краев провести по две пунктирные линии.
Склеить лист Мёбиуса. Разрезать по пунктирным линиям. Описать полученный результат.
Прошу дать прогноз для подобного эксперимента, но когда лента не была перекручена. (Два тонких кольца и центральная часть).
б) Приготовьте ленту шириной 5 см, на которой нанесите пунктир, отступив от края на
1 см, 2 см, 3 см и 4 см. Сделайте из неё лист Мёбиуса. Что получится, если разрезать его по пунктиру?
Можно ставить еще немало экспериментов по разрезанию лент. Попробуйте придумать и поставить свой эксперимент, суть которого отразить на отдельном листе бумаги.
-
Международный символ переработки представляет собой Лист Мёбиуса.
-
Благодаря ленте Мебиуса возникло множество самых разнообразных изобретений. Например, были созданы особые кассеты для магнитофона, которые дали возможность слушать магнитофонные кассеты с "двух сторон" не меняя их местами. Скольких людей приводили в восторг аттракционы "Американские горки". Лента Мебиуса наблюдается в форме абразивных ремней для заточки инструмента, красящей ленты для печатающих устройств.
Математическая шутка
Теорема: Ученики ничего не делают.
Доказательство:
-
1. По ночам занятий нет, значит, половина суток свободна. Остается
365-182=183 (дня).
-
2. В школе ученики занимаются половину дня, значит, вторая половина (т.е. четвертая часть суток) может быть свободна. Остается
183-183:4=137 (дней).
-
3. В году 52 воскресенья. Из них на каникулы приходится 15 дней, таким образом, выходных в учебном году 52-15=37 (дней).
Итого остается 137-37=100 (дней).
-
4. Но есть еще каникулы: осенние ( 5 дней), зимние ( 10 дней), весенние ( 7 дней), летние ( 78 дней).
Всего 100 (дней).
-
5. Итак, школьники заняты в году
100-100=0 (дней).
Ч.т.д.
Вопрос: А когда же учиться?
Где ошибка в рассуждениях?
Выходные и каникулы считались дважды.
Вот ещё один пример интересной математической ситуации.
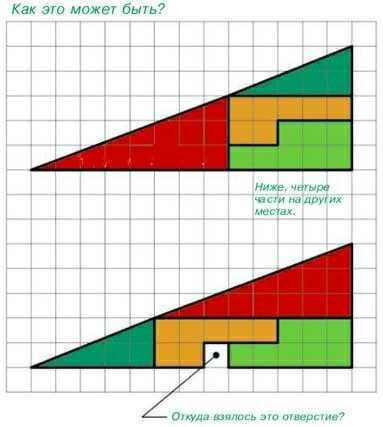
Попробуйте и вы составить теоремы- шутки или математические казусы.
Подведение уроков урока.
«Математика во всем», - нам твердят.
Многие не верят, спорить норовят:
«Математика от нас далеко…
Жить на свете без нее так легко!»
Но пойдет однажды вечером дождь,
Подойдешь ты к окну и поймешь:
Все на свете, что видишь, давно
Математикой отражено.
Ты вглядись: от фонаря свет
Векторами разлетается. Нет?
Точки капель, окружности луж -
Неужели ты не видишь? Ну ж…
Окошек плоскости отрезками полны…
И вечна траектория Луны…
А по параболе летит метеорит.
Через мгновенье в атмосфере он сгорит…
Многоугольники, квадраты и круги…
Пространства-времени неслышные шаги…
Все движется и мчится, все улетает вдаль.
А кто не видит этого…
того мне просто жаль…