Текст для подготовки к ГИА в форме ЕГЭ

1. Задание 1 № 318753.

Бегун пробежал 300 м за 30 секунд. Найдите среднюю скорость бегуна на дистанции. Ответ дайте в километрах в час.

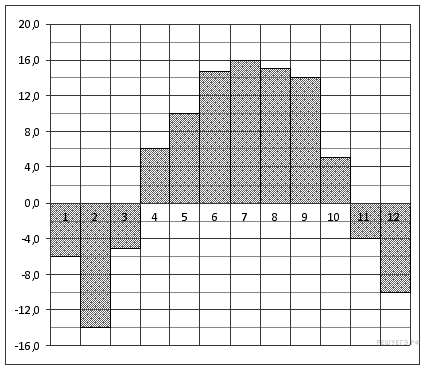
2. Задание 2 № 27519. На диаграмме показана среднемесячная температура воздуха в Нижнем Новгороде (Горьком) за каждый месяц 1994 года. По горизонтали указываются месяцы, по вертикали - температура в градусах Цельсия. Определите по диаграмме, сколько было месяцев с положительной среднемесячной температурой.

3. Задание 3 № 57051.

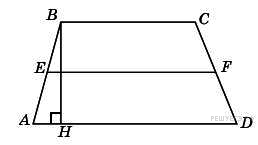Высота трапеции равна 12, площадь равна 48. Найдите среднюю линию трапеции.

4. Задание 4 № 320571. В магазине стоят два платёжных автомата. Каждый из них может быть неисправен с вероятностью 0,05 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.

5. Задание 5 № 509879. Найдите корень уравнения

6. Задание 6 № 27810.

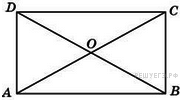Меньшая сторона прямоугольника равна 6, диагонали пересекаются под углом 60°. Найдите диагонали прямоугольника.

7. Задание 7 № 8045.

На рисунке изображен график производной функции f(x), определенной на интервале (−10; 8). Найдите количество точек максимума функции f(x) на отрезке [−9;6].

8. Задание 8 № 505467.

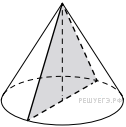Площадь основания конуса равна 36π, высота - 10. Найдите площадь осевого сечения конуса.

9. Задание 9 № 245172. Найдите значение выражения .

10. Задание 10 № 43873.

Груз массой 0,8 кг колеблется на пружине со скоростью, меняющейся по закону , где - время в секундах. Кинетическая энергия груза, измеряемая в джоулях, вычисляется по формуле , где - масса груза (в кг), - скорость груза (в м/с). Определите, какую долю времени из первой секунды после начала движения кинетическая энергия груза будет не менее Дж. Ответ выразите десятичной дробью, если нужно, округлите до сотых.

11. Задание 11 № 99620. В помощь садовому насосу, перекачивающему 5 литров воды за 2 минуты, подключили второй насос, перекачивающий тот же объем воды за 3 минуты. Сколько минут эти два насоса должны работать совместно, чтобы перекачать 25 литров воды?

12. Задание 12 № 26717. Найдите наибольшее значение функции на отрезке

13. Задание 13 № 507668. Решите уравнение

14. Задание 14 № 511603. Все рёбра правильной треугольной призмы ABCA₁B₁C₁ имеют длину 12. Точки M и N- середины рёбер AA₁ и A₁C₁ соответственно.

а) Докажите, что прямые BM и MN перпендикулярны.

б) Найдите угол между плоскостями BMN и ABB₁.

15. Задание 15 № 508507. Решите неравенство:

16. Задание 16 № 512885. Радиусы окружностей с центрами O₁ и O₂ равны соответственно 1 и 3. Найдите радиус третьей окружности, которая касается двух данных и прямой O₁O₂, если O₁O₂ = 14.

17. Задание 17 № 513369. По вкладу «А» банк в конце каждого года планирует увеличивать на 20% сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» - увеличивать эту сумму на 10% в первый год и на одинаковое целое число n процентов и за второй, и за третий годы. Найдите наименьшее значение n, при котором за три года хранения вклад «Б» окажется выгоднее вклада «А» при одинаковых суммах первоначальных взносов.

18. Задание 18 № 500390. Найдите все значения , при каждом из которых уравнение имеет более двух корней.

19. Задание 19 № 500412. В ряд выписаны числа: Между ними произвольным образом расставляют знаки «» и «» и находят получившуюся сумму.

Может ли такая сумма равняться:

а) 12, если ?

б) 0, если ?

в) 0, если ?

г) 5, если ?