«Таблицы и опорные схемы по математике в 5 классе (ЗПР), как средство развития познавательной деятельности детей с ограниченными возможностями в здоровье»

Областное государственное бюджетное образовательное учреждение для детей, нуждающихся в психолого-педагогической и медико-социальной помощи -

областной центр диагностики и консультирования «Развитие»

Вейер Татьяна Викторовна

«Таблицы и опорные схемы по математике

в 5 классе (ЗПР), как средство развития познавательной деятельности детей с ограниченными возможностями в здоровье»

г.Ульяновск

2014

Пояснительная записка.

Практический опыт работы с опорными схемами заметно повышает результативность обучения программного материала по математике детей с ограниченными возможностями здоровья с ЗПР. В своей работе использовала свои разработанные схемы. В схемах, таблицах и опорных конспектах правила, алгоритмы выглядят вполне доступно, понятно, можно разобраться и выучить гораздо легче. Схемы помогают выделить конкретные действия, обозначить их связи. Таблицы, опорные конспекты и схемы могут быть использованы учителем в ходе урока, объяснения нового материала, и также учащимися для самостоятельного выполнения заданий, повторения, восполнения пробелов знаний, для самопроверки. Предложенные наглядные средства могут применяться в качестве материалов на зачетах, тестах, при написании контрольных работ. Они помогают детям не только строить свои рассуждения, но и выполнять действия по предложенному плану, избавляют от механического зазубривания правил и формулировок и способствуют более глубокому осмыслению и усвоению детьми соответствующего материала. Работа с опорными схемами требует известной оперативности, поэтому учитель должен продумать способы их предъявления на уроках. Некоторые из схем можно сделать элементами постоянной экспозиции классной комнаты, другие - поместить во временную экспозицию, третьи - использовать только на отдельных уроках по мере необходимости.

Важную функцию в опорных схемах могут выполнять цветовые сигналы, стрелки и другие условные обозначения. Каждый из этих символов имеет свою смысловую нагрузку, понятную ученикам. Поэтому при введении новых схем следует соблюдать единообразие в обозначениях и уделять особое внимание впервые появляющимся символам.

Хорошими помощниками служат детям и памятки, отражающие пошаговые операции при вычислениях. Особенно они пригодятся при изучении письменных приемов вычислений. Такие памятки могут быть демонстрационными (в виде таблицы вывешиваются в классе) и индивидуальными (находятся в пользовании у каждого ученика). Предлагая памятку, учитель должен обучить детей работе с ней. Вначале действия по каждому пункту памятки выполняются под руководством учителя, с проговариванием вслух. Выполнив одну операцию, учитель показывает, в каком пункте памятки о ней сказано. Затем дети приступают к процессу математического действия, прочитав соответствующий пункт и выполнив описанное в нем действие. Постепенно руководство процессом действия со стороны учителя прекращается и дети переходят на самостоятельное использование памятки.

Работу со схемами по решению задач, предусматривает применение любых рациональных чисел и решению более сложных задач. Такую работу можно строить по- разному. Вот некоторые из возможных вариантов:

- после чтения текста задачи предложить детям выбрать нужную схему

(предложить для выбора 2-3 схемы);

- по данной схеме с готовым числовым набором составить текст;

- по данной схеме с готовым числовым набором дать задание, назвать действия, необходимые для решения задачи, и объяснить их выбор;

- по данной схеме с готовым числовым набором и решением дать задание, проверить и обосновать верность предложенного решения или опровергнуть его;

- сравнить тексты двух задач, предложить детям выбрать для каждой из них схему и указать, чем будут отличаться их решения.

При решении составных задач опорные схемы помогут в формировании умения разбивать составную задачу на простые. Таким образом, опорные схемы по разным темам и разделам математики дают учителю возможность:

- облегчить и ускорить изучение нового материала;

- уменьшить количество ошибок, допущенных детьми;

- успешно повторять необходимый материал, а также решать ряд других

учебных задач.

Включать каждого ученика в активную деятельность на всех уроках, довести представления по изучаемой теме до формирования понятий, устойчивых навыков - вот моя цель. Опорные схемы - это выводы, которые рождаются на глазах учеников в момент объяснения и оформляются в виде таблиц, карточек, наборного полотна, чертежа, рисунка. Активный ответ - первостепенное условие высокой обратной связи, доброго делового контакта на уроке. Этому и помогают схемы-опоры.
Когда ученик отвечает на вопрос учителя, пользуясь схемой (читает ее), снимаются скованность, страх ошибки. Схема становится алгоритмом рассуждения и доказательства, а все внимание направлено не на запоминание или воспроизведение заученного, а на суть, размышление, осознание причинно-следственных зависимостей и связей. Дети дома не учат у нас правила и формулировки. Ни один даже самый слабый ученик не чувствует себя беспомощным. Опоры на наших уроках стали постоянными помощниками моим ученикам, условием бесконфликтного, делового, дружеского общения, основой уверенности детей в своих способностях преодолеть трудности учения, импульсом к активному, заинтересованному труду.

ТАБЛИЦА РАЗРЯДОВ И КЛАССОВ

ЦЕЛЫЕ ЧИСЛА

Десятичные доли

Класс миллионов

Класс тысяч

Класс единиц

Единицы

сотни

десятки

единицы

сотни

десятки

единицы

десятые

сотые

тысячные

ЧИТИАЕМ: 456.758.609.231

сде

сде

сде

сде

456

.

758

.

609

.

231

М

И

Л

Л

И

А

Р

Д

О

В

М

И

Л

Л

И

О

Н

О

В

Т

Ы

С

Я

Ч

Таблица. Геометрические фигуры.

Прямая

А В

АВ прямая

Отрезок.

• •

АВ отрезок

Луч.

В

• А АВ луч

Параллельные прямые.

А В

С D

АВ || СD

Перпендикулярные прямые. А

С D

В

АВ СD

Ломаная.

А С

D

В

АВ+ВС+СД -длина ломаной

Линия

Треугольник

В

А С

Р = АВ+ВС+АС

Прямоугольник

Р = 2 · (а + b)

P = 2a + 2b

S = a·b

Квадрат.

P = 4 · a

S = a · a = a²

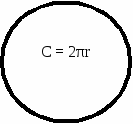
Круг.

Окружность

Овал.

Угол.

Параллелограмм

Ромб.

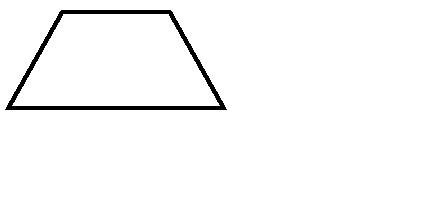
Трапеция.

Многоугольник

(шестиугольник)

Прямоугольник. Квадрат.

Д - длина, Ш - ширина. a - длина, b - ширина.

Название

Изображение

Площадь (S)

Периметр (Р)

Прямоугольник

b

(Ширина)

a

(Длина)

S = Д × Ш

S = a · b

Р = Д + Ш + Д + Ш

Р = 2· а + 2· в

Р = 2· (а + в)

Квадрат

a

(Ширина)

a

(Длина)

S = Д × Ш

или

S = Д × Д

S = a · a

Р = Д + Ш + Д + Ш

или

Р = Д + Д + Д + Д

Р = 4· а

ПЕРИМЕТР треугольника

АВ = 55мм А

АС = 4см = 40 мм

ВС = 6см 5 мм = 65мм

Периметр треугольника АВС

55 + 40 + 65 = 160мм = 16 см В С

Меры.

Меры

Соотношения мер

Стоимости

копейка к.

рубль р.

1к.

1 р. = 100к.

1 к = 0, 01р

Длины

миллиметр мм

сантиметр см

дециметр дм

метр м

километр км

1 мм

1 см = 10 мм

1 дм = 10 см

1 дм = 100 мм

1 м = 10 дм

1 м = 100 см

1 м = 10 000 мм

1 км = 1 000 м

1 км = 100 000 см

1 мм = 0, 1см

1 см = 0, 1 дм

1мм = 0,01дм

1дм = 0, 1 м

1 см = 0, 01 м

1 мм = 0, 0001 мм

1 м = 0, 001 км

1 см = 0, 00001км

Площади

квадратный миллиметр (кв.мм.) мм²

квадратный сантиметр (кв.см.) см²

квадратный дециметр (кв. дм.) дм²

квадратный метр (кв. м.) м²

квадратный километр (кв.км.) км²

1 мм²

1 см² = 100 мм²

1 дм² = 100 см²

1 м² = 100 дм²

1 м² = 10 000 см²

1 м² = 1 000 000 мм²

1 км² = 1 000 000 м²

1 мм² = 0, 01 см²

1 см² = 0, 01 дм²

1 дм² = 0,01 м²

1 см² = 0, 0001 м²

1 мм² = 0, 000001 м²

1 м² = 0, 000001 км²

Земельных площадей.

квадратный километр (кв.км.) км²

гектар га

ар а

1 км² = 1 000 000 м²

1 га = 100 а

1 га = 10 000 м²

1 а = 100 м²

1 м² = 0, 000001км²

1 а = 0, 01 га

1 м² = 0, 0001 га

1 м² = 0, 01 а

Объёма

кубический миллиметр мм³

кубический сантиметр см³

кубический дециметр дм³

кубический метр м³

кубический километр км³

1 мм³

1 см³ = 1 000 мм³

1л= 1 дм³ = 1 000 см³

1л =1 дм³ = 1 000 000 мм³

1 м³ = 1 000 дм³

1 м³ = 1 000 000 см³

1 мм³ = 0, 001 см³

1 см³ = 0, 001 дм³

1 мм³ = 0, 000001дм³

1 дм³ = 0, 001 м³

1 см³ = 0, 000001 м³

Массы

грамм г

килограмм кг

центнер ц

тонна т

1 г

1 кг = 1 000г

1 ц = 100 кг

1 ц = 100 000 г

1 т = 10 ц

1 т = 1 000 кг

1 т = 1 000 000 г

1 г = 0, 001 кг

1 кг = 0, 01 ц

1 г = 0, 00001 ц

1 ц = 0, 1т

1 кг = 0, 001 т

1 г = 0, 000001 т

Времени

секунда с

минута мин

час ч

сутки сут.

неделя нед.

месяц мес.

год год

век век

1с

1 мин = 60 с

1 ч = 60 мин

1 сут. = 24 ч

1 нед. = 7 сут.

1 мес. = 28 ( 29, 30, 31 ) сут.

1 год = 12 мес.

1 век = 100 лет

Шкалы и координаты

0 1 2 3 4 5 6 7 8 9 10 11 ___.___.___.___.___.___.___.___.___.___.____________

О Е А В С Р К Х

О(0) - начало координатного луча

Е(1) единичный отрезок

О(0), Е(1), А(2), В(3), …

Числа 0, 1, 2, 3, 4, … соответствующие точкам О, Е, А, В, С, … называют координатами этих точек

МЕНЬШЕ или БОЛЬШЕ

4 < 6 точка С(4) лежит ЛЕВЕЕ точки К(6)

6 >4 точка К(6) лежит ПРАВЕЕ точки С(4)

4 < 6 6 >4 НЕРАВЕНСТВО

3 < 5 < 7 ДВОЙНОЕ НЕРАВЕНСТВО

СЛОЖЕНИЕ и ВЫЧИТАНИЕ

НАТУРАЛЬНЫХ ЧИСЕЛ

Компоненты сложения и вычитания

Первое слагаемое

Второе слагаемое

Сумма +

170

55

170 + 55 = 225

сумма сумма

Уменьшаемое

Вычитаемое

Разность -

170

55

170 - 55 = 115 разность разность

Свойства сложения

1. ПЕРЕМЕСТИТЕЛЬНОЕ свойство

2 + 8 = 8 + 2

2. СОЧЕТАТЕЛЬНОЕ свойство

2 + (8 + 7) = (2 + 8) + 7 = 10 + 7 = 17

3. 7 + 0 = 7 или 0 + 7 = 7

Свойства вычитания

1. Вычитание суммы из числа

12 - (3 + 2) = (12 - 3) - 2 = 12 - 2 - 3 = 7

2. Вычитание числа из суммы

(13 + 6) - 3 = 13 + 6 - 3 = 13 - 3 + 6 = 16

3. 8 - 0 = 8

4. 8 - 8 = 0

ЧИСЛОВЫЕ и БУКВЕННЫЕ выражения

670 + 330 - 50 = 950

числовое значение

выражение выражения

670 + а буквенное выражение

Если а = 30, то 670 + 30 = 700

Если а = 430, то 670 + 430 = 1100

Буквенная запись свойств сложения и вычитания

1. Переместительное свойство

a + b = b + a

2. Сочетательное свойство

a + (b + c) = (a + b) + c = a + b + c

3. Свойство нуля при сложении

a + 0 = 0 + a = a

4. Свойство вычитания суммы из числа

a - (b + c) = a - b - c

b + c < a b + c = a

5. Свойство вычитания числа из суммы

(a + b) - c = a + (b - c), если с < b или с = b

(a + b) - c = (a- c) + b, если с < а или с = а

6. Свойство нуля при вычитании

а - 0 = а; а - а = 0

УПРОСТИТЬ выражение:

а) 38 + х + 22 = 38 + 22 + х = 60 + х

б) 38 - (12 + х) = 38 - 12 - х = 26 - х

в) х - 38 - 12 = х - (38 + 12) = х - 50

г) 38 - х - 12 = 38 - (х + 12) = 38 - (12 + х) = 38 - 12 - х

= 26 - х

д) (38 + х) - 12 = (38 - 12 ) + х = 26 - х

е) х - 12 + 38 = (х - 12) + 38 = 38 + (х - 12) = 38 + х - 12

= 38 - 12 + х = 26 + х

Решение уравнений.

Повторяют алгоритм нахождения неизвестного компонента. На месте однозначного числа могут быть любые многозначные (рациональные) числа.

Слаг-ое слаг-ое сумма

2. + х = 5

Слаг-ое

х = 5 - 2

Слаг-ое

х = 3

Умен-ое выч-ое разность

7 - х = 3

Выч-ое

х = 7 - 3

Выч-ое

х = 4

Множ-ль множ-ль произ-е

2. × х = 6

Множ-ль

х = 6 : 2

Множ-ль

х = 3

Дел-ое дел-ль частное

10. : х = 5

Дел-ль

х = 10 : 5

Дел-ль

х = 2

Слаг-ое слаг-ое сумма

х + 2 = 5

Слаг-ое

х = 5 - 2

Слаг-ое

х = 3

Умен-ое выч-ое разность

х - 3 = 5

Умен-ое

х = 5 + 3

Умен-ое

х = 8

Множ-ль множ-ль произ-е

х × 2 = 6

Множ-ль

х = 6 : 2

Множ-ль

х = 3

Дел-ое дел-ль частное

х : 5 = 2

Дел-ое

х = 5 × 2

Дел-ое

х = 10

Компоненты умножения.

Первый множитель

Второй множитель

Произведение

43

2

43 · 2 = 86

43 · 2 - произведение чисел 43 и 2

86 - значение произведения чисел 43 и 2Свойства умножения

Название свойства

Числовая запись

Буквенная запись

переместительное

2 · 5 = 5 · 2

a · b = b · a

сочетательное

5 · (2 · 3) = (5 · 2) · 3

a · (b · c) = (a · b) · c

умножение на 1

1 · 5 = 5 5 · 1 = 5

1· a = а a · 1 = а

умножение на 0

0 · 5 = 0 5 · 0 = 0

0· a = 0 a · 0 = 0

₁²

₂²

×

2

3

4

6

5

+

1

1

7

0

1

4

0

4

1

5

2

1

0

8 · х пишут 8х

5 · (a + b) пишут 5(a + b)

a · b пишут ab

(a + b) · (3 + c) пишут (a + b)(3 + c)

Компоненты деления.

Делимое

Делитель

Частное

86

2

86 : 2 = 43

86 : 2 частное чисел 86 и 2

43 - частное (значение частного чисел 86 и 2)

Числовая запись

Буквенная запись

3 : 1 = 3

а : 1 = а

3 : 3 = 1

а : а = 1

0 : 3 = 0

0 : а = 0

3 : 0 - нельзя

а : 0 - нельзя

·

·

·

·

₁

₁

-

1

3

1

3

2

0

5

6

×

5

6

×

5

6

1

1

2

·2

·3

4·

·5

2

3

-

1

9

3

1

1

2

1

6

8

1

6

8

-

2

5

2

2

2

4

-

2

8

0

2

8

0

0

Деление с остатком

_ 23 |_4__

20 | 5

3

делимое

делитель

неполное частное

остаток

23

==

4

·

5

+

3

a

=

b

·

q

+

r

Упрощение выражений

Распределительное свойство умножения относительно сложения

(a + b)c = a c + b c

a c + b c = (a + b)c

буквенное выражение

(65 + b)·2 = 65 ·2 + b·2 = 130+2b

3х + 12х = (3+12)х = 15х

числовое выражение

107·4= (100+7) ·4 = 100·4+7·4 = 400+28=428

23· 34+77· 34 = 34· (23+77) = 34·100= 3 400 или

23· 34+77· 34 = (23+77) · 34 = 100 · 34= 3 400

Распределительное свойство умножения относительно вычитания

(a - b)c = a c - b c

a c - b c = (a - b)c

буквенное выражение

(65 - b)·2 = 65 ·2 - b·2 = 130-2b

12х - 3х = (12 - 3)х = 9х

числовое выражение

93·4= (100-7) ·4 = 100·4-7·4 = 400-28=372

77· 34 - 67· 34= (77-67)· 34 = 10· 34= 340 или

77· 34 - 67· 34= 34 · (77-67) = 34·10= 340

Степень числа. Квадрат и куб числа.

3·3·3·3·3= 3⁵

3- основание степени,

5 - показатель степени

3⁵ = 3·3·3·3·3 = 243

243- значение степени

Квадрат числа

р² = р · р

4² = 4·4 = 16

Куб числа

р² = р · р· р

4³ = 4·4 ·4 = 64

3¹ = 3 34¹ = 34 1¹ = 1

Формулы

Формула пути.

s - путь, v - скорость, t - время.

Скорость

Время

Путь

v = s : t

t = s: t

s = v · t

50 км/ч

2 ч

?

Решение:

50 км/ч × 2 ч = 100 км

80 км/ч

?

Решение:

160 км : 80 км/ч = 2 ч

160 км

?

Решение:

80 км : 4 ч = 20 км/ч

4ч

80км

Прямоугольный параллелепипед

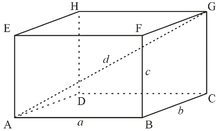
Прямоугольный параллелепипед - объёмная фигура, у которой шесть граней, и каждая из них является прямоугольником. Имеет 12 рёбер и 8 вершин.

Длины трёх рёбер прямоугольного параллелепипеда, имеющих общий конец, называют его измерениями:

a - длина, b - ширина, с - высота

Площадь поверхности прямоугольного параллелепипеда

S_п.п. = 2 a b + 2 b с + 2 a с или

S_п.п. = 2 (a b + b с + a с)
Формула нахождения объёма прямоугольного параллелепипеда:

V=abс

Куб

Прямоугольный параллелепипед с равными измерениями называется .

Все шесть граней куба - равные .

Площадь поверхности куба S_п.п.к = 6 a²

Формула нахождения объёма куба V=a³

Круг.

А В

Окружность

А В

О- центр окружности /круга

ОА - радиус окружности /круга

АВ - диаметр окружности /круга

АВ = 2· ОА

Полукруг

Полуокружность

Дуга окружности

Обыкновенные дроби.

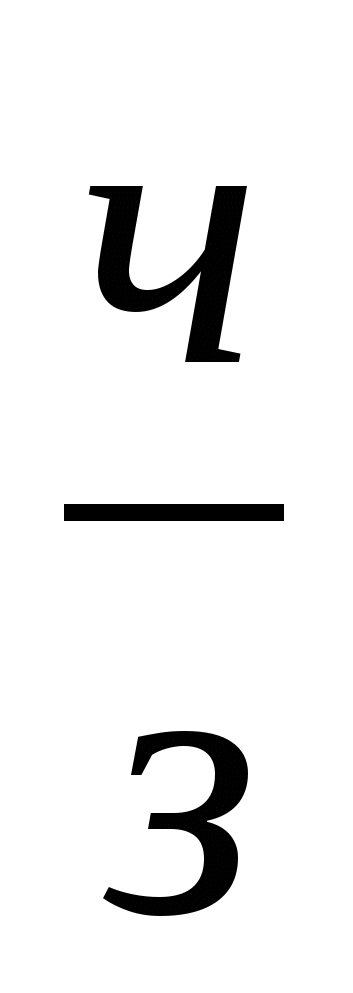
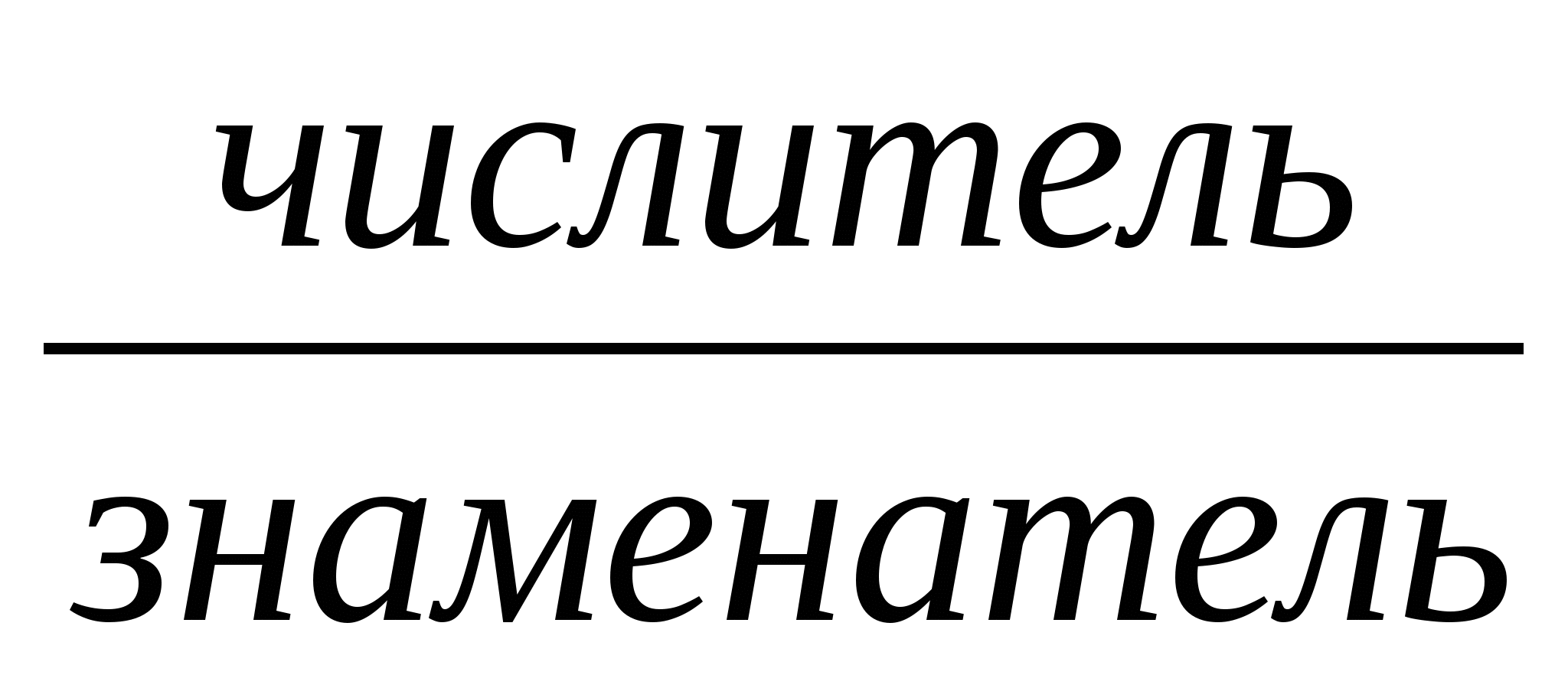
0 1 ___.___.___.___.___.___.___.___.___.___.____________

О А В С D К Е Х

О(0) - начало координатного луча

Е(1) единичный отрезок = 6 клеток

О(0), Е(1), А(), В(),С(), D(), К (), …

Е(),

Правильные и неправильные дроби. Смешанные числа.

Правильные дроби

( ч < з )

ч- числитель,

з- знаменатель.

Неправильные дроби

( ч > з, ч = з )

ч- числитель,

з- знаменатель.

Смешанные числа

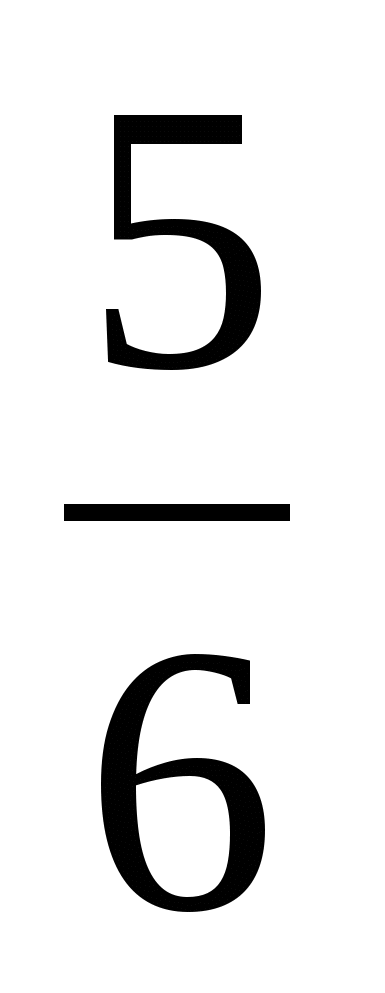
Ц - целая часть,

ч- числитель,

з- знаменатель.

; ;

; ; ; ; ; ; .

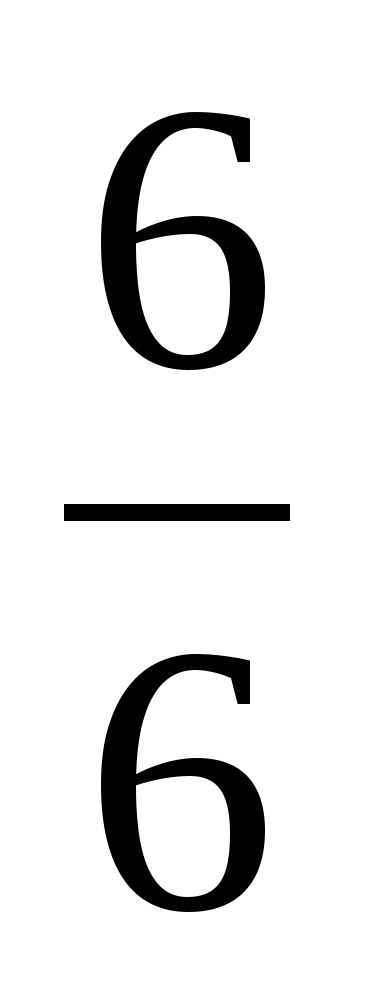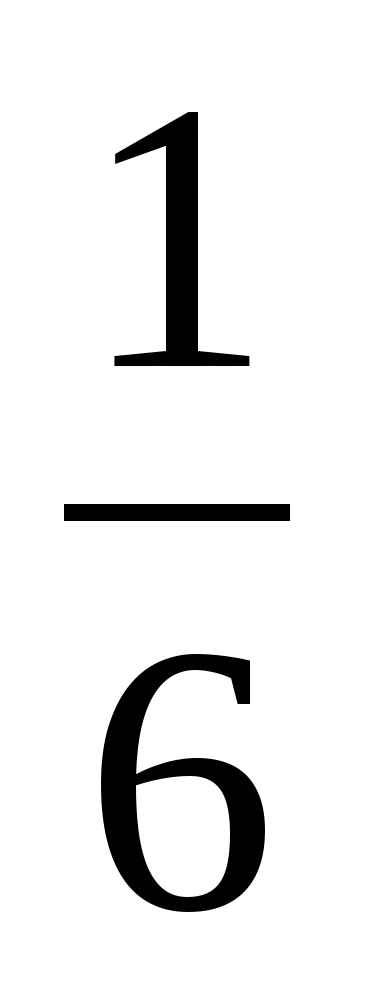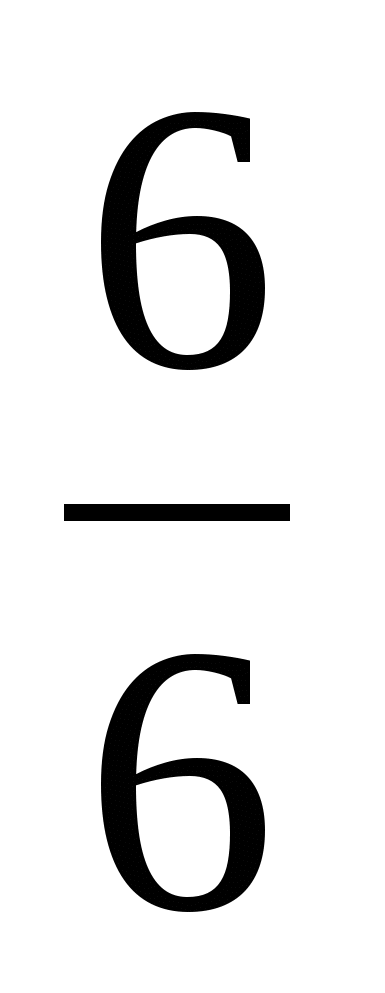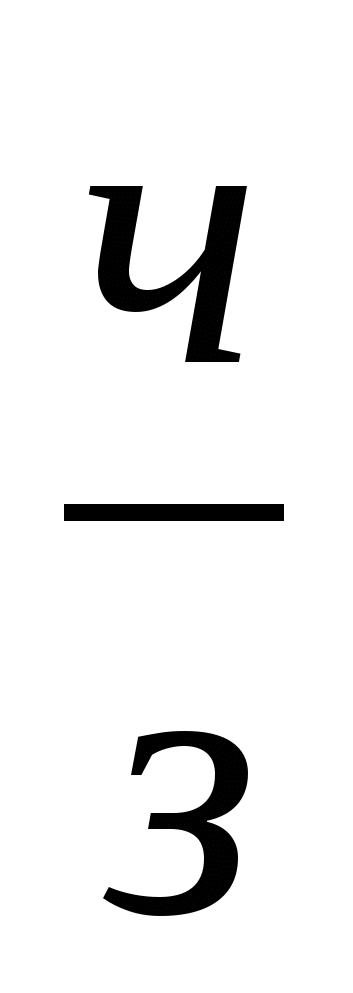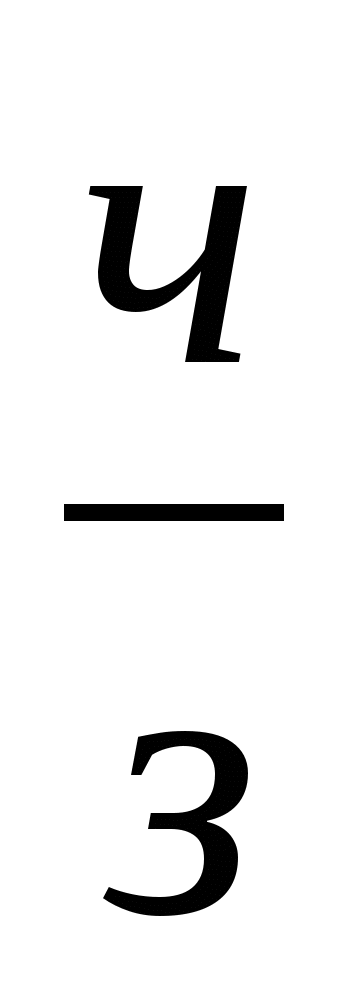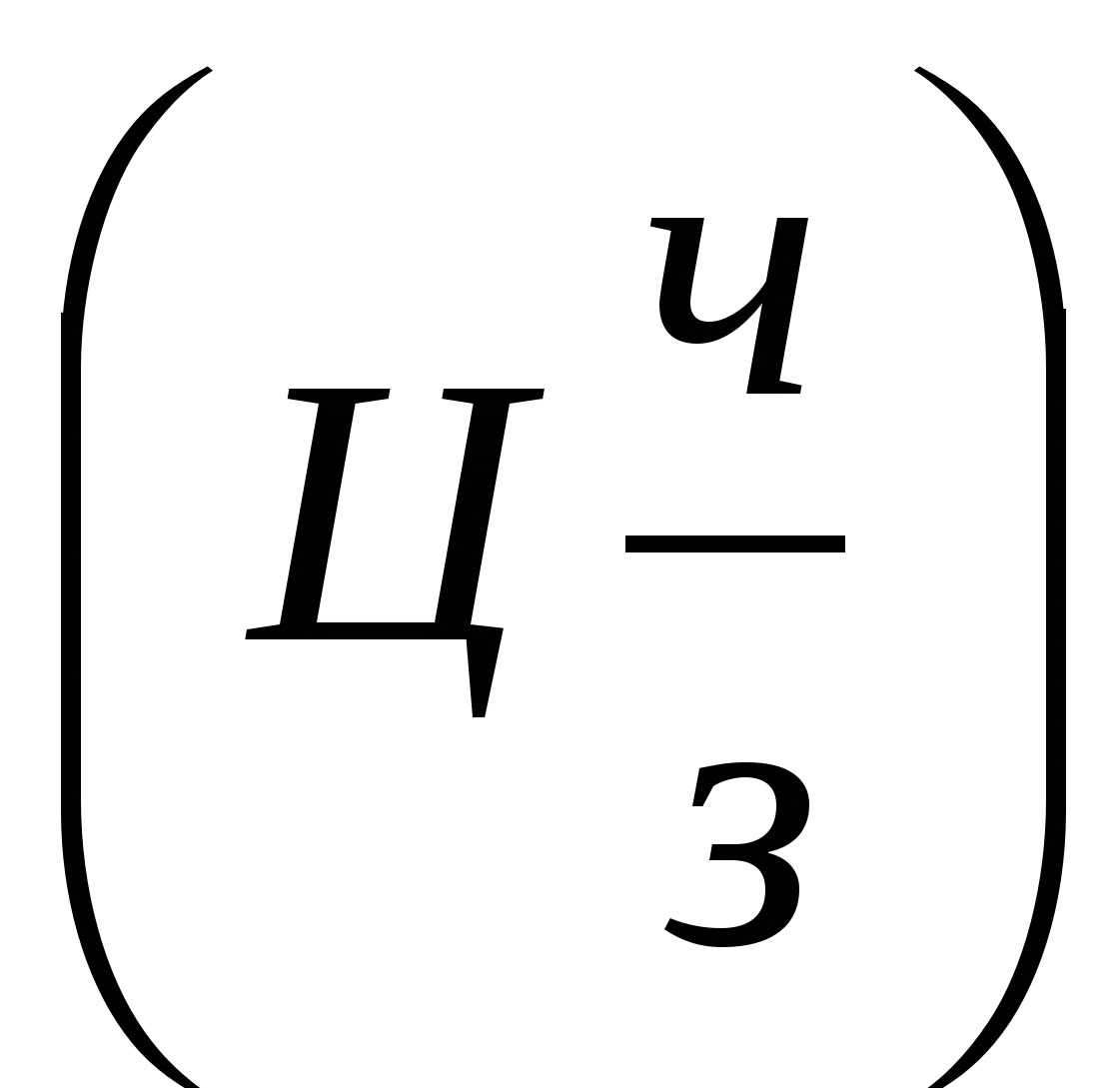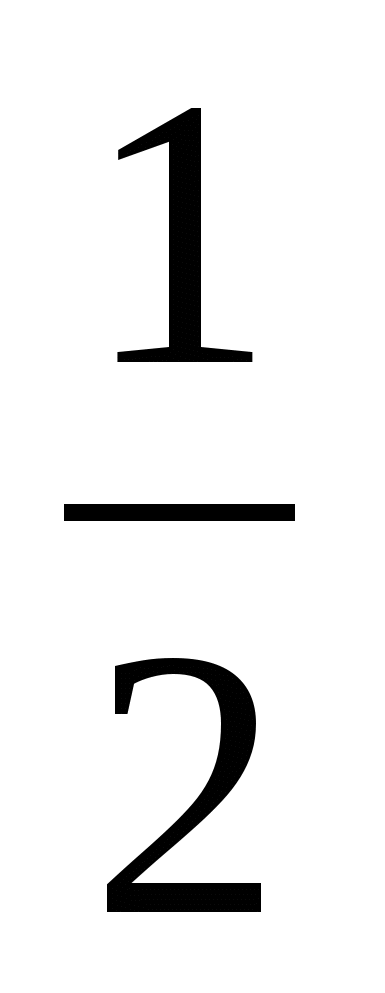; 91.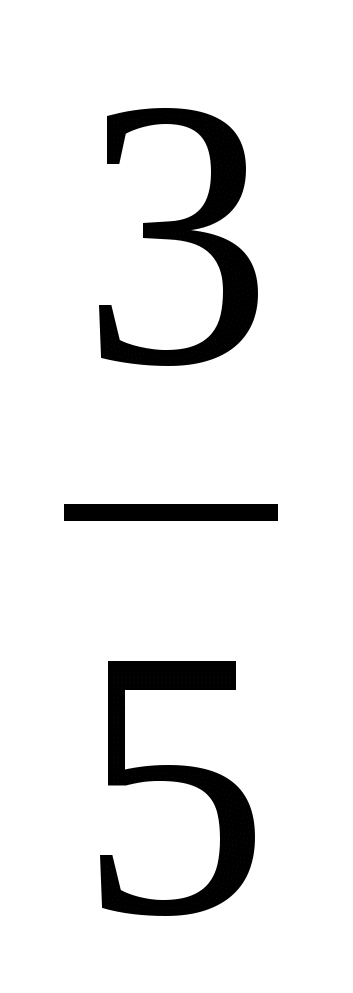

Основное свойство дроби.

Дробь не изменится, если числитель и знаменатель дроби

умножить на одно и то же число

разделить на одно и то же число

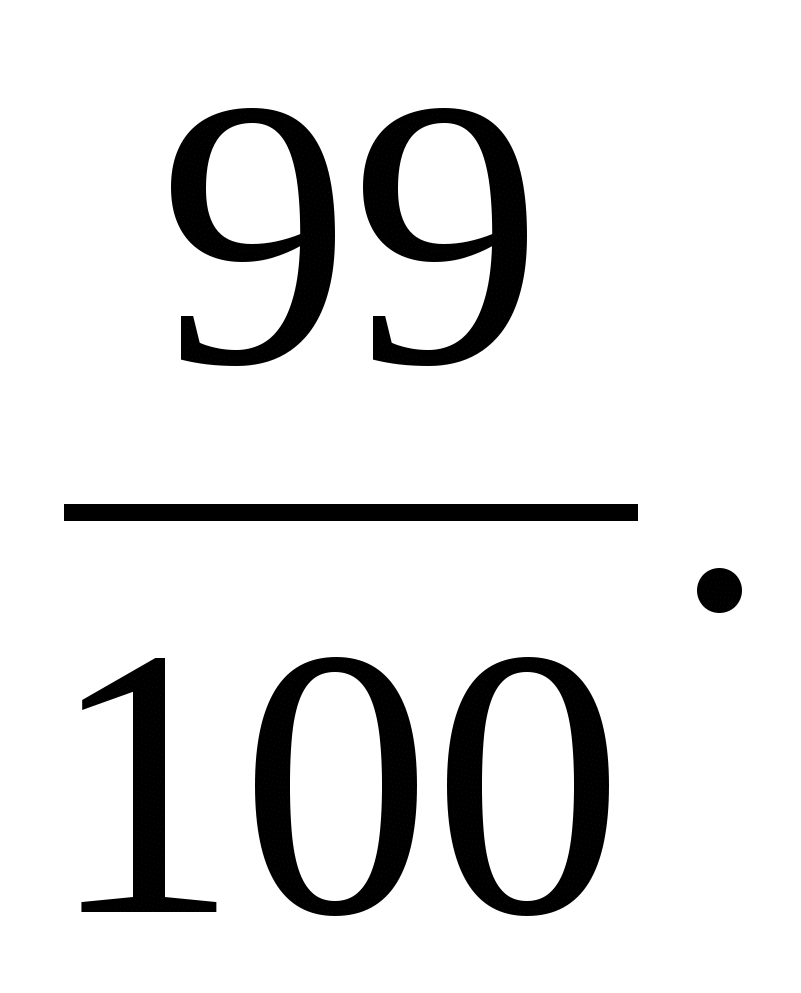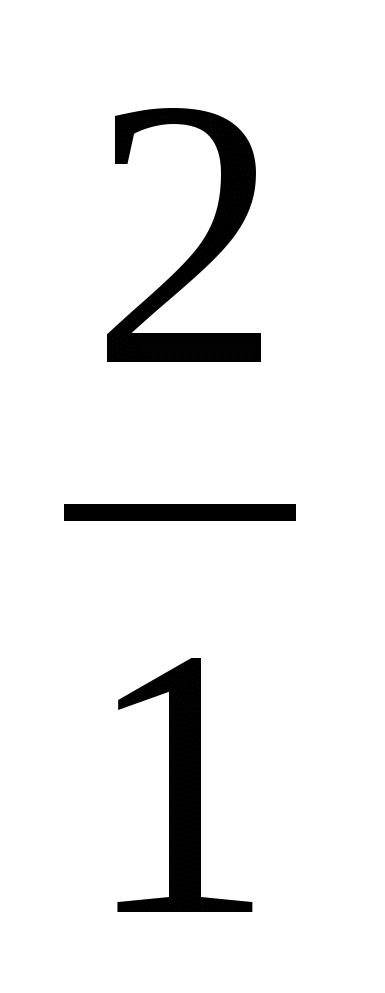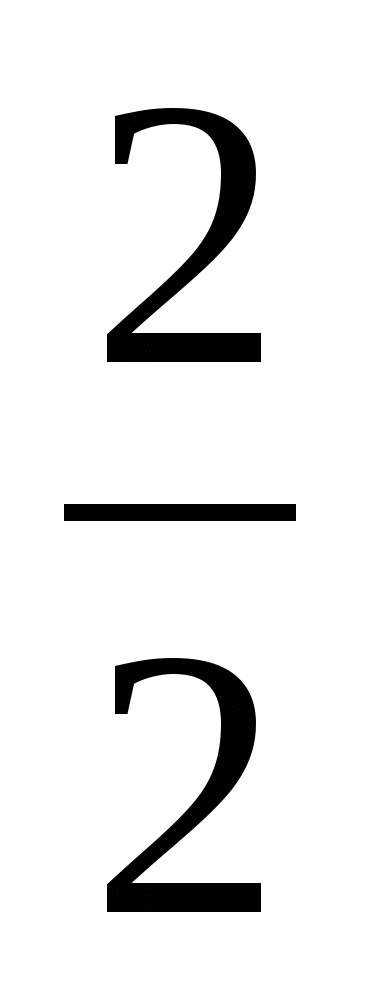; 3.

; 3.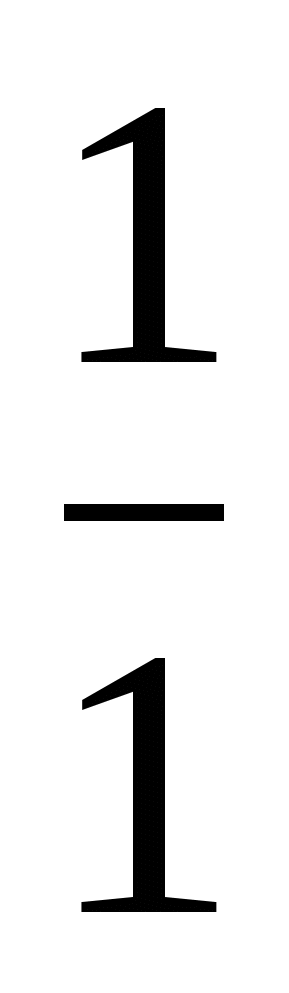

Нахождение части от числа.

Нахождение одной части от числа.

Нахождение нескольких частей от числа.

Найти 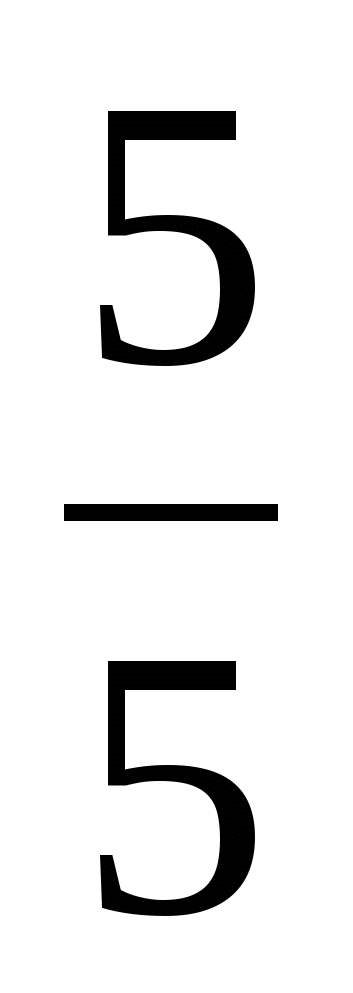от 300.

Найти 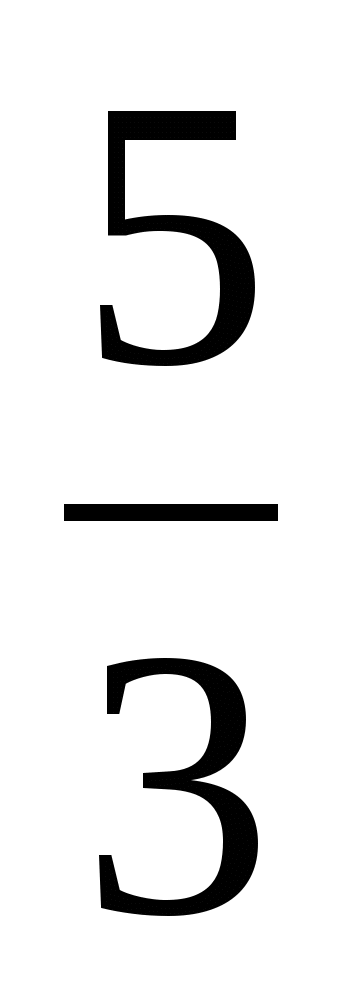от 300.

Решение:

300 : 5 × 1 = 60

Решение:

300 : 5 × 2 = 120

Нахождение дроби от числа.

Нахождение числа по его дроби.

Найти от 10см.

Решение: 10 : 5 × 2 = 4 (см)

Найти число, если его составляет 10см.

Решение: 10 : 2 × 5 = 25 (см)

Сравнение дробей.

Сравнение дробей с одинаковыми знаменателями

Сравнение дробей с одинаковыми числителями

Сравнение дробей с 1

Сравнение правильных и неправильных дробей

Сравнение смешанных чисел

Сравнение дробей с разными знаменателями

<

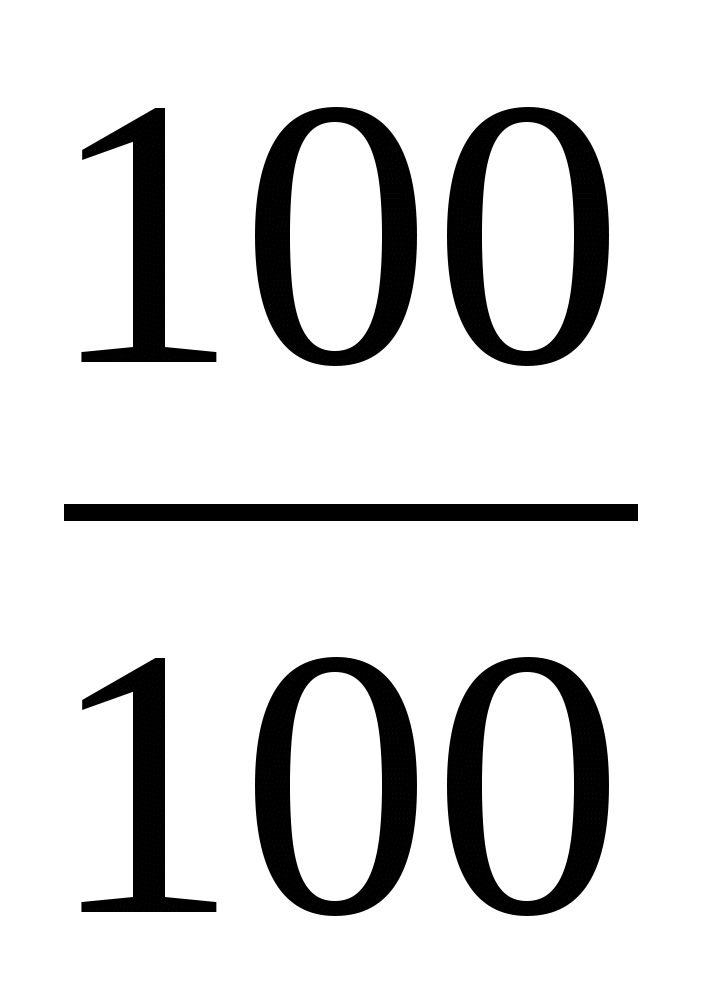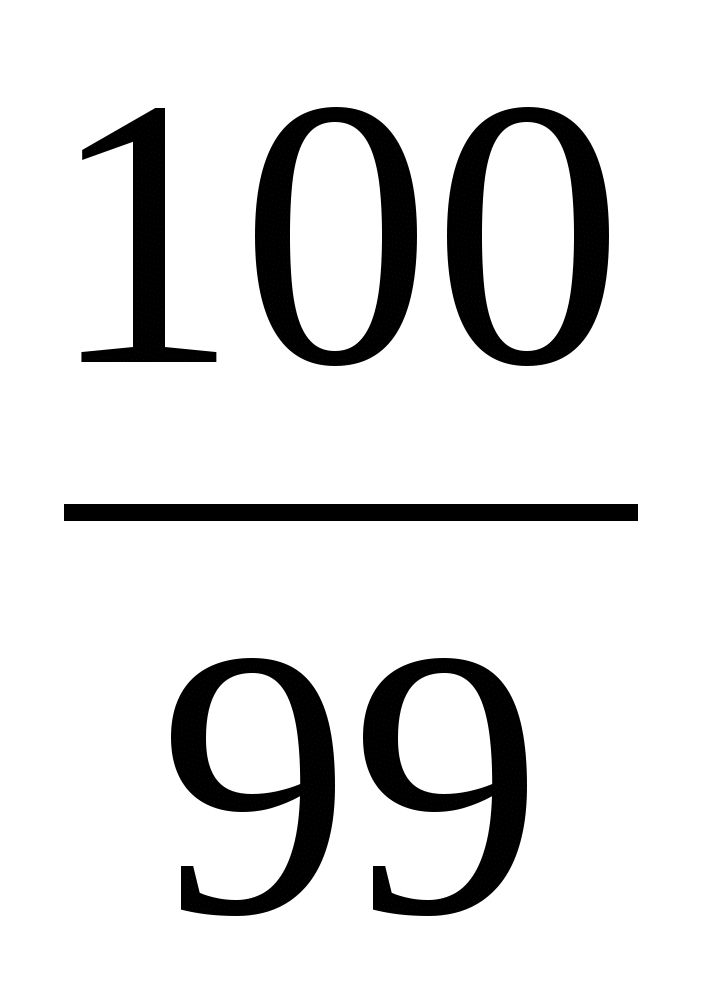
( 3 < 5 )

Больше та, у которой числитель больше.

<

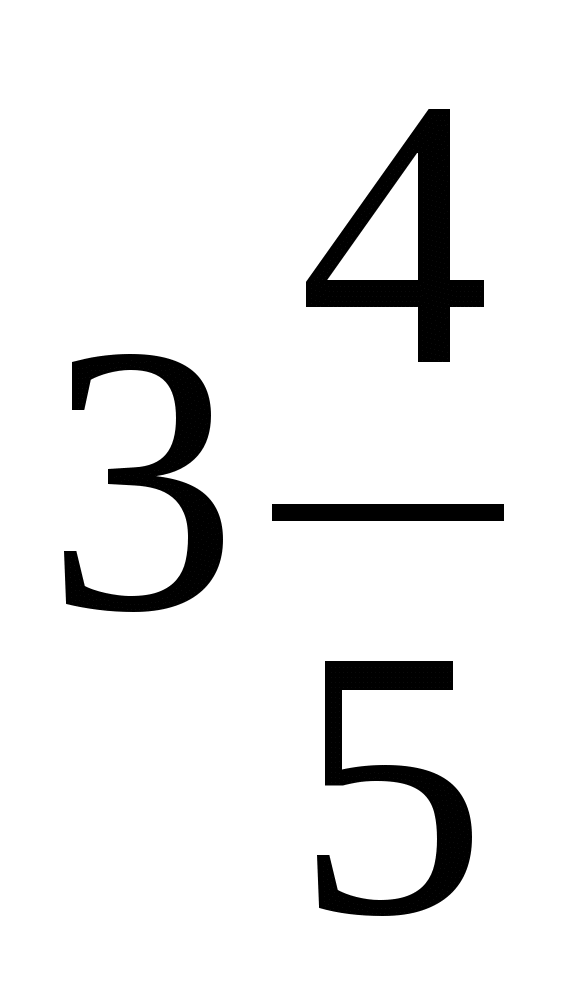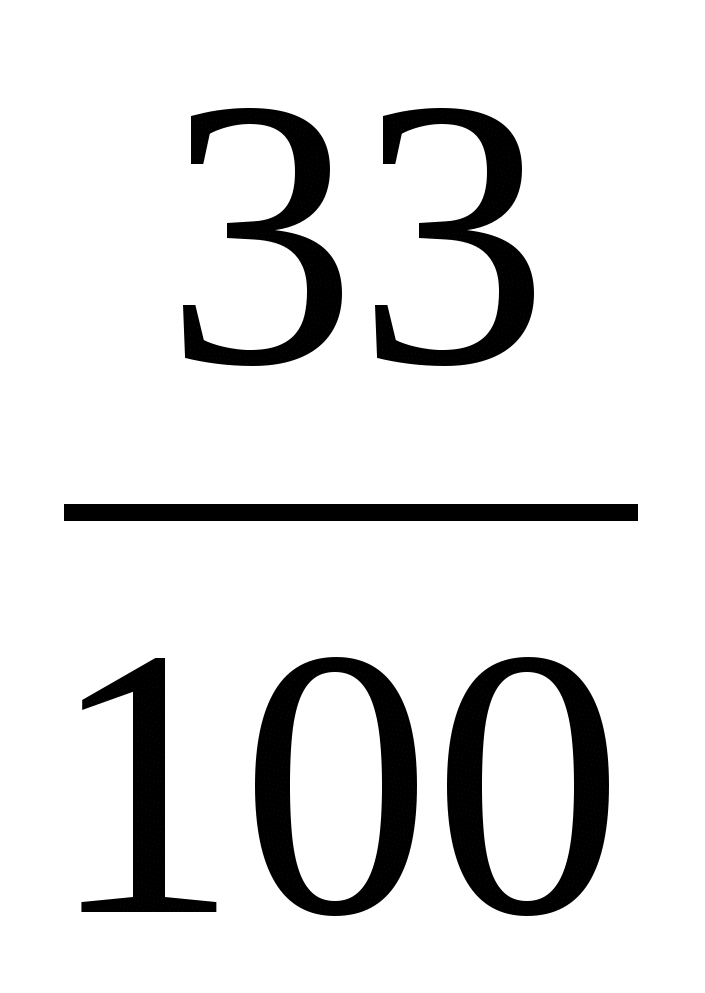
( 8 > 2 )

Больше та, у которой знаменатель меньше.

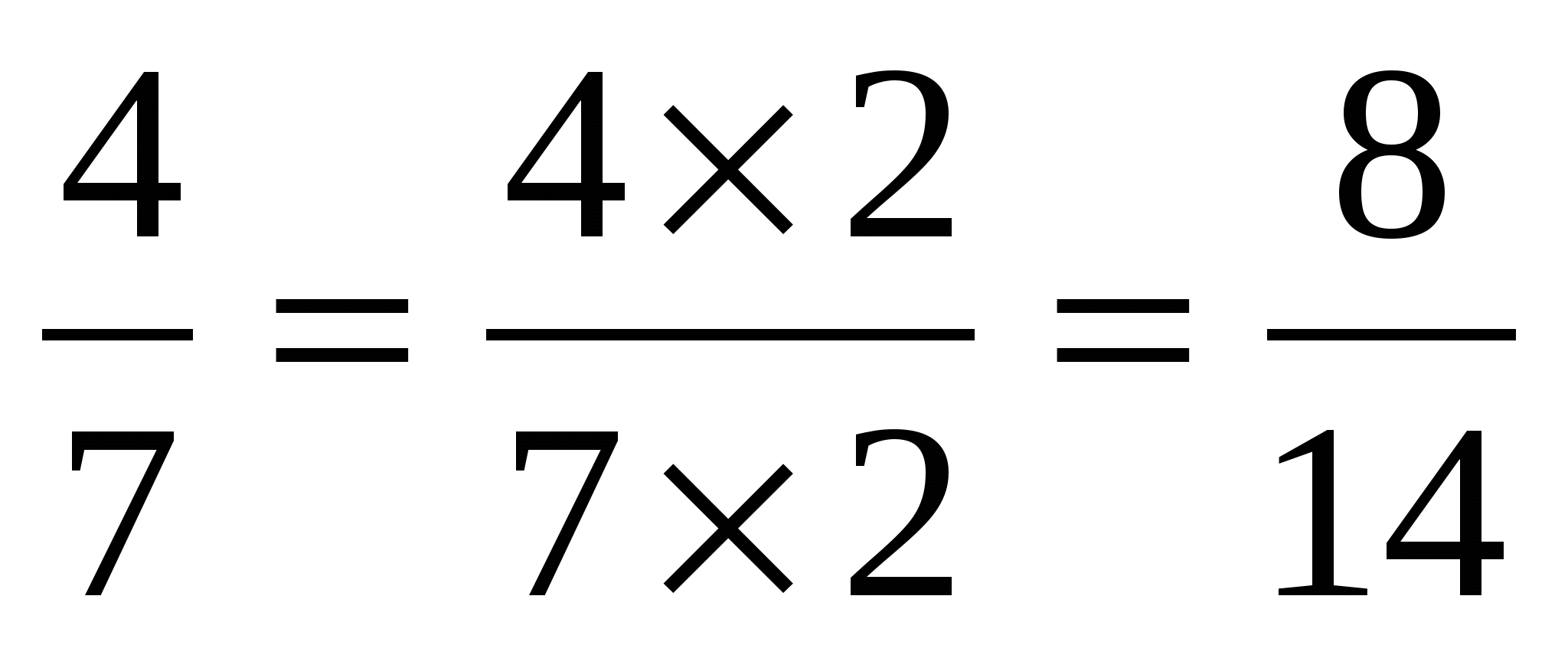
Любая правильная дробь меньше 1

;

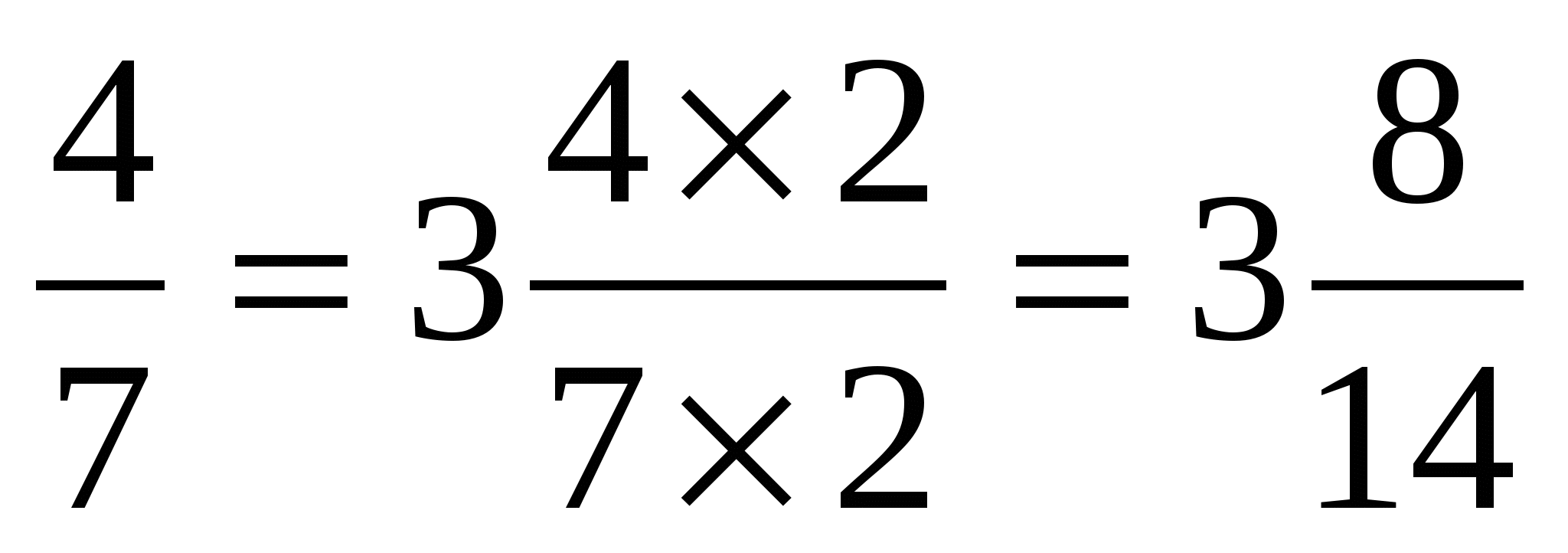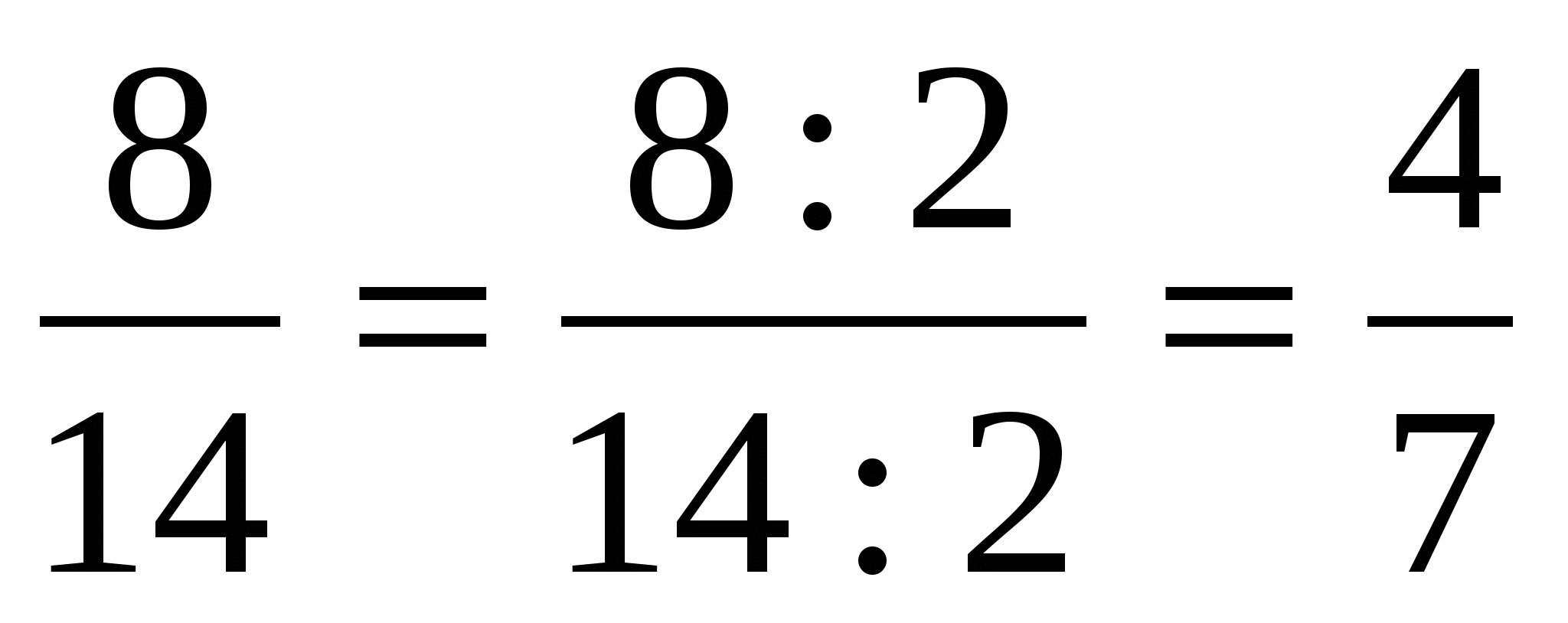
Любая неправильная дробь больше1 или равна 1.

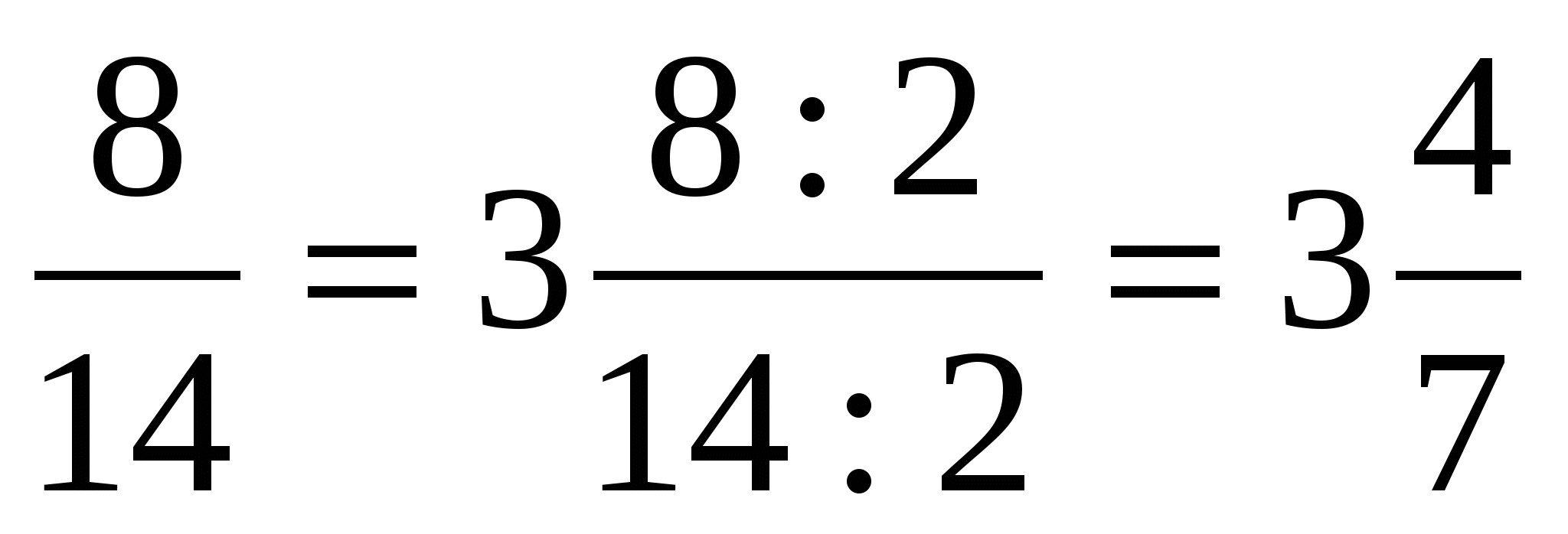
Любая правильная дробь меньше неправильной

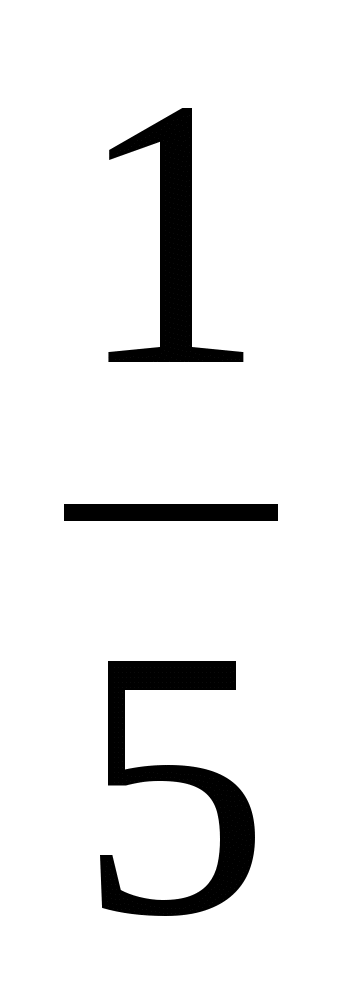
(4 > 1)

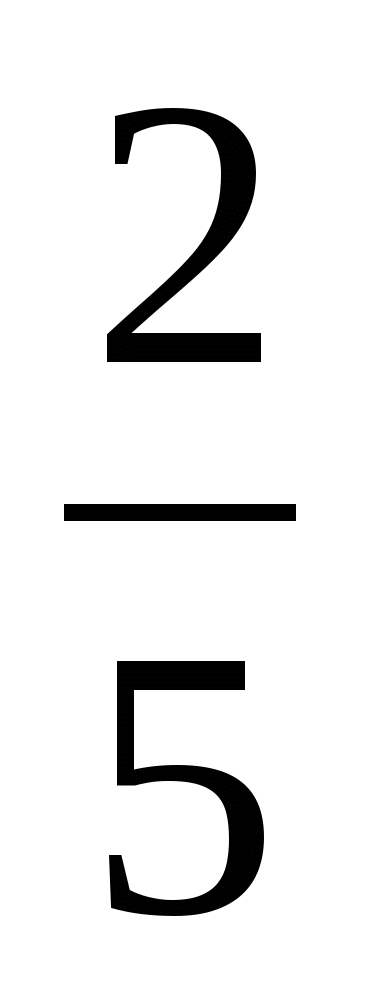
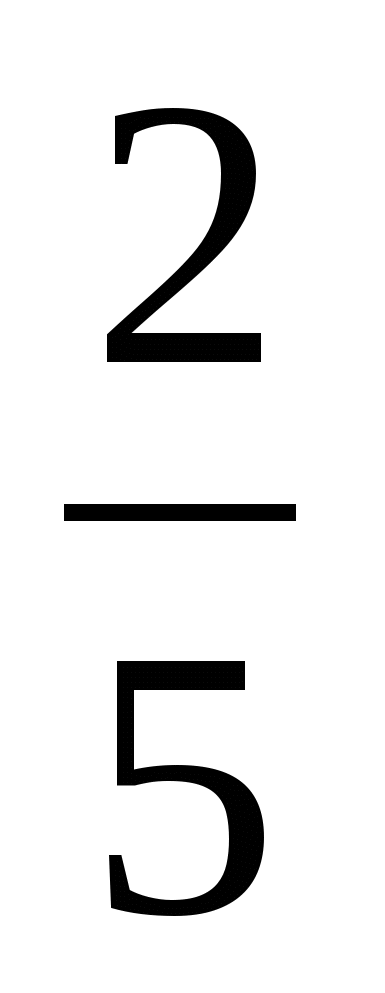
4 7

<

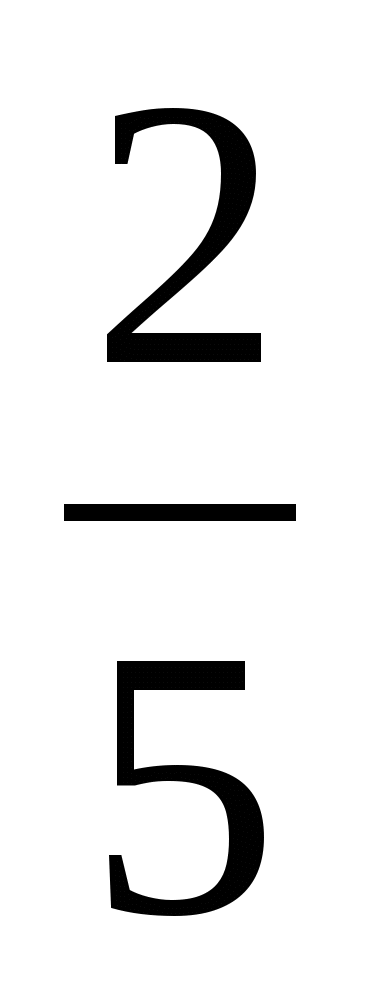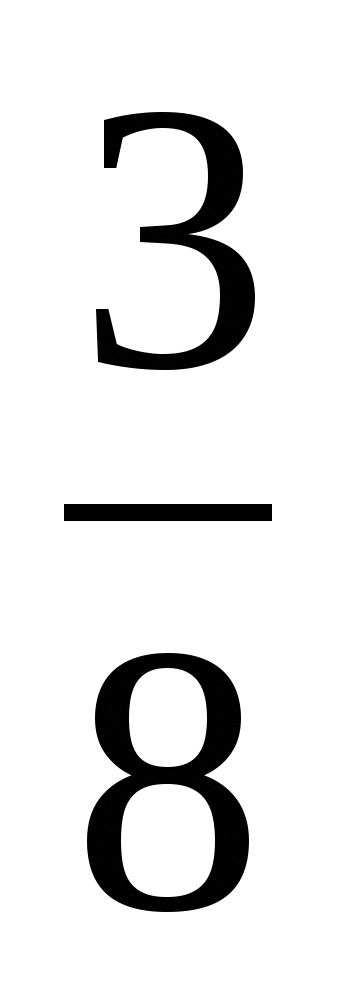
28

<

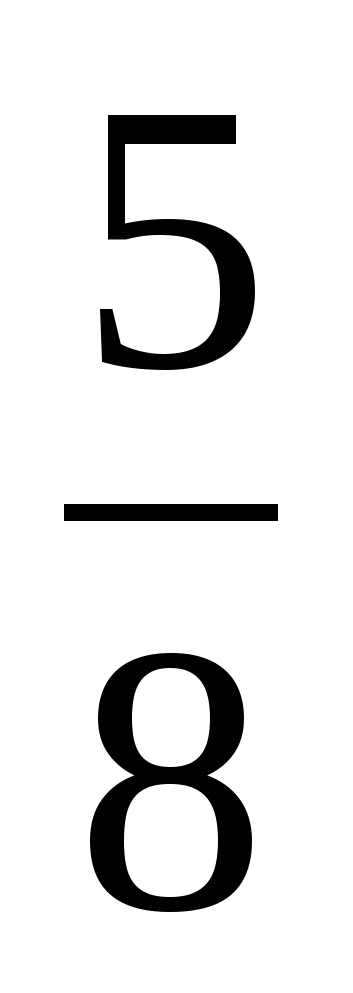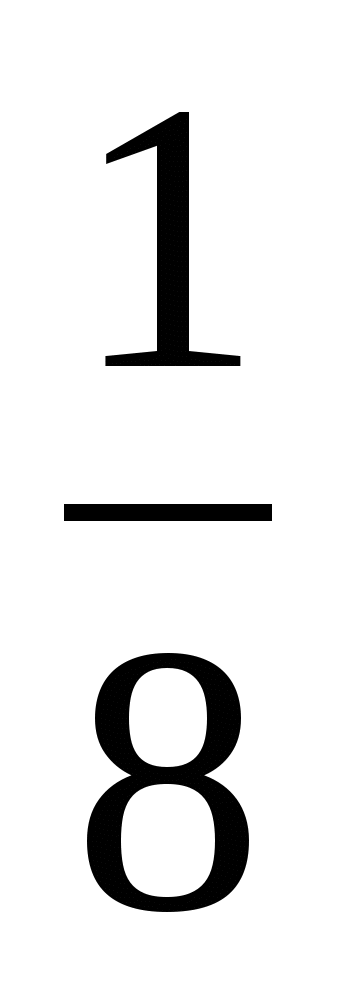
Таблица 15. Преобразование обыкновенных дробей.

Запись неправильной дроби в виде смешанного числа.

Запись неправильной дроби в виде целого числа.

Запись смешанного числа в виде неправильной дроби.

Запись целого числа в виде неправильной дроби.

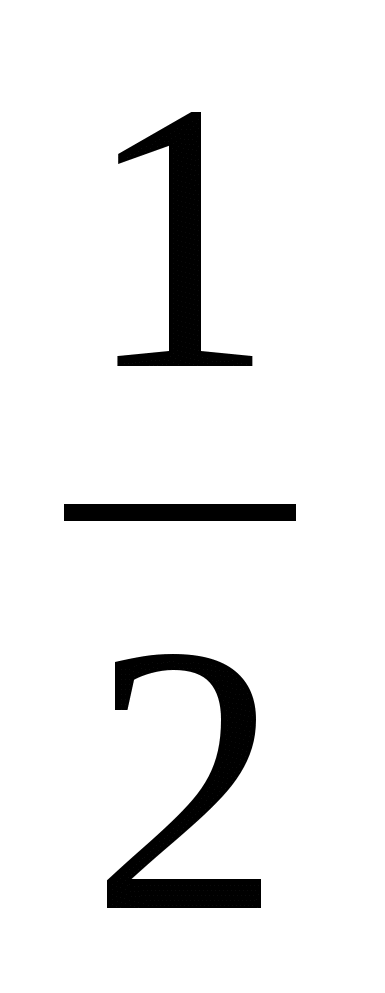
_ 23 | 4 .

20 | 5 (ц)

3 (ч)

;

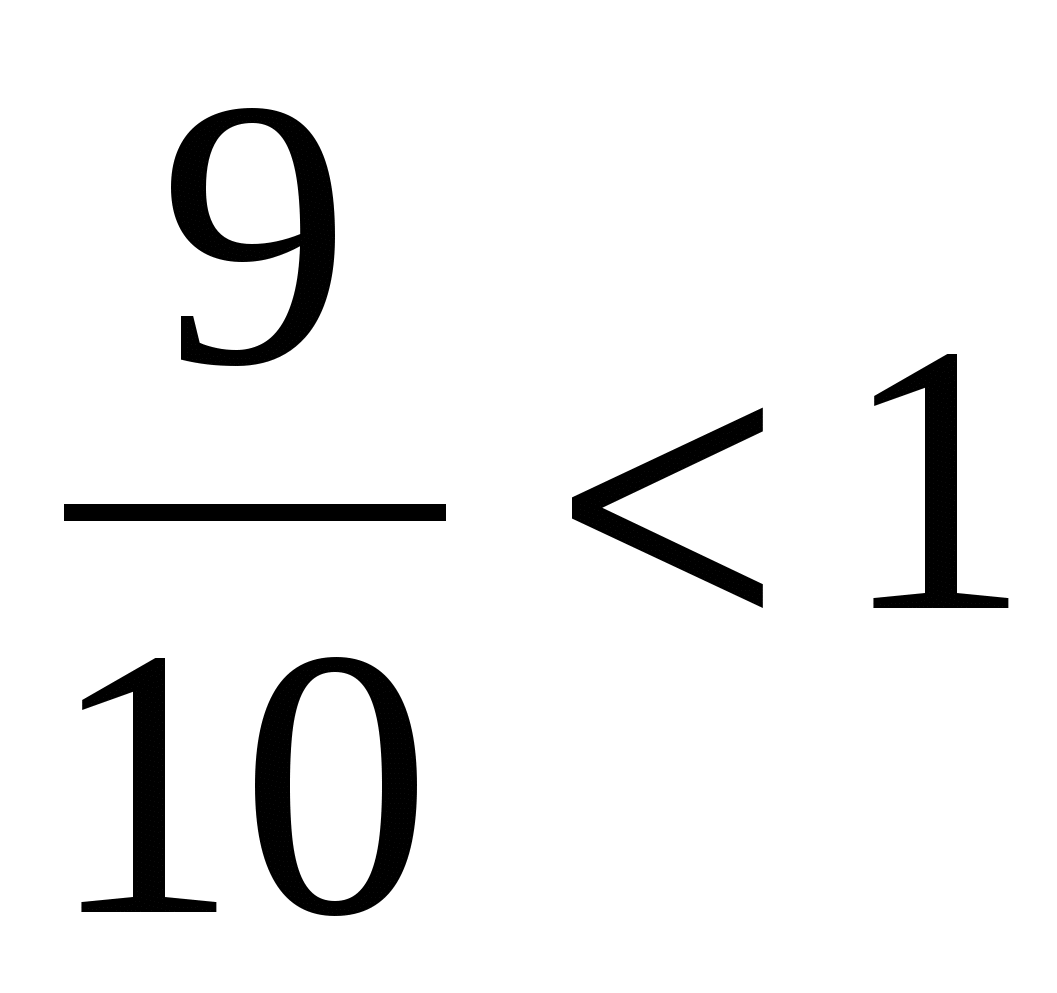
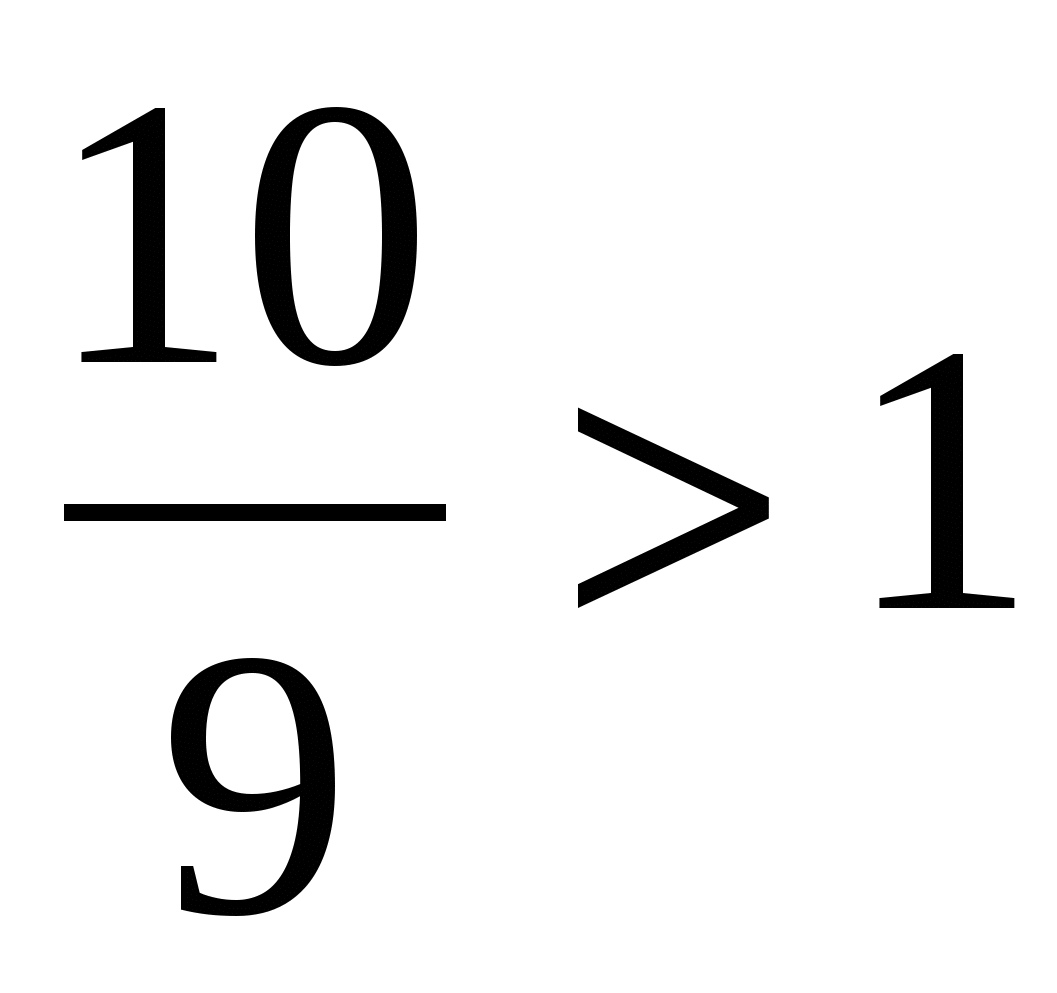
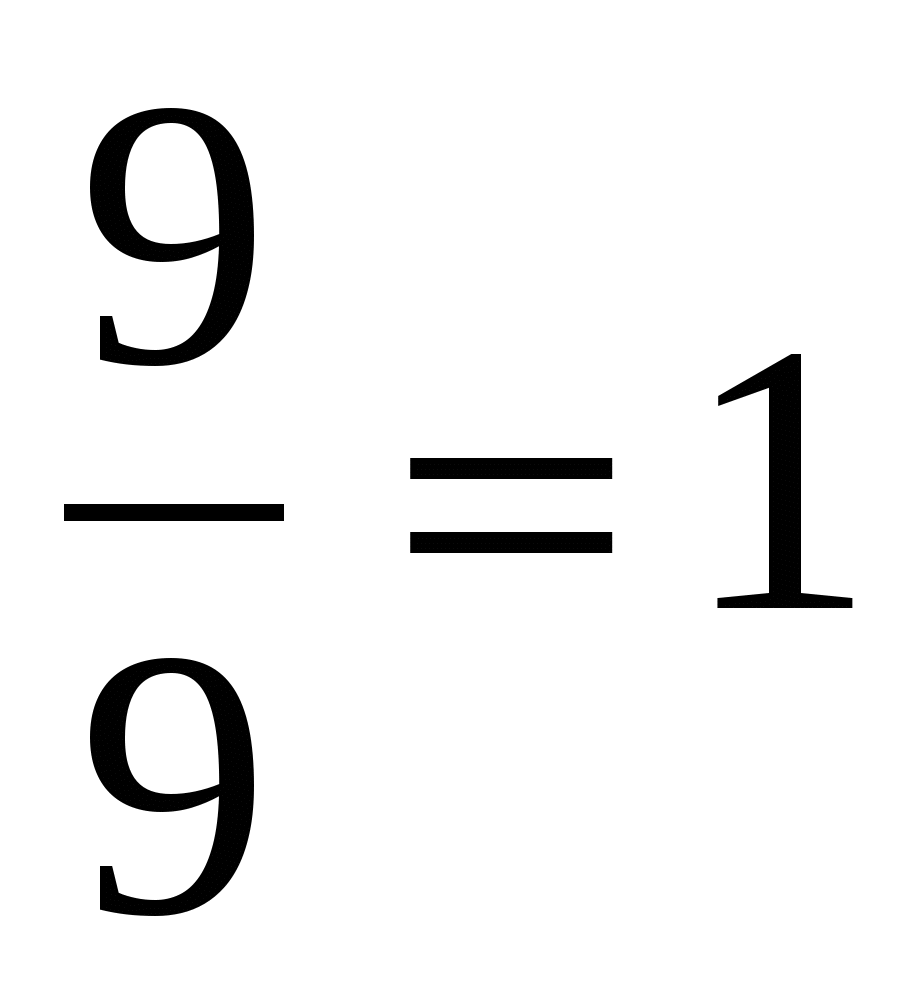6 = .

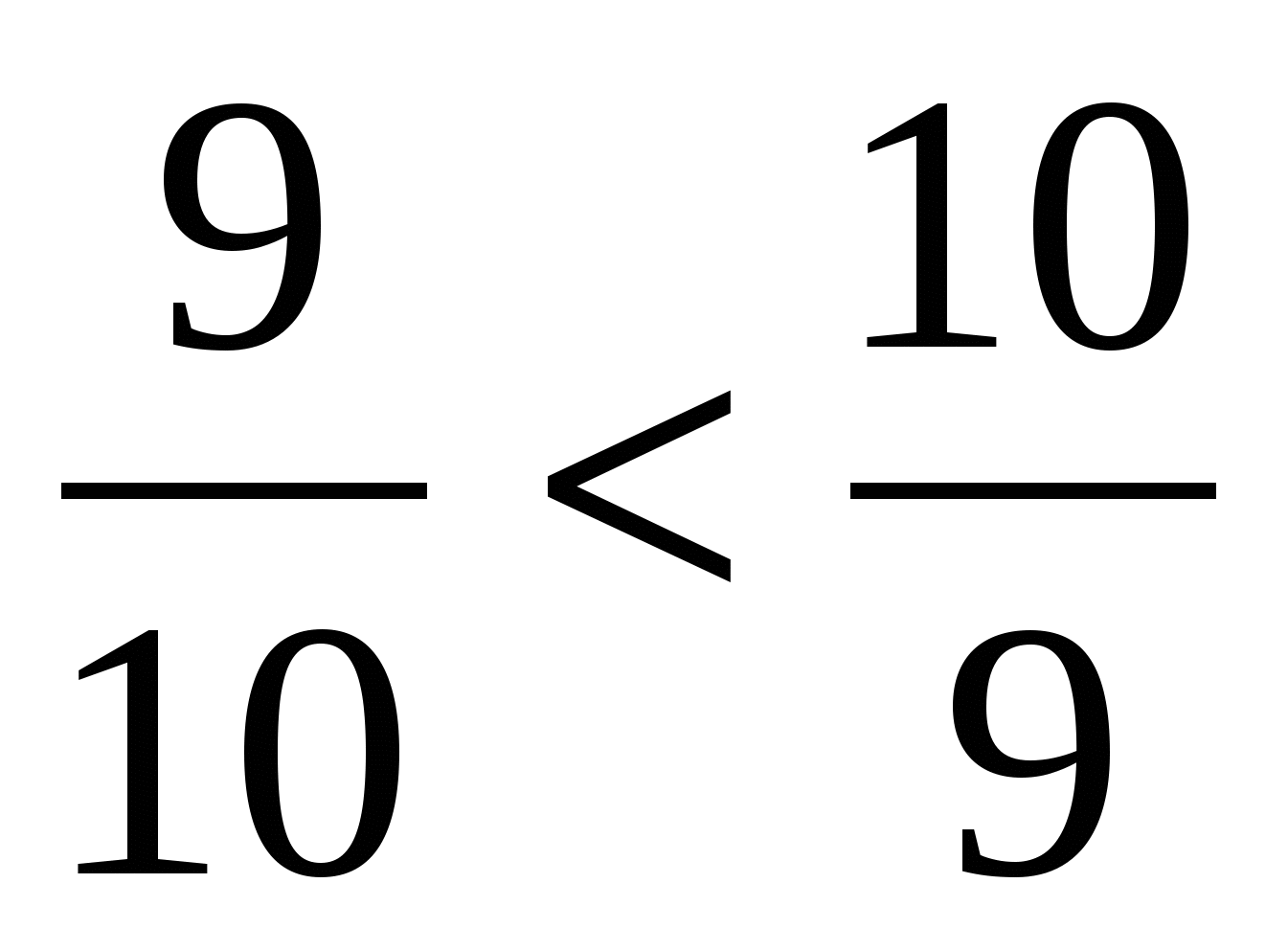Действия с обыкновенными дробями.

1. Сложение дробей

с одинаковыми

знаменателями.

а) ; б) 3;

в) ; г) 3;

д) ; е) 3

1. Вычитание дробей

с одинаковыми

знаменателями

а) ; б) 5;

в) 1 - ; г) 5 -;

д) ;

е);

ж) .

3. Сложение дробей с разными знаменателями.

а) (см. п.1. примеры а), в), д)).

б) 3(см. п.1. примеры б), г), е)).

4. Вычитание дробей с разными знаменателями.

а) (см. п.1. пример а)).

б) 3; в)

Десятичная запись дробных чисел

7

=

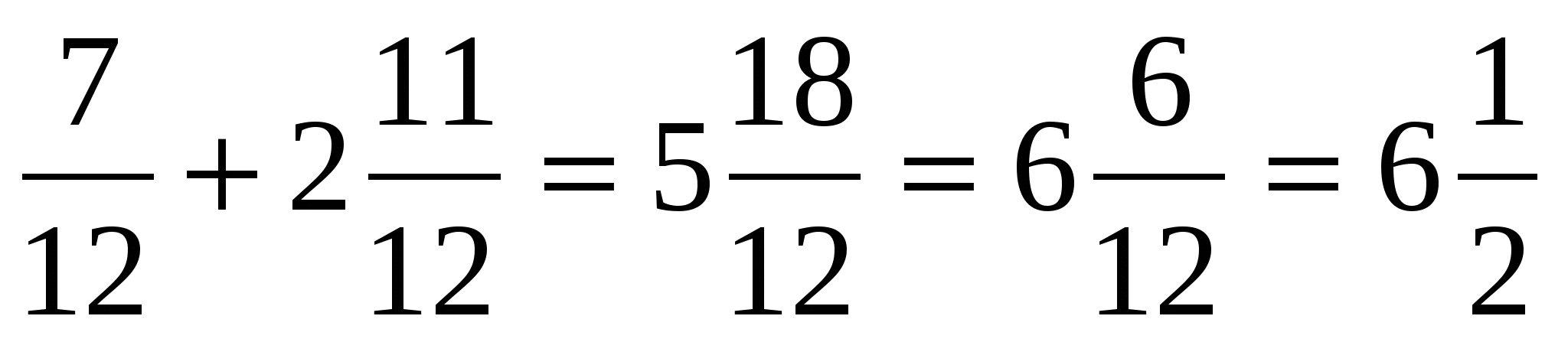
7

,

28

Целая часть

Дробная часть

Целая часть

Дробная часть

Сложение и вычитание десятичных дробей

3,7 + 2, 651 3,7 - 2, 651

+

3,

7

0

0

-

3,

7

0

0

2,

6

5

1

2,

6

5

1

,

,

Умножение десятичных дробей

1,25 · 8 1,25 · 3,8

×

1,

2

5

×

1,

2

5

8

3,

8

1

0,

0

0

=

1

0

+

1

0

0

0

3

7

5

4,

7

7

0

=

4,

7

7

Деление десятичных дробей

4,77:3,8 = 47,7 : 38 = 1.25 2,44 : 0,8 = 24,4 : 8 = 3,05

-

4

7,

7

0

3

8

-

2

4,

4

8

3

8

1,

2

5

2

4

3,

0

5

-

9,

7

-

0

4

7

6

0

-

2

1

0

-

4

0

2

1

0

4

0

0

0

Среднее арифметическое

Среднее арифметическое = (сумма чисел): (количество слагаемых)

Задача. Найти среднее арифметическое чисел 3,28; 4; 6,7; 0,45; 2,07.

Решение:

Средняя скорость

Средняя скорость = (весь пройденный путь) : (всё время движения)

Задача. Поезд шёл 2 ч со скоростью 60 км/ч и 3 ч со скоростью 70 км/ч. Найдите среднюю скорость поезда на пройденном за это время пути.

2+3

Решение: (60 · 2 + 70 · 3) : 5 = 66 (км/ч)

Ответ: 66 км/ч средняя скорость поезда на пройденном пути.

Сумма чисел = (среднее арифметическое) × (Количество чисел)

Запись обыкновенных и десятичных дробей в процентах. Перевод процентов в обыкновенную и десятичную дробь.

Запись обыкновенных дробей в процентах.

Запись десятичных дробей в процентах.

Запись процентов в виде обыкновенных и десятичных дробей.

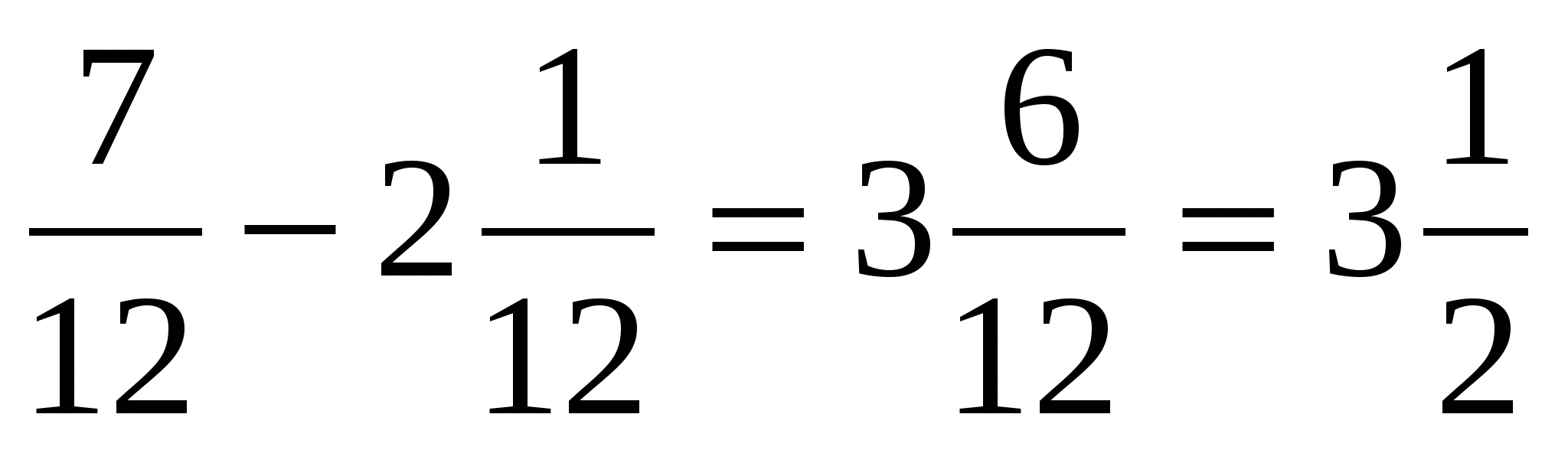
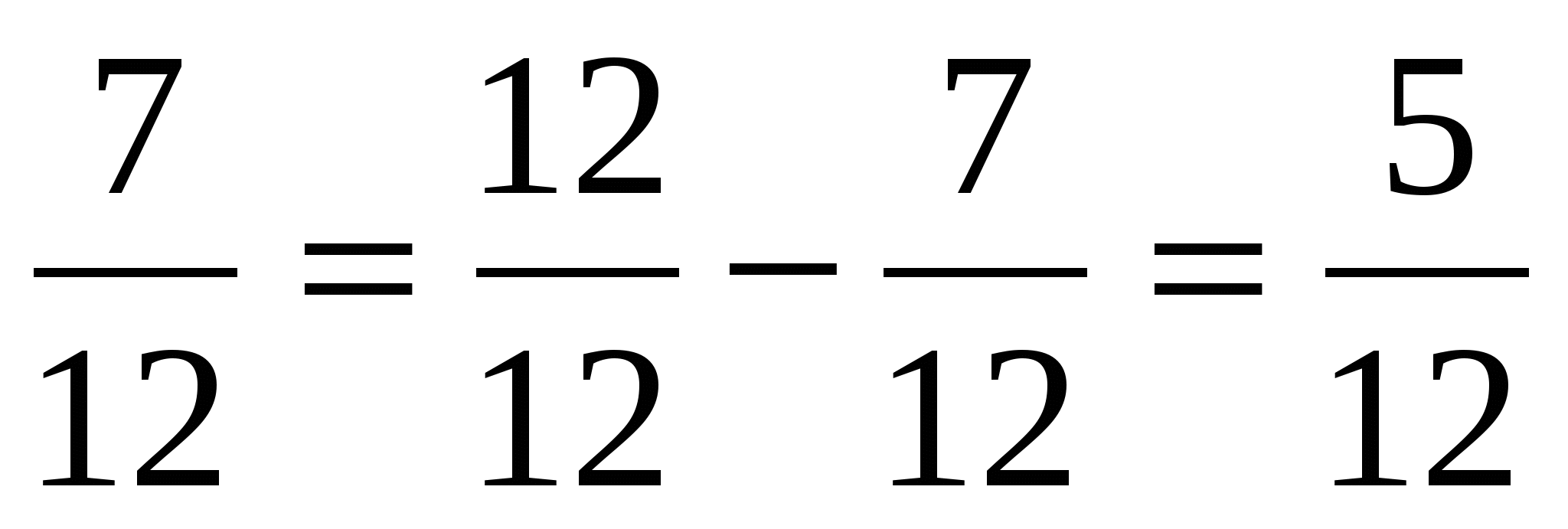
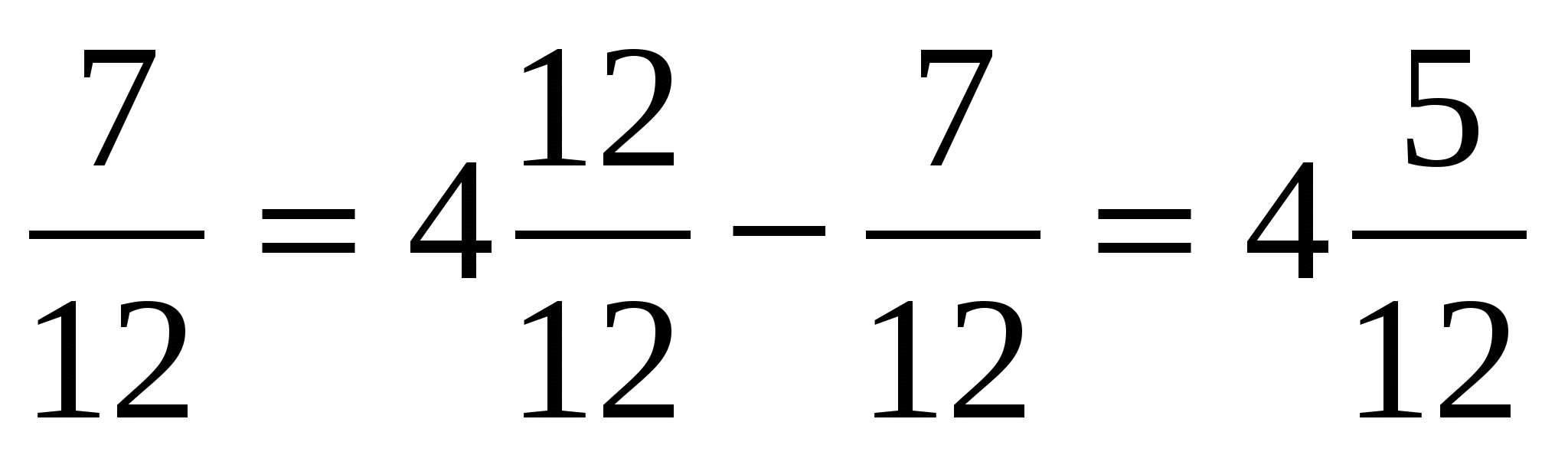
0,04 = 0,04 · 100% = 4%

0,33 =0,33 · 100% = 33%

4,77 = 4,77 · 100% = 477%

3% =

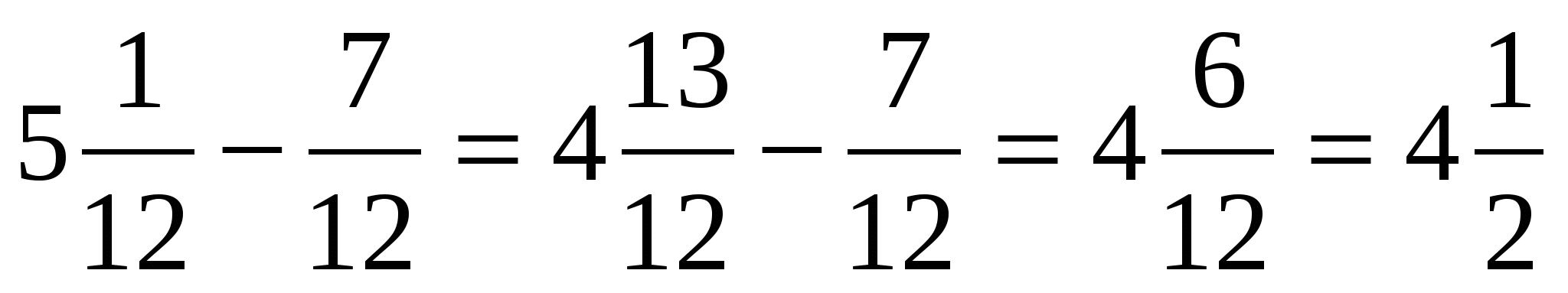
28% =

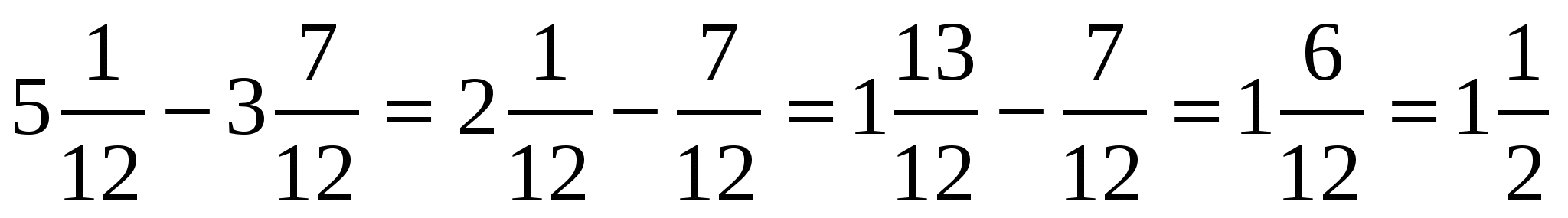
635% =

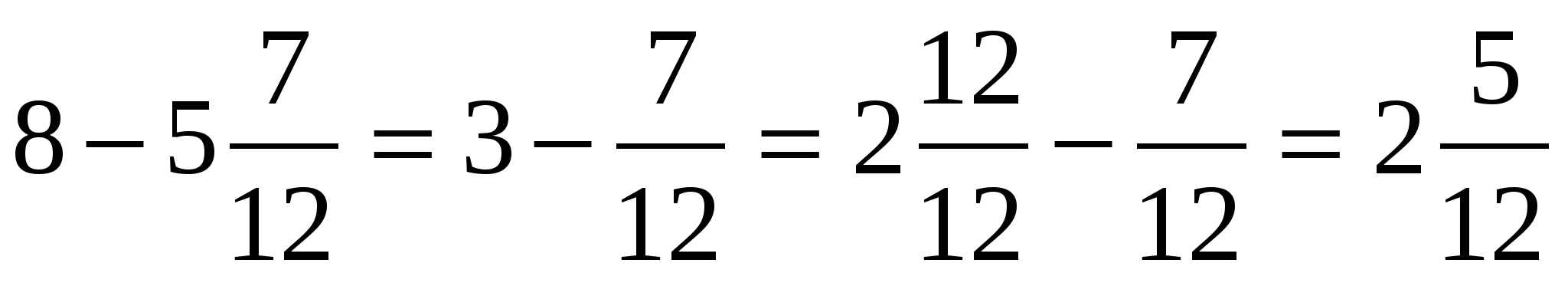
Замена процентов дробью.

Проценты

1%

2%

5%

10%

20%

25%

50%

75%

100%

Десятичная дробь

0,01

0,02

0,05

0,1

0,2

0,25

0,5

0,75

1

(1,0)

Обыкновенная дробь

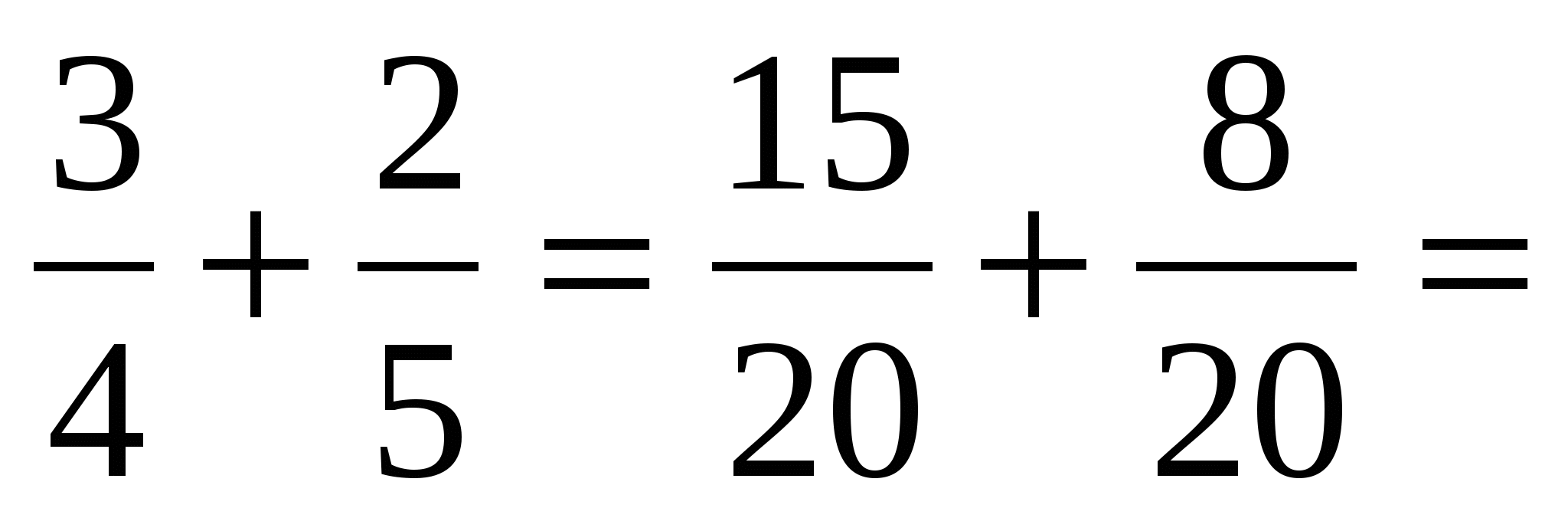
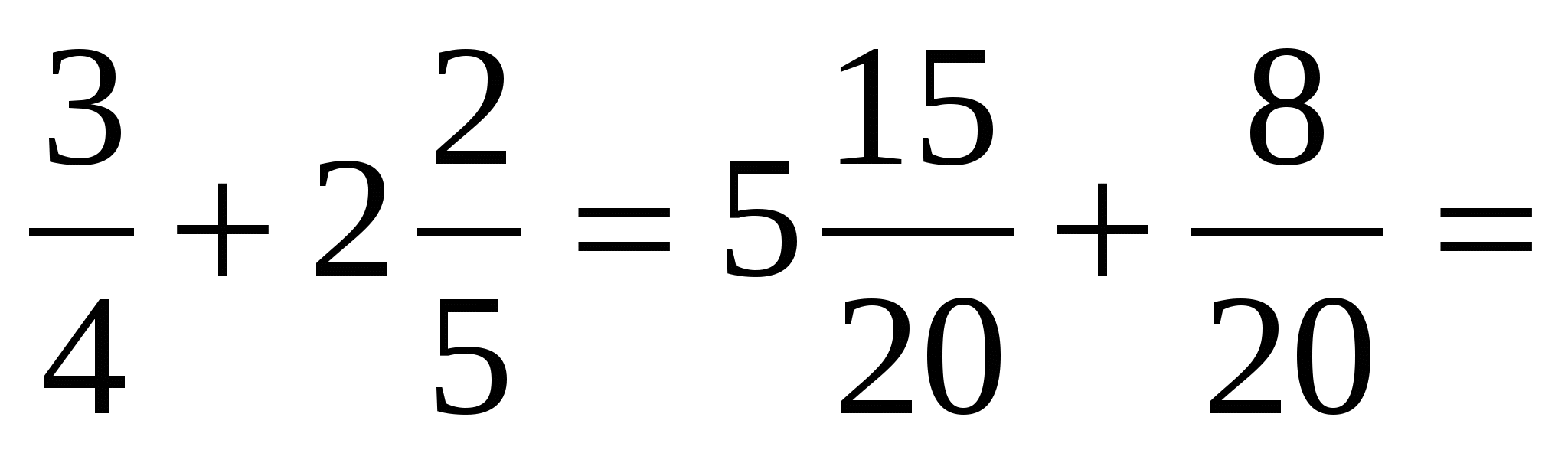
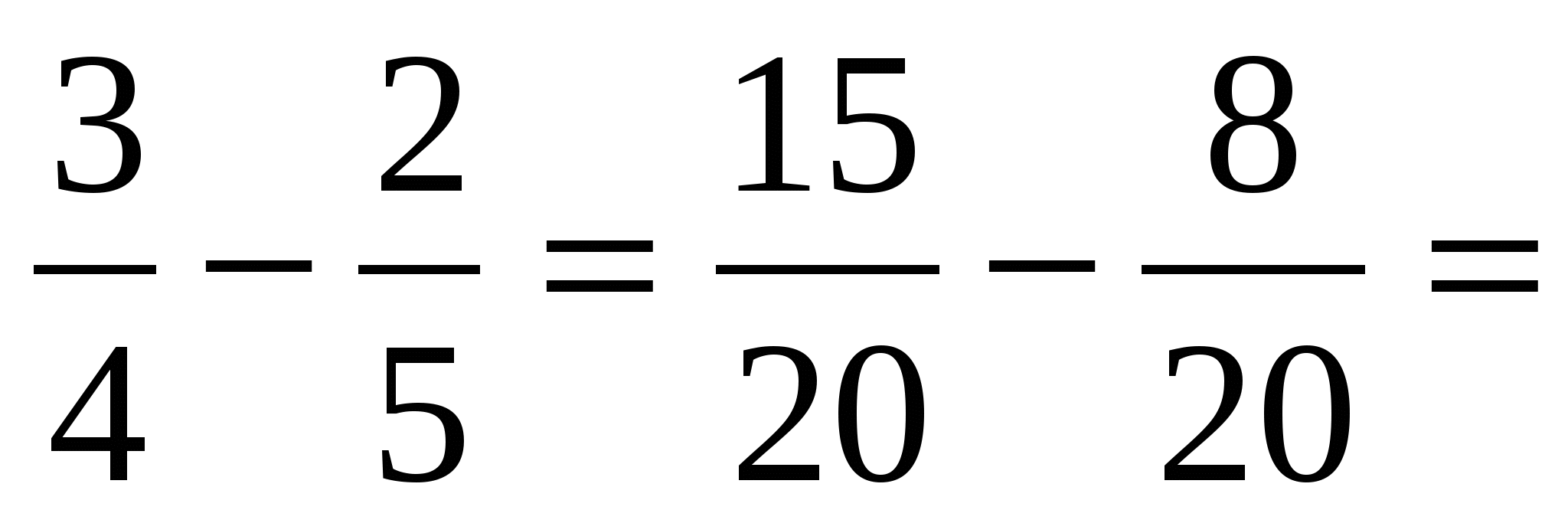
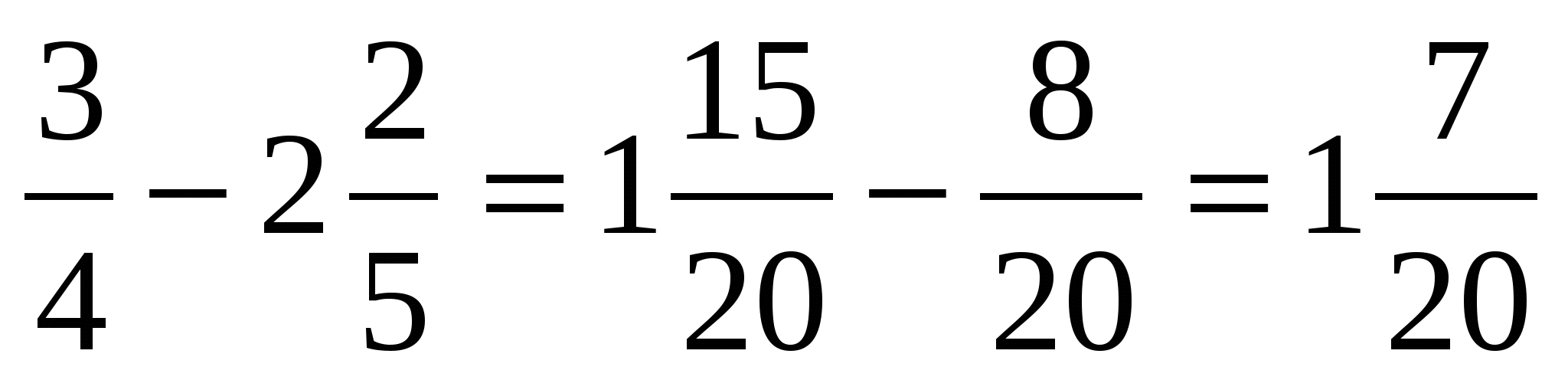
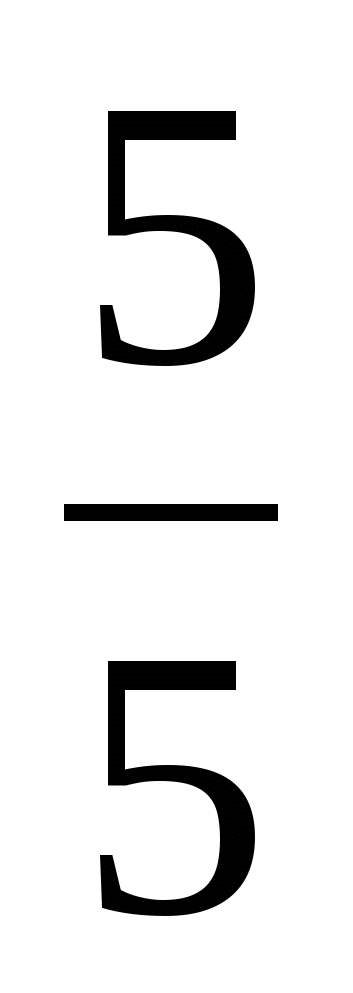
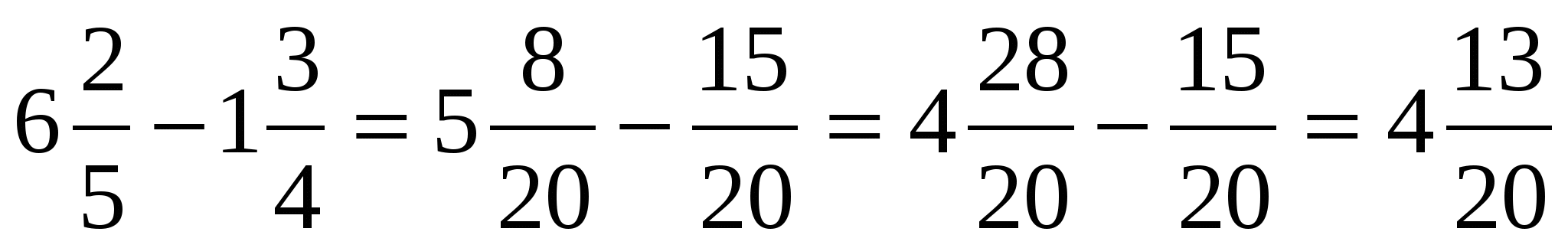
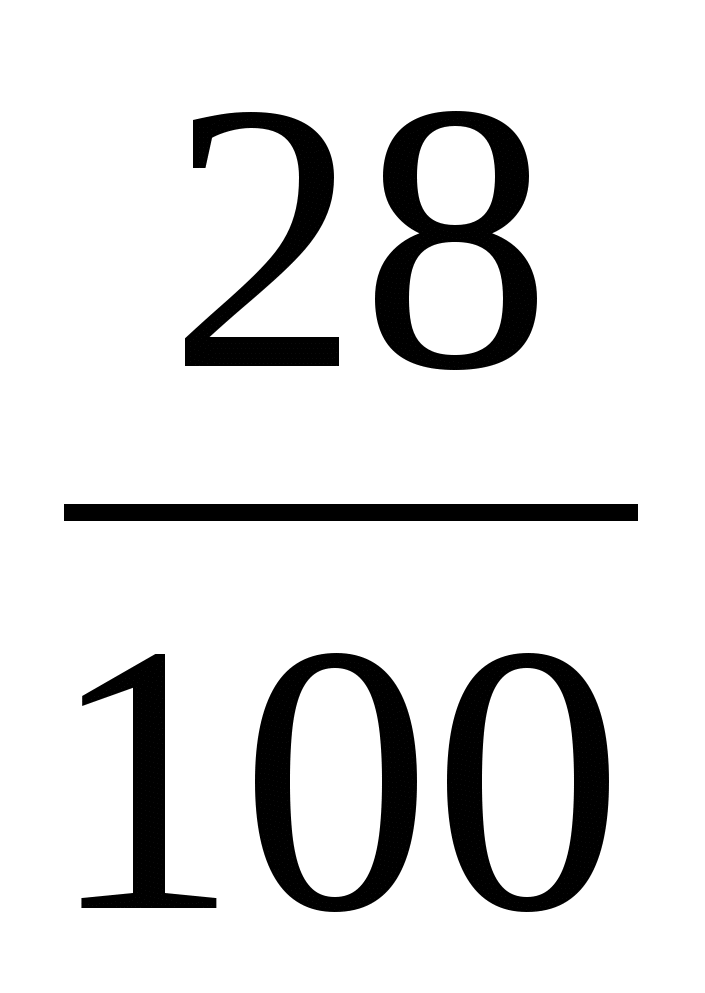
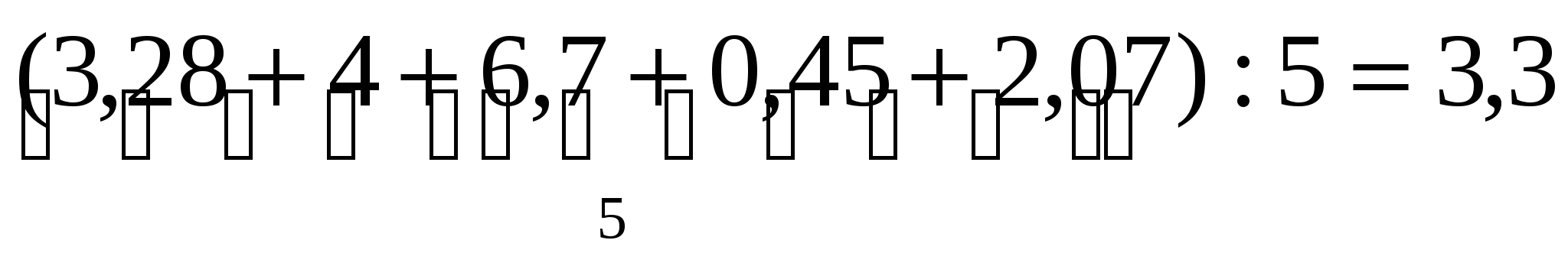
1

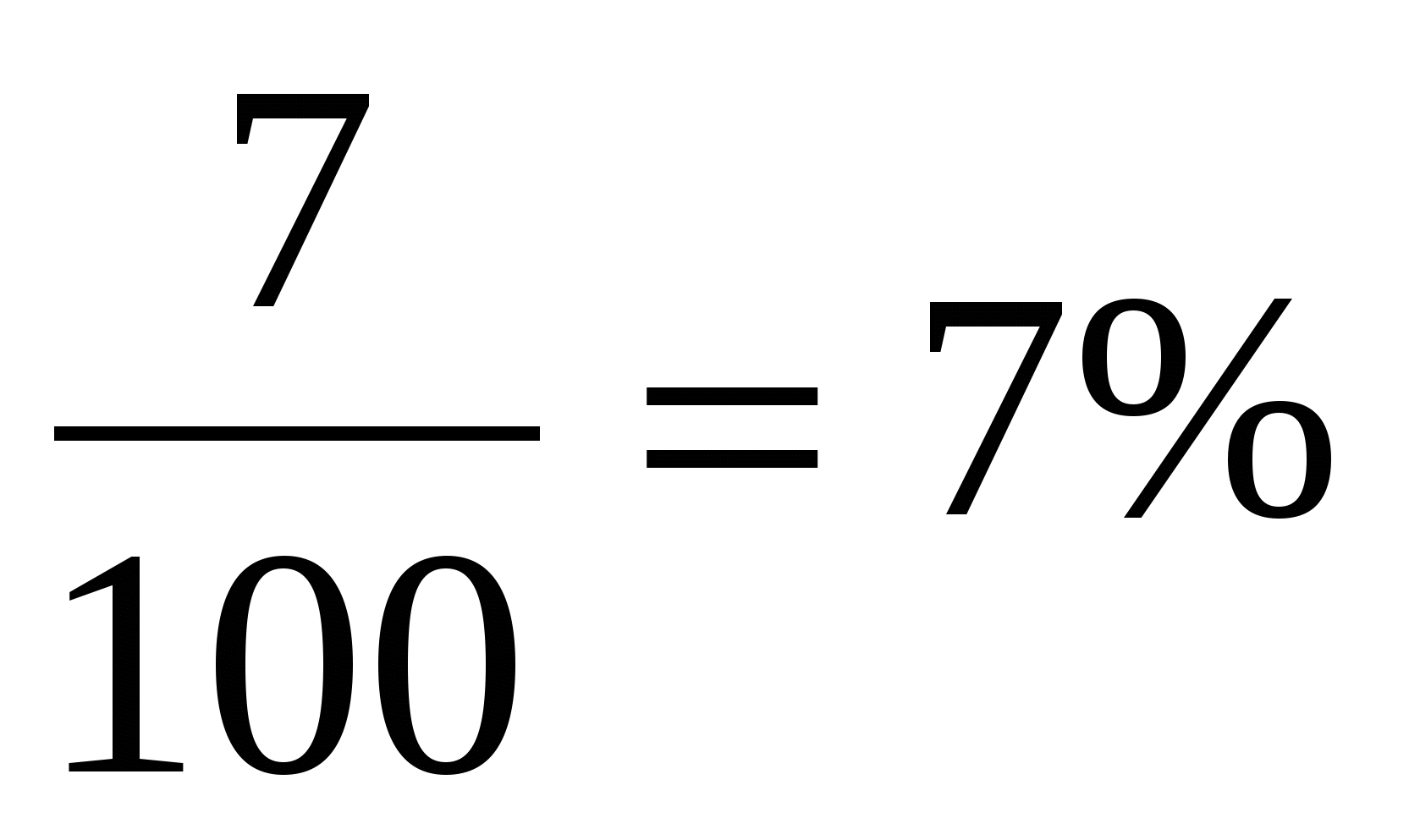
Решение задач по теме: «Проценты»

Нахождение процента от числа.

Найти 1% от 200.

Найти 75% от 200.

Решение: 1% = .

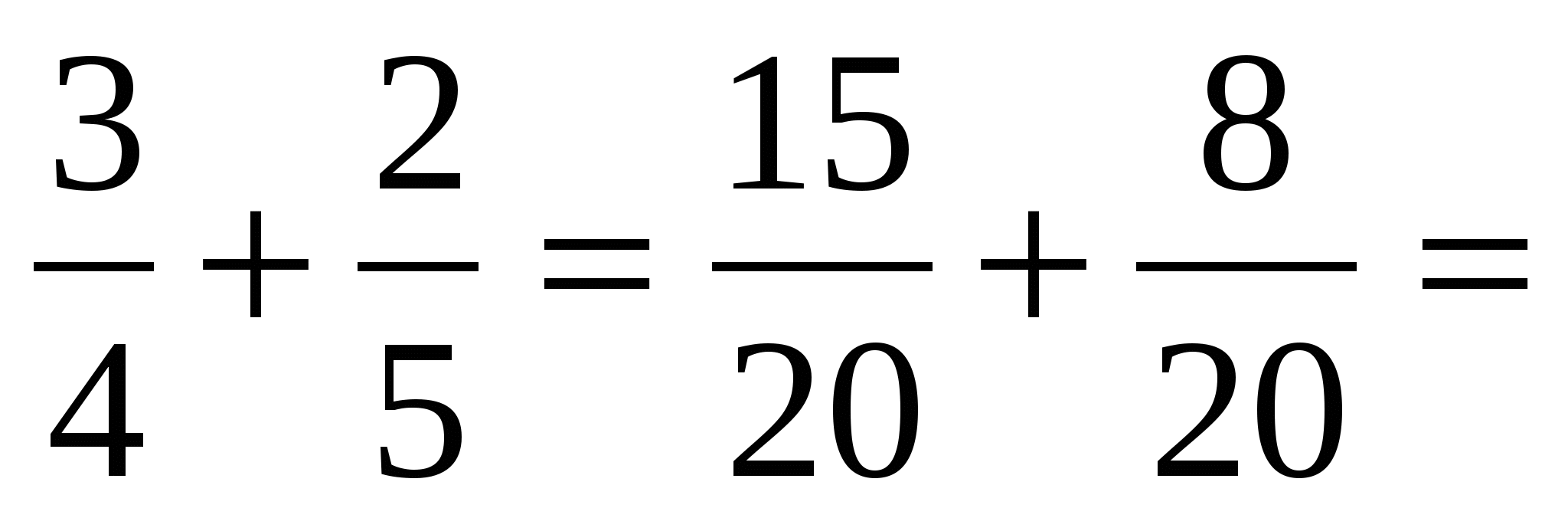200 : 100 × 1 = 2

1 способ. Решение: 75% = .

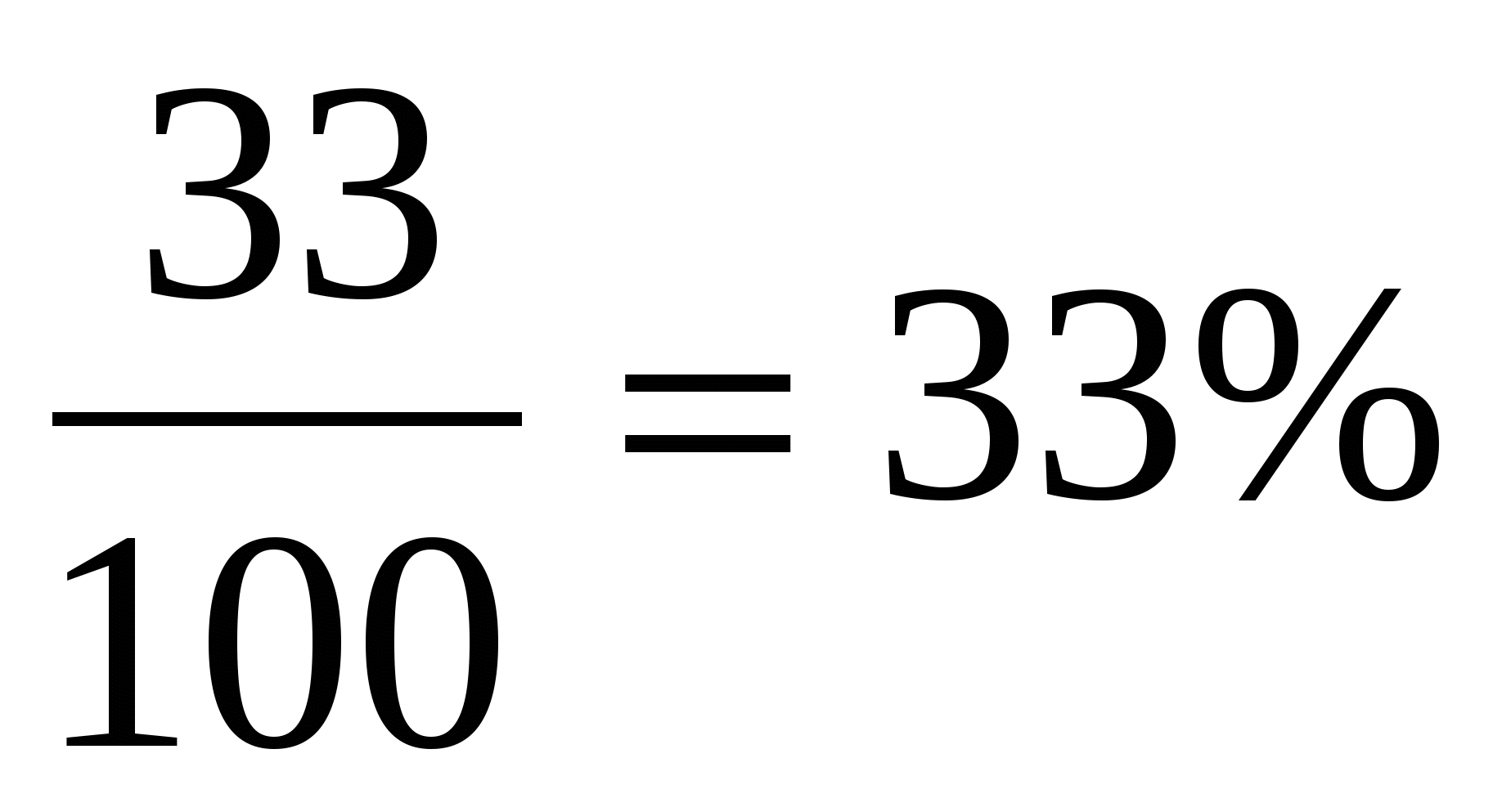200 : 100 × 75 = 150

2 способ. Решение: 75% = 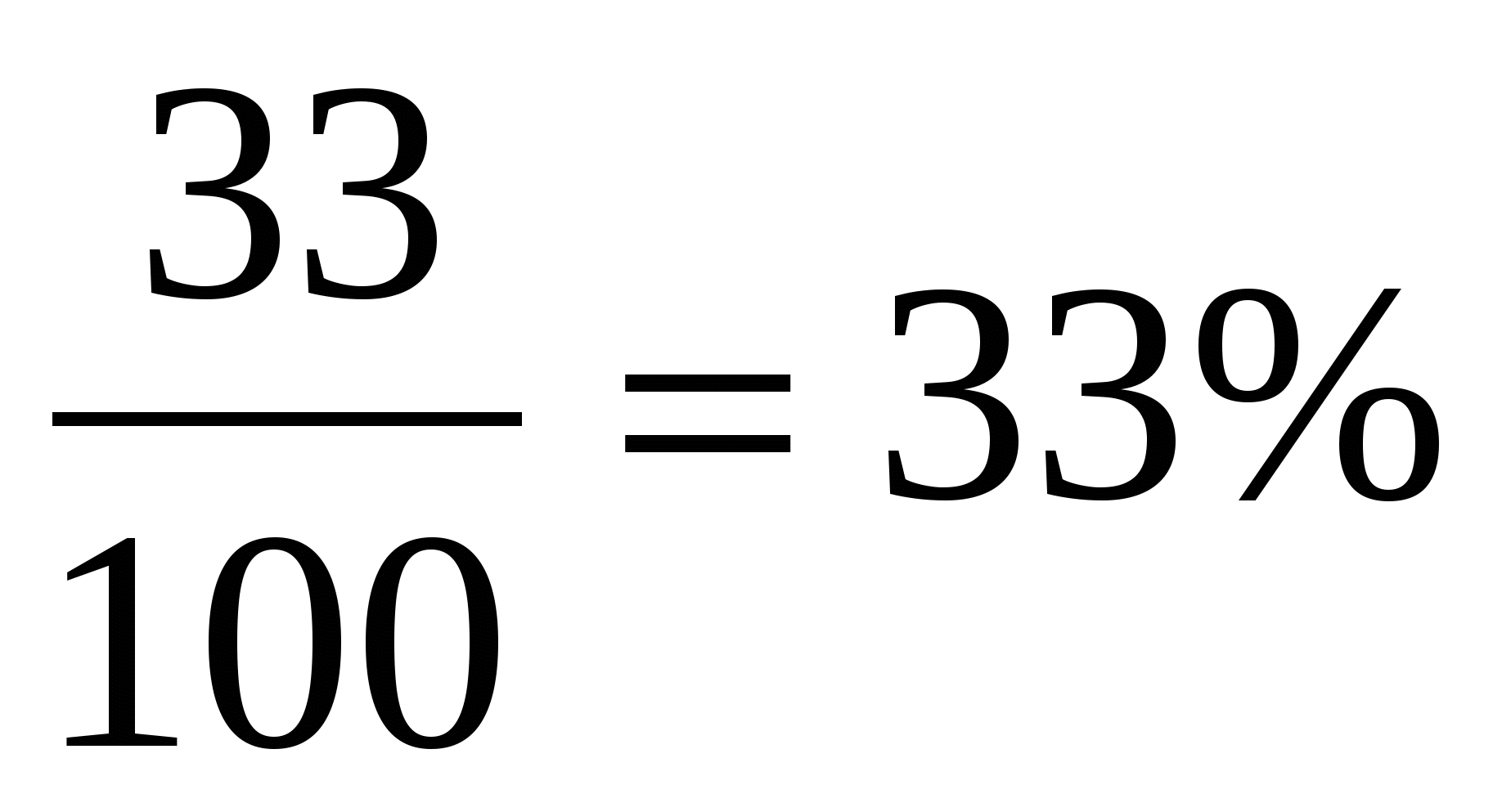= 0,75

200 × 0,75 = 150

3 способ. Решение: 75% = = .

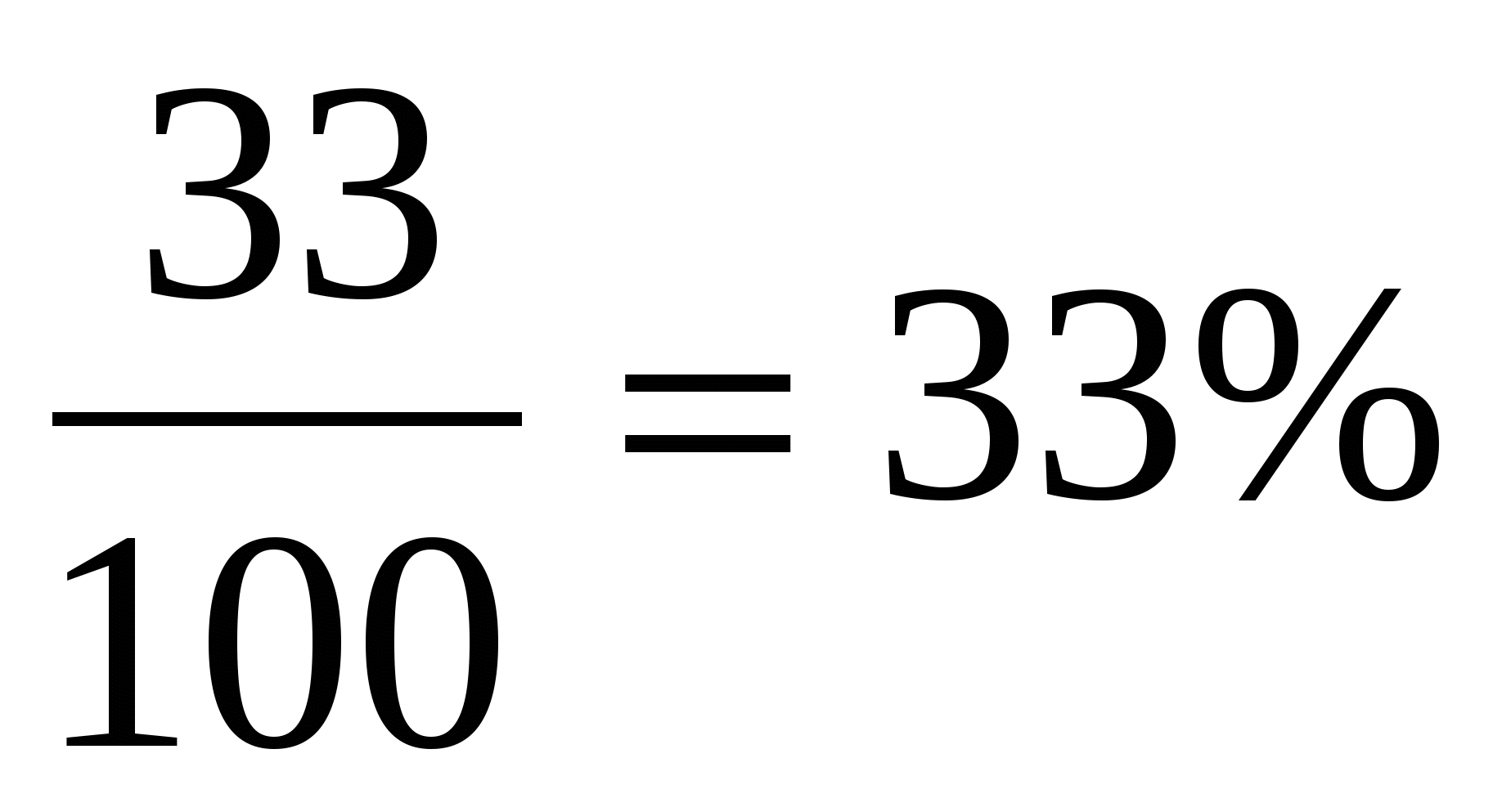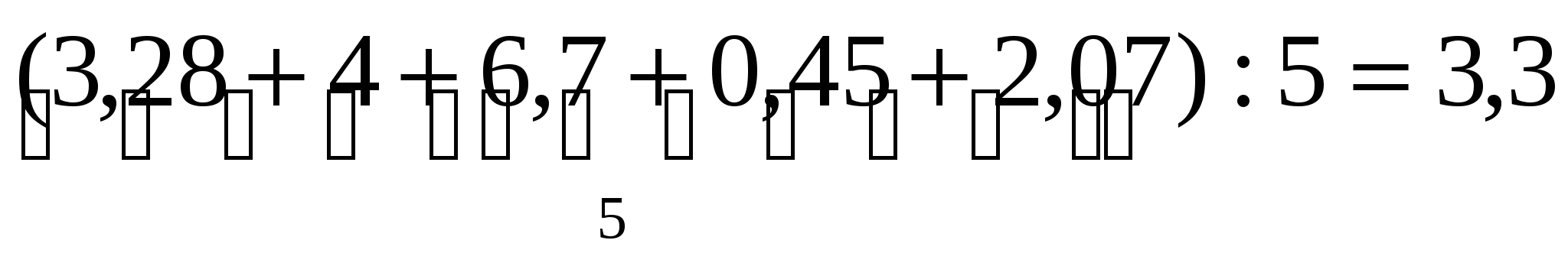200 : 4 × 3 = 150.

Нахождение числа по проценту.

Найти число, если 1% от него (составляет) равно 600.

Найти число, если 75% от него (составляет) равно 600.

Решение: 1% = .

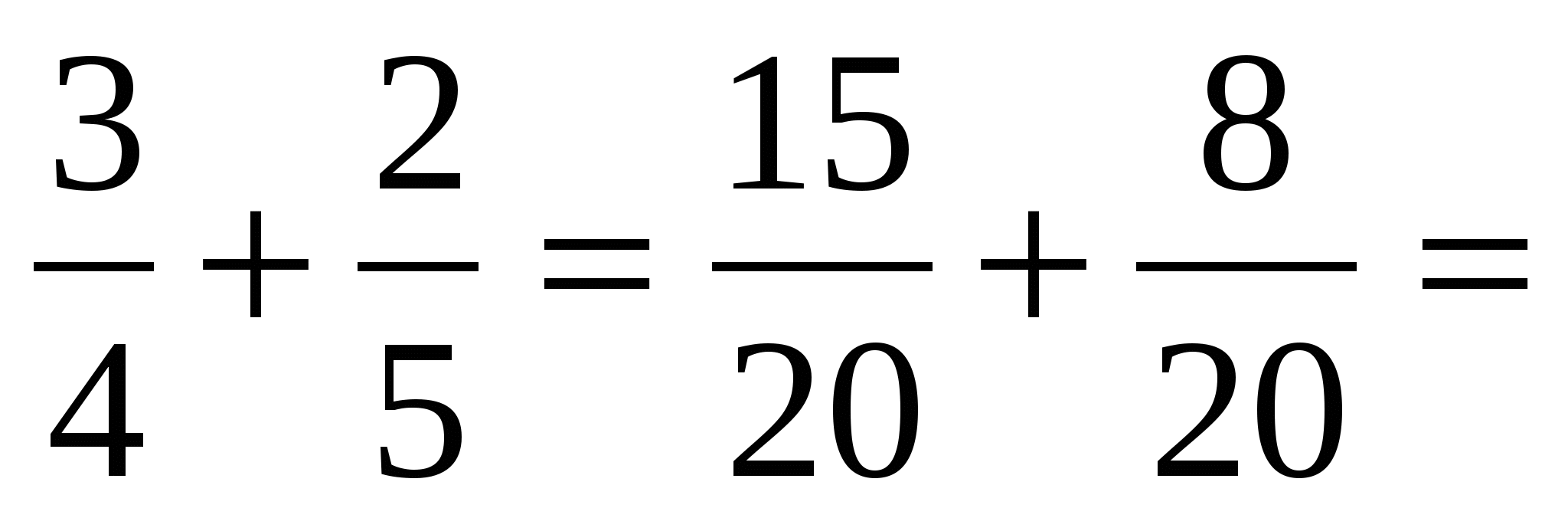600 : 1 × 100 = 60 000.

Или 600 × 100 = 60 000.

1 способ. Решение: 75% = .

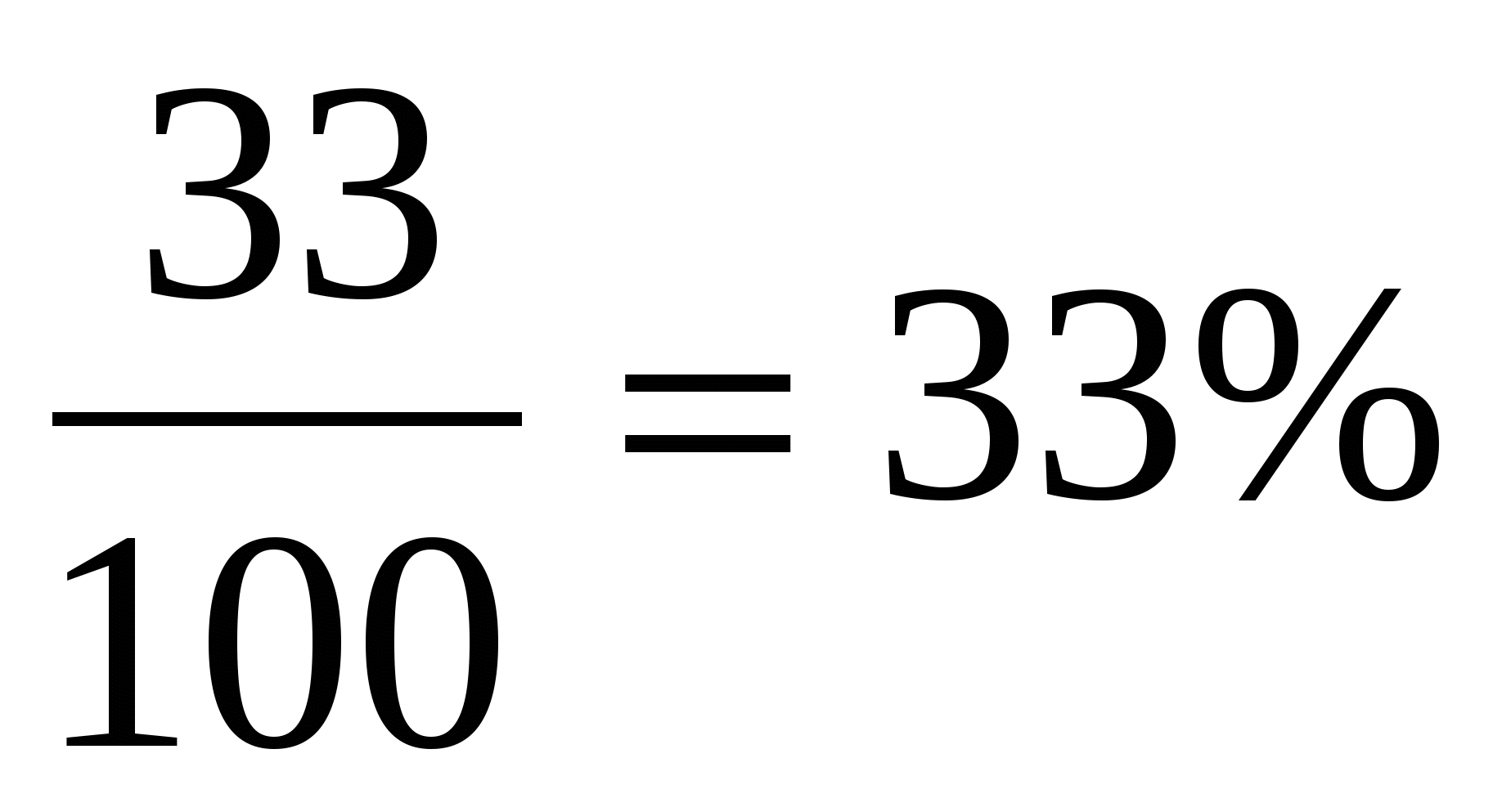600 : 75 × 100 = 800

2 способ. Решение: 75% = 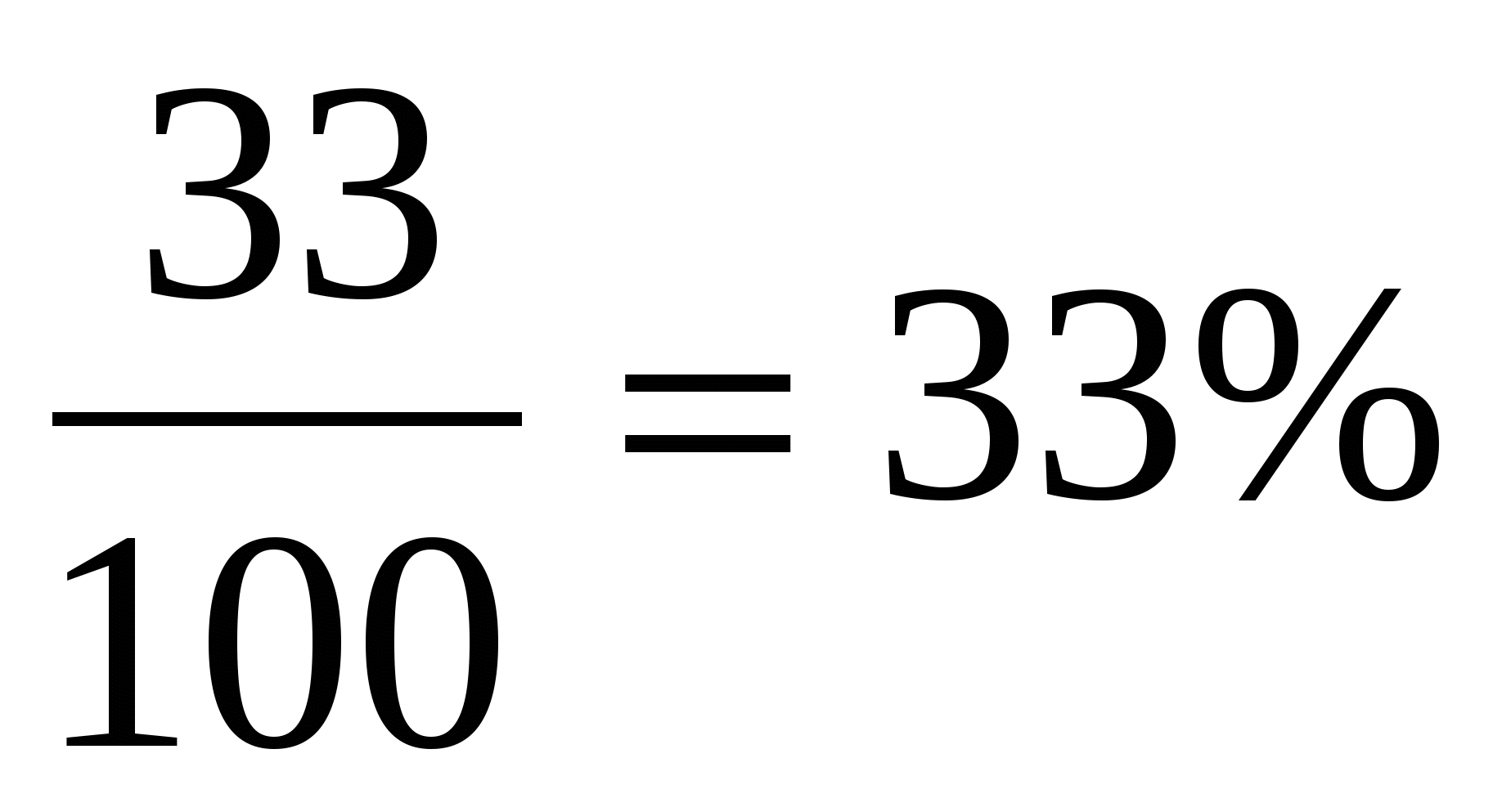= 0,75

600 : 0,75 = 800

3 способ. Решение: 75% = = .

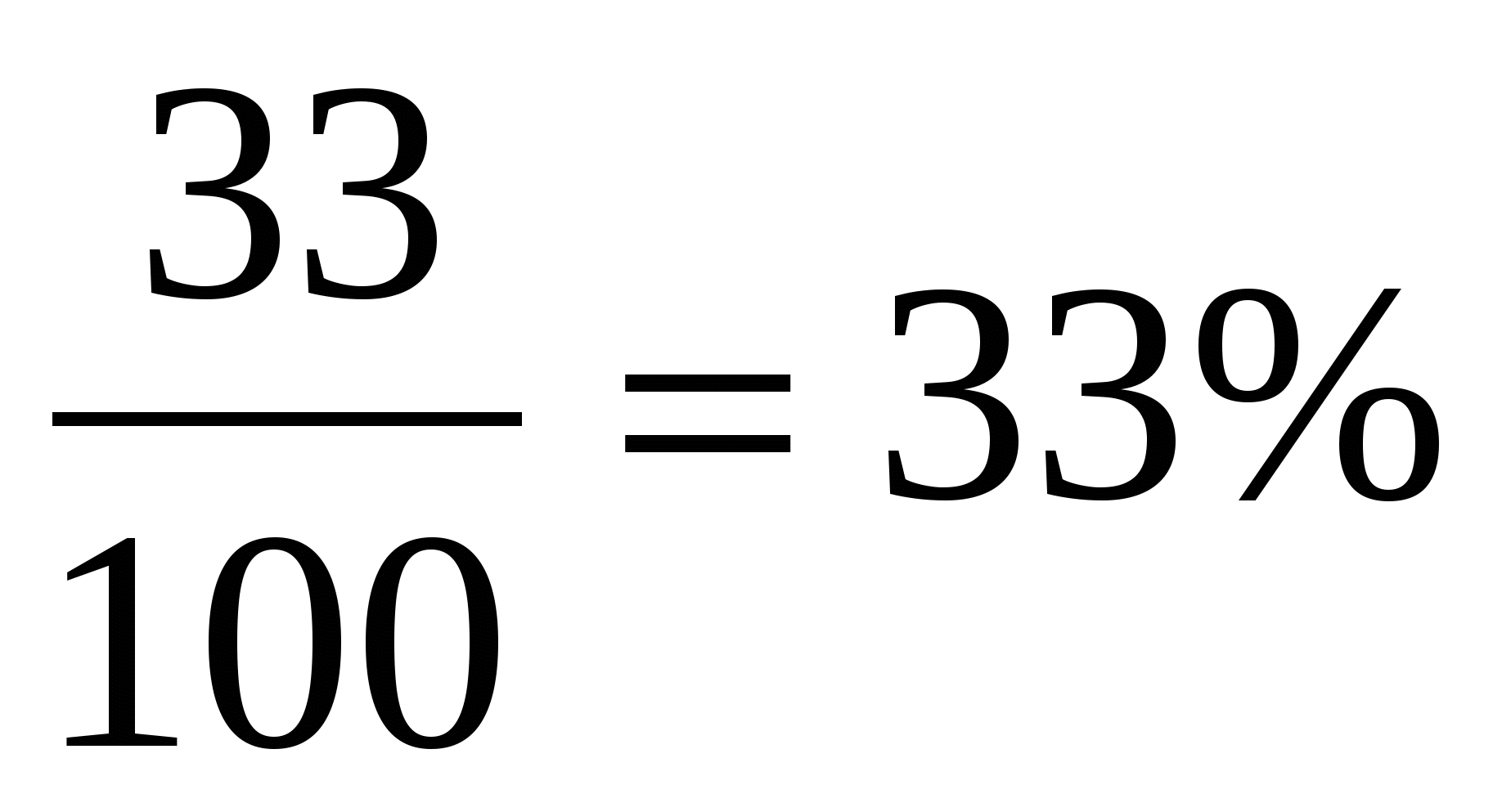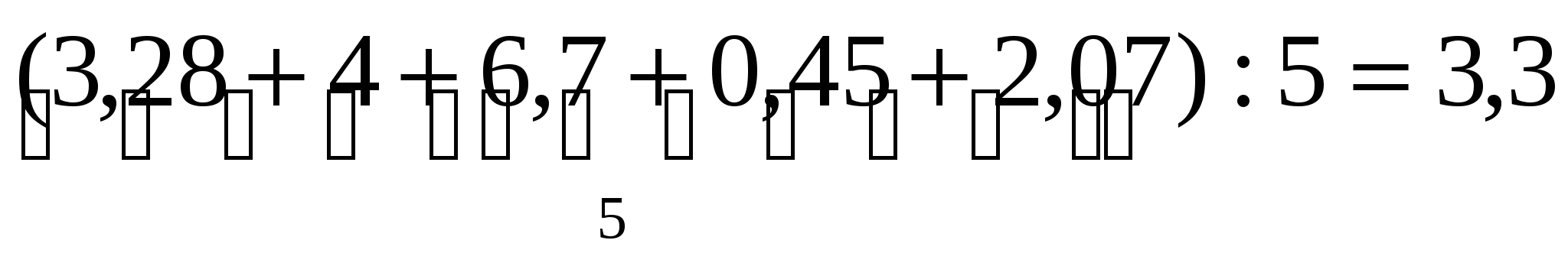600 : 3 × 4 = 800

Нахождение

процентного отношения.

В школе учатся 800 учащихся. Среди них 385 девочек. Сколько процентов учащихся этой школы составляют девочки?

Решение: 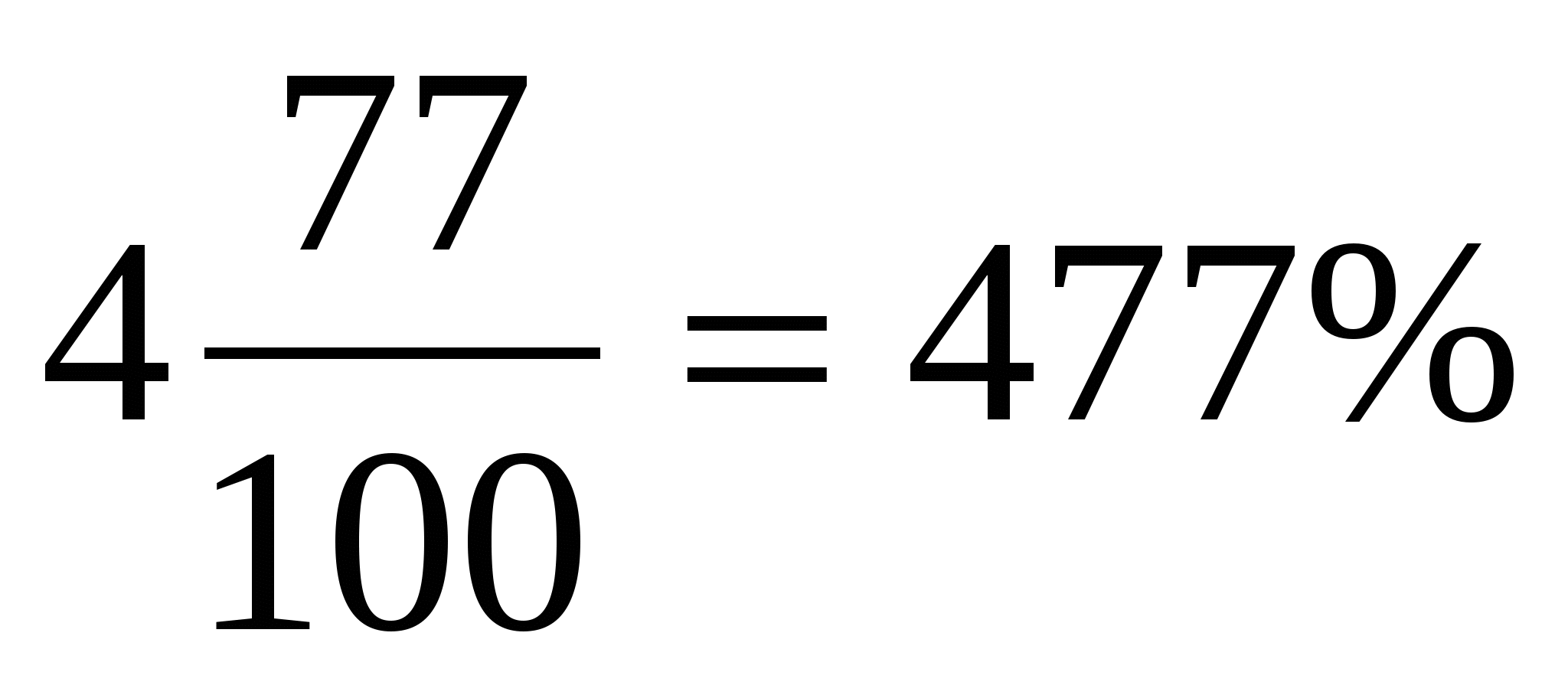0,45 = 0,45 · 100 = 45%

Округление чисел.

Примеры

Правило

Округлить число до десятков :

+1 0 +1 0

2 8 ≈ 30 2 8 5 ≈ 2 9 0

* *

+0 0 +0 0

2 3 ≈ 20 2 3 4 ≈ 230

• •

Если * = 5,6,7,8,9 то + 1

Если ● = 0,1,2,3,4 то + 0

Округлить число до сотен::

+0 0 0 +1 0 0

2 3 8≈200 2 8 3 ≈ 300

• *

Углы.

Название

Изображение

Градусная мера

Острый угол.

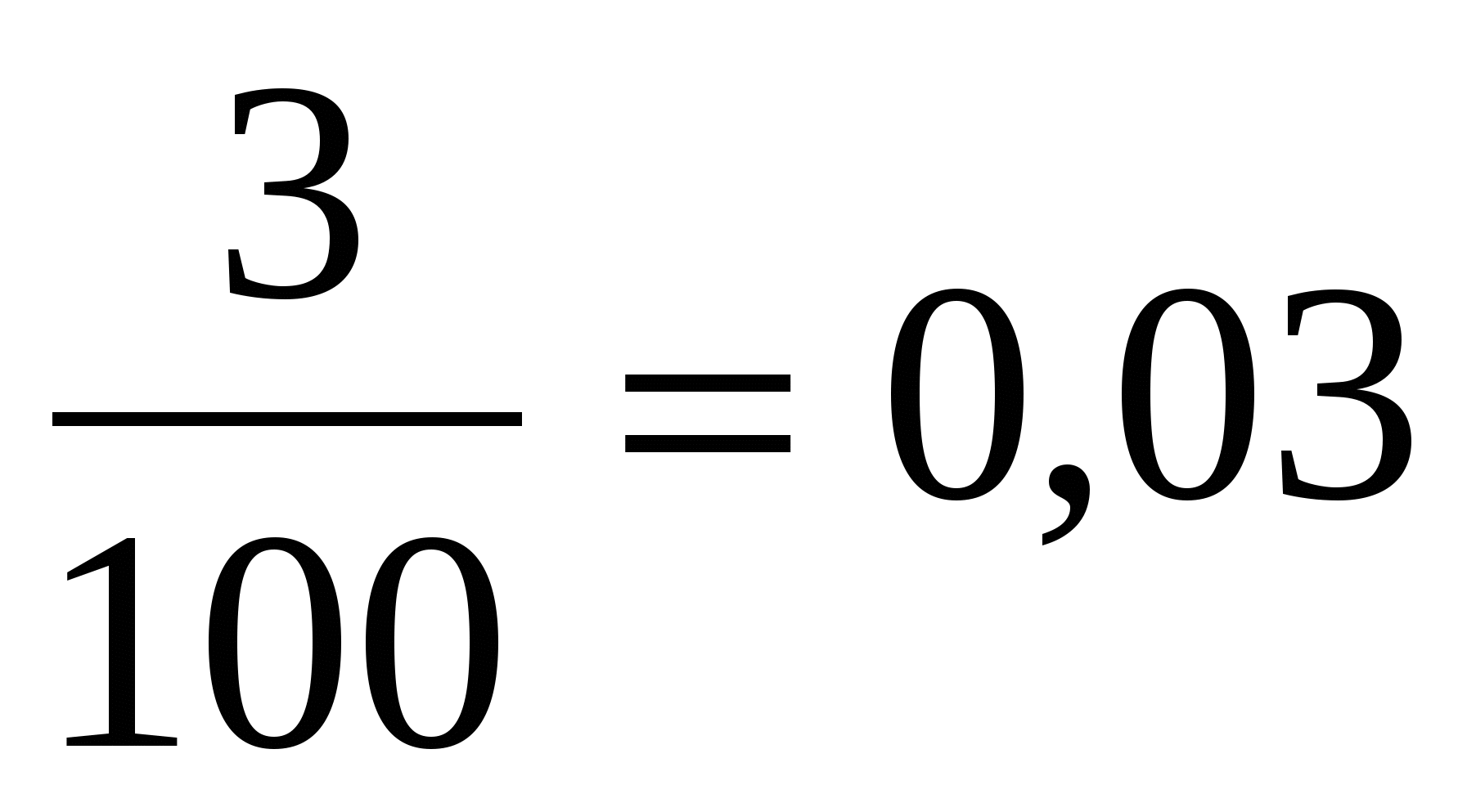
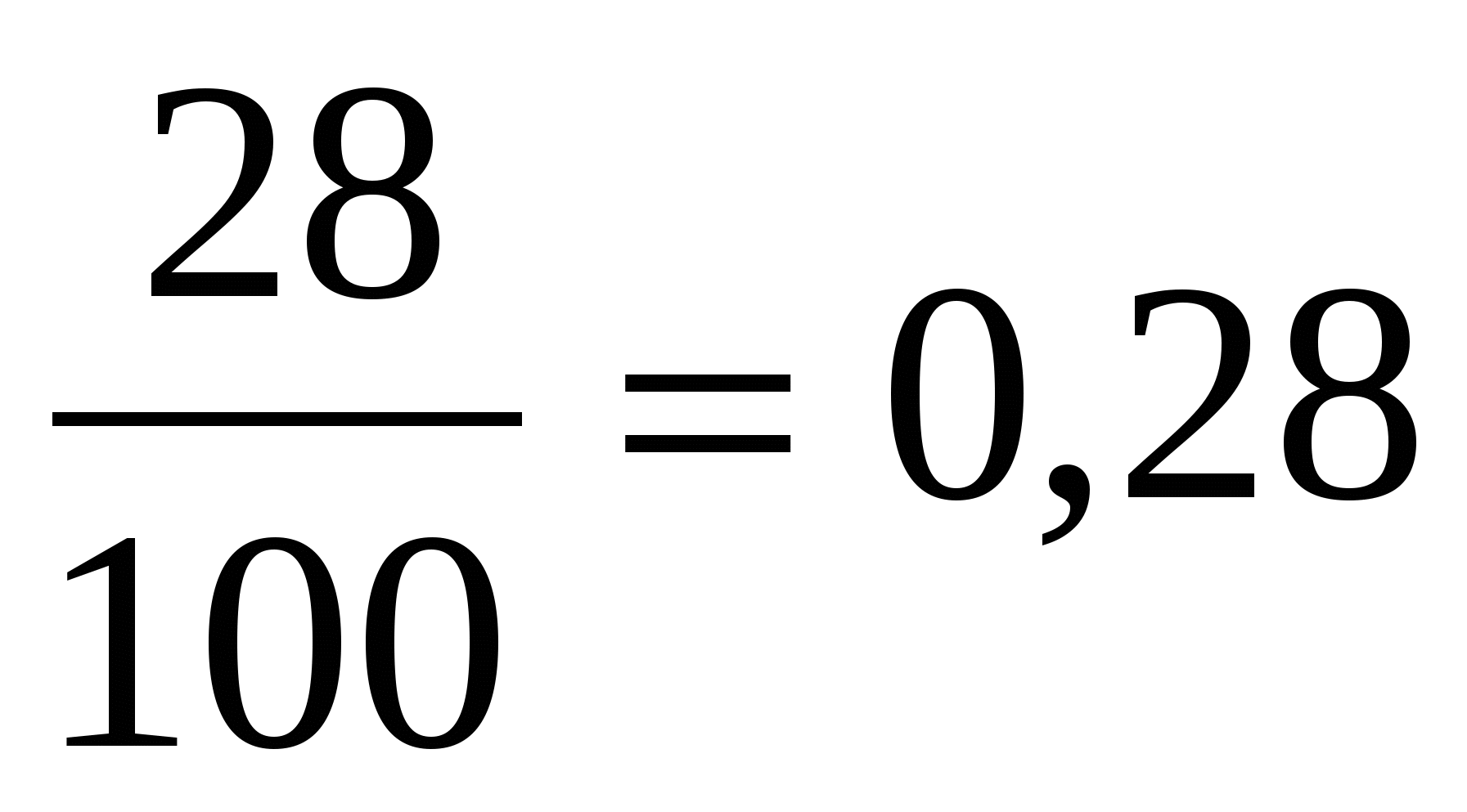
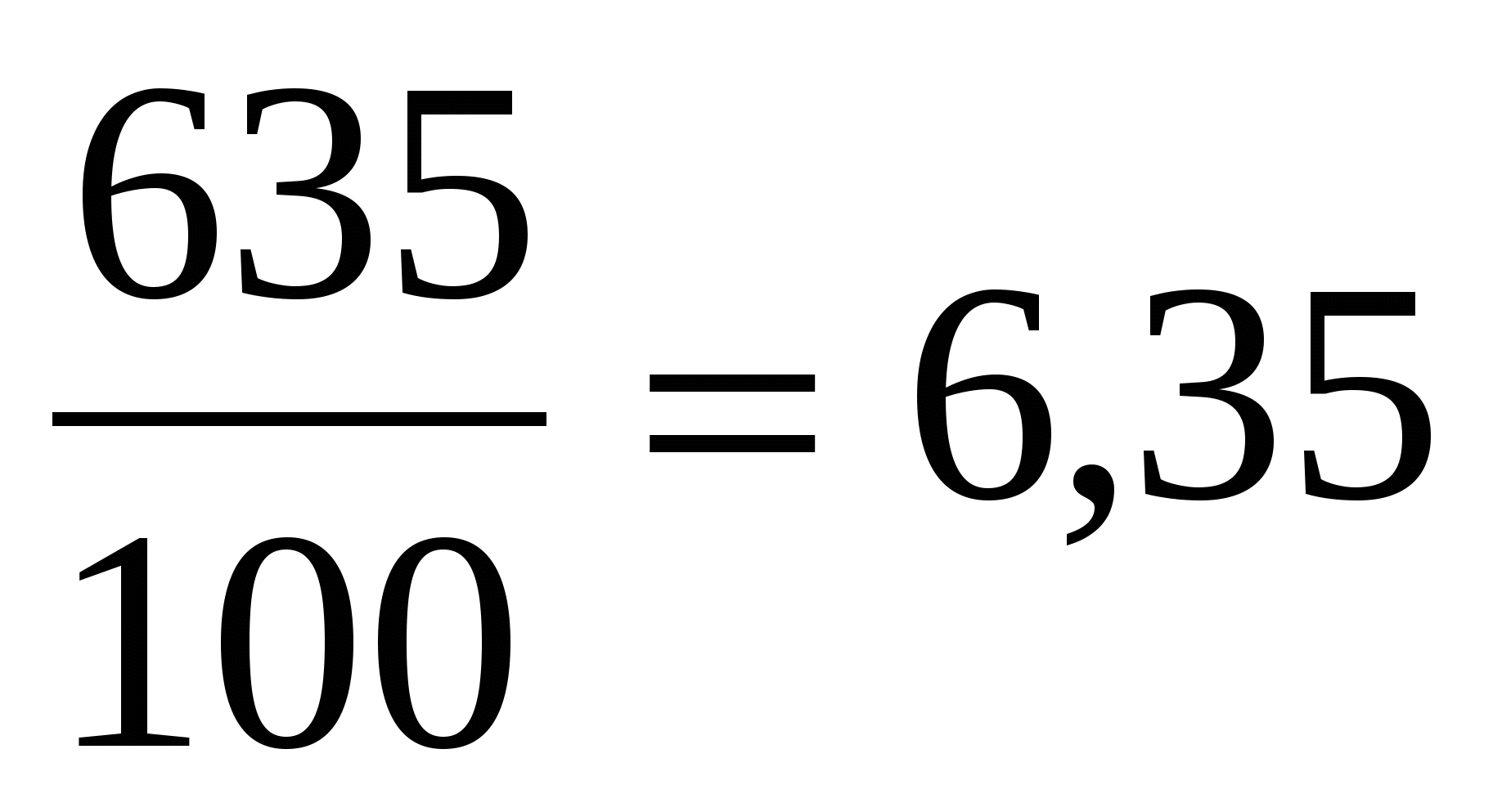
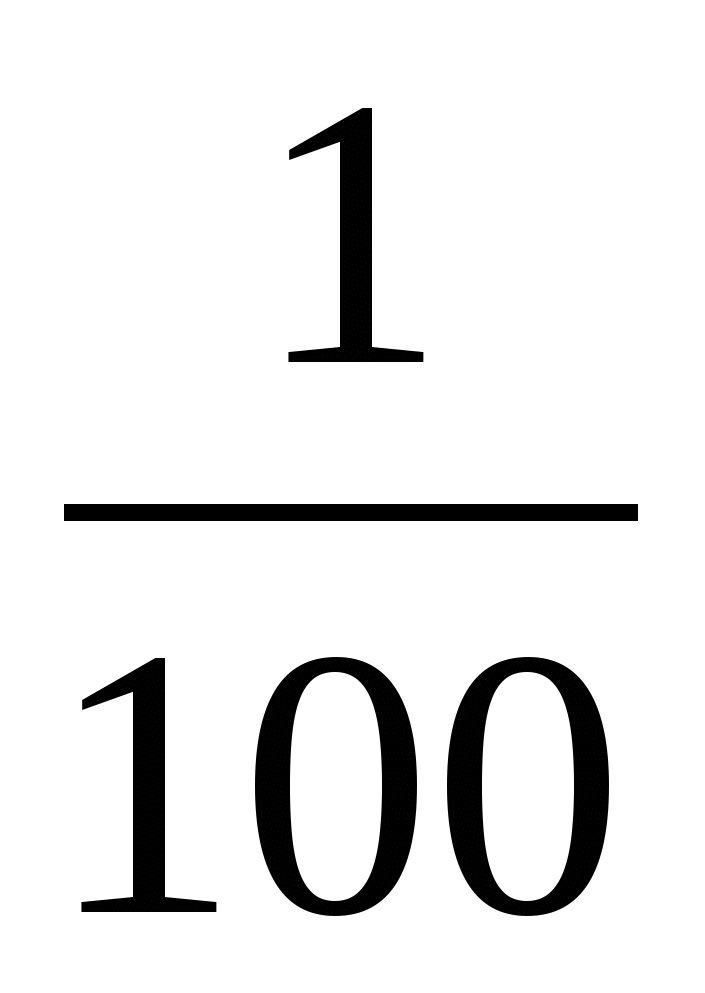1 1

1 - острый

Острый угол меньше 90°.

1< 90°

Прямой угол.

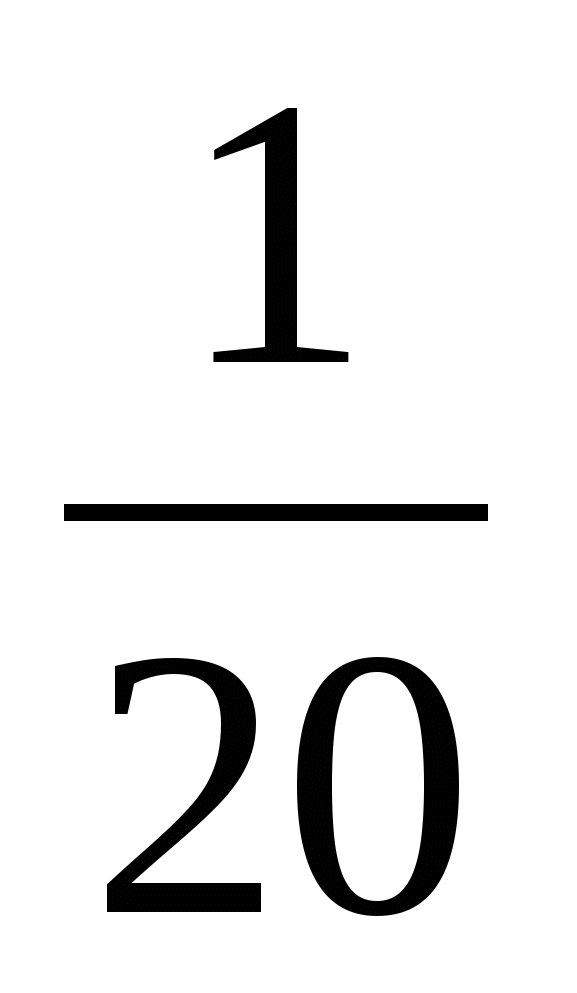
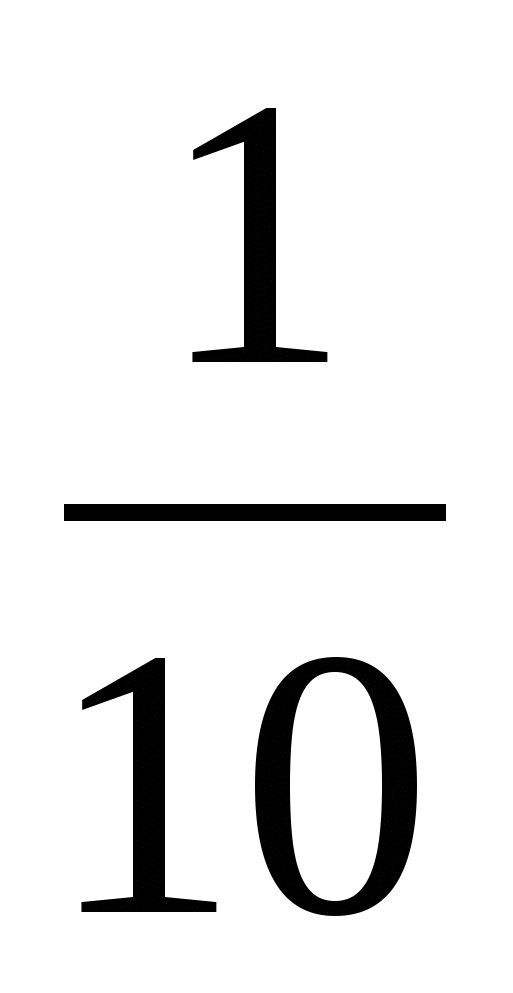
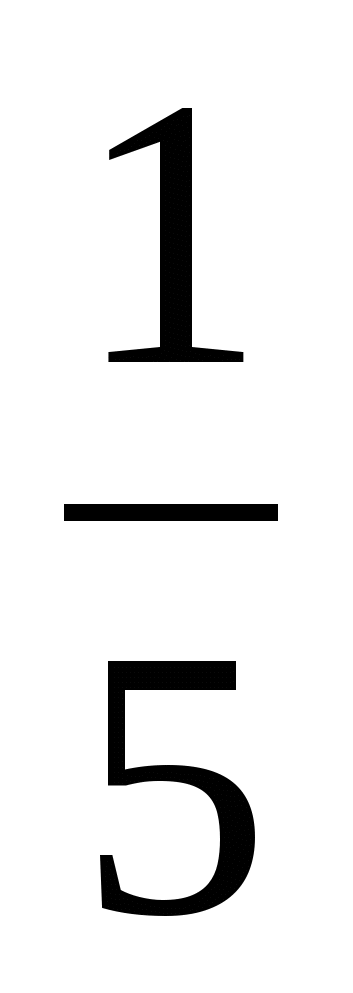
2

2

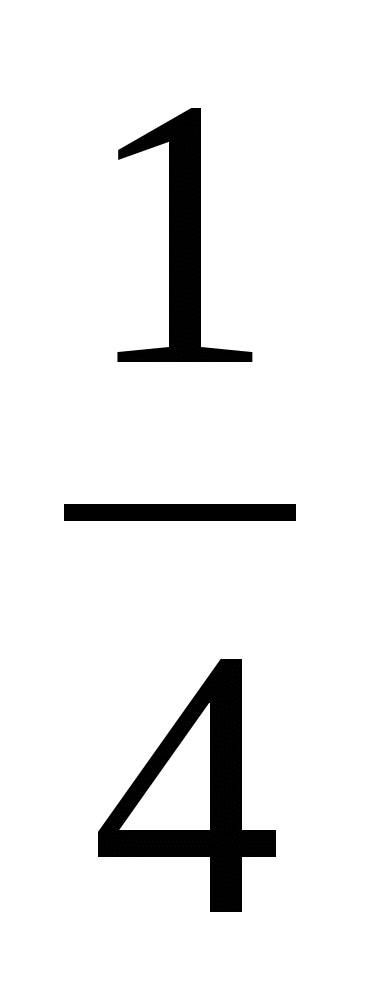
2 - прямой

Прямой угол равен 90°.

2 = 90°

Тупой угол.

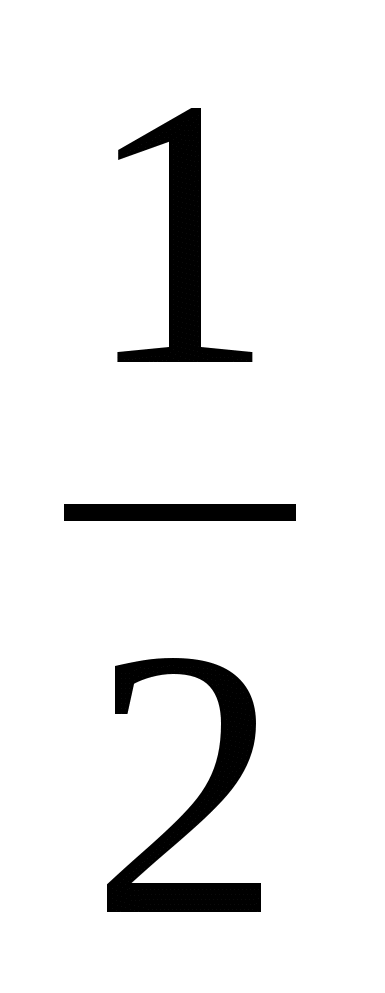
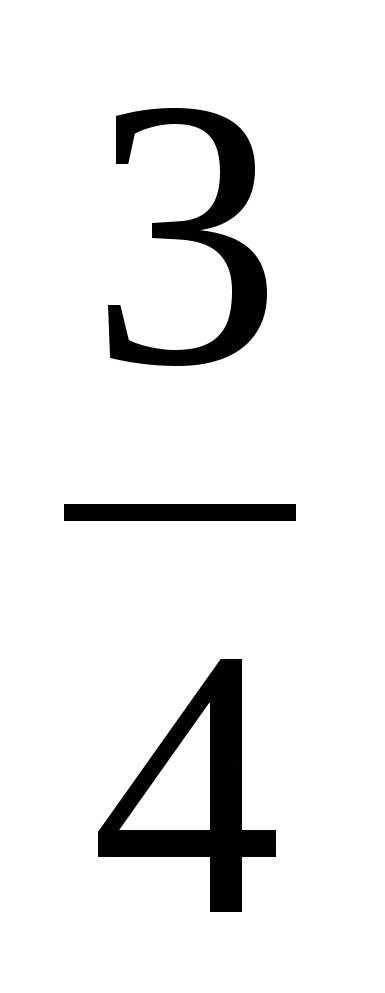
3 3

3 - тупой

Тупой угол больше 90°.

90° < 3 <180°

Развёрнутый угол.

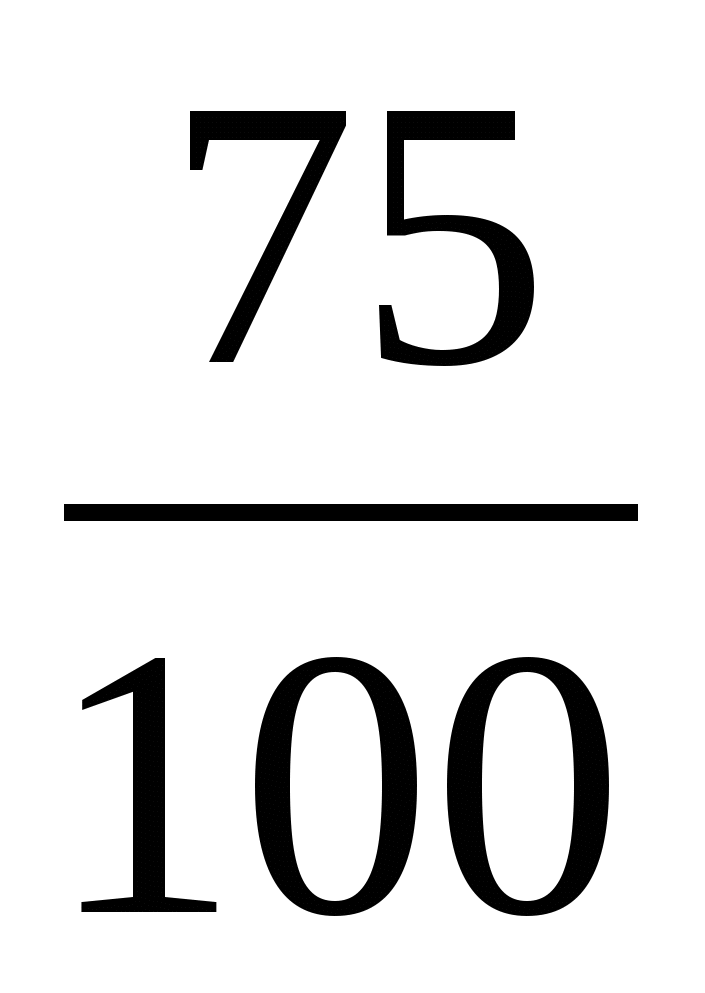
4

.

4 - развёрнутый

Развёрнутый угол равен 180°.

4 = 180°

Математические действия при решении задач.

В условии требуется узнать

Действия

На … больше

+ складываем

На … меньше

- вычитаем

В … раз(а) больше

• × умножаем

В … раз(а) меньше

: делим

На сколько больше?

На сколько меньше?

- вычитаем

Во сколько раз больше?

Во сколько раз меньше?

: делим

Всего

+ складываем

Задачи и опорные схемы к ним. ПОВТОРЕНИЕ за 1-4 классы.

Алгоритм решения задачи предусматривает работу со всеми рациональными числами и решению более сложных задач.

Задачи на нахождение суммы

Решение

1

У дома росло 4 дерева. Весной посадили еще 7 деревьев. Сколько деревьев растет у дома?

Б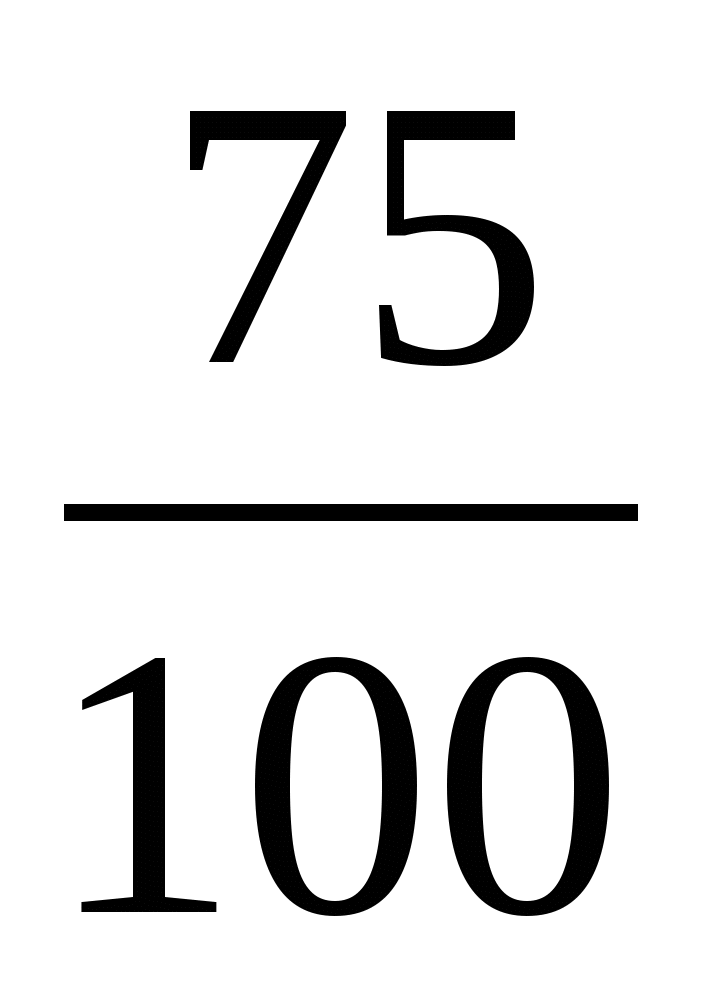ыло -4д.

?

Посадили-7 д.

1. 4+7 = 11 (д) - посадили весной

2. 4 + 11 = 15 (д) - растет у дома

Ответ: 15 деревьев растет у дома

2

В первый день Митя нарисовал 4 рисунка. Во второй день столько же. Сколько рисунков нарисовал Митя?

I-4 р.

II-?, столько же

1. 4 +4 = 8 (р) - нарисовал Митя.

Ответ: 8 рисунков нарисовал Митя

3

На день рождения Маше подарили 3 куклы, 5 мишек, а воздушных шариков столько же, сколько кукол и мишек вместе. Сколько воздушных шариков подарили Маше?

К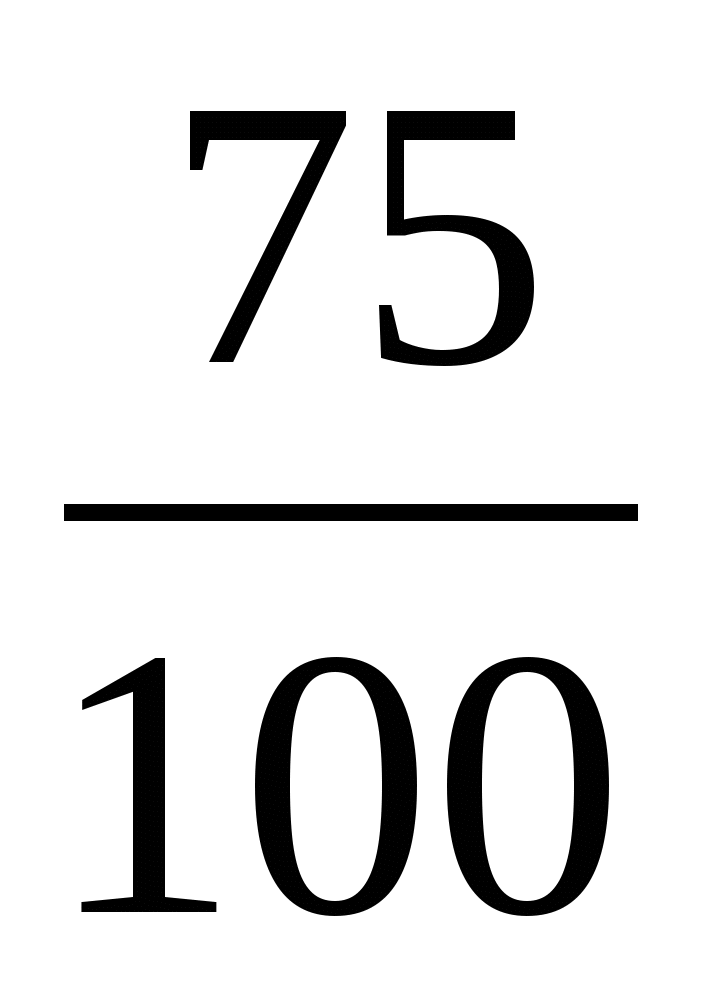.-3

Ш.-?

М.-5

1) 3 + 5 = 8 (ш) подарили Маше

Ответ: 8 воздушных шариков подарили Маше.

Задачи на увеличение и уменьшение числа НА несколько единиц

4

В магазин привезли 7 ящиков хурмы, а винограда на 5 ящиков больше. Сколько ящиков винограда привезли в магазин?

Х.-7 ящ.

В.-?, на 5 ящиков больше

1) 7+5 = 12 (ящ)

Ответ: 12 ящиков винограда привезли в магазин

5

В автобусе ехало 15 взрослых пассажиров, а детей на 10 человек меньше. Сколько детей ехало в автобусе?

В.-15п.

Д. ?, на 10 человек меньше

1) 15-10 = 5 (д)

Ответ: 5 детей ехало в автобусе

Задачи на нахождение остатка

6

В вазе было 10 яблок. 8 яблок съели. Сколько яблок осталось?

Было -10 яб.

Съели-8 яб.

Осталось-?

1) 10-8 = 2 (я)

Ответ: 2 яблока осталось?

Задачи на нахождение неизвестного слагаемого

7

За 2 дня девочка прочитала 10 страниц. В первый день она прочитала 7 страниц. Сколько страниц она прочитала во второй день?

I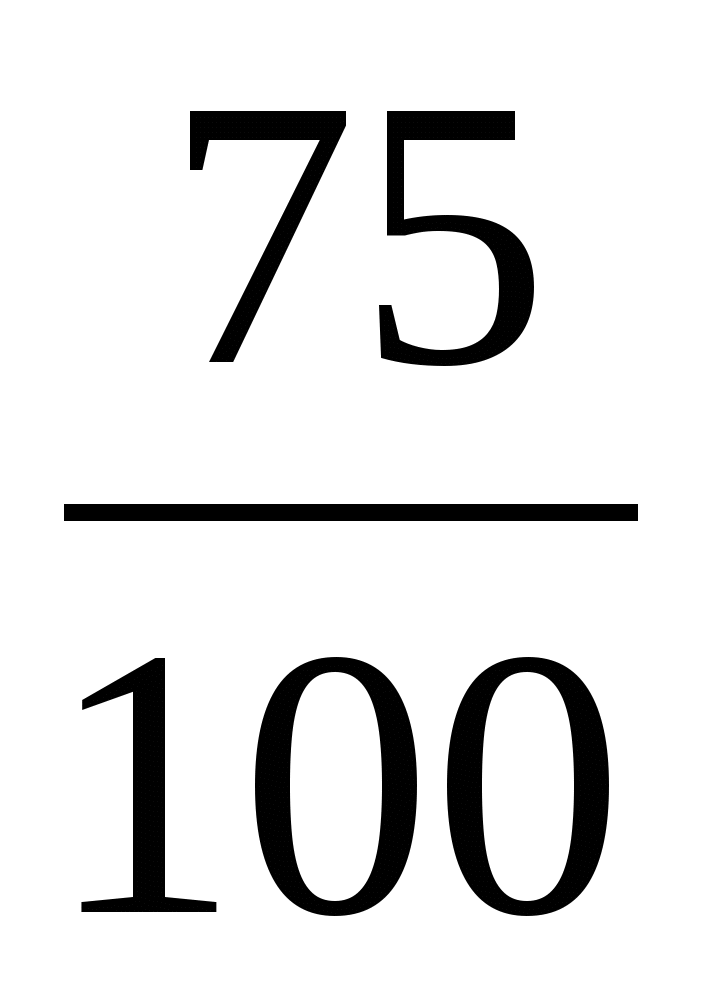-7 стр.

10 стр.

II-?

1) 10-7 = 3 (стр)

Ответ: 3 страницы девочка прочитала во второй день

Задачи на нахождение неизвестного уменьшаемого и вычитаемого

8

У Иры было несколько тетрадей. Когда она исписала 3 тетради, у нее осталось 6. Сколько тетрадей было у Иры?

Было ?

Исписала-3т.

Осталось-6т.

1) 3 + 6 = 9 (т)

Ответ: 9 тетрадей было у Иры

9

У Иры было 9 тетрадей. Когда несколько тетрадей она исписала, у нее осталось 6. Сколько тетрадей исписала Ира?

Было-9т.

Исписала-?

Осталось-6т.

1) 9 - 6 = 3 (т)

Ответ: 3 тетради исписала Ира

Задачи на разностное сравнение

10

Катя нашла 8 грибов, а Аня - 10. На сколько больше грибов нашла Аня?

На сколько меньше грибов нашла Катя?

К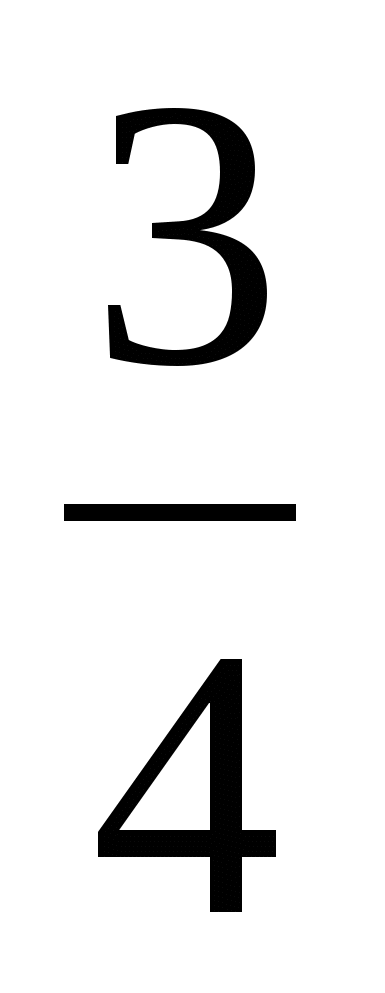.-8г.

На ? > (<)

А.-10г.

1) 10 - 8 = 2 (г)

Ответ: на 2 гриба больше нашла Аня. На 2 гриба меньше нашла Катя.

Задачи, выраженные в косвенной форме

11

Оле 10 лет. Она на 3 года старше своего брата. Сколько лет брату?

О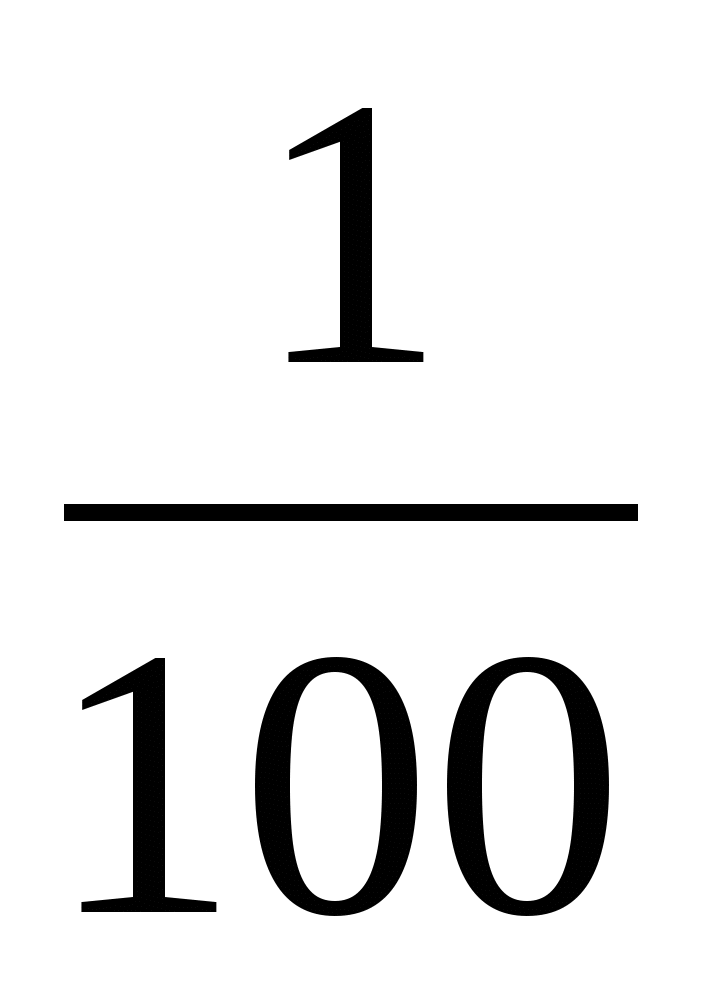.-10 лет, она на 3 года старше

Б.-?,

1) 10 - 3 = 7 (л)

Ответ: 7 лет брату.

Умножение.

Простые задачи на умножение

12

В двух вазах по 3 розы. Сколько роз в этих вазах?

III III

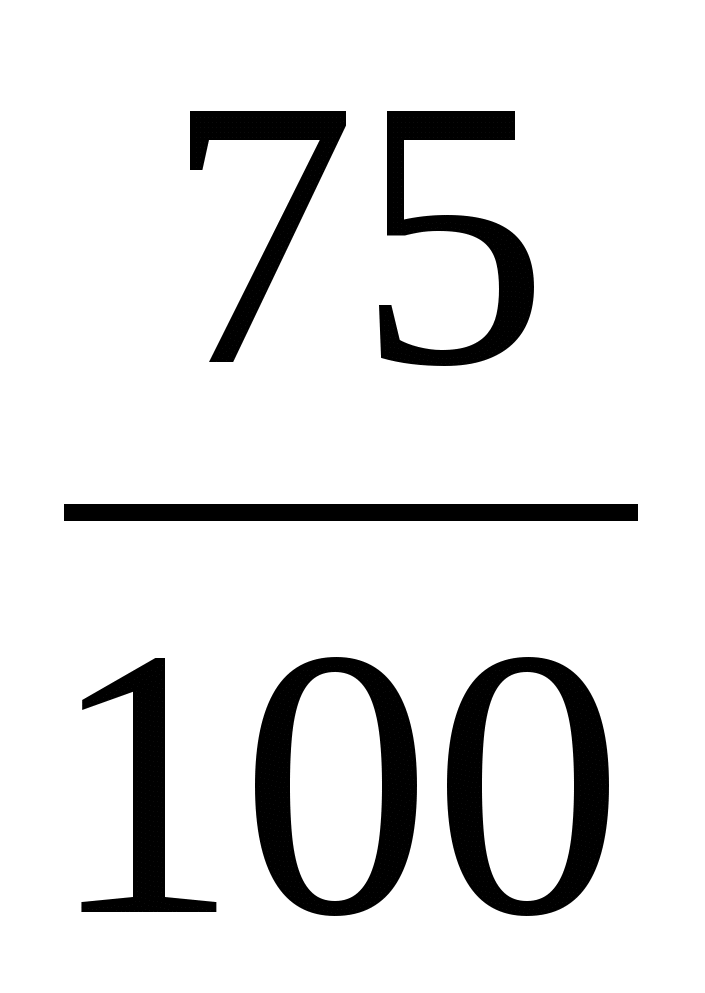3 3

?

1. 3 · 2 = 6 (р)

Ответ: 6 роз в двух вазах.

Задачи на увеличение и уменьшение числа В несколько раз

13

В кружке занимаются 5 мальчиков, а девочек в 2 раза больше. Сколько девочек занимаются в кружке?

М.-5

Д.-?, в 2 раза больше

1) 5 · 2 = 10 (д)

Ответ: 10 девочек занимаются в кружке

14

В кружке занимаются 12 мальчиков, а девочек в 3 раза меньше. Сколько девочек занимаются в кружке?

М.-12

Д.-?, в 3 раза меньше

1) 12 : 3 = 6 (д)

Ответ: 6 девочек занимаются в кружке

Задачи на деление по содержанию

15

8 кустов астр посадили на клумбы, по 4 куста на каждую. Сколько клумб засадили астрами?

4

? …

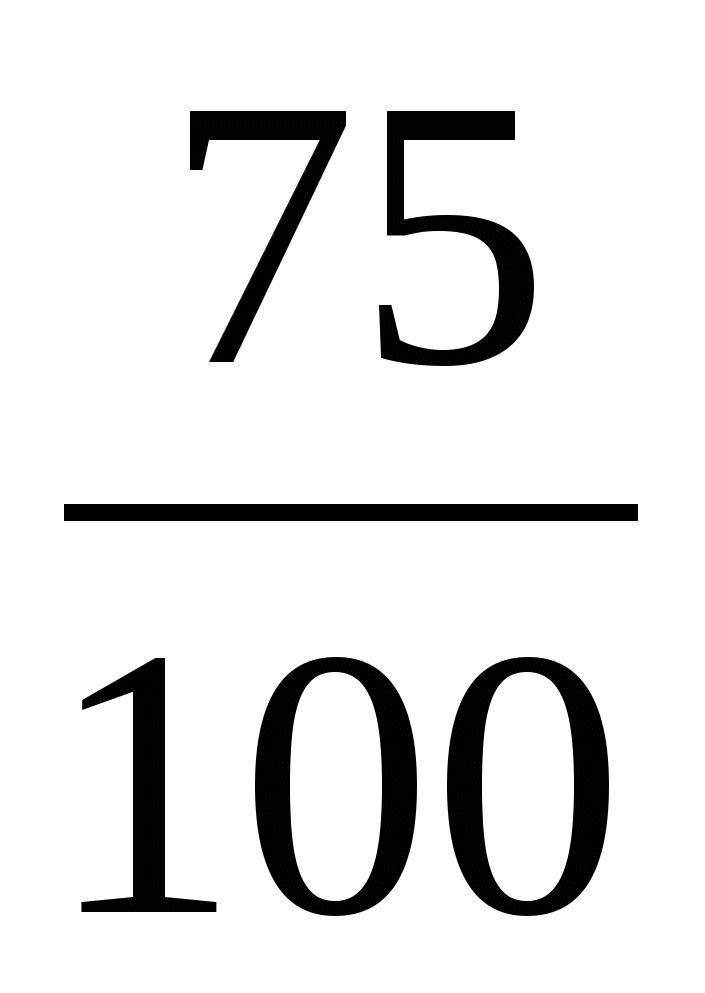8 к.

1) 8 : 4 = 2 (к)

Ответ: 2 клумбы засадили астрами

Задачи на деление на равные части

16

8 кустов астр посадили на 2 клумбы. Сколько кустов астр на каждой клумбе?

?

?

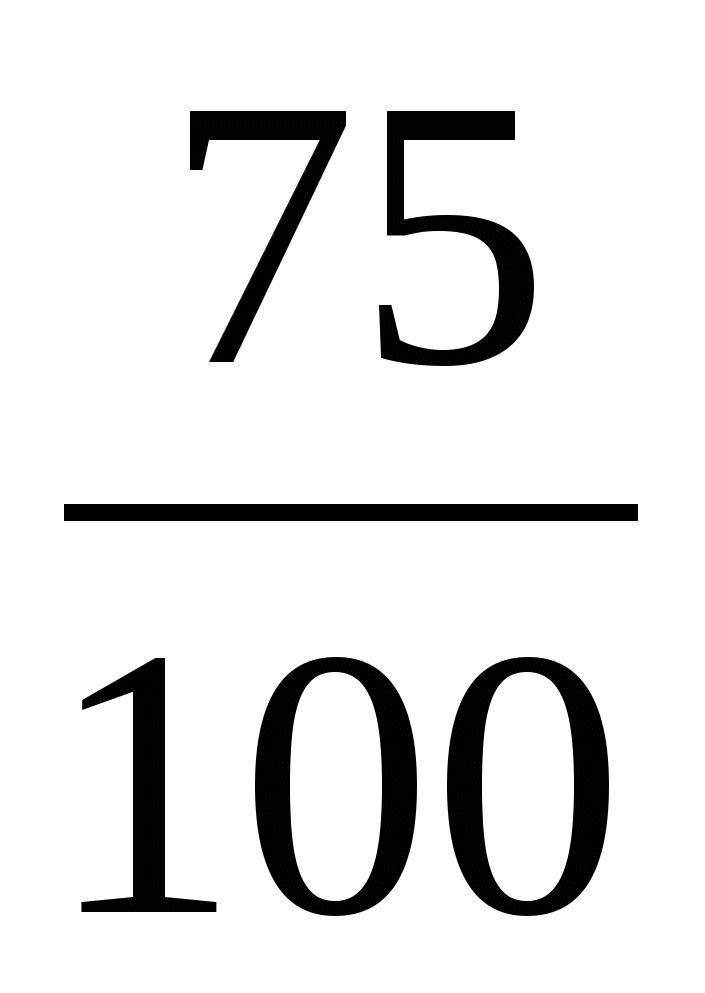
8 к.

1) 8 : 2 = 4 (к)

Ответ: 4 куста астр на каждой клумбе

Задачи на кратное сравнение

17

Высота дома 12 метров, а высота сарая - 3 метра. Во сколько раз дом выше сарая?

Во сколько раз сарай ниже дома?

Д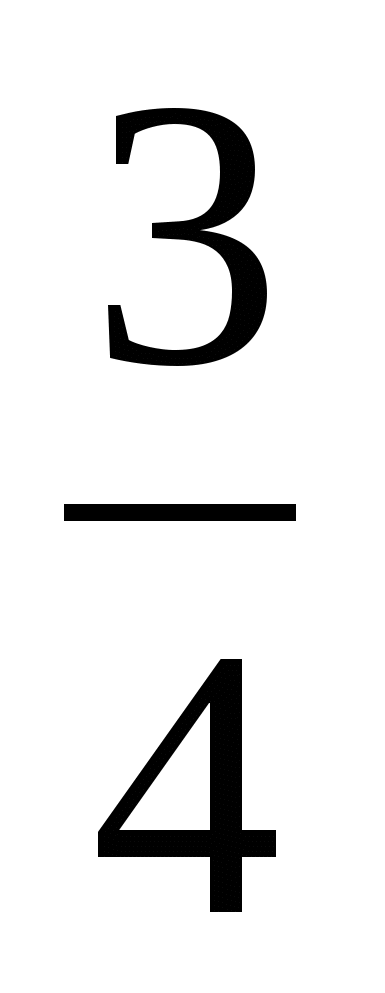.12 м

Во ? > (<)

С.-3 м

1) 12: 3 = 4 (раза)

Ответ: в 4 раза дом выше сарая. В 4 раза сарай ниже дома

Задачи на увеличение и уменьшение числа в несколько раз, выраженные в косвенной форме.

18

На озере плавало 6 селезней, что в 2 раза меньше, чем уток. Сколько уток плавало на озере?

На озере плавало 12 уток. Это в 2 раза больше, чем селезней. Сколько селезней плавало на озере?

С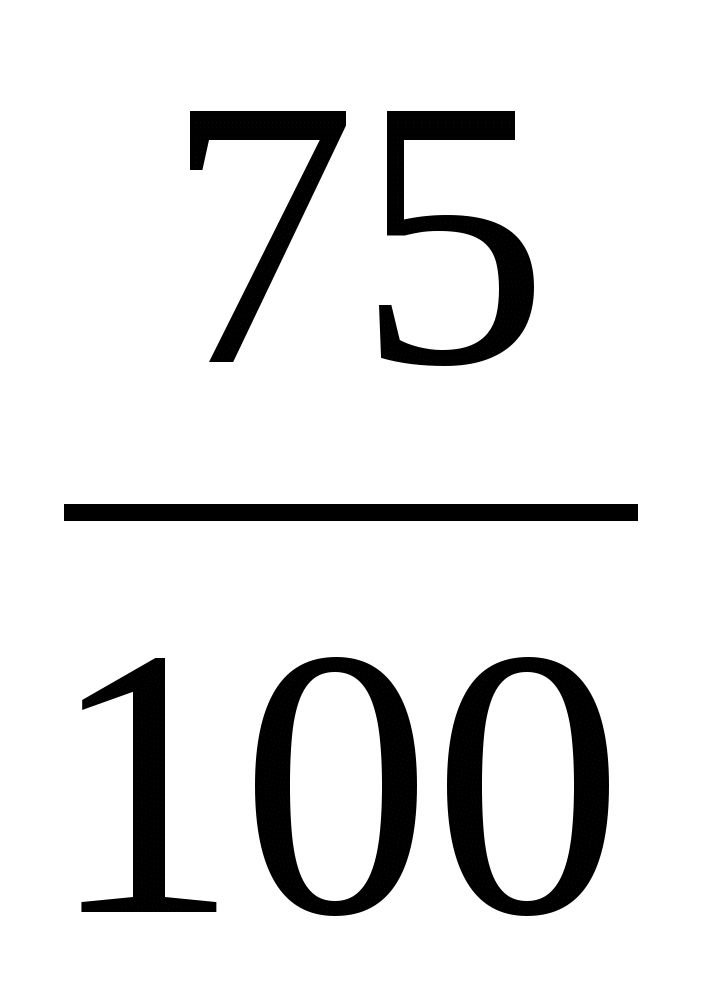.-6, это в 2 раза меньше

У.-?

У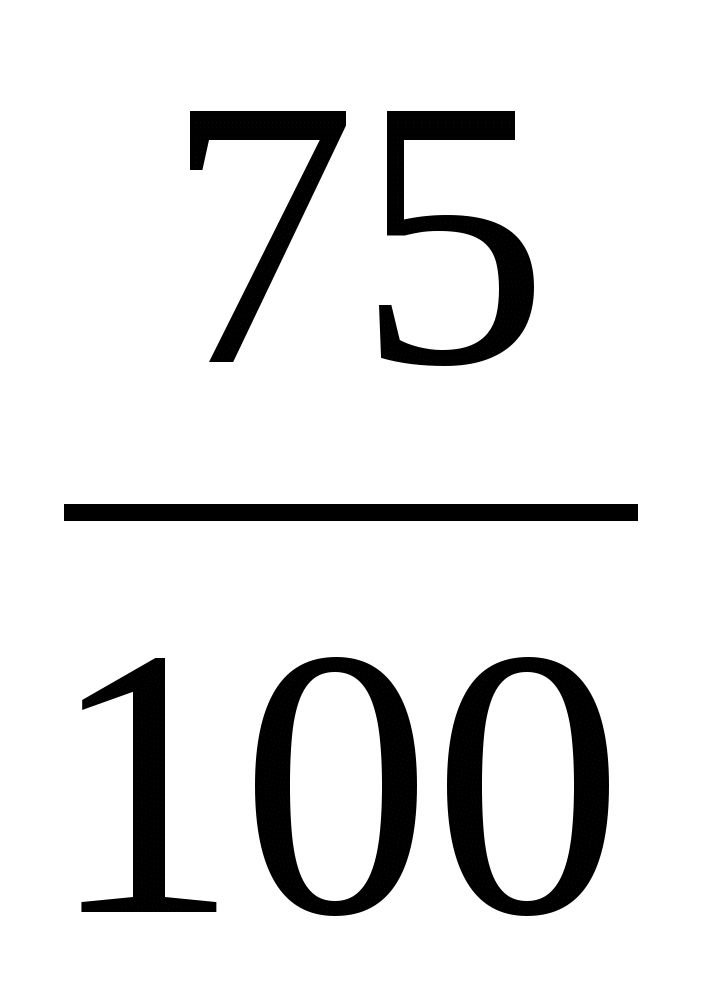.-12, это в 2 раза больше

С.-?

1. 6 · 2 = 12 (у)

Ответ: 12 уток плавало на озере

1. 12 : 2 = 6 (с)

Ответ: 6 селезней плавало на озере

Задачи на приведение к единице

19

В трех пачках 12 фломастеров. Сколько фломастеров в 2 таких пачках?

?

?

?

?

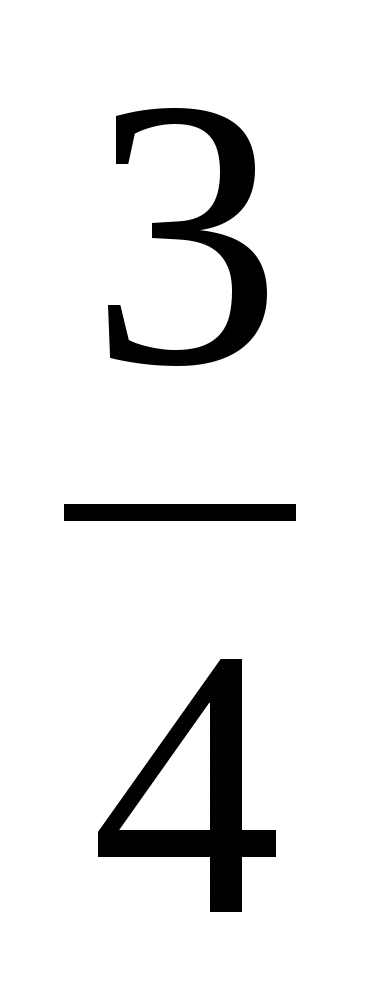
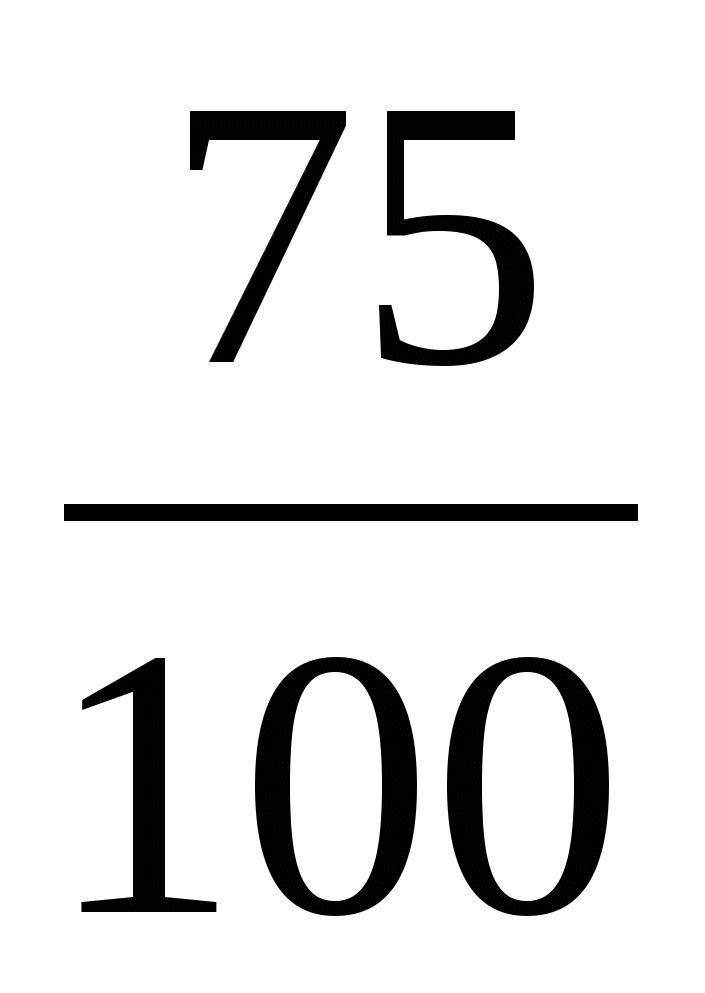
12ф.

1. 12 : 3 = 4 (ф) в одной пачке.

2. 4 · 2 = 8 (ф) в 2 таких пачках

Ответ: 8 фломастеров в 2 таких пачках.

Простые задачи на цену, количество, стоимость

20

1. Тарелка стоит 5 рублей. Сколько стоят 6 тарелок?

2. Тарелка стоит 5 рублей. Сколько тарелок можно купить на 30 рублей?

3. За 6 тарелок заплатили 30 рублей. Сколько стоит одна тарелка?

Цена

Кол-во

Стоим.

5р.

6

?

Цена

Кол-во

Стоим.

5 р.

?

30 р.

Цена

Кол-во

Стоим.

?

6

30 р.

1.

1) 5 · 6 = 30 (р)

Ответ: 30 рублей стоят 6 тарелок.

2.

1) 30 : 5 = 6 (т)

Ответ: 6 тарелок можно купить на 30 рублей

3.

1) 30 : 6 = 5 (р)

Ответ: 5 рублей стоит одна тарелка

Составная задача

21

В магазин привезли 7 ящиков хурмы, а винограда на 5 ящиков больше. Сколько ящиков хурмы и винограда привезли в магазин?

Х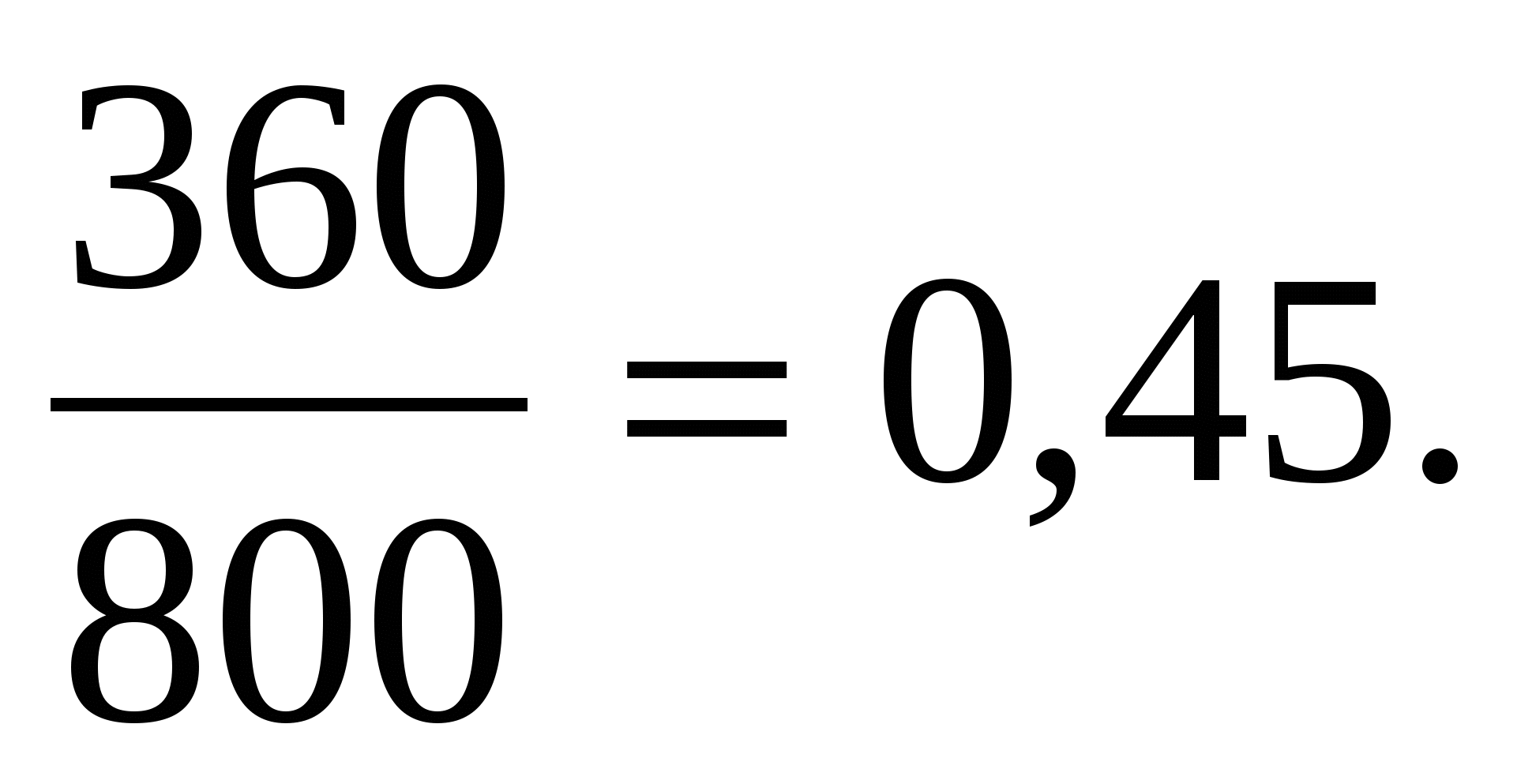.-7 ящ.

?

В.-?, на 5 ящиков больше

1) 7+5 = 12 (ящ) винограда

2) 7 + 12 = 19 (ящ)

Ответ: 19 ящиков хурмы и винограда привезли в магазин