- Учителю
- Открытый урок Многочлены.Формулы квадрата суммы и квадрата разности двух выражений
Открытый урок Многочлены.Формулы квадрата суммы и квадрата разности двух выражений
Открытый урок по алгебре в 7 классе.
Тема: « Галактика формул и уравнений».
Цели урока:
-
Образовательные:
выработать навыки возведения в квадрат суммы и разности двух выражений;
б)
закрепить буквенную запись формул квадрата суммы и квадрата разности и их словесные формулировки;
в)
выработать умение применять формулы квадрата двучлена для преобразования квадрата суммы или разности в трехчлен вида
a2 ± 2ab + b2;
г)
закрепить и усовершенствовать навыки решения уравнений и тождественных преобразований целых выражений;
д)
углубить знания учащихся за счет возрастающей сложности примеров, практического применения полученных знаний по теме в новых нестандартных условиях с возрастающей степенью самостоятельности;
-
Развивающие:
развитие грамотной устной и письменной математической речи, формирование языка и аппарата математики, выработка умения читать математическую, а следовательно, и техническую литературу;
б)
повышение познавательной активности учащихся в учебном процессе, интереса к предмету, логического мышления;
в)
развитие элементов творческой деятельности как качеств мышления - интуиции, пространственного воображения, смекалки;
г)
развитие зрительной памяти, сознательного восприятия учебного материала;
д)
развитие мировоззрения, понимания философской стороны математики как науки об определенных свойствах действительного мира и ее роли в освоении научной картины мира.
-
Воспитательные:
формирование навыков самоконтроля, самопроверки и взаимопроверки;
б)
воспитание коммуникативной культуры, умения работать в паре, оценивать себя и своих товарищей;
в)
эстетическое формирование личности учащегося; воспитание учащегося по критериям «научной» красоты.
г)
воспитание познавательной активности, чувства ответственности, культуры общения, культуры диалога;
-
Задачи:
провести диагностику усвоения системы знаний и умений и её применения для выполнения практических заданий стандартного уровня с переходом на более высокий уровень.
б)
систематизировать материал по данной теме.
в)
развивать познавательные процессы, память, мышление, внимание, наблюдательность, сообразительность
г)
выработать критерии оценки своей работы, умение анализировать проделанную работу и адекватно её оценивать.
-
Тип урока:
По методам - урок-практикум
б)
по назначению - урок тренинга, повторения навыков;
в)
по содержанию - урок применения полученных знаний на практике;
г)
по месту проведения - урок в кабинете математики.
-
Оборудование:
мультимедийный проектор
б)
Экран
в)
презентация по теме
Ход урока:
-
Организационный момент.
Представим себе, что сегодня наш класс - отправляется в межгалактическое путешествие и мы посетим различные планеты. Вас всех пригласили принять участие в путешествии, чтобы обсудить с вами тему «Многочлены. Формулы сокращенного умножения их применение». И вы будите исследователями этих планет. В процессе путешествия вы должны: закрепить изученный материал, показать уровень усвоения темы, разобраться в непонятных ранее моментах, проконтролировать и оценить свои знания. У каждого из вас на столе оценочный лист, где вы будете фиксировать свои результаты исследования:
Оценочный лист.Планета теоретических знаний
Планета формул
Планета
испытаний
Планета
секретов
Планета нахождения истины
Активность
во время путешествия
Всего баллов
Оценка
Девизом нашего заседания является лозунг:
«Дорогу осилит идущий, а математику мыслящий» - запись на доске.
А сейчас открыли тетради и записали тему урока.
«Многочлены и формулы сокращенного умножения»
II. Актуализация опорных знаний.
Но прежде, чем войти в космический корабль, вам необходимо пройти испытание, которое будет пропуском на корабль.
Экспресс - опрос.

![]()
Выражение, представляющее собой сумму одночленов - многочлен.


да
или
нет
![]()
Выражение 2x2y4x - одночлен в стандартном виде.
да
или
нет
![]()
Одночлены с одинаковой буквенной частью - подобные члены.
да
или
нет
![]()
Квадрат двучлена
(a - 2b) равен
a2 - 2ab + 4b2.
да
или
нет
![]()
Выражение (x2 + y2) представляет собой квадрат суммы.
да
или
нет
Итак, мы получили пропуск на корабль. Мы уже летим в галактике. Перед нами планета теоретических знаний.
Планета теоретических знаний.
Давайте примем участие в изучении этой планеты. В ней много законов, по которым мы будем работать.
У некоторых учащихся имеется карточка-домино. Карточка содержит вопрос и ответ. Первым начинает ученик, у которого карточка содержит слова «Старт» и «Финиш». Он задаёт стартовый вопрос. Он же даёт финишный ответ. Каждый ученик должен внимательно следить за ходом игры, чтобы не пропустить свой ответ. Ответив, ученик задаёт свой вопрос и т.д. Учитель указывает на ошибку, если прозвучал неправильный ответ. Все учащиеся одновременно следят и за тем, чтобы был дан правильный ответ. За игру в домино в оценочный лист вы себе поставите один балл, если верно ответите на вопрос, и 0 баллов, если пропустите свой ответ.
Итак «Математическое домино».
Финиш: Ответ: Произведению суммы этих выражений на неполный квадрат их разности.
Старт: Вопрос: Что называют многочленом?
Ответ: Сумму одночленов.
Вопрос: Что называют одночленом?
Ответ: Произведение чисел, переменных и их степеней.
Вопрос: Как умножить одночлен на многочлен?
Ответ: Одночлен умножить на каждый член многочлена, а результаты сложить.
Вопрос: Как перемножить одночлены?
Ответ: Перемножить числовые коэффициенты, а затем перемножить степени с одинаковыми основаниями и результаты перемножить.
Вопрос: Как умножить две степени с одинаковыми основаниями?
Ответ: Основание оставить тем же, а показатели степеней сложить.
Вопрос: Как возвести степень в степень?
Ответ: Основание оставить тем же, а показатели степеней перемножить.
Вопрос: Как умножить многочлен на многочлен?
Ответ: Каждый член одного многочлена умножить на каждый член другого многочлена и результаты сложить.
Вопрос: Чему равен квадрат суммы двух выражений?
Ответ: Квадрату первого выражения плюс удвоенное произведение первого на второе плюс квадрат второго выражения.
Вопрос: Чему равен квадрат разности?
Ответ: Квадрату первого выражения минус удвоенное произведение первого на второе плюс квадрат второго выражения.
Вопрос: Чему равно произведение разности и суммы двух выражений?
Ответ: Разности квадратов этих выражений.
Вопрос: Чему равно произведение разности двух выражений на неполный квадрат их суммы?
Ответ: Разности кубов этих выражений.
Вопрос: Чему равна сумма кубов двух выражений?
Планета формул.
На этой планете много формул сокращённого умножения. Объясните, для чего они нужны и в каких случаях вы их применяете?Установите соответствие:
Вариант 1.
Вариант 2.

(a + b)2

(t - p)2


a2-2ab+b2
a2+ab+b2

a2+2ab+b2


t2+2pt+p2
t2-pt+p2

t2-2pt+p2
Комментарий учителя
!
Ребята! Обменяйтесь работами и сверьте полученные результаты с изображенным на экране.
За верный ответ 2 балла.
Установите соответствие:
Вариант 1.
Вариант 2.

(a + b)2

(t - p)2


a2-2ab+b2
a2+ab+b2

a2+2ab+b2


t2+2pt+p2
t2-pt+p2

t2-2pt+p2
Комментарий учителя
!
Ребята! Обменяйтесь работами и сверьте полученные результаты с изображенным на экране.
За верный ответ 2 балла.
Планета испытаний
Комментарий учителя
!
Выберите верный вариант ответа и сверьте полученные результаты с изображенным на экране.
За верный ответ в оценочный лист 2 балла.
![]()
z2 - 16z + 64
16y2 + 40ay+25a2

Вариант 1.

(z + 8)2 =
(4y+5a)2 =
![]()
![]()
z2 +16z+64
40ay -16y2+ 25a2
z2 + 8z + 64
16a2 + 40ay+25y2
*****************************************************************************
![]()


Вариант 2.
49y2 + 84y + 36
81 +90h +25h2
(6 + 7y)2 =
(9 - 5h)2 =

![]()
![]()
49y2 +42y + 36
81 - 90h +25h2
49y2 + 84y2 + 36
812 + 90h -25h2
![]()

z2 - 16z + 64
16y2 + 40ay+25a2

Вариант 1.

(z + 8)2 =С1
(4y+5a)2 =A2
(2x + 5g)2 =A2
![]()
![]()
z2 +16z+64
40ay -16y2+ 25a2
z2 + 8z + 64
16a2 + 40ay+25y2
*****************************************************************************
![]()


Вариант 2.
49y2 + 84y + 36
81 +90h +25h2
(6 + 7y)2 = A1
(9 - 5h)2 =C2

![]()
![]()
49y2 +42y + 36
81 - 90h +25h2
49y2 + 84y2 + 36
812 + 90h -25h2
Планета секретов.
Межпланетный корабль подлетел к неизвестной планете, произвел фотосъёмку её поверхности. А мы с вами взяли пробы грунта этой планеты. Вместе с пробами обнаружился кусок твёрдого сплава с таинственными обозначениями. Так вот необходимо, чтобы вы объяснили, что обозначают эти таинственные знаки.
Вариант 1.
![]()

(* - f )2 = ( f - e)2
![]()
(* + 2w )2 = * + 12t w +
*
![]()
(* - 2m )2 = 100 -
40m + 4m2
*****************************************************************************
Вариант 2.
![]()

(* - r )2 = ( d + r)2
![]()
(3i +* )2 = * + * +
49q2
![]()
(3n + * )2 = 9n2
+ 6nv + v2
Комментарий учителя
!
Ребята! Обменяйтесь работами и сверьте полученные результаты с изображенным на экране.
Если верен 1 ответ - 1 балл, 2 ответа - 2 балла, 3 ответа - 3 балла.
Вариант 1.
![]()

(e - f )2 = ( f - e)2
![]()
(3t + 2w )2 = 9t2+ 12t w +
4w2
![]()
(10 - 2m )2 = 100 - 40m +
4m2
*****************************************************************************
Вариант 2.
![]()

(-d - r )2 = ( d + r)2
![]()
(3i +7q )2 = 9i2 + 42iq +
49q2
![]()
(3n + v )2 = 9n2 + 6nv +
v2
Планета нахождения истины.
Перед нами планета нахождения истины. Давайте примем участие в изучении этой планеты. На этой планете мы попробуем найти истину, решая уравнения.
Выдающийся физик Альберт Эйнштейн - основоположник теории относительности - говорил так: «Мне приходится делить время между политикой и уравнениями. Однако уравнения, по-моему, гораздо важнее. Политика существует только для данного момента, а уравнения будут существовать вечно».
Вот и займёмся уравнениями. Попробуем применить формулы к решению уравнений. На доске написаны 8 уравнений. Каждый из вас будет решать 2 уравнения. Затем нужно будет подойти к доске, отыскать полученный результат и прикрепить его обратной стороной (буквой) к своему уравнению. Если вашего результата нет, значит, уравнение решено неверно.
Реши уравнения
-
(6y+2)(5-y)=47-(2y-3)(3y-1) 2 - А
-
(x+6)²-(x-5)(x+5)=79 1,5 - Л
-
-
9x·(x+6)-(3x+1)²=1
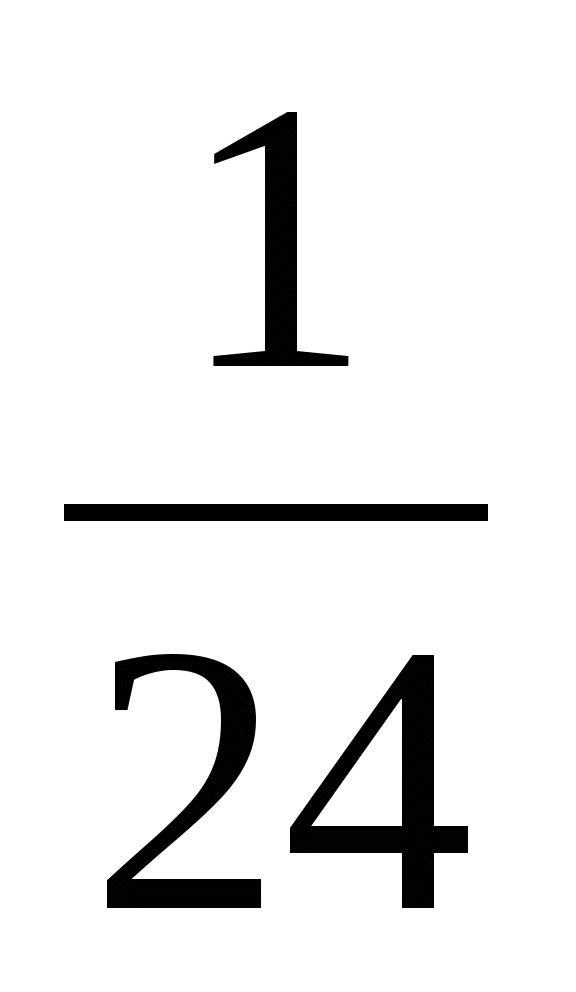 - Д
- Д
-
a·(8-9a)+40=(6-3a)(6+3a) -0,5 - Ж
-
16y·(2-y)+(4y-5)²=0
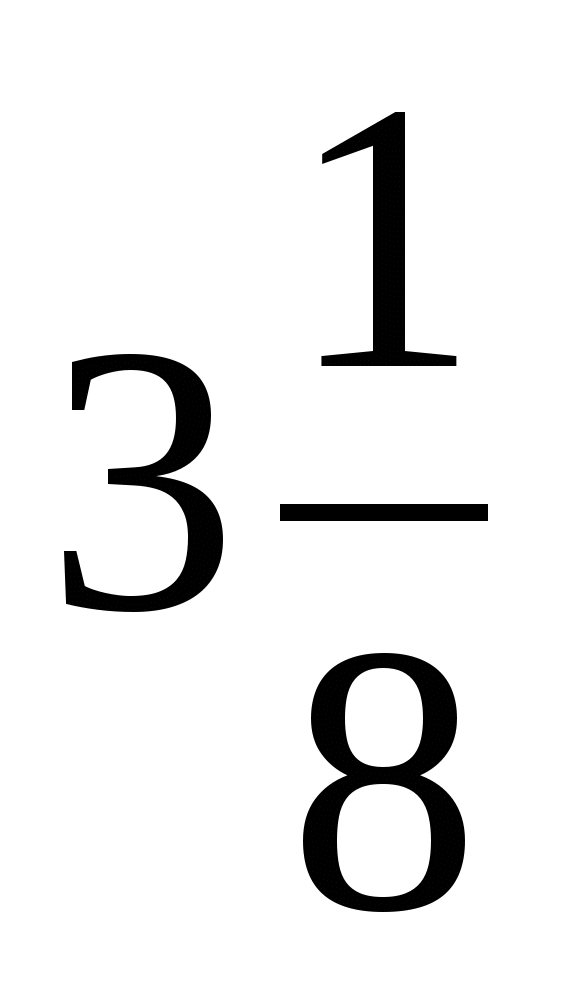 - А
- А
-
(х-7)²+3=(х-2)(х+2) 4 - Б
-
(2-х)²-х·(х+1,5)=4 0 - Р
-
(2х-3)(2х+3)-8х=7+4х² -2 - А
Мы получили загадочное слово АЛ-ДЖАБРА. Что же это за слово?
Сообщение учащегося:
Занимаясь математикой, вы не могли не заметить, что она состоит из нескольких частей. Вы научились оперировать с натуральными и дробными числами, знаете положительные и отрицательные числа. «Число» - по-гречески звучит арифмос. Поэтому наука о числе получила греческое название арифметика. Другой раздел математики посвящён различным фигурам и их свойствам и называется «Геометрия». Гео - по-гречески земля, метрио - мерею. Но вот слово алгебра - раздел математики, где решаются уравнения, рассматриваются преобразования выражений, составленные из чисел и букв - не греческое. В чём тут дело? Разве у греков не было алгебры. Была. Но решали древние греки алгебраические задачи геометрически.
А вот слово алгебра произошло от слова ал-джабра, взятого из названия книги узбекского математика, астронома и географа Мухамеда Ал-Хорезми «Краткая книга об исчислениях ал-джабры и ва-л-мукабалы». Арабское слово аль-джебр переводчик не стал переводить, а записал его латинскими буквами algebr. Так возникло название науки, которую мы изучаем. «Ал-джабра» - операция переноса отрицательных членов из одной части уравнения в другую, но уже с положительным знаком. По-русски это слово означает «восполнение».
Интересно, что «алгебраистами» в средние века называли вовсе не математиков, а арабских хирургов-костоправов. Об одном таком алгебраисте написал Сервантес в своём знаменитом романе «хитроумный Идальго Дон Кихот Ламанческий»
Друзья! А мы возвращаемся из нашего межпланетного путешествия, чтобы оно закончилось успешно Вам необходимо преодолеть ступеньки вместе с шагающим человечком и подняться на вершину успеха нашего загадочного урока.
Задание заключается в следующем: используя формулу квадрата суммы или квадрата разности, вычислите:
Вариант 1.
![]()





9,92
В ариант
2.
ариант
2.
![]()





10,22
Комментарий учителя
!
Друзья! Убедитесь, что Вы правы!
9,92 = (10 - 0,1)2 = 100 - 2 + 0,01 = 98,01.
10,22 = (10 + 0,2)2 = 100 + 4 + 0,04 = 104,04.
III Итог урока.
Каждый ученик сегодня принимал участие в нашем путешествии. Сегодня, выполняя разнообразные задания, вы иногда допускали ошибки. И это неудивительно, любой человек не застрахован от ошибок, особенно, когда он только учится овладевать какой-либо наукой. Важно вовремя найти и исправить эти ошибки, понять, почему они появились, и стараться впредь не допускать их.
Давайте, оценим свою активность во время путешествия(1-3 балла) и поставим себе оценку за урок: 12-15 баллов -«5», 10-12 баллов -«4», 7-9 баллов -«3» .
Домашнее задание №880, 888, 892 .
</