Пробные экзаменационные варианты работ профильного уровня

Вариант № 1

Часть 1

Задание 1 . На автозаправке клиент отдал кассиру 1000 рублей и залил в бак 29 литров бензина по цене 33 руб. 70 коп.за литр. Какую сумму сдачи он должен получить у кассира? Ответ запишите в рублях.

Задание 2 .

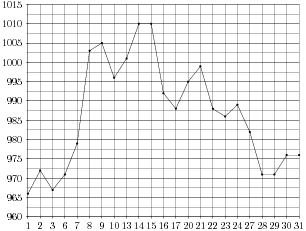
На рисунке жирными точками показана цена золота, установленная Центробанком РФ во все рабочие дни в октябре 2009 года. По горизонтали указываются числа месяца, по вертикали - цена золота в рублях за грамм. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку наибольшую цену золота за указанный период. Ответ дайте в рублях за грамм.

Задание 3 .

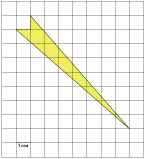
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

Задание 4 .

В среднем из 1500 садовых насосов, поступивших в продажу, 9 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.

Задание 5 . Найдите корень уравнения: Если уравнение имеет более одного корня, укажите меньший из них.

Задание 6 . 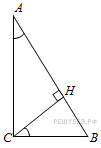В треугольнике угол равен 90°, высота равна 24, . Найдите .

Задание 7 . Прямая является касательной к графику функции . Найдите b, учитывая, что абсцисса точки касания больше 0.

Задание 8 . 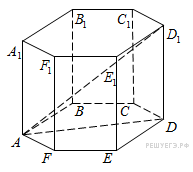В правильной шестиугольной призме все ребра равны 1. Найдите тангенс угла

Часть 2

Задание 9 . Найдите значение выражения .

Задание 10 . Скорость автомобиля, разгоняющегося с места старта по прямолинейному отрезку пути длиной км с постоянным ускорением , вычисляется по формуле . Определите наименьшее ускорение, с которым должен двигаться автомобиль, чтобы, проехав один километр, приобрести скорость не менее 110 км/ч. Ответ выразите в км/ч.

Задание 11 . Путешественник переплыл море на яхте со средней скоростью 30 км/ч. Обратно он летел на спортивном самолете со скоростью 370 км/ч. Найдите среднюю скорость путешественника на протяжении всего пути. Ответ дайте в км/ч.

Задание 12 . Найдите точку максимума функции .

1Задание 13 . а) Решите уравнение .

б) Укажите корни этого уравнения, принадлежащие промежутку .

Задание 14. В правильной шестиугольной пирамиде SABCDEF стороны основания которой равны 1, а боковые ребра равны 2, найдите угол между прямыми SB и CD.

Задание 15 . Решите неравенство:

Задание 16 . Высоты BB₁ и CC₁ остроугольного треугольника ABC пересекаются в точке H.

а) Докажите, что ∠AHB₁ = ∠ACB.

б) Найдите BC, если AH = 21 и ∠BAC = 30°.

Задание 17 . В январе 2000 года ставка по депозитам в банке «Возрождение» составила х % годовых, тогда как в январе 2001 года - у % годовых, причем известно, что x + y = 30%. В январе 2000 года вкладчик открыл счет в банке «Возрождение», положив на него некоторую сумму. В январе 2001 года, попрошествии года с того момента, вкладчик снял со счета пятую часть этой суммы. Укажите значение х при котором сумма на счету вкладчика в январе 2002 года станет максимально возможной.

Задание 18 . Найдите все значения a, при которых уравнение

имеет ровно два различных корня.

Задание 19 . а) Можно ли число 2014 представить в виде суммы двух различных натуральных чисел с одинаковой суммой цифр?

б) Можно ли число 199 представить в виде суммы двух различных натуральных чисел с одинаковой суммой цифр?

в) Найдите наименьшее натуральное число, которое можно представить в виде суммы пяти различных натуральных чисел с одинаковой суммой цифр.

Вариант № 2

Часть 1

Задание 1 . Выпускники 11а покупают букеты цветов для последнего звонка: из 3 роз каждому учителю и из 7 роз классному руководителю и директору. Они собираются подарить букеты 15 учителям (включая директора и классного руководителя), розы покупаются по оптовой цене 35 рублей за штуку. Сколько рублей стоят все розы?

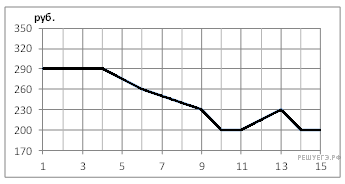
Задание 2 . На рисунке показано изменение биржевой стоимости акций целлюлозно-бумажного завода в первой половине апреля. 2 апреля бизнесмен приобрёл 250 акций этого завода. 6 апреля он продал 150 акций, а оставшиеся акции продал 11 апреля. Сколько рублей потерял бизнесмен в результате этих операций?

Задание 3 .

Средняя линия и высота трапеции равны соответственно 40 и 4. Найдите площадь трапеции.

Задание 4 . Вероятность того, что на тесте по биологии учащийся П. верно решит больше 9 задач, равна 0,59. Вероятность того, что П. верно решит больше 8 задач, равна 0,65. Найдите вероятность того, что П. верно решит ровно 9 задач.

Задание 5 .

Найдите корень уравнения: .

Задание 6 . 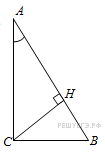В треугольнике ABC угол C равен 90°, CH - высота, , . Найдите AH.

Задание 7 . 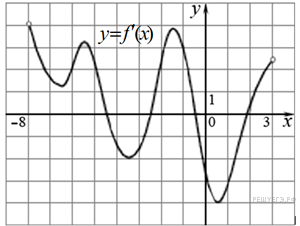На рисунке изображен график y=f'(x) - производной функции f(x), определенной на интервале (−8; 3). Найдите промежутки возрастания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.

.

Задание 8 . В правильной четырёхугольной призме известно, что . Найдите угол между диагоналями и . Ответ дайте в градусах.

Часть 2

Задание 9 . Найдите значение выражения .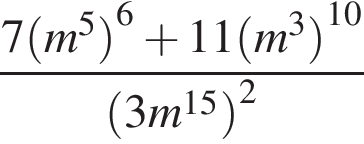

Задание 10 . При нормальном падении света с длиной волны нм на дифракционную решeтку с периодом d нм наблюдают серию дифракционных максимумов. При этом угол (отсчитываемый от перпендикуляра к решeтке), под которым наблюдается максимум, и номер максимума k связаны соотношением . Под каким минимальным углом (в градусах) можно наблюдать второй максимум на решeтке с периодом, не превосходящим 1800 нм?

Задание 11 . Теплоход, скорость которого в неподвижной воде равна 25 км/ч, проходит по течению реки и после стоянки возвращается в исходный пункт. Скорость течения равна 3 км/ч, стоянка длится 5 часов, а в исходный пункт теплоход возвращается через 30 часов после отплытия из него. Сколько километров прошел теплоход за весь рейс?

Задание 12 .Найдите наименьшее значение функции на отрезке .

Задание 13 . Решите уравнение .

Задание 14 . В конус, радиус основания которого равен 6, вписан шар радиуса 3.

а) Изобразите осевое сечение комбинации этих тел.

б) Найдите отношение площади полной поверхности конуса к площади поверхности шара.

Задание 15 . Решите неравенство:

Задание 16 . Основание равнобедренного треугольника равно косинус угла при вершине равен Две вершины прямоугольника лежат на основании треугольника, а две другие - на боковых сторонах. Найдите площадь прямоугольника, если известно, что одна из его сторон вдвое больше другой.

Задание 17 . Алексей приобрёл ценную бумагу за 8 тыс. рублей. Цена бумаги каждый год возрастает на 1 тыс. рублей. В любой момент Алексей может продать бумагу и положить вырученные деньги на банковский счёт. Каждый год сумма на счёте будет увеличиваться на 8%. В течение какого года после покупки Алексей должен продать ценную бумагу, чтобы через двадцать пять лет после покупки этой бумаги сумма на банковском счёте была наибольшей?

Задание 18 . Найдите все значения при каждом из которых график функции

пересекает ось абсцисс более чем в двух различных точках.

Задание 19 . Найдите все целые значения и такие, что

Вариант № 3

Часть 1

Задание 1 . Бегун пробежал 180 метров за 20 секунд. Найдите среднюю скорость бегуна. Ответ дайте в километрах в час.

Задание 2 . 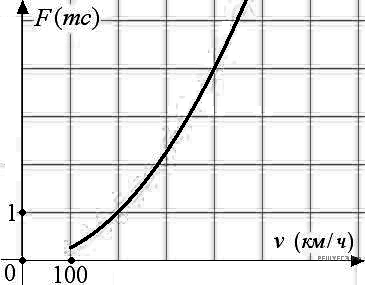Когда самолет находится в горизонтальном полете, подъемная сила, действующая на крылья, зависит только от скорости. На рисунке изображена эта зависимость для некоторого самолета. На оси абсцисс откладывается скорость (в километрах в час), на оси ординат - сила (в тоннах силы). Определите по рисунку, чему равна подъемная сила (в тоннах силы) при скорости 200 км/ч?

Задание 3 . 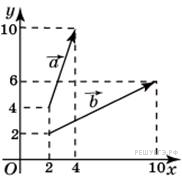Найдите сумму координат вектора + .

Задание 4 . В магазине стоят два платёжных автомата. Каждый из них может быть неисправен с вероятностью 0,05 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.

Задание 5 . Найдите решение уравнения: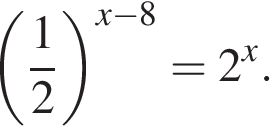

Задание 6 . 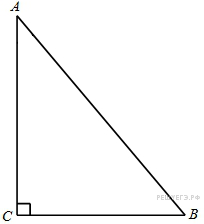В треугольнике ABC угол C равен 90°,AB = 25, BC = 20. Найдите .

Задание 7 .Прямая является касательной к графику функции . Найдите b, учитывая, что абсцисса точки касания меньше 0.

Задание 8 .Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 2 и 3. Объем призмы равен 18. Найдите ее боковое ребро.

Часть 2

Задание 9 .Найдите значение выражения , если .

Задание 10 . При адиабатическом процессе для идеального газа выполняется закон, где p - давление в газе в паскалях, V - объeм газа в кубических метрах. В ходе эксперимента с одноатомным идеальным газом (для него ) из начального состояния, в котором Па, газ начинают сжимать. Какой наибольший объeм V может занимать газ при давлениях p не ниже Па? Ответ выразите в кубических метрах.

Задание 11 . Смешали некоторое количество 13-процентного раствора некоторого вещества с таким же количеством 15-процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?

Задание 12 . Найдите точку максимума функции .

Задание 13 . а) Решите уравнение

б) Укажите корни этого уравнения, принадлежащие отрезку

Задание 14 . В правильной треугольной призме ABCA'B'C' стороны основания равны 6, а боковые ребра равны 4. Изобразите сечение, проходящее через вершины A, B и середину ребраA'C'. Найдите его площадь

Задание 15 . Решите неравенство: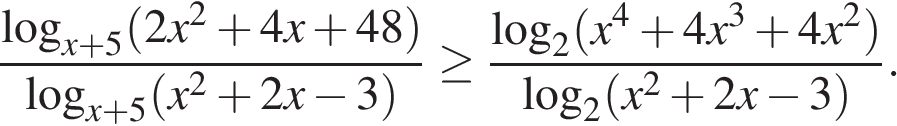

Задание 16 . Окружность радиуса вписана в прямой угол. Вторая окружность также вписана в этот угол и пересекается с первой в точках M и N. Известно, что расстояние между центрами окружностей равно 12. Найдите MN.

Задание 17 . Оля хочет взять в кредит 1 200 000 рублей. Погашение кредита происходит раз в год равными суммами (кроме, может быть, последней) после начисления процентов. Ставка процента 10 % годовых. На какое минимальное количество лет может Оля взять кредит, чтобы ежегодные выплаты были не более 320 000 рублей?

Задание 18 . Найдите все значения a, для каждого из которых существует хотя бы одна пара чисел x и y, удовлетворяющих неравенству

Задание 19 . Натуральные числа образуют возрастающую арифметическую прогрессию, причём все они больше 500 и являются квадратами натуральных чисел. Найдите наименьшее возможное, при указанных условиях, значение

Вариант № 4

Часть 1

Задание 1 . Флакон шампуня стоит 200 рублей. Какое наибольшее число флаконов можно купить на 1000 рублей во время распродажи, когда скидка составляет 15%?

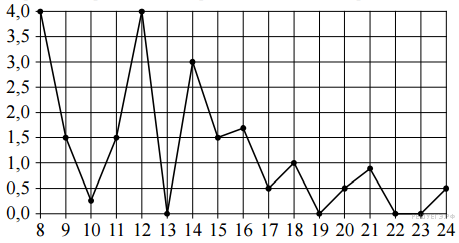
Задание 2 . На рисунке жирными точками показано суточное количество осадков, выпадавших в Томске с 8 по 24 января 2005 года. По горизонтали указываются числа месяца, по вертикали - количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, сколько дней выпадало более 2 миллиметров осадков.

Задание 3.Вектор с концом в точке B(5; 3) имеет координаты (3; 1). Найдите абсциссу точки A.

Задание 4 . Вероятность того, что на тесте по биологии учащийся О. верно решит больше 11 задач, равна 0,67. Вероятность того, что О. верно решит больше 10 задач, равна 0,74. Найдите вероятность того, что О. верно решит ровно 11 задач.

Задание 5 . Найдите корень уравнения: .

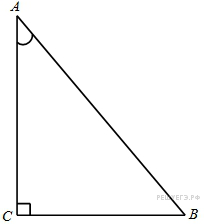
Задание 6. В треугольнике ABC угол C равен 90°, AC = 8, BC = 4. Найдите .

Задание 7 .

Материальная точка движется прямолинейно по закону (гдеx - расстояние от точки отсчета в метрах, t - время в секундах, измеренное с начала движения). Найдите ее скорость (в м/с) в момент времени t = 4 с.

Задание 8 . Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 4 и 16. Найдите ребро равновеликого ему куба.

Часть 2

Задание 9 . Найдите значение выражения

Задание 10 . При адиабатическом процессе для идеального газа выполняется законpV^k = const , где p - давление в газе в паскалях, V - объём газа в кубических метрах. В ходе эксперимента с одноатомным идеальным газом (для него k = ) из начального состояния, в котором const = 7,29·10⁷ Па·м⁵, газ начинают сжимать. Какой наибольший объём V может занимать газ при давленииp не ниже 3·10⁵ Па ? Ответ выразите в кубических метрах.

Задание 11 . Компания "Альфа" начала инвестировать средства в перспективную отрасль в 2001 году, имея капитал в размере 5000 долларов. Каждый год, начиная с 2002 года, она получала прибыль, которая составляла 200% от капитала предыдущего года. А компания «Бета» начала инвестировать средства в другую отрасль в 2003 году, имея капитал в размере 10000 долларов, и, начиная с 2004 года, ежегодно получала прибыль, составляющую 400% от капитала предыдущего года. На сколько долларов капитал одной из компаний был больше капитала другой к концу 2006 года, если прибыль из оборота не изымалась?

Задание 12 . Найдите наименьшее значение функции на отрезке .

Задание 13 а) Решите уравнение

б) Найдите все корни этого уравнения, принадлежащие отрезку

Задание 14. Длина ребра правильного тетраэдра ABCD равна 1. Найдите угол между прямыми DM и CL, где M - середина ребра BC, L - середина ребра AB.

Задание 15 . Решите неравенство:

Задание 16 . Угол C треугольника ABC равен 60°, D - отличная от A точка пересечения окружностей, построенных на сторонах AB и AC как на диаметрах. Известно, что ВD : DC = 1 : 3. Найдите синус угла A.

Задание 17 . Алексей приобрёл ценную бумагу за 8 тыс. рублей. Цена бумаги каждый год возрастает на 1 тыс. рублей. В любой момент Алексей может продать бумагу и положить вырученные деньги на банковский счёт. Каждый год сумма на счёте будет увеличиваться на 8%. В течение какого года после покупки Алексей должен продать ценную бумагу, чтобы через двадцать пять лет после покупки этой бумаги сумма на банковском счёте была наибольшей?

Задание 18 . Найдите все значения параметра при каждом из которых уравнение

имеет единственное решение. Найдите это решение для каждого значения a.

Задание 19 . Известно, что a, b, c, и d - попарно различные положительные двузначные числа.

а) Может ли выполняться равенство

б) Может ли дробь быть в 11 раз меньше, чем сумма

в) Какое наименьшее значение может принимать дробь если и

Вариант № 5

Часть 1

Задание 1 . Шоколадка стоит 35 рублей. В воскресенье в супермаркете действует специальное предложение: заплатив за две шоколадки, покупатель получает три (одну в подарок). Сколько шоколадок можно получить на 200 рублей в воскресенье?

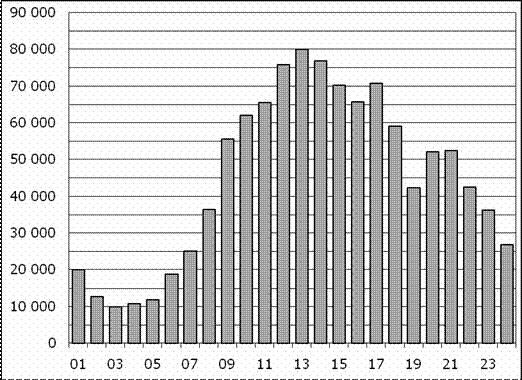
Задание 2 .На диаграмме показано количество посетителей сайта РИА Новости в течение каждого часа 8 декабря 2009 года. По горизонтали указывается номер часа, по вертикали - количество посетителей сайта за данный час. Определите по диаграмме, каким было наибольшее количество посетителей в час с 1:00 до 7:00 в данный день на сайте РИАН.

Задание 3 . 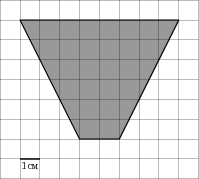На клетчатой бумаге с клетками размером 1 см 1 см изображена трапеция (см. рисунок). Найдите ее площадь в квадратных сантиметрах.

Задание 4 . Биатлонист пять раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,8. Найдите вероятность того, что биатлонист первые три раза попал в мишени, а последние два промахнулся. Результат округлите до сотых.

Задание 5 . Найдите корень уравнения: Если уравнение имеет более одного корня, укажите меньший из них.

Задание 6 . Точки A, B, C, расположенные на окружности, делят ее на три дуги, градусные величины которых относятся как 1 : 6 : 11. Найдите больший угол треугольника ABC. Ответ дайте в градусах.

Задание 7 . На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите , где - одна из первообразных функции

Задание 8 . В прямоугольном параллелепипеде известно, что , , Найдите длину диагонали

Часть 2

Задание 9 . Найдите значение выражения .

Задание 10 . Расстояние от наблюдателя, находящегося на небольшой высоте километров над землeй, до наблюдаемой им линии горизонта вычисляется по формуле , где (км) - радиус Земли. С какой высоты горизонт виден на расстоянии 28 километров? Ответ выразите в километрах.

Задание 11 . Первая труба пропускает на 1 литр воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если резервуар объемом 110 литров она заполняет на 2 минуты дольше, чем вторая труба заполняет резервуар объемом 99 литров?

Задание 12 . Найдите точку максимума функции .

Задание 13 . а) Решите уравнение

б) Укажите корни этого уравнения, принадлежащие отрезку

Задание 14 . Основание прямой четырехугольной призмы - прямоугольник в котором Найдите угол между плоскостью основания призмы и плоскостью, проходящей через середину ребра перпендикулярно прямой если расстояние между прямыми и равно

Задание 15 . Решите неравенство:

Задание 16 . Окружности радиусов 2 и 3 с центрами O₁ и O₂ соответственно касаются в точке A. Прямая, проходящая через точку A, вторично пересекает меньшую окружность в точке B, а большую - в точке C. Найдите площадь треугольника BCO₂ , если ∠ABO₁ = 30°.

Задание 17 . 31 декабря 2013 года Сергей взял в банке 9 930 000 рублей в кредит под 10% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Сергей переводит в банк определённую сумму ежегодного платежа. Какой должна быть сумма ежегодного платежа, чтобы Сергей выплатил долг тремя равными ежегодными платежами?

Задание 18 . Найдите все значения a, для каждого из которых существует хотя бы одна пара чисел x и y, удовлетворяющих неравенству

Задание 19 . Имеется 8 карточек. На них записывают по одному каждое из чисел:

−11, 12, 13, −14, −15, 17, −18, 19.

Карточки переворачивают и перемешивают. На их чистых сторонах заново пишут по одному из чисел:

−11, 12, 13, −14, −15, 17, −18, 19.

После этого числа на каждой карточке складывают, а полученные восемь сумм перемножают.

а) Может ли в результате получиться 0?

б) Может ли в результате получиться 117?

в) Какое наименьшее целое неотрицательное число может в результате получиться

Вариант № 6

Часть 1

Задание 1. Система навигации, встроенная в спинку самолетного кресла, информирует пассажира о том, что полет проходит на высоте 21 910 футов. Выразите высоту полета в метрах. Считайте, что 1 фут равен 30,5 см.

Задание 2 .

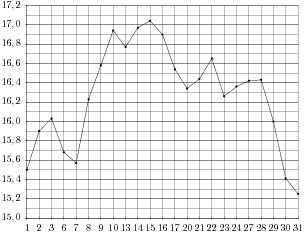
На рисунке жирными точками показана цена серебра, установленная Центробанком РФ во все рабочие дни в октябре 2009 года. По горизонтали указываются числа месяца, по вертикали - цена серебра в рублях за грамм. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку наименьшую цену серебра в период с 1 по 17 октября. Ответ дайте в рублях.

Задание 3 .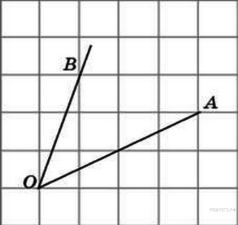

Найдите тангенс угла AOB.

Задание 4 . Какова вероятность того, что случайно выбранное натуральное число от 10 до 19 делится на три?

Задание 5 . Решите уравнение .

Задание 6 . 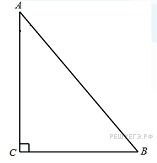В треугольнике ABC угол C равен 90°, АВ = 8. Найдите ВС.

Задание 7 . На рисунке изображён график функции и одной из первообразных некоторой функции , определённой на интервале Пользуясь рисунком, определите количество решений уравнения на отрезке

Задание 8 . Площадь осевого сечения цилиндра равна 7. Найдите площадь боковой поверхности цилиндра, деленную на .

Часть 2

Задание 9 . Найдите значение выражения .

Задание 10 . Некоторая компания продает свою продукцию по цене руб. за единицу, переменные затраты на производство одной единицы продукции составляют руб., постоянные расходы предприятия руб. месяц. Месячная операционная прибыль предприятия (в рублях) вычисляется по формуле . Определите наименьший месячный объeм производства (единиц продукции), при котором месячная операционная прибыль предприятия будет не меньше 300000 руб.

Задание 11 . Смешав 11-процентный и 72-процентный растворы кислоты и добавив 10 кг чистой воды, получили 31-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 51-процентный раствор кислоты. Сколько килограммов 11-процентного раствора использовали для получения смеси?

Задание 12 . Найдите наибольшее значение функции .

Задание 13 . а) Решите уравнение

б) Найдите все корни этого уравнения, принадлежащие промежутку

Задание 14 . В правильной треугольной призме ABCA'B'C' стороны основания равны 6, а боковые ребра равны 4. Изобразите сечение, проходящее через вершины A, B и середину ребраA'C'. Найдите его площадь

Задание 15 . Решите неравенство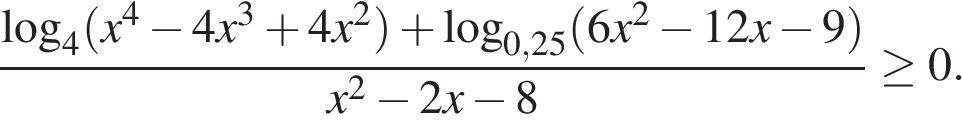

Задание 16 . Две окружности касаются внутренним образом в точке A, причём меньшая проходит через центр большей. Хорда BC большей окружности касается меньшей в точке P. Хорды AB и AC пересекают меньшую окружность в точках K и M соответственно.

а) Докажите, что прямые KM и BC параллельны.

б) Пусть L - точка пересечения отрезков KM и AP. Найдите AL, если радиус большей окружности равен 10, а BC = 12.

Задание 17 . Транcнациональная компания AmakoInc. решила провести недружественное поглощение компании FirstAluminumCompany (FAC) путем скупки акций миноритарных акционеров. Известно, что Amako было сделано три предложения владельцам акций FAC, при этом цена покупки одной акции каждый раз повышалась на 1/3. В результате второго предложения Amako сумела увеличить число выкупленных акций на 20%, а в результате скупки по третьей цене - еще на 20%. Найдите цену третьего предложения и общее количество скупленных акций FAC, если начальное предложение составляло $27 за одну акцию, а по второй цене Amako скупила 15 тысяч акций.

Задание 18 . При каждом значении а решите систему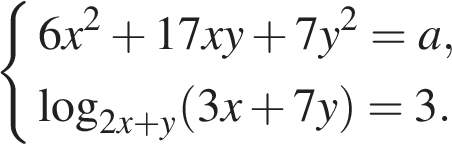

Задание 19 . На доске написано более 27, но менее 45 целых чисел. Среднее арифметическое этих чисел равно −5, среднее арифметическое всех положительных из них равно 9, а среднее арифметическое всех отрицательных из них равно −18.

а) Сколько чисел написано на доске?

б) Каких чисел написано больше: положительных или отрицательных?

в) Какое наибольшее количество положительных чисел может быть среди них?

Вариант № 7

Часть 1

Задание 1 .Студент получил свой первый гонорар в размере 900 рублей за выполненный перевод. Он решил на все полученные деньги купить букет лилий для своей учительницы английского языка. Какое наибольшее количество лилий сможет купить студент, если удержанный у него налог на доходы составляет 13% гонорара, лилии стоят 120 рублей за штуку и букет должен состоять из нечетного числа цветов?

Задание 2 . На диаграмме показан средний балл участников 10 стран в тестировании учащихся 4-го класса, по математике в 2007 году (по 1000-балльной шкале). По данным диаграммы найдите число стран, в которых средний балл ниже, чем в Нидерландах.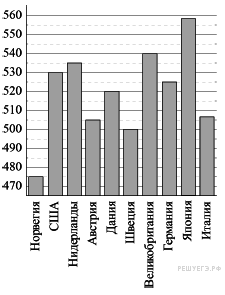

Задание 3 . 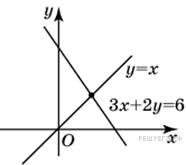Найдите абсциссу точки пересечения прямых, заданных уравнениями 3x + 2y = 6 и y = x.

Задание 4 . В чемпионате мира участвуют 15 команд. С помощью жребия их нужно разделить на пять групп по три команды в каждой. В ящике вперемешку лежат карточки с номерами групп:

1, 1, 1, 2, 2, 2, 3, 3, 3, 4, 4, 4, 5, 5, 5.

Капитаны команд тянут по одной карточке. Какова вероятность того, что команда России окажется в четвёртой группе?

Задание 5 .Решите уравнение . Если уравнение имеет более одного корня, в ответе укажите меньший из них.

Задание 6 . 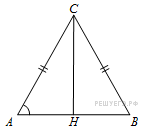В треугольнике ABC AC = BC, AB = 30, Найдите AC.

Задание 7 .

На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x₀. Найдите значение производной функции f(x) в точке

Задание 8 . 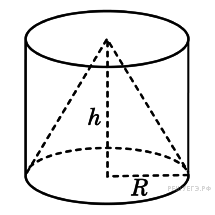Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 25.

Часть 2

Задание 9 . Найдите значение выражения 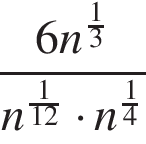при .

Задание 10 . При температуре рельс имеет длину м. При возрастании температуры происходит тепловое расширение рельса, и его длина, выраженная в метрах, меняется по закону , где - коэффициент теплового расширения, - температура (в градусах Цельсия). При какой температуре рельс удлинится на 7,5 мм? Ответ выразите в градусах Цельсия.

Задание 11 . В помощь садовому насосу, перекачивающему 9 литров воды за 1 минуту, подключили второй насос, перекачивающий тот же объем воды за 2 минуты. Сколько минут эти два насоса должны работать совместно, чтобы перекачать 54 литра воды?

Задание 12 . Найдите точку максимума функции .

Задание 13 . а) Решите уравнение

б) Найдите все корни этого уравнения, принадлежащие промежутку

Задание 14 . Ребро куба ABCDA₁B₁C₁D₁ равно 1. Найдите расстояние от вершины Bдо плоскости ACD₁.

Задание 15 . Решите неравенство:

Задание 16 . В остроугольном треугольнике ABC проведены высоты AP и CQ.

а) Докажите, что угол PAC равен углу PQC.

б) Найдите радиус окружности, описанной около треугольника ABC, если известно, что PQ=10 и

Задание 17 . 31 декабря 2014 года Алексей взял в банке 6 902 000 рублей в кредит под 12,5% годовых. Схема выплаты кредита следующая - 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 12,5%), затем Алексей переводит в банк X рублей. Какой должна быть сумма X, чтобы Алексей выплатил долг четырьмя равными платежами (то есть за четыре года)?

Задание 18 . Найдите все значения а, при каждом из которых уравнение имеет ровно три различных решения.

Задание 19 . Найдите все простые числа b, для каждого из которых существует такое целое число а, что дробь можно сократить на b.

Вариант № 8

Часть 1

Задание 1 .Летом килограмм клубники стоит 80 рублей. Мама купила 1 кг 200 г клубники. Сколько рублей сдачи она должна получить с 500 рублей?

Задание 2 . На рисунке жирными точками показано суточное количество осадков, выпадавших в Томске с 8 по 24 января 2005 года. По горизонтали указываются числа месяца, по вертикали - количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какое наибольшее количество осадков выпадало в период с 13 по 20 января. Ответ дайте в миллиметрах.

Задание 3 . 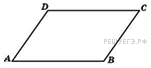Две стороны параллелограмма относятся как , а периметр его равен 40. Найдите большую сторону параллелограмма.

Задание 4 . Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 25 этих стекол, вторая - 75. Первая фабрика выпускает 4 бракованных стекол, а вторая - 2. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.

Задание 5 . Найдите корень уравнения .

Задание 6 . 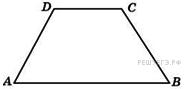В равнобедренной трапеции основания равны 12 и 27, острый угол равен . Найдите ее периметр.

Задание 7 . 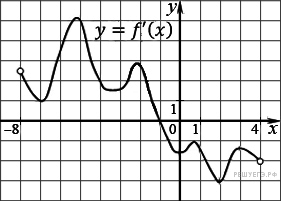На рисунке изображен график производной функции f(x), определенной на интервале (−8; 4). В какой точке отрезка [−7; −3] f(x) принимает наименьшее значение?

Задание 8 . 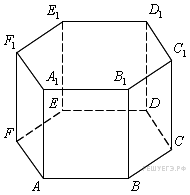Найдите объем многогранника, вершинами которого являются точки , , , , , , , правильной шестиугольной призмы , площадь основания которой равна 5, а боковое ребро равно 15.

Часть 2

Задание 9 .Найдите значение выражения .

Задание 10 .На верфи инженеры проектируют новый аппарат для погружения на небольшие глубины. Конструкция имеет форму сферы, а значит, действующая на аппарат выталкивающая (архимедова) сила, выражаемая в ньютонах, будет определяться по формуле: , где - постоянная, - радиус аппарата в метрах, - плотность воды, а - ускорение свободного падения (считайте Н/кг). Каков может быть максимальный радиус аппарата, чтобы выталкивающая сила при погружении была не больше, чем 2 491 398 Н? Ответ выразите в метрах.

Задание 11 . Два велосипедиста одновременно отправились в 240-километровый пробег. Первый ехал со скоростью, на 1 км/ч большей, чем скорость второго, и прибыл к финишу на 1 час раньше второго. Найти скорость велосипедиста, пришедшего к финишу первым. Ответ дайте в км/ч.

Задание 12 . Найдите наименьшее значение функции на отрезке .

Задание 13 . Решите уравнение:

Задание 14 . Дана правильная треугольная пирамида DABC с вершиной D. Сторона основания пирамиды равна , высота равна . Найдите расстояние от середины бокового ребраBD до прямой МТ, где точки М и Т - середины ребер АС и AВ соответственно.

Задание 15 . Решите неравенство

Задание 16 . В прямоугольнике ABCD со сторонами AB = 4 и BC = 10 на стороне ADрасположены точки M и N таким образом, что DM = 4, при этом P - точка пересечения прямых BN иCM. Площадь треугольника MNP равна 1. Найдите длину отрезка, соединяющего точки M и N.

Задание 17 . В январе 2000 года ставка по депозитам в банке «Возрождение» составила х % годовых, тогда как в январе 2001 года - у % годовых, причем известно, что x + y = 30%. В январе 2000 года вкладчик открыл счет в банке «Возрождение», положив на него некоторую сумму. В январе 2001 года, попрошествии года с того момента, вкладчик снял со счета пятую часть этой суммы. Укажите значение х при котором сумма на счету вкладчика в январе 2002 года станет максимально возможной.

Задание 18 . Найдите все значения a, при каждом из которых функция имеет более двух точек экстремума.

Задание 19 . Найдите все пары натуральных чисел m и k, являющиеся решениями уравнения 9^k − 2^m = 1.

Вариант № 9

Часть 1

Задание 1 . Шоколадка стоит 40 рублей. В воскресенье в супермаркете действует специальное предложение: заплатив за две шоколадки, покупатель получает три (одну в подарок). Сколько шоколадок можно получить на 320 рублей в воскресенье?

Задание 2 .На диаграмме показано количество посетителей сайта РИА Новости в течение каждого часа 8 декабря 2009 года. По горизонтали указывается номер часа, по вертикали - количество посетителей сайта за данный час. Определите по диаграмме, каким было наибольшее количество посетителей в час с 1:00 до 7:00 в данный день на сайте РИАН.

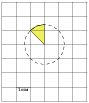
Задание 3 . 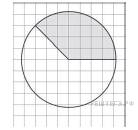Площадь закрашенного сектора, изображённого на клетчатой бумаге (см. рис.), равна 6. Найдите площадь круга.

Задание 4 . За круглый стол на 9 стульев в случайном порядке рассаживаются 7 мальчиков и 2 девочки. Найдите вероятность того, что обе девочки будут сидеть рядом.

Задание 5 .Найдите корень уравнения .

Задание 6 . 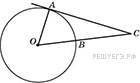Угол ACO равен 39°. Его сторона CA касается окружности. Найдите градусную величину большей дуги AD окружности, заключенной внутри этого угла. Ответ дайте в градусах.

Задание 7 . На рисунке изображён график функции - одной из первообразных некоторой функции , определённой на интервале . Пользуясь рисунком, определите количество решений уравнения на отрезке

Задание 8 . 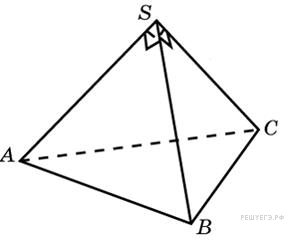Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из них равно 27. Найдите объем пирамиды.

Часть 2

Задание 9 . Найдите , если и .

Задание 10 .Перед отправкой тепловоз издал гудок с частотой Гц. Чуть позже издал гудок подъезжающий к платформе тепловоз. Из-за эффекта Доплера частота второго гудка больше первого: она зависит от скорости тепловоза по закону 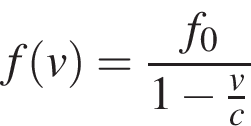(Гц), где - скорость звука в звука (в м/с). Человек, стоящий на платформе, различает сигналы по тону, если они отличаются не менее, чем на 7 Гц. Определите, с какой минимальной скоростью приближался к платформе тепловоз, если человек смог различить сигналы, а м/с. Ответ выразите в м/с.

Задание 11 . Первый сплав содержит 5% меди, второй - 12% меди. Масса второго сплава больше массы первого на 9 кг. Из этих двух сплавов получили третий сплав, содержащий 10% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.

Задание 12 . Найдите точку максимума функции .

Задание 13 . а) Решите уравнение

б) Найдите все корни этого уравнения, принадлежащие промежутку

Задание 14 . В правильной треугольной пирамиде с основанием известны рёбра: Найдите угол, образованный плоскостью основания и прямой, проходящей через середины рёбер и

Задание 15 . Решите уравнение

Задание 16 . Медианы AA₁, BB₁ и CC₁ треугольника ABC пересекаются в точке M. Точки A₂, B₂ и C₂ - середины отрезков MA, MB и MC соответственно.

а) Докажите, что площадь шестиугольника A₁B₂C₁A₂B₁C₂ вдвое меньше площади треугольникаABC.

б) Найдите сумму квадратов всех сторон этого шестиугольника, если известно, что AB = 4, BC = 7 и AC = 8.

Задание 17 . Алексей приобрёл ценную бумагу за 7 тыс. рублей. Цена бумаги каждый год возрастает на 2 тыс. рублей. В любой момент Алексей может продать бумагу и положить вырученные деньги на банковский счёт. Каждый год сумма на счёте будет увеличиваться на 10 %. В течение какого года после покупки Алексей должен продать ценную бумагу, чтобы через тридцать лет после покупки этой бумаги сумма на банковском счёте была наибольшей?

Задание 18 . Найдите все значения параметра a, при каждом из которых система

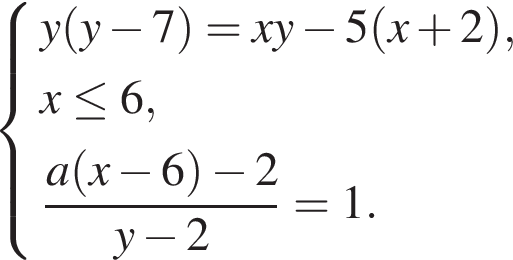
имеет единственное решение.

Задание 19 . Красный карандаш стоит 18 рублей, синий - 14 рублей. Нужно купить карандаши, имея всего 499 рублей и соблюдая дополнительное условие: число синих карандашей не должно отличаться от числа красных карандашей больше чем на шесть.

а) Можно ли купить 30 карандашей?

б) Можно ли купить 33 карандаша?

в) Какое наибольшее число карандашей можно купить?

Вариант № 10

Часть 1

Задание 1 . Розничная цена учебника 180 рублей, она на 20% выше оптовой цены. Какое наибольшее число таких учебников можно купить по оптовой цене на 10 000 рублей?

Задание 2 . На рисунке жирными точками показана среднесуточная температура воздуха в Пскове каждый день с 15 по 28 марта 1959 года. По горизонтали указываются числа месяца, по вертикали - температура в градусах Цельсия. Для наглядности жирные точки соединены линией. Определите по рисунку, сколько дней из данного периода среднесуточная температура была от 2 до 7 градусов Цельсия.

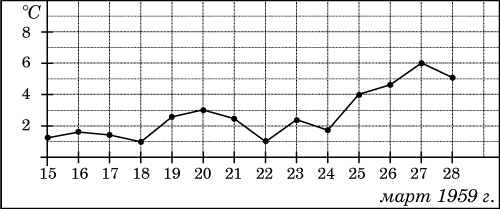
Определите по рисунку, сколько дней из данного периода выпадало от 2 до 8 мм осадков.

Задание 3 . Найдите (в см²) площадь S закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки

1 см 1 см (см. рис.). В ответе запишите .

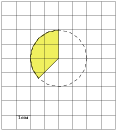
Задание 4 . Агрофирма закупает куриные яйца в двух домашних хозяйствах. 40% яиц из первого хозяйства - яйца высшей категории, а из второго хозяйства - 20% яиц высшей категории. Всего высшую категорию получает 35% яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.

Задание 5 . Решите уравнение

Задание 6 . В треугольнике ABC AC = BC, AB = 30, Найдите AC.

Задание 7 . На рисунке изображён график производной функции и восемь точек на оси абсцисс: ,. В скольких из этих точек функция убывает?

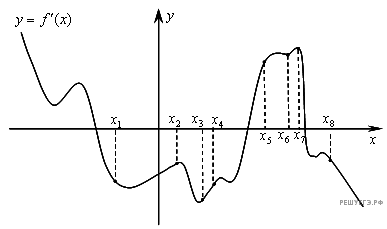
Задание 8 . 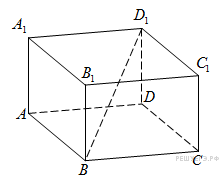В прямоугольном параллелепипеде известно, что Найдите длину ребра .

Часть 2

Задание 9 . Найдите , если и .

Задание 10 . Небольшой мячик бросают под острым углом к плоской горизонтальной поверхности земли. Расстояние, которое пролетает мячик, вычисляется по формул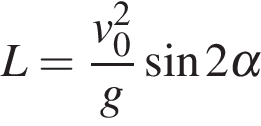е (м), где м/с - начальная скорость мячика, а - ускорение свободного падения (считайте м/с). При каком наименьшем значении угла (в градусах) мячик перелетит реку шириной 20 м?

Задание 11 . Имеется два сплава. Первый сплав содержит 10% никеля, второй - 35% никеля. Из этих двух сплавов получили третий сплав массой 250 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава меньше массы второго?

Задание 12 . Найдите точку минимума функции .

Задание 13 . Решите уравнение .

Задание 14 . Все рёбра правильной треугольной пирамиды SBCD с вершиной Sравны 9.

Основание O высоты SO этой пирамиды является серединой отрезка SS₁, M - середина ребра SB, точка L лежит на ребре CD так, что CL : LD = 7 : 2.

а) Докажите, что сечение пирамиды SBCD плоскостью S₁LM - равнобокая трапеция.

б) Вычислите длину средней линии этой трапеции.

Задание 15 . Решите неравенство:

Задание 16 . Вневписанной окружностью треугольника называется окружность, касающаяся одной стороны треугольника и продолжений двух других его сторон. Радиусы двух вневписанных окружностей прямоугольного треугольника равны 7 и 17. Найдите расстояние между их центрами.

Задание 17 . В конце августа 2001 года администрация Приморского края располагала некой суммой денег, которую предполагалось направить на пополнение нефтяных запасов края. Надеясь на изменение конъюнктуры рынка, руководство края, отсрочив закупку нефти, положила эту сумму 1 сентября 2001 года в банк. Далее известно, что сумма вклада в банке увеличивалась первого числа каждого месяца на 26% по отношению к сумме на первое число предыдущего месяца, а цена барреля сырой нефти убывала на 10% ежемесячно. На сколько процентов больше (от первоначального объема закупок) руководство края смогло пополнить нефтяные запасы края, сняв 1 ноября 2001 года всю сумму, полученную из банка вместе с процентами, и направив ее на закупку нефти?

Задание 18 . Найдите все значения параметра , при каждом из которых наименьшее значение функции больше

Задание 19 . Каждый из группы учащихся сходил в кино или в театр, при этом возможно, что кто-то из них мог сходить и в кино, и в театр. Известно, что в театре мальчиков было не более от общего числа учащихся группы, посетивших театр, а в кино мальчиков было не более от общего числа учащихся группы, посетивших кино.

а) Могло ли быть в группе 10 мальчиков, если дополнительно известно, что всего в группе было 20 учащихся?

б) Какое наибольшее количество мальчиков могло быть в группе, если дополнительно известно, что всего в группе было 20 учащихся?

в) Какую наименьшую долю могли составлять девочки от общего числа учащихся в группе без дополнительного условия пунктов а) и б)?

Вариант № 11

Часть 1

Задание 1 .В доме, в котором живет Гриша, один подъезд. На каждом этаже находится по 10 квартир. Гриша живет в квартире № 46. На каком этаже живет Гриша?

Задание 2 . На рисунке жирными точками показано суточное количество осадков, выпадавших в Томске с 8 по 24 января 2005 года. По горизонтали указываются числа месяца, по вертикали - количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, сколько дней выпадало более 2 миллиметров осадков.

Задание 3 . Найдите (в см²) площадь S закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки

1 см 1 см (см. рис.). В ответе запишите .

Задание 4 . В кармане у Пети было 2 монеты по 5 рублей и 4 монеты по 10 рублей. Петя, не глядя, переложил какие-то 3 монеты в другой карман. Найдите вероятность того, что пятирублевые монеты лежат теперь в разных карманах.

Задание 5 . Решите уравнение . В ответе напишите наименьший положительный корень.

Задание 6 .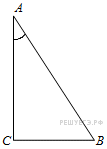В треугольнике ABC угол C равен 90°, , . Найдите AB.

Задание 7 . На рисунке изображён график функции y = f(x) и восемь точек на оси абсцисс: x₁, x₂, x₃, …, x₈. В скольких из этих точек производная функции f(x) положительна?

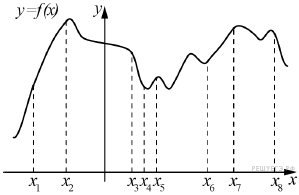
Задание 8 . От треугольной призмы, объем которой равен 150, отсечена треугольная пирамида плоскостью, проходящей через сторону одного основания и противоположную вершину другого основания. Найдите объем оставшейся части.

Часть 2

Задание 9 .Найдите значение выражения

Задание 10 . Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковые импульсы частотой 749 МГц. Скорость спуска батискафа, выражаемая в м/с, определяется по формуле , где м/с - скорость звука в воде, - частота испускаемых импульсов (в МГц), - частота отражeнного от дна сигнала, регистрируемая приeмником (в МГц). Определите наибольшую возможную частоту отраженного сигнала , если скорость погружения батискафа не должна превышать 2 м/с.

Задание 11 . Смешали некоторое количество 11-процентного раствора некоторого вещества с таким же количеством 17-процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?

Задание 12 . Найдите наименьшее значение функции на отрезке .

Задание 13 . Решите уравнение

Задание 14 . В правильной четырёхугольной призме стороны основания равны а боковые ребра равны На ребре отмечена точка так, что Найдите угол между плоскостями и

Задание 15 . Решите неравенство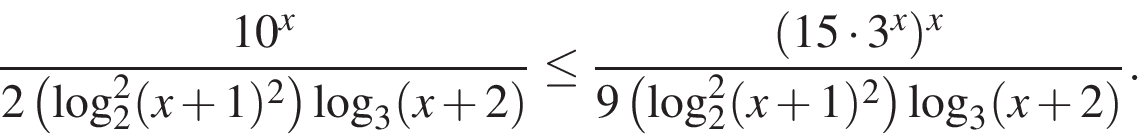

Задание 16 . Медианы AA₁, BB₁ и CC₁ треугольника ABC пересекаются в точке M. Известно, что AC = 3MB.

а) Докажите, что треугольник ABC прямоугольный.

б) Найдите сумму квадратов медиан AA₁ и CC₁, если известно, что AC = 12.

Задание 17 . Известно, что вклад, находящийся в банке с начала года, возрастает к концу года на определенный процент, свой для каждого банка. В начале года Степан положил 60% некоторой суммы денег в первый банк, а оставшуюся часть суммы во второй банк. К концу года сумма этих вкладов стала равна 590 000 руб., а к концу следующего года 701 000 руб. Если бы Степан первоначально положил 60% своей суммы во второй банк, а оставшуюся часть в первый, то по истечении одного года сумма вкладов стала бы равной 610 000 руб. Какова была бы сумма вкладов в этом случае к концу второго года?

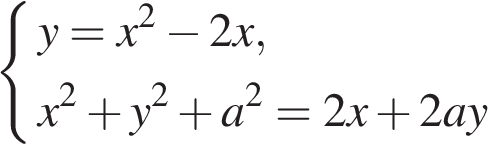Задание 18 . При каких значениях параметра система имеет решения?

Задание 19 . Пусть q - наименьшее общее кратное, а d - наибольший общий делитель натуральных чисел x и y, удовлетворяющих неравенству 3x = 8y − 29.

а) Может ли быть равным 170?

б) Может ли быть равным 2?

в) Найдите наименьшее значение .

Вариант № 12

Часть 1

Задание 1 . Цена на электрический чайник была повышена на 16% и составила 3480 рублей. Сколько рублей стоил чайник до повышения цены?

Задание 2 . На рисунке жирными точками показано суточное количество осадков, выпадавших в Мурманске с 7 по 22 ноября 1995 года. По горизонтали указываются числа месяца, по вертикали - количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, сколько дней из данного периода выпадало менее 3 миллиметров осадков.

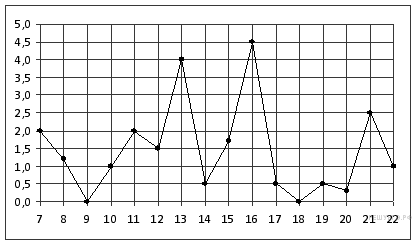
Задание 3 . 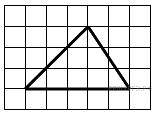На клетчатой бумаге с размером клетки 1 × 1 изображен треугольник. Найдите его площадь.

Задание 4 . На экзамене 40 вопросов, Коля не выучил 4 из них. Найдите вероятность того, что ему попадется выученный вопрос.

Задание 5 . Найдите корень уравнения

Задание 6 . 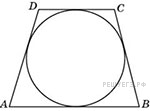Найдите высоту трапеции, в которую вписана окружность радиуса 47.

Задание 7 .Прямая параллельна касательной к графику функции . Найдите абсциссу точки касания.

Задание 8 . 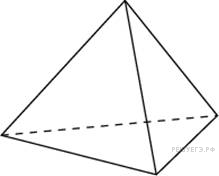Во сколько раз увеличится объем правильного тетраэдра, если все его ребра увеличить в два раза?

Часть 2

Задание 9 .Найдите значение выражения 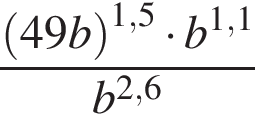при .

Задание 10 . Плоский замкнутый контур площадью м находится в магнитном поле, индукция которого равномерно возрастает. При этом согласно закону электромагнитной индукции Фарадея в контуре появляется ЭДС индукции, значение которой, выраженное в вольтах, определяется формулой , где - острый угол между направлением магнитного поля и перпендикуляром к контуру, Тл/с - постоянная, - площадь замкнутого контура, находящегося в магнитном поле (в м). При каком минимальном угле (в градусах) ЭДС индукции не будет превышать В?

Задание 11 . Первая труба пропускает на 1 литр воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает вторая труба, если резервуар объемом 930 литров она заполняет на 1 минуту быстрее, чем первая труба?

Задание 12 . Найдите точку минимума функции .

Задание 13 . а) Решите уравнение

б) Укажите корни этого уравнения, принадлежащие отрезку

Задание 14 . В кубе ABCDA₁B₁C₁D₁ все ребра равны 1. Найдите расстояние от точкиC до прямой AD₁

Задание 15 . Решите неравенство:

Задание 16 . Точка О - центр окружности, вписанной в треугольник ABC. На продолжении отрезка AO за точку О отмечена точка K так, что BK = OK.

а) Докажите, что четырехугольник ABKC вписанный.

б) Найдите длину отрезка AO, если известно, что радиусы вписанной и описанной окружностей треугольника ABC равны 3 и 12 соответственно, а OK = 5.

Задание 17 . Консервный завод выпускает фруктовые компоты в двух видах тары - стеклянной и жестяной. Производственные мощности завода позволяют выпускать в день 90 центнеров компотов в стеклянной таре или 80 центнеров в жестяной таре. Для выполнения условий ассортиментности, которые предъявляются торговыми сетями, продукции в каждом из видов тары должно быть выпущено не менее 20 центнеров. В таблице приведены себестоимость и отпускная цена завода за 1 центнер продукции для обоих видов тары.

Вид тары

Себестоимость,

1 ц.

Отпускная цена,

1 ц.

стеклянная

1500 руб.

2100 руб.

жестяная

1100 руб.

1750 руб.

Предполагая, что вся продукция завода находит спрос (реализуется без остатка), найдите максимально возможную прибыль завода за один день (прибылью называется разница между отпускной стоимостью всей продукции и её себестоимостью).

Задание 18 . Найдите все значения а, при каждом из которых уравнение имеет ровно три различных решения.

Задание 19 . Длины сторон прямоугольника ― натуральные числа, а его периметр равен 4000. Известно, что длина одной стороны прямоугольника равна n% от длины другой стороны, где n ― также натуральное число.

а) Какое наибольшее значение может принимать площадь прямоугольника?

б) Какое наименьшее значение может принимать площадь прямоугольника?

в) Найдите все возможные значения, которые может принимать площадь прямоугольника, если дополнительно известно, что n <100.

Вариант № 13

Часть 1

Задание 1 .1 киловатт-час электроэнергии стоит 1 рубль 10 копеек. Счетчик электроэнергии 1 ноября показывал 7061 киловатт-час, а 1 декабря показывал 7249 киловатт-часов. Сколько рублей нужно заплатить за электроэнергию за ноябрь?

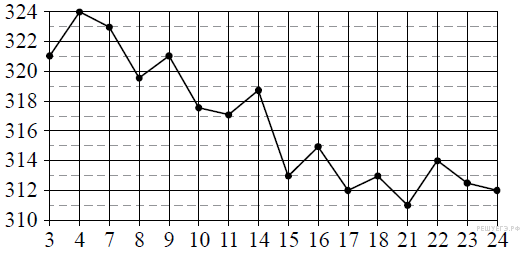
Задание 2 . На рисунке жирными точками показана цена золота на момент закрытия биржевых торгов во все рабочие дни с 3 по 24 марта 2002 года. По горизонтали указываются числа месяца, по вертикали - цена унции золота в долларах США. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку наибольшую цену золота на момент закрытия торгов в период с 8 по 21 марта (в долларах США за унцию).

Задание 3 . Найдите сумму координат вектора .

Задание 4 .Вероятность того, что новый ноутбук в течение года поступит в гарантийный ремонт, равна 0,091. В некотором городе из 1000 проданных ноутбуков в течение года в гарантийную мастерскую поступило 96 штук. На сколько отличается частота события «гарантийный ремонт» от его вероятности в этом городе?

Задание 5 . Решите уравнение . В ответе напишите наибольший отрицательный корень.

Задание 6 . Чему равен вписанный угол, опирающийся на диаметр окружности? Ответ дайте в градусах.

Задание 7 . 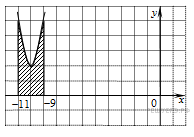На рисунке изображён график функцииy = f(x). Функция - одна из первообразных функции y = f(x). Найдите площадь закрашенной фигуры.

Задание 8 . В правильной четырехугольной пирамиде высота равна 3, боковое ребро равно 5. Найдите ее объем.

Часть 2

Задание 9 .Найдите значение выражения .

Задание 10 .Опорные башмаки шагающего экскаватора, имеющего массу тонн представляют собой две пустотелые балки длиной метров и шириной метров каждая. Давление экскаватора на почву, выражаемое в килопаскалях, определяется формулой , где - масса экскаватора (в тоннах), - длина балок в метрах, - ширина балок в метрах, - ускорение свободного падения (считайте м/с). Определите наименьшую возможную ширину опорных балок, если известно, что давление не должно превышать 250 кПа. Ответ выразите в метрах.

Задание 11 . Теплоход проходит по течению реки до пункта назначения 247 км и после стоянки возвращается в пункт отправления. Найдите скорость течения, если скорость теплохода в неподвижной воде равна 16 км/ч, стоянка длится 7 часов, а в пункт отправления теплоход возвращается через 39 часов после отплытия из него. Ответ дайте в км/ч.

Задание 12 . Найдите наименьшее значение функции на отрезке .

Задание 13 . а) Решите уравнение

б) Найдите все корни этого уравнения, принадлежащие промежутку

Задание 14 . В правильной четырёхугольной пирамиде SABCD с основанием ABCDпроведено сечение через середины ребер АВ и ВС и вершину S. Найдите площадь этого сечения, если все ребра

пирамиды равны 4.

Задание 15 . Решите неравенство:

Задание 16 . Радиус окружности, описанной около треугольника , равен 5, высота, проведённая к стороне равна 2. Найдите длину той хорды описанной окружности, которая делится пополам стороной

Задание 17 . В 1-е классы поступает 43 человека: 23 мальчика и 20 девочек. Их распределили по двум классам: в одном должно получиться 22 человека, а в другом ― 21. После распределения посчитали процент мальчиков в каждом классе и полученные числа сложили. Каким должно быть распределение по классам, чтобы полученная сумма была наибольшей?

Задание 18 . Найдите все значения a, для каждого из которых существует хотя бы одна пара чисел x и y, удовлетворяющих неравенству

Задание 19 . Имеется 8 карточек. На них записывают по одному каждое из чисел 1, -2, -3, 4, -5, 7, -8, 9. Карточки переворачивают и перемешивают. На их чистых сторонах заново пишут по одному каждое из чисел 1, -2, -3, 4, -5, 7, -8, 9. После этого числа на каждой карточке складывают, а полученные восемь сумм перемножают.

а) Может ли в результате получиться 0?

б) Может ли в результате получиться 1?

в) Какое наименьшее целое неотрицательное число может в результате получиться?

Вариант № 14

Часть 1

Задание 1 . Клиент взял в банке кредит 12 000 рублей на год под 16%. Он должен погашать кредит, внося в банк ежемесячно одинаковую сумму денег, с тем чтобы через год выплатить всю сумму, взятую в кредит, вместе с процентами. Сколько рублей он должен вносить в банк ежемесячно?

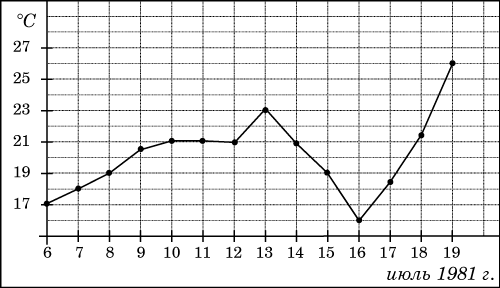
Задание 2 . На рисунке жирными точками показана среднесуточная температура воздуха в Бресте каждый день с 6 по 19 июля 1981 года. По горизонтали указываются числа месяца, по вертикали - температура в градусах Цельсия. Для наглядности жирные точки соединены линией. Определите по рисунку, какого числа среднесуточная температура была наименьшей за указанный период.

Задание 3 . 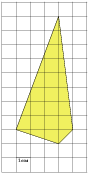Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

Задание 4 .Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали ходить. Найдите вероятность того, что часовая стрелка застыла, достигнув отметки 10, но не дойдя до отметки 4 часа.

Задание 5 . Решите уравнение . Если уравнение имеет более одного корня, в ответе запишите больший из корней.

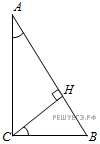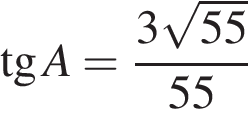Задание 6 . В треугольнике ABC угол C равен 90°, , . Найдите высоту CH.

Задание 7 . На рисунке изображён график функции и одной из первообразных некоторой функции , определённой на интервале Пользуясь рисунком, определите количество решений уравнения на отрезке

Задание 8 . 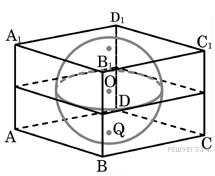В куб вписан шар радиуса 7. Найдите объем куба.

Часть 2

Задание 9 . Найдите значение выражения

Задание 10.Груз массой 0,25 кг колеблется на пружине со скоростью, меняющейся по закону , где - время в секундах. Кинетическая энергия груза вычисляется по формуле , где - масса груза (в кг), - скорость груза (в м/с). Определите, какую долю времени из первой секунды после начала движения кинетическая энергия груза будет не менее Дж. Ответ выразите десятичной дробью, если нужно, округлите до сотых.

Задание 11 . Первая труба пропускает на 5 литров воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает вторая труба, если резервуар объемом 375 литров она заполняет на 10 минут быстрее, чем первая труба заполняет резервуар объемом 500 литров?

Задание 12 . Найдите точку минимума функции .

Задание 13 . а) Решите уравнение

б) Найдите все корни этого уравнения, принадлежащие отрезку

Задание 14 . Сторона правильной треугольной призмы ABCA₁B₁C₁ равна 8. Высота этой призмы равна 6. Найти угол между прямыми CA₁ и AB₁.

Задание 15 . Решите неравенство:

Задание 16 . На прямой, содержащей медиану AD прямоугольного треугольника ABCс прямым углом C, взята точка E, удаленная от вершины A на расстояние, равное 4. Найдите площадь треугольника BCE, если BC = 6, AC = 4.

Задание 17 . 31 декабря 2013 года Сергей взял в банке 9 930 000 рублей в кредит под 10% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Сергей переводит в банк определённую сумму ежегодного платежа. Какой должна быть сумма ежегодного платежа, чтобы Сергей выплатил долг тремя равными ежегодными платежами?

Задание 18 . Найдите все значения при каждом из которых уравнение имеет хотя бы один корень.

Задание 19 . На доске написано более 40, но менее 48 целых чисел. Среднее арифметическое этих чисел равно −3, среднее арифметическое всех положительных из них равно 4, а среднее арифметическое всех отрицательных из них равно −8.

а) Сколько чисел написано на доске?

б) Каких чисел написано больше: положительных или отрицательных?

в) Какое наибольшее количество положительных чисел может быть среди них?

Вариант № 15

Часть 1

Задание 1 . В школе 800 учеников, из них 30% - ученики начальной школы. Среди учеников средней и старшей школы 20% изучают немецкий язык. Сколько учеников в школе изучают немецкий язык, если в начальной школе немецкий язык не изучается?

Задание 2 . На рисунке жирными точками показан курс доллара, установленный Центробанком РФ, во все рабочие дни в октябре 2010 года. По горизонтали указываются числа месяца, по вертикали - цена доллара в рублях. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку наибольший курс доллара за указанный период. Ответ дайте в рублях.

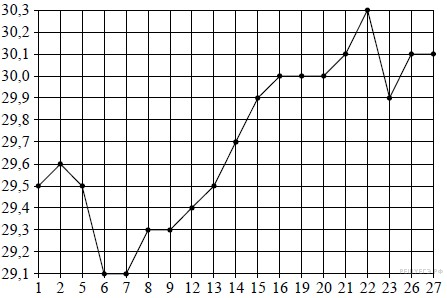
Задание 3 . Найдите площадь параллелограмма, изображенного на рисунке.

Задание 4 . Вероятность того, что на тесте по истории учащийся Т. верно решит больше 8 задач, равна 0,76. Вероятность того, что Т. верно решит больше 7 задач, равна 0,88. Найдите вероятность того, что Т. верно решит ровно 8 задач.

Задание 5 .Найдите корень уравнения:

Задание 6 .Через концы A, B дуги окружности в проведены касательные AC и BC. Найдите угол ACB. Ответ дайте в градусах.

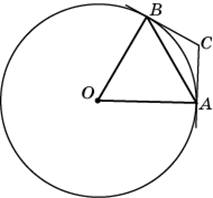
Задание 7 . На рисунке изображен график функции y = f(x), определенной на интервале (−5; 7). Найдите сумму точек экстремума функции y = f(x).

Задание 8 . В правильной шестиугольной призме все ребра равны 40. Найдите расстояние между точками и .

Часть 2

Задание 9 .Найдите значение выражения .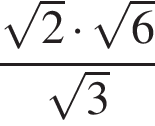

Задание 10 . Зависимость температуры (в градусах Кельвина) от времени для нагревательного элемента некоторого прибора была получена экспериментально. На исследуемом интервале температура вычисляется по формуле T(t) = T₀ + bt + at² , где t - время в минутах, T₀ = 1380 К, а = −15 К/мин², b= 165 К/мин. Известно, что при температуре нагревателя свыше 1800 К прибор может испортиться, поэтому его нужно отключить. Определите, через какое наибольшее время после начала работы нужно отключить прибор. Ответ выразите в минутах.

Задание 11 .Два пешехода отправляются одновременно в одном направлении из одного и того же места на прогулку по аллее парка. Скорость первого на 0,5 км/ч больше скорости второго. Через сколько минут расстояние между пешеходами станет равным 25 метрам?

Задание 12 . Найдите точку максимума функции .

Задание 13 . а) Решите уравнение

б) Найдите все корни этого уравнения, принадлежащие промежутку

Задание 14 . В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁, у которого AB = 4,BC = 6, CC₁ = 4, найдите тангенс угла между плоскостью ABC и прямой EF, проходящей через середины ребер AA₁ и С₁D₁.

Задание 15 . Решите неравенство

Задание 16 . В треугольнике Точка D лежит на прямой BC причем . Окружности, вписанные в каждый из треугольников ADC иADB касаются стороны AD в точках E и F. Найдите длину отрезка EF.

Задание 17 . 31 декабря 2014 года Савелий взял в банке 7 378 000 рублей в кредит под 12,5% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 12,5%), затем Савелий Переводит в банк платёж. Весь долг Савелий выплатил за 3 равных платежа. На сколько рублей меньше он бы отдал банку, если бы смог выплатить долг за 2 равных платежа?

Задание 18 . Найдите все значения параметра a, при каждом из которых система 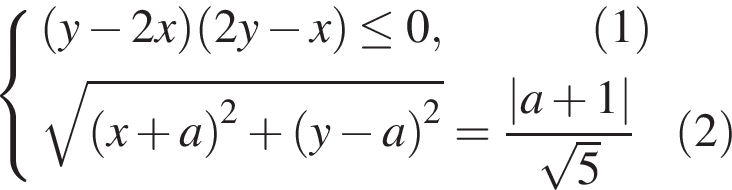имеет ровно два решения.

Задание 19 . Каждое из чисел a₁, a₂, …, a₄₅₀ равно 1, 2, 3 или 4. Обозначим

S₁ = a₁+a₂+...+a₄₅₀,

S₂ = a₁²+a₂²+...+a₄₅₀²,

S₃ = a₁³+a₂³+...+a₄₅₀³,

S₄ = a₁⁴+a₂⁴+...+a₄₅₀⁴.

Известно, что S₁ = 739.

а) Найдите S₄, если еще известно, что S₂ = 1779, S₃ = 5611.

б) Может ли S₄ = 6547 ?

в) Пусть S₄ = 6435. Найдите все значения, которые может

Ответы к вариантам административной работы по математике 11 класс февраль 201622,7

1010

7

0,994

-9

0,28

-35

2

64

6050

55,5

0

Вар2

1855

13500

160

0.06

7

9,6

-19

60

2

30

616

73

Вар3

32,4

1

20

0,9975

4

0,6

21

6

12,8

0,512

14

0

Вар4

5

3

2

0,07

0,3

0,5

39

4

-6

27

35000

0

Вар5

7

25000

30

0,02

-9

110

7

3

14

0,06125

10

3

Вар6

6682,55

15,5

1

0,3

-1,5

4

8

7

2

5000

5

4

Вар7

5

7

1,2

0,2

10

25

-1,25

75

6

62,5

4

1

Вар8

404

3

17

0,025

2

69

-7

50

16

3,9

16

-1

Вар9

12

25000

16

0,25

23

129

8

3280,5

-3

3,5

21

100

Вар10

66

8

1,5

0,75

-17

25

5

3

-3

15

50

196

Вар11

5

3

0,25

0,6

1

18

5

100

2

751

14

-1

Вар12

3000

14

7,5

0,9

-2

94

-4

8

343

60

31

-2,5

Вар13

206,8

321

-4

0,005

-2

90

6

32

8

2

3

9

Вар14

1160

16

18

0,5

4

15

8

2744

1

0,33

25

-2

Вар15

112

30,3

6

0,12

-9

66

10

80

2

4

3

4

: а) б) и

№16

№17

№18

№19

25.

а) да; б) нет; в) 110.

№13

№14

№15

Вар2

8:3

№16

№17

№18

№19

в течение шестого года

№13

№14

№15

Вар 3

: а)

б)

№16

№17

№18

№19

или

5

[−2; 1].

1369

№13

№14

№15

Вар 4

а) ; б)

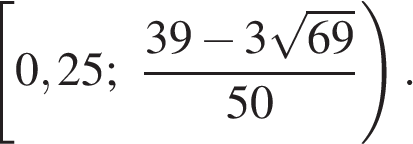
№16

№17

№18

№19

или

в течение шестого года

при единственное решение

а) Да, например, если и

б) нет; в)

№13

№14

№15

Вар 5

а)

б)

№16

№17

№18

№19

3 993 000 рублей

[−5; −1].

а) нет; б) нет; в) 4.

№13

№14

№15

Вар 6

а) б)

№16

№17

№18

№19

$48

108000

акций

при решений нет, при

а) 36;

б) отрицательных;

в) 16.

№13

№14

№15

Вар 7

а) б) и

№16

№17

№18

№19

2 296 350.

3,5; 4; 4,5

2

№13

№14

№15

Вар 8

№16

№17

№18

№19

2 или 2,5

25

№13

№14

№15

Вар 9

а) б)

№16

№17

№18

№19

21,5

в течение восьмого года

а) да; б) нет; в) 31.

№13

№14

№15

Вар 10

5,75

№16

№17

№18

№19

26 или

96

а) да: б) 10; в) .

№13

№14

№15

Вар 11

№16

№17

№18

№19

180

749 000

а) да; б) нет) в) 4.

№13

№14

№15

Вар 12

а) где б)

№16

№17

№18

№19

14,4

53 500 руб

3,5; 4; 4,5.

а) 1 000 000;

б) 1999;

в) 937 500 или

640 000.

№13

№14

№15

Вар 13

а) б)

№16

№17

№18

№19

В одном классе ― 21 мальчик, в другом ― 20 девочек и 2 мальчика

[−5; −1].

а) нет; б) нет; в) 4.

№13

№14

№15

Вар 14

а) ,

б)

№16

№17

№18

№19

3 993 000

рублей

а) 44;

б) отрицательных; в) 17.

№ 13

№14

№15

Вар 15

а)

б)

№16

№17

№18

№19

1 или 1,5

506250

или .

a) 19995;

б) нет;

в) 1371 или 1383