- Учителю
- Научно-исследовательская работа учащегося 9 класса по теме
Научно-исследовательская работа учащегося 9 класса по теме
Автор: Губайдуллина Наталья, ученица 9 Б класса
Руководитель: Кудрявцева Наталья Николаевна, учитель математики МОУ «СОШ № 30» г. Абакан Республики Хакасия
«Рекуррентные соотношения и их применение»
Содержание.
1. Введение.
2. Числовые последовательности.
3. Способы задания последовательности.
3.1 Задачи на рекуррентный способ задания последовательности
4. Арифметическая и геометрическая прогрессии.
4.1. Арифметическая прогрессия.
4.1.1. Задачи на арифметическую прогрессию.
4.2. Геометрическая прогрессия.
4.2.1. Задачи на геометрическую прогрессию.
5. Задачи прикладного характера.
6. Вывод формулы сложных процентов.
7. Исследовательский проект «Изучение процентной ставки вкладов банков города Абакана».
8. Доказательство правильности полученных результатов.
9. Заключение.
10. Литература.
ВВЕДЕНИЕ,
Последовательность является одним из основных понятий математики, изучаемых в школах. Она довольно часто используется в различных областях науки, самый распространенный пример использования последовательностей - это банковские расчеты.
Помимо этого можно встретить последовательности в биологии, химии, медицине и других областях наук.
При изучении многих явлений сначала получают некоторые данные, которые представляют собой последовательность величин, а уже после этого составляют формулы, выражающие определённую зависимость между изучаемыми величинами. Часто наиболее простыми такими формулами являются рекуррентные соотношения. Наиболее изученными в школьном курсе являются арифметическая и геометрическая прогрессии, являющиеся частным случаем рекуррентных соотношений.
В работе представлены нестандартные задачи на тему «Прогрессии».
Также рассмотрены задачи, позволяющие решить отдельные бытовые проблемы каждого человека, задачи технологии производства, задачи, дающие возможность предвидеть результат размножения бактерий в биологии, рассчитать схему приема лекарства, наиболее эффективную для больного, позволяющие рассчитать увеличение нагрузки спортсменов, улучшающие их результат, а также решить много других проблем, стоящих перед человеком.
Практическое применение прикладных задач настолько велико, что текстовые задачи на рекуррентные соотношения ( арифметическую и геометрическую прогрессии, банковские расчеты) включены в материал итоговой аттестации за курс основной и средней школы, в КИМы и ЕГЭ, в конкурсные экзаменационные работы в высшие учебные заведения.
Цель и задачи работы:
- рассмотрение применения рекуррентных соотношений в различных областях науки.
- подборка задач на рекуррентные соотношения из различных областей наук;
- проведение исследования с целью сравнения полученных доходов по некоторым вкладам банков города Абакана на 3 месяца, 6 месяцев и год, для выявления наиболее выгодных условий капиталовложений.
В ввек технического прогресса и развития коммуникаций на каждого человека выливается большой поток информации, поступает несколько деловых предложений одновременно, что обуславливает необходимость
просчитывать предлагаемые варианты и выбор наиболее благоприятного из них.
Деньги играют немаловажную роль в жизни человека. Поэтому возникает естественный вопрос, в какой банк выгоднее положить определённую сумму денег, для получения в дальнейшем прибыли.
Я посетила несколько банков города Абакана с целью ознакомления с предлагаемыми процентными ставками по отдельным вкладам и сравнила полученные доходы. Результаты исследования приведены в данной работе. А также приведено доказательство правильности, полученных опытным путем, результатов.
Числовые последовательности.
Выпишем в порядке возрастания двузначные числа, оканчивающиеся цифрой 3:
13; 23; 33; 43; 53; 63; 73; 83; 93.
Получим девять идущих одно за другим чисел. Они образуют числовую последовательность. Первым записано число 13, вторым - число 23, третьим - число 33, девятым (последним) - число 93. Каждому натуральному числу от 1 до 9 соответствует единственное двузначное число. Значит, задана функция, областью определения которой служит множество{1,2,3,4,5,6,7,8,9}, а областью значений - множество {13; 23;33;43; 53;63;73;83;93}.
Если мы будем выписывать в порядке возрастания все натуральные числа, оканчивающиеся цифрой 3:
3;13;23;33;43;…
то этот процесс мы не закончим никогда, т. к. таких чисел бесконечно много.
Очевидно, что на шестом месте будет число 53, на седьмом - 63 , на десятом- 93, на одиннадцатом- 103, на пятнадцатом -143. Рано или поздно, мы выпишем число, стоящее на 100-м месте, на 10000000-м месте и вообще, для любого натурального n мы укажем единственное соответствующее ему число, оканчивающееся цифрой 3.
Т.о. и в данном случае задана функция. Но ее областью определения служит все множество натуральных чисел N, а областью значений - множество натуральных чисел, оканчивающихся цифрой 3.
Определение. Функция f , область определения которой - множество натуральных чисел или множество первых n натуральных чисел, называется последовательностью.
Т.о. любые подряд выписанные n чисел образуют последовательность.
Если последовательность определена на множестве всех натуральных чисел, то ее называют бесконечной.
Например, вторая рассмотренная нами последовательность, или последовательность четных чисел:
2; 4; 6; 8; 10; 12…
Если последовательность определена на множестве первых n натуральных чисел, то ее называют конечной. Например, последовательность натуральных двузначных чисел: 10; 11;12;13;…;99, или первая рассмотренная нами последовательность.
Пусть некоторая функция f является последовательностью. Значения функции
f(1); f(2); f(3);…;f(n);…,
соответствующие значениям аргумента, равным 1,2,3,…,n называют первым, вторым, третьим,…, энным;… членами последовательности.
Математики условились обозначать члены последовательности буквами с индексами. Обозначим первый член последовательности символом а1(а первое); второй - символом а2 , третий - символом а3 ,…, член с номером n символом аn (а энное). Тогда,
f(1)= а1; f(2)= а2; f(3)= а3;… ;f(n)= аn;
В этом обозначении индекс (порядковый номер числа) равен значению аргумента. Саму последовательность будем обозначать (аn).
Способы задания последовательности.
Последовательность, также как и функцию, можно задать несколькими способами, среди которых являются особенно важными:
1. Конечная последовательность может быть задана путем перечисления ее членов в порядке возрастания их номеров. Например, последовательность (аn): 1; 4; 9; 16; 25; 49; 64; 81; 100. Заметим, что бесконечную последовательность перечислением первых членов задать нельзя. Порядок расположения членов последовательности играет важную роль, поэтому последовательности 1;2;3;4, и 4; 3; 2; 1 различны.
2. Говорят, что последовательность задана аналитически, если указана формула ее n-го члена. Например, последовательность (аn) такова, что для каждого номера n соответствующий член аn можно найти по формуле:
аn=n2-n+1.
Тогда подставляя в формулу вместо n последовательно натуральные числа
1; 2; 3; 4;… получим:
а1=1+1-1=1; а2=3; а3=7; а4=13; и т.д.
Формула, выражающая энный член последовательности через его номер, называется формулой n -го члена последовательности или общего члена последовательности.
Например, формулой аn=![]() задается последовательность, члены которой арифметические квадратные корни из натуральных чисел:
задается последовательность, члены которой арифметические квадратные корни из натуральных чисел:
![]()
3. Словесное задание последовательности используется тогда, когда правило составления последовательности задать формулой невозможно. ![]() Например, последовательность десятичных приближений числа
Например, последовательность десятичных приближений числа ![]() по недостатку: 1; 1,4; 1,41; 1,414; 1,4142; 1,41421;…
по недостатку: 1; 1,4; 1,41; 1,414; 1,4142; 1,41421;…
последовательность десятичных приближений числа ![]() по избытку: 2; 1,5; 1,42; 1,415; 1,4143; 1,41422;…
по избытку: 2; 1,5; 1,42; 1,415; 1,4143; 1,41422;…
последовательность простых чисел: 2; 3; 5; 7; 11; 13; 17; 19; 23; 29; …
Во всех случаях правило составления последовательности описано словами.
4. Последовательность, в отличие от функции, можно задать еще одним способом, который заключается в следующем: указывается правило, позволяющее вычислить n -й член последовательности, если известны ее предыдущие члены.
Например, пусть известно, что каждый член последовательности, начиная со второго, равен квадрату предыдущего.
Таких последовательностей сколько угодно:
2;4;16;256;…
![]() и т.д.
и т.д.
Чтобы задать одну из таких последовательностей, например 2;4;16;256;… достаточно указать первый ее член. Таким образом, эта последовательность задается условиями:
Первый член равен 2; каждый член, начиная со второго, равен квадрату предыдущего.
Если последовательность обозначить (аn), то предыдущим для члена аn будет член аn+1, последующий - аn-1. Тогда условия можно переписать так:
а1=1; аn+1=![]()
Рассмотрим последовательность (аn), первый член которой равен единице, второй - двум, а каждый член, начиная с третьего, равен сумме двух предыдущих членов. Эти условия можно записать в виде:
а1=1; а2=1; аn+2= аn+1+ аn; Зная эти условия можно найти любой член последовательности: а1=1; а2=1; а3=1+1=2; а4=1+2=3; а5=2+3=5; а6=3+5=8; и т.д. - эта последовательность называется последовательностью Фибоначчи (по имени итальянского математика ХШ века).
Рассмотрим решение следующих задач:
1.Сколько n-значных чисел можно составить из цифр 2 и 5, так, чтобы никакие две двойки не стояли рядом?
Решение:
Обозначим количество искомых способов через аn, тогда
а1=2;(это числа 2 и 5);
а2=3 (25; 52; 55);
а3=5 (252; 255; 525; 552; 555);
а4=8 (5252; 5255;5525; 5552; 5555; 2525; 2552; 2555)
Каждое n- значное число начинается либо с двойки, либо с пятерки.
Если число начинается с двойки, то за ним должна идти пятерка и любое из (n-2) - значных чисел (всего таких чисел аn-2). Если число начинается с пятерки, то за ней может стоять любое (n-1) значных чисел (всего таких чисел аn-1).
Т.о. мы получим рекуррентную формулу
аn= аn-2+ аn-1; или аn+2= аn+1+ аn, с начальными значениями а1=2; а2=3.
2. Задача о прыгуне.
Прыгун может прыгать в одном направлении вдоль разделенной на клетки полосы, перемещаясь при каждом прыжке либо в соседнюю клетку, либо через клетку. Сколькими способами может он сдвинуться на n-1 клетку, и, в частности, переместиться из первой клетки в n - ю?
(Способы прыганья считать одинаковыми, если в ходе каждого из них прыгун побывает в одних и тех же клетках).
Решение: Обозначим искомое число способов через хn.
Переход из первой клетки в первую же осуществляется одним способом- отсутствием прыжков ( х1=1). Переместиться во вторую клетку можно единственным способом- прыжком в соседнюю клетку (х2=1). Прыжок на третью клетку можно осуществить из первой клетки, либо из второй. Значит
х3=2. Чтобы достигнуть 4-й клетки, прыжки можно осуществлять либо со второй клетки, в которую прыгун переместится одним прыжком, либо с третьей, в которую можно переместиться двумя способами: х4=1+2=3.
Пусть целью прыгуна является достижение n+2 клетки. Общее число способов осуществления этой цели - хn+2. Эти способы разбиваются на два класса: начинающиеся с прыжка во вторую клетку и начинающиеся с прыжка в третью клетку. Из второй клетки прыгун может переместиться в (n+2) хn+1 способами, из третьей - хn способами. Получим рекуррентное соотношение:
хn+2= хn+1+ хn; х1=1; х2=1.
Эта последовательность совпадает с последовательностью Фибоначчи.
Рано или поздно мы найдем любой член последовательности, но для этого нам придется вычислить значение и всех предыдущих членов.
При вычислении членов последовательности по этому правилу мы как бы все время возвращаемся назад, выясняя чему равны предыдущие члены. Поэтому такой способ задания последовательности назвали рекуррентным (от лат слова recurrere - бегу назад, возвращаюсь).
Формулу, выражающую любой член последовательности, начиная с некоторого, через предыдущие (один или несколько), называют рекуррентным соотношением.
При рекуррентном способе задания последовательности обычно указывают:
1) первый член последовательности (или несколько первых членов);
2) рекуррентное соотношение.
Приведём примеры:
1.При нахождении приближенного значения квадратного корня из положительного числа а выбирают какое либо начальное приближение х1 и строят затем последовательность чисел х1, х2, х3, х4, … хn, используя рекуррентное соотношение:
![]()
2.Последовательность (аn) задана первыми двумя членами а1=2; а2=3 и условием ![]() . Найдите
. Найдите ![]() .
.
Решение: Выпишем несколько первых членов последовательности:
а1=2; а2=3; а3=1,5; а4=0,5; а5=![]() ; а6=
; а6=![]() ; а7=2; а8=3 ; а9=1,5; а10=0,5;..
; а7=2; а8=3 ; а9=1,5; а10=0,5;..
а1= а7=2; а2= а8=3; а9=![]() =1,5 …, то последовательность является периодической (Т=6) 1986:6=331. Значит
=1,5 …, то последовательность является периодической (Т=6) 1986:6=331. Значит ![]() =
=![]() =
=![]()
Ответ: ![]()
Арифметическая и геометрическая прогрессии
Среди последовательностей выделяют арифметическую и геометрическую прогрессии:
Определение. Арифметической прогрессией называют числовую последовательность (аn), члены которой удовлетворяют рекуррентному соотношению:
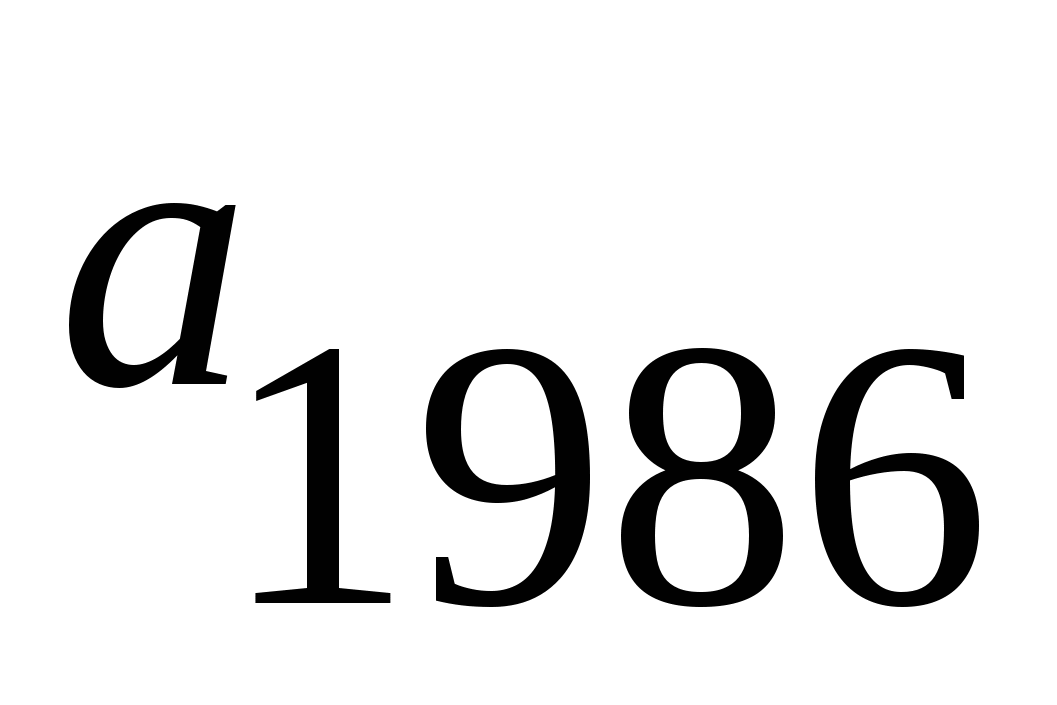 ,
,
где d разность прогрессии (некоторая константа, не зависящая от n). Исходя из определения d= аn+1-аn, а аn=аn+1-d.
Например, арифметическая прогрессия встречается в литературе:
Напомним строки из романа А.С.Пушкина «Евгений Онегин», сказанные о его
герое: «…Не мог он ямба от хорея, как мы не бились отличить». Отличие ямба от хорея состоит в различных расположениях ударных слогов стиха.
Ямб - стихотворный метод с ударениями на чётных слогах стиха (Мой дядя самых честных правил), т.е. ударными являются второй, четвёртый, шестой, восьмой и т. д. слоги. Номера ударных слогов образуют арифметическую прогрессию с первым членом 2 и с разностью, равной двум: 2, 4, 6, 8, … .
Хорей - стихотворный размер с ударением на нечётных слогах стиха (Буря мглою небо кроет). Номера ударных слогов также образуют арифметическую прогрессию, но её первый член равен единице, а разность по-прежнему равна двум: 1, 3, 5, 7, … .
Рассмотрим примеры задач на арифметическую прогрессию:
1. Доказать, что среди любых 22 последовательных натуральных чисел найдётся число, не делящееся на сумму своих цифр.
Решение. Пусть n, n+1, n+2, …, n+21 - натуральные числа. Среди чисел n+1, n+2, …, n+20 рассмотрим число k, последняя цифра которого - нуль, предпоследняя отлична от нуля. Сумма цифр числа k на 1 меньше суммы цифр числа k+1 и на 8 меньше суммы цифр числа k-1. Отсюда следует, что суммы цифр чисел k+1 и k-1 отличаются на 7, и потому одна из этих сумм чётна. Но числа k+1 и k-1 оба нечётны, значит, по крайней мере одно из них не делится на сумму своих цифр.
2.(МГУ -2004) Найдите арифметическую прогрессию, в которой сумма любого числа первых членов равна утроенному квадрату числа этих членов.
Решение. По условию для любого числа n первых членов их сумма равна 3n2:

Обратно, для прогрессии с первым членом 3 и разностью 6 указанное тождество, как легко проверить, выполняется.
3. (ЕГЭ) В арифметической прогрессии сумма первых семи членов равна 21, разность пятого и третьего членов равна - 6. На каком месте в этой прогрессии стоит число - 21?
Решение. Пусть a1 и d - соответственно первый член и разность прогрессии. Поскольку
![]()
![]()
![]()
поэтому a1= 12. Осталось определить n из условия an= a1 + d(n - 1) = -21. Подставляя сюда найденные выше значения a1 и d, получаем, что n = 12.
Ответ: 12.
4. (МГУ -2003) Турист, поднимаясь в гору, в первый час достиг высоты 800 м, а каждый следующий час поднимался на высоту, на 25 м меньшую, чем в предыдущий. За сколько часов он достигнет высоты в 5700 м?
Решение:
Арифметическая прогрессия, ![]()
Найти: n
S![]() =
=![]() , тогда получим
, тогда получим
![]()
5700=![]()
25n![]() - 1625 n+11400=0
- 1625 n+11400=0
n![]() - 65n +456=0
- 65n +456=0
D=4225-1824=2401=49![]()
n![]() =
=![]() =8; n
=8; n![]() =
=![]() =57
=57![]() не удовлетворяет условию задачи.
не удовлетворяет условию задачи.
Ответ: За 8 часов турист достигнет вершины горы.
5. Сумма трех последовательных членов арифметической прогрессии в 5 раз больше их произведения. Найдите эти члены, если они являются целыми числами.
Решение:
Пусть аn ; аn+1 ; аn+2 ; - три последовательных члена арифметической прогрессии, разность которой равна d.
Тогда аn+2= аn+1+d; аn= аn+1-d.
5(аn + аn+1 +аn+2 )=аn аn+1 аn+2;
5(аn+1 -d + аn+1 +аn+1 +d)=(аn+1 -d)(аn+1 +d) аn+1;
15 аn+1 =(![]() -d) аn+1;
-d) аn+1;
аn+1=0 или (![]() -d)=15;
-d)=15;
(аn+1 -d)(аn+1 +d)= 15 ![]() ;
;
аn ; аn+1 ; аn+2 целые числа.
Два целых числа в произведении дадут 15 если:
-
аn=3; аn+2= 5;
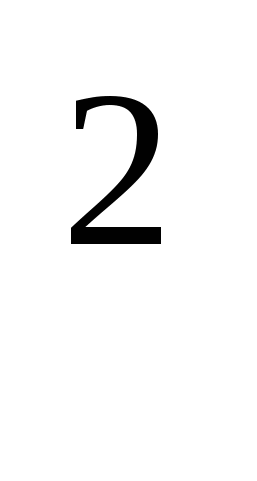
-
аn=5; аn+2= 3;
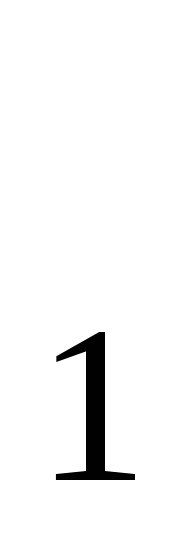
-
аn=1 ; аn+2= 15;
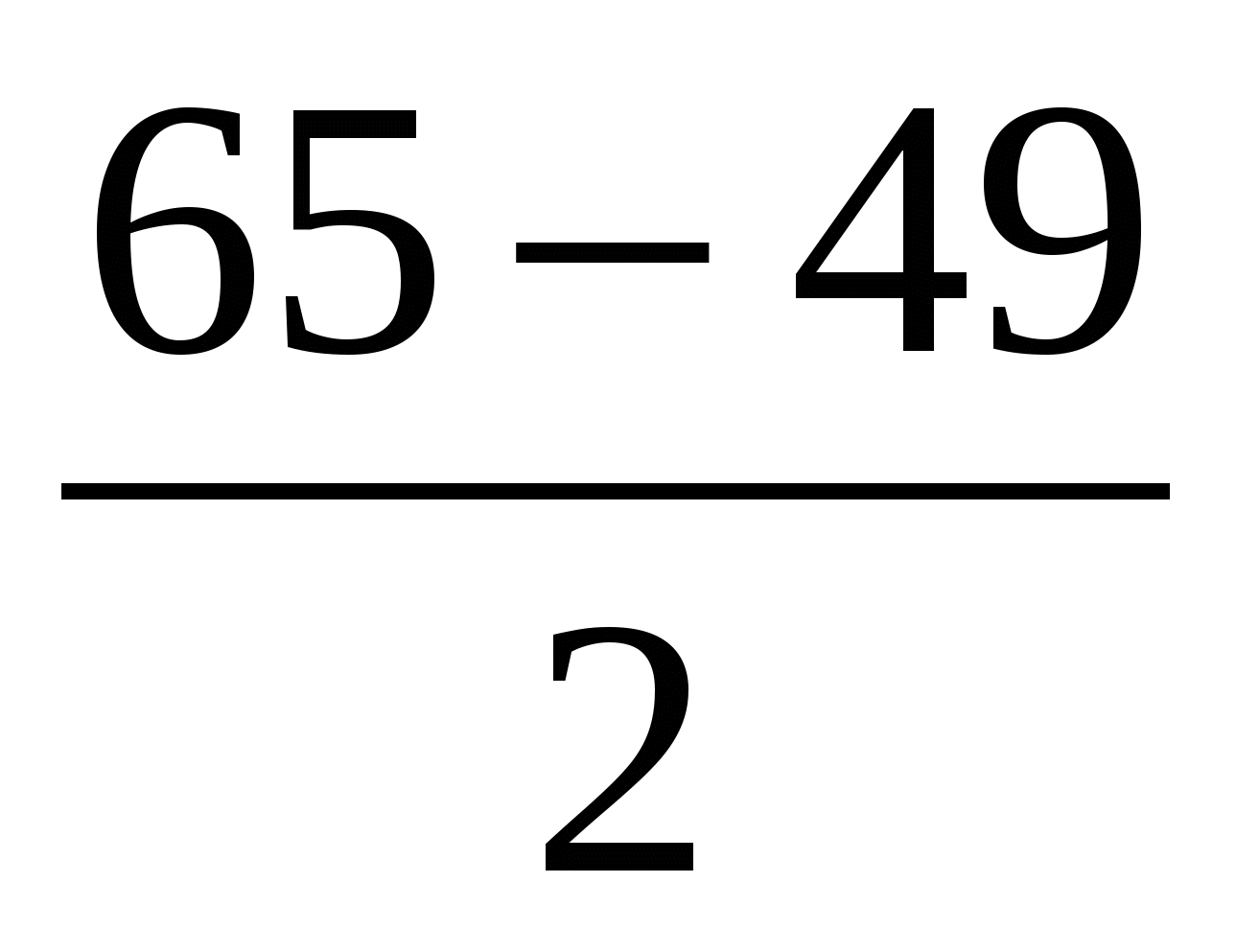
-
аn=15 ; аn+2= 1;
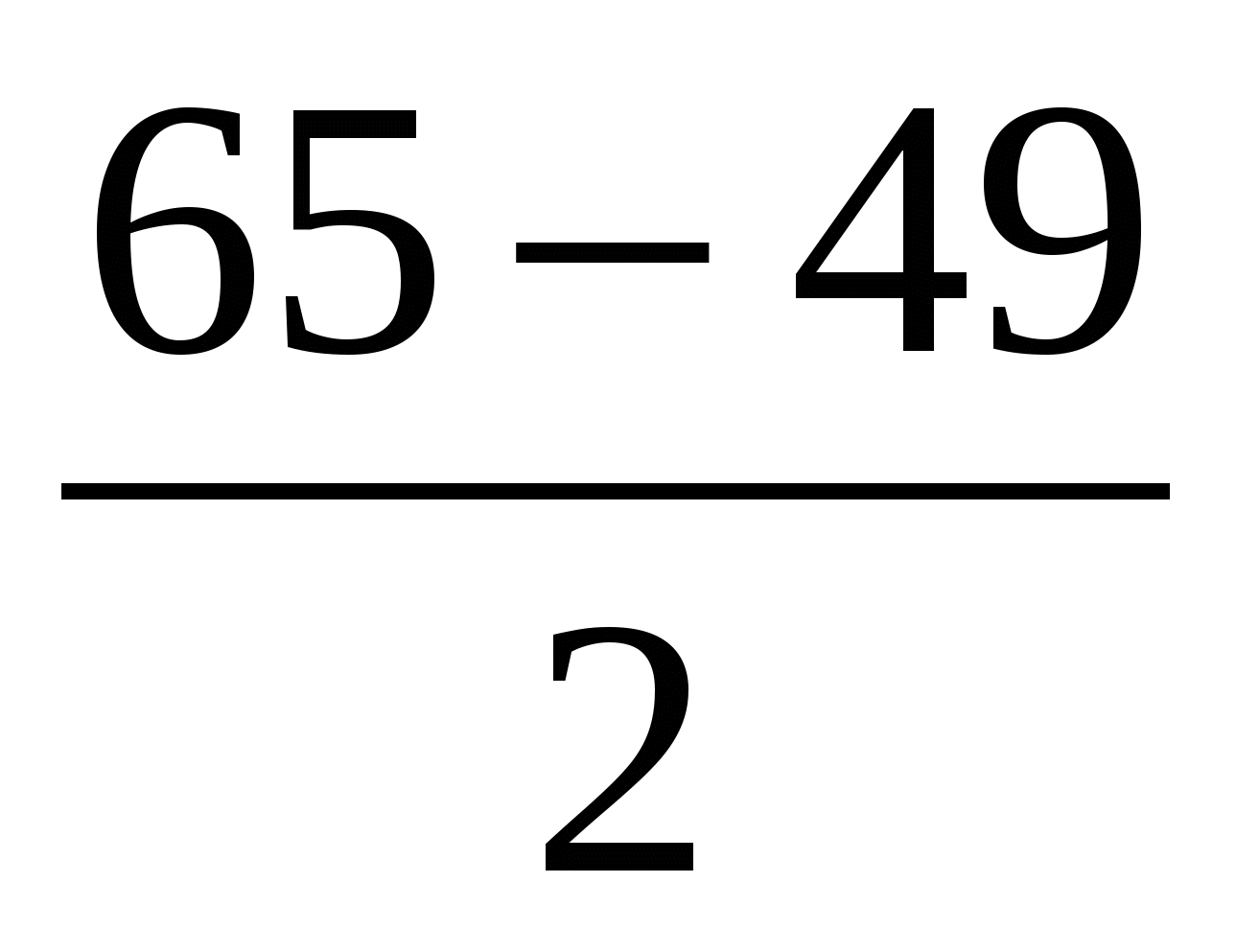
если аn+1=0, то аn=0 и аn+2=0
Ответ: (3;4;5) (5;4;3) (15;8;1) (1;8;15)
6. Докажите, что числа вида ![]() , где
, где ![]() , не образуют арифметическую прогрессию.
, не образуют арифметическую прогрессию.
Доказательство:
Предположим, что числа ![]() образуют арифметическую прогрессию, тогда должно выполняться равенство:
образуют арифметическую прогрессию, тогда должно выполняться равенство:
![]()
В обеих частях этого равенства находятся положительные числа, поэтому
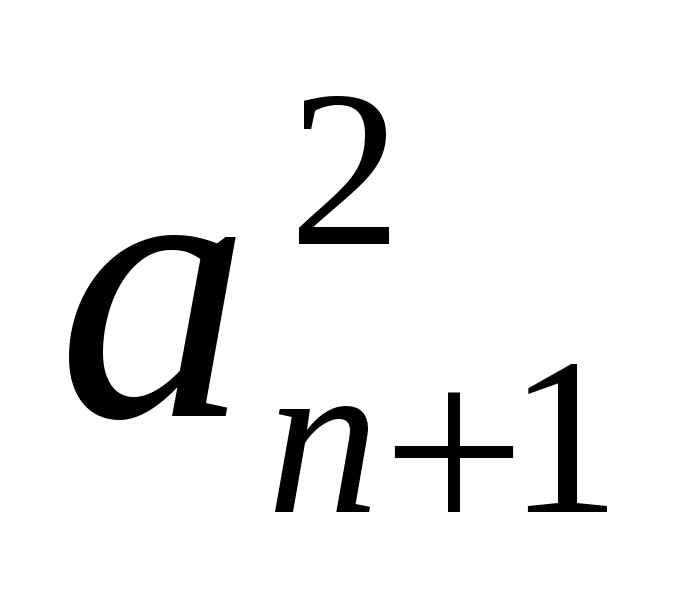
Равенство не выполняется, поэтому наше предположение неверно.
Значит, числа![]() не образуют арифметическую прогрессию.
не образуют арифметическую прогрессию.
7.Положительные числа ![]() образуют арифметическую прогрессию. Докажите, что
образуют арифметическую прогрессию. Докажите, что
![]()
Решение: Домножим числитель и знаменатель каждой из дробей суммы левой части равенства на сопряженное выражение
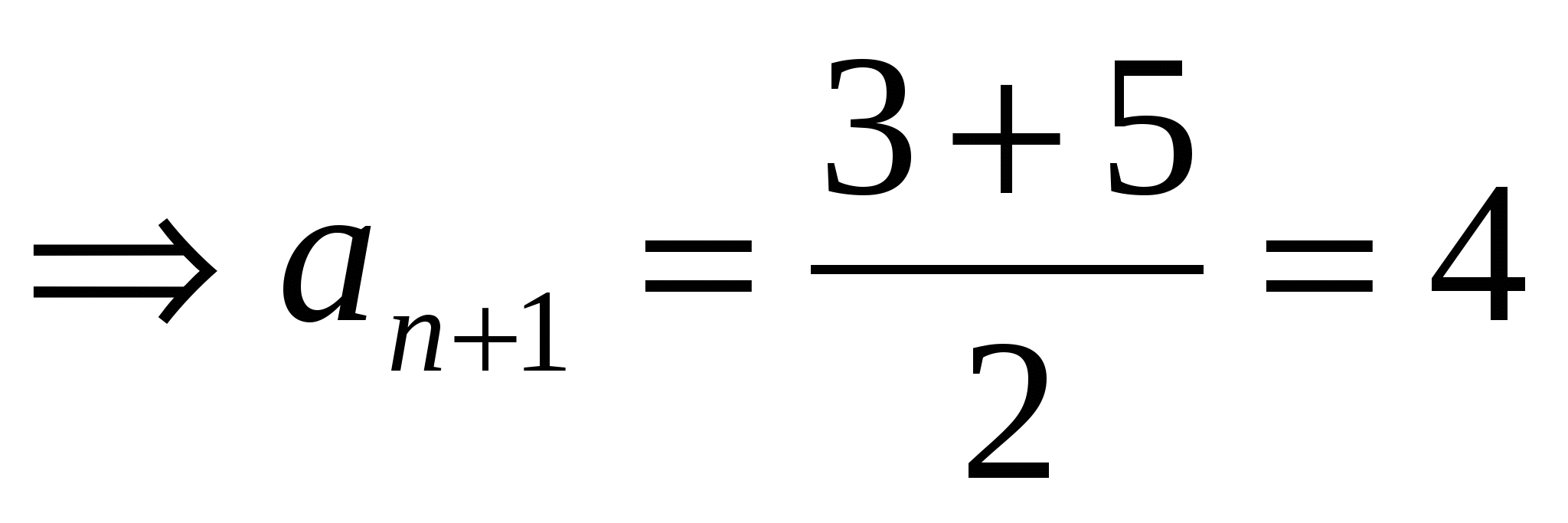
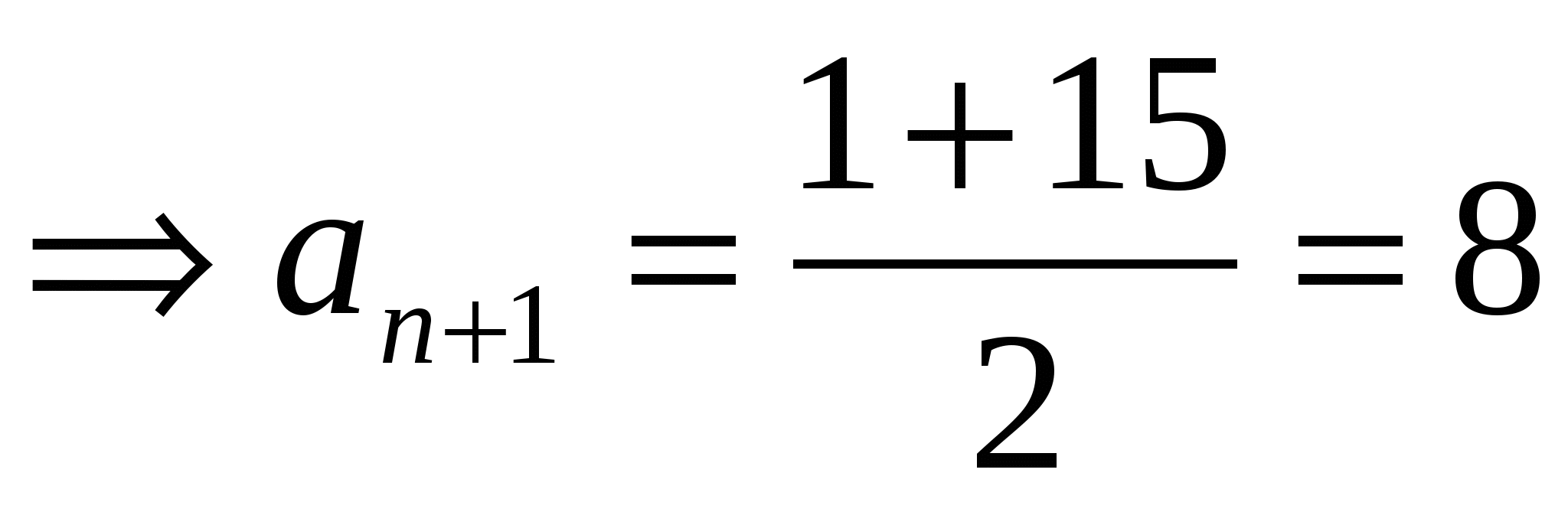 Что и требовалось доказать.
Что и требовалось доказать.
8. Могут ли цифры простого трехзначного числа образовывать арифметическую прогрессию с положительной разностью? Если могут, то найдите все такие числа.
Решение:
Пусть ![]() трехзначное число, цифры которого a,b,c, образуют арифметическую прогрессию с разностью d.
трехзначное число, цифры которого a,b,c, образуют арифметическую прогрессию с разностью d.
Тогда a=b-d; c=b+ d.
S=a+b+c=b-d+b+b+d=3b![]() , значит S не может быть простым числом.
, значит S не может быть простым числом.
Ответ: не могут.
9. Три числа, являющиеся длинами рёбер прямоугольного параллелепипеда с диагональю 6, образуют арифметическую прогрессию. Кубы этих чисел тоже образуют арифметическую прогрессию. Найдите эти числа.
Решение. Для рёбер a ≤ b≤ c параллепипеда имеем:
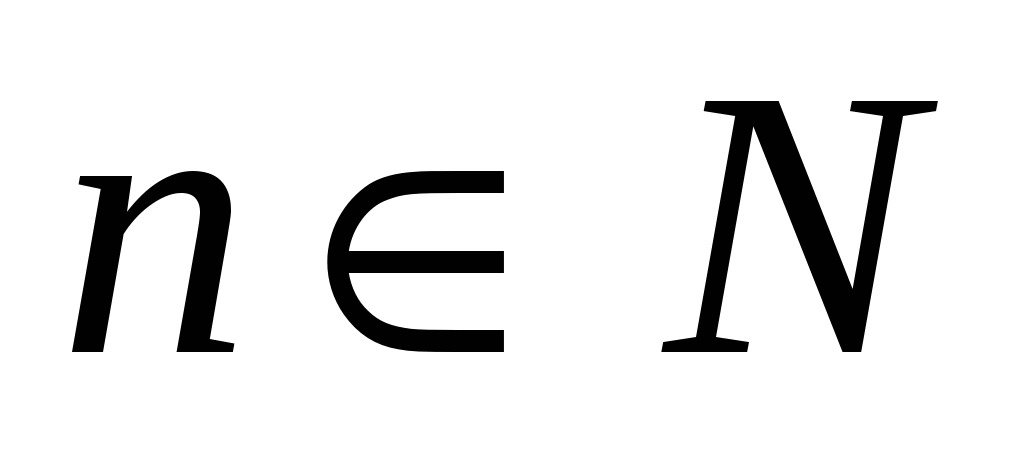
Отсюда следует, что числа a и c являются корнями квадратного уравнения
x2 - 2bx + b2 = 0, т.е. a = b = c.
Из равенства a2 + b2 + c2= 62 находим a = c = b = 2![]()
Ответ: 2![]() , 2
, 2![]() , 2
, 2![]() .
.
.
10. В соревновании по стрельбе за каждый промах в серии из 25 выстрелов стрелок получал штрафные очки: за первый промах - одно штрафное очко, а за каждый последующий - на ½ очка больше, чем за предыдущий. Сколько раз попал в цель стрелок, получивший 7 штрафных очков.
Решение: Найдем число промахов.
Арифметическая прогрессия, в которой ![]()
Найдем n
![]()
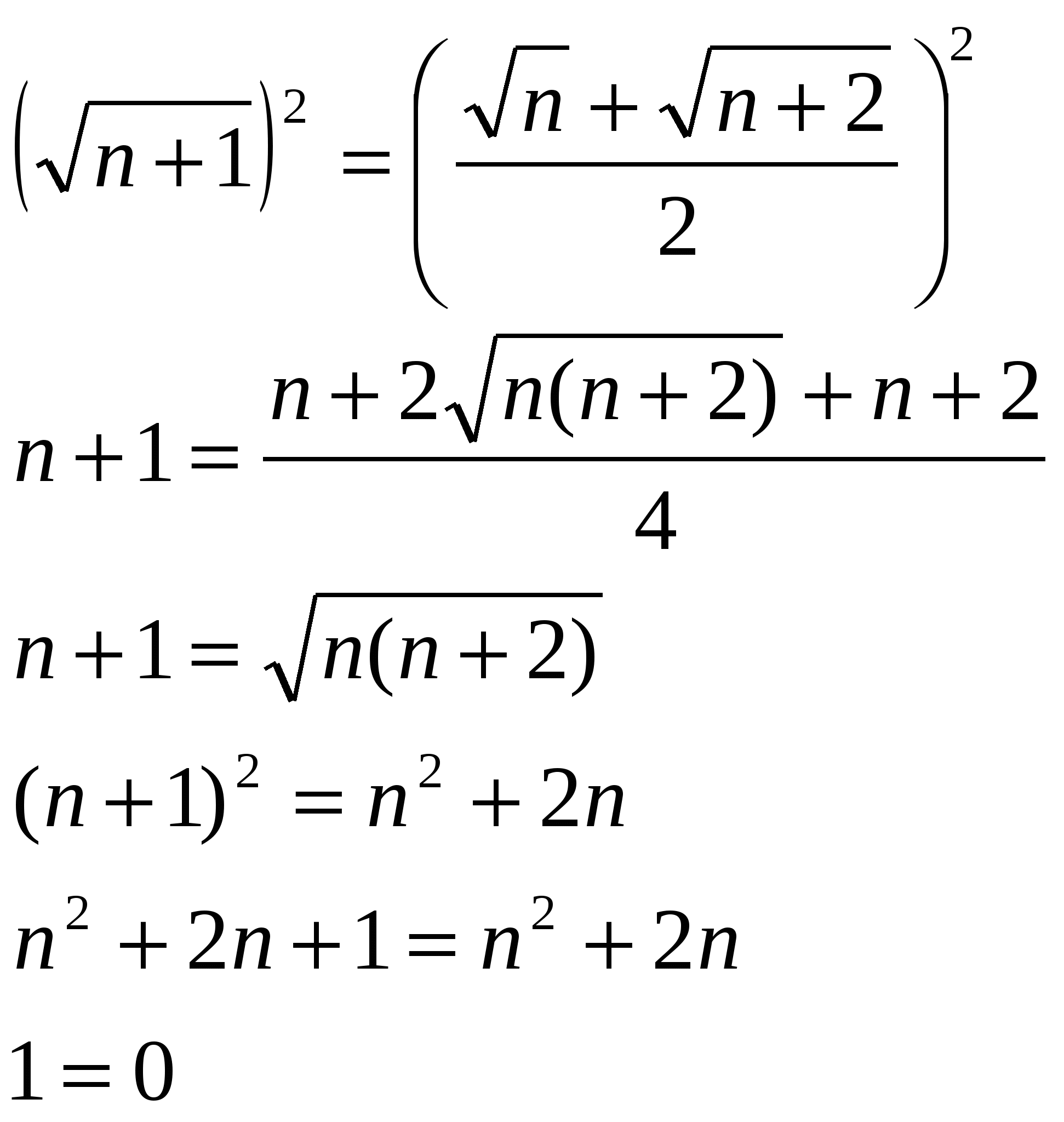
-7 не удовлетворяет условию задачи.
4 раза промахнулся стрелок.
25-4=21 раз стрелок попал в цель.
Ответ: 21 раз стрелок попал в цель.
11. Первоначальная цена товара на торгах повышалась несколько раз на одно и тоже количество рублей. После третьего повышения цена равнялась 1200 рублям, а после двенадцатого повышения - 1650 рублям. Через сколько повышений первоначальная цена удвоилась?
Решение: В условии задачи ничего не говорится ни об арифметической, ни о геометрической прогрессии. Поэтому решение можно строить так.
Пусть x - первоначальная цена товара на торгах. Пусть после первого повышения цена стала x + a рублей, после второго x + 2a рублей и после третьего повышения цена стала равной x + 3a рублям, что по условию равно 1200 рублям. То есть x + 3a =1200. После двенадцатого повышения цена стала равной x + 12a = 1650. Отсюда 9a = 450 и a = 50. Следовательно, x = 1200 - 3 · 50 = 1050 (рублей). Теперь пусть число повышений равно n. Составим равенство: 1050 + 50n = 2100. Отсюда n = 21. Следовательно, цена товара удвоится через 21 повышение первоначальной цены.
Ответ: 21.
Определение. Геометрической прогрессией называют числовую последовательность (bn), члены которой удовлетворяют рекуррентному соотношению:
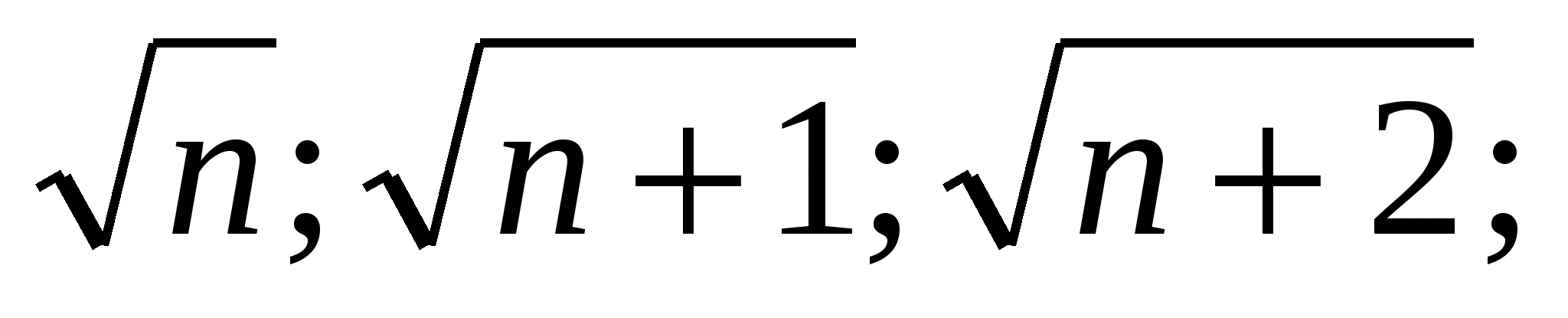
где q - знаменатель прогрессии ( некоторая константа, не зависящая от n).
Из определения следует, что ![]() и
и ![]()
1. Отношение девятого члена геометрической прогрессии к её шестому члену равно 1 .
8
Найдите первый член прогрессии, если её пятый член равен 3.
Решение. Если q - знаменатель прогрессии, то
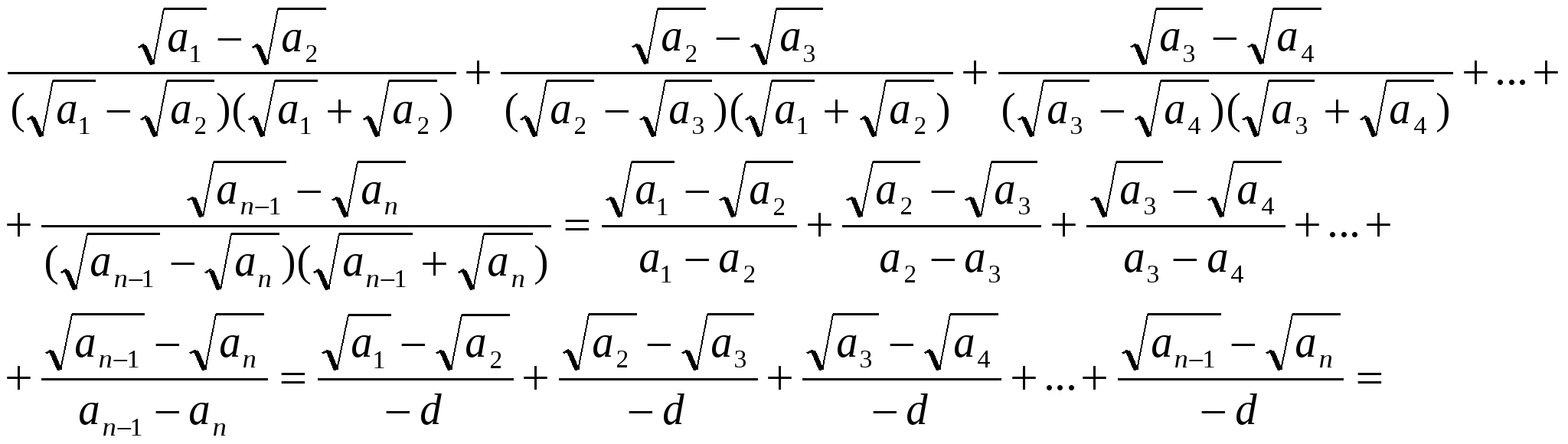
Ответ: 48.
2. Докажите, что между каждыми двумя последовательными членами геометрической прогрессии с положительными членами можно вставить по k чисел так, что вся последовательность составит геометрическую прогрессию.
Решение:
Пусть числа b1, b2, b3, b4, …, bn, составляют геометрическую прогрессию, знаменатель которой равен q.
Определим знаменатель искомой прогрессии q по первому ее члену b1 и (k+2) - му - b2,
b2= b1qk+1.![]()
последовательность будет иметь вид:
b1, b1![]() ,b1
,b1 ,…, b1
,…, b1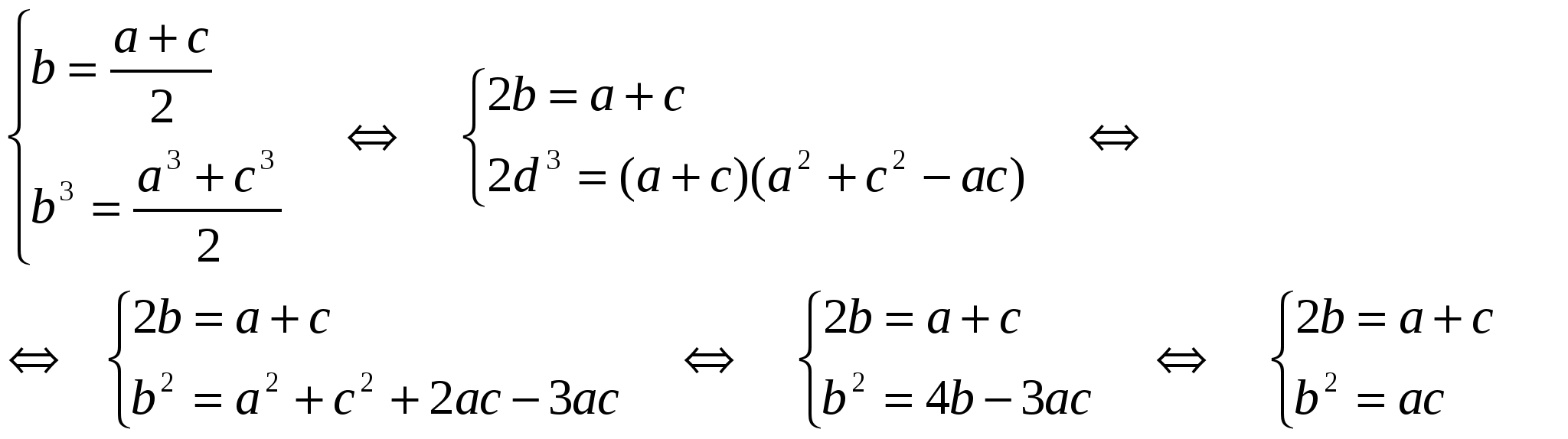 , b2.
, b2.
Аналогично между числами b2и b3 можно вставить k членов, так, что образуется геометрическая прогрессия со знаменателем![]() и т.д.
и т.д.
По условию задачи ![]() , значит, вся последовательность составит геометрическую прогрессию со знаменателем
, значит, вся последовательность составит геометрическую прогрессию со знаменателем
![]()
![]() =… , что и требовалось доказать.
=… , что и требовалось доказать.
3. Завод приобрел 5 электромоторов, мощности которых составляет геометрическую прогрессию. Рассчитать мощности трех средних моторов, если известно, что наименьшая мощность мотора 5 квт, наибольшая 12,5 квт
Решение: В задаче речь идет о геометрической прогрессии в которой ![]() ,необходимо найти
,необходимо найти ![]() .
.
![]() не удовлетворяет условию задачи. Тогда
не удовлетворяет условию задачи. Тогда ![]() .
.
Ответ: мощность второго мотора ![]() кВт, мощность третьего мотора
кВт, мощность третьего мотора ![]() кВт, мощность третьего мотора
кВт, мощность третьего мотора ![]() кВт.
кВт.
Рассмотрим решение следующих задач прикладного характера:
1. Отряд механизаторов в весенне-посевную компанию в первый день вспахал 100 га пашни, а в каждый следующий день - на 3 га больше, чем в предыдущий. Найти, сколько гектаров пашни отряд механизаторов вспахал за 19 дней.
Решение:
Рассмотрим арифметическую прогрессию, в которой
![]() Найти S19
Найти S19
![]()
Ответ: 2413 га отряд механизаторов вспахал за 19 дней.
2.Игорь начал утренние тренировки в беге с 2 км в день. Он решил каждую неделю увеличивать эту дистанцию в арифметической прогрессии так, чтобы в одиннадцатую неделю пробегать 4 км в день. На какое расстояние ему надо увеличить дистанцию еженедельно?
Решение: Рассмотрим арифметическую прогрессию, в которой ![]()
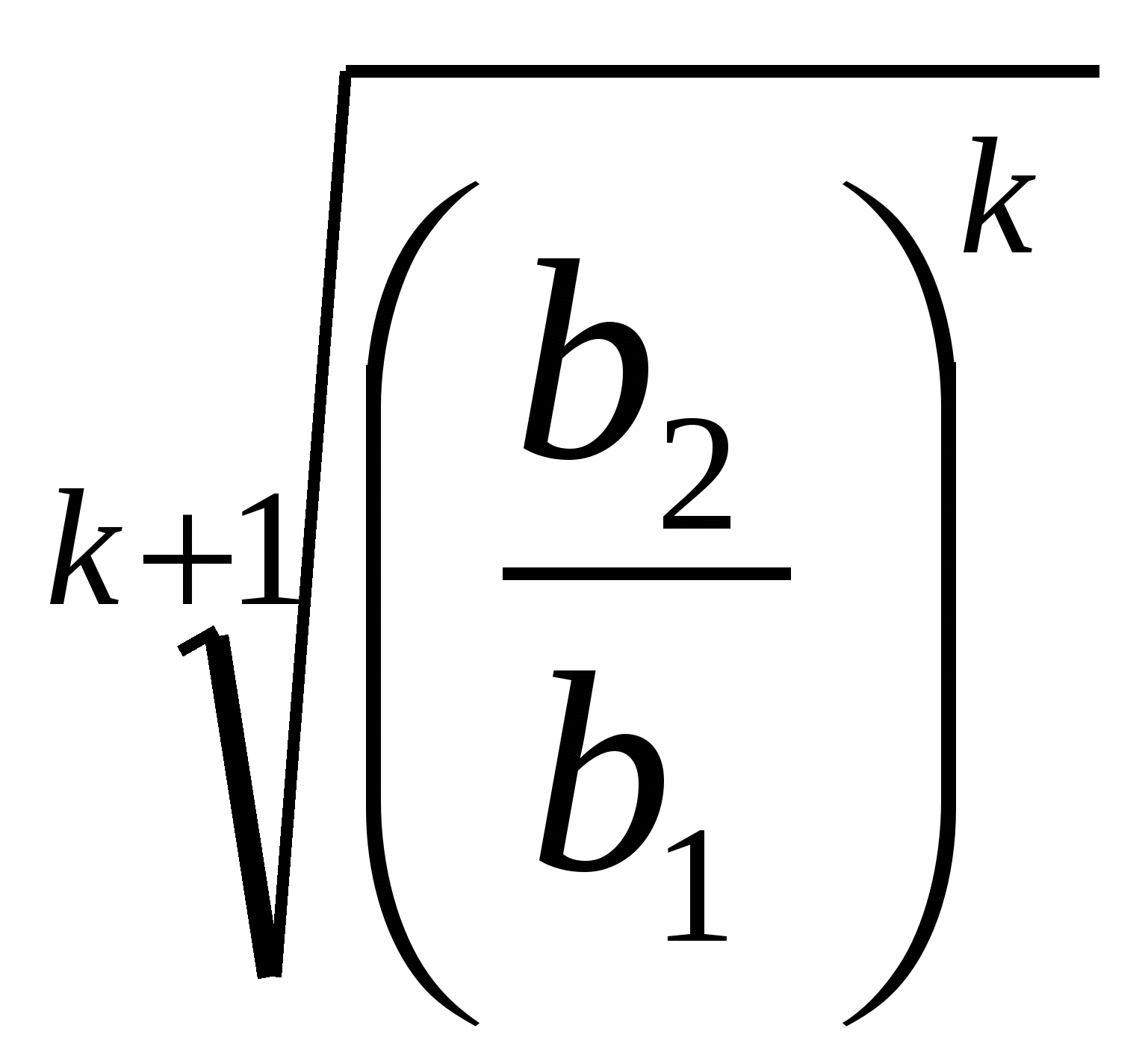
Ответ: На 0,2 км Игорю надо увеличивать дистанцию еженедельно.
3. В горных местностях температура воздуха летом при подъеме на каждые 100 м в среднем понижается на 0,70 С. В 11 часов на горе термометр показывал 14,7 0С. Как высоко находится наблюдатель, если у подножия в это время температура 280С?
Решение: Рассмотрим арифметическую прогрессию, в которой ![]() . Найти n.
. Найти n.
14,7 = 28 - 0,7(n-1)
0,7n = 14
n = 20.
20 · 100 =2000 м = 2км
Ответ: находится на высоте 2 км.
4. Шар. катящийся по желобу, в первую секунду проходит 0,6 м, а путь, пройденный в каждую следующую, увеличивается на 0,6 м. Сколько времени будет двигаться шар по шестиметровому желобу?
Решение:
Рассмотрим арифметическую прогрессию, где
S = 6 м, 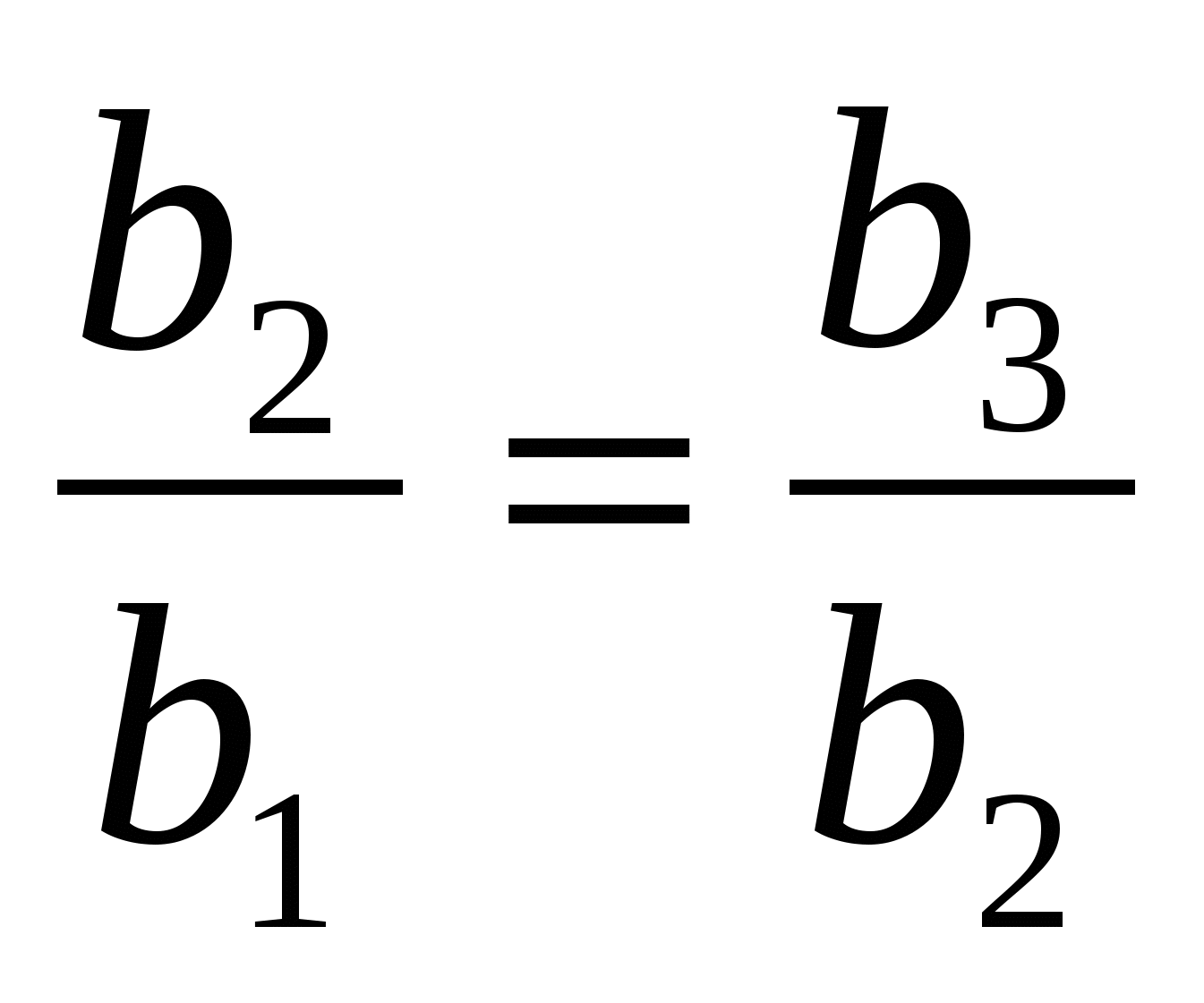
5. В сентябре семья Савельевых заплатила 240 руб. за школьные завтраки. В дальнейшем плата за завтраки ежемесячно увеличивалась на 2 % от суммы, внесенной в сентябре. а) Сколько заплатили Савельевы за завтраки в декабре?
б) Сколько всего было заплачено за завтраки с сентября по декабрь?
Решение:
а) Сентябрь - 240 р.
Октябрь: 240 + 240 · 0.02 = 244.8 р.
Ноябрь: 244.8 + 244.8 · 0.02 = 249.7 р.
Декабрь: 249.7 + 249.7 · 0.02 = 254.7 р.
б) 240 + 244.8 +249.7 + 254.7 = 989.2
Ответ: в декабре 254.7 р. заплатили Савельевы за завтраки в декабре, 989.2 р. было заплачено за завтраки с Сентября по Декабрь.
6.Лекарственную настойку пьют каплями: в 1-й день 6 капель, а в каждый следующий на 3 капли больше. Начиная, с 11 дня дневную дозу ежедневно убавляют на 3 капли и заканчивают курс лечения на 19 день после его начала.
Сколько капель лекарства примет больной за первые 10 дней лечения?
Решение:
Рассмотрим арифметическую прогрессию в которой
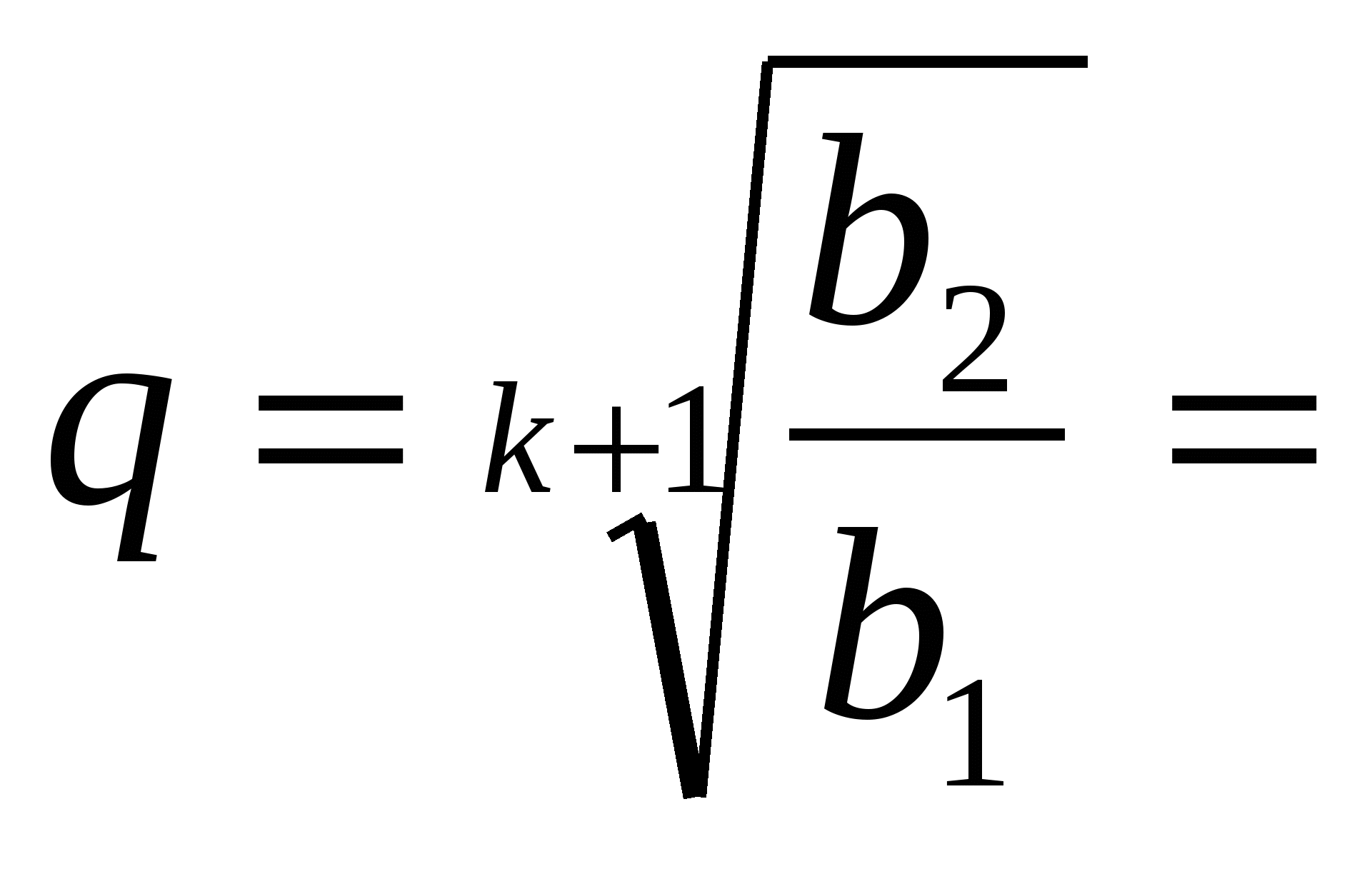
Значит 195 капель примет больной за первые 10 дней лечения.
Ответ: 195 капель.
7. Рост дрожжевых клеток происходит делением каждой клетки на две части. Сколько стало клеток после десятикратного их деления, если первоначально было 6 клеток?
Решение:
Т.к. каждая клетка делится на 2 части, то количество клеток увеличивается в 2 раза. Получим геометрическую прогрессию, в которой
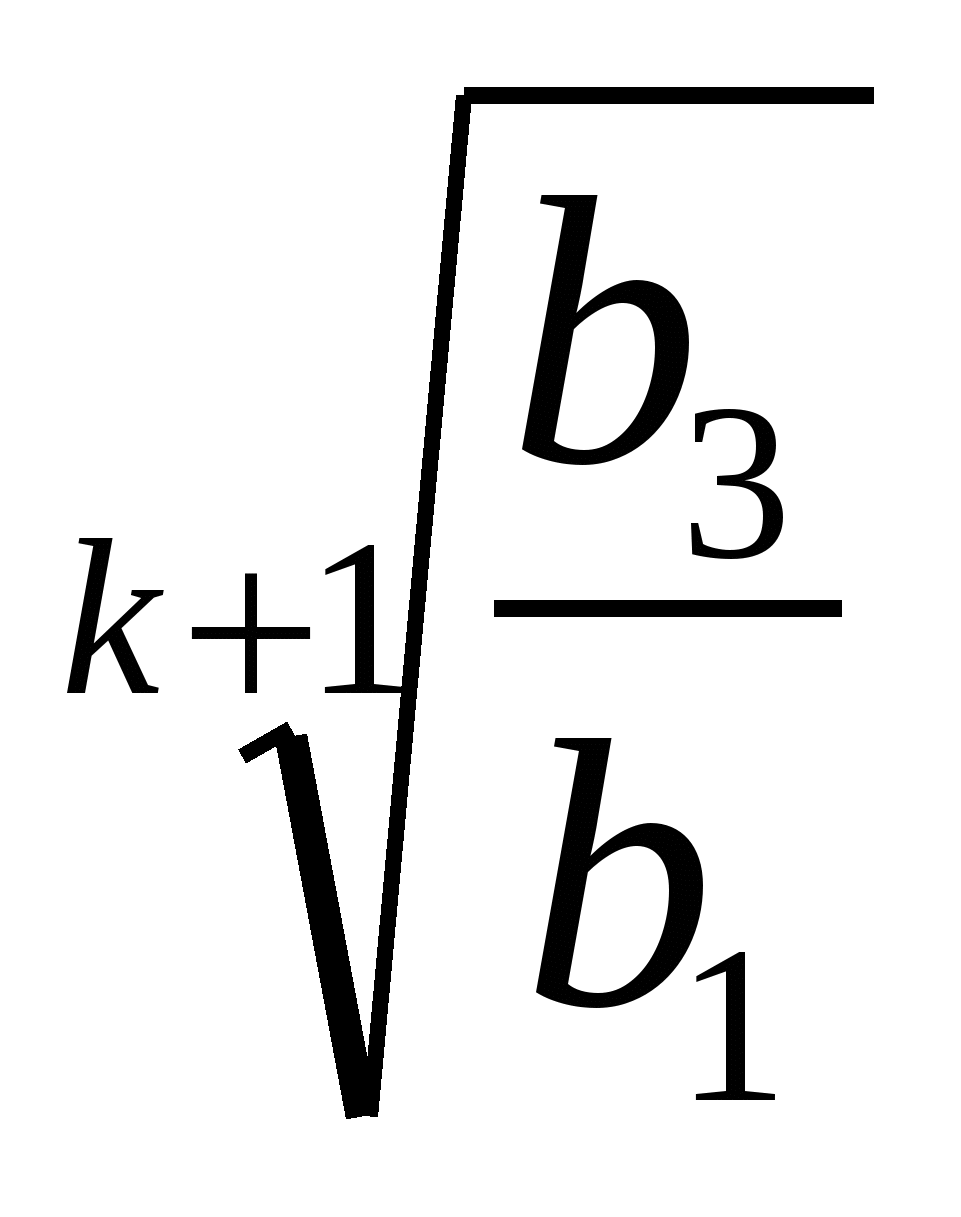
Ответ: 6138 клеток стало после десятикратного их деления, если первоначально было 6 клеток.
8. На озере растет одна лилия. Она покрывает цветами все озеро за 10 дней, причем за каждый день площадь, покрытая цветами, становится в два раза больше, чем была до этого. За сколько дней это озеро покроют две такие лилии?
Решение: Если площадь озера, которое покрывает цветами одна лилия, в первый день равна 1, то площадь, покрываемая за два дня равна 2, за три - 22, за четыре - 2 3, … На 10 день цветы покроют площадь, равную 29. Точно такую же площадь озера покроют цветы двух лилий за 9 дней.
Ответ: 9 дней.
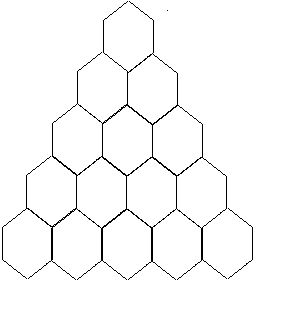
9.Фигура составлена из правильных шестиугольников так, что в верхнем ряду находится один шестиугольник, а в каждом следующем ряду на один шестиугольник больше, чем в предыдущем. Известно, что для составления фигуры потребовалось 45 шестиугольников. В скольких рядах размещены шестиугольники?
Решение:
Дано:
(÷) an: a1 = 1, d = 1, Sn = 45.
Найти: n.
Решение:
Sn= 2a1 + d (n - 1) . n
2
2 + 1(n - 1) . n = 45 2 + n - 1 . n = 45 1 + n . n = 45 n2 = 90
2 2 2
n + n2 = 90
n2 + n - 90 = 0
D = 12 - 4·1·(-90) = 1 + 360 = 361 = 192
n1 = -1 - 19 = -10 n1< 0 не является решением; n2 = -1 + 19 = 9
2 2
Ответ: 9 рядов.
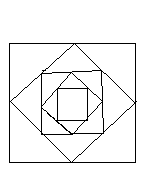
10.Дан квадрат, сторона которого равна 4 см. Середины его сторон являются вершинами второго квадрата, середины сторон второго квадрата являются вершинами третьего квадрата и т. д. Найти сумму площадей всех квадратов.
Решение:
Из геометрических соображений ясно, что площадь каждого следующего квадрата равна половине площади предыдущего. Таким образом, последовательность площадей квадратов является геометрической прогрессией, первый член которой равен 16, а знаменатель равен ![]() . Найдём сумму этой геометрической прогрессии:
. Найдём сумму этой геометрической прогрессии:
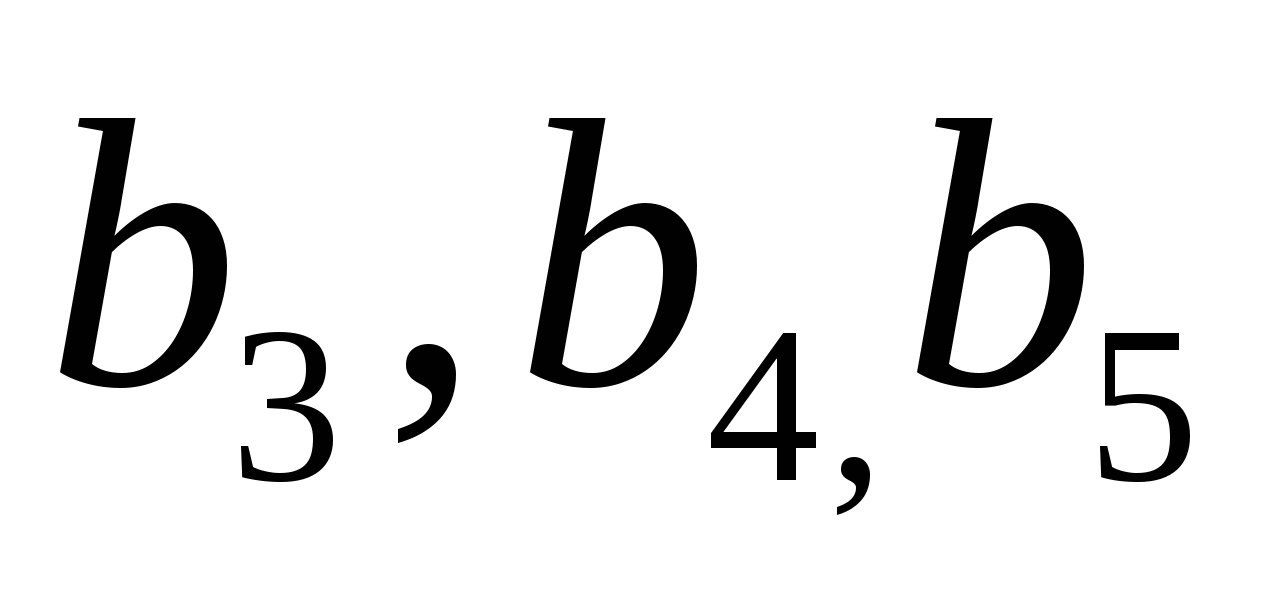 .
.
Значит, сумма площадей всех квадратов равна 32 см2.
Ответ: 32 см2.
ФОРМУЛА СЛОЖНЫХ ПРОЦЕНТОВ.
1. Клиент банка внес 1500 р. на вклад с годовым доходом 5%. Если никакие суммы со счета не снимаются и никаких дополнительных вложений не делается, то сколько денег будет на счете через 1 год, 2 года?
Решение:
Через год на сумму 1500 р. начислят ![]() р., значит, будет 1575 р.
р., значит, будет 1575 р.
Через 2 года на сумму 1575 р. начислят ![]() р., значит, будет 1653.75 р.
р., значит, будет 1653.75 р.
Решим задачу в общем виде:
2. В банк положен вклад Н рублей, доход от которого в год составляет х%. Какая сумма будет на счете через n лет?
Решение: Пусть Кn сумма вклада на счете через n лет. Тогда,
через 1 год на сумму Н начислят х% от Н (равную Н![]() ), значит К1=Н+ Н
), значит К1=Н+ Н![]() = Н(1+
= Н(1+![]() );
);
Через 2 года уже на сумму К1 начислят х%, значит К2 =К1 +К1![]() =К1 (1+
=К1 (1+![]() ).
).
Через 3 года К3 =К2 +К2![]() = К2 (1+
= К2 (1+![]() ).
).
Через 4 года К4 =К3 +К3![]() = К3 (1+
= К3 (1+![]() ).
).
…
Через n лет Кn =Кn-1 +Кn-1![]() = Кn-1 (1+
= Кn-1 (1+![]() ).
).
Т.о. мы пришли к рекуррентному соотношению:
Кn=Кn-1 (1+![]() ); К0=Н.
); К0=Н.
По этому соотношению можно найти сумму вклада за любое число лет, но для этого нам придется сначала вычислить сумму вклада за предыдущий год. Например, чтобы вычислить сумму вклада за 30 лет, необходимо знать сумму вклада за 29 лет, чтобы вычислить сумму вклада за 29 лет, необходимо знать сумму вклада за 28 лет и т.д. Эти вычисления довольно громоздкие. Было бы намного удобнее знать аналитическую формулу, выражающую прямую зависимость суммы вклада от количества лет. Преобразуя данное соотношение такую формулу получить можно:
Кn=Кn-1 (1+![]() )= Кn-2 (1+
)= Кn-2 (1+![]() )2= Кn-3 (1+
)2= Кn-3 (1+![]() )3=…= К1 (1+
)3=…= К1 (1+![]() )n-1=Н(1+
)n-1=Н(1+![]() )n. Итак,
)n. Итак,
Кn= Н(1+![]() )n;- формула сложных процентов. Эта формула широко используется в банках, для начисления процентов.
)n;- формула сложных процентов. Эта формула широко используется в банках, для начисления процентов.
3. Ежемесячно семья Комаровых платит за электроэнергию 60 р. За каждый просроченный день взимается пеня в размере 0,5% с оплачиваемой суммы.
Сколько платят Комаровы за электроэнергию, если они просрочат оплату за 5 день?
Решение:
По формуле сложных процентов Кn= Н(1+![]() )n получим
)n получим
К5= 60(1+![]() )5= 60 · 1.0055 = 60 · 1.025 = 61.5 р.
)5= 60 · 1.0055 = 60 · 1.025 = 61.5 р.
Ответ: 61.5 р. оплатят Комаровы за электроэнергию, если они просрочат 5 дней.
Исследовательский проект
Объект: Банки города Абакана
Цель исследования: Определить вид вклада в банках города Абакана, приносящего наибольшую прибыль населению.
В городе Абакан несколько акционерных банков, предлагающих населению разнообразные вклады. Я решила проанализировать процентные ставки предлагаемых вкладов нескольких банков для определения наиболее выгодного для населения.
Рассмотрим фиксированный вклад размером 1000 руб., получим предполагаемую сумму дохода через год (предполагается, что деньги в течении года не снимаются со счета)
О.А.О. Банк Хакасии.
Виды вкладов
Процентные ставки
Сумма вклада
Полученная сумма
3 месяца
6 месяцев
1 год
3×4
6×2
1
Накопительный
6.5%
9%
11%
1000 руб.
1286 р.
1188 р.
1110 р.
Классический
7%
10%
11%
1000 руб.
1311 р.
1210 р.
1110 р.
Пенсионный
7%
10%
11%
1000 руб.
1311 р.
1210 р.
1110 р.
О.А.О. Муниципальный Банк Хакасии.
Виды вкладов
Процентные ставки
Сумма вклада
Полученная сумма
3 месяца
6 месяцев
1 год
3×4
6×2
1
Городской
7%
8.5%
10.5%
1000 руб.
1311 р.
1177 р.
1105 р.
Универсальный
8%
10.5%
11%
1000 руб.
1360 р.
1221 р.
1110 р.
Ветеран
7%
9%
11%
1000 руб.
1311 р.
1188 р.
1110 р.
О.А.О. Россельхозбанк.
Виды вкладов
Процентные ставки
Сумма вклада
Полученная сумма
3 месяца
6 месяцев
1 год
3×4
6×2
1
Срочный
8.5%
9.5%
11%
1000 руб.
1386 р.
1199 р.
1110 р.
Накопительный
7.75%
8.75%
10.25%
1000 руб.
1348 р.
1183 р.
1102 р.
Кубышка
7.75%
8.75%
10.25%
1000 руб.
1348 р.
1183 р.
1102 р.
О.А.О. Сбербанк России.
Виды вкладов
Процентные ставки
Сумма вклада
Полученная сумма
3 месяца
6 месяцев
1 год
3×4
6×2
1
Особый
-
6.75%
7.5%
1000 руб.
-
1140 р.
1075 р.
Депозит
5.25%
7.75%
9.25%
1000 руб.
1227 р.
1161 р.
1093 р.
Пополняемый депозит
-
7.5%
9%
1000 руб.
-
1156 р.
1090 р.
О.А.О. Банк Кедр.
Виды вкладов
Процентные ставки
Сумма вклада
Полученная сумма
3 месяца
6 месяцев
1 год
3×4
6×2
1
С определённым сроком хранения и выплатой процентов в конце срока
3.5%
6%
9%
1000 руб.
1147 р.
1124 р.
1090 р.
Накопительный
4%
6%
9%
1000 руб.
1170 р.
1124 р.
1090 р.
Пенсионный
-
6%
10.5%
1000 руб.
-
1124 р.
1105 р.
О.А.О. Банк Енисей
Виды вкладов
Процентные ставки
Сумма вклада
Полученная сумма
3 месяца
6 месяцев
1 год
3×4
6×2
1
Универсальный
3.5%
7%
9%
1000 руб.
1147 р.
1070р.
1090 р.
Накопительный
4%
7,5%
9%
1000 руб.
1170 р.
1156р.
1090 р.
Пенсионный
-
7,5%
10.5%
1000 руб.
-
1156р.
1105 р.
О.А.О. Центрально-Азиатский Банк
Виды вкладов
Процентные ставки
Сумма вклада
Полученная сумма
3 месяца
6 месяцев
1 год
3×4
6×2
1
Особый
3.5%
6%
9%
1000 руб.
1147 р.
1124 р.
1090 р.
Накопительный
4%
8%
9%
1000 руб.
1170 р.
1080 р.
1090 р.
Пенсионный
-
8,5%
10.5%
1000 руб.
-
1085 р.
1105 р.
Сравним доходы, полученные через год вкладов на 3 месяца:
Банк, название вклада
сумма
Банк Хакасии
Накопительный
1286 р.
Классический
1311 р.
Пенсионный
1311 р.
Муниципальный Банк Хакасии
Городской
1311 р.
Универсальный
1360 р.
Ветеран
1311 р.
Россельхозбанк
Срочный
1386 р.
Накопительный
1348 р.
Кубышка
1348 р.
Сбербанк России
Особый
0
Депозит
1227 р.
Пополняемый депозит
0
Банк Кедр
С определённым сроком хранения и выплатой процентов в конце срока
1147 р.
Накопительный
1170 р.
Пенсионный
0
Банк Енисей
Универсальный
1147 р.
Накопительный
1170 р.
Пенсионный
0
Банк Центрально-Азиатский
Особый
1147 р.
Накопительный
1170 р.
Пенсионный
0
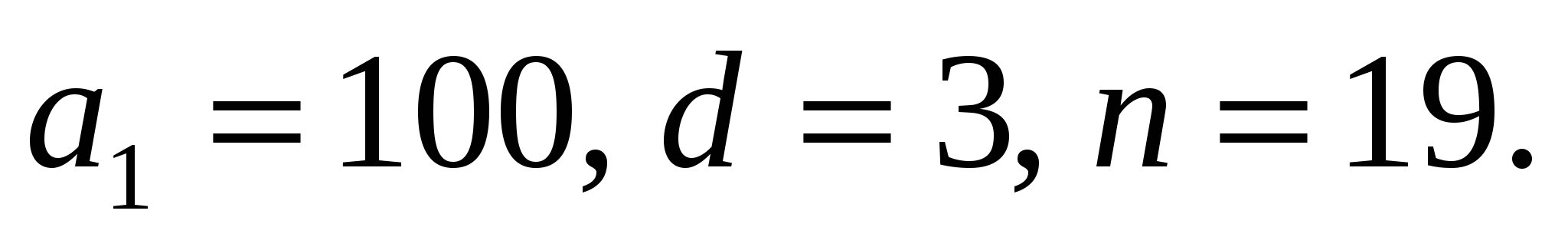 Наибольшая сумма будет получена 1386 рублей по «Срочному» вкладу в Россельхозбанке.
Наибольшая сумма будет получена 1386 рублей по «Срочному» вкладу в Россельхозбанке.
Сравним доходы, полученные через год вкладов на 6 месяца:
Банк, название вклада
сумма
Банк Хакасии
Накопительный
1188 р.
Классический
1210 р.
Пенсионный
1210 р.
Муниципальный Банк Хакасии
Городской
1177 р.
Универсальный
1221 р.
Ветеран
1188 р.
Россельхозбанк
Срочный
1199 р.
Накопительный
1183 р.
Кубышка
1183 р.
Сбербанк России
Особый
1140 р.
Депозит
1161 р.
Пополняемый депозит
1156 р.
Банк Кедр
С определённым сроком хранения и выплатой процентов в конце срока
1147 р.
Накопительный
1170 р.
Пенсионный
-
Банк Енисей
Универсальный
1070р.
Накопительный
1156р.
Пенсионный
1156р.
Банк Центрально-Азиатский
Особый
1124 р.
Накопительный
1080 р.
Пенсионный
1085 р.
Наибольшая сумма будет получена 1221 рубль по «Универсальному» вкладу в Муниципальном Банке Хакасии.
Сравним доходы, полученные через год вкладов на 1 год:
Банк, название вклада
сумма
Банк Хакасии
Накопительный
1110 р.
Классический
1110 р.
Пенсионный
1110 р.
Муниципальный Банк Хакасии
Городской
1105 р.
Универсальный
1110 р.
Ветеран
1110 р.
Россельхозбанк
Срочный
1110 р.
Накопительный
1102 р.
Кубышка
1102 р.
Сбербанк России
Особый
1075 р.
Депозит
1093 р.
Пополняемый депозит
1090 р.
Банк Кедр
С определённым сроком хранения и выплатой процентов в конце срока
1090 р.
Накопительный
1090 р.
Пенсионный
1105 р.
Банк Енисей
Универсальный
1090 р.
Накопительный
1090 р.
Пенсионный
1105 р.
Банк Центрально-Азиатский
Особый
1090 р.
Накопительный
1090 р.
Пенсионный
1105 р.
Наибольшая сумма будет получена 1110 рублей по «Срочному» вкладу в Россельхозбанке и по вкладам «Универсальный» и «Ветеран» в Муниципальном Банке Хакасии и по вкладам «Накопительный», «Классический», «Пенсионный» в Банке Хакасии.
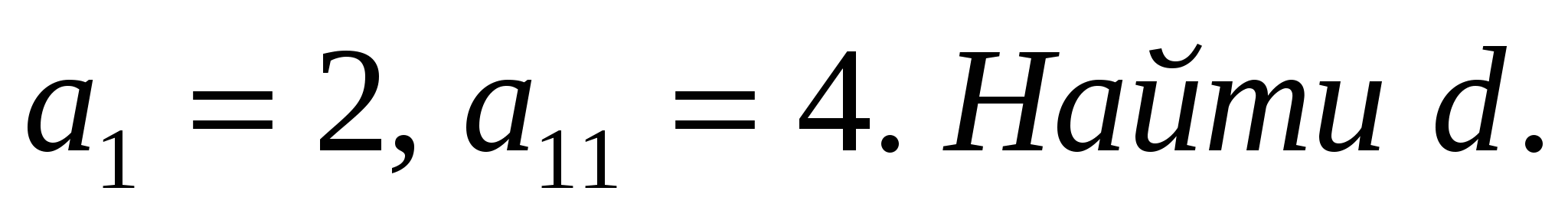
Наибольшая сумма будет получена 1386 рублей по «Срочному» вкладу в Россельхозбанке на 3 месяца.
Докажем, что наибольший доход получат вкладчики Россельхозбанка по «Срочному» вкладу на 3 месяца по сравнению с доходом, полученным вкладчиками по этому вкладу на 1 год.
Доказательство:
Пусть в начале года положили Н рублей под х% годовых.
В конце года получат
Н+ Н ![]() = Н(1+
= Н(1+![]() ) руб.
) руб.
Пусть теперь положили Н рублей под х% годовых на 3 месяца и не снимали их в течении года Н(1+![]() )4 руб. Сравним полученные величины:
)4 руб. Сравним полученные величины:
![]() >0, так как Н>0, (1+
>0, так как Н>0, (1+![]() )>0,
)>0, ![]() >0. Значит Н(1+
>0. Значит Н(1+![]() )4 > Н(1+
)4 > Н(1+![]() ), т.е. по вкладу на 3 месяца по истечении года вкладчики получат большую сумму.
), т.е. по вкладу на 3 месяца по истечении года вкладчики получат большую сумму.
ЗАКЛЮЧЕНИЕ.
В данной работе мы рассмотрели последовательности, способы задания последовательностей, более подробно остановились на рекуррентных соотношениях и их применении в различных областях науки: экономика, биология, информатика и т.д.
При решении задач прикладного характера было выявлено, что наиболее распространённым и применяемым способом задания последовательностей, является рекуррентное соотношение.
Среди рекуррентных соотношений особое место занимают арифметическая и геометрическая прогрессии и банковские расчёты. Поэтому в работе были представлены нестандартные задачи на тему «Прогрессии», предлагаемые на вступительных экзаменах и олимпиадах по математике.
Проведённое исследование помогло выявить наилучший вариант вклада для вложения некоторой суммы денег.
Приведены решения задач, позволяющих решить отдельные бытовые проблемы каждого человека; задачи технологии производства, дают возможность предвидеть результат размножения бактерий в биологии, рассчитать схему приема лекарства, наиболее эффективную для больного, позволяют рассчитать увеличение нагрузки спортсменов, улучшающие их результат, а также решить много других проблем, довольно часто стоящих перед человеком.
Современному человеку необходимо просчитывать предлагаемые варианты какого-либо вопроса и выбор наиболее благоприятного из них.
В наше время деньги - едва ли не самое главное в жизни человека, в результате перед нами стоит проблема в решении выбора банка, в который выгоднее внести взнос, для приобретения в дальнейшем времени прибыли.
Впоследствии я посетила некоторые банки города Абакана и, ознакомившись с предлагаемыми процентными ставками по отдельным вкладам, сравнила полученные доходы по этим вкладам. Я получила определённые результаты исследования и привела их в данной работе, а также доказала правильность моих результатов.
Полученные результаты помогут многим решить проблему вложения денег в коммерческие и некоммерческие банки. Жители города Абакана смогут получить больший доход от вклада, что, в общем, и являлось главной сутью моего исследования.
Список литературы
-
Алгебра для 9 класса: Учеб. пособие для учащихся шк. и кл. с углубл. изуч. математики/ Н.Я. Виленкин, Г.С. Сурвилло, А.С. Симонов, А.И. Кудрявцев/ Под ред. Н.Я. Виленкина. - 2-е изд.- М.: Просвещение, 1998.- 384с.
-
Алгебра и начала анализа.8-11кл.: Пособие для школ и классов с углубл. изучением математики/ Л.И.Звавич, Л.Я.Шляпочник, М.В. Чинкина.- 2-е изд., стереотип. -М.: Дрофа,2001.-352с.
-
Васильев Н.Б., Гутенмахер В.Л., Работ Ж.М., Тоом А.Л. Заочные математические олимпиады.-2-е изд., перераб.-М.: Наука. Гл. ред. физ.-мат. лит., 1987.-176с.
-
Виленкин Н.Я. Комбинаторика. -М.: Наука. Гл. ред. физ.-мат. лит.,1969.-328с.
-
Г.П. Мещерякова. Нестандартные задачи на прогрессии//МШ.-1998.- №6-с.47.
-
Дополнительные главы по курсу математики. Учебное пособие по факультативному курсу для учащихся 9 классов. Сборник статей. Сост. П.В.Стратилатов, изд. 2-е, испр. и доп. М.: Просвещение, 1974.-144с.
-
Кострикина Н.П. Задачи повышенной трудности в курсе алгебры 7-9 кл.: Кн. для учителя. -М.: Просвещение, 1991.-237с.
-
М.Г. Лускина. Из опыта изучения темы «Прогрессии»// МШ.-1973.-№1.-с.31-36
-
Н.А. Петровская. Коллекция нестандартных задач «на прогрессии»// МШ. №2.-1991.-с.60.
-
Перельман Я.И. Живая математика. -М.: Триада-литера.-1994.-175с.
-
Пичурин Л.Ф.За страницами учебника алгебры: Кн.для учащихся 7-9 кл. средн. шк.- М.: Просвещение,1990.-224с.
-
Рязановский А.Р. Алгебра и начала анализа: 500 способов и методов решения задач по математике для школьников и поступающих в вузы.-М.:Дрофа,2001.-480с.
-
Сборник задач по алгебре для 8-9 классов: Учеб. Пособие для учащихся шк. И кл. с углубл. изуч. математики/ М.Л. Галицкий, А.М. Гольдман, Л.И.Звавич.- 5-е изд.- М.: Просвещение, 1999. - 271 с.
-
Сборник задач по математике для поступающих в втузы: Учеб. пособие. /Егерев В.К., Кордемский Б.А., Зайцев В.В. и др. .; под.ред. М.И.Сканави.- М.: Высш. Шк,2005.-528с.
-
Фоминых Ю.Ф. Прикладные задачи по алгебре для 7-9 классов: Кн.для учителя.- М. : Просвещение, 1999.-112с.
22