Разработка Подробное доказательство теоремы об ортогональной проекции многоугольника (10 класс)

_{Подробное доказательство теоремы об ортогональной проекции многоугольника}

Если - проекция плоского n-угольника на плоскость, то , где - угол между плоскостями многоугольников и . Иными словами, площадь проекции плоского многоугольника равна произведению площади проецируемого многоугольника на косинус угла между плоскостью проекции и плоскостью проецируемого многоугольника.

Доказательство. I этап. Проведём доказательство сначала для треугольника . Рассмотрим 5 случаев.

1 случай. лежат в плоскости проекции.

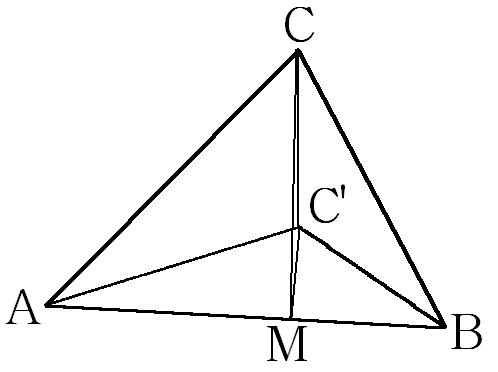
Пусть - проекции точек на плоскость соответственно. В нашем случае . Положим, что . Пусть - высота , тогда по теореме о трёх перпендикулярах мы можем заключить, что - высота ( - проекция наклонной , - её основание и прямая проходит через основание наклонной, причём ).

Рассмотрим . Он прямоугольный. По определению косинуса :

С другой стороны, так как и , тогда по определению - линейный угол двугранного угла, образованного полуплоскостями плоскостей и с граничной прямой , а, следовательно, его мера является также и мерой угла между плоскостями проекции треугольника и самого треугольника, то есть .

Найдём отношение площади к :

Заметим, что формула остаётся верной даже когда . В этом случае

2 случай. Тольколежит в плоскости проекции и параллельна плоскости проекции.

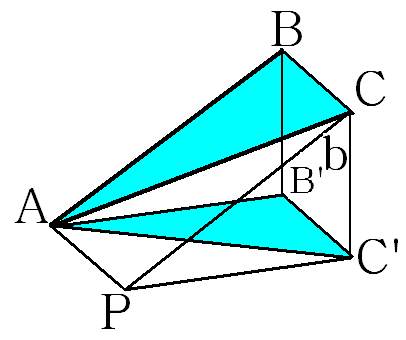
Пусть - проекции точек на плоскость соответственно. В нашем случае .

Проведём через точку прямую . В нашем случае прямая пересекает плоскость проекции, значит, по лемме, и прямая пересекает плоскость проекции. Пусть это будет в точке Так как , то точки лежат в одной плоскости, а так как параллельна плоскости проекции, то по следствию из признака параллельности прямой и плоскости следует, что . Следовательно, - параллелограмм. Рассмотрим и . Они равны по трём сторонам (- общая, , , как противолежащие стороны параллелограмма). Заметим, что четырёхугольник - прямоугольник и равен (по катету и гипотенузе), следовательно, равен по трём сторонам. Поэтому и .

Для применим 1 случай: , т. е..

3 случай. Тольколежит в плоскости проекции и не параллельна плоскости проекции.

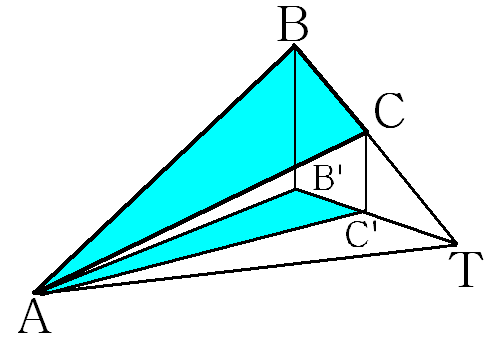
Пусть точка - точка пересечения прямой с плоскостью проекции. Заметим, что и . По 1 случаю: и . Таким образом получаем, что

4 случай. Вершины не лежат в плоскости проекции. Рассмотрим перпендикуляры . Возьмём среди этих перпендикуляров наименьший. Пусть это будет перпендикуляр . Может оказаться, что , либо только , либо только . Тогда всё равно берём .

Отложим от точки на отрезке точку , так, чтобы и от точки на отрезке точку , так, чтобы . Такое построение возможно, так как - наименьший из перпендикуляров . Заметим, что является проекцией и , по построению. Докажем, что и равны.

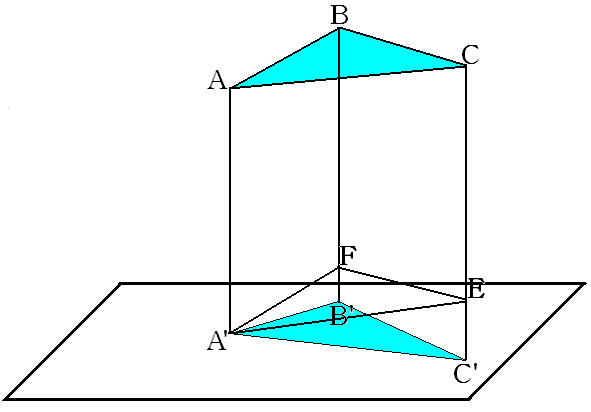
Рассмотрим четырёхугольник . По условию - перпендикуляры к одной плоскости, следовательно, по теореме , поэтому . Так как по построению , тогда по признаку параллелограмма (по параллельным и равным противолежащим сторонам) мы можем заключить, что - параллелограмм. Значит, . Аналогично доказывается, что , . Следовательно, и равны по трём сторонам. Поэтому . Заметим, что и , как противолежащие стороны параллелограммов, следовательно, по признаку параллельности плоскостей, . Так как эти плоскости параллельны, то они образуют один и тот же угол с плоскостью проекции.

Для применимы предыдущие случаи:.

5 случай. Плоскость проекции пересекает стороны . Рассмотрим прямые . Они перпендикулярны к плоскости проекции, поэтому по теореме они параллельны. На сонаправленных лучах с началами в точках соответственно отложим равные отрезки , таким образом, чтобы вершины лежали вне плоскости проекции. Заметим, что является проекцией и , по построению. Покажем, что равен.

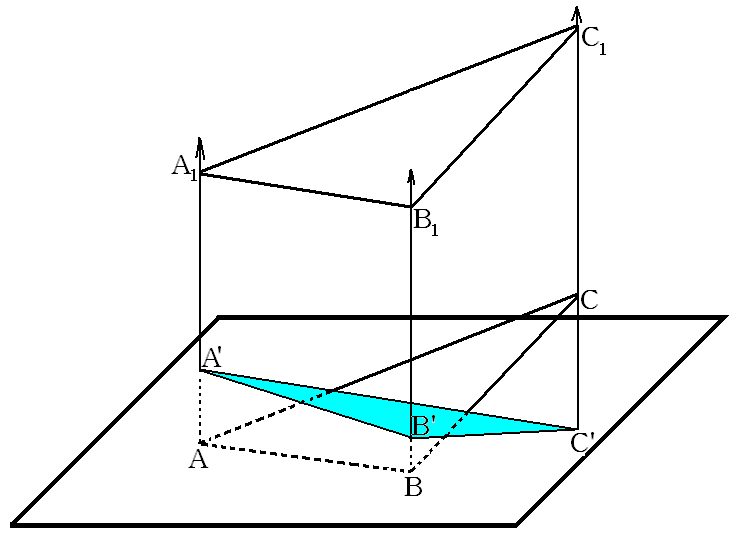
Так как и , по построению, тогда . Следовательно, по признаку параллелограмма (по двум равным и параллельным сторонам), - параллелограмм. Аналогично доказывается, что и - параллелограммы. Но тогда , и (как противолежащие стороны), поэтому равен по трём сторонам. Значит, .

Кроме того, , и , поэтому , по признаку параллельности плоскостей. Так как эти плоскости параллельны, то они образуют один и тот же угол с плоскостью проекции.

Для применим 4 случай:.

II этап. Разобьем плоский многоугольник на треугольники с помощью диагоналей, проведенных из вершины : Тогда по предыдущим случаям для треугольников: .

Что и требовалось доказать.