- Учителю
- Упражнения на закрепление и проверки знаний по теме «Прогрессии»
Упражнения на закрепление и проверки знаний по теме «Прогрессии»
Учитель математики Кожахметова Клара Есмаганбетовна
Упражнения на закрепление и проверки знаний по теме «Прогрессии»
Пример1.Найдите номер члена арифметической прогрессии, равного
47, если 
Решение:
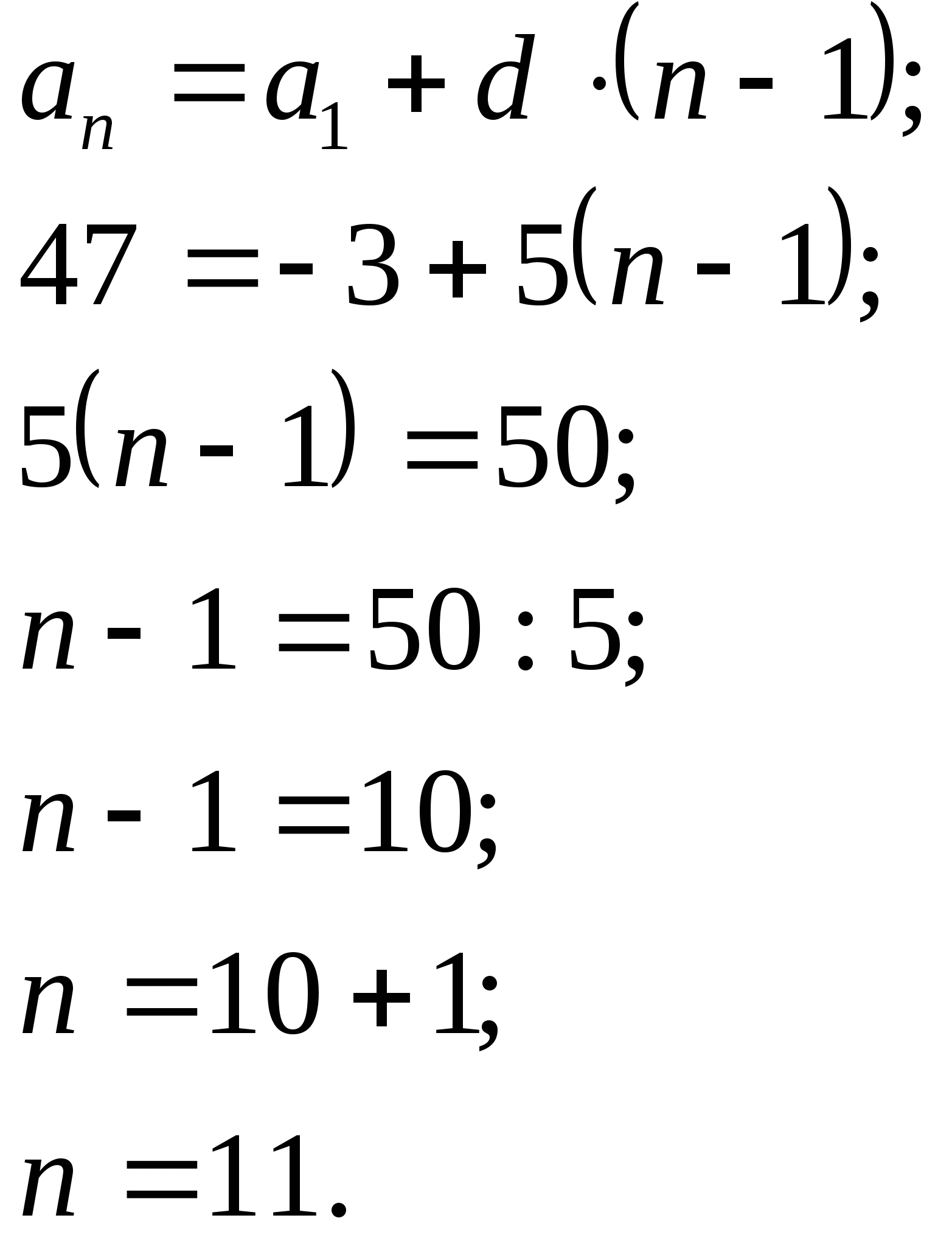
Ответ:11.
Пример2. Найдите первый член арифметической прогрессии, если
,
.
Решение:
.
48=23+5d;
5d=48-23;
5d=25;
d=25:5;
d=5.
Ответ: -2.
Пример3. Найдите разность арифметической прогрессии, если
Решение
а
67=7+15d;
15d=67-7;
15d=60;
d=60:15;
d=4.
Ответ d=4.
Пример4. В арифметической прогрессии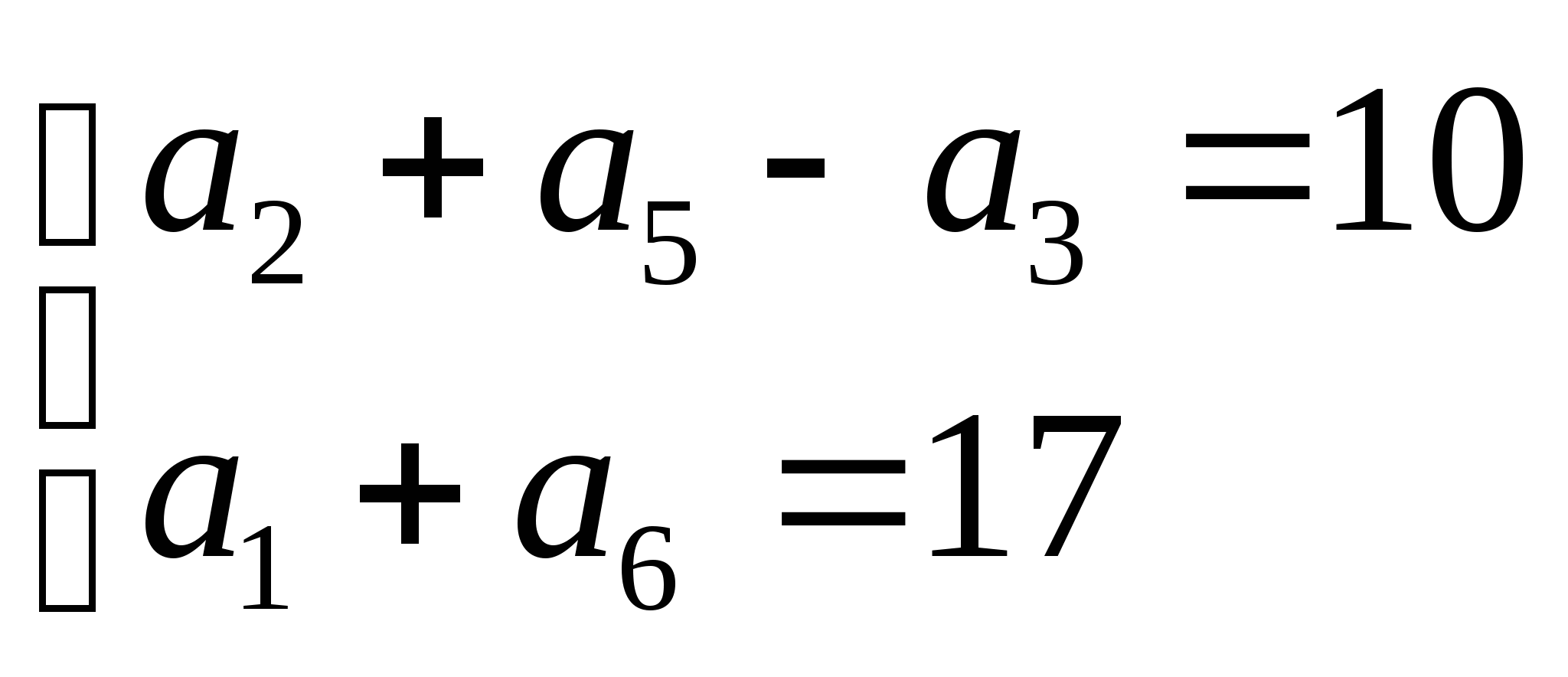 
.
Найдите а
.
Решение: ;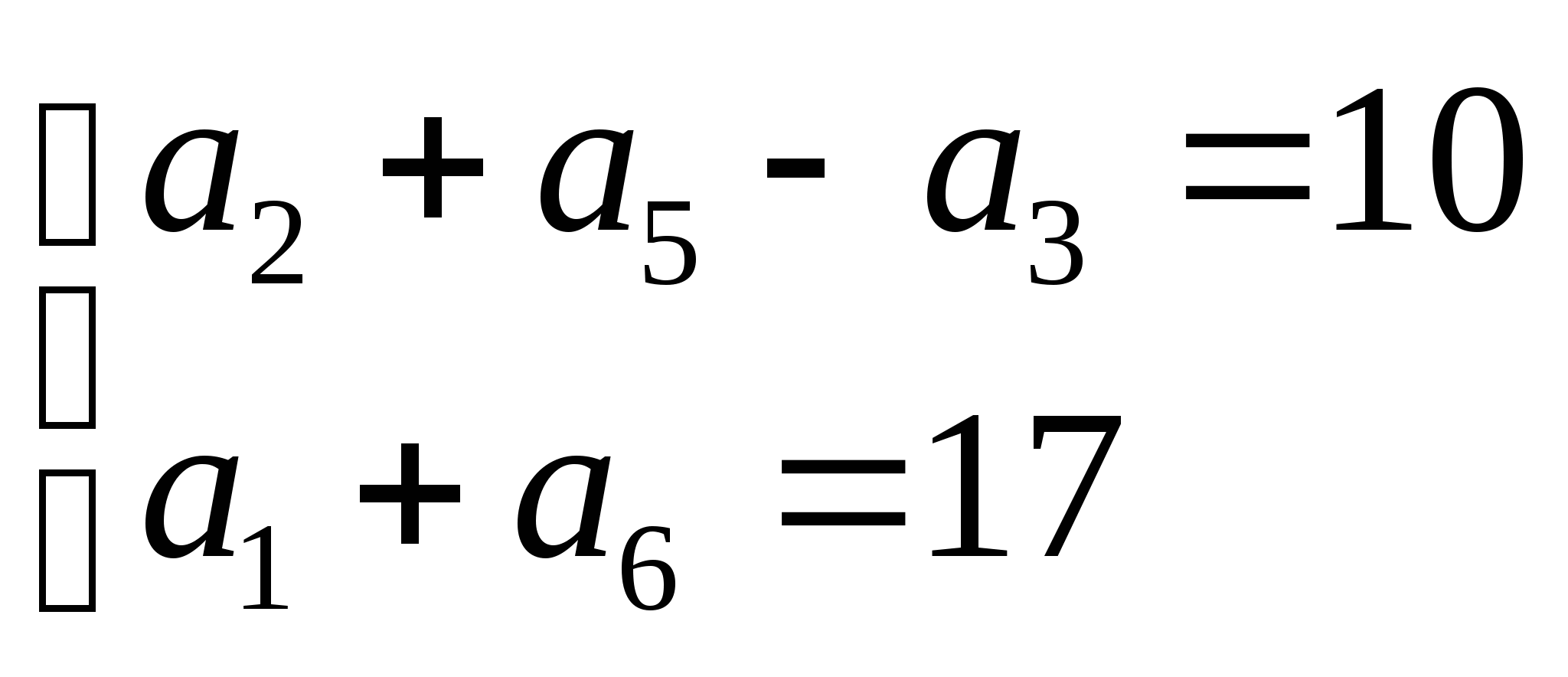
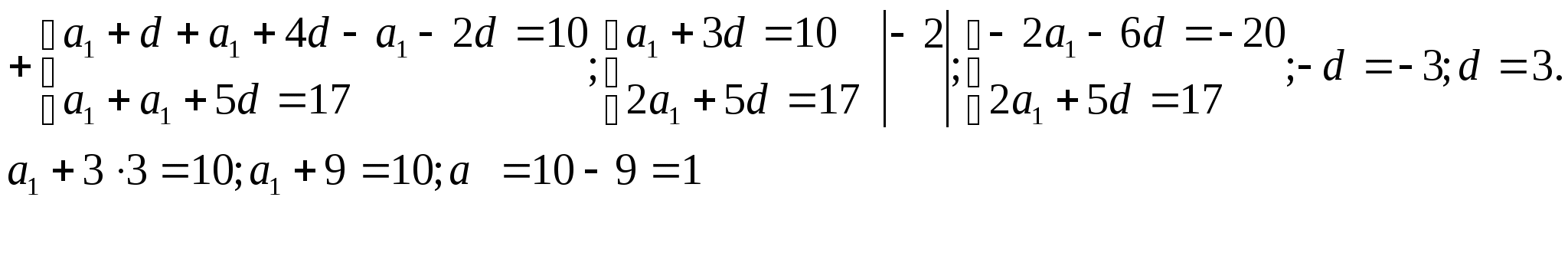Ответ:1.
Пример5.Между числами 8 и 26 вставьте пять чисел, которые вместе с данными числами составят арифметическую прогрессию.
Решение:
8; 
.
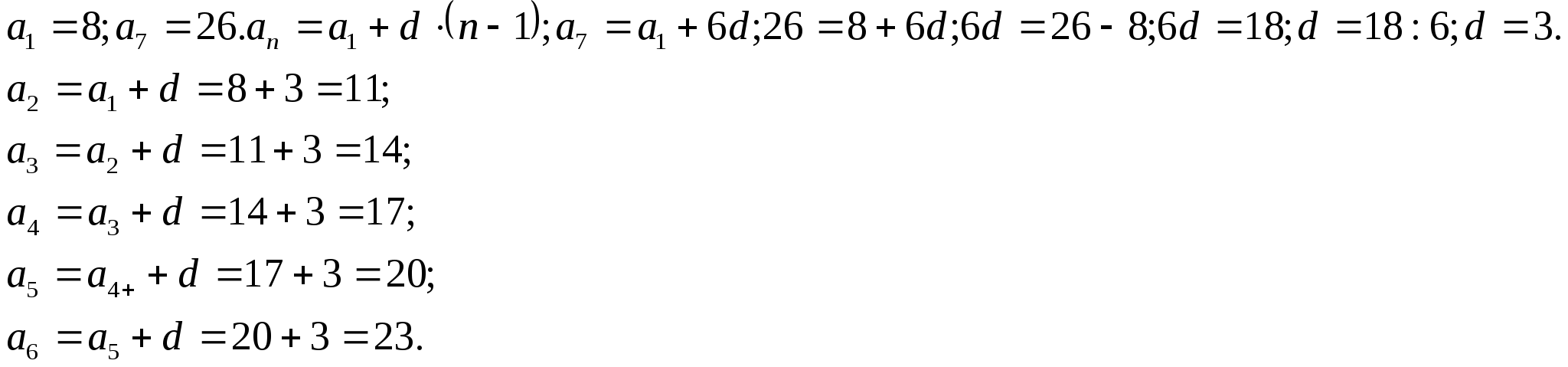Ответ:
11; 14;17;20;23.
Пример6. В арифметической прогрессии а
Найдите
Решение: а
Ответ:102.
Пример7. В арифметической прогрессии 
,
,
.
Найдите n.
Решение: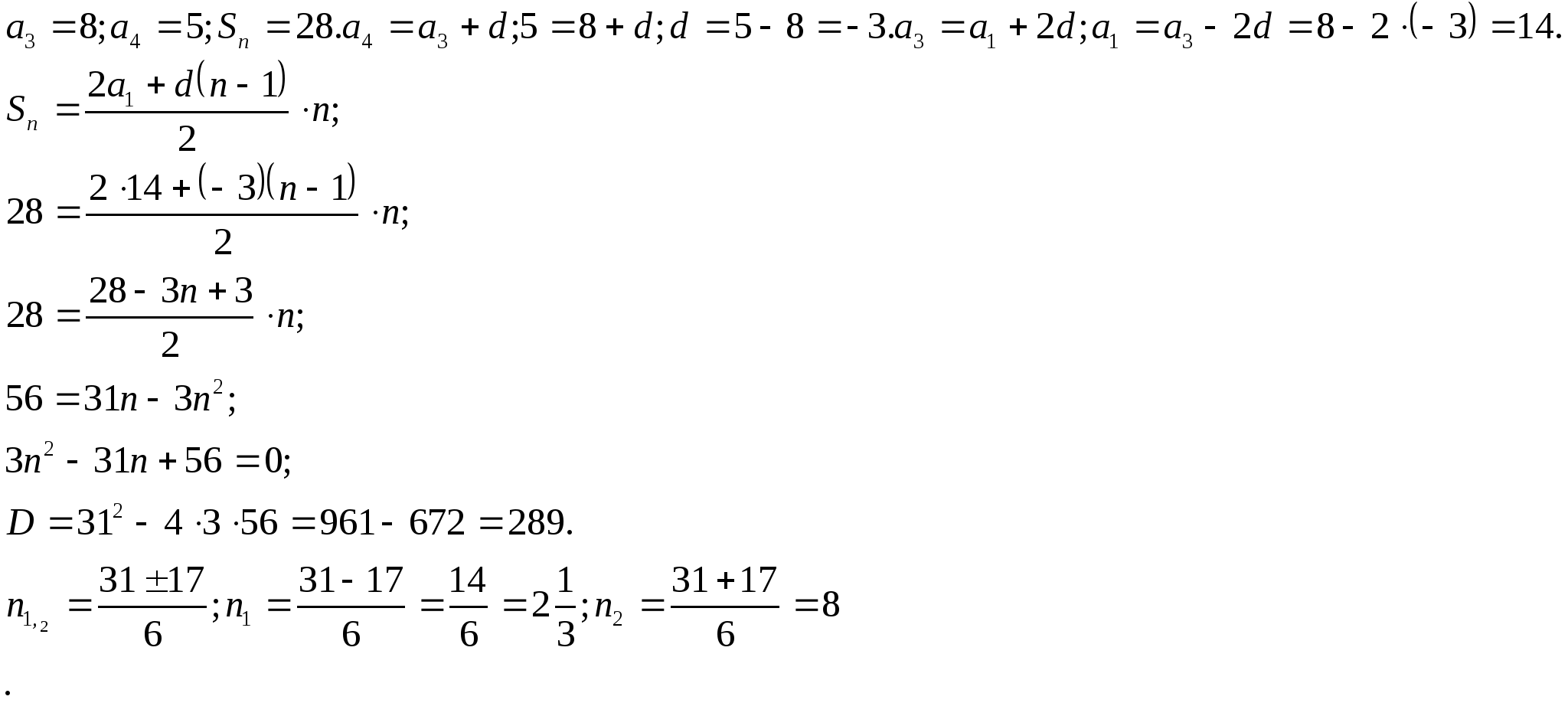 
Ответ:n=8
Пример8. Найдите сумму всех натуральных чисел, кратных 6 и не превышающих 70.
Решение.
Из условия следует:
: 
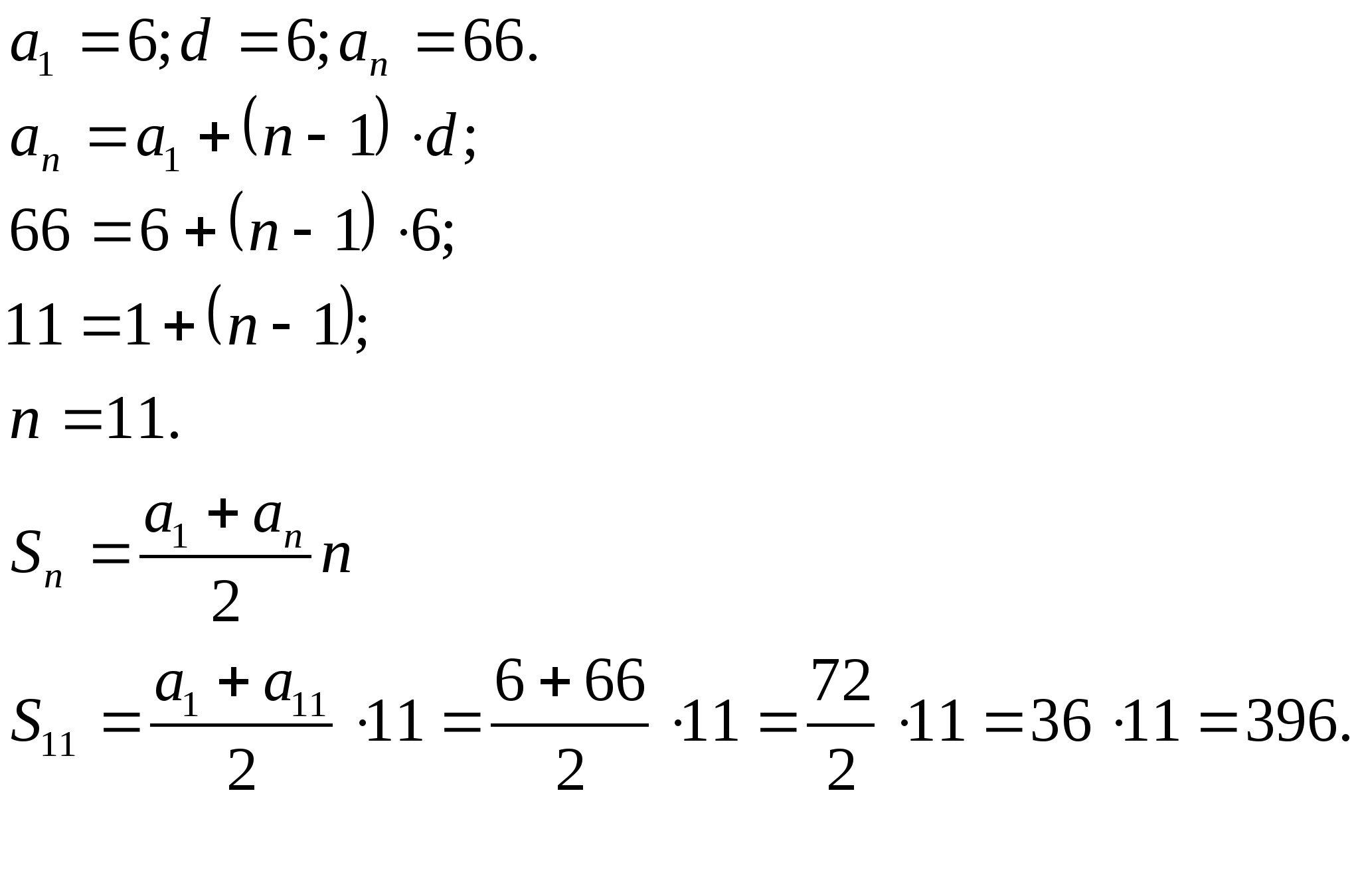
Ответ:396.
Пример9. В арифметической прогрессии 
,
.
Найдите d.
Решение:
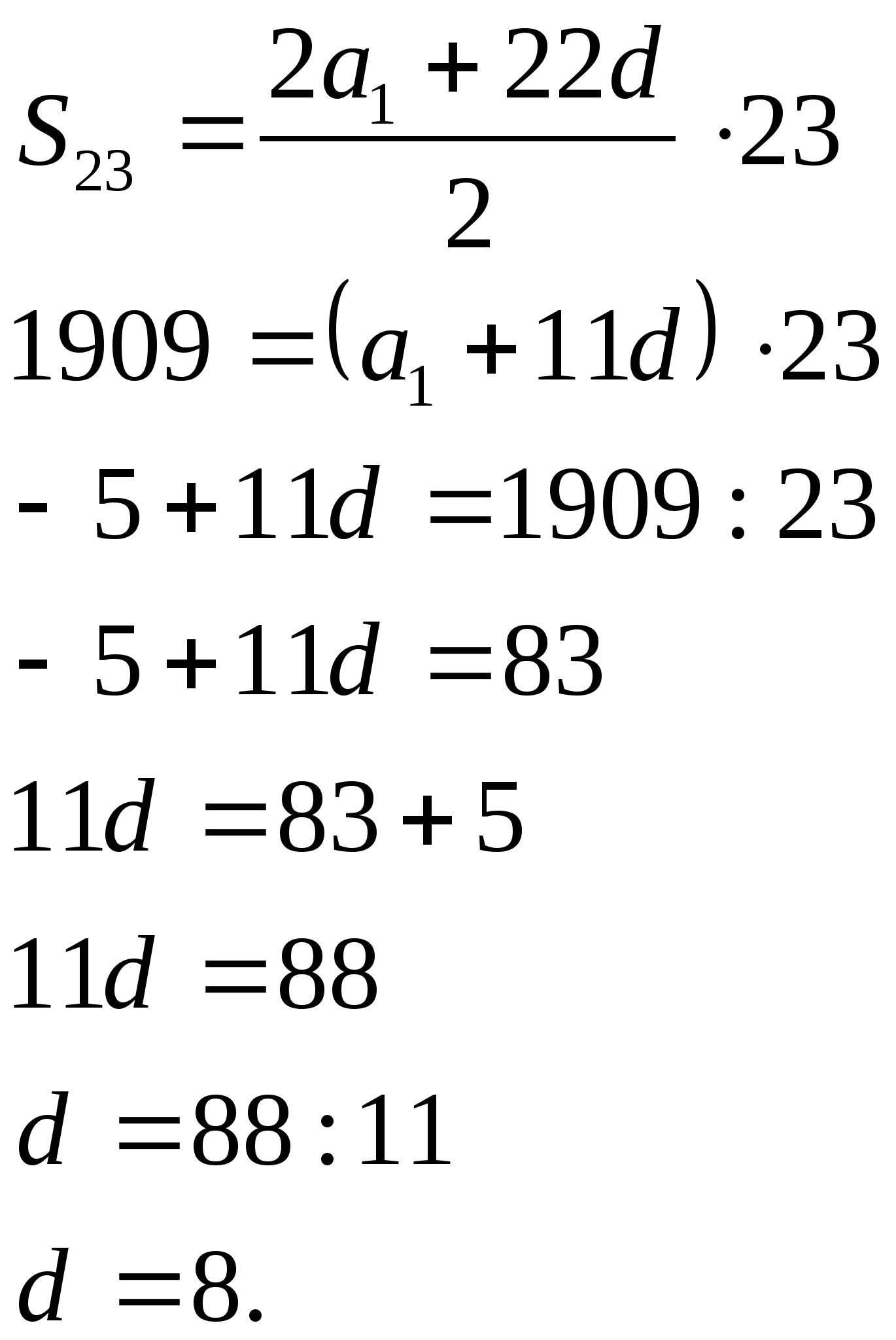
Ответ:8.
Пример10. Сколько членов арифметической прогрессии
105, 98, 91, … нужно взять , чтобы их сумма была равна нулю?.
Решение:
Из условия следует , что а
,
.
Значит d=
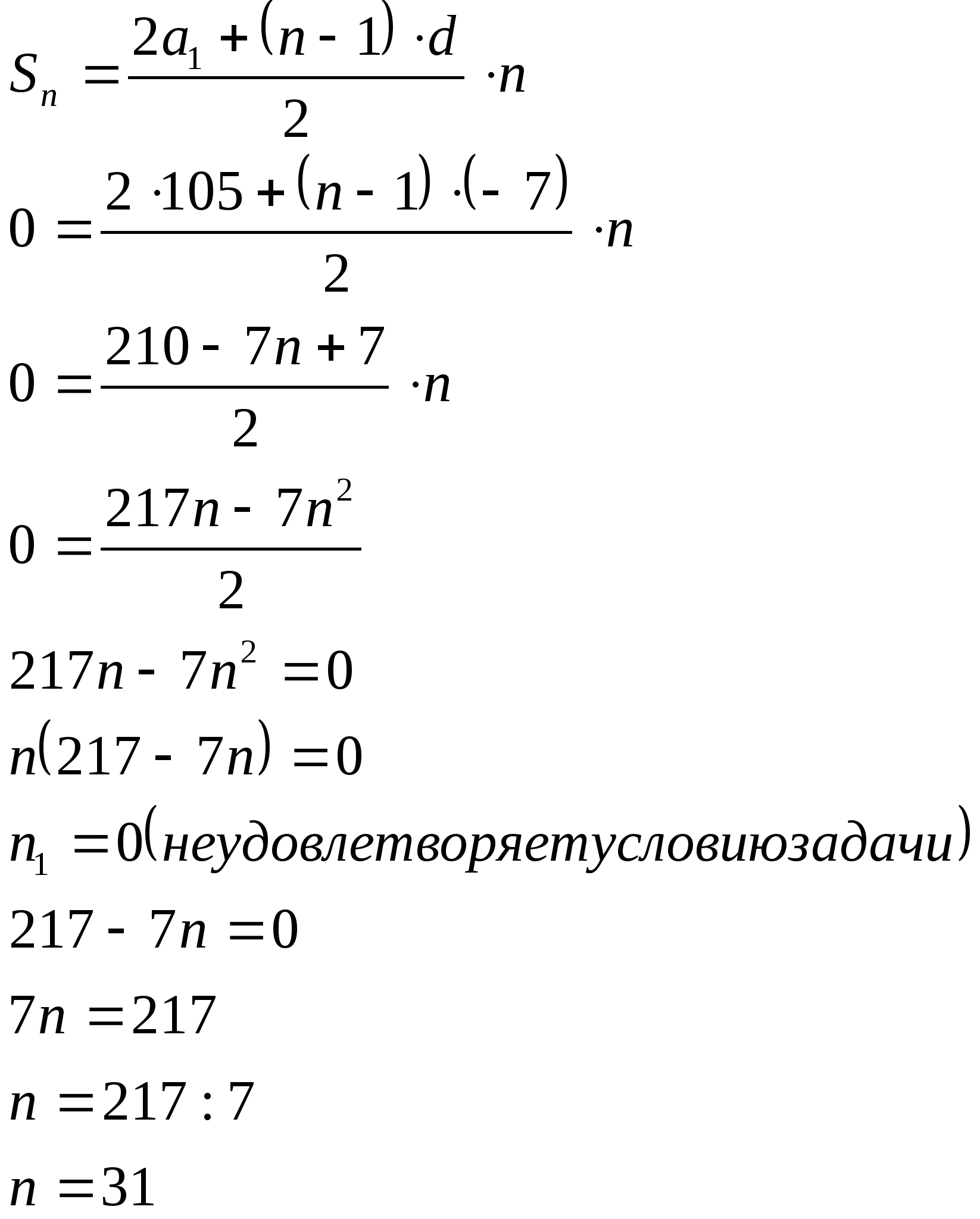
Ответ: 31.
Пример11.Найти сумму десяти первых членов арифметической
прогрессии 
.
Решение:
Так как
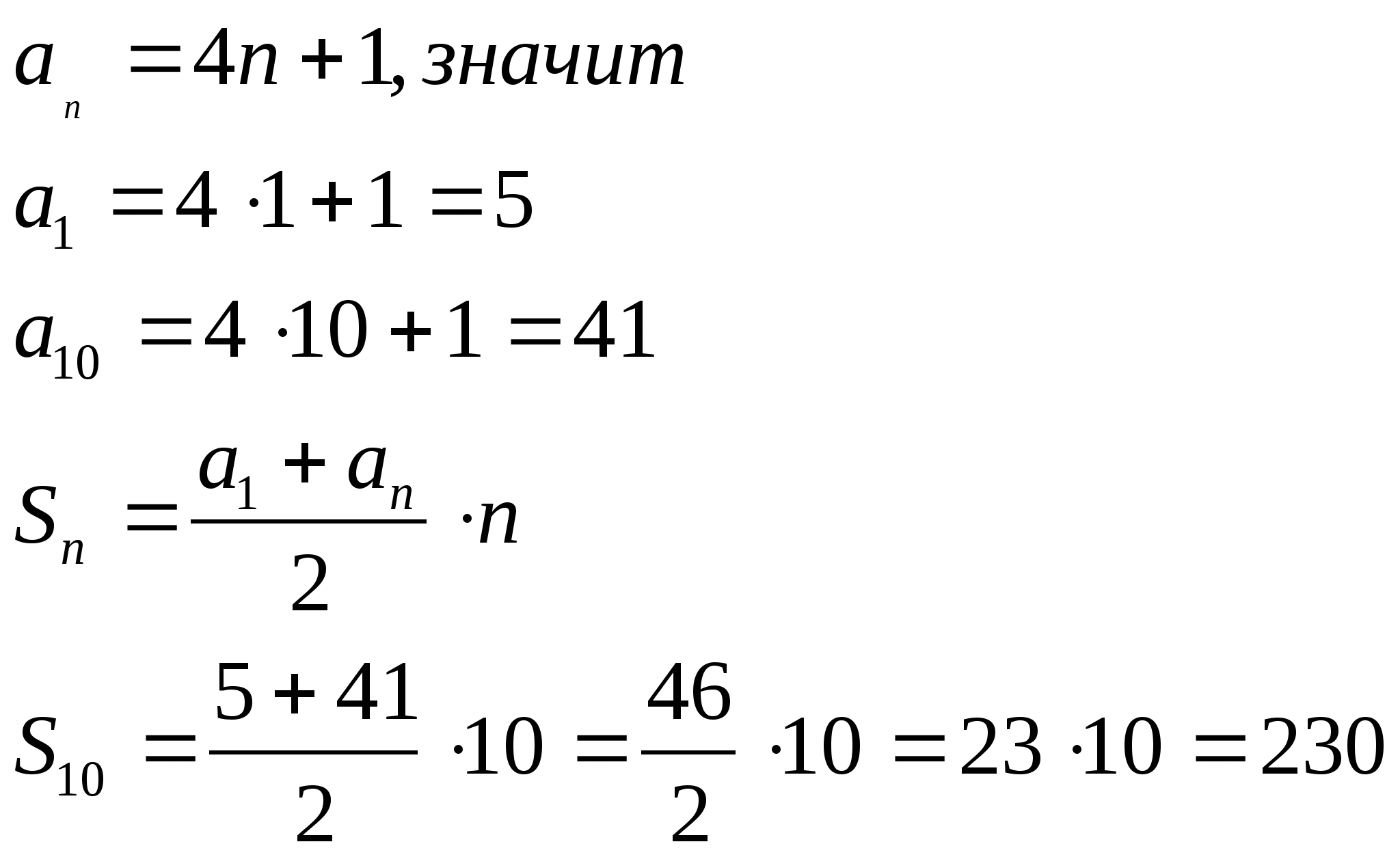
Ответ: 230.
Пример 12. В арифметической прогрессии 
,
=
16.
Найдите а
.
Решение:
По признаку арифметической прогрессии: каждый член арифметической прогрессии, начиная со второго, есть среднее арифметическое соседних с ним членов, имеем:
Ответ: 15,6
Пример13.Найти сумму 19 первых членов арифметической прогрессии,
если известно, что 
Решение:
..
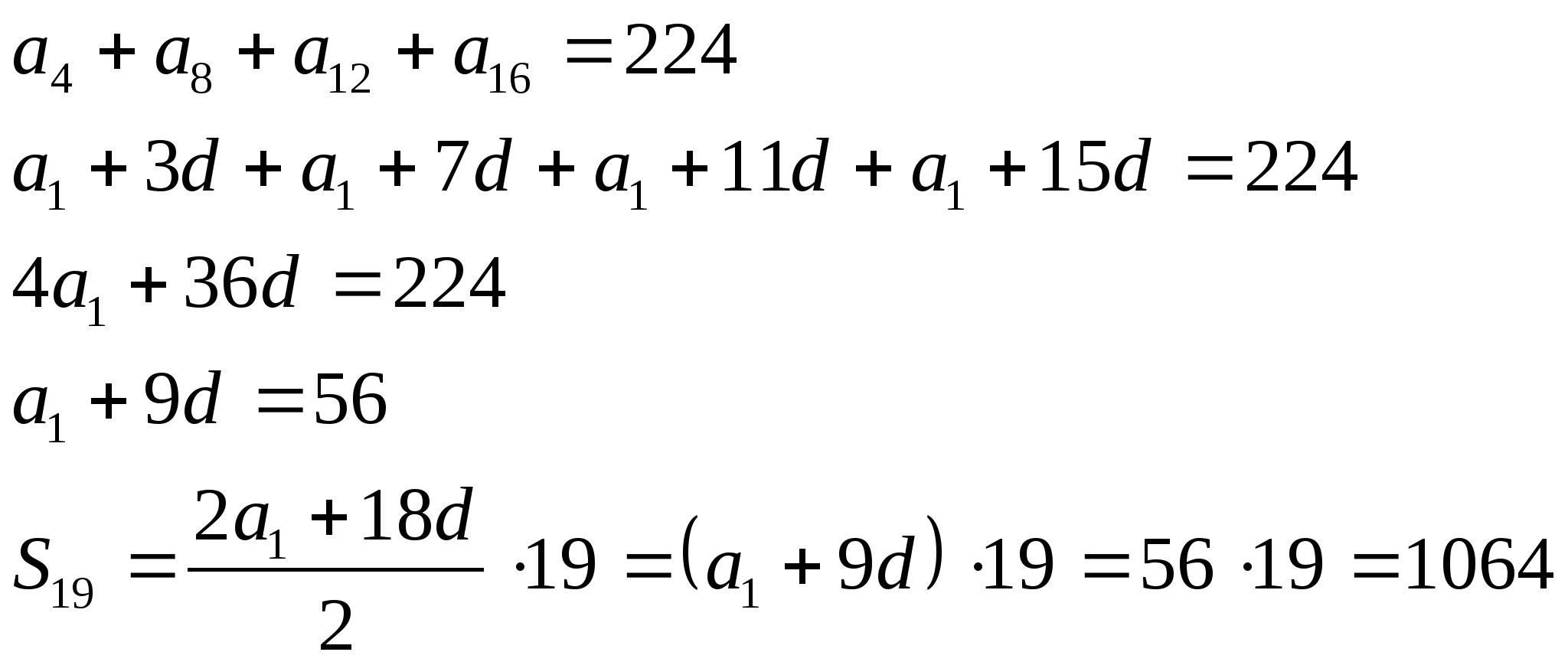Ответ:1064.
Пример14.Найдите пятый член геометрической прогрессии, в которой
,
Решение:
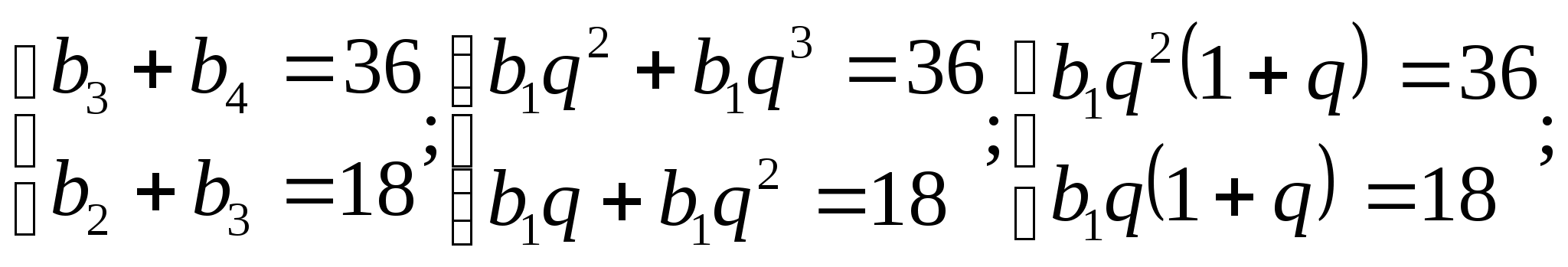
Разделим первое уравнение на второе: q=2; b
;
b
;
.
Ответ: 48.
Пример15. Между числами 243 и 1 поместите четыре числа , которые вместе с данными числами образовали бы геометрическую прогрессию.
Решение:
243; b
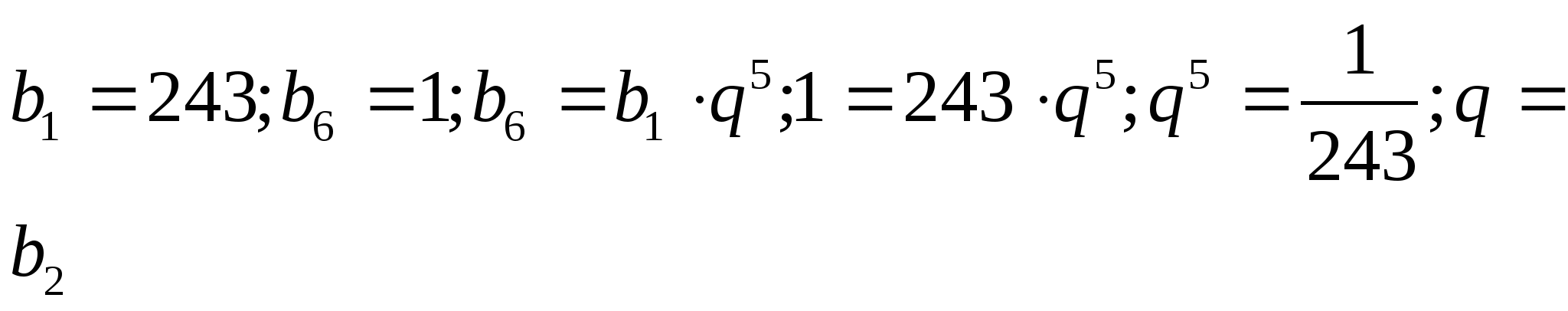
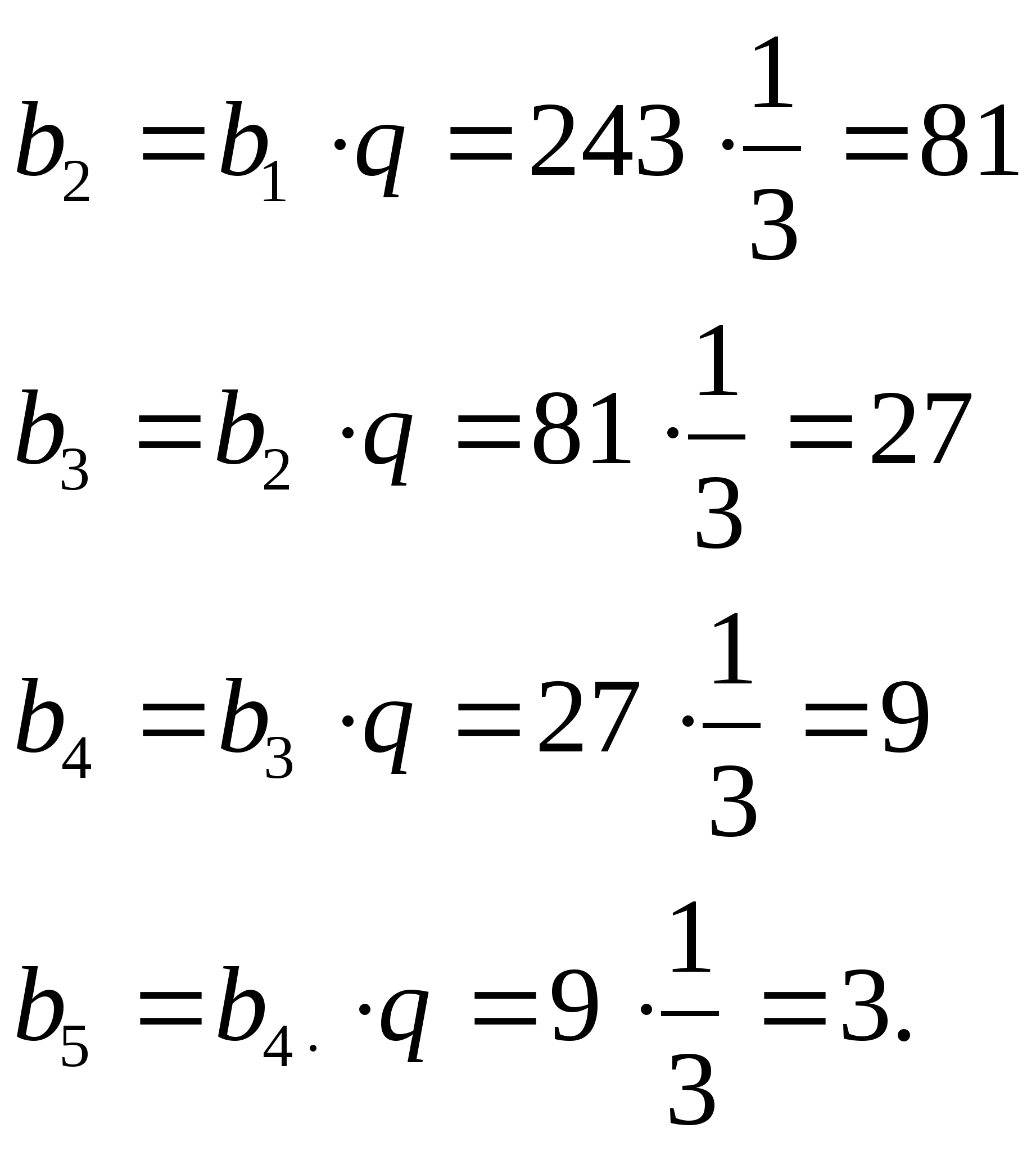
Ответ: 81; 27;9;3.
Пример16.Последовательность 3; 6; … - геометрическая прогрессия.
Найдите 
.
Решение:
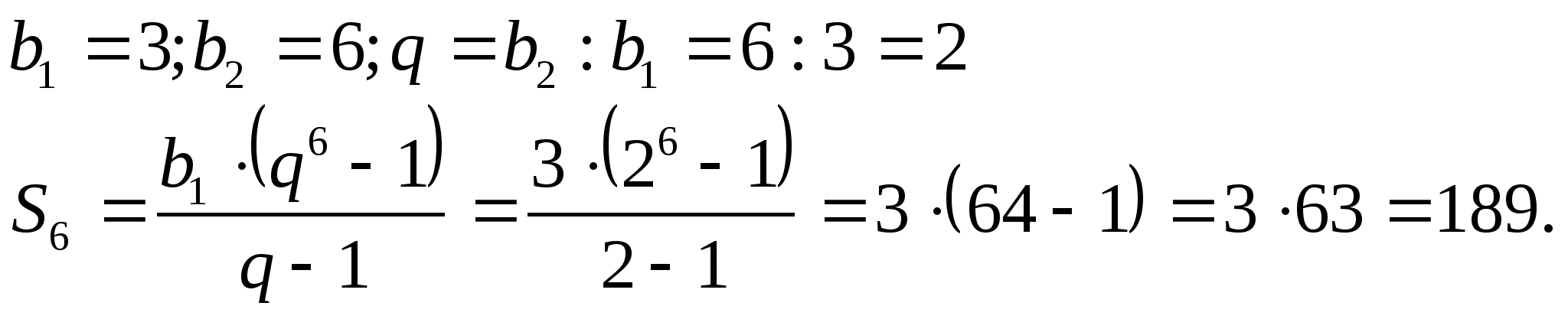
Ответ: 189.
Пример17.Найдите 
геометрической прогрессии, если 
и 
.
Решение:
Пользуясь признаком геометрической прогрессии 
найдем b
Ответ: 24
Пример18.Найдите знаменатель геометрической прогрессии,
если
и 
.
Решение:
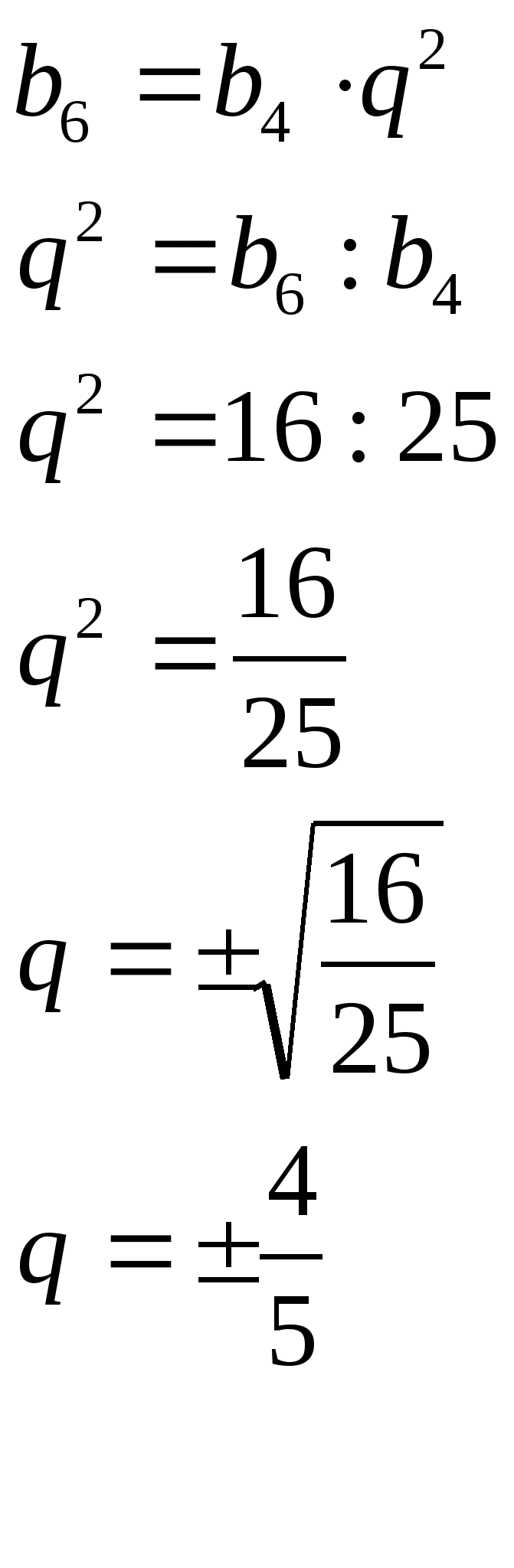
Ответ: 
Пример19. В арифметической прогрессии 
и 
Найдите 
и d.
Решение.
;
;
;
42=
;
;
;
2
;
(*) 
;
132=
;
:4
; 
;
(**).Подставив
значение
равенства
(*) в равенство (**) получим:
33-7d;
-3d+7d=33-21; 4d=12; d=12:4=3.
Найдем значение 
из равенства (*).
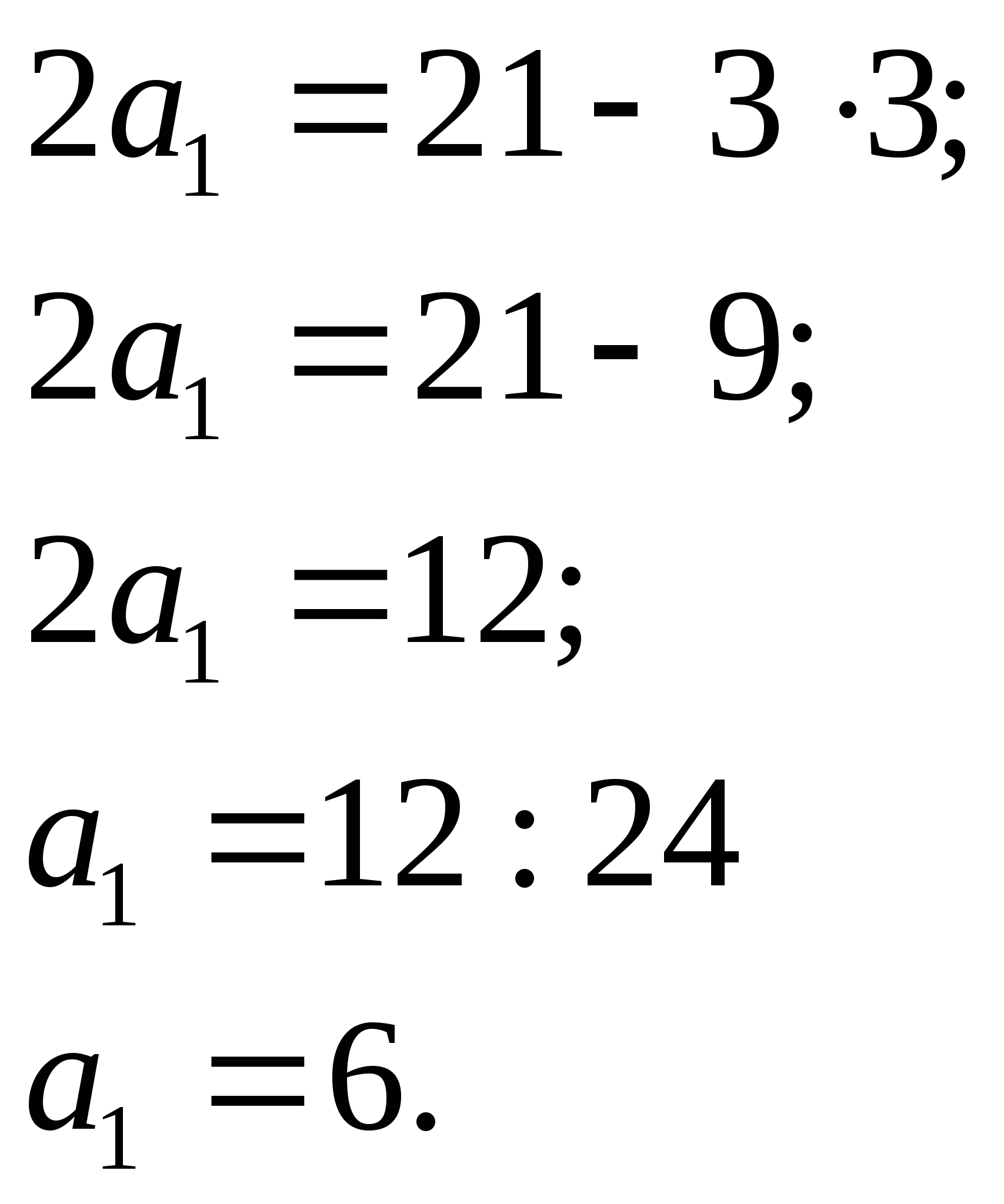
Ответ: 
Пример 20. Дана арифметическая прогрессия -18; -14; -10; ….
Укажите номер её первого положительного члена.
Решение.
Так как данная последовательность является арифметической и каждый член начиная со второго больше предыдущего на 4, то получим последовательность: -18;-14; -10; -6; -2; 2;..
Значит , шестой член данной последовательности является положительным числом.
Ответ:n=6.
Пример 21. В геометрической прогрессии
и 
Найдите 
.
Решение:
и
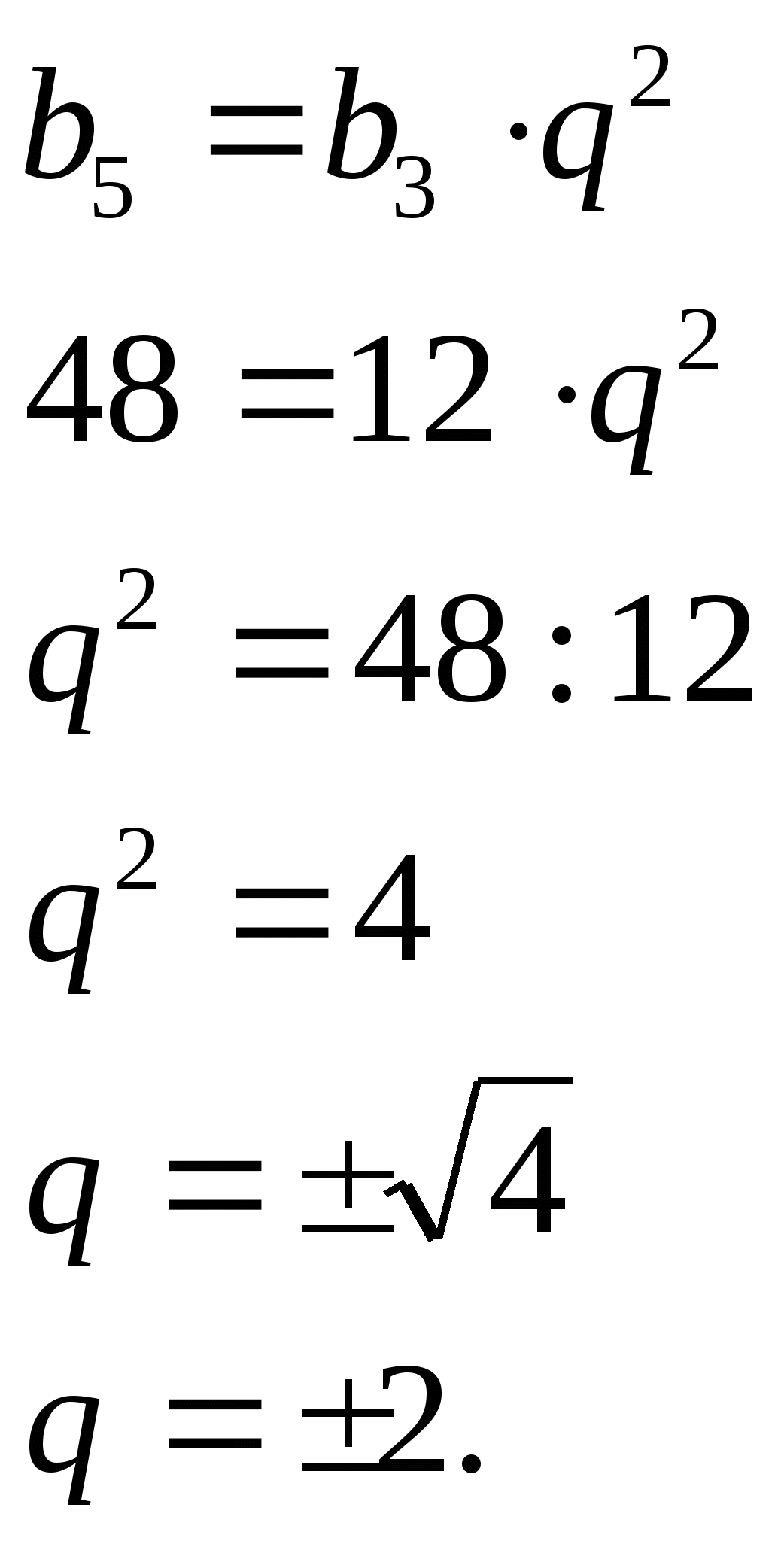
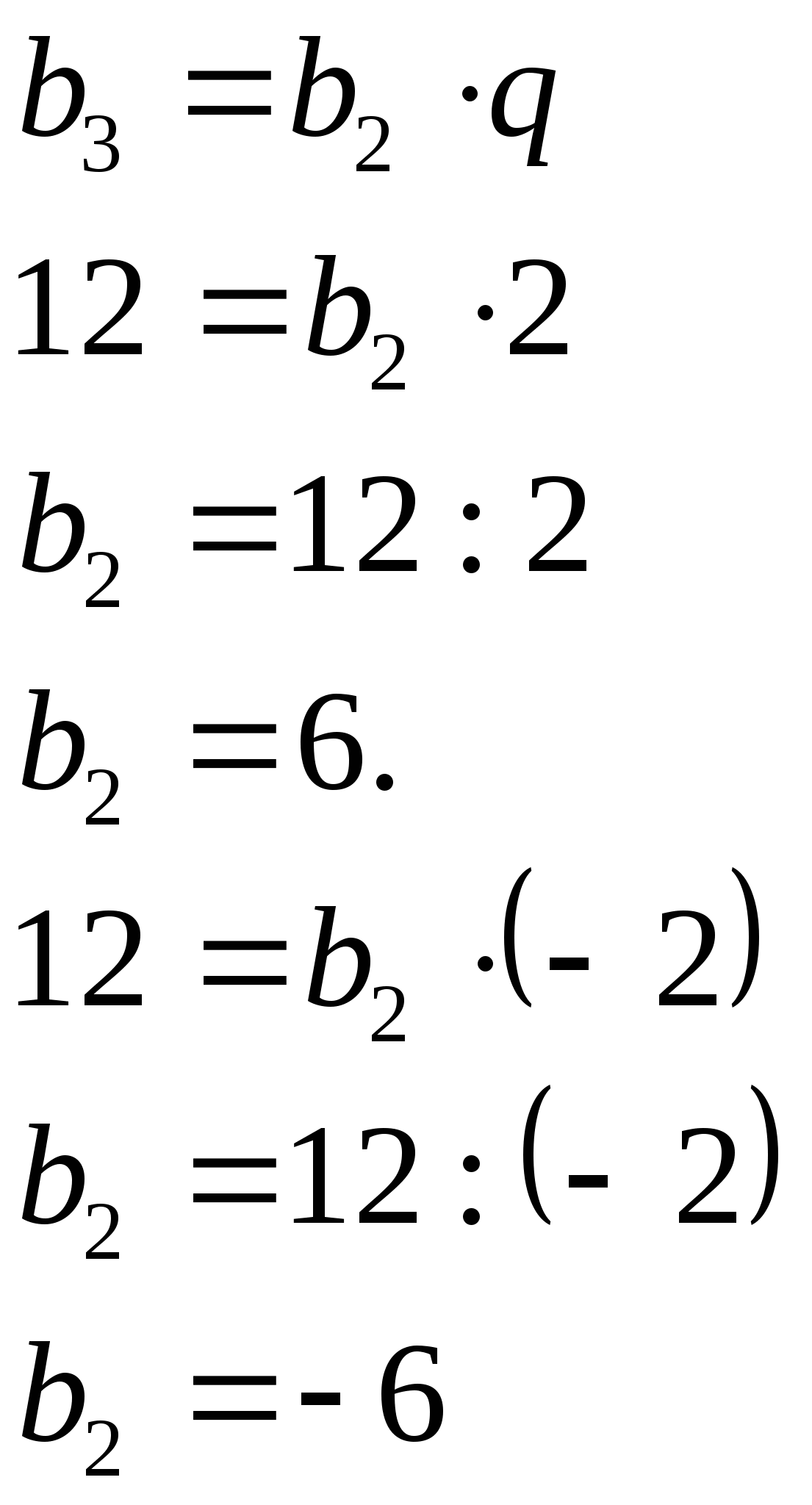
Ответ:±6
Пример 22. Дана арифметическая прогрессия (а
,
где
.
Найдите сумму её членов с 11-го по 20-й включительно.
Решение:
Так как ,
найдем 
и 
.
.
Число членов , начиная с 11-го по 20 -й включительно , равно
10.Значит надо найти сумму десяти членов данной прогрессии, где
первым членом будет .
Ответ: 320.
Пример23. Дана бесконечная геометрическая прогрессия (с
с
суммой 42 и знаменателем 
.Найти
.
Решение:
Найдем
по формуле 
.
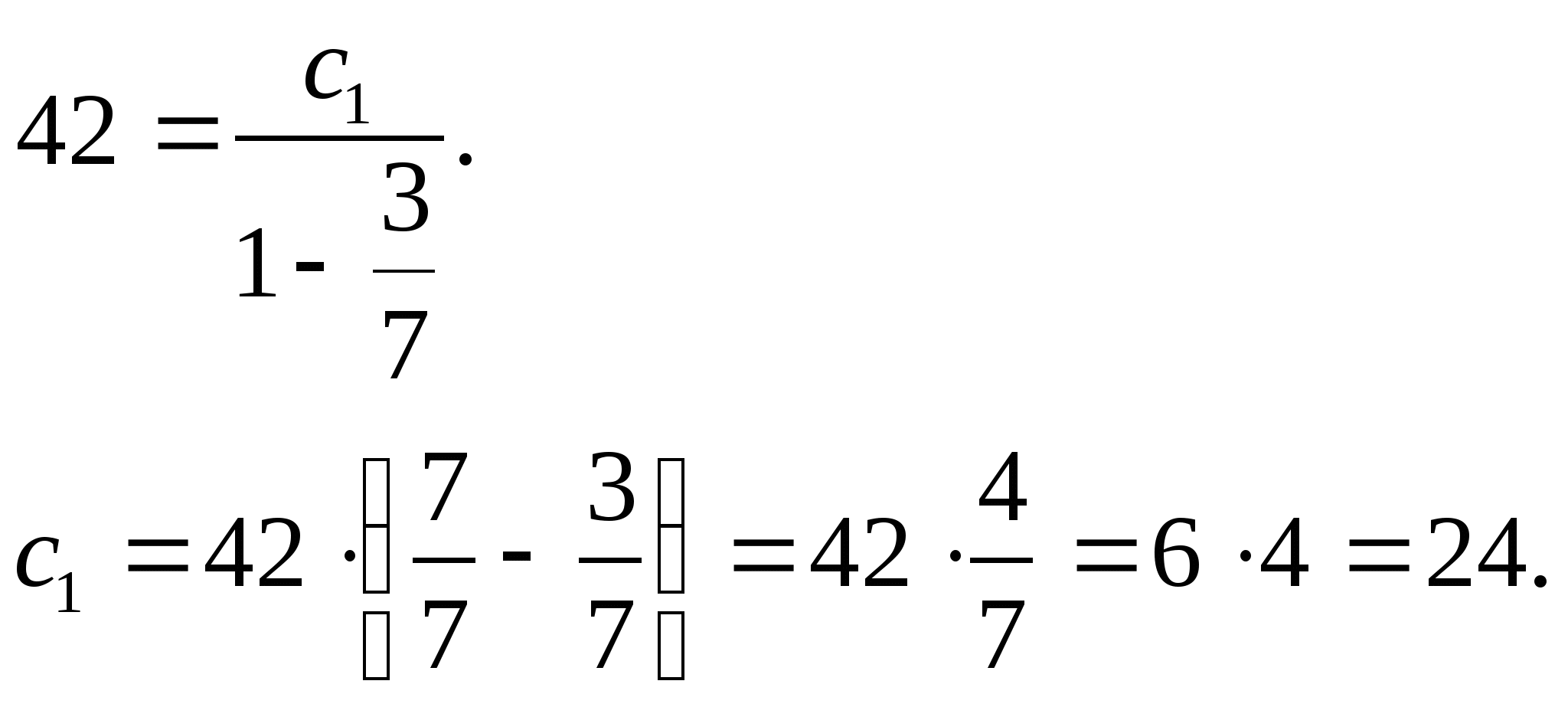
Ответ:24.
Пример24. В арифметической прогрессии 
Найдите число её членов и сумму n первых членов.
Решение.
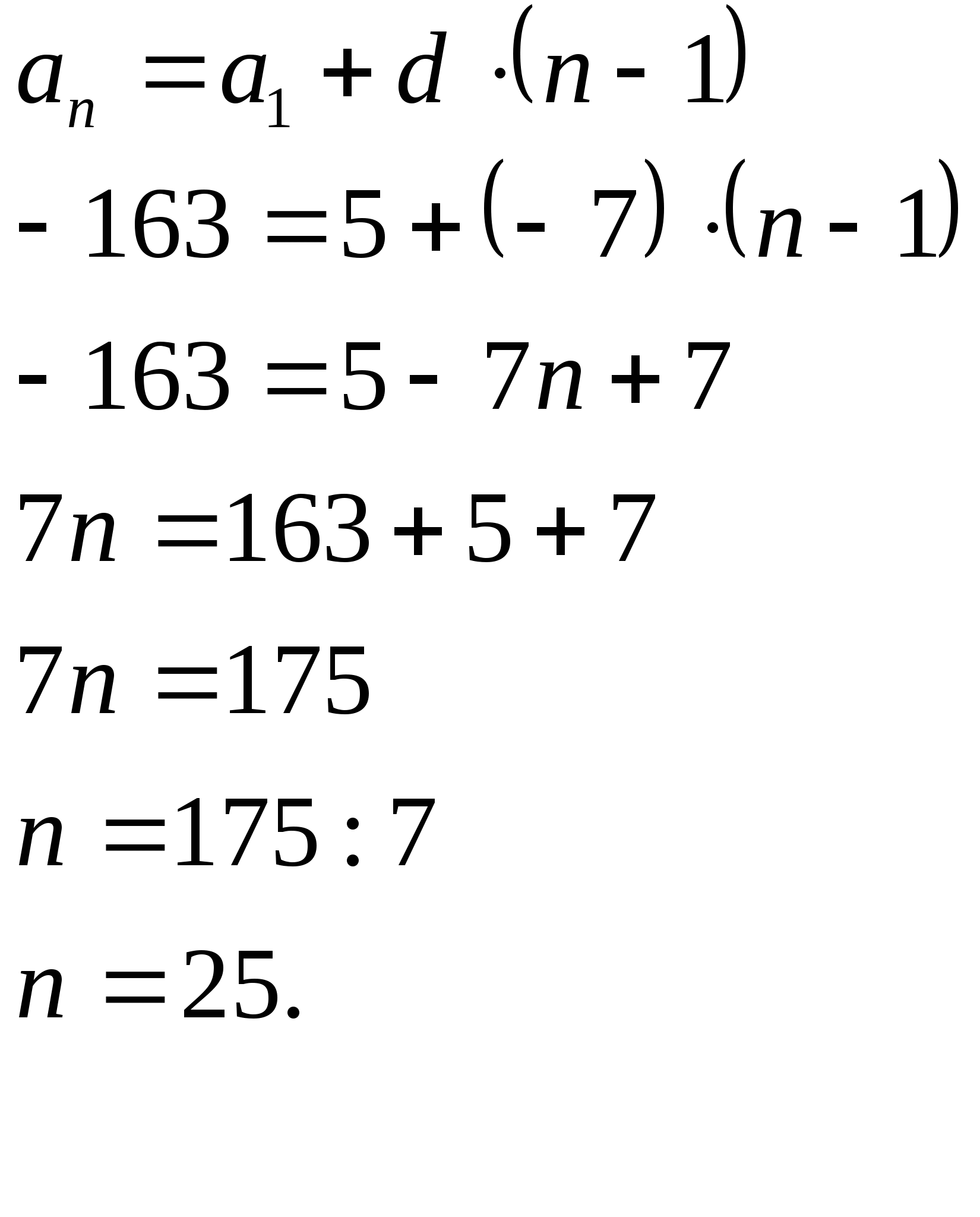
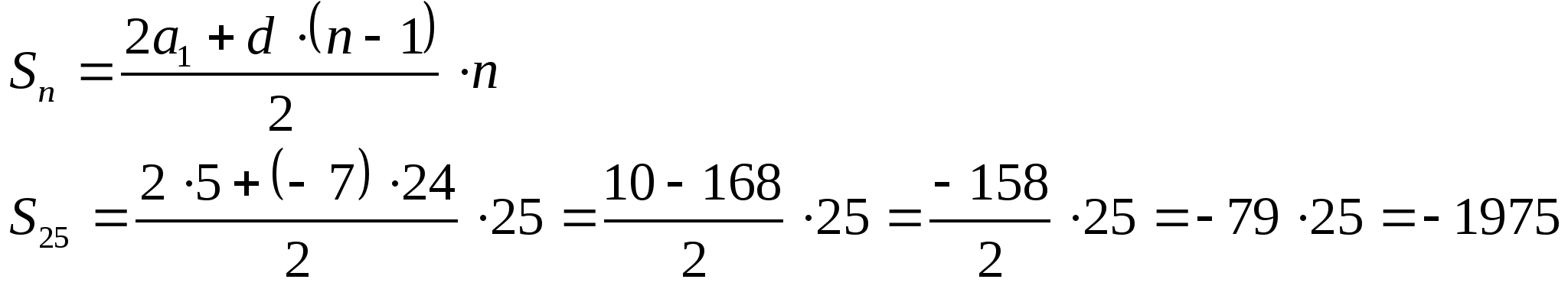
Ответ: -1975.
Пример25. Найдите сумму шести членов геометрической прогрессии, у которой второй член равен (-2) , а пятый член
равен 16.
Решение:
По условию известно, что прогрессия является геометрической, у
которой 
.
Вычислим значение q.
;
:
Найдем 
по определению геометрической прогрессии.
;
.
Зная
и q можно найти сумму шести членов данной прогрессии.
.
Ответ:21
Пример26. Является ли число 
членом геометрической прогрессии 4; 2; 1; …? Если является, то
укажите его номер.
Решение.
;
.
Зная ,значение
и 
найдем q .
q=
Найдем
номер члена данной геометрической прогрессии пользуясь формулой
n-го члена геометрической прогрессии.
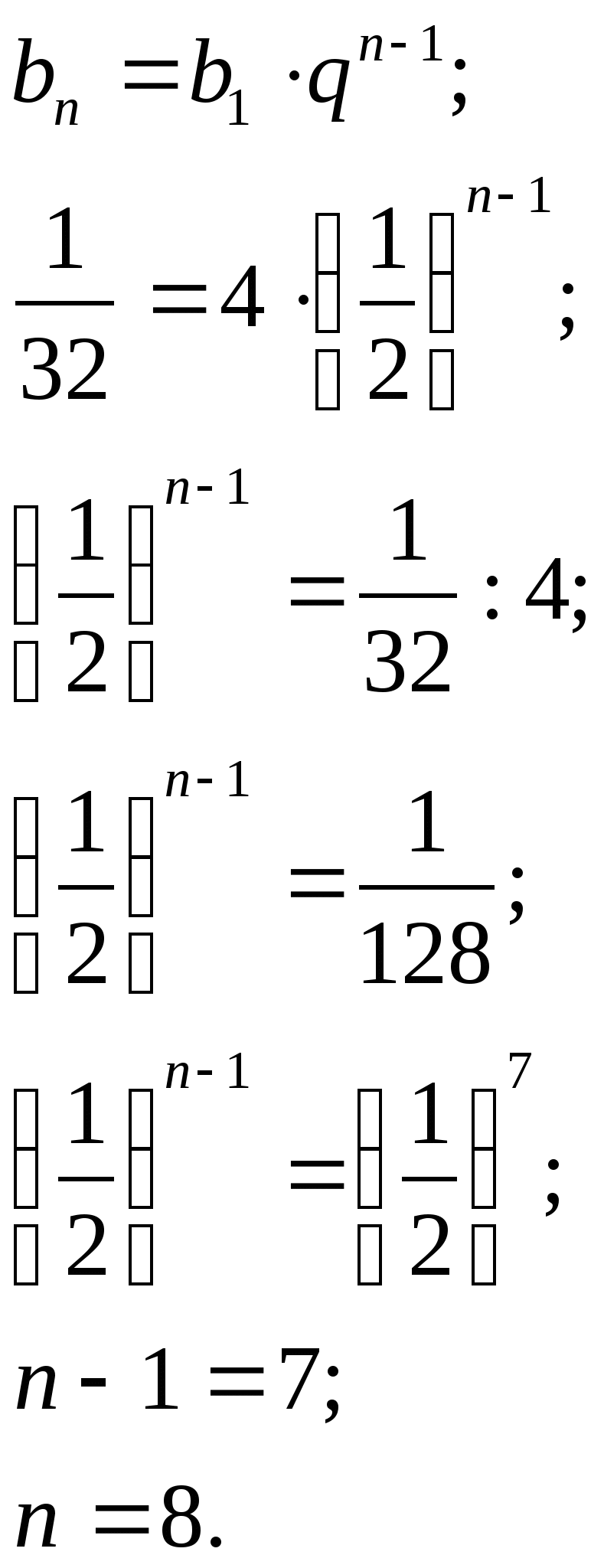
Ответ :является, n=8.
