Разработка урока 'Площадь треугольника' 8 класс

Тема: Площадь треугольника

Цель:

Образовательная:

- расширить и углубить представление учащихся об измерении площадей, закрепить знание формул площади прямоугольника, квадрата, параллелограмма;

- создать содержательные и организационные условия для самостоятельного поиска учащимися формул площади треугольника;

-учить применять эти формулы при решении задач.

Развивающая:

-создать условия для развития у школьников умений формулировать проблемы, предлагать пути их решения;

-самостоятельности на основе создания проблемной ситуации при изучении нового материала;

-развитие творческих способностей учащихся, умственной и мыслительной активности, развитие умения учиться, навыков самоконтроля.

Воспитательная:

-способствовать в ходе урока воспитанию воли и настойчивости для достижения конечных результатов.

Оборудование:

-интерактивная доска, компьютер-1, тестирующее устройство - Activote -30 шт, раздаточный материал (математическое лото-15 шт, спички по 6 шт), Activpen-2 шт.

Тип урока:

По основной дидактической цели - урок ознакомления с новым материалом.

По основному способу проведения - проблемно-поисковая деятельность.

Основные этапы урока:

1. Сообщение темы, цели, задач урока и мотивация учебной деятельности.

(1 мин.)

2. Подготовка к изучению нового материала через повторение и актуализацию опорных знаний. (5 мин.)

3. Повторение основных видов многоугольников и формул площади.(3 мин)

4. Создание проблемной ситуации при самостоятельном решении задач. Выдвижение гипотез и их проверка. (8 мин.)

5. Ознакомление с новым материалом. (8 мин.)

6. Проверка умений учащихся самостоятельно применять знания в стандартных ситуациях (устная работа). (7 мин.)

7. Проверка умений учащихся применять знания в нестандартных задачах.

Дополнительный материал. (10 мин.)

8. Домашнее задание. (2 мин.)

9. Подведение итогов. (1 мин.)

Учащиеся должны усвоить: формулы для нахождения площади треугольника,

способы их применения в различных задачах.

Учащиеся должны научиться: применять формулы для нахождения площадей фигур, доказывать одну из формул площади треугольника.

Этап

урока

Деятельность учителя

Деятельность учащихся

Записи на доске

1

Тема: Площадь треугольника

Цель: вывести формулы для нахождения площади треугольника.

Кто не слышал о загадочном бермудском треугольнике (находится в Атлантическом океане между бермудскими островами, государством Пуэрто-Рико и полуостровом Флорида), в котором бесследно исчезают корабли и самолёты?

А ведь знакомый всем с детства треугольник таит в себе немало интересного и загадочного.

Часто знает и дошкольник,
Что такое треугольник.
А уж вам-то, как не знать!
Но совсем другое дело -
Очень быстро и умело
Его площадь подсчитать.

Мы с вами научимся точно вычислять площадь треугольника, используя различные формулы, которые сегодня будем выводить вместе.

Запись с доски темы урока.

2

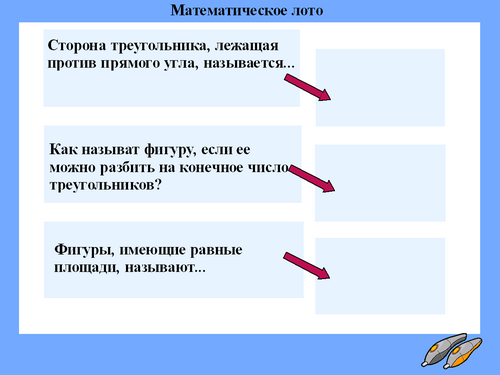
Для того чтобы вывести формулу площади треугольника нам необходимо вспомнить пройденный ранее материал. В этом нам поможет игра «Математическое лото».

У вас на столах лежат карточки с вопросами и ответами, необходимо совместить их так, чтобы определения были верными.

Двое учащихся по очереди пишут на доске ответы.

1 Сторона треугольника, лежащая против прямого угла, называется…(гипотенузой).

2 Как называется фигура, если ее можно разбить на конечное число треугольников?

(простой)

3 Фигуры, имеющие равные площади, называют… (равновеликими)

4 Перпендикуляр, опущенный из любой вершины, на противоположную сторону треугольника, называется… (высотой).

5 В зависимости от длины сторон треугольники бывают…

(разносторонние, равносторонние, равнобедренные).

6 Чтобы найти площадь прямоугольника, надо… (длину умножить на ширину).

Для проверки ваших ответов необходимо вытянуть верные ответы из-под прямоугольников.

Самопроверка.

Учитель вытягивает ответы, учащиеся проверяют.

Учащиеся записывают на полях тетради количество верных ответов.

7 Равенство, устанавливающее взаимосвязь между величинами называется… (формулой).

8 Сторона треугольника, на которую опущен перпендикуляр, называется… (основанием).

9 Отношение противолежащего катета к прилежащему катету в прямоугольном треугольнике называется… (тангенсом).

Учащиеся записывают на полях тетради количество верных ответов.

3

4

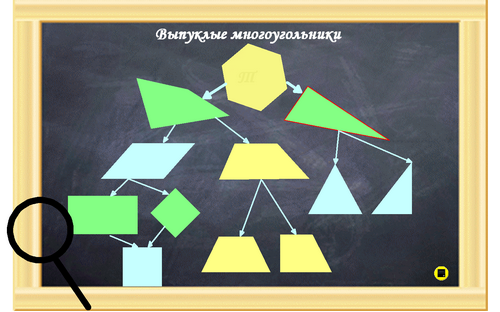
Треугольник является одним из видов многоугольника, давайте вспомним какие еще многоугольники мы изучили.

Инструмент «шторка» закрывает доску, затем постепенно открывается, и вы называете фигуру.

Когда все фигуры открыты, инструмент «Лупа»

при наведении на них показывает буквы из которых надо составить слово.

Об этом мы узнаем чуть позже. А пока решим задачу.

Гипотеза:

При нажатии на стрелку на доске появляется гипотеза - достроим треугольник до прямоугольника.

При нажатии на вторую стрелку чертеж достраивается до фигуры, площадь которой уже изучена.

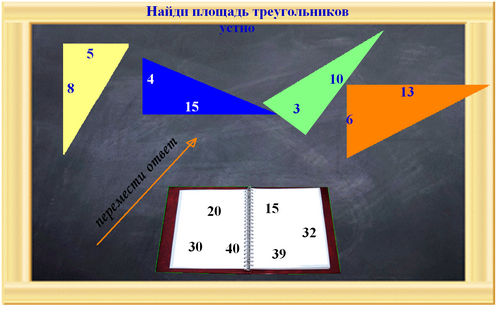
Устно, найдите площадь прямоугольных треугольников.

Многоугольник

Четырехугольник Треугольник

Парал-м Трапеция Прям-ый Остр-ый

Прям-ик Ромб Равн-ая Прям-ая

Квадрат

Тетраэдр

Что оно означает?

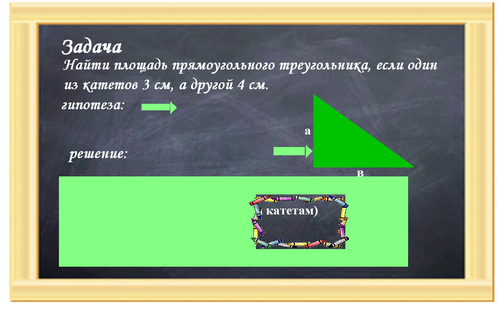Задача.

Найти площадь прямоугольного треугольника, если один из катетов 3 см, а другой 4 см.

Выдвижение гипотез…

Проверка гипотез…

Устные рассуждения…

Чтобы решить эту проблему, дети предлагают: достроить данный треугольник до прямоугольника.

Объясняется, почему: если прямоугольный треугольник достроим до прямоугольника, то мы получим два равных треугольника, которые равны по двум катетам.

А так как площадь прямоугольника равна произведению его смежных сторон, то площадь прямоугольного треугольника равна половине произведения его катетов. Значит, (см²).

У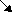стная работа

Теперь обращаю внимание учащихся на то, что решена пока только часть основной проблемы.

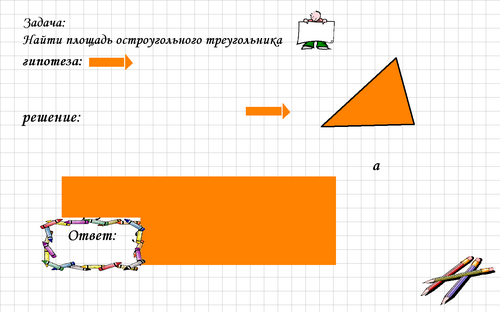
Далее предлагаю ученикам решить другую задачу "Найти площадь любого остроугольного треугольника". При помощи наводящих вопросов ученики находят способ. Они предлагают дополнить остроугольный треугольник до параллелограмма. Дополняем треугольник до параллелограмма. Затем доказываем, что полученные 2 треугольника равны по 3-му признаку равенства треугольников. Ставлю вопрос: "чему равна площадь любого остроугольного треугольника?"

Задача.

Найдите площадь остроугольного треугольника.

Предлагают дополнить остроугольный треугольник до параллелограмма.

Затем доказываем, что полученные 2 треугольника равны по 3-му признаку равенства треугольников.

Ученики отвечают, что площадь любого остроугольного треугольника равна половине произведения его основания на высоту.

У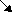стная работа

закрепление

5

Теперь решаем проблему: "найти площадь произвольного треугольника".

Учащиеся самостоятельно справляются с этой проблемой. Ученики отвечают, что площадь произвольного треугольника равна половине произведения его основания на высоту.

- Это утверждение есть теорема о площади треугольника.

Мы с вами изучили теорему о площади произвольного треугольника. Проведем доказательство. Учитель.

Доказательство записано на доске, учитель, используя «шторку» поэтапно знакомит учащихся с его основными элементами.

6

Творческое задание.

Постройте с помощью шести палочек четыре равносторонних треугольника.

Эта фигура называется «тетраэдр».

Пирамида- это….

Творческое задание. (Д/з)

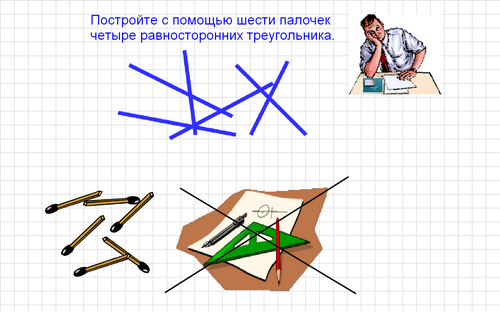
На картинке фигуры, которые состоят из четырех фигур. Площадь фигур из которых они состоят одинаковы. Если фигуры переставить, то останется лишняя клетка. Поясните, откуда она взялась?

Учащиеся кратко записывают.

Учащиеся выдвигают гипотезы.

Вначале пытаются построить на плоскости.

Затем предполагают объемное решение.

Смотрят фильм о Дворце «Мира и Согласия» в Астане, который имеет форму пирамиды.

7

Обобщение.

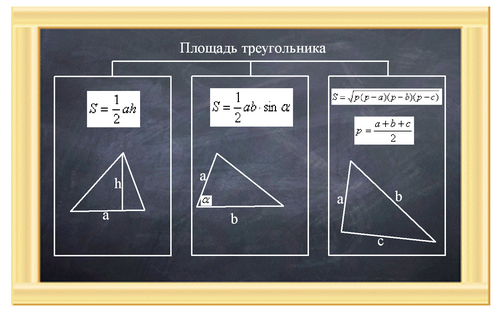
Для нахождения площади треугольника существуют 3 основные формулы.

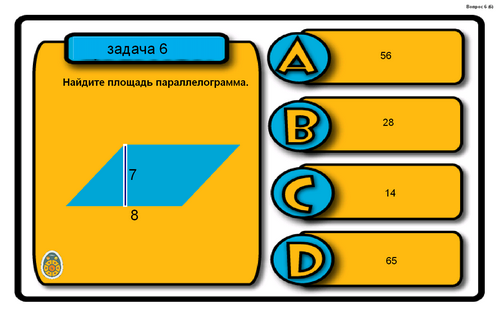
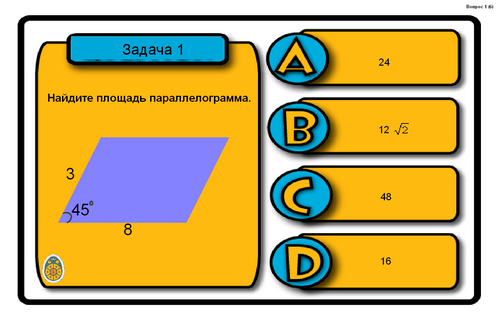
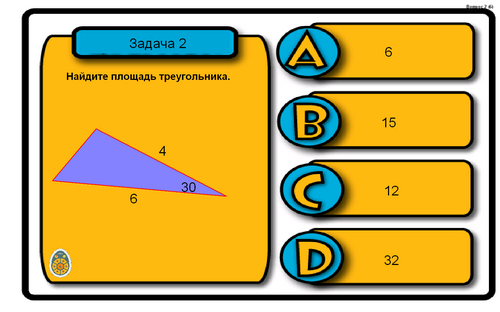
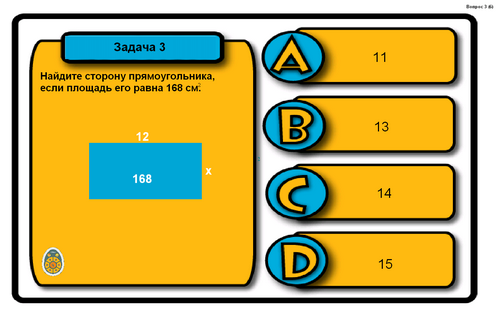
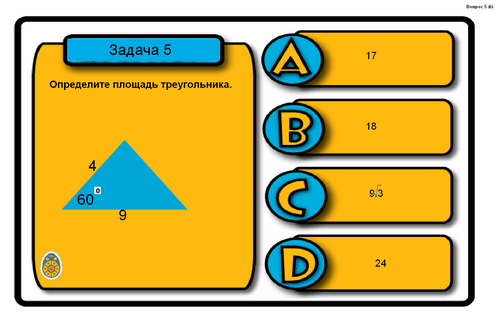
Используя формулы, решите следующие задачи-рисунки.

Подведение итогов теста по решению задач-рисунков. Выставление оценок за урок.

Запись в тетради

Используя тестирующее устройство

Activote, отвечают на вопросы.

Ответ: В

S=

Ответ: А

Ответ: С

Ответ: Д

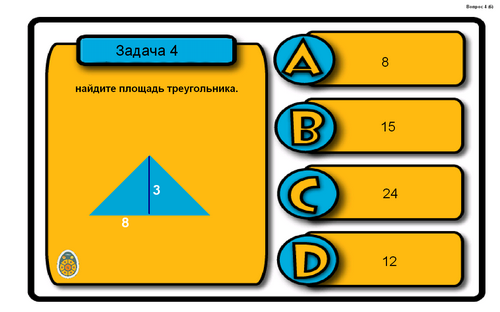
S=

Ответ: С

Ответ: А