- Учителю
- Сборник уроков для 5 класса
Сборник уроков для 5 класса
















































 Сборник уроков
Сборник уроков
по математике для 5 класса
Тема: Понятие об обыкновенной дроби.
Цели:
-
Познакомить учащихся с основными понятиями: обыкновенная дробь, числитель дроби, знаменатель дроби; сформировать умение записывать и читать обыкновенные дроби,
-
Создавать у школьников положительную мотивацию к выполнению умственных и практических занятий.
-
Воспитывать чувство удовлетворения от возможности показать на уроке свои знания.
Ход урока.
1. Организационный момент.
2. Мотивация урока.
С древних времен людям приходилось не только считать предметы (для чего требовались натуральные числа), но и измерять длину, время проданные товары. Не всегда результат измерения или стоимости удавалось выразить натуральным числом. Приходилось учитывать и части, доли меры. Так появились дроби.
Такие слова, как полхлеба, полчаса, треть пути, ты слышишь каждый день. Это примеры дробных чисел, с которыми нам и предстоит познакомиться.
3. Актуализация опорных знаний.
Математика - это наука, которая всегда сопровождала человечество. Она призвана развивать логическое мышление, внимание, тренировать мозг. Недаром ее называют «гимнастикой ума». Так давайте выполним небольшую математическую разминку.
-
Первое слагаемое 64, второе 29. Найти сумму.
-
Уменьшите 81 в 3 раза.
-
Из числа 340 вычесть число 80 и прибавить 70.
-
К какому числу прибавили 44, и получили 80?
-
7000 уменьшить в 100 раз.
-
7000 уменьшить на 100.
-
Запиши число 90003.
-
Сколько см в 5 дм?
4. Изучение нового материала.
Постановка проблемы.
Учитель показывает детям апельсин и задает вопрос.
Апельсин один, а нас в классе восемь человек. Как сделать так, чтобы апельсин достался каждому?
Ребята выдвигают версии. Когда один из ребят дает правильную версию, учитель повторяет ее.
Апельсин нужно разделить. Сколько апельсина получит каждый из вас?
Ребята выдвигают версии. Когда ребята найдут правильную версию, учитель озвучивает и закрепляет ее.
Все ребята проговаривают правильную версию.
Каждый получит дольку апельсина.
Вот эта долька от апельсина и называется дробью.
ДРОБЬ - одна или несколько равных долей.
Дробь записывают двумя натуральными числами, которые разделены чертой.
5 - числитель дроби

8 - знаменатель дроби
- Что показывает знаменатель 8? (на сколько долей делят целое)
- Что показывает числитель 5? (сколько таких долей взяли)
Например: 
 - одна пятая;
- одна пятая;  - две шестых;
- две шестых;  - семь десятых;
- семь десятых;  - восемьдесят три сто пятьдесят вторых.
- восемьдесят три сто пятьдесят вторых.
Какую часть круга составляет доля на каждом из кругов?
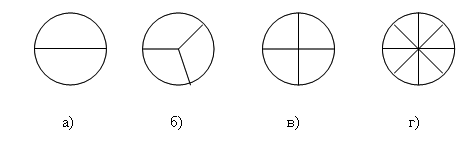
Прочитать дроби № .
Записать дроби №
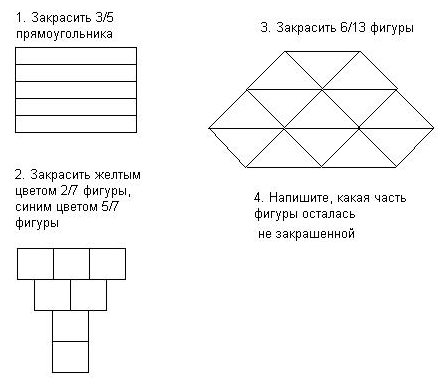
Исторические сведения:
В русском языке слово «дробь» появилось в VIII веке, оно происходит от глагола «дробить» - разбивать, ломать на части. В первых учебниках математики (в VIII веке) дроби так и назывались - «ломаные числа». У других народов название дроби также связано с глаголами «ломать», «разбивать», «раздроблять».
Современное обозначение дробей берет свое начало в Древней Индии; его стали использовать и арабы, а от них в XII - XIV веках оно было заимствовано европейцами. Вначале в записи дробей не использовалась дробная черта; например, числа записывались так: Черта дроби стала постоянно использоваться лишь около 300 лет тому назад. Первым европейским ученым, который стал использовать и распространять современную запись дробей, был итальянский купец и путешественник, сын городского писаря Фибоначчи (Леонардо Пизанский) в 1202 г. Он ввел слово «дробь». Названия «числитель» и «знаменатель» ввел в XIII веке Максим Плануд - греческий монах, ученый-математик.
5. Закрепление нового материала.
Решить № №
6. Физкультминутка.
Провести физкультминутку, применив математическую считалочку:
« Один, два - не собьюсь,
Четыре, пять - не собьюсь,
Семь, восемь - не собьюсь,
Десять, одиннадцать - не собьюсь,
Тринадцать, четырнадцать - не собьюсь,
Шестнадцать, семнадцать - не собьюсь,
Девятнадцать, двадцать - не собьюсь.»
7. Самостоятельная работа.
Решить №
На повторение: №
8. Итоги урока. Рефлексия. Д/з.
«Дерево удовлетворённости»
По окончании урока дети прикрепляют на дереве листья, цветы, плоды:
-
Плоды - урок прошёл полезно, плодотворно;
-
Цветок - урок прошёл довольно неплохо;
-
Зелёный листок - не совсем удовлетворён уроком;
-
Жёлтый листок - урок не понравился, скучно.
Выучить п., решить № №
Каждый может за версту
Видеть дробную черту.
Над чертой - числитель, знайте,
Под чертою - знаменатель.
Дробь такую, непременно,
Надо звать - обыкновенной.
Тема: Понятие об обыкновенной дроби. Нахождение дроби от числа и числа по его дроби.
Цели:
-
Закрепить понятия: обыкновенная дробь, числитель дроби, знаменатель дроби; сформировать умение записывать и читать обыкновенные дроби, изучить правила нахождения дроби от числа и числа по его дроби.
-
Создавать у школьников положительную мотивацию к выполнению умственных и практических занятий.
-
Воспитывать чувство удовлетворения от возможности показать на уроке свои знания.
Ход урока.
1. Организационный момент.
Посмотрите, всё ль в порядке:
Книжка, ручки и тетрадки.
Прозвенел сейчас звонок.
Начинается урок.
2. Мотивация урока.
Есть у нас поговорка «попал в тупик», т.е. попал в такое положение, откуда нет выхода. У немцев аналогичная поговорка гласит, «попасть в дроби». Она означает, что человек, попавший в «дроби», попал в очень трудное положение.
Поговорка эта напоминает нам о тех временах, когда дроби считались самым трудным и самым запутанным отделом математики. Освоить же дроби было тяжело. Даже самые образованные люди считали действия с дробями весьма трудными. Это происходило потому, что общих приемов действия с дробями и записи дробей не было.
Именно обыкновенные дроби помогут нам сегодня сделать очередное открытие в изучении математики.
3. Актуализация опорных знаний. Проверка д/з.
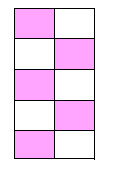
Какая фигура изображена?
Какой дробью можно представить закрашенную часть?
Сколько можно представить таких дробей?
На основании чего это можно сделать?
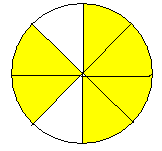
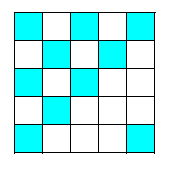
-
Что называют долями?
-
Как называют доли
 ,
,  ,
,  ?
? -
Что показывает знаменатель обыкновенной дроби?
-
Что показывает числитель обыкновенной дроби?
4. Решение упражнений на нахождение дроби от числа и числа по его дроби.
Чтобы найти дробь от числа, надо число разделить на знаменатель и умножить на числитель дроби.
Решить № №
Чтобы найти число по его дроби, надо число разделить на числитель и умножить на знаменатель дроби.
Решить № №
Разминка - шуточная задача.
История о том, как я ходил на рыбалку.
Я встал пораньше, в четыре килограмма утра. Позавтракал плотно, выпил один километр молока. Потом отправился на озеро. Расстояние до него не малое, пять градусов. Утром было прохладно, температура всего десять часов тепла. Поэтому я шел быстро, со скоростью шесть литров. Пришел, закинул удочки. Не прошло и двадцати сантиметров, как я поймал первую рыбу. Большую - длиной пятьдесят минут и весом три километра в час. Отличная получилась уха.
Повторение: №
5. Самостоятельная работа.
Незнайка решил начать новую жизнь. Он составил себе такое расписание на сутки:
1 \ 6 часть суток - чтение умных книг;
3 \ 8 часть суток - совершение добрых дел;
1 \ 12 часть суток - на прием пищи (завтрак, обед, ужин);
2 \ 8 часть суток с - занятия спортом;
8 часов на сон.
Сможете ли вы помочь Незнайке и сказать, выполним ли его план?
6. Итоги урока. Д/з.
-
Как найти
 от числа 42?
от числа 42? -
Как найти число, если известно, что
 от него равны 4?
от него равны 4?
Решить № №
Тема: Правильные и неправильные дроби.
Цели урока:
-
образовательная - расширение и углубление знаний, умений и навыков по программному материалу (правильные и неправильные дроби, нахождение части от числа и числа по его части).
-
развивающая - приобщение учащихся к творческой деятельности, расширение математического кругозора и представлений о практической значимости математики.
-
воспитательная - развитие у учащихся интереса к математике, воспитание коммуникативной культуры, умения оценивать себя и своих товарищей.
Ход урока.
1. Организационный момент.
2. Мотивация урока.
3. Актуализация опорных знаний. Проверка д/з.
Какую запись называют обыкновенной дробью?
Запись вида а/в, где а- числитель , а в- знаменатель называют обыкновенной дробью .
Что показывает знаменатель дроби?
Знаменатель показывает, на сколько долей делят.
Что показывает числитель дроби?
Числитель показывает, сколько таких долей взято.
1.Назовите пять любых дробей.
2.Назовите их числители и знаменатели.
3.Любое ли натуральное число считается дробью ?
4.Какое число называется дробью?
5.Сколько граммов в половине килограмма?
6.Сколько часов в одной трети суток?
7. Сколько килограммов в четверти тонны?
8. Сколько метров в 1/8 части километра?
9. Сколько миллиметров в ½ сантиметра?
10. Сколько минут в 1/3 часа?
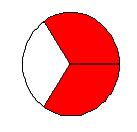
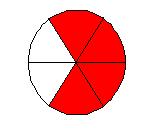
Какая часть круга закрашена?
Как найти дробь от числа? число по его дроби?
Решить № №
4. Изучение нового материала.
В некотором царстве, в некотором государстве «Обыкновенным дроби» жили-были дроби:![]() (Прочитайте дроби). Они веселились: некоторые порхали, как бабочки; другие важно прыгали и переваливались на месте (Почему? - ответы учеников « Дроби правильные и неправильные»). За их играми наблюдала «Царица единица», ведь она имела отношение ко всем этим дробям. (Какое? - ответы учеников «правильные дроби < 1, неправильные дроби > 1).
(Прочитайте дроби). Они веселились: некоторые порхали, как бабочки; другие важно прыгали и переваливались на месте (Почему? - ответы учеников « Дроби правильные и неправильные»). За их играми наблюдала «Царица единица», ведь она имела отношение ко всем этим дробям. (Какое? - ответы учеников «правильные дроби < 1, неправильные дроби > 1).
И решила «Царица - единица», что эти их игры надо упорядочить, для этого она классифицировала дроби. (Как?) Правильно, развела их жить в разные города.
-« Город правильных дробей» и «Город неправильных дробей».
Работа с учебником.
-
Дробь, в которой числитель меньше знаменателя, называют правильной дробью.
-
Дробь, в которой числитель больше знаменателя или равен ему, называют неправильной дробью.
В этом ряду есть лишняя дробь. Найдите ее и назовите.

( - неправильная дробь)
- неправильная дробь)
5. ФИЗКУЛЬТМИНУТКА
Сели удобно, почувствовали спинку стула, взглядом пишем сегодняшнюю дату, не отрывая взгляда от бумаги и не проводя по одной линии дважды, обведите следующие фигурки. (Плакаты)
6. Закрепление нового материала.
Решить № №
7. Итоги урока. Д/з.
Выучить п.. Решить № №
Тема: Сравнение дробей.
Цели урока:
Обучающая:
-
познакомить с правилом сравнения обыкновенных дробей с одинаковыми знаменателями; сформировать первые навыки записи дробей в порядке возрастания (убывания); закрепить знание взаимного расположения точек на луче в зависимости от их координат.
Развивающая:
-
развивать способность применять знания в новой ситуации;
-
учить формулировать самостоятельно вывод.
Воспитательная: воспитывать скромность и аккуратность.
Ход урока.
1. Организационный момент.
2. Мотивация урока.
Мы с вами продолжаем изучать обыкновенные дроби. На предыдущих уроках вы научились отмечать эти дроби на координатном луче. Изучая натуральные числа, вы научились их сравнивать, а также складывать, вычитать, умножать и делить, т. е. выполнять 4 арифметических действия. Сегодня нам предстоит освоить такую математическую операцию как сравнение обыкновенных дробей. Какие знаки сравнения вы знаете?
3. Актуализация опорных знаний. Проверка д/з.
О С А В Е
0 1
Рис. 1
Какая из отмеченных точек имеет координату 1/2, 1/8, 1/4?
В(1/2), С(1/8), А(1/4).
Сколько клеток нужно отсчитать от начала отсчета, что бы отметить на рисунке 1точку М(3/4), Д(7/8)?
Решить № 671.
4. Изучение нового материала.
Как узнать какая дробь больше?
Возьмите четвертые доли круга. Выложите слева 1 долю, а справа 3. Сравните, где большая часть? Запишите.
Записали 1/4<3/4.
Возьмите восьмые доли круга. Выложите слева 4 доли, а справа 2. сравните, где большая часть? Запишите.
Записали 4/8>2/8.
Посмотрите, чем отличатся дроби, которые мы сравнили?
Числителем.
От чего зависит знак?
От числителя. Чем больше числитель, тем больше дробь.
Из двух дробей с одинаковыми знаменателями, какая дробь меньше?
Меньше та, у которой меньше числитель.
Подтверждают полученный вывод чтением учебника.
Из двух дробей с одинаковыми знаменателями меньше та, у которой меньше числитель, и больше та у которой больше числитель.
Решаем № .
Посмотрите внимательно, чем отличаются эти дроби?
Знаменателем.
А знаменатель показывает, на сколько долей делят.
Сформулируйте правило сравнения дробей, числитель которых равен единице.
Чем больше число, на которое делят единицу, тем меньше дробь.
Вывод: из двух дробей с равными числителями, чем больше знаменатель, тем меньше дробь; чем меньше числитель, тем больше дробь.
Решить №
5. Закрепление нового материала.
Отметьте на координатном луче точки, координаты которых равны:
1/5; 2/5; 3/5;4/5.
О А В С D Е
0 1/5 2/5 3/5 4/5 1
Какая дробь самая маленькая из всех отмеченных? 4/5
Решить № №
Точка на координатном луче, имеющая меньшую координату, лежит слева от точки, имеющей большую координату.
Дроби
Жили-были в одном городе числа. Однажды решили они организовать свой кружок по тяжелой атлетике. Стали числа выполнять упражнения: большие числа поднимали над головой на перекладине меньшие числа. Такое упражнение судьи называли правильным. Когда же меньшие числа поднимали большие над головой, то судьи называли такое упражнение неправильным.
Так появились правильные и неправильные дроби. Разделились они на две команды: одна команда правильных дробей, а другая команда неправильных. Только неправильные дроби почему то всегда выигрывали у правильных.
Ребята, а как вы думаете почему?
6. Итоги урока. Д/з.
Какая дробь из двух дробей с одинаковыми знаменателями меньше, а какая больше?
Интересное и меткое арифметическое сравнение делал писатель Л. Н. Толстой: «Человек подобен дроби, числитель которой есть то, что человек представляет собой, а знаменатель - то, что он думает о себе». Еще раз посмотрите на зависимость, если знаменатель (самомнение) становится больше, то значение дроби (личности) становиться … меньше.
Решить № №
Тема: Сложение и вычитание дробей с одинаковыми знаменателями.
Цели урока:
-
изучить новый материал, научить складывать и вычитать дроби с одинаковыми знаменателями,
-
развивать математическую речь, внимание,
-
воспитывать аккуратность, интерес к предмету, активность, усидчивость
Ход урока.
1. Организационный момент.
Друзья мои! Я очень рада
Войти в приветливый ваш класс
И для меня уже награда
Вниманье ваших умных глаз.
2. Мотивация урока.
Начать наш урок хочу пословицей. Прочитайте её. Как вы понимаете смысл пословицы?
МАТЕМАТИКЕ УЧИТЬСЯ - ВСЕГДА ПРИГОДИТЬСЯ.
2) Ребята, а зачем заниматься математикой?
Не зря говорят: МАТЕМАТИКА - КОРОЛЕВА НАУК!
БЕЗ НЕЁ НЕ ЛЕТЯТ КОРАБЛИ,
БЕЗ НЕЁ НЕ ПОДЕЛИШЬ НИ АКРА ЗЕМЛИ,
ДАЖЕ ХЛЕБА НЕ КУПИШЬ, РУБЛЯ НЕ СОЧТЁШЬ,
ЧТО ПОЧЁМ, НЕ УЗНАЕШЬ, А УЗНАВ, НЕ ПОЙМЁШЬ!
Над какой темой мы работали на предыдущих уроках?
Как вы думаете, всё ли вы знаете о дробях? Хотите узнать новое? Не боитесь трудностей? А что (кто) поможет вам справиться с трудностями? Пожелайте друг другу удачи.
3. Актуализация опорных знаний. Проверка д/з.
1) Из двух дробей с одинаковыми знаменателями меньше та, у которой
а) больше числитель;
б) меньше числитель;
в) среди ответов нет правильных
2). Расставьте в порядке возрастания дроби:

3). Расставьте дроби в порядке убывания:

4). Найдите ошибку в записях:
а) б)
б)  в)
в)  г)
г)  д)
д) 
5). Дробь, в которой числитель меньше знаменателя, называют
а) правильной дробью б) неправильной дробью г) среди ответов нет правильных
6). При каких значениях, а дробь  будет правильной.
будет правильной.
7). Может ли правильная дробь быть больше, чем 1?
Решить № №
4. Изучение нового материала.
Буханку хлеба разделили на 8 равных частей (долей) (на доске висит наглядность). Сначала на тарелку положили 2 доли, а потом еще 5 долей.
На тарелке оказалось 7 долей, то есть  буханки:
буханки: 
- При сложении дробей с одинаковыми знаменателями числители складывают, а знаменатель оставляют тот же.
С помощью букв правило сложения можно записать так:

- Буханку хлеба разрезали на 8 равных частей.
- На тарелку положили 7 долей, а потом 4 доли съели. Осталось три доли, то есть  буханки:
буханки:  .
.
- При вычитании дробей с одинаковыми знаменателями из числителя уменьшаемого вычитают числитель вычитаемого, а знаменатель оставляют тот же.
С помощью букв правило вычитания можно записать так:

Как складывают дроби с одинаковыми знаменателями?
При сложении дробей с одинаковыми знаменателями числители складывают а знаменатель оставляют тот же.
- Как вычитают дроби с одинаковыми знаменателями?
При вычитании дробей с одинаковыми знаменателями из числителя уменьшаемого вычитают числитель вычитаемого, а знаменатель оставляют тот же.
- Запишите правила сложения и вычитания дробей с одинаковыми знаменателями с помощью букв.
 ;
; 
5. Закрепление нового материала.
Решить № №
6. Зарядка для глаз
(Звучит музыка) Реснички опускаются...
Глазки закрываются...
Мы спокойно отдыхаем...
Сном волшебным засыпаем...
Дышится легко... ровно... глубоко...
Наши руки отдыхают...
Отдыхают... Засыпают...
Шея не напряжена
И рассла-бле-на...
Губы чуть приоткрываются...
Все чудесно расслабляется...
Дышится легко... ровно... глубоко...
(Пауза.)
Мы спокойно отдыхаем...
Сном волшебным засыпаем...
(Громче, быстрей, энергичней.)
Хорошо нам отдыхать!
Но пора уже вставать!
Крепче кулачки сжимаем.
Их повыше поднимаем.
Пoтянулись! Улыбнулись!
7. Самостоятельная работа.
Решить №
8. Итоги урока. Рефлексия. Д/з.
- Что нового узнали на уроке?
- Чему научились?
- Оцените свои знания по таблице:
Знаю: (что такое умножение)
Сомневаюсь:
Не знаю:
Выучить п. . Решить № №
Тема: Сложение и вычитание дробей с одинаковыми знаменателями.
Цели урока:
-
закрепить правила сложения и вычитания дробей с одинаковыми знаменателями,
-
развивать математическую речь, внимание, память;
-
воспитывать аккуратность, интерес к предмету, активность, усидчивость.
Ход урока.
1. Организационный момент.
Здравствуйте, садитесь!
Я знаю каждый в классе гений,
Но без труда талант не впрок
Скрестите шпаги ваших мнений
Мы вместе сочиним урок!
Мои соавторы и судьи,
Оценкой вас не накажу
За странный слог не обессудьте,
2. Мотивация урока.
3. Актуализация опорных знаний. Проверка д/з.
- Как складывают дроби с одинаковыми знаменателями?
- Как вычитают дроби с одинаковыми знаменателями?
- Запишите правила сложения и вычитания дробей с одинаковыми знаменателями с помощью букв.
Вычислить:
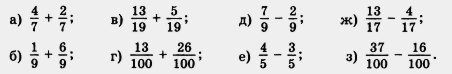
Найти значения выражений:
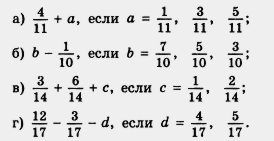
4. Решение упражнений на сложение и вычитание дробей с одинаковыми знаменателями.
Решить № №
5. Физкультминутка.
Поднимает руки класс - это "раз"
Повернулась голова - это "два"
"Руки вниз, вперёд смотри - это "три".
Руки в стороны пошире развернули на "четыре"
С силой их к плечам прижать - это "пять"
Всем ребятам надо сесть - это "шесть".
6. Самостоятельная работа.
Решить №
7. Итоги урока. Рефлексия. Д/з.
Решить № №
Тема: Дроби и деление натуральных чисел.
Цели урока:
-
обобщить понятие обыкновенной дроби,
-
развивать математическую речь, внимание, память;
-
воспитывать аккуратность, интерес к предмету, активность, усидчивость.
Ход урока.
1. Организационный момент.
Эмоциональный настрой на урок.
Дети, вам тепло? (Да!)
В классе светло? (Да!)
Прозвенел уже звонок? (Да!)
Уже закончился урок? (Нет!)
Только начался урок? (Да!)
Хотите учиться? (Да!)
Значит можно всем садиться!
2. Мотивация урока.
3. Актуализация опорных знаний. Проверка д/з.
Вспомним определения правильных и неправильных дробей. И поиграем в игру «Хлопушка». Я читаю дроби, а если вы услышали среди них неправильную дробь, то ваша задача хлопнуть.

Расположить числа в порядке возрастания.
 ,
,  ,
,  ,
,  ,
,  ,
, 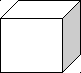 .
.
В порядке убывание
 ,
,  ,
, 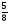 ,
,  ,
, 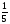 ,
, 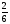 .
.
Какая из точек лежит на координатном луче левее?
А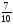 , С
, С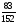 , Е
, Е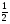
4. Изучение нового материала.
Разделим 2 одинаковых яблока между тремя детьми. Число 2 не делится нацело на 3. Поэтому разделим каждое яблоко на 3 равные части и дадим каждому ребенку по одной части от каждого яблока.
Каждая часть - это 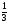 яблока, а две такие части - это
яблока, а две такие части - это 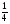 яблока. Значит, каждый ребенок получит
яблока. Значит, каждый ребенок получит 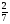 яблока.
яблока.
Дробь получилась при делении 2 яблок на 3 равные части. Поэтому черту дроби можно понимать как знак деления: 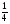 =2:3.
=2:3.
С помощью дробей можно записать результат деления двух любых натуральных чисел.
Если деление выполняется нацело, то частное является натуральным числом.
Если же разделить нацело нельзя, то частное является дробным числом.
Например, ![]()
Запишем число 3 в виде дроби со знаменателем 5. Для этого надо найти такое число, при делении которого на 5 получилось бы 3. Таким числом является
3 • 5, то есть 15.
Значит, ![]()
Запишите в виде дроби частные:
2:5; 1 : 10; 15 : 8; 7:1; 20 : 4; 77: 10
5. Закрепление нового материала.
Решить № №
6. Самостоятельная работа.
Решить №
7. Итоги урока. Рефлексия. Д/з.
Каким числом является частное, если деление выполняется нацело?
Каким числом является частное, если деление не выполняется нацело?
Выучить п., решить № №
Тема: Смешанные числа.
Цели:
-
образовательные: совершенствовать навыки учащихся в работе с обыкновенными дробями, закрепить навыки выделения целой части из неправильной и представления смешанного числа в виде неправильной дроби; проверить знания и умение учащихся по изученному материалу.
-
развивающие: развитие логического мышления, памяти, внимания, развития самостоятельности.
-
воспитательные: развитие интереса к предмету, формирование умения осуществлять самоконтроль.
Ход урока.
1. Организационный момент.
Здравствуйте, ребята!
Прошу занять свои места.
Слушайте меня внимательно,
На вопросы отвечайте,
Всё, ребята, подмечайте,
Ничего не забывайте,
Меня, прошу, не подкачайте.
2. Мотивация урока.
А знаете ли вы, что названия "числитель" и "знаменатель" ввёл в употребление греческий учёный-математик Максим Плануд. Долгое время дроби считались самым трудным разделом математики. У нас есть поговорка: "попал в тупик", т.е. попал в такое положение, откуда нет выхода. У немцев аналогичная поговорка гласит: "попасть в дроби". Она означает, что человек, попавший в "дроби", оказался в затруднительном положении.
Но сегодня на уроке мы докажем, что дроби не смогут нас поставить в трудное положение.
3. Актуализация опорных знаний. Проверка д/з.
Каким числом является частное, если деление выполняется нацело?
Каким числом является частное, если деление не выполняется нацело?
1. Вычислить:
2/9+5/9; 4/12+6/12; 9/15 - 6/15; 12/18 - 10/18;
2. Найти ошибку:
а) правильные дроби: 3/7; 3/3; 18/9; 1/5; 4 3/8; 5.
б) 3/4меньше 1/4; 10/7 больше 1; 6/6 больше 1; 3/5=1; 8/7 меньше 1;
3. Вычислить:
а) 15/19 - (2/19+3/19) (1 уч.) (10/19)
20/23 - 10/23 + 3/23 (2 уч.) (13/23)
Математический диктант.
Записать в тетрадь полученные ответы. Затем сравнить с ответами на доске.
1)Сколько минут в 1 часе?
2)Какую часть составляют семь часов от суток?
3)Какую часть составляет 1 метр от 1 км?
4)Записать правильную дробь со знаменателем 5.
5)Записать неправильную дробь с числителем 4.
6) 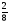 -
- 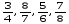
7)Незнайка решил совершить за день 10 хороших поступков. Но, к сожалению, ему удалось сделать 1 часть того, что он запланировал. Сколько хороших поступков совершил
5
Незнайка за день?
8)Знайка прочитал за день 1 части книги. Сколько надо дней, чтобы прочитать всю
4
книгу?
9)Мама купила 6 кг конфет. Витя сразу съел 2 всех конфет и у него заболел живот.
3
Сколько кг конфет съел Витя?
Ответы на доске: учащиеся проверяют и подсчитывают количество правильных ответов.
60 мин; 7 ; 1 ; 1,2,3,4 ; 4 ; 5; 2; 4 дня; 4 кг.
24 1000 5 1,2,3,4 9
4. Изучение нового материала.
1)Поработайте в парах. На партах у вас по 5 конфет. Разделите их поровну. Сколько конфет получит каждый? Запишите результат на листочке.
2)Проверим, что получилось. (2 целых конфеты и 1/2 )
Что можете сказать об этой записи? (В записи есть натуральное число и правильная дробь)
3)В ответе задачи получили правильную дробь? (Да) Прочитайте число. Цель достигли? Как бы вы назвали такое число?
4)В математике такие числа называются СМЕШАННЫЕ.
5)Какая у нас тема урока?
ТЕМА УРОКА: СМЕШАННЫЕ ЧИСЛА (запишем тему урока в тетрадь)
6)В словаре Сергея Ивановича Ожегова слово смешанный имеет следующие значения:
а) Образовавшийся путём смешения чего-нибудь
б) Составленный или составившийся из разных частей, элементов, участков.
Что же мы смешиваем в нашем числе? (целое число и дробное)
7)Где мы можем проверить наши выводы? Откройте учебник на стр. 183, прочитайте правило про себя.
8)Из каких частей состоит смешанное число? (Смешанное число состоит из целой части и дробной части)
Чтобы из неправильной дроби выделить целую часть, надо:
-
разделить с остатком числитель на знаменатель;
-
неполное частное будет целой частью;
-
остаток (если есть) дает числитель, а делитель - знаменатель дробной части.
- Как записать смешанное число в виде неправильной дроби?
Чтобы представить смешанное число в виде неправильной дроби, нужно:
-
умножить его целую часть на знаменатель дробной части;
-
к полученному произведению прибавить числитель дробной части;
-
записать полученную сумму числителем дроби, а знаменатель дробной части оставить без изменения.
5. Закрепление нового материала.
Решить №№
6. Физкультминутка.
Поднимает руки класс - это "раз"
Повернулась голова - это "два"
"Руки вниз, вперёд смотри - это "три".
Руки в стороны пошире развернули на "четыре"
С силой их к плечам прижать - это "пять"
Всем ребятам надо сесть - это "шесть".
7. Самостоятельная работа.
Решить № №
8. Итоги урока. Рефлексия. Д/з.
Выучить п. , решить №№
1)Какую цель ставили перед собой на уроке? Добились цели?
С какими числами познакомились?
Из каких частей состоит смешанное число? Какую дробь можно записать в виде смешанного числа? Где будем использовать смешанные числа?
2)Кто испытывал затруднения при работе со смешанными числами? А у кого всё получалось? С каким настроением пойдёте домой?
3)Всё ли мы теперь узнали с вами о дробях? На следующем уроке продолжим знакомиться с дробями.
Тема: Сложение и вычитание смешанных чисел.
Цель:
-
Познакомить учащихся с алгоритмами сложения и вычитания смешанных чисел путем включения учащихся в практическую деятельность.
-
Совершенствовать вычислительные навыки, развивать познавательный интерес, внимание, логическое мышление учащихся через игровые моменты.
-
Воспитывать чувство товарищества и взаимовыручки.
Ход урока.
1. Организационный момент.
Каждый день - всегда, везде,
На занятиях, в игре
Смело четко говорим
И тихонько сидим.
2. Мотивация урока.
Сегодня на уроке мы будем изучать тему «Сложение и вычитание смешанных чисел» и научимся применять новые знания на практике. А урок наш будет необычным - урок-сказка «Цветик-семицветик».
В Математическом царстве, в Арифметическом государстве, в городе Обыкновенная дробь жила-была девочка. Учительница математики дала ей задание: приготовить вопросы и упражнения для урока. Утром девочка отправилась в школу. Идет, по сторонам зевает, вывески читает, ворон считает. Вдруг из-за угла выскочила злая собака, сумку выхватила и убежала.
Села девочка на скамейку и заплакала. Вдруг откуда ни возьмись, Математика - царица наук. И говорит она девочке:
- Не плачь, я тебе помогу. Ты девочка хорошая, хоть и любишь зевать по сторонам. Вот тебе «цветик-семицветик». Он волшебный. Надо только оторвать лепесток и прочитать, что на нем записано.
3. Актуализация опорных знаний. Проверка д/з.
Этот красный лепесток
Начинает наш урок.
Устный счет мы проведем
И рекорды все побьем.
Проверка д/з. Сверка с верными ответами.
Вдруг наш желтый лепесток
Улетает на восток.
К нам с востока возвращается
И работа продолжается.
Фронтальный опрос:
а) Какую дробь называют правильной?
б) Сравните правильную дробь с 1?
в) Какую дробь называют неправильной?
г) Сравните неправильную дробь с 1? 5/6,7/7,2/5,3/10,13/10,18/5
д) Назовите правильные (неправильные) дроби?
е) Как из неправильной дроби выделить целую часть?
ж) Выделите целую часть из неправильных дробей?
з) Как складываются (вычитают) дроби с одинаковыми знаменателями?
Оранжевый лепесток
Продолжает наш урок.
Математический диктант решаем,
Без ошибок отвечаем.
Математический диктант:
Двое учащихся работают на доске, остальные на листах.
1). Из дробей: 7/8, 11/11, 9/4, 16/9, 3/5, 6/13 выберите правильные дроби и неправильные.
2). Сравните выписанные дроби с 1.
3). Выделите в дробях целую часть:
19/8
16/5
25/4
27/11
4). Запишите смешанные числа в виде неправильной дроби:
2 3/7
5 2/3
9 1/12
8 3/7
Поменялись листочками. Сегодня у нас взаимоконтроль, оцените друг друга.
4. Изучение нового материала.
Зеленый цвет весьма приятный,
Лепесточек аккуратный.
Оторвем его мы дружно
И узнаем все, что нужно.
Ребята, а знаете ли вы, как складывают и вычитают смешанные числа?
3 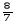 + 2
+ 2 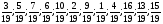 = (3 +
= (3 + 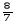 ) + (2 +
) + (2 +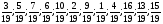 ) = (3 +2) + (
) = (3 +2) + (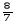 +
+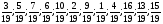 ) = 5 +
) = 5 + 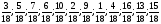 = 5
= 5 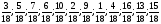
Чтобы смешанные числа сложить
Надо их на части разложить:
3 - это целая часть, прибавим к ней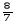 - это дробная часть;
- это дробная часть;
2- это целая часть, прибавим к ней- 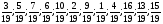 это дробная часть.
это дробная часть.
И между суммами поставим знак сложенья.
Чтобы удобно нам было считать
Мы эти числа должны сгруппировать:
Целые части мы сложим отдельно,
И дробные части мы сложим отдельно.
Получили 5- это целая часть,
А-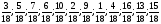 это дробная часть.
это дробная часть.
Что делать с ними мне скажите
И ответ скорее подскажите. (5 + 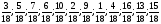 = 5
= 5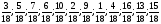 - получили смешанное число)
- получили смешанное число)
Кто может сам сформулировать правило сложения смешанных чисел?
Краткая запись: 3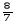 + 2
+ 2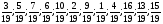 = 5
= 5 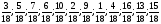
Давайте попробуем выполнить вычитание смешанных чисел (по аналогии):
5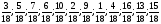 - 3
- 3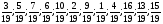 = (5 +
= (5 +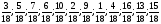 ) - (3 +
) - (3 +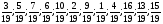 )= (5 - 3) + (
)= (5 - 3) + (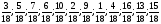 -
-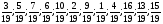 ) = 2+
) = 2+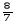 = 2
= 2 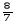
Сформулируйте правило вычитания смешанных чисел.
Краткая запись: 5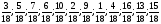 - 3
- 3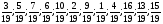 = 2
= 2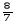 .
.
5. Физминутка
Потрудились - отдохнём,
Встанем, глубоко вздохнём.
Руки в стороны, вперёд,
Влево, вправо поворот.
Три наклона, прямо встать.
Руки вниз и вверх поднять.
Руки плавно опустили,
Всем улыбки подарили.
6. Закрепление нового материала.
Бордовый лепесток мы сорвем,
Ручки в руки мы возьмем.
Смело порешаем
И ответы мы узнаем.
Решить № №
7. Самостоятельная работа.
Серебристый лепесток мы отрываем,
Замок волшебный открываем.
Чтоб в царство знаний нам попасть
Самостоятельно нам надо порешать.
Решить №
8. Итоги урока. Д/з.
- Что такое смешанное число?
- Как сложить смешанные числа?
- Как вычесть смешанные числа?
-Чему мы сегодня научились? ( Складывать и вычитать смешанные числа.)
Это вам поможет справиться с домашним заданием.
Выучить п., решить № №
Салатовый цветок,
Интересный лепесток.
Его мы отрываем
И кое-что узнаем.
Расшифруйте слова!
1 группа

2 группа

3 группа

4 группа

Ответы:
-
Смешанных
-
Чисел
-
Сложение
-
Вычитание
(Представитель каждой группы записывает на доске расшифрованное слово).
Изрядно потрудились, собрали вы слова.
Слова же следует теперь соединить,
В какую фразу можно их объединить?
(Сложение и вычитание смешанных чисел).
Вот и закончилась сказка. Добрая волшебница-Математика спасла девочку, а цветик-семицветик помог вам сделать еще один шаг на пути к новым знаниям.
Тема: Сложение и вычитание смешанных чисел.
Цель:
-
Закрепит алгоритм сложения и вычитания смешанных чисел;
-
Создание условий для формирования мыслительных операций.
-
Воспитывать чувство товарищества и взаимовыручки, настойчивости, привычки работать упорядоченно, самостоятельно.
Ход урока.
1. Организационный момент.
2. Мотивация урока.
Здравствуйте! Я надеюсь, что Вы все готовы к уроку? Тогда мы отправляемся в лес смешанных чисел. А почему в лес? А потому что в Англии в 18 веке говорили, что смешанные числа приводят учащихся в уныние, заставляя восклицать: «В эти дебри мы не пойдём! ». Но сегодня на улице 21 век и мы постараемся доказать обратное. Поэтому сегодня тема нашего урока - «Действия со смешанными числами». На уроке мы готовимся к контрольной работе и наша задача вспомнить и закрепить всё, что знаем о смешанных числах. Должны повторить правила сложения и вычитания смешанных чисел и применять наши знания для решения задач и уравнений. Развивать внимание и трудолюбие.
3. Актуализация опорных знаний. Проверка д/з.
Фронтальная работа с классом:
установить верно или неверно утверждение, с использованием сигнальных карточек.
1 -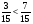 =
=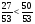 ; 5 - 2
; 5 - 2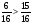 = 3
= 3![]() ; 4 - 2
; 4 - 2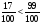 = 1
= 1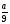 ; 3
; 3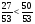 - 2 =1
- 2 =1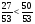 .
.
Дробь 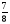 равна смешанной дроби:
равна смешанной дроби:
А) 4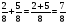 ; Б) 3
; Б) 3 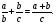 ; В) 1
; В) 1 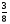 .
.
Число 7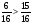 равно неправильной дроби:
равно неправильной дроби:
А) 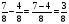 ; Б)
; Б) 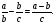 ; В)
; В)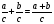 .
.
Сколько натуральных чисел заключено между числами 8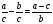 и 18
и 18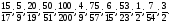 ?
?
А) 10; Б) 9; В) 12.
Вычислить устно:
1) 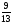
2) 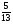
3) 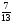
4) 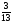
5) 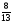
6) 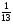
4. Решение упражнений на сложение и вычитание смешанных чисел.
Решить № №
5. Физкультминутка.
Кто проснуться не успел
Тот остался не у дел!
Остальные повернулись
И соседу улыбнулись!
2/4 приседают
3/6 им помогают!
5/10 потянулись
И в окошки улыбнулись!
7/7 сказали вдруг
Математика - наш друг!
Дроби снова изучаем
И друг другу помогаем!
6. Самостоятельная работа в парах.
Решить № №
7. Итоги урока. Д/з.
Решить № №
Урок сегодня завершён,
Но каждый должен знать:
Познание, упорство, труд
К успеху в жизни приведут!
Тема: Обобщение и систематизация знаний по теме «Обыкновенные дроби»
Цель:
-
Образовательные: обобщить и систематизировать знания об обыкновенных дробях; закрепить и усовершенствовать навыки действия над обыкновенными дробями, навыки сравнения обыкновенных дробей;
-
Развивающие: навыки реализации теоретических знаний в практической деятельности; сообразительность, стремление к преодолению трудностей; интеллектуальные навыки (мыслительные операции: анализ, синтез, сравнение, обобщение).
-
Воспитывающие: чувство ответственности за качество и результат выполняемой работы; культуру общения, коммуникабельность (умение слушать друг друга, учителя, отстаивать свою точку зрения).
Ход урока.
1. Организационный момент.
Поэт Р.Сеф написал такие строчки:
Кто ничего не изучает,
Тот ничего не замечает.
Кто ничего не замечает
Тот вечно хнычет и скучает.
А чтобы не было вам, ребята, скучно на уроке, каждый должен принимать активное участие.
2. Мотивация урока.
В мире много сказок
Грустных и смешных.
И прожить на свете
Нам нельзя без них!
Пусть герои сказок
Дарят нам тепло,
Пусть добро навеки
Побеждает зло!
«В некотором царстве, в некотором государстве жил-был Иван-царевич, и было у него три сестры: Ольга, Марья и Анна. Отец и мать у них умерли, и отдал Иван-царевич сестер своих замуж за царей медного, серебряного и золотого царства. Целый год жил без сестер, и сделалось ему скучно. Решил он проведать сестриц и отправился в путь. По дороге Иван-царевич повстречал Елену-Прекрасную и они полюбили друг друга. Но злой Кощей похитил Елену и спрятал в глубокое подземелье. Погоревал-погоревал Иван-царевич, да делать нечего, взял он своих верных воинов и отправился в путь».
- А наша с вами задача: помочь им на их нелегком пути. Мы с вами начали знакомство с обыкновенными дробями, научились сравнивать, складывать и вычитать дроби с одинаковыми знаменателями, выделять целую часть из неправильной дроби, находить дробь от числа и число по его дроби. И чтобы перейти на следующем уроке к решению более сложных примеров, мы с вами сегодня еще раз все должны вспомнить и повторить.
«Итак, шли они шли до синего моря, видят: у берега корабль. Сели они на него, а корабль ни с места. Волшебный был корабль, и чтобы он поплыл, нужно выполнить задание, которое на его дне лежит».
3. Актуализация опорных знаний. Проверка д/з.
Математический диктант.
1. Запишите: а) - правильные дроби; б) - неправильные дроби.
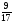 В - I
В - I
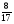
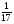
В - II
2. Сравните:
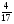
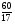 В - I
В - I
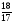
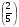 В - II
В - II
3. Выделите целую часть из неправильной дроби:
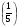
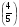
В - I
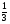
В - II
(Проверка диктанта)
4. Закрепление и обобщение материала, изученного на прошлых уроках.
«Корабль подплыл к другому берегу, а берег тот: одни горы, да такие высокие, что собой солнце закрывают. Не знает Иван-царевич, как через них перебраться. Но вдруг вспомнил он, что царь золотого царства подарил ему ковер-самолет. Но не взлетает ковер-самолет, тянут его к земле нерешенные задания».
1) Выполните действия:
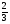
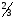
«Выполнили они задание, перелетели через горы и опустились у дремучего леса. Шли они шли по лесу и пришли к избушке Бабы-Яги. А Баба-Яга давно враждовала с Кощеем и решила Ивану-царевичу помочь, но при условии, что он выполнит ее задание».
2) Решите уравнение:
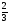
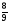
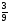
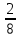
«Показала Баба-Яга дорогу в царство Кощея. Долго ли, коротко ли шел Иван-царевич и пришел в Кощеево царство, нашел он подземелье, а вход в него 3-х главый Змей - Горыныч охраняет, и чтобы его победить волшебный меч нужен. Чтобы его получить, выполним следующее задание».
Физкультминутка.
1. Исходное положение - сидя, откинувшись на спинку стула, глубокий вздох, наклоняемся вперед - выдох (4 раза )
2. Сидя, откинувшись на спинку стула, прикрыть веки, крепко зажмурить глаза, открыть веки (4 раза)
3. Сидя, руки на поясе. Повернуть голову вправо, посмотреть на локоть правой руки, повернуть голову влево, посмотреть на локоть левой руки (4 раза)
4. Глазами нарисовать 4 окружности по часовой стрелке 4- против часовой стрелке .
3) Найдите значение выражения:
В - I 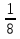
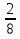
В - I I 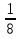
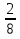
«Взял Иван-царевич меч и одним махом отрубил Змею все головы, добрался до подземелья, а дверь на большой замок закрыта и нужен к нему ключ не простой, а волшебный. Тогда Иван-царевич принялся за последнее задание».
4) Решите задачу:
а) В школу привезли 300 новых учебников, из них учебники по математике составляли 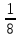 всех книг, учебники по русскому языку
всех книг, учебники по русскому языку 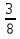 всех книг, а остальные книги были по литературе. Сколько привезли книг по литературе?
всех книг, а остальные книги были по литературе. Сколько привезли книг по литературе?
б) Поезд прошел 840 км, что составляет 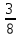 его пути. Какое расстояние ему осталось пройти?
его пути. Какое расстояние ему осталось пройти?
5. Логическое задание.
«Открыл Иван-царевич подземелье, освободил Елену-Прекрасную. В тот же день сыграли они свадьбу, проведали сестер и отправились домой. Но чтобы они благополучно добрались до дома, нужно выполнить последнее задание».
5) Выпишите точки, которые соответствуют дробям:
0 Я 1 К П Н А Б И Е З
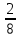
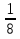
6. Подведение итогов. Д/з.
Вот закончена игра,
Результат узнать пора.
Кто же лучше всех трудился?
Кто же в сказке отличился?
Для подведения итогов дети сами должны сказать, что вспомнили и закрепили на уроке. Преподаватель должен выставить оценки. Особенно обратить внимание на тех, кто отвечал у доски. Если с последним заданием были трудности, не стоит торопиться объяснять его. Нужно дать детям обдумать его дома, что бы им было интересно самим решить и довести до конца это задание. На следующий день можно с этого задания начать урок. А так же задать домашнее задание из учебника.
Сложение и вычитание дробей с разными знаменателями.
Тип урока: комбинированный.
Место данного урока: первый урок по данной теме.
Метод: использовался метод проблемного изложения.
Цели:
-
Обеспечить усвоение учащимися темы "Сложение и вычитание дробей с разными знаменателями"
-
Развивать культуру математической речи, интерес к предмету.
-
Воспитывать аккуратность и точность при работе с обыкновенными дробями.
Ход урока
1) Организационный момент.
Сообщается тема урока , цель и план.
2) Устный счет:
1. Прочитать дроби : ![]() ;
;
2. Сократить дроби: (ребята повторяют правило сокращения дробей)
![]() ;
;
3. Сравнить: (ученики повторяют правило сравнения дробей с одинаковыми знаменателями, правило сравнения обыкновенных дробей с единицей и правило сравнения дробей с разными знаменателями)
![]() ;
;
4. Выделить целую часть из дробей: (ребята проговаривают правило выделения целой части из неправильной дроби) ![]()
![]()
![]()
5. Вычислить: (повторили правило сложения и вычитания дробей с одинаковыми знаменателями) ![]()
![]()
![]()
![]()
3) Изучение нового материала. Правило сложения и вычитания дробей с разными знаменателями
Выполнить действия : ![]()
![]()
![]()
4) Закрепление. Работа по учебнику №
а) ![]()
б) ![]()
в) ![]()
5) Физкультминутка.
6) Закрепление изученного(продолжение).
Задача. В первый день магазин получил ![]() т овощей, а во второй - на
т овощей, а во второй - на ![]() т меньше. Сколько тонн овощей магазин получил за два дня?
т меньше. Сколько тонн овощей магазин получил за два дня?
7) Тестовая работа.
1. Вычислить ![]()
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ;
;
2. Найти сумму дробей ![]()
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ;
;
3. Найдите разность дробей ![]()
4. В первый день в магазине было продано 3/ 10 лука, а во второй ![]() т. Сколько тонн лука было продано за два дня?
т. Сколько тонн лука было продано за два дня?
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
8) Проверка тестовой работы.
1
2
3
4
а
б
а
б
9) Домашнее задание.
выучить правило сложения и вычитания дробей с разными знаменателями.
-
№ №
10) Итог урока.
-
Что нового узнали на уроке?
-
Чему научились?
-
Сформулируйте правило сложения и вычитания дробей с разными знаменателями.
«Сложение и вычитание обыкновенных дробей»
Тип урока: повторительно- обобщающий.
Вид урока: смешанный ( разные формы работы: беседа, устная фронтальная работа, индивидуальная работа с учащимися, выполнение задания с элементом исследования, самостоятельная работа)
Цели урока: обучающая- обобщение и систематизация знаний по темам « Сравнение дробей, Сложение и вычитание обыкновенных дробей»
развивающая - развитие математической речи учащихся при проговаривании правил, развитие внимания ( при заполнении таблицы), развитие исследовательских навыков ;
воспитательная - развитие коммуникативных способностей ( консультанты), воспитание чувства товарищества.
-
Организационный момент.
-
Целеполагание.
1) ![]() ( на доске записаны дробь и стихотворение с пропусками)
( на доске записаны дробь и стихотворение с пропусками)
Каждый может за версту
Видеть дробную ……….
Над чертой ……… . Знайте!
Под чертою …………. .
Дробь такую непременно
Надо звать ……………. .
Фронтальное задание: Ребята! Давайте дружно вместе прочитаем стихотворение, вставляя пропущенные слова ( черту, числитель, знаменатель, обыкновенной).
-
( на доске записать ряд чисел)
![]() 189, 1,
189, 1, ![]() ? Фронтальная беседа по вопросам:
? Фронтальная беседа по вопросам:
- Что вы видите в этой записи? (числа)
- Какие числа?
- Какие действия вы учились выполнять с натуральными
числами, начиная с первого класса?
- Выберите из этой записи дробные числа и назовите их.
- Какие действия вы уже научились выполнять с дробными
числами?
Далее акцентируется внимание на последнем ответе: действия сравнения дробей с одинаковыми знаменателями, сравнение дробей с одинаковыми числителями, сложение и вычитание дробей с одинаковыми знаменателями и дробей с разными знаменателями
и формируется цель урока: повторить и закрепить материал по темам «Сравнение дробей» и «Сложение и вычитание дробей». А основой всех наших действий являются следующие правила: ![]() и
и ![]() ( правила записаны на листах ватмана и два ученика вслух
( правила записаны на листах ватмана и два ученика вслух
должны сформулировать эти правила)
III. Актуализация знаний.
-
Индивидуальные задания для слабых учащихся (карточки - консультанты):
-
повтори правило на стр.
-
а) сократи дроби:
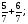
-
б) приведи дроби к знаменателю 30: ![]() .
.
3) повтори правила на стр.
4) выполни действия с дробями:
а) ![]() подумай над ответом); б)
подумай над ответом); б) ![]() в)
в) ![]() (подумай над ответом);
(подумай над ответом);
г) ![]() (выдели целую часть в полученном ответе).
(выдели целую часть в полученном ответе).
5) прочти выделенный текст на стр .
6) выполни действия: а) ![]() б) 1-
б) 1- ![]() в)
в) ![]()
(2) Устные упражнения для остальных учащихся класса:
1) ( работа с черновиком) Каждый ученик одного ряда просчитывает свою цепочку вычислений и тот, кто получит ответ первым, может выйти и записать свои результаты
I ряд ![]()
II ряд 1 - ![]()
III ряд ![]()
2)найдите закономерность и заполните таблицу ( 1 мин. на размышление)
![]()
![]()
*
![]()
![]()
*
![]()
![]()
![]()
*
1
1
1
*
1
(при проверке данного задания - вопрос:
какая закономерность? Докажите, что эта закономерность выполняется и в четвёртом столбце)
3)Найди ошибку! И запиши номера неверных сравнений на черновик крупными цифрами, затее свою запись молча поднять вверх по просьбе учителя :
![]()
![]()
1 2 3 4 5 ![]() ( Ваш верный ответ 25)
( Ваш верный ответ 25)
IV. Отработка умений и навыков
-
Выполните действия(сначала все учащиеся работают самостоятельно, затем один ученик зачитывает свои ответы и каждое задание комментирует, а второй прописывает решение пункта г) на доске):
а) ![]() б)
б)![]() в)
в) ![]() г)
г) ![]()
( Одновременно два сильных ученика проверяют работавших индивидуально)
-
№ ( найдите два способа решения) При устной поверке задания повторяется правило нахождения части от целого.
-
Самостоятельная работа ( 7-8 мин.) с последующей самопроверкой
( ответы заранее записаны на доске и закрыты таблицей)
Вариант 1 Вариант 2
-
Выполните действия: (3 балла)
а) ![]() ; б) 1-
; б) 1- ![]() в)
в)![]() / а)
/ а) ![]() б)
б)![]() в) 1-
в) 1- ![]()
-
Сравните дроби: ( вместо звёздочки поставьте нужный знак) (1 балл)
а) ![]() б)
б)![]() / а)
/ а) ![]() б)
б)![]()
-
Решите уравнение: ( 1 балл)
![]() /
/ ![]()
-
Домашнее задание: Составьте либо 4 примера с дробями, либо две задачи для своего друга и оформите их на отдельном двойном листе.
-
Итог урока.
Сложение и вычитание обыкновенных дробей.
Цели урока:
Образовательные:
-
систематизировать знания об обыкновенных дробях;
-
повторить правила сложения и вычитания дробей с одинаковыми знаменателями;
-
повторить правила сложение и вычитание дробей с разными знаменателями.
Развивающие:
-
развивать внимание, речь, память, логическое мышление, самостоятельность.
Воспитательные:
-
воспитывать стремление достигать поставленную цель; уверенности в себе, умение работать в коллективе.
Знать: правила сложения и вычитания дробей с одинаковыми и разными знаменателями.
Уметь: складывать и вычитать обыкновенные дроби.
Тип урока: урок обобщения и систематизации знаний.
Ход урока
1). Организационный момент.
Учащимся предлагается прочитать тему урока.
- "Сложение и вычитание обыкновенных дробей".
Предлагается сформулировать цели и задачи урока, в ходе обсуждения они формулируются (учитель может их записать на доске).
2). Актуализация знаний. Повторение пройденного материала.
а) Сегодня урок мы начнём с аукциона. Выставлен единственный лот "обыкновенная дробь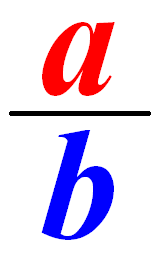 Вспомним, что мы знаем об обыкновенных дробях:
Вспомним, что мы знаем об обыкновенных дробях:
- числитель;
- знаменатель;
- дробная черта - деление;
- на b частей делим, берём а таких частей ;
- правильная;
- неправильная;
- выделить целую часть;
- сократить;
- привести к новому знаменателю;
- примеры.
Кто последний сказал об обыкновенной дроби, тому достаётся модель обыкновенной дроби.
б) Закрепим наши знания при выполнении теста
ТЕСТ
1. Найдите правильную дробь:
А)![]() ; Б)
; Б) ![]() ; В)
; В) ![]() .
.
2. Найдите неправильную дробь:
А)![]() ; Б)
; Б) ![]() ; В)
; В) ![]() .
.
3. Сократите дробь ![]() :
:
А)![]() ; Б)
; Б) ![]() ; В)
; В) ![]() .
.
4. Приведите дробь ![]() к знаменателю 28:
к знаменателю 28:
А)![]() ; Б)
; Б) ![]() ; В)
; В) ![]() .
.
5. Выделите целую часть ![]() :
:
А)![]() ; Б)
; Б) ![]() ; В)
; В) ![]() .
.
Ответы вписывают в таблицу.
1
2
3
4
5
Обменяться тетрадями, выполнить взаимопроверку.
Подвести итог:
-
5 "+" отметка 5,
-
4 "+" отметка 4 ,
-
3 "+" отметка 3.
3).Применение правил сложения и вычитания обыкновенных дробей с одинаковыми знаменателями.
Какие обыкновенные дроби мы умеем складывать?
- дроби с одинаковыми и разными знаменателями
Повторим сложение дробей с одинаковыми знаменателями.
- чтобы сложить две дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить без изменения.
- чтобы вычесть дроби с одинаковыми знаменателями, надо из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить без изменения.
Закрепим знания на практике.
Учащимся предлагается вычислить устно примеры и ответы записать в бланк ответов задания № 2.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Обменяться тетрадями, выполнить взаимопроверку.
Подвести итог:
-
9-8 "+" отметка 5,
-
7-6 "+" отметка 4 ,
-
5 "+" отметка 3.
4). Физкультминутка.
5). Применение правил сложения и вычитания обыкновенных дробей с разными знаменателями.
Мы складывали дроби с одинаковыми знаменателями. Что необходимо выполнить, чтобы сложить обыкновенные дроби с разными знаменателями?
- чтобы выполнить сложение и вычитание дробей с разными знаменателями, надо привести дроби к общему знаменателю, найдя дополнительные множители. Выполнить сложение и вычитание обыкновенных дробей уже с одинаковыми знаменателями.
Закрепим знания на практике. Ученик вызывается к доске, остальные в тетради. После выполнения 3-4 примеров ребятам предложено решать самостоятельно.
Вычисли:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Дополнительно:
Вычисли:
1. а) ![]() б)
б) ![]() в)
в) ![]() ; г)
; г) ![]()
2. а) ![]() б)
б) ![]() в)
в) ![]() ; г)
; г) ![]()
3. а) ![]() б)
б) ![]() в)
в) ![]() ; г)
; г) ![]()
Подвести итог решения примеров.
6. Домашнее задание
Правило,решить№№; дополнительно: составить 4 примера на сложение и вычитание дробей и оформить на листах.
7. Подведение итогов (каждый учащийся выставляет себе оценку за работу на уроке).
Учитель оценивает работу учащихся на уроке и выставляет оценки.
Рефлексия
"Ёлочка настроения"
По окончании урока дети рисуют рот у шара-смайлика и прикрепляют его на ёлочку.
-
Я доволен своей работай на уроке.
-
На уроке я работал неплохо.
-
На уроке мне было трудно.





Урок по теме "Сложение и вычитание обыкновенных дробей с разными знаменателями"
Цель: обобщить знания учащихся по данной теме, скорректировать возможно неверное применение знаний.
На предыдущем уроке проводится самостоятельная работа.
Вариант 1
1. Выполните действия:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]()
2. Отрезок АВ равен ![]() м, и он длиннее отрезка CD на
м, и он длиннее отрезка CD на ![]() м. Найдите длину CD.
м. Найдите длину CD.
3. Решите уравнение: ![]()
Вариант 2
1. Выполните действия:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]()
2. Отрезок МК равен ![]() м, и он короче отрезка АС на
м, и он короче отрезка АС на ![]() м. Найдите длину АС.
м. Найдите длину АС.
3. Решите уравнение: ![]()
Работа проверяется и оценивается учителем. В зависимости от полученной оценки учащиеся получают различные задания на следующий урок.
Перед началом урока на парте у каждого учащегося находится цветной конверт:
-
красный - соответствует оценке "5"
-
синий - соответствует оценке "4"
-
желтый - соответствует оценке "3".
Учащиеся знакомы с данными цветами и соответствующими им оценками.
Ход урока
I. Организационный момент
(Организация класса, постановка цели)
Дроби всякие нужны,
Дроби всякие важны.
Дробь учи, тогда сверкнёт удача.
Если дроби будешь знать ,
Точно смысл их понимать,
Станет легкой даже сложная задача.
II. Устная работа
(Работа на карточках.)
1. Сократите дроби:
![]()
![]()
![]() ;
; ![]()
![]()
![]()
![]()
![]()
![]()
2. Приведите дроби к знаменателю 45
![]()
![]()
![]()
![]()
![]()
![]()
3. Представьте неправильные дроби в виде смешанных чисел
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
III. Повторение
-
Верно ли, что при делении на 2 числителя и знаменателя неправильной дроби получится неправильная дробь
-
Можно ли сократить дробь, если ее числитель и знаменатель четные числа
-
Можно ли сократить дробь, если ее числитель и знаменатель взаимно простые числа
-
Может ли НОК двух чисел равняться их произведению
-
Верно ли, что дробь
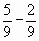 можно сократить на 9
можно сократить на 9 -
Верно ли, что
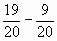
-
Верно ли, что из двух дробей с одинаковым числителем больше та, у которой знаменатель меньше
IV. Анализ самостоятельной работы
По результатам самостоятельной работы вы получили конверты разного цвета. Ваша оценка соответствует цвету конверта.
Типичные ошибки:
-
при сокращении дробей
-
при выделении целой части неправильной дроби
-
нахождение наименьшего общего знаменателя.
V. Решение задач
1. Сократите дроби ![]() ,
, ![]()
2. Приведите дроби к знаменателю 28 ![]() ,
, ![]()
3. Приведите дроби к общему знаменателю ![]() и
и ![]() ,
, ![]() и
и ![]() - один ученик у доски.
- один ученик у доски.
4. Выполните действия ![]() ,
, ![]()
5. Решите уравнение: х - ![]() =
= ![]() - у доски.
- у доски.
VI. Физкультминутка
VII. Самостоятельная работа
(У каждого учащегося на конверте прикреплена карточка с индивидуальным заданием, соответствующим предыдущей оценке. В конверте находится решение данного задания и карточка с домашним заданием.)
Вариант 1 (желтая карточка)
Выполните действия:
а) ![]() б)
б) ![]() в)
в) ![]()
г) ![]()
***Дополнительное задание:
Сократите дроби: ![]()
![]()
Вариант 2 (желтая карточка)
Выполните действия:
а) ![]() б)
б) ![]() в)
в) ![]()
г) ![]()
***Дополнительное задание:
Сократите дроби: ![]()
![]()
Вариант 3 (синяя карточка)
Выполните действия:
а) ![]() б)
б) ![]() в)
в) ![]()
г) ![]()
***Дополнительное задание:
Сократите дроби:
![]()
![]() ;
; ![]()
Вариант 4 (синяя карточка)
Выполните действия:
а) ![]() б)
б) ![]() в)
в) ![]()
г) ![]()
***Дополнительное задание:
Сократите дроби:
![]()
![]() ;
; ![]()
Вариант 5 (красная карточка)
Выполните действия:
а) ![]() б)
б) ![]() в)
в) ![]()
Решите уравнение ![]()
***Дополнительное задание:
Решите уравнение
![]()
Вариант 6 (красная карточка)
Выполните действия:
а) ![]() б)
б) ![]() в)
в) ![]()
Решите уравнение ![]()
***Дополнительное задание:
Решите уравнение
![]()
Учащиеся выполняют задание на карточке, работа рассчитана на 5-6 мин. Затем учащиеся меняются работами , вскрывают конверты , проверяют работу соседа по парте сверяясь с решением из конверта. Выставляют оценку и опять меняются тетрадями.
Критерии оценок:
-
"5" верно выполнено 5 заданий
-
"4" верно выполнено 4 задания
-
"3" верно выполнено 3 задания
-
"2" 2 задания и меньше
Каждая карточка содержит дополнительное задание, которое выполняется при наличии времени. Оценивается дополнительное задание учителем.
VIII. Предварительный мониторинг
Поднимают руку те, кто повысил свою оценку.
Поднимают руку те, кто подтвердил свою оценку.
Поднимают руку те, кто понизил свою оценку.
IX.Домашнее задание
На карточках внутри конверта

Х. Итог урока
Л. Толстой:
"Человек подобен дроби: в знаменателе то, что он о себе думает
В числителе, то что он есть на самом деле.
Чем больше знаменатель, тем меньше дробь".
Пусть ваша дробь всегда будет неправильной,
А в идеале - равной единице!
Умножение обыкновенных дробей.
Цели:
-
Образовательная: систематизировать и обобщить знания учащихся по теме, закрепить умения применять правила умножения обыкновенных дробей при решении задач и примеров;
-
Развивающая: активизировать деятельность учащихся через разнообразные виды самостоятельных работ и игровые формы урока;
-
Воспитательная: формировать у учащихся такие качества, как нравственность, гражданственность, взаимопомощь и взаимовыручка.
Ход урока
I. Организационный момент
Учитель: На предыдущих уроках мы с вами познакомились с правилом умножения обыкновенных дробей. Сегодня нам эти знания пригодятся для того, чтобы совершить путешествие на корабле в страну «Дроби». А капитаном этого корабля буду я.
II. Основная часть урока
1) Учитель: Французский писатель Анатоль Франс однажды заметил: «Учиться можно весело. Чтобы переварить знания надо поглощать их с аппетитом». Пусть эти слова послужат девизом сегодняшнего урока-путешествия.
2) Учитель: Для путешествия на корабле мы все должны быть в хорошей форме. Давайте проведем с небольшую разминку.
- Сформулировать правило умножения обыкновенных дробей;
- Сформулировать правило умножения обыкновенных дробей на натуральное число;
- Сформулировать правило умножения смешанных чисел.
- Устный счёт.
а) преобразуйте смешанные числа в обыкновенные дроби:
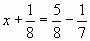
б) преобразуйте обыкновенные дроби в смешанные числа:
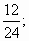
в) выполните умножение:
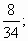
3) Учитель: Прежде, чем отплыть на корабле, необходимо проверить его исправность и устранить все неполадки.
На доске записаны примеры, в которых имеются скрытые ошибки. Вам необходимо эти ошибки выявить и исправить, тем самым устранив неисправность корабля.
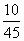
Учитель: Молодцы, ребята! Неисправности устранены, корабль к выходу из гавани готов!
4) Учитель: Перед отплытием необходимо проверить готовность экипажа к отплытию.
Вам нужно выполнить умножение дробей. Ответам соответствуют буквы, из которых вы должны составить кодовое слово.
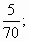
5) Учитель: Первой дробью, с которой познакомились люди, была половина, затем появилась треть. Египтяне умели умножать и делить дроби.
Современную систему записи дробей создали в Индии. Только там писали знаменатель сверху, а числитель - снизу, и не писали дробную черту. Записывать дроби в точности так, как сейчас стали арабы.
Следует отметить, что раздел арифметики о дробях долгое время был одним из наиболее трудных. Недаром, у немцев сохранилась поговорка: «Попасть в дроби», что означало зайти в безысходное положение. В то время считалось, что тот, кто не знает дроби, не знает и арифметики.
6) Учитель: Итак, все неисправности устранены, экипаж готов, приступаем к путешествию. Отплываем!
Давайте вычислим, сколько времени продлится наше путешествие.
На доске записано уравнение, решив которое, вы найдете количество дней, которое продлится наше путешествие.
![]()
Итак, наше путешествие продлится 4 дня
7) Учитель: Опасность! На горизонте появились пираты! Они могут потопить наш корабль! Необходимо поскорее уплывать от них! Как это сделать? Правильно решив задачу, мы ускоримся.
Задача: завод изготовил 120 телевизоров. ![]() этих телевизоров было отправлено в школы. Сколько телевизоров было отправлено в школы?
этих телевизоров было отправлено в школы. Сколько телевизоров было отправлено в школы?
Ответ: 90 телевизоров
8) Учитель: Итак, путешествие наше подходит к концу. Нужно найти спокойную бухту, куда причалит наш корабль. А для этого вам нужно решить задания.№№
9) Учитель: Наше путешествие завершено. Оно прошло благополучно! Благодарю за службу!
А закончить наш урок мне хотелось бы словами Л.Н. Толстого: «Человек есть дробь. Числитель - это достоинство человека, знаменатель - это оценка человеком себя самого. Увеличить своего числителя - свои достоинства, не во власти человека, но всякий может уменьшить своего знаменателя - свое мнение о самом себе, и этим уменьшением приблизиться к совершенству»
III. Подведение итогов урока. Домашнее задание
Умножение обыкновенных дробей
Цель урока:
1. Сформировать умения умножать дробь на дробь, дробь на число, смешанные числа.
2. Интенсифицировать самостоятельную познавательную деятельность наиболее подготовленных учащихся и активизировать помощь слабоуспевающим.
3. Воспитывать сознательную дисциплину учащихся через вовлечение каждого ученика в активную и посильную самостоятельную учебную деятельность, воспитания воли и характера.
4. Развивать навыки самоконтроля, математическую речь.
5. Формировать логическое, эвристическое мышление.
Форма урока: комбинированный
1. Сообщение темы и цели урока.
Ребята! Минздрав предупреждает: правильно умножая обыкновенные дроби, вы будете всегда поддерживать себя в правильной форме. Сегодня на уроке мы повторим основные правила умножения обыкновенных дробей, будем учиться применять эти правила при нахождении значения выражений.
2. Актуализация опорных знаний и умений учащихся.
Учитель обращается к табличке на доске.
Что умеем:
-
" + "Об. Др.
-
" - " Об. Др.
Обращать
Должны знать: 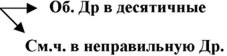
-
Др.
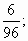 Др.
Др. -
Др.
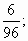 Ч
Ч -
См.
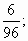 См.
См.
На доске картина с богатырем и замком 
Учитель обращается к учащимся:
- Три дороги надо пройти богатырю, чтобы научиться действовать дробями и попасть в Царство ДРОБИ. Надо помочь!
Учащиеся в парах, за партой, друг другу повторяют 3 правила умножения обыкновенных дробей. После этого выходят к доске три ученика и вслух рассказывают каждое правило.
На доске закрыты 5 примеров.
Учитель:
- Не пропускают нас в Царство Дроби, пока мы не найдем с вами числа, которые делятся на 8.
Учащиеся находят на картине числа, которые делятся на 8, и открывают задание.
№32 ![]()
![]()
![]() № 56 3
№ 56 3![]()
![]() 1
1![]() № 64
№ 64 ![]()
![]() 0 +
0 + ![]()
![]()
![]()
№ 72 ![]()
![]() 3
3
№ 88 4![]() =
= ![]()
![]()
![]()
10![]() =
= ![]()
20![]() =
=![]()
![]()
Работа с математическим тренажером.
Итак, теперь мы попали в Царство Дроби, работаем с тренажером. Нашли столбик с буквой А. Учащиеся по цепочке считают устно.
4. Работа по учебнику .
Обучающая самостоятельная работа №
Учащиеся выполняют самостоятельно № , учитель подходит к учащимся, проверяет, помогает тем, кто еще затрудняется в умножении дробей.
5. Дифференцированная проверочная работа.
На доске импровизированный светофор
Задания на карточках (они прикреплены на магнитах) записаны по мере сложности. Учащимся сообщаются критерии оценки за выполненную работу. Зеленый кружок - самый высокий бал, желтый - на 1 бал ниже, красный еще на 1 бал ниже.
Красный кружок на "3"
Желтый кружок на "4"
Зеленый кружок на "5".
Карточки:
Красный цвет: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ;
;
Желтый цвет: а) ![]()
![]() ; б)
; б) ![]() ; в) 2,4
; в) 2,4![]() ; г)
; г) ![]() ;
;
Зеленый цвет: а) 3![]()
![]() ; б) 2
; б) 2![]() ; в) 7
; в) 7![]() ; г) 0,4
; г) 0,4![]() ;
;
5. Подводится итог урока:
-
Оценки за работу на уроке.
-
Чему сегодня учились на уроке?
-
Что нужно знать, чтобы себя поддерживать в "правильной форме"?
Математический тренажер.
Каждое число в столбце умножь на число в рамке.
А ![]()
Б![]()
В![]()
Г![]()
Д![]()
![]()
![]()
![]()
![]()
![]()
---------------
![]()
![]()
![]()
![]()
![]()
---------------
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
-------------
![]()
![]()
![]()
![]()
![]()
-------------
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
3
----------------
![]()
![]()
![]()
2
![]()
----------------
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
3
---------------
![]()
![]()
![]()
![]()
![]()
--------------
![]()
4
![]()
![]()
![]()
![]()
![]()
6
![]()
![]()
-------------
![]()
![]()
1
![]()
![]()
-------------
5
![]()
0
![]()
![]()
Обобщающий урок по теме "Умножение обыкновенных дробей"
Цели урока:
Образовательные:
-
закрепить навыки умножения дробей
-
систематизировать знания учащихся по данной теме
Воспитательные:
-
воспитать внимание, аккуратность
Развивающие:
-
развить умение слушать, работать, самостоятельность, развитие речи.
Эпиграф:
"Я слышу - я забываю,
Я вижу - я запоминаю,
Я делаю - я усваиваю"
/Китайская мудрость/.
Ход урока:
1. Организационный момент
Здравствуйте! Садитесь! Сегодня на уроке мы должны показать свои знания по теме "Умножение дробей". Эпиграфом к уроку я взяла такие слова из китайской мудрости:
"Я слышу - я забываю,
Я вижу - я запоминаю,
Я делаю - я усваиваю"
Будем активны и внимательны на уроке.
"Что бы спорилось нужное дело,
Что бы в жизни не знать неудач,
Мы в поход отправляемся смело. -
В мир загадок и сложных задач.
Не беда что идти далеко
Не боимся, что путь будет труден.
Достижения крупные людям
Никогда не давались легко."
2. Проверка д/з
а) ![]()
б) ![]()
в) ![]()
г) ![]()
д) ![]()
№
1. 40% от 40 км ![]()
![]()
2. 30% 0т 40 км 40 км ![]()
![]()
3. ? ост. км![]()
![]()
Есть ли вопросы по домашнему заданию?
При решении задач мы использовали следующие правила: умножение дробей, нахождение дроби от числа.
Тетради с домашним заданием мы сдадим в конце урока.
В тетрадях запишите число, тему урока.
3. Индивидуальная работа, "Торопись, да не оступись!"
4 человека работают индивидуально. 2 человека у доски и 2 на местах. Уч-ся после решения - осуществляют взаимопроверку.
После проверки небольшой анализ выполненной работы.
Сколько заданий выполнено и я ставлю такую оценку.
Карточка №1
-
Найдите
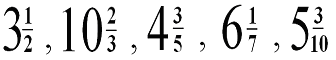 0т 28
0т 28 -
Вычислите
-
Вычислите
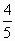
-
Выделите целую часть
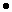
-
Найдите 50% от 104
Ответы:
Карточка №2
-
Найдите
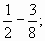 от 18
от 18 -
Вычислите
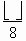
-
Вычислите

-
Выделите целую часть
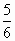
-
Найдите 50% от 98
Ответы:
4. Устные упражнения "Думай и соображай".
Сядьте удобно. Считаем устно.
Теоретическая часть.
![]()
А) назовите правильные дроби
Б) выделите целую часть из неправильной дроби
В) назовите равные дроби
Г) найдите произведение 1 и 3 дроби; 3 и 5 дроби
Выполните действия отгадайте слово
а) ![]()
б) ![]()
в) ![]()
г) ![]()
д) ![]()
1) ![]()
2) ![]()
3) ![]()
4) ![]()
5) ![]()
6) ![]()
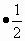
Можно решать и считать в тетрадях.
5. Решение задачи"Помоги Незнайке"
Задача.
Как то раз Незнайка решил начать новую жизнь. Он составил себе такое расписание на сутки: ![]() часть суток - чтение умных книг,
часть суток - чтение умных книг, ![]() - совершение добрых дел,
- совершение добрых дел, ![]() - прием пищи,
- прием пищи, ![]() - занятие спортом, 8 часов - сон. Сможете ли вы помочь Незнайке и сказать выполним ли его план?
- занятие спортом, 8 часов - сон. Сможете ли вы помочь Незнайке и сказать выполним ли его план?
Решение:
Чтение книг ![]() от 24ч
от 24ч
Добрые дела ![]() от 24ч
от 24ч
Прием пищи ![]() от 24ч
от 24ч
Занятие спортом ![]() от 24ч
от 24ч
Сон 8ч
1) ![]() ч.
ч.
2) ![]() ч.
ч.
3) ![]() ч.
ч.
4) ![]() ч.
ч.
5) 4+9+2+3+8=26ч
Ответ: план не выполним
6. Физминутка
Поработали, отдохнем. Сядьте прямо, руки свободно лежат на парте, закройте глаза, вспомните приятное, можете даже улыбнуться.
В течении одной минуты.
7. Задача "на внимательность".
-
К серой цапле на урок прилетело 7 сорок, а из них лишь 3 сороки приготовили уроки. Сколько лодырей сорок прилетело на урок? (4)
-
Мы - большущая семья, самый младший это я. Сразу нас не сосчитать!
-
Юра, Шура, Саша и Наташа тоже наша. Мы по улице идем, говорят, что детский дом. Сосчитайте поскорей сколько нас в семье детей? (6)
8. Решение примеров. Уравнений.
1) ![]()
2) ![]()
3) ![]()
4) ![]()
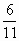
9. Работа с тестами "Проверь себя сам"
Задание: выбери ответ из числа предложенных, По выбранным ответам составь слово.
Вариант 1.
Найдите ![]() от 25
от 25
О. ![]()
М. 10
К. ![]()
2. Найдите ![]()
Л. ![]()
С. ![]()
О. ![]()
3. В одной коробке было ![]() кг. яблок, а в другой в 2 раза больше. Сколько яблок во второй коробке?
кг. яблок, а в другой в 2 раза больше. Сколько яблок во второй коробке?
Л. 11
Н. ![]()
К. 15
4. От рулона обоев длина которого ![]() м отрезали
м отрезали ![]() сер. длины. Сколько обоев осталось в рулоне?
сер. длины. Сколько обоев осталось в рулоне?
![]()
![]()
И. 5
О. ![]()
А. ![]()
5. Вычислите: ![]()
К. ![]()
Т. ![]()
Д. 100
6. Вычислите: ![]()
Е. ![]()
О. ![]()
И. ![]()
7. Решите уравнение ![]()
Ш. ![]()
Ц. 5
П. 5,2
МОЛОДЕЦ
10.Рефлексия,итог урока,д/з
Урок математики "Деление обыкновенных дробей"
Цели: ввести понятие взаимно обратных чисел; определять взаимнообратных чисел ввести понятие деления дроби на дробь, развивать логическое мышление учащихся.
Ход урока
I. Создание учебной ситуации
Учитель: Учитель. Какая учебная задача решается нами на протяжении последних уроков?
Ученики: Учимся выполнять действия с обыкновенными дробями.
Ученики: Как вы считаете, мы выполнили поставленную перед нами задачу?
Ученики: Нет. Мы еще не умеем делить дроби.
Учитель: А выполнять остальные действия вы умеете хорошо?
Ученики: Иногда вызывают затруднения действия…
Учитель: В чем причина затруднения?
Ученики: Невнимательность при выполнении действия.
Учитель: Как нам эту причину устранить?
Учащиеся высказывают свои предложения.
Учитель: Хорошо, ребята. Я думаю, что начнем мы сегодня урок с устного счета, который послужит разминкой к нашей дальнейшей работе.
1. В записи вычислений цепочкой поставьте необходимые числа
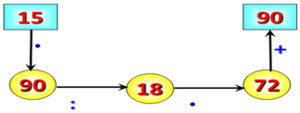
2. Не прошла разминка зря!
Дальше нам бежать пора!
а) ![]()
-
Назовите правильные дроби.
-
Назовите неправильные дроби.
-
Выделите целую часть неправильной дроби.
-
Найдите произведение первой и третьей дроби.
-
Назовите равные дроби.
б) Представьте смешанное число в виде неправильной дроби
![]()
3. Повторим алгоритм
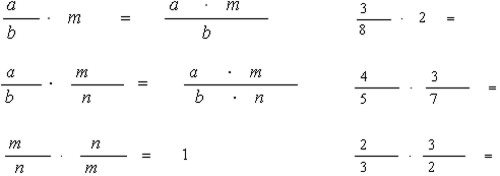
4. Посмотрите, ребята, привычные действия в разных ситуациях:
а) 1/4 ∙ 1; б) 3/8: 0; в) 1/2 : 3/8
Учитель: Почему последнее действие вызвало затруднение? Вы знаете как его выполнять? Кто знает?
У доски ученик выполняет запись: ![]()
Учитель: Ребята, я думаю, нам нет основания, не доверять правильности выполнения действия.
- Открыли тетради, записываем тему урока «Деление обыкновенных дробей»
- Но меня интересует другое. Посмотрите на эти дроби 3/8 и 8/3.
- Давайте выясним, какая связь существует между этими дробями?
II. Постановка учебной задачи.
Учитель: Чем отличаются эти дроби?
Ученик: Числитель 1 дроби является знаменателем 2 дроби и знаменатель 1 дроби - числитель 2 дроби.
Учитель: Даёт определение взаимно обратных дробей.
Конспект (на доске) а/в и в/а - взаимно обратные числа.
Учитель: Как можно получить дробь, обратную данной?
Ученик: Дробь надо перевернуть. (Или другие варианты ответов)
Учитель: Найдите произведение этих дробей. Сделайте это самостоятельно.
Учащиеся в тетрадях выполняют умножение.
Учитель: Какие результаты у вас получились? Какой вывод мы можем сделать?
Конспект (на доске) ![]() , при а ≠ 0 и в ≠ 0.
, при а ≠ 0 и в ≠ 0.
Учитель: Итак, чтобы числа были взаимно обратными, какое условие должно выполняться?
Ученики: Произведение дробей должно быть равно 1.
Учитель: Назовите дробь обратную 1 и 0.
Ученики: 1 и 0.
Учитель: Подводим итог конспект
Учитель: Используя взаимно обратные дроби, мы можем деление дробей свести к умножению. Вернёмся к примеру ![]() .
.
- Сформулируйте правило деления дробей.
Конспект (продолжение)
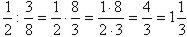
Решить пример
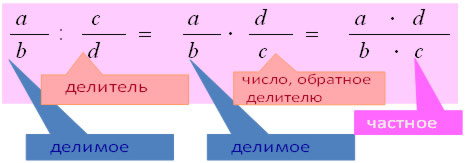
III. Физминутка
Чтобы в форме быть всегда
Двигаться нужно, друзья,
Приседаем раз и два,
Наклоняемся раз-два,
Поскакали, побежали,
Руки вверх, вы не устали?
А теперь все улыбнитесь,
Настроеньем зарядитесь.
IV. Закрепление изученного материала.
1. Найти число, обратное числу ![]() .
.
Учитель: (подробно объясняет) Запишем число ![]() в виде неправильной дроби:
в виде неправильной дроби: ![]() Значит, обратным
Значит, обратным ![]() будет число 6/23.
будет число 6/23.
2. Определи число взаимно обратное для:
![]()
3. Являются ли числа взаимно обратными?
![]()
4. Решить № №
V. Домашнее задание: ,решить № №,учить правило
VI. Итог урока.
-
Что нового вы узнали на уроке?
-
Для чего необходимо уметь делить обыкновенные дроби?
-
Где данное умение может пригодиться?
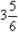
Обобщающий урок по теме "Деление обыкновенных дробей"
Цель для учителя: систематизировать, расширить и углубить знания, умения и навыки учащихся по теме.
Цель здоровьесберегающая: четкое разделение урока на определенные этапы и контроль усвоения на каждом этапе, который создает картину успеха.
Цели для учащихся:
-
Знать правило деления обыкновенных дробей, свойства деления;
-
Применять полученные знания при решении заданий.
Ход урока
I. Организационный момент
а) Ребята, вы сядете, когда услышите взаимно обратные числа:
4; ![]() ;
; ![]() ;
; ![]()
б) Что нужно нам знать, чтобы приступить к работе?
Т Е А М
-
расшифруйте запись
в) Помогите мне собрать слова в логическое предложение:
-
урок;
-
Обобщающий;
-
по теме;
-
обыкновенных;
-
Деление;
-
дробей.
г) Как вы понимаете тему нашего урока? Чем будем заниматься? Что для этого нужно знать? (см. цель учащихся)
Договор:
-
Слушать;
-
Слышать;
-
Не отвлекаться.
II. Актуализация опорных знаний
Сегодня мы должны повторить весь материал по теме и для этого отправимся в страну "Обыкновенных дробей". Т.к. всякое путешествие требует закалки и тренировки, то проверим готовы ли мы к путешествию:
а : b = с
а : b = ![]()
(а-числитель; b-знаменатель)
Назовите компоненты деления
Назовите обратную дробь данной дроби
Устно:
1) Выбери взаимно обратные числа.
![]() ;
; ![]() ;
; ![]() ;
; ![]() ; p
; p
k; 2; ![]() ;
; ![]() ;
; ![]()
Вопросы:
а) Закончи формулировку: взаимно обратными числами называют…
б) Если данная дробь правильная, то обратная ей дробь будет…
в) Если данная дробь не правильная, то обратная ей дробь будет…
г) Существует ли число, для которого нет обратного числа?
2) Придумать три пары взаимно обратных дробей.
а) ![]() ;
;
б) ![]() ;
;
в) ![]() .
.
3) Вместо звездочки поставьте знак: =; >; <.
а) ![]() ?
?
б) ![]() ?
?
Повторение
Сформулируйте правило деления двух дробей.
![]()
Свойства:
-
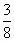 ;
; -
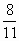 ;
; -
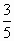 ;
; -
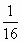 ;
; -
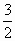 ;
; -
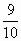 ;
; -
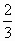
Алгоритм 1
(по правилу)
![]()
Алгоритм 2
Перевести смешанное число в неправильную дробь.
Делим как дробь на дробь.
![]()
Алгоритм 3
Запишем целое число в виде дроби со знаменателем один.
Делим как дробь на дробь.
![]() - Как измениться число, если разделить его на правильную дробь? (получим число больше делимого)
- Как измениться число, если разделить его на правильную дробь? (получим число больше делимого)
![]() - Как измениться число, если разделить его на неправильную дробь? (получим число меньше делимого)
- Как измениться число, если разделить его на неправильную дробь? (получим число меньше делимого)
Алгоритм 4
1) Заменим целое число на дробь со знаменателем один.
2) Делим как дробь на дробь.
![]()
III. Тест: проверь сам себя.
1) Запиши число обратное числу
I в.
II в.
![]()
а) ![]() ;
;
б) ![]() ;
;
в) ![]()
![]()
а) ![]() ;
;
б) ![]() ;
;
в) ![]()
Выполни действие
I в.
II в.
1) ![]()
а) ![]() ;
;
б) ![]() ;
;
в) ![]()
2) ![]()
а) ![]() ;
;
б) ![]() ;
;
в) ![]()
3) ![]()
а) ![]() ;
;
б) ![]() ;
;
в) ![]()
4) ![]()
а) ![]() ;
;
б) ![]() ;
;
в) ![]()
1) ![]()
а) ![]() ;
;
б) ![]() ;
;
в) ![]()
2) ![]()
а) ![]() ;
;
б) ![]() ;
;
в) ![]()
3) ![]()
а) ![]() ;
;
б) ![]() ;
;
в) ![]()
4) ![]()
а) ![]() ;
;
б) ![]() ;
;
в) ![]()
Работа в группах
1) Выполните действия.
а) ![]() ;
;
б) ![]() ;
;
в) ![]() ;
;
г)  .
.
2) Найдите значение выражения.
а) 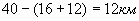
3) Реши уравнение.
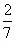
4) Задача.
Длина одного отрезка равна ![]() см. Второй отрезок короче первого в
см. Второй отрезок короче первого в ![]() раза. Найдите сумму длин этих отрезков.
раза. Найдите сумму длин этих отрезков.
5) Задача.
В два вагона погрузили 119 тонн зерна. В один погрузили зерна в ![]() раза больше, чем в другой. Сколько тонн зерна в каждом вагоне?
раза больше, чем в другой. Сколько тонн зерна в каждом вагоне?
В ответах закодировано слово "ДРОБЬ"
IV. Экскурс в историю
1) О происхождении дробей.
В первых учебниках дроби так и назывались "ломаные числа". Современное обозначение дробей берет свое начало в Древней Индии. В начале в записи дробей не использовалась дробная черта. Она появилась около 300 лет назад. Автором первого европейского учебника в котором использовалась современная запись дробей был итальянский купец и путешественник Кибоначчи Леонардо Пизанский. Название числитель и знаменатель ввел в 13 веке Максим Пиануд - греческий монах ученый - математик.
Метод "Паука".
![]()
V. Самостоятельная работа на карточках по вариантам
1 вариант
1. Выполните действия:
а) ![]()
б) ![]()
в) ![]()
г) 4![]() +1
+1![]()
2. Решите уравнение: ![]()
Задача: В двух цистернах 120 т. нефти. В одной из них нефти было в 1![]() раза меньше, чем в другой. Сколько тонн нефти было в каждой цистерне?
раза меньше, чем в другой. Сколько тонн нефти было в каждой цистерне?
2 вариант
1. Выполните действия:
а) ![]()
б) ![]()
в) ![]()
г) 3:![]()
![]()
2. Решите уравнение: ![]()
3. Задача: Масса двух электромоторов 52 кг. Масса одного из них в 2![]() раза больше другого. Найдите массу каждого электромотора.
раза больше другого. Найдите массу каждого электромотора.
VI. Итог урока
VII. Домашнее задание
Тема: Десятичные дроби. Чтение и запись десятичных дробей.
Цели:
-
Формирование знаний и умений записывать и читать десятичные дроби. Познакомить учащихся с новыми числами - десятичными дробями (новым способом записи числа)
-
Развивать культуру математического мышления, интуицию, догадку, эрудицию и владение методами математики.
-
Пробудить математическую любознательность и инициативу, развивать устойчивый интерес к математике.
Ход урока.
1. Организационный момент.
2. Мотивация урока.
Я рада вас видеть. Мы начинаем наш урок. Сегодня на уроке вы узнаете, что знания математики нам нужны в реальной жизни. Я хочу, чтобы этот урок принес вам новые открытия, и надеюсь, что вы с успехом будете применять имеющиеся у вас знания в решении практических задач. Я предлагаю вам отгадать задуманное мною слово, которое будет ключевым словом нашего урока. У вас есть три попытки. В словаре С.И. Ожегова о нем написано так:
- это мелкие свинцовые шарики для стрельбы из охотничьего ружья;
- это частые прерывистые звуки, например "барабанная…";
- она может быть правильной или неправильной, обыкновенной или десятичной.
(Это слово - "Дробь".)
Как сказал Р.Декарт: "Любопытный отыскивает редкости только затем, чтобы им удивляться; любознательный же затем, чтобы узнать их и перестать удивляться". Так будем же любознательными!
3. Актуализация опорных знаний.
Записать числа в виде суммы разрядных слагаемых.
2973=2000+900+70+3
4706=
5005=
5900=
20010=
Записать сумму как одно число:
8000 + 700 + 20+9=
6000+400+70+4=
7000+40+2=
Запомните, что единица каждого следующего разряда в 10 раз больше от единицы предыдущего разряда. Если какого - либо разряда нет, то в записи числа на его месте ставим 0.
Работа по группам:
1 группа: Представить в метрах:
7 дм = 28 см = 4 см =
2 группа: Представить в центнерах:
4 кг = 23 кг = 5 г = 78 г =
3 группа: Представить в часах:
20 мин = 3 мин = 17 сек =
4. Изучение нового материала.
Обратите внимание на знаменатели полученных дробей. Согласны ли вы с тем, что в заданиях знаменателями являются числа, записанные единицей и нулями, т.е. 10, 100, 1000 и т.д.? с такими дробями, как видно, часто приходится иметь дело в повседневной жизни, выполнять над ними вычисления. А поэтому для записи дробей, у которых знаменатели 10, 100, 1000 и т.д., используют позиционный принцип изображения чисел в десятичной системе счисления и называют их десятичными.
Изобретение десятичных дробей является одним из величайших достижений человеческой культуры. Правила вычислений с десятичными дробями описал знаменитый ученый средневековья аль-Каши Джемшид Ибн Масуд, работавший в Узбекистане, вблизи города Самарканда в обсерватории Улегбека в начале ХV века. Аль-Каши записывал дроби в одну строчку с числами в десятеричной системе, чтобы отделить целое от десятеричного , он пользовался вертикальной чертой или чернилами разного цвета. Его труды долго не были известны европейским ученым, и только через 150 лет десятичные дроби были заново изобретены.
Новый вид дробей более простой и более удобный, с которым мы сегодня и познакомимся.
Дробь десятичная,
Такая отличная.
Обыкновенной сестрица, -
В знаменателе у нее
Разрядная единица.
Чтобы ее прочитать,
Нужно разряды десятых долей знать.
Вопросы:
-
Какой наименьший разряд для натуральных чисел? (Разряд единиц)
-
Может ли быть еще меньший разряд? (да, если использовать дроби)
-
Как вы считаете, во сколько раз может быть меньше разряд, который мы располагаем на первом месте правее от разряда единиц? (в 10 раз)
Этот разряд мы называем десятые доли единиц. Вопрос:
Следующий за разрядом десятых долей разряд, как вы считаете, во сколько раз будет меньше чем единица? (в 100 раз)
Вопросы:
-
Как бы вы назвали следующий разряд? (тысячные доли единиц)
-
А еще дальше?
5. Осмысление нового материала.
У нас есть все основания для того, чтобы записывать и читать десятичные дроби. Но запомним, что разряды долей будем записывать справа от разряда единиц. Между целыми и дробными частями ставят запятую. При отсутствии какого - либо разряда долей, его заменяем 0 при записи числа.
Например: 4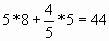 =4,1,
=4,1, 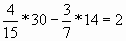 , 2
, 2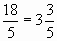 .
.
Если имеем правильную дробь, то на месте целых записываем 0.
Например: 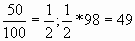 ,
, 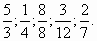 ,
, 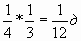 .
.
Обратите внимание на то, что количество цифр после запятой равно количеству нулей, которые стоят после единицы в знаменателе.
1) Записать десятичной дробью:
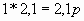 .
.
2) Прочитать десятичные дроби (по записи на доске):
А) 2,7; 11,4; 401,1; 0,8; 99,9; 909,9.
Б) 5,64; 21,87; 381, 77; 54,60; 0,55; 0,09; 2,02.
В) 1,597; 12,882; 326,703; 0,321; 0,049; 0,001.
Г) 203,6; 20,36; 0,0236; 2,0306; 0,010101.
3) Записать десятичные дроби под диктовку.
-
7 целых 8 десятых
-
2 целые 25 сотых
-
0 целых 92 сотые
-
12 целых 3 сотых
-
5 целых 187 тысячных
-
24 целые 24 тысячные
-
7 целых 7 десятых
-
7 целых 7 сотых
-
7 целых 7 тысячных
-
0 целых 5 десятитысячных
-
2 целые 2 тысячи 35 миллионных
-
Решить устно №
6. Историческая справка
Впервые понятие абстрактной десятичной дроби возникло в 15 ст. Его ввел видающийся математик и астроном ал - Коши (полное имя Джемиад ибн - Масуд ал - Коши) в работе «Ключ к арифметике» (1427 г). Открытие ал - Коши в Европе стало известным только через 300 лет.
Ничего, не зная об открытии ал - Коши, десятичные дроби открыл второй раз, приблизительно через 150 лет, после него, фламандский ученый математик и инженер Симон Стевин в труде «Децималь» (1585 г).
В России учение о десятичных дробях впервые выдал Л.П. Магницкий в своей « Арифметике» - первом российском учебнике математике. (1703 г)
Отделять целую часть от дробной предлагали по - разному. Ал - Коши целую и дробную части писал в один ряд, хотя записывал разными чернилами, или ставил между ними вертикальную черту. С. Стевин для отделения целой части от дробной ставил нуль в кружочке. Принятую в наше время запятую предложил немецкий астроном Й. Кеплер (1571 - 1630).
7. Самостоятельная работа.
Решить №
8. Подведение итогов урока.
Рефлексия.
- Что нового для себя узнали?
- В чём затруднялись?
- Чему научились?
- Какую проблему ставили на уроке?
- Удалось ли нам её решить?
Напишите, как усвоили материал урока на листах обратной связи.
-
Получил хорошие знания.
-
Усвоил весь материал.
-
Усвоил материал частично.
9. Домашнее задание.
Выучить п..
Повторить п.
решить № №
Творческое задание: сообщении е «Из истории десятичных дробей».
А вот о том, как важна точность в расчетах, послушайте отрывок из стихотворения "Три десятых"
Три десятых… Скажи про такую ошибку,
И, пожалуй, на лицах увидишь улыбку.
Три десятых… И все же об этой ошибке
Я прошу вас послушать меня без улыбки.
Если б, строя ваш дом, тот, в котором живете,
Архитектор немного ошибся в расчете -
Что б случилось, ты знаешь ли, Костя Жигалин?
Этот дом превратился бы в груду развалин!
Ты вступаешь на мост, он надежен и прочен,
А не будь инженер в чертежах своих точен,
Ты бы, Костя, свалившись в холодную реку,
Не сказал бы спасибо тому человеку!
Вот турбина, в ней вал токарями расточен.
Если б токарь в работе не очень был точен,
Совершилось бы, Костя, большое несчастье,
Разнесло бы турбину на мелкие части.
Три десятых - и стены возводятся косо!
Три десятых - и рухнут вагоны с откоса!
Ошибись только на три десятых аптека -
Станет ядом лекарство, убьет человека…
Тема: Сравнение десятичных дробей.
Цель урока:
-
создать условия для вывода правила сравнения десятичных дробей и умения его применять; повторить запись обыкновенных дробей в виде десятичных;
-
развивать логическое мышление, способность к обобщению, исследовательские умения, речь;
-
воспитывать соблюдение норм поведения в коллективе, навыков совместной деятельности при работе в группах, умения аргументировать свои действия.
Ход урока.
1. Организационный момент.
2. Мотивация урока.
Решение задач - практическое искусство, подобное плаванию, катанию на лыжах или игре на фортепиано, научиться ему можно. «Если вы хотите плавать, смело входите в воду, а если хотите научиться решать задачи, то решайте их»,- советовал учащимся известный американский математик Джорж Пойа в книге «Как решить задачу». Решение любой достаточно трудной задачи требует напряжённого труда, воспитывает волю, упорство, развивает любознательность, смекалку. Это очень нужные качества в жизни человека, ведь даже в пословице говорится: «ум без догадки гроша не стоит».
Сегодня у нас урок по теме «Сравнение десятичных дробей».
3. Актуализация опорных знаний.
1. Прочитайте дроби:
17,3; 0,07; 53,2; 1,251; 0,26; 7,1027;
2,7; 0,127; 0,1; 0,34; 2,141; 0,0537;
2. В каждой дроби перенесите запятую через один разряд влево. Прочитайте
полученные числа:
34,1; 310,2; 110,1; 105,007; 2,7; 3,4;
3. В каждой дроби перенесите запятую через один разряд вправо. Прочитайте
полученные числа:
1,37; 0,1401; 3,017; 1,7; 37,4; 350,4.
Решить № №
Сравнить натуральные числа:
345 и 1872;
371 и 317;
4086 и 4806.
Решить № №
Повторить правило сравнения натуральных чисел.
4. Изучение нового материала.
Задание: сравните числа (на доске записаны)
18,625 и 5,784 15,200 и 15,200
3,0251 и 21,02 7,65 и 7,8
23,0521 и 0,0521 0,089 и 0,0081
- Сначала открываем левую часть. Целые части разные. Делаем вывод о сравнении десятичных дробей с разными целыми частями. Открываем правую часть. Целые части - одинаковые числа. Как сравнить?
Я выписала правило сравнения десятичных дробей, которое предлагает автор. Давайте сравним.
-
Правило сравнения десятичных дробей
-
Если целые части десятичных дробей различны, то больше та дробь, у которой больше целая часть.
-
Если целые части десятичных дробей равны, то больше та дробь, у которых больше десятых.
-
Если же и десятых поровну, то больше та дробь, у которых больше сотых и т.д.
- Мы с вами сделали открытие. И это открытие - правило сравнения десятичных дробей. Оно у нас совпало с правилом, которое предложил автор учебника.
Если в конце десятичной дроби приписать нуль или отбросить нуль, то получится дробь, равная данной.
Например,
0,87 = 0,870 = 0,8700; 141 = 141,0 = 141,00 = 141,000;
26,000 = 26,00 = 26,0 = 26; 60,00 = 60,0 = 60;
0,900 = 0,90 = 0,9.
Сравним две десятичные дроби 5,345 и 5,36. Уравняем число десятичных знаков, приписав к числу 5,36 справа нуль. Получаем дроби 5,345 и 5,360.
Найдите равные дроби:
0,89; 1,700; 0,30000; 1,7; 1,0000; 3,0; 2,3; 2,300; 1,00; 2,30; 0,3; 1,00000; 0,300; 0,03.
Приписав справа нули, уравняйте число знаков после запятой в десятичных дробях:
1,8; 13,54 и 0,789.
Запишите короче дроби:
2,5000; 3,02000; 20,010.
5. Осмысление нового материала.
Задание: сравните
Работа в парах.
0,3 и 0,8
0,90 и 0,9
5,6 и 3,6
2,99 и 13,1
0,759 и 0,76
3,4208 и 3,4028
- Итак, что мы научились сегодня делать? Давайте себя проверим. Ученики сравнивают десятичные дроби, ставя знаки >, <, =.
Самостоятельная работа.
(Проверка - ответы на обратной стороне доски.)
Сравните:
1,21 и 1,2
3,34 и 3,4
8,6 и 8,37
23,43 и 23,9
3,5601 и 4,48
85,113 и 85,13
148,05 и 14,805
6,44806 и 6,44863
35,601 и 35,6010
Что интересного заметили? Были ли среди них легкие?
Некоторые числа можно было сравнить по целой, а у некоторых пришлось сравнивать по дробной части.
Какие было интереснее сравнивать? Почему?
23,43 < 23,9. Там целые равны, а в дробной части, если не знать правило, можно сравнить как 9 и 43, и можно допустить ошибку.
Решить № №
6. Физкультминутка.
Мы устали чуточку,
Отдохнем минуточку.
Поворот, наклон, прыжок,
Улыбнись, давай, дружок.
Еще попрыгай: раз, два, три!
На соседа посмотри,
Руки вверх и тут же вниз
И за парту вновь садись.
Стали мы теперь бодрее,
Будем думать мы быстрее.
7. Самостоятельная работа.
Работа в парах.
Замените значок «*» цифрой так, чтобы полученная запись была верной:
1) 5,688 < 5,6*1;
2) 71,09* < 71,091;
3) 9,*57 > 9,499;
4) 0,7*5 < 0,725;
5) 5*,67 < 52,31;
6) 3,*2 < 3,93.
8. Итог урока. Рефлексия.
Выучить п.
Решить № №
Учащиеся заполняют карточки.
Карточка__________________________________________________
Я, ____________(имя), сегодня на уроке научился
(что делать)__________________________________________
Действовать нужно по такому алгоритму:
Если _____________части десятичных дробей неравные, то________________________________________
Пример:_________________
Если _____________части десятичных дробей равны,
то нужно (что сделать) _______________________________десятичных знаков.
Сравнить (что)__________________________________________
и________________________________________________________
Пример:___________________
Тема: Сравнение десятичных дробей.
Цель урока:
-
Закрепить правила сравнения десятичных дробей и умения его применять; повторить запись обыкновенных дробей в виде десятичных;
-
развивать логическое мышление, способность к обобщению, исследовательские умения, речь.
-
воспитывать соблюдение норм поведения в коллективе, навыков совместной деятельности при работе в группах, умения аргументировать свои действия.
Ход урока.
1. Организационный момент.
2. Мотивация урока.
Девиз урока: «Знания имей отличные по теме дроби десятичные».
Раз, два, три, четыре, пять
С детства учимся считать.
А как только подрастем
Мы учиться все идем.
Умножаем, прибавляем
Дроби тоже мы считаем,
А иначе как? Нельзя?
Математика - она
В мире каждому нужна
В магазин идешь ты, в банк
Надо деньги посчитать
А иначе разоришься,
Будешь ты рыдать.
3. Актуализация опорных знаний. Проверка д/з.
По одному ученику от каждой команды выходят к доске, на которой записаны столбики из шести пар десятичных дробей. Ребята должны поставить знак < ; > или =.
4.08
4,01
0,06
0,051
3,15
3,015
25,90
25,900
0,9090
0,0909
2,71
2,710
Как короче записывают дроби, знаменатель которых единица с несколькими нулями?
Как называют такую запись дроби?
Запишите в виде десятичных дробей:
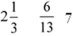
Решить №
4. Решение упражнений на сравнение десятичных дробей.
Решить № №
5. Самостоятельная работа.
I вариант
-
Сравнить числа:
-
3,61 и 1,69
-
0,034 и 0,035
-
0,6 и 0,59
-
0,6 и 0,600
-
Записать в порядке возрастания числа:
8,02; 9,4; 8,2; 8,22.
-
Вместо звездочки подставить цифру так, чтобы образовалось верное неравенство:
-
2,*1 < 2,02
-
0,39826 < 0,3*845
-
1,892 < 1,*0765
-
Поставьте нужный знак < или >:
-
**,412 и *,9*
-
0,742 и 0,741**
-
Найти 2 значения х, при которых верно неравенство:
2 < x < 2,0001
Дополнительно:
-
Сравните величины:
-
6,7 м и 6690 мм
-
83,62 ц и 8,362 т.
II вариант
-
Сравнить числа:
-
8,57 и 4,56
-
0,7 и 0,69
-
0,957 и 0,964
-
0,90 и 0,900
-
Записать в порядке убывания числа:
4,5; 5,72; 4,05; 4,55.
-
Вместо звездочки подставить цифру так, чтобы образовалось верное неравенство:
-
6,413 > 6,4*8
-
4,5*8 > 4,593
-
5*,683 < 50,6*1
-
Поставьте нужный знак < или >:
-
4,3** и 4,7**
-
*,*** и **,**.
-
Найти 2 значения х, при которых верно неравенство:
1,999 < x < 2
Дополнительно:
-
Сравните величины:
-
18,34 кг и 243,6 г
-
7,3 дм и 8,6 см.
6. Логическое задание.
Взвесили пять цыплят разной породы: белого, серого, черного, рыжего и пестрого. Получили следующие результаты: 0,3 кг; 0,52 кг; 0,16 кг; 0,88 кг; 0,28 кг. Известно, что рыжий цыпленок легче серого, но тяжелее белого. Черный тяжелее пестрого цыпленка, а пестрый тяжелее серого. Сколько весит каждый цыпленок?
7. Подведение итогов урока. Д/з.
1.Кто может сформулировать название темы урока?
2. Что нового вы узнали на уроке? Какие навыки приобрели?
Решить № №
Тема: Округление десятичных дробей.
Цели урока:
-
повторить ранее изученный материал, научить детей округлять десятичные дроби;
-
развивать математическую речь, внимание,
-
воспитывать аккуратность, интерес к предмету, активность, усидчивость.
Ход урока.
1. Организационный момент.
2. Мотивация урока.
3. Актуализация опорных знаний. Проверка д/з.
1. Укажите, какие из чисел равны 2,034.
А) 2,34; Б) 2,03; В) 2,0340; Г) 2,03400.
2. Расположите числа 4,28; 3,289; 4,249; 3,78 по возрастанию.
А) 4,28; 4,249; 3,78; 3,289;
Б) 3,289; 3,78; 4,249; 4,28;
В) 4,249; 4,28; 3,289; 3,78;
Г) 3,78; 3,289; 4,28; 4,249.
3. Каким числом можно заменить х в неравенстве 0,03 < х < 0,031, чтобы оно было верным?
А) 0,030; Б) 0,0301; В) 0,0309; Г) такого числа нет.
4. Укажите те неравенства, которые верны при замене звездочки любой цифрой, отличной от цифры 0.
А) 67,28*>67; Б) 75,62*<75,629* В) 564,2*7>564,27 Г) *,**>**,*
5. Укажите все цифры, которые можно поставить вместо * с тем, чтобы запись 0,7*5<0,*62 выражала верное неравенство А) 0; Б) 8, 9; В) 9; Г) 1, 2, 3, 4, 5, 6.
Вспомни правила округления натуральных чисел и округли данные числа:
a) до тысяч: 34 457; 120 089; 43 609 780; 56 009
b) до миллионов: 45 890 654; 139 870 000; 754 389 008
Решить № - самостоятельно.
4. Изучение нового материала.
При округлении десятичной дроби используют те же правила, что и при округлении натуральных
чисел.
-
Чтобы округлить число до указанного разряда, надо:
-
Отделить все цифры, стоящие после этого разряда;
-
Подчеркнуть первую из тех цифр, которые отделены, и установить, среди каких цифр: 0; 1; 2; 3; 4 или 5; 6; 7; 8; 9 она находится;
-
Если подчеркнута цифра 0; 1; 2; 3; 4, то все цифры, которые отделены, заменяются нулями; если же подчеркнута цифра 5; 6; 7; 8; 9, то к разряду, до которого ведется округление, прибавляется 1, а все цифры, которые отделены, заменяются нулями;
-
В ответе отбрасываются все нули в дробной части десятичной дроби, стоящие правее разряда, до которого ведется округление.
5. Осмысление нового материала.
Решить№№
До какого разряда выполнено округление?
43,281 ![]()
![]() 43,28;
43,28;
12771 ![]()
![]() 12800;
12800;
18,457 ![]()
![]() 18,46;
18,46;
328,3601![]()
![]() 328,0
328,0
6. Релаксация.
Реснички опускаются…
Глазки закрываются…
Мы спокойно отдыхаем… (два раза).
Сном волшебным засыпаем…
Дышатся легко… ровно… глубоко…
Наши руки отдыхают…
Отдыхают, засыпают… (два раза).
Шея не напряжена…
Губы чуть приоткрываются…
Всё чудесно расслабляется… (два раза).
Дышится легко… ровно… глубоко.
7. Самостоятельная работа.
Решить №
Ученик работает на скрытой доске. Затем проверка.
8. Итог урока. Рефлексия.
Выучить п
Решить № №
-
Какая тема рассматривалась сегодня на уроке?
-
Какие правила мы сегодня повторили?
-
Какие еще действия можно делать над десятичными дробями?
-
Как вы думаете, какая тема урока будет у нас завтра?
Тема: Округление десятичных дробей.
Цели урока:
-
Закрепление навыков при сравнении и округлении десятичных дробей;
-
развивать культуру устной и письменной математической речи,
внимание,
-
воспитывать аккуратность, интерес к предмету, активность, усидчивость.
Ход урока.
1. Организационный момент.
2. Мотивация урока.
3. Актуализация опорных знаний. Проверка д/з.
1. Какие виды чисел вы знаете?
2. Какие числа называются натуральными?
3. Ноль натуральное число?
4. Какие числа называются десятичными дробями?
5. Какие разряды десятичных дробей вы знаете?
6. Что вы умеете делать с десятичными дробями?
7. Сформулируйте правило сравнения десятичных дробей.
8. Сформулируйте правило округления десятичных дробей.
Расположить числа в таблице в порядке возрастания.
0,08; 0,29; 0,3; 1,48; 1,5; 2,06; 2,1; 5,39; 5,4.
Работа в парах.
Даны десятичные дроби и их округление. Найти соответствие и указать до какого разряда выполнено округление:
0,32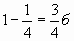 0,3 25,186
0,3 25,186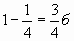 25,2 183,809
25,2 183,809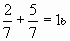
19,0273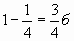 19,027 37,1951
19,027 37,1951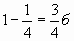 37,195 81,2587
37,195 81,2587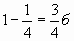 81,26
81,26
193,76021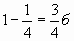 193,7602 125,30507
193,7602 125,30507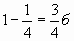 125,3051 83,6209
125,3051 83,6209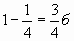 83,62
83,62
4. Решение упражнений на округление и сравнение десятичных дробей.
Решить № №
5. Физкультминутка.
Одолела вас дремота,
(Зеваем.)
Шевельнуться неохота?
Ну-ка, делайте со мною
Упражнение такое:
Вверх, вниз потянись,
(Руки вверх, потянулись.)
Окончательно проснись.
Руки вытянуть пошире.
(Руки в стороны.)
Раз, два, три, четыре.
Наклониться - три, четыре
(Наклоны туловища.)
И на месте поскакать.
(Прыжки на месте.)
На носок, потом на пятку.
Все мы делаем зарядку.
6. Самостоятельная работа.
Вариант 1
Подставьте вместо * цифру, чтобы равенство было верным:
а) 0,35*7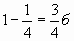 0,352;
0,352;
б) 16,114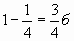 16,1*;
16,1*;
в) 25,8*1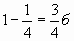 25,84;
25,84;
г) 37,562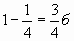 3*;
3*;
д) 23,*756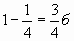 23,9.
23,9.
Вариант 2
Подставьте вместо * цифру, чтобы равенство было верным:
а) 14,225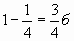 14,2*;
14,2*;
б) 0,7*81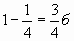 0,74;
0,74;
в) 57,5*5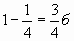 57,58;
57,58;
г) 20,*916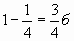 20,5;
20,5;
д) 76,892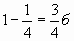 7*.
7*.
7. Итоги урока. Д/з.
-
Решить № №
-
Повторить п.
Сейчас я вам расскажу одну притчу.
Шел мудрец, а навстречу ему три человека, которые везли под горячим солнцем тележки с камнями для строительства. Мудрец остановился и каждому задал по вопросу. У первого спросил: «Что ты делал целый день?». И тот с ухмылкой ответил, что целый день возил проклятые камни. У второго мудрец спросил: «А что ты делал целый день?», и тот ответил: «А я добросовестно выполнял свою работу». А третий улыбнулся, его лицо засветилось радостью и удовольствием: «А я принимал участие в строительстве храма!».
-Ребята! Давайте мы попробуем оценить каждый свою работу за урок.
-Кто работал так, как первый человек, поднимают синие квадратики.
-Кто работал добросовестно, поднимают зеленые квадратики.
-Кто принимал участие в строительстве храма «Знаний», поднимают красные квадратики.
Тема: Сложение и вычитание десятичных дробей.
Цели урока:
образовательная: формирование знаний об алгоритме сложения и вычитания десятичных дробей;
развивающая: развивать логическое мышление, память, познавательный интерес;
продолжить формирование математической речи; вырабатывать умение анализировать и сравнивать, проводить аналогии;
воспитательная: развитие любознательности и интереса к предмету; совершенствование навыков эстетического оформления записи в тетради.
Ход урока.
1. Организационный момент.
Добрый день!
Сели ровно, оглянулись.
Друг другу улыбнулись
И в работу окунулись.
2. Мотивация урока.
Дроби десятичные - новые для Вас
Лишь совсем недавно, их узнал ваш класс
Сразу прибавилось всем теперь мороки
Учим, учим правила, готовимся к уроку.
3. Актуализация опорных знаний. Проверка д/з.
Блиц-опрос (заполнить пропуски):
Обыкновенные дроби, в знаменателе которых стоят числа 10,100, 1000, и т. д., короче записываются без знаменателя.
Целую часть от дробной части отделяет запятая.
Запись дроби с использованием запятой, которая отделяет целую часть от дробной, называется десятичной записью дробного числа.
В десятичной дроби перед запятой записывают целую часть, а после запятой - дробную часть.
Если обыкновенная дробь правильная, то в десятичной записи перед запятой пишем цифру 0.
В десятичной дроби после запятой слева направо следуют разряды:
Десятые
Сотые
Тысячные
Десятитысячные
Стотысячные
Миллионные
Чтобы сравнить две десятичные дроби, надо…
Чтобы округлить десятичную дробь, надо…
Заполни пробел…
Озеро Байкал - самое глубокое место на земном шаре. Его глубина достигает 1622 м. или 1,622 км
Самое глубокое место в мировом океане - 11 022 м - зафиксировано в Тихом океане вблизи Марианских островов. В километрах это будет 11,022 км
Сибирский осётр - одна из крупных рыб. Длина его достигает 3 м, (0,003 км) вес более 100 кг (0,1 т).
Наивысший материк земного шара - это Антарктида. Его средняя высота 2040 м над уровнем моря. (2,04 км) Единственные обитатели - учёные и исследователи этого материка.
Самое длинное животное - ленточный червь - был найден в прибрежных водах Южного моря. Его длина равнялась 54 м 90 см . (54,9 м)
4. Изучение нового материала.
Чтобы сложить (вычесть) десятичные дроби, нужно:
-
Уравнять в этих дробях количество знаков после запятой;
-
Записать их друг под другом так, чтобы запятая была записана под запятой;
-
Выполнить сложение (вычитание), не обращая внимания на запятую;
-
Поставить в ответе запятую под запятой в данных дробях.
5. Закрепление нового материала.
Решить № №
6. Из истории математики:
Правила вычислений с десятичными дробями описал знаменитый ученый аль - Каши Джемшид Ибн Масуд в начале XV века.Записывал он дроби так же, как принято сейчас, но не использовал запятой: дробную часть записывал красными чернилами или отделял вертикальной чертой. Но в Европе об этом не узнали и только через 150 лет учёный Симон Стивен записал десятичные дроби довольно сложно: в место запятой нуль в кружке. Запятая или точка для отделения целой части стали использоваться с XVII века. В России о десятичных дробях изложил Л. Ф. Магнитский в 1703 году в первом учебнике математики "Арифметика, сиречь наука числительная".
7. Логическое задание.
Работа в парах. Восстановите в записи примеров запятые:
48 + 22 = 7
1 + 308 = 408
12 + 92 = 212
945 - 545 = 4
53 - 17 = 513
8. Итоги урока. Д/з.
1. Что нового вы узнали, чему научились, что вспомнили, повторили?….
2. Чьи ответы вам понравились больше всего?
3. Что запомнится надолго после сегодняшнего урока?
4. Ваши впечатления об уроке. Эмоциональный настрой.
На дом:
Выучить п.
Решить № №
Придумать и красиво оформить на альбомном листе задачу, которая была бы
решена с помощью сложения и вычитания десятичных дробей, записать на листок условие
задачи и нарисовать рисунок по этому условию, а в тетрадь записать её решение.
Постарайтесь, чтобы ваша задача понравилась учащимся класса, чтобы данные в условии
соответствовали реальности.
Чтоб десятичные дроби сложить,
Нам не приходится долго мудрить:
Выстроим все запятые мы в ряд,
Цифра под цифрой строго стоят.
И в результате получим мы вновь,
Побольше других, десятичную дробь.
Или такой алгоритм:
Десятичные дроби вычти, сложи,
Цифру под цифрой строго пиши,
И запятые все сохраняй,
В ряд их пиши, не забывай!
Тема: Сложение и вычитание десятичных дробей.
Цели урока:
образовательная: формирование знаний об алгоритме сложения и вычитания десятичных дробей;
развивающая: развивать логическое мышление, память, познавательный интерес;
продолжить формирование математической речи; вырабатывать умение анализировать и сравнивать, проводить аналогии;
воспитательная: развитие любознательности и интереса к предмету; совершенствование навыков эстетического оформления записи в тетради.
Ход урока.
1. Организационный момент.
2. Мотивация урока.
3. Актуализация опорных знаний. Проверка д/з.
Правило сложения и вычитания десятичных дробей.
а) Впишите в кружочки знаки "+" или "-" так, чтобы равенства были верными.
0,5 О 2,7 О 0,2 = 3; 7,4 О (12,3 О 9,2) = 4,3.
б) Между числами 5,2 и 5,3 поставьте число, большее 5,2 и меньшее 5,3.
в) Как быстрее и проще найти сумму данных сумм 2,18+4,36+6,53+8,77 и
7,82+5,64+3,47+1,23
Выполни действия по схеме:
1,8
+
0,9
7
+
0,9
4
-
10
-
+
4. Решение упражнений на сложение и вычитание десятичных дробей.
Решить № №
5. Физкультминутка.
Дышим носом глубоко
Дышим носом глубоко-
Поднимаемся легко.
(Приседания.)
Наклоняемся вперёд.
Прогибаемся назад.
Как деревья ветер гнёт.
Так качаемся мы в лад-
(Наклоны взад-вперёд.)
Головой теперь покрутим-
Так мы лучше думать будем.
Поворот и поворот,
А потом наоборот.
(Вращения головой в стороны.)
Встанем, дети, на носочки -
(Потягивания - руки вверх.)
На зарядке ставим точку.
6. Самостоятельная работа проверочного характера
I вариант
II вариант
-
Найти сумму
-
52 + 0,084
-
25,49 + 0,375
-
0,0374 + 49,9626
-
0,096 + 63
-
0,598 + 32,24
-
29,9738 + 0,0262
-
Выполнить вычитание:
-
2,56 - 0,468
-
8 - 0,9328
-
0,4008 - 0,243
-
7,82 - 0,746
-
6 - 0,8736
-
0,3007 - 0,189
7. Подведение итогов урока. Д/з.
Рефлексия.
- Что нового для себя узнали?
- В чём затруднялись?
- Чему научились?
- Какую проблему ставили на уроке?
- Удалось ли нам её решить?
Напишите, как усвоили материал урока на листах обратной связи.
-
Получил хорошие знания.
-
Усвоил весь материал.
-
Усвоил материал частично.
Решить № №
Тема урока: «Сложение и вычитание десятичных дробей».
Цели урока:
1.Систематизировать материал по теме «Сложение и вычитание десятичных дробей». Обогатить знания, установить связи между теорией и практикой.
2.Развивать вычислительные навыки, память, мышление и смекалку.
3.Воспитывать познавательный интерес к предмету.
Ход урока.
1. Организационный момент.
2. Мотивация урока.
"Недостаточно овладеть премудростью,
Нужно так же уметь пользоваться ею"
Цицерон
Обсудить высказывание с учащимися.
Вывод: недостаточно знать правила, надо уметь их применять.
3. Актуализация опорных знаний. Проверка д/з.
Зачем нам понадобились десятичные дроби? Может быть, можно было обойтись
натуральными числами и обыкновенными дробями?
Запись удобна, действия над десятичными дробями похожи на действия с
натуральными числами, которые мы хорошо знаем, можно считать с помощью
калькулятора.
Известно, какое важное значение имеет запятая в русском языке. От неправильной
расстановки запятых смысл предложения может резко измениться. Например, «Казнить,
нельзя помиловать» и «Казнить нельзя, помиловать». В математике от положения запятой
зависит верность или неверность равенства.
Расставить запятые так, чтобы получились верные равенства.
3,2 + 1,8 = 5
3 + 1,08 = 4,08
0,42 + 1,7 = 2,12
7,36 - 3,36 = 4
63 - 2,7 = 60,3
5,7 - 4 = 1,7
4. Решение упражнений.
1. Укажите примеры, где сложение выполнено верно.
А) 279,04 Б) 37,284 в) 28,145 г)42,790
0,28 + 221,37 +454,37 + 0,284
279,32 59,421 735,82 43,074
2. Укажите значение суммы 42,7 + 0,56.
А) 48,3; Б) 43,26; В) 4,83; Г) 44,26.
3. Укажите значение разности 34,7 - 2,729.
А) 32,071; Б) 7,41; В) 3,1971; Г) 31,971.
4. Укажите значение выражения 19 - 11,08 + 8,5 + 6,24.
А) 21,76; Б) 22,66; В) 15,01; Г) 23,66.
5. Корнем уравнения 2,73 - х = 0,219 является число:
А) 2,511; Б) 2,949; В) 0,074; Г) 2,611.
6.По течению реки плывет катер со скоростью 28,7 км/ч. Скорость течения 3,1 км/ч. Укажите верные утверждения о движении катера.
A) Скорость катера в стоячей воде 31,8 км/ч.
Б) Скорость катера против течения 22,5 км/ч.
B) Против течения катер движется быстрее, чем в стоячей воде.
Г) В стоячей воде скорость катера 25,6 км/ч.
7. Какую цифру нужно поставить в равенстве 19,7+*,* = 2*,5 вместо звездочки, чтобы оно было верным?
Решить № №
5. Самостоятельная работа
(работают в парах, повторяют правила сложения и вычитания десятичных дробей с последующей проверкой).
Найдите пропущенное число:
1. _______+3,015 = 3,605
2. 21,035 - ________=11,3
3. 106,314+________=120,404
4. 0,35+10,7+16,05 =________
5. (18,325+10,7) - ________=0,375
6. Логическая пауза.
В пословице говориться: «Ум без догадки гроша не стоит».
Решение любой достаточно трудной задачи требует напряженного труда,
воспитывает волю, упорство, развивает любознательность, смекалку. Это очень важные
качества в жизни человека.
1. Даны две суммы:
7,82 + 5,64 + 3,47 + 1,23 и 2,18 + 4,36 + 6,53 + 8,77
Найдите сумму этих сумм. Ответ: 40.
2. Найдите значение выражения:
(0,5 - ½) (13 - 2,46 - 3,54). Ответ: 0.
3. Вычислите наиболее простым способом:
5,94 * 2,67 + 0,33 * 5,94 + 3* 0,06. Ответ: 18.
7. Подведение итогов урока.
Рефлексия.
- Что нового для себя узнали?
- В чём затруднялись?
- Чему научились?
8. Домашнее задание.
Повторить п. Решить №№
Тема урока: Обобщение и систематизация знаний и умений по теме «Сложение и вычитание десятичных дробей».
Цели:
1. Обобщение и систематизация знаний учащихся по теме «Сложение и вычитание десятичных дробей», закрепление умений и навыков применения правил сравнений, округления, сложения и вычитания десятичных дробей при решении задач;
2. Развивать логическое мышление учащихся, познавательную активность учащихся, самостоятельность.
3. Воспитывать аккуратность и внимательность учащихся, культуру письма, интерес к предмету, эрудицию, упорство.
Ход урока.
1. Организационный момент.
Эмоциональный настрой.
- Как живете? (дети отвечают жестами и движениями)
- Как идёте?
- Как бежите?
- Ночью спите?
- Как даёте?
- Как берёте?
- Как шалите?
- Как грозите?
- Как сидите?
- А математику как знаете?
2. Мотивация урока.
Сегодня наш урок называется общественный смотр знаний по теме «Десятичные дроби». И вот сегодня каждый из вас должен отчитаться по изученному материалу. Результаты будем заносить в оценочный лист.
Итак, совершим путешествие по городу «Десятичные дроби».
Сегодня на уроке
Мы во дворец Математики за знаниями пойдем.
Смекалку, фантазию с собой возьмем.
Дорогой с пути никуда не свернем.
Но чтобы цели нам поскорее достичь,
Должны мы подняться
По лестнице ввысь.
3. Актуализация опорных знаний. Проверка д/з.
Чтобы войти в этот город необходимо ответить на следующие вопросы:
Опрос учащихся: «Ты - мне, я - тебе» (за каждый правильный ответ ученик получает 1 балл)
-
Что такое десятичная дробь?
-
Из чего состоит десятичная дробь?
-
Как называют разряды десятичной дроби, стоящей справа от запятой?
-
По какому принципу записывают десятичные дроби?
-
Как записать десятичную дробь в виде смешанного числа?
-
Сформулируйте правило сравнения десятичных дробей?
-
Сформулируйте правило округления десятичных дробей?
-
Что значит округлить десятичную дробь до десятых? сотых?
-
Как сложить десятичные дроби?
-
Как вычесть десятичные дроби?
Максимум -5 баллов.
4. Обобщение и систематизация знаний и умений по теме «Сложение и вычитание десятичных дробей».
Первая улица «Дробная».
Записать десятичные дроби.
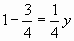 ;
; 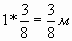 ;
; 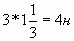 ;
; 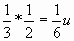 ;
; 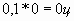 ;
; 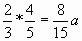 ;
;
Учащиеся меняются тетрадями и по ответам, написанным на доске проверяют правильность решения. (За каждое правильно выполненное задание - 1 балл). Максимум -6 баллов.
Следующая улица называется «Сравнительная».Десятичные дроби очень удобно сравнивать, что не скажешь об обыкновенных дробях. Например, легче сравнивать 0,375 и 0,4 чем 28 и 3/5.
Как сравнивать десятичные дроби?
Сравнение - очень важная операция. В медицине известно, что «великан» среди микробов имеет размер 0,1 мм, а наиболее мелкий вирус 0,0000016мм. Сравнивая размеры, медики определяют, чем вызвано заболевание микробом или вирусом и узнают, какая это болезнь. Мои слова подтвердит и прочитает стихотворение 3/10.
А теперь проверим, как вы научились сравнивать десятичные дроби.
Решить № .
Улица «Округлительная».
Сформулируйте правило округления десятичных дробей.
Найдите ошибки, которые допустили при округлении чисел. Работа у доски.
3,27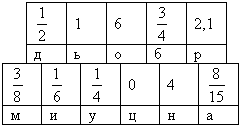 3,3 0,75
3,3 0,75 0,7
0,7
2,99 3,0 8,18
3,0 8,18 8,2 12,34
8,2 12,34 12,4
12,4
Переулок «Спортивный»