Конспект урока по геометрии на тему «Средняя линия треугольника» (8 класс)

План-конспект урока геометрии в 8 классе по теме

«Средняя линия треугольника».

Кошаева Зоя Михайловна - учитель математики МОУ «Петъяльская средняя общеобразовательная школа»

Цель урока: ознакомление учащихся с понятием средней линии треугольника; формирование умения применять свойство средней линии треугольника к решению задач..

Учебные задачи, направленные на достижение:

Личностного развития:

• продолжать развивать умение ясно, точно и грамотно излагать свои мысли в устной и письменной речи,

• развивать креативность мышления, инициативу, находчивость, активность при решении математических задач.

Метапредметного развития:

• расширять кругозор, прививать умение совместно работать (чувство товарищества и ответственности за результаты своего труда);

• продолжать развивать умение понимать и использовать математические средства наглядности.

Предметного развития:

• формировать теоретическое и практическое представление о средней линии треугольника и об её свойстве;

• формировать умение применять изученные понятия для решения задач практического характера.

Тип урока: урок получения новых знаний (с проблемной ситуацией)

Формы работы учащихся:

• индивидуальная;

• фронтальная;

• работа в парах.

Необходимое оборудование:

• Проектор и экран.

• Презентация "Средняя линия треугольника".

Структура и ход урока:

1. Организационный момент. (Слайд №1). Сообщение темы урока. Настрой учащихся на работу.

2. Устные упражнения:

Решите задачи:

1. (слайд №2): Диагонали четырёхугольника АВСД пересекаются в точке О, причём АО:ОС = ВО:ОД. Докажите, что АВСД - трапеция.

(Док-во: Рассмотрим треугольники АОВ и ДОС. В них: АО:ОС = ВО:ОД - по условию задачи, угол АОВ равен углу ДОС - как вертикальные. Значит, треугольник АОВ подобен треугольнику ДОС по двум пропорциональным сторонам и углу между ними. В подобных треугольникам соответственные углы равны, значит, угол АВО равен углу ВДС, а они накрест лежащие при прямых АВ и ДС и секущей ВД. Значит, отрезок АВ параллелен отрезку ДС.

Четырёхугольник, в котором две стороны параллельны, а две другие - нет, является трапецией. АВСД - трапеция).

Структура и ход урока

№

Этап урока

Название используемых ЭОР

Деятельность учителя

(с указанием действий с ЭОР, например, демонстрация)

Деятельность ученика

1

2

3

4

5

1

Организационный момент. Вступительное слово учителя.

Презентация.

Слайд №1

Эпиграфом к сегодняшнему уроку взяты слова французского писателя XIX столетия. Анатоль Франс однажды заметил: "Учиться можно только весело… Чтобы переваривать знания, надо поглощать их с аппетитом" (демонстрация слайда №1).

Давайте последуем совету писателя и на сегодняшнем уроке: будьте активны, внимательны, поглощайте с большим желанием знания, которые пригодятся вам в дальнейшей жизни.

Ученики слушают.

2

Актуализация.

Повторение пройденного материала.

Проводится аукцион знаний по теме «Треугольник». Проводится в виде игры «Угадай мелодию».

Слайд №2

Сегодня мы с вами отправимся в путешествие в один из уголков страны Геометрии в край Треугольник. Выясним, что вы знаете о треугольниках. А сегодняшний наш урок мы построим в идее аукциона.

Нельзя идти в гости не зная порядков и законов страны. Поэтому послушаем краткую информацию о треугольниках, которую подготовила Мария Масякова.

На доске демонстрируется слайд с темами и номерами заданий.

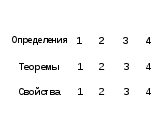
Определения:

1. Сформулируйте определение треугольника.

2. Сформулируйте определение высоты, биссектрисы, медианы треугольника.

3. Виды треугольников и их определения.

4. Определение периметра треугольника.

Теоремы:

1. Признаки равенства треугольников.

Класс разбивается на 3 команды (группы). Ученик слушают учителя.

Ученица делает сообщение о треугольниках.

Каждая команда по очереди выбирает задания и отвечает.

2. Признаки подобия треугольников.

3. Признаки равенства прямоугольных треугольников.

4. Теорема Пифагора.

Свойства:

1. Свойства равнобедренного треугольника.

2. Свойства прямоугольных треугольников.

3. Соотношение между сторонами и углами треугольника.

4. Площадь треугольника.

4

Операционно-познавательный этап.

1. Осознание проблемы.

Слайд № 3

На слайде даны рисунки. Ученики должны по рисункам определить названия элементов треугольника.

На 1 рисунке ВД -медиана.

На 2 рис. ВД высота.

На 3 рис. ВД биссектриса.

На 4 рис. Учащиеся не могут определить элемент треугольника. Возникает проблема.

Ученики отвечают.

2.Формулирование гипотезы.

Из рисунка

АК=КВ =>К середина

ВЕ=ЕС => Е середина

Ученики делают вывод что, КЕ - отрезок, соединяющий середину сторон треугольника.

3.Решение проблемы.

Слайд № 4

Учитель подсказывает, что этот отрезок называется средней линией треугольника.

Учитель сообщает тему урока «Средняя линия треугольника». Демонстрирует слайд с темой урока.

С помощью учителя учащиеся формулируют цель урока.

5

Изучение нового материала.

Слайд №5

Учитель задаёт вопрос классу: «Ребята, как вы думаете, чему равна средняя линия треугольника?»

Учитель оказывает консультативную помощь.

Ученикам предлагается в парах обсудить доказательство параллельности средней линии треугольника противоположной стороне.

Учитель излагает окончательную формулировку теоремы.

Теорема:

Средняя линия треугольника параллельна его стороне и равна её половине.

Учитель предлагает в парах доказать теорему, оказывая при этом консультативную помощь. Обращает внимание ребят на учебник, где есть доказательство данной теоремы.

Демонстрирует теорему и доказательство теоремы на слайде.

Возможные ответы:

1. Разбивает треугольник на два подобных треугольника.

2. Средняя линия параллельна противоположной стороне.

Возможно, кто-нибудь из ребят догадается, что средняя линия треугольника равна половине противоположной стороны.

Ученики пытаются в парах доказать теорему. В учебнике ученики прочитают теорему о средней линии треугольника.

Слайд №6

Ученики решают устно и отвечают с места.

6

Закрепление материала.

Устное решение задач.

Слайд №7

Решите устно:

Задание 1.

Будет ли ЕF средней линией треугольника?

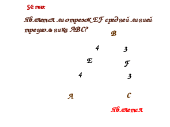
Ученики решают устно и отвечают с места.

Слайд №8

Слайд №9

Задание 2.

Является ли отрезок СD средней линией треугольника?

Задание 3.

KL - средняя линия треугольника DFE, DF =10см, FE= 12 см. Чему равны отрезки DK, KF, FL, LE?

Слайд №10

Задание 4.

MK и PK - средние линии треугольника АВС. Является ли отрезок МР средней линией этого треугольника?

Слайд №11

Задание 5.

Стороны треугольника равны 4 м, 6 м, 8 м. Чему равны средние линии этого треугольника?

Слайд №12

Решите задачу № 567 из учебника в тетрадях.

Ученики письменно в тетрадях решают задачу. Один ученик решает на переносной доске.

7

Домашнее задание.

Демонстрация слайда

Домашнее задание: П. 62. Задачи № 565, 566.

Ученики записывают домашнее задание.

8

Подведение итогов. Рефлексия.

Спрашивает формулировки определения средней линии и теорем. По таблице, вместе с учениками, пересказывает доказательство.

Ставит оценки.

Слушают учителя. Вместе с учителем вкратце пересказывают доказательства, отвечают на вопросы.