- Учителю
- Рабочая программа по алгебре 8 класс
Рабочая программа по алгебре 8 класс
Пояснительная записка
Рабочая программа по алгебре для 8 класса 2013-2014 учебный год составлена на основе примерной программы основного общего образования по математике М.: Дрофа, 2007 в соответствии с содержанием указанного учебника Макарычев Ю.Н., Миндюк Н. Г. Нешков К.И., Суворова С.Б. «Алгебра» 8 кл. - Просвещение, 2009-2012
Данная рабочая программа рассчитана на 102 учебных часа (3 часа в неделю), в том числе контрольных работ - 10.
Срок реализации рабочей учебной программы - один учебный год.
Используется учебно-методический комплект:
-
Макарычев, Ю. Н. Алгебра: учебник для 8 класса общеобразовательных учреждений / Ю.Н. Макарычев, К.И. Нешков, Н.Г. Миндюк, С.Б. Суворова; под ред. С.А. Теляковского. - М.: Просвещение, 2010.
-
Звавич, Л.И. Дидактические материалы по алгебре. 8 класс / Л.И. Звавич, Л.В. Кузнецова, С.Б. Суворова. - М.: Просвещение, 2010.
-
Рурукин А.Н., Лупенко Г.В., Масленникова И.А. Поурочные разработки по алгебре: 8 класс. - М.: ВАКО, 2011. - 416с.
Рабочая программа конкретизирует содержание предметных тем образовательного стандарта и дает распределение учебных часов по разделам курса.
Рабочая программа выполняет две основные функции:
-
Информационно-методическая функция позволяет всем участникам образовательного процесса получить представление о целях, содержании, общей стратегии обучения, воспитания и развития учащихся средствами данного учебного предмета.
-
Организационно-планирующая функция предусматривает выделение этапов обучения, структурирование учебного материала, определение его количественных и качественных характеристик на каждом из этапов, в том числе для содержательного наполнения промежуточной аттестации учащихся.
Основное общее образование в современных условиях призвано обеспечить функциональную грамотность и социальную адаптацию обучающихся на основе приобретения ими опыта в сфере учения, познания, профессионально-трудового выбора, личностного развития, ценностных ориентаций и смыслотворчества. Это предполагает направленность целей обучения на формирование компетентной личности, способной к жизнедеятельности и самоопределению в информационном обществе, ясно представляющей свои потенциальные возможности, ресурсы и способы реализации выбранного жизненного пути.
Цели обучения математике:
-
формирование представлений о математике как универсальном языке науки, средство моделирования явлений и процессов; об идеях и методах математики;
-
развитие логического мышления, пространственного воображения, алгоритмической культуры, критичности мышления на уровне, необходимом для будущей профессиональной деятельности, а также последующего обучения в высшей школе;
-
овладение математическими знаниями и умениями, необходимыми в повседневной жизни, для изучения школьных естественнонаучных дисциплин на базовом уровне, для получения образования в областях, не требующих углубленной математической подготовки;
-
воспитание средствами математики культуры личности, понимания значимости математики для научно - технического прогресса, отношения к математике как к части общечеловеческой культуры через знакомство с историей развития математики, эволюцией математических идей.
Практическая значимость школьного курса алгебры обусловлена тем, что её объектом являются количественные отношения действительного мира. Математическая подготовка необходима для понимания принципов устройства и использования современной техники, восприятия научных и технических понятий и идей. Математика является языком науки и техники. С её помощью моделируются и изучаются явления и процессы, происходящие в природе.
В ходе преподавания математики в 8 классах работа ведется так, чтобы учащиеся овладевали умениями общеучебного характера, разнообразными способами деятельности, приобретали опыт:
-
планирования и осуществления алгоритмической деятельности, выполнения заданных и конструирования новых алгоритмов;
-
решения разнообразных классов задач из различных разделов курса, в том числе задач, требующих поиска пути и способов решения;
-
исследовательской деятельности, развития идей, проведения экспериментов, обобщения, постановки и формулирования новых задач;
-
ясного, точного, грамотного изложения своих мыслей в устной и письменной речи, использования различных языков математики (словесного, символического, графического);
-
проведения доказательных рассуждений, аргументации, выдвижения гипотез и их обоснования;
-
поиска, систематизации, анализа и классификации информации, использования разнообразных информационных источников, включая учебную и справочную литературу, современные информационные технологии.
Задача образовательного процесса - обеспечить усвоение учащимися обязательного минимума содержания на основе требований государственного образовательного стандарта.
Программа составлена на основе федерального компонента государственного Стандарта основного общего образования по математике
Цели изучения курса алгебры 8 класса:
-
Овладения системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин;
-
Интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, способности к преодолению трудностей;
-
Формирование представлений об идеях и методах математики как универсального языка науки и техники , овладение системой математических знаний и умений , необходимых для применения в практической средства моделирования явлений и процессов;
-
Воспитание культуры личности, отношения к математике как части общечеловеческой культуры, играющей особую роль в общественном развитии.
Содержание учебного предмета
Рациональные дроби
Рациональная дробь. Основное свойство дроби, сокращение дробей.
Тождественные преобразования рациональных выражений. Функция ![]() и ее график.
и ее график.
Квадратные корни
Понятие об иррациональных числах. Общие сведения о действительных числах.
Квадратный корень. Понятие о нахождении приближенного значения квадратного корня.
Свойства квадратных корней. Преобразования выражений, содержащих квадратные корни.
Функция у = √х, ее свойства и график.
Квадратные уравнения
Квадратное уравнение. Формула корней квадратного уравнения. Решение рациональных
уравнений. Решение задач, приводящих к квадратным уравнениям и простейшим
рациональным уравнениям.
Неравенства
Числовые неравенства и их свойства. Почленное сложение и умножение числовых
неравенств. Погрешность и точность приближения. Линейные неравенства с одной
переменной и их системы.
Степень с целым показателем. Элементы статистики
Степень с целым показателем и ее свойства. Стандартный вид числа. Начальные сведения
об организации статистических исследований.
Повторение
Требования к уровню подготовки и освоению содержания курса
Рациональные дроби
В результате изучения курса математики учащиеся должны:
-
знать основное свойство дроби, рациональные, целые, дробные выражения;
-
правильно употреблять термины «выражение», «тождественное преобразование»,
-
понимать формулировку заданий: упростить выражение, разложить на множители, привести к общему знаменателю, сократить дробь;
-
знать и понимать формулировку заданий: упростить выражение, разложить на множители, привести к общему знаменателю, сократить дробь, свойства обратной пропорциональности;
-
осуществлять в рациональных выражениях числовые подстановки и выполнять соответствующие вычисления;
-
выполнять действия сложения и вычитания с алгебраическими дробями, сокращать дробь;
-
выполнять разложение многочлена на множители применением формул сокращенного умножения, выполнять преобразование рациональных выражений;
-
осуществлять в рациональных выражениях числовые подстановки и выполнять соответствующие вычисления;
-
выполнять действия умножения и деления с алгебраическими дробями, возводить дробь в степень, выполнять преобразование рациональных выражений;
-
правильно употреблять функциональную терминологию (значение функции, аргумент, график функции), строить график обратной пропорциональности, находить значения функции y=k/x по графику, по формуле.
Квадратные корни
В результате изучения курса математики учащиеся должны:
-
знать определения квадратного корня, арифметического квадратного корня, какие числа называются рациональными, иррациональными, как обозначается множество рациональных чисел; свойства арифметического квадратного корня;
-
выполнять преобразование числовых выражений, содержащих квадратные корни;
-
решать уравнения вида x2=а;
-
находить приближенные значения квадратного корня;
-
находить квадратный корень из произведения, дроби, степени;
-
строить график функции
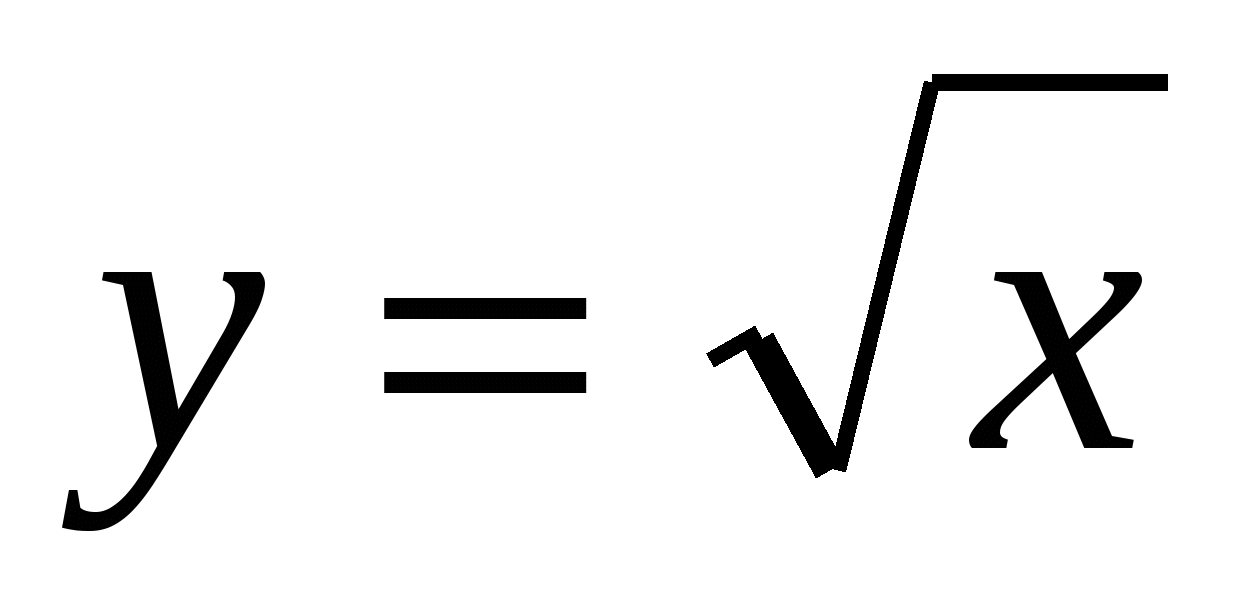 и находить значения этой функции по графику или по формуле;
и находить значения этой функции по графику или по формуле; -
выносить множитель из-под знака корня, вносить множитель под знак корня;
-
выполнять преобразование выражений, содержащих квадратные корни.
Квадратные уравнения
В результате изучения курса математики учащиеся должны:
-
знать, что такое квадратное уравнение, неполное квадратное уравнение, приведенное квадратное уравнение; формулы дискриминанта и корней квадратного уравнения, терему Виета и обратную ей;
-
решать квадратные уравнения выделением квадрата двучлена;
-
решать квадратные уравнения по формуле;
-
решать неполные квадратные уравнения;
-
решать квадратные уравнения с помощью теоремы, обратной теореме Виета;
-
использовать теорему Виета для нахождения коэффициентов и свободного члена квадратного уравнения;
-
решать текстовые задачи с помощью квадратных уравнений.
-
знать какие уравнения называются дробно-рациональными, какие бывают способы решения уравнений;
-
понимать, что уравнение - это математический аппарат решения разнообразных задач математики, смежных областей знаний, практики;
-
решать дробно-рациональные уравнения, решать уравнения графическим способом, решать текстовые задачи с помощью дробно-рациональных уравнений.
Неравенства
В результате изучения курса математики учащиеся должны:
-
знать определение числового неравенства с одной переменной, что называется решением неравенства с одной переменной, что значит решить неравенство, свойства числовых неравенств;
-
понимать формулировку задачи «решить неравенство»;
-
уметь записывать и читать числовые промежутки, изображать их на числовой прямой;
-
решать линейные неравенства с одной переменной, решать системы неравенств с одной переменной;
-
уметь применять свойства неравенства при решении неравенств и их систем.
Степень с целым показателем. Элементы статистики
В результате изучения курса математики учащиеся должны:
-
знать определение степени с целым и целым отрицательным показателем; свойства степени с целым показателями;
-
выполнять действия со степенями с натуральным и целым показателями;
-
приводить числа к стандартному виду;
-
записывать приближенные значения чисел, выполнять действия над приближенными значениями;
-
собирать и группировать статистические данные;
-
строить столбчатые и линейные диаграммы и графики.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
-
выполнения расчетов по формулам, составления формул, выражающих зависимости между реальными величинами; нахождения нужной формулы в справочных материалах;
-
моделирования практических ситуаций и исследовании построенных моделей с использованием аппарата алгебры;
-
описания зависимостей между физическими величинами соответствующими формулами при исследовании несложных практических ситуаций;
-
интерпретации графиков реальных зависимостей между величинами;
Фактически курс алгебры в 8-х классах разделен на 6 тем:
Средства контроля
Контроль знаний учащихся - неотъемлемая часть процесса обучения, оценки качества образования.
Контроль знаний осуществляется как традиционными методами, так и с использованием компьютерных технологий.
Программа предусматривает использование следующих методов контроля:
Устные (опрос).
Письменные (математический диктант, контрольная работа, тестирование).
Практические (самостоятельные работы, зачеты).
Результаты контроля выражаются в оценке. В зависимости от типа контроля эта оценка будет либо внешней, либо внутренней (самооценкой). Всякая оценка выражает уровень соответствия результатов учебных действий ученика проверяемым параметрам этих действий. Для оценки существует шкала этого соответствия, которая может быть бинарной (выполнил - не выполнил), или более сложной, выражающейся в виде 5-и балльной шкалы отметок.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни:
-
Выполнения расчетов по формулам, составления формул, выражающих зависимости между реальными величинами; нахождения нужной формулы в справочных материалах;
-
Моделирования практических ситуаций и исследования построенных моделей с использованием аппарата алгебры;
-
Описания зависимостей между физическими величинами соответствующими формулами при исследовании несложных практических ситуаций;
-
Интерпретации графиков реальных зависимостей между величинами;
-
Анализа реальных числовых данных, представленных в виде диаграмм, графиков, таблиц;
-
Понимания статистических утверждений.
Учебно-дидактическое сопровождение
Учебник: Алгебра. 8 класс: учеб. для общеобразоват. учреждений / [ Ю.Н. Макарычев, Н.Г. Миндюк , К.И. Нешков, С.Б. Суворова ] ; под ред. С.А. Теляковского. - 17-е изд. -М. : Просвещение, 2009.
Методические пособия для учителя
-
Изучение алгебры в 7-9 классах: пособие для учителей / [ Ю.Н. Макарычев, Н.Г. Миндюк , С.Б. Суворова, И.С. Шлыкова]. -3-е изд., дораб.- М.: Просвещение, 2009.
-
Уроки алгебры в 8 классе: кн. для учителя / В.И. Жохов, Г.Д. Карташева.- 3-е изд., дораб. - М.: Просвещение,2009.
-
Поурочное планирование по алгебре: 8 класс: к учебнику Ю.Н. Макарычева, Н.Г. Миндюк, К.И. Нешкова, С.Б. Суворова. Алгебра: 8 класс» / Т.М. Ерина.- М.: Издательство « Экзамен», 2008. 2009.
-
Поурочные разработки по алгебре: 8 класс. / А.Н. Рурукин. и др. - М. : ВАКО, 2008,2009.
-
Алгебра. 8 класс: поурочные планы по учебнику Ю.Н. Макарычева и др. /авт.- сост. Т.Л. Афанасьева, Л.А. Тапилина. - Волгоград: Учитель, 2007,2008,2009.
-
Диктанты по алгебре. 7-11 классы. Дидактические материалы. /Г.Г. Левитас - М.: Издательство «Илекса»,2005-2009.
-
Сборник задач по алгебре: 7-8 кл.: к учебникам «Алгебра. 7 класс» и «Алгебра. 8 класс» под редакцией С.А. Теляковского /П.И. Алтынов.- М.: Издательство « Экзамен»,2008,2009.
-
Алгебра: Доп. главы к шк. учеб. 8 кл.: Учеб. пособие для учащихся шк. и классов с углубленным изуч. математики / Ю.Н. Макарычев, Н.Г. Миндюк, Под ред. Г.В. Дорофеева.- М.: Посвещение,1996-2008.
-
Занимательные материалы по математике .7-8 классы./Сост. Е.А. Галаева - Волгоград: ИТД «Корифей», 2006-2009.
-
Алгебра: математические диктанты. 7-9 классы / авт.- сост. А.С. Конте.- Волгоград: Учитель,2007-2009.
-
Нестандартные уроки алгебры.8 класс./Сост. Н.А. Ким.- Волгоград, ИТД «Корифей»,2006-2008.
-
. Алгебра. Тесты для промежуточной аттестации. 7-8 класс. Издание четвертое, переработанное и дополненное. /Под ред. Ф.Ф. Лысенко.- Ростов-на-Дону: Легион-М, 2009.
-
Открытые уроки алгебры: 7-8 классы. / Н.Л. Барсукова. - М.: ВАКО,2010.
Дидактические материалы
Алгебра: дидактические материалы для 8 кл. /В.И. Жохов, Ю.Н. Макарычев, Н.Г. Миндюк . - М.: Просвещение, 2008, 2009.
Инструментарий по отслеживанию результатов
-
Контрольные работы по алгебре: 8 класс / Ю.П.Дудницын, В.Л. Кронгауз.- М.: Издательство «Экзамен», 2010.
-
Контрольно-измерительные материалы. Алгебра: 8 класс. / Сост. Л.Ю. Бабушкина.- М.: ВАКО,2010.
-
Тесты по алгебре: 8 класс.: к учебнику Ю.Н. Макарычева и др. «Алгебра. 8 класс». / Ю.А. Глазков, М.Я. Гаиашвили. - М.: Издательство «Экзамен», 2011.
-
Самостоятельные и контрольные работы по алгебре и геометрии для 8 класса. / Ершова А.П. и др. - М.: Илекса,2009.
-
Контрольные и зачетные работы по алгебре: 8-й кл.: К учебнику «Алгебра 8 кл. общеобразоват. учреждений.Авт. Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова; Под ред. С.А. Теляковского / Алтынов П.И.- М.: Издательство «Экзамен»,2004-2009.
-
Алгебра: Тестовые задания к основным учебникам: 8 класс: Рабочая тетрадь / В.В. Кочагин, М.Н. Кочагина.- М.: Эксмо, 2007-2009.
-
Дидактические материалы по алгебре для 8 класса с углубленным изучением математики. / Ю.Н. Макарычев, Н.Г. Миндюк. - М.: Просвещение, 1998-2008.
Цифровые образовательные ресурсы
-
Уроки алгебры.7-8 классы. - М.: ООО «Кирилл и Мефодий», 2008-2010.
-
Алгебра. 7-9 классы. - М.: Просвещение, 2008-2010.
-
Алгебра.7-11 классы. - М.: «Фирма 1С», 2008-2010.
Интернет-ресурсы представлены в таблице:
№ п/п
Название
Электронный адрес
1.
МО и Н РФ
www. edu.ru
2.
Российский образовательный портал
www.school.edu.ru
3.
Федеральный институт педагогических измерений
www.fipi.ru
4.
Московский институт открытого образования (МИОО)
www.mioo.ru
5.
Институт новых технологий
www.int-edu.ru
6.
Интернет-поддержка учителей математики
www.math.ru
7.
Сеть творческих учителей
www.it-n.ru
8.
Сайт газеты «Математика»
http:// mat. 1 september.ru
9.
Единая коллекция образовательных ресурсов
http: / school.collection.informatika.ru
10.
Челябинский городской методический центр
www.chel-edu.ru
Дополнительная литература для учащихся:
-
За страницами учебника алгебры. / Л.Ф. Пичурин. - М.: Просвещение, 2008,2009.
-
Сборник заданий для проведения письменного экзамена по алгебре за курс основной школы.9 класс. /Л.В. Кузнецова, Е.А. Бунимович, С.Б. Суворова.- М.: Дрофа, 2008,2009.
-
Сборник задач для подготовки и проведения письменного экзамена по алгебре за курс основной школы: 9-й класс. /С.А. Шестаков, И.Р. Высоцкий, Л.И. Звавич ; Под ред. С.А. Шестакова. - М.: ООО Издательство «АСТ»; ООО Издательство «Астрель»,2008,2009.
-
Математика: 7-9 классы. Основные понятия, формулы, графики: Пособие для учащихся. /Сост. А.А. Лаврентьев.- М.: Школьная Пресса,2005.
-
Алгебра в таблицах. 7-11 классы. Справочное пособие./авт.-сост. Л.И. Звавич, А.Р. Рязановский.- М.: Дрофа, 1997-2009.
Календарно-тематическое планирование
№ п/п
Раздел, тема
Кол-во часов
Обязательные результаты обучения
дата
план
факт
ТСО, ЦОР
Глава 1. Рациональные дроби и их свойства
23
Цель: выработать умение выполнять тождественные преобразования рациональных выражений.
1-3
Рациональные выражения
3
Знать и понимать:
понятие целых выражений, рациональных выражений;
основное свойство дроби;
формулы сокращенного умножения и уметь их применять;
правила умножения дробей и возведения в степень, уметь применять их.
Уметь
находить ОДЗ;
сокращать дробь;
складывать и вычитать дроби с одинаковыми знаменателями;
находить общий знаменатель;
применять знания при преобразовании выражений;
преобразовывать рациональные выражения;
строить графики функций;
по графику находить значения х и у.
Презентация
ЦОР
4-6
Основное свойство дроби. Сокращение дробей. Приведение дробей к новому знаменателю.
3
Презентация
ЦОР
7-8
Сложение и вычитание дробей с одинаковыми знаменателями
2
9-11
Сложение и вычитание дробей с разными знаменателями
3
Презентация
ЦОР
12
Контрольная работа №1: "Рациональные выражения. Сложение и вычитание дробей"
1
13-14
Анализ контрольной работы.
Умножение дробей. Возведение дроби в степень
2
Презентация
ЦОР
15-16
Деление дробей
2
17-20
Преобразование рациональных выражений
4
21-22
Функция у = k / x и ее график
2
Презентация
ЦОР
23
Контрольная работа №2: "Произведение и частное дробей. Преобразование рациональных выражений "
1
Глава 2. Квадратные корни
19
Цель: систематизировать сведения о рациональных числах и дать представление об иррациональных числах, расширив тем самым понятие числа; выработать умение выполнять простейшие преобразования выражений, содержащих квадратные корни.
24
Анализ контрольной работы.
Рациональные числа
1
Знать и понимать:
преобразование обыкновенных дробей в десятичные;
теоремы о квадратном корне из произведения, дроби и степени.
Уметь:
сравнивать рациональные числа;
находить квадратные корни из неотрицательных чисел;
решать уравнения х2=а;
находить приближенные значения квадратного корня;
составлять таблицу значений и строить график функции √х;
применять теоремы о квадратном корне из произведения, дроби и степени;
находить корень из произведения, дроби, степени;
выносить множитель за знак корня;
вносить множитель под знак корня;
выполнять преобразования выражений с квадратным корнем.
Презентация
ЦОР
25
Иррациональные числа
1
26-27
Квадратные корни. Арифметический квадратный корень
2
Презентация
ЦОР
28-30
Уравнение х2 = а
3
31
Нахождение приближенных значений квадратного корня
1
32-33
Функция у = √х и ее график
2
Презентация
ЦОР
34
Квадратный корень из произведения и дроби
1
35
Квадратный корень из степени
1
36
Квадратный корень из произведения, дроби, степени
1
37
Контрольная работа № 3: "Квадратные корни"
1
38-39
Анализ контрольной работы.
Вынесение множителя из-под знака корня. Внесение множителя под знак корня
2
40-41
Преобразование выражений, содержащих квадратные корни
2
42
Контрольная работа № 4:"Преобразование выражений, содержащих квадратные корни»
1
Глава 3. Квадратные уравнения
21
Цель: выработать умения решать квадратные уравнения, простейшие рациональные уравнения и применять их к решению задач.
43-44
Анализ контрольной работы.
Определение квадратного уравнения. Неполные квадратные уравнения
2
Знать и понимать:
формулу корней квадратного уравнения;
теорему Виета.
Уметь:
решать неполные квадратные уравнения;
применять формулу корней квадратного уравнения при решении уравнений;
решать квадратные уравнения с помощью теоремы Виета;
решать задачи с использованием формулы и теоремы Виета, а так же с помощью рациональных уравнений.
Презентация
ЦОР
45
Решение квадратных уравнений выделением квадрата двучлена
1
46-48
Формула корней квадратного уравнения
3
49
Обобщающий урок
1
Презентация
ЦОР
50
Контрольная работа №5: «Квадратное уравнение и его корни»
1
51-52
Решение задач с помощью квадратных уравнений
2
53-54
Теорема Виета
2
Презентация
ЦОР
55-57
Решение дробных рациональных уравнений
3
58-60
Решение задач с помощью рациональных уравнений
3
61
Контрольная работа №6 «Дробные рациональные уравнения»
1
62
Анализ контрольной работы
1
63
Урок зачет по теме «Квадратные уравнения»
1
Глава 4. Неравенства
20
Цель: выработать умения решать линейные неравенства с одной переменной и их системы.
64-65
Числовые неравенства
2
Знать и понимать:
обозначение числовых неравенств;
теоремы о свойствах числовых неравенств;
теоремы о сложении и умножении числовых неравенств;
обозначение пересечения и объединения множеств и обозначение числовых промежутков.
Уметь:
читать числовые неравенства;
применять свойства числовых неравенств;
решать неравенства с одной переменной;
находить общее решение системы;
решать системы неравенств с одной переменной;
доказывать неравенства.
66-67
Свойства числовых неравенств
2
68-70
Сложение и умножение числовых неравенств
3
71
Погрешность и точность приближения
1
72-73
Пересечение и объединение множеств
2
74-75
Числовые промежутки
2
Презентация
ЦОР
76-77
Решение неравенств с одной переменной
2
78
Контрольная работа №7 «Числовые неравенства и их свойства. Числовые промежутки»
1
79
Анализ контрольной работы
Решение неравенств с одной переменной
1
80-82
Решение систем неравенств с одной переменной
3
Презентация
ЦОР
83
Контрольная работа №8:"Неравенства с одной переменной и их системы "
1
Глава 5. Степень с целым показателем. Элементы статистики
11
Цель: сформировать умение выполнять действия над степенями с целыми показателями, ввести понятие стандартного вида числа.
83-84
Определение степени с целым отрицательным показателем
2
Знать и понимать:
определение степени с целым отрицательным показателем;
свойства степени с целым показателем;
правила умножения и деления десятичных дробей.
Уметь:
находить значение степени с целым отрицательным показателем;
преобразовывать выражения, содержащие степени с целым показателем;
приводить числа к стандартному виду;
выполнять действия со степенями.
строить столбчатые и линейные диаграммы и графики.
Презентация
ЦОР
85-86
Свойства степени с целым показателем
2
87-88
Стандартный вид числа
2
Презентация
ЦОР
89
Контрольная работа №9 «Степень с целым показателем»
1
90-91
Сбор и группировка статистических данных
2
Цель: сформировать начальные представления о сборе и группировке статистических данных, их наглядной интерпретации
Уметь:
собирать и группировать статистические данные;
строить столбчатые и линейные диаграммы и графики.
92-94
Наглядное представление статистической информации
2
Итоговое повторение
8
Цель: обобщение и систематизация основного материала, изученного в курсе алгебры 8 класса
Рациональные дроби
1
Знать и понимать:
формулу корней квадратного уравнения и теорему Виета;
свойства числовых неравенств.
Уметь:
приводить дроби к общему знаменателю;
складывать, вычитать, умножать и делить рациональные дроби;
решать квадратные уравнения;
решать задачи с помощью квадратных уравнений;
решать числовые неравенства;
преобразовывать выражения с корнями;
решать неравенства с переменной и системы неравенств.
Квадратные корни и квадратные уравнения
1
Решение задач с помощью составления квадратных уравнений
2
Неравенства
1
Степень с целым показателем
1
Контрольная работа №10: «Итоговое повторение»
1
Анализ контрольной работы
Обобщение изученного материала
1
Всего
102
Литература
-
Федеральный государственный образовательный стандарт основного общего образования, утвержден Приказом Министерства образования и науки РФ от 17 декабря 2010 г. № 1897
-
Приказ Минобразования РФ от 5 марта 2004 г. N 1089 "Об утверждении федерального компонента государственных образовательных стандартов начального общего, основного общего и среднего (полного) общего образования"
-
Макарычев, Ю. Н. Алгебра: учебник для 8 класса общеобразовательныхучреждений / Ю.Н. Макарычев, К.И. Нешков, Н.Г. Миндюк, С.Б. Суворова; под ред. С.А. Теляковского. - М.: Просвещение, 2010
-
Звавич, Л.И. Дидактические материалы по алгебре. 8 класс / Л.И. Звавич, Л.В. Кузнецова, С.Б. Суворова. - М.: Просвещение, 2010.
-
Рурукин А.Н., Лупенко Г.В., Масленникова И.А. Поурочные разработки по алгебре: 8 класс. - М.: ВАКО, 2011. - 416с.
