- Учителю
- Практические работы по математике
Практические работы по математике
Одним из важнейших требований к профессиональному образованию в концепции модернизации российского образования выделяется требование подготовки конкурентноспособного на рынке труда, компетентного, ответственного, свободно владеющего своей профессией и ориентированного в смежных областях деятельности, способного к эффективной работе по специальности на уровне мировых стандартов, готового к постоянному профессиональному росту социальной и профессиональной мобильности специалиста. Новые требования ориентируют систему начального профессионального образования на переход от традиционного подхода - к компетентностному, призванному удовлетворить потребности современного общества, и самих обучающихся. Обучающиеся намерены получить такое образование, которое в наибольшей степени содействует развитию их личностных сил и благоприятно скажется на профессиональной карьере .
Показателем качества подготовки специалиста, определяющим его поведенческие качества на рынке труда является профессиональная компетентность.
Под профессиональной компетентностью понимаем интегральное качество личности, характеризующее владение ключевыми и профессиональными компетенциями. Именно компетентность характеризует профессионализм специалиста. Компетентного специалиста отличает самостоятельность, ответственность, способность к творчеству, стремление к постоянному обновлению знаний, овладению новой информацией для успешного решения профессиональных задач, как в стандартных, так и проблемных ситуациях. При этом компетентность будущего специалиста формируется в процессе обучения не только специальным, но общеобразовательным, в том числе и математическим циклом.
Результатом освоения программы профессионального модуля является овладение обучающимися видом профессиональной деятельности, в том числе профессиональными и общими компетенциями
Так с целью овладения профессиональными компетенциями
по профессии НПО 270802.10 Мастер отделочных строительных работ в части освоения основного вида профессиональной деятельности:
ПМ. 01 Выполнение штукатурных работ
ПК 1.1. Выполнять подготовительные работы при производстве
штукатурных работ.
ПК 1.2. Производить оштукатуривание поверхностей различной
степени сложности.
ПК 1.3. Выполнять отделку оштукатуренных поверхностей.
ПК 1.4. Выполнять ремонт оштукатуренных поверхностей.
обучающийся в ходе освоения профессионального модуля должен
уметь: просчитывать объемы работ и потребности в материалах;
Знать: нормы расходов сырья и материалов на выполняемые работы.
А также выпускник, освоивший ОПОП НПО, должен обладать общими
компетенциями, включающими в себя способность:
ОК 1. Понимать сущность и социальную значимость своей будущей
профессии, проявлять к ней устойчивый интерес.
ОК 2. Организовывать собственную деятельность, исходя из цели и
способов ее достижения, определенных руководителем.
ОК 3. Анализировать рабочую ситуацию, осуществлять текущий и
итоговый контроль, оценку и коррекцию собственной деятельности, нести
ответственность за результаты своей работы.
ОК 4. Осуществлять поиск информации, необходимой
для эффективного выполнения профессиональных задач.
ОК 5. Использовать информационно-коммуникационные технологии
в профессиональной деятельности.
ОК 6. Работать в команде, эффективно общаться с коллегами,
руководством, клиентами.
Поэтому математику следует рассматривать, как важнейшую составляющую качественной подготовки будущих специалистов. Это обусловлено не только тем, что математика является важным элементом общей культуры, универсальным языком науки, в целом, но и, главным образом, тем, что она является мощным средством решения прикладных и практико-ориентированных задач.
В этой связи акценты при изучении математики переносятся на процесс познания, эффективность которого полностью зависит от познавательной активности самого обучающегося. Успешность достижения этой цели зависит не только оттого, что усваивается, но и от того, как усваивается.
Выполнение лабораторных работ позволяет сформировать математическую, учебно-познавательную, информационную, коммуникативно-интерактивную и профессиональную, общую другие компетенции.
В процессе выполнения лабораторных работ обучающиеся могут закрепить не только навыки практического характера, но и умения и навыки интеллектуального труда: умений самостоятельно выполнять учебные задания, умений наблюдать, экспериментировать, рассуждать, обобщать и критически мыслить, умений самостоятельно искать ответы на интересующие вопросы и делать выводы, умений использовать приборы и различного рода оборудование в самостоятельной работе, умений опираться на практику и связывать ее с теорией.
Таким образом выполняются условия для подготовки компетентного специалиста, которого отличает самостоятельность, ответственность, способность к творчеству, стремление к постоянному обновлению знаний, овладению новой информацией для успешного решения профессиональных задач, как в стандартных, так и проблемных ситуациях.
Таким образом, использование лабораторных работ при обучении математике помогут достичь следующих целей:
образовательные:
усвоение математических знаний, формирование практических умений и навыков, усвоение принципов действия и навыков использования различных счетных, измерительных и чертежных инструментов, совершенствование знаний учащихся и обучение их самостоятельному применению этих знаний, обучение решению практико-ориентированных задач;
воспитательные:
формирование аккуратности и ответственности за свою деятельность, активизация учебной деятельности исследовательского характера;
развивающие:
развитие наблюдательности, умения выдвигать и проверять гипотезы и предположения, опровергать ошибочные обобщения и суждения, развитие способности учащихся работать в коллективе, а также интереса к изучаемому предмету.
Применение лабораторных работ, систематическое включение их в учебную деятельность обучающегося для повышения научно-теоретического уровня, для усиления творческого характера процесса обучения математике помогает улучшить качество математических знаний, является средством формирования прочных конструктивных, измерительных и вычислительных умений и навыков.
Анализ литературы по дидактике и методике преподавания математики позволяет видеть многоаспектность такого понятия, как лабораторная работа.
Лабораторная работа может выступать в качестве метода, формы и средства обучения.
Лабораторная работа - это такой метод обучения, при котором учащиеся под руководством учителя и по заранее намеченному плану проделывают опыты или выполняют определенные практические задания и в процессе их воспринимают и осмысливают новый учебный материал, закрепляют полученные ранее знания.
В классификации по основным этапам учебного процесса также можно выделить место лабораторной работе. Так контрольные уроки подразделяются на следующие виды: уроки устного опроса, уроки письменного опроса, зачеты, лабораторные и практические работы. Таким образом, лабораторные работы используются в качестве контроля и проверки знаний и умений учеников
Лабораторную работу можно рассматривать как средство обучения - средство развития профессиональной компетенции обучающихся , средство формирования необходимых умений и навыков, как средство формирования понимания практической значимости предмета, как средство развития поисковой активности учащихся, как средство контроля знаний.
В процессе выполнения лабораторных работ обучающиеся могут закрепить не только навыки практического характера, но и умения и навыки интеллектуального труда: умений самостоятельно выполнять учебные задания, умений наблюдать, экспериментировать, рассуждать, обобщать и критически мыслить, умений самостоятельно искать ответы на интересующие вопросы и делать выводы, умений использовать приборы и различного рода оборудование в самостоятельной работе, умений опираться на практику и связывать ее с теорией.
Виды лабораторных работ, их классификация.
В соответствии с важнейшими дидактическими функциями лабораторных работ целесообразно разделить их на три группы:
1. Лабораторные работы, после выполнения которых можно высказать определенную догадку, гипотезу о рассматриваемой зависимости.
2. Лабораторные работы, в которых требуется подтвердить рассмотрением частных случаев правильность только что найденной формулы, только что доказанной теоремы (или свойства, которое дано в учебнике без вывода). Лабораторные работы этого типа особенно эффективны для проверки умозаключений, сделанных по аналогии, ведь в случае неправильности такого суждения опыт доказывает его ложность. Темой такой работы может быть проверка любой обратной теоремы после доказательства прямой.
3. Лабораторные работы, в которых требуется применить знания для решения определенной практической задачи. Можно рассматривать лабораторные работы комбинированного типа, в которых можно найти элементы всех перечисленных выше лабораторных исследовательских задач.
Также можно разделить все лабораторные работы по видам используемых средств на занятии. Например, можно выделить лабораторные работы на измерения, то есть лабораторные работы с использованием различных измерительных инструментов, или лабораторные работы с применением информационных технологий.
Выделим следующие виды лабораторных работ:
лабораторные работы по обучению использованию чертежных и измерительных инструментов;
на измерения;
на конструирование;
на вычисления;
на построения;
с использованием ИКТ.
Выделяют следующие основные требования к организации лабораторной работы по математике:
Лабораторная работа должна соответствовать теме урока.
Лабораторная работа должна быть направлена на достижение поставленных целей.
Инструкция к лабораторной работе должна быть четко, грамотно составлена.
Каждый шаг инструкции должен быть понятен обучающимся.
При организации лабораторной работы должны быть подготовлены все необходимые инструменты, раздаточные материалы.
Лабораторная работа должна укладываться во временные рамки урока.
Обучающиеся должны быть заранее разделены на группы.
При составлении лабораторной работы, важно учитывать то, чтобы все учащиеся группы были задействованы в ее выполнении.
При выполнении этих требований к организации лабораторной работы и правильном ее проведении обучающиеся быстро усвоят материал и смогут самостоятельно сделать нужные выводы.
Лабораторные работы в курсе математики по профессии: «Мастер отделочных строительных работ»
Лабораторная работа
Формула боковой поверхности призмы. Применение формулы боковой поверхности прямой призмы и формулы площади прямоугольника для вычисления количества отделочных материалов и времени выполнения работ в помещении, указанном на плане.
Цель работы: научиться применять формулу боковой поверхности прямой призмы и площади прямоугольника для вычисления количества отделочных материалов и времени выполнения работ в помещении, указанном на плане.
Оборудование: ИЛР, калькулятор.
Предварительная работа: измерение размеров стен и пола мастерской по профессии «Мастер отделочных строительных работ»
Ход работы
I. Теоретическая часть.
Используя формулы для вычисления площади боковой поверхности прямой призмы и площади прямоугольника, вывести формулу для расчета количества плиток в общем виде.
II. Практическая часть.
Задание 1. Рассчитать количество плиток, необходимых для облицовки стен и пола мастерской по профессии «Мастер отделочных строительных работ».
Размеры плитки:
Для стен

Елена Бежевый 20х30
Для пола

Антей Бежевый пол 30х30
Задание 2. Рассчитать время выполнения работ в помещении
Таблица расхода рабочего времени:
№
п/п
Наименование
Количества часов
1
Рабочий день
8
2
Облицовка стен (1 м2)
2
3
Облицовка пола
1
Задание 3. Заполните таблицу
Количество плиток для облицовки стен
Количество плиток для облицовки пола
Расход рабочего времени
Сделайте вывод .
ЛАБОРАТОРНАЯ РАБОТА
Объем прямоугольно параллелепипеда. Применение формулы объема прямого параллелепипеда для вычисления массы плитки по объему и объемной массе.
Цель: развивать мыслительную деятельность учащихся, самостоятельность, логическое мышление, умение анализировать. Показать необходимость: знаний по геометрии для овладения их будущей профессии, применение формулы объема прямого параллелепипеда для вычисления массы плитки по объему и объемной массе.
Тип урока: совершенствование знаний.
Методы: лабораторная работа, беседа.
Оборудование: керамическая плитка, ИЛР, измерительная линейка с миллиметровыми делениями, справочник по гражданскому строительству, МК.
Ход урока.
Организация учащихся на проведение лабораторной работы.
Выполнение лабораторной работы .
Инструкционная карта для выполнения лабораторной работы.
1
Лабораторная работа
Применение формулы объема прямого параллелепипеда для вычисления массы плитки по объему и объемной массе.
Цель работы: применить формулу объема прямого параллелепипеда для вычисления массы плитки по объему и объемной массе.
Оборудование: керамическая плитка, измерительная линейка с миллиметровыми делениями, справочник по гражданскому строительству, МК.
Теоретическое обоснование.
Керамические плитки - это обоженные глинянные плитки с окрашивающими примесями или без них.
Плитки класса А применяются для полов с повышенной истираемостью, при влажном режиме помещений или химических воздействиях на пол. Плитки класса Б применяют во всех остальных случаях.
Водопоглащение для плиток А - не болеее 2%, для плиток класса Б - не более 4%. Коэффициент истираемости класса А не более 0, 65; класс - не боле 1,3. Плитки должны выдержать испытание на удар.
Характеристика основных видов керамических плиток для полов.
(ГОСТ 6787 - 80).
Тип
Размеры, мм
Количество плиток на
1 м²
длина
ширина
толщина
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Квадратные плитки
300
200
170
150
100
85
80
70
60
50
48
300
200
170
150
100
85
80
70
60
50
48
13; 15
11; 13: 15
11; 13: 15
11; 13: 15
10; 11; 13: 15
11; 13: 15
11; 13: 15
11; 13: 15
11; 13: 15
11; 13: 15
4; 6
11
25
35
45
100
140
157
205
278
400
435
Прямоугольные плитки
300
200
170
150
48
150
100
100
74
22
11; 13: 15
11; 13: 15
11; 13: 15
11; 13: 15
4; 6
23
50
60
90
905
Порядок выполнения работы.
Снимите размеры данной плитки:
а) сторона а = ;
б) сторона в = ;
в) толщина с = .
Запишите размеры данной плитки с учетом абсолютной погрешности измерения (абсолютная погрешность измерения при однократном измерении берется равной цене деления или половине цены деления прибора):
а) сторона а = ;
б) сторона в = ;
в) толщина с = .
Вычислите объем данной плитки, используя формулу объема прямого параллелепипеда:
V = .
Найдите абсолютную погрешность вычисления объема плитки ( для А*В абсолютная погрешность вычисляется по формуле А*∆В + В*∆А) и запишите результат вычисления объема.
∆V =
V ± ∆V =
Запишите , используя справочник по гражданскому строительству, объемный вес керамической плитки
Объемный вес (ρ) = кг/м³.
Расчитайте массу плитки по формуле:
m = V* ρ =
Найдите абсолютную погрешность массы плитки и запишите результат вычисления массы плитки.
∆m =
m ± ∆m = .
Вывод:
Обобщение и выводы по уроку.
Задание на дом: составить отчет о работе.
Лабораторная работа. Формула боковой поверхности призмы. Применение формулы площади боковой поверхности прямой призмы и формулы площади прямоугольника для вычисления количества плитки для облицовки поверхности .
Спецтехнология. Облицовка поверхности керамической плиткой.
Цель работы. Научиться применять формулы площади боковой поверхности прямой призмы и формулы площади прямоугольника для вычисления количества плитки для облицовки поверхности .
Содержание работы. Измерить необходимые линейные размеры облицовочной поверхности, по данным измерениям записать выражения для вычисления площади поверхности, вычислить количество плитки для облицовки.
Оборудование. И.Л.Р., измерительная линейка, карандаш, микрокалькулятор.
ХОД РАБОТЫ
1. Измерить длину и ширину двери кабинета.
2. Вычислить площадь двери.
3. Измерить длину и ширину окна.
4. Вычислить площадь окна.
5. Измерить длину и ширину керамической плитки.
6. Вычислить площадь плитки.
7. Записать формулу площади боковой поверхности прямой призмы. S=ph , где р - периметр основания, h- высота призмы.
8. Записать формулу для вычисления облицовочной поверхности. S=s - (s + 3s)
9. Выполнить вычисления задания 8.
10. Записать формулу для вычисления количества плитки 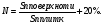 , вычислить количество плитки.
, вычислить количество плитки.
Сделать вывод.
Лабораторная работа
Объем прямоугольного параллелепипеда. Применение формулы объема прямоугольного параллелепипеда и формулы площади прямоугольника для вычисления количества штукатурки.
Спецтехнология. Оштукатуривание поверхностей.
Цель работы. Учиться применять формулы объема прямоугольного параллелепипеда и формулы площади прямоугольника для вычисления количества штукатурки.
Оборудование. Измерительная линейка, карандаш, микрокалькулятор, И.Л.Р.
ХОД РАБОТЫ
1. Запишите данные для выполнения работы:
а) площадь оштукатуриваемой поверхности (см. Лаб. Работу №1.);
б) высоту штукатурного намета (15 мм).
2. Запишите формулу объема прямоугольного параллелепипеда
V=SH , где S-площадь основания, Н - высота.
3. Вычислите количество штукатурки, необходимой для оштукатуривания панелей класса по формуле объема прямоугольного параллелепипеда v=sh, где для данной работы s-площадь оштукатуриваемой поверхности, h- высота штукатурного намета.
4. Вычислите время выполнения работы по формуле t=s*0,6 чел/час.
Сделайте вывод.
Лабораторная работа
Объем прямоугольного параллелепипеда. Применение формулы объема прямого параллелепипеда для вычисления массы плитки по объему и объемной массе.
Цель работы: применить формулу объема прямого параллелепипеда для вычисления массы плитки по объему и объемной массе.
Оборудование: керамическая плитка, измерительная линейка с миллиметровыми делениями., справочник по гражданскому строительству, МК.
Теоретическое обоснование.
Керамические плитки -это обоженные глинянные плитки с окрашивающими примесями или без них.
Плитки класса А применяютсядля полов с повышенной истираемостью, при влажном режиме помещений или химических воздействиях на пол. Плитки класса Б применяют во всех остальных случаях.
Водопоглащение для плиток А - не болеее 2%, для плиток класса Б - не более 4%. Коэффициент истираемости класса А не более 0, 65; класс - не боле 1,3. Плитки должны выдержать испытание на удар.
Характеристика основных видов керамических плиток для полов.
(ГОСТ 6787 - 80).
Тип
Размеры, мм
Количество плиток на
1 м²
длина
ширина
толщина
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Квадратные плитки
300
200
170
150
100
85
80
70
60
50
48
300
200
170
150
100
85
80
70
60
50
48
13; 15
11; 13: 15
11; 13: 15
11; 13: 15
10; 11; 13: 15
11; 13: 15
11; 13: 15
11; 13: 15
11; 13: 15
11; 13: 15
4; 6
11
25
35
45
100
140
157
205
278
400
435
Прямоугольные плитки
300
200
170
150
48
150
100
100
74
22
11; 13: 15
11; 13: 15
11; 13: 15
11; 13: 15
4; 6
23
50
60
90
905
Ход выполнения работы.
1. Снимите размеры данной плитки:
а) сторона а = ;
б) сторона в = ;
в) толщина с = .
2. Запишите размеры данной плитки с учетом абсолютной погрешности измерения (абсолютная погрешность измерения при однократном измерении берется равной цене деления или половине цены деления прибора):
а) сторона а = ;
б) сторона в = ;
в) толщина с = .
3. Вычислите объем данной плитки, используя формулу объема прямого параллелепипеда:
V = .
4. Найдите абсолютную погрешность вычисления объема плитки ( для А*В абсолютная погрешность вычисляется по формуле А*∆В + В*∆А) и запишите результат вычисления объема.
∆V =
V ± ∆V =
5. Запишите , используя справочник по гражданскому строительству, объемный вес керамической плитки
Объемный вес (ρ) = кг/м³.
6. Расчитайте массу плитки по формуле:
m = V* ρ =
7. Найдите абсолютную погрешность массы плитки и запишите результат вычисления массы плитки.
∆m =
m ± ∆m = .
Сделайте вывод.
ОБЛАСТНОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
НАЧАЛЬНОГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ ПРОФЕССИОНАЛЬНОЕ УЧИЛИЩЕ № 6 Г. ЛЬГОВА КУРСКОЙ ОБЛАСТИ
Лабораторные работы
как средства развития профессиональной компетенции обучающихся
Подготовила преподаватель математики:
Францева С.А.
2012ОБЛАСТНОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
НАЧАЛЬНОГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ ПРОФЕССИОНАЛЬНОЕ УЧИЛИЩЕ № 6 Г. ЛЬГОВА КУРСКОЙ ОБЛАСТИ
Лабораторные работы
по математике
по профессии НПО
270802.10 Мастер отделочных строительных работ
Подготовила
преподаватель математики:
Францева С.А.
2012