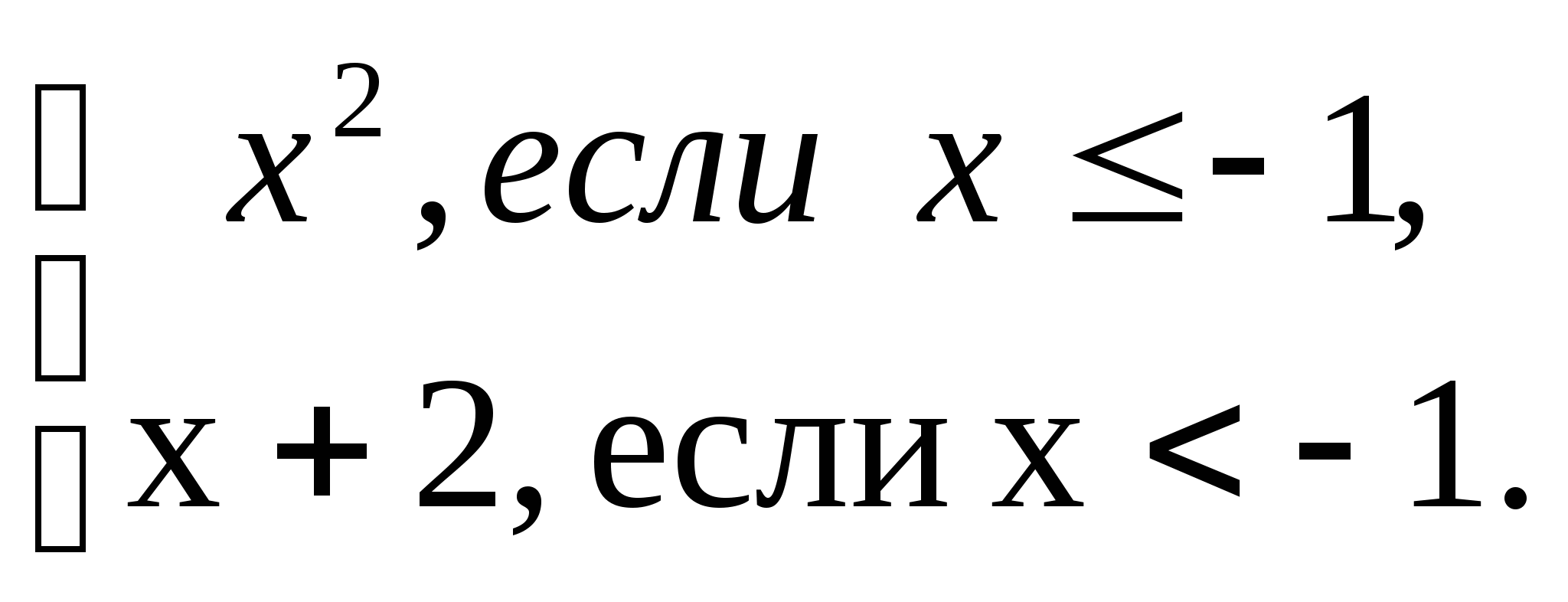Рабочая программа по алгебре 7 класс Мордкович

МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

«УСТЬ-КИРАНСКАЯ СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА-ИНТЕРНАТ»

на заседании МО учителей

Протокол № _____

от _____________ 20___г.

Руководитель МО

_________ /Лебедева Т.С./

«Согласовано»

Зам. директора по УВР школы

_____________ /Нечаева Т.С./

________________ 20______ г.

«Утверждаю»

Директор

___________/Имыгиров С.Л./

Приказ № _____

от _______________ 20 ____ г.

Рабочая программа

по алгебре

7 класс

Лебедевой Татьяны Сергеевны

2016 г.

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

Рабочая программа по математике составлена в соответствии со стандартом общего образования (приказ Минобразования России «Об утверждении федерального компонента государственных стандартов начального общего, основного общего и среднего (полного общего образования» от 05.03.2004 года №1089), с авторской программой для общеобразовательных учреждений И. И. Зубаревой, А.Г. Мордкович. Алгебра. 7-9 классы авт.-сост. И.И. Зубарева, А.Г. Мордкович. - М.: Мнемозина, 2011; с авторской программой Л.С. Атанасяна, В.Ф. Бутузова и др. «Программа по геометрии (базовый и профильный уровни)» - Программы общеобразовательных учреждений. Геометрия 10-11 классы. / Сост. Т.А. Бурмистрова. - М.: Просвещение, 2009.

Разработана программа по учебнику А.Г. Мордковича «Алгебра. 7 класс » и задачнику к этому учебнику. Планирование проведено из расчёта: 1 четверть - 5 часов в неделю, 2 - 4 четверти - 3 часа в неделю, согласно программе, рекомендованной Департаментом образовательных программ и стандартов общего образования Министерства образования РФ. Всего 120 часов.

Методологической основой программы, заложенной в УМК А. Г. Мордковича является функциональная линия.

Целью изучения курса является систематизация и обобщение понятия «математическая модель», развитие умения составлять словесную, аналитическую и графическую модели и научить переходить от одного вида модели к другому; познакомить учащихся с основными функциональными понятиями и с графиком линейной функции и функций y=x²; выработать умение выполнять действия над степенями с натуральными показателями; выполнять сложение, вычитание, умножение, деление одночленов и многочленов, разложение многочленов на множители, применять в несложных случаях формулы сокращённого умножения; познакомить учащихся со способами решения систем линейных уравнений с двумя переменными, применять их при решении текстовых задач.

Развитие учащихся, формирование у них умений и способностей будут оцениваться при выполнении самостоятельных и контрольных работ.

Рабочая программа выполняет две основные функции.

Информационно-методическая функция позволяет всем участникам образовательного процесса получить представление о целях, содержании, общей стратегии обучения, воспитания и развития учащихся средствами данного учебного предмета.

Организационно-планирующая функция предусматривает выделение этапов обучения, структурирование учебного материала, определение его количественных и качественных характеристик на каждом из этапов, в том числе для содержательного наполнения промежуточной аттестации учащихся.

Изучение алгебры 7 класса нацелено на формирование математического аппарата для решения задач из математики, смежных предметов, окружающей реальности. Язык алгебры подчеркивает значение математики как языка для построения математических моделей, процессов и явлений реального мира (одной из основных задач изучения алгебры является развитие алгоритмического мышле­ния, необходимого, в частности, для освоения курса информатики; овладение навыками дедуктивных рассуждений. Преобразование символических форм вносит свой специфический вклад в развитие воображения, способностей к математическому творчеству. Другой важной задачей изучения алгебры является получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов (равномерных, равноускоренных, экспоненциальных, периодических и др.), для формирования у обучающихся представлений о роли математики в развитии цивилизации и культуры.

Целевой ориентир в уровне сформированности ключевых компетенций, соответствует целям изучения математики в основной школе, ставит следующие цели обучения:

• овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;

• интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе, свойственных математической деятельности: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, пространственных представлений, способность к преодолению трудностей;

• формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;

• воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, играющей особую роль в общественном развитии.

В рабочей программе представлены содержание математического образования, требования к базовому и продвинутому уровню подготовки обучающегося, виды контроля, а также компьютерное сопровождение урока.

В данном классе ведущими методами обучения предмету являются: объяснительно-иллюстративный и репродуктивный, хотя используется и частично-поисковый. На уроках используются элементы следующих технологий: личностно ориентированное обучение, обучение с применением опорных схем, ИКТ.

Общеучебные умения, навыки и способы деятельности.

В ходе преподавания алгебры в основной школе, работы над формированием у учащихся перечисленных в программе знаний и умений, следует обращать внимание на то, чтобы они овладевали умениями общеучебного характера, разнообразными способами деятельности, приобретали опыт:

• планирования и осуществления алгоритмической деятельности, выполнения заданных и конструирования новых алгоритмов;

• решения разнообразных классов задач из различных разделов курса, в том числе задач, требующих поиска пути и способов решения;

• исследовательской деятельности, развития идей, проведения экспериментов, обобщения, постановки и формулирования новых задач;

• ясного, точного, грамотного изложения своих мыслей в устной и письменной речи, использования различных языков математики (словесного, символического, графического), свободного перехода с одного языка на другой для иллюстрации, интерпретации, аргументации и доказательства;

• проведения доказательных рассуждений, аргументации, выдвижения гипотез и их обоснования;

• поиска, систематизации, анализа и классификации информации, использования разнообразных информационных источников, включая учебную и справочную литературу, современные информационные технологии.

УЧЕБНО-ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ

КАЛЕНДАРНО-ТЕМАТИЧЕСКИЙ ПЛАН

Дата

проведения

По плану

Фактически

Математический язык. Математическая модель (18 часов)

1/1

Числовые выражения

2/2

Числовые выражения

3/3

Алгебраические выражения

4/4

Алгебраические выражения

5/5

Допустимые значения переменных в выражениях

6/6

Язык математики

7/7

Математическая модель задачи

8/8

Математическая модель задачи

9/9

Математическая модель задачи

10/10

Линейное уравнение с одной переменной

11/11

Линейное уравнение с одной переменной

12/12

Решение задач с помощью линейных уравнений

13/13

Решение задач с помощью линейных уравнений

14/14

Координатная прямая

15/15

Изображение точек на координатной прямой

16/16

Изображение точек на координатной прямой

17/17

Контрольная работа № 1 «Математический язык. Математическая модель»

18/18

Анализ контрольной работы

Линейная функция (12 часов)

19/1

Изображение точки на координатной плоскости

20/2

Изображение точки на координатной плоскости

21/3

Уравнения с двумя переменными

22/4

Уравнения с двумя переменными

23/5

График линейной функции

24/6

График линейной функции

25/7

Прямая пропорциональность

26/8

Прямая пропорциональность

27/9

Расположение прямых на координатной плоскости

28/10

Расположение прямых на координатной плоскости

29/11

Расположение прямых на координатной плоскости

30/12

Контрольная работа № 2 по теме «Линейная функция»

Системы двух линейных уравнений с двумя переменными (13 часов)

31/1

Системы двух линейных уравнений

32/2

Системы двух линейных уравнений

33/3

Метод подстановки решения систем уравнений

34/4

Использование метода подстановки для решения систем уравнений

35/5

Использование метода подстановки для решения систем уравнений

36/6

Метод алгебраического сложения решения систем уравнений

37/7

Использование метода алгебраического сложения для решения систем уравнений

38/8

Использование метода алгебраического сложения для решения систем уравнений

39/9

Решение текстовых задач с помощью систем уравнений

40/10

Решение текстовых задач с помощью систем уравнений

41/11

Решение текстовых задач с помощью систем уравнений

42/12

Контрольная работа № 3 по теме «Системы двух линейных уравнений с двумя переменными»

43/13

Анализ контрольной работы

Степень с натуральным показателем и ее свойства (12 часов)

44/1

Определение степени с натуральным показателем

45/2

Определение степени с натуральным показателем

46/3

Определение степени с натуральным показателем

47/4

Умножение и деление степеней

48/5

Умножение и деление степеней

49/6

Умножение и деление степеней

50/7

Возведение в степень произведения и частного чисел

51/8

Возведение в степень произведения и частного чисел

52/9

Возведение в степень произведения и частного чисел

53/10

Понятие степени с нулевым показателем

54/11

Контрольная работа № 4 по теме «Степень с натуральным показателем и ее свойства»

55/12

Анализ контрольной работы

Одночлены. Арифметические операции над одночленами (12 часов)

56/1

Одночлен и его стандартный вид

57/2

Одночлен и его стандартный вид

58/3

Сумма и разность одночленов

59/4

Сумма и разность одночленов

60/5

Произведение одночленов. Степень одночлена

61/6

Произведение одночленов. Степень одночлена

62/7

Произведение одночленов. Степень одночлена

63/8

Частное одночленов

64/9

Частное одночленов

65/10

Частное одночленов

66/11

Контрольная работа № 5 по теме «Одночлены. Арифметические операции над одночленами»

67/12

Анализ контрольной работы

Многочлены. Арифметические операции над многочленами (19 часов)

68/1

Многочлен. Стандартный вид многочлена

69/2

Многочлен. Стандартный вид многочлена

70/3

Сумма и разность многочленов

71/4

Сумма и разность многочленов

72/5

Произведение многочлена и одночлена

73/6

Произведение многочлена и одночлена

74/7

Произведение многочлена и одночлена

75/8

Произведение многочленов

76/9

Произведение многочленов

77/10

Произведение многочленов

78/11

Формулы квадрата суммы и разности

79/12

Формулы квадрата суммы и разности

80/13

Формулы квадрата суммы и разности

81/14

Разность квадратов

82/15

Разность квадратов

83/16

Разность кубов и сумма кубов

84/17

Разность кубов и сумма кубов

85/18

Контрольная работа № 6 по теме «Многочлены. Арифметические операции над многочленами»

86/19

Анализ контрольной работы

Что такое разложение многочленов на множители и зачем оно нужно (17 часов)

87/1

Применение разложения многочленов на множители

88/2

Применение разложения многочленов на множители

89/3

Способ вынесения общего множителя за скобки

90/4

Способ вынесения общего множителя за скобки

91/5

Группировка членов при разложении

92/6

Группировка членов при разложении

93/7

Применение формул сокращенного умножения для разложения многочленов

94/8

Применение формул сокращенного умножения для разложения многочленов

95/9

Применение формул сокращенного умножения для разложения многочленов

96/10

Применение формул сокращенного умножения для разложения многочленов

97/11

Разложение многочленов различными способами

98/12

Разложение многочленов различными способами

99/13

Алгебраическая дробь. Сокращение дроби

100/14

Алгебраическая дробь. Сокращение дроби

101/15

Тождественно равные выражения

102/16

Контрольная работа № 7 по теме «Разложение многочленов на множители»

103/17

Анализ контрольной работы

Функция y=x² (8 часов)

104/1

Квадратичная функция

105/2

Квадратичная функция

106/3

Решение уравнений с помощью графиков

107/4

Решение уравнений с помощью графиков

108/5

Расширение понятия функции

109/6

Расширение понятия функции

110/7

Контрольная работа № 8 по теме «Функция y=x² и ее график»

111/8

Анализ контрольной работы

Повторение (9 часов)

112/1

Функции и их графики

113/2

Функции и их графики

114/3

Линейные уравнения и системы уравнений

115/4

Степень с натуральным показателем

116/5

Итоговая контрольная работа

117/6

Сумма и разность многочленов

118/7

Произведение многочленов

119/8

Формулы сокращенного умножения

120/9

Функции у=х² и у=х³ и их графики

СОДЕРЖАНИЕ КУРСА

1. Математический язык. Математическая модель (18 часов)

Числовые и алгебраические выражения. Переменная. Допустимое значение переменной. Недопустимое значение переменной. Первые представления о математическом языке и о математической модели. Линейные уравнения с одной переменной. Линейные уравнения как математические модели реальных ситуаций. Координатная прямая, виды промежутков на ней.

Основная цель изучения данной темы - выработать у учащихся умение выполнять действия над степенями с натуральным показателем.

2. Линейная функция (12 часов)

Координатная плоскость. Алгоритм отыскания координат точки. Алгоритм построения точки М(а;b) в прямоугольной системе координат.

Линейное уравнение с двумя переменными. Решение уравнение. График уравнения. Алгоритм построения графика уравнения.

Линейная функция. Независимая переменная (аргумент). Зависимая переменная. График линейной функции. Наибольшее и наименьшее значения линейной функции на заданном промежутке. Возрастание и убывание линейной функции. Взаимное расположение графиков линейных функций.

3. Системы двух линейных уравнений с двумя переменными (13 часов)

Система уравнений. Решение системы уравнений. Графический способ решения уравнений. Метод подстановки. Метод алгебраического сложения.

Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций (текстовые задачи)

4. Степень с натуральным показателем (12 часов)

Степень. Основание степени. Показатель степени. Свойства степени с натуральным показателем. Умножение и деление степеней с одинаковыми показателями. Степень с нулевым показателем.

5. Одночлены. Операции над одночленами (12 часов)

Понятие одночлена. Коэффициент одночлена. Стандартный вид одночлена. Подобные одночлены. Арифметические операции над одночленами.

6. Многочлены. Арифметические операции над многочленами (19 часов)

Многочлен. Члены многочлена. Двучлен. Трехчлен. Приведение подобных слагаемых членов многочлена. Стандартный вид многочлена.

Формулы сокращенного умножения. Деление многочлена на одночлен.

6. Разложение многочленов на множители (17 часов)

Разложение многочлена на множители: с помощью формул сокращенного умножения, способ группировки, вынесение общего множителя за скобки, комбинированный способ. Метод выделения полного квадрата.

Основная цель изучения данной темы - выработать умение выполнять сложение, вычитание, умножение многочленов и разложение многочлена на множители.

Данная тема играет фундаментальную роль в формировании умения выполнять тождественные преобразования алгебраических выражений.

Понятие алгебраической дроби. Сокращение алгебраической дроби.

Тождество. Тождественно равные выражения. Тождественные преобразования.

6. Квадратичная функция (8 часов)

Квадратичная функция, ее свойства и график. Графическое решение уравнений. Кусочная функция. Чтение графика функции. Область определения функции. Первое представление о непрерывных функциях. Точка разрыва. Функциональная символика.

6. Итоговое повторение (9 часов).

ТРЕБОВАНИЯ К УРОВНЮ ПОДГОТОВКИ ОБУЧАЮЩИХСЯ

В результате изучения курса алгебры 7 класса обучающиеся должны:

знать/понимать

• существо понятия математического доказательства; примеры доказательств;

• существо понятия алгоритма; примеры алгоритмов;

• как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;

• как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;

• как потребности практики привели математическую науку к необходимости расширения понятия числа;

• вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов;

• каким образом геометрия возникла из практических задач землемерия; примеры геометрических объектов и утверждений о них, важных для практики;

• смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации;

уметь

• составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные;

• выполнять основные действия со степенями с натуральными показателями, с многочленами; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражений;

• решать линейные уравнения решать линейные решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;

• изображать числа точками на координатной прямой;

• определять координаты точки плоскости, строить точки с заданными координатами;

• находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;

• применять графические представления при решении уравнений, систем, неравенств;

• описывать свойства изученных функций (у=кх, где к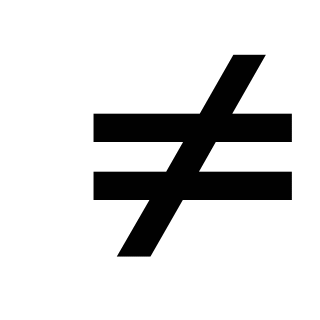0, у=кх+b, у=х², у=х³), строить их графики.

использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

• выполнения расчетов по формулам, составления формул, выражающих зависимости между реальными величинами; нахождения нужной формулы в справочных материалах;

• моделирования практических ситуаций и исследовании построенных моделей с использованием аппарата алгебры;

• описания зависимостей между физическими величинами соответствующими формулами при исследовании несложных практических ситуаций;

• интерпретации графиков реальных зависимостей между величинами.

КОНТРОЛЬНО-ИЗМЕРИТЕЛЬНЫЕ МАТЕРИАЛЫ

Контрольная работа № 1«Математический язык. Математическая модель»

Вариант 1

1. Найдите значение алгебраического выражения 4(4с - 3) + 8(5 - 2с) - (10с + 8), при с = 0,12

2. Решите уравнение: а) 2х + 3 = 0; б) 6х - 7 = 15 + 2х

3. Запишите обозначение, аналитическую и геометрическую модели числового промежутка: «Луч с началом в точке (-5). Сколько отрицательных чисел принадлежит данному промежутку?

4. Постройте прямую, проходящую через данные точки, и запишите ее аналитическую модель: А(-3; 1); В(-3; 4)

5. Решите задачу:

В книге 190 страниц. В пятницу Знайка прочитал в 1,2 раза меньше страниц, чем в субботу, а в субботу на 20 страниц меньше, чем в воскресенье. Сколько страниц он прочитал в субботу?

Вариант 2

1. Найдите значение алгебраического выражения 2(12с - 7) + 6(5 - 4с) - 3(2с + 5), при с =

2. Решите уравнение: а) 3х - 2 = 0; б) 7х + 1,5 = 10х - 3

3. Запишите обозначение, аналитическую и геометрическую модели числового промежутка: «Открытый луч с концом в точке 7. Сколько натуральных чисел принадлежит данному промежутку?

4. Постройте прямую, проходящую через данные точки, и запишите ее аналитическую модель: А(-2; 3); В(1; 3)

5. Решите задачу:

Капитан Врунгель загрузил на свой корабль в трех ящиках 44 кг бананов. В первом ящике было в 1,5 раза больше бананов, чем во втором, и на 4 кг меньше, чем в третьем. Сколько килограммов бананов в первом ящике?

Контрольная работа № 2 «Линейная функция»

Вариант 1

1. а) Найдите координаты точек пересечения графика линейного уравнения - 3х + 2у - 6 = 0 с координатными осями и постройте его график.

б) Принадлежит ли графику данного уравнения точка К?

2. а) Преобразуйте линейное уравнение с двумя переменными 2х + у - 1 = 0 к виду линейной функции и постройте ее график.

б) Найдите наименьшее и наибольшее значение этой функции на отрезке [-1;2].

3. Найдите координаты точки пересечения прямых у = 3 - х и у = 2х.

4. а) Задайте прямую пропорциональность формулой, если известно, что ее график параллелен графику линейной функции у = 3х - 4.

б) Определите, возрастает или убывает заданная функция. Ответ объясните.

Вариант 2

1. а) Найдите координаты точек пересечения графика линейного уравнения 2х - 5у - 10 = 0 с координатными осями и постройте его график.

б) Принадлежит ли графику данного уравнения точка М?

2. а) Преобразуйте линейное уравнение с двумя переменными -2х + у + 3 = 0 к виду линейной функции и постройте ее график.

б) Найдите наименьшее и наибольшее значение этой функции на отрезке [-2;1].

3. Найдите координаты точки пересечения прямых у = - х и у = 2х - 3.

4. а) Задайте прямую пропорциональность формулой, если известно, что ее график параллелен графику линейной функции у = -4х + 7.

б) Определите, возрастает или убывает заданная функция. Ответ объясните.

Контрольная работа № 3 «Системы двух линейных уравнений с двумя переменными»

Вариант 1

1. Решите методом подстановки систему уравнений.

2. Решите методом алгебраического сложения систему уравнений .

3. Решите графически систему уравнений .

4.В туристический поход ребята взяли двухместные и трехместные палатки. Сколько человек разместилось в трехместных палатках, если на 26 человек взяли 10 палаток?

5. Дана система уравнений . Пара чисел (2;-1) является ее решением. Найти значения a и b.

Вариант 2

1. Решите методом подстановки систему уравнений.

2. Решите методом алгебраического сложения систему уравнений .

3. Решите графически систему уравнений .

4.В копилку складывали двухрублевые и пятирублевые монеты. Когда копилку вскрыли, в ней оказалось пятирублевых монет на 12 меньше, чем двухрублевых, а всего денег на сумму 178 руб. Сколько рублей пятирублевыми монетами было в копилке?

5. Дана система уравнений Пара чисел (1;-2) является ее решением. Найти значения a и b.

Контрольная работа № 4 «Степень с натуральным показателем и ее свойства»

Вариант 1

1. Упростить выражение: а) б) в) .

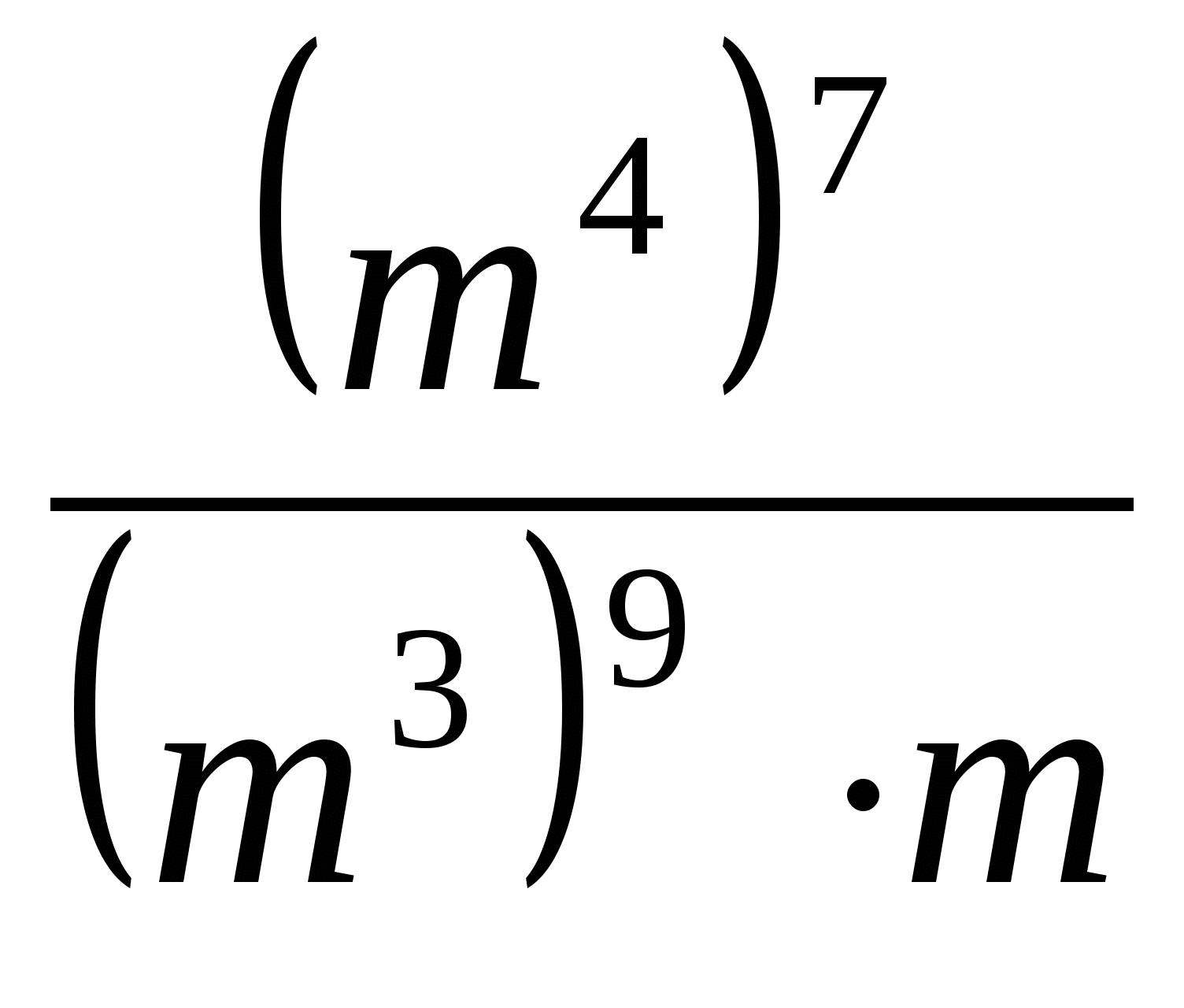2. Вычислите: .

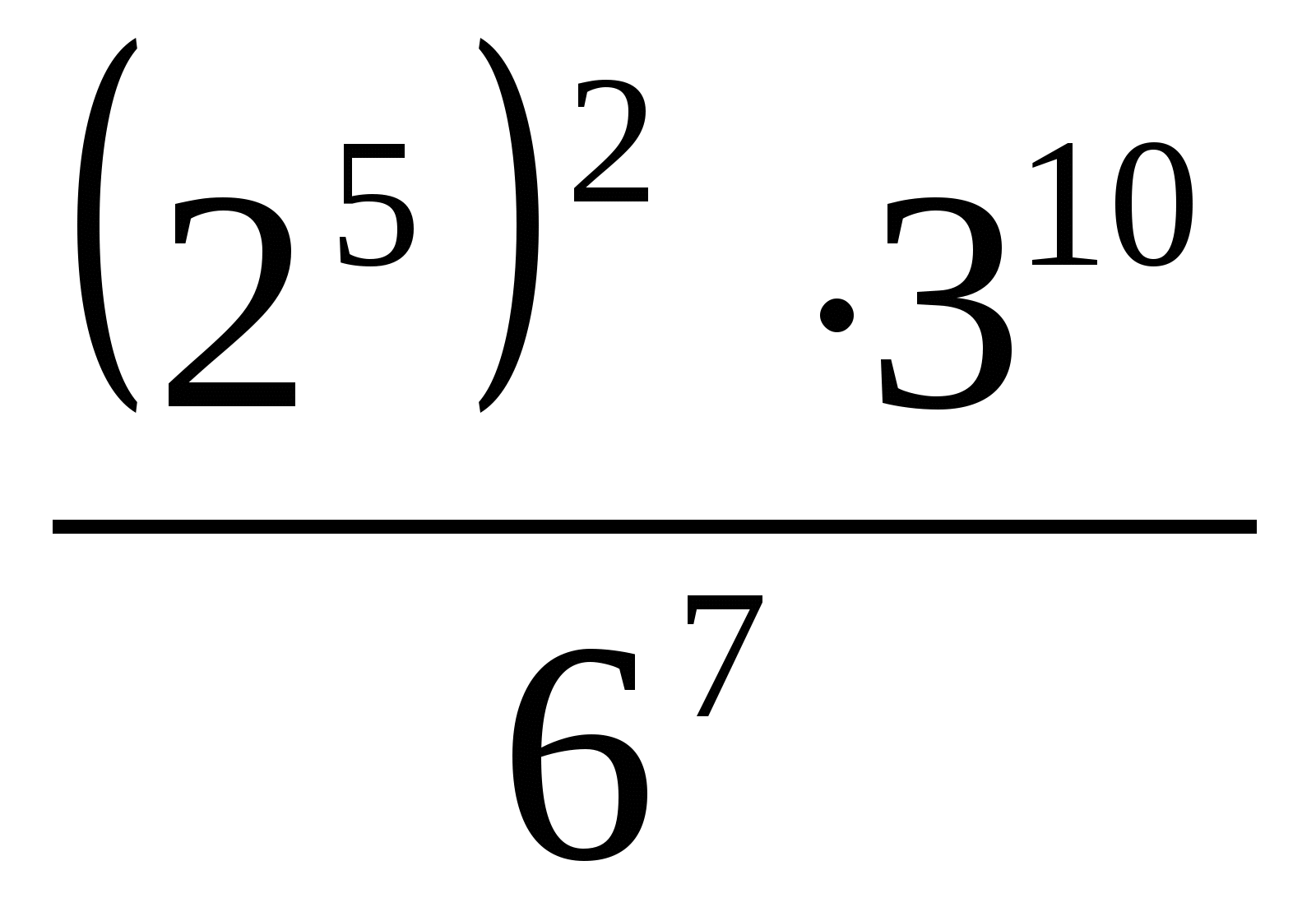3. Сравните значения выражений 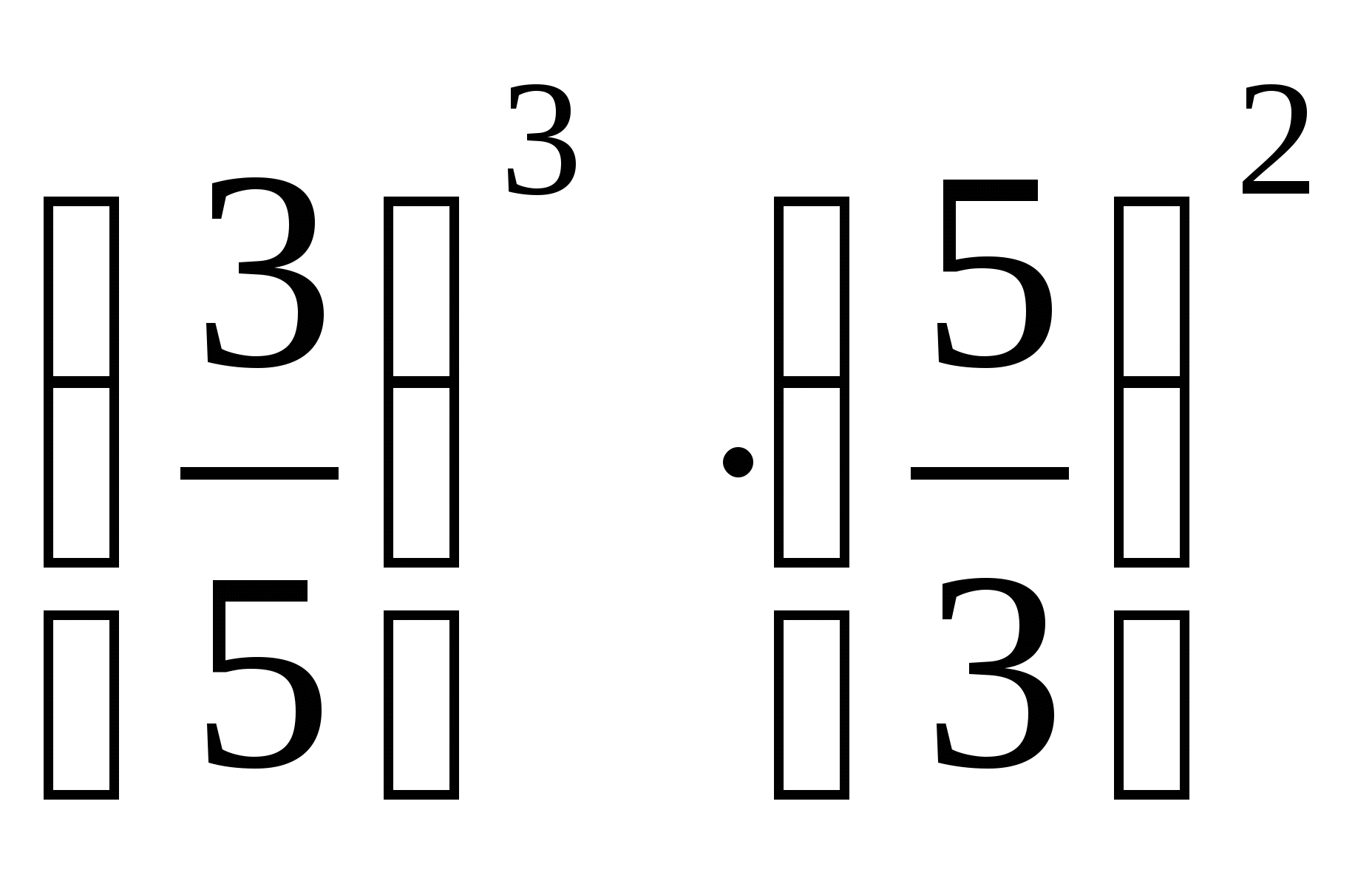и 1,6^о.

4. Объем куба равен 27 см³. Найти длину ребра куба и площадь полной поверхности куба.

5. Решите уравнение: 10^х = 10000000.

Вариант 2

1. Упростить выражение: а) б) в).

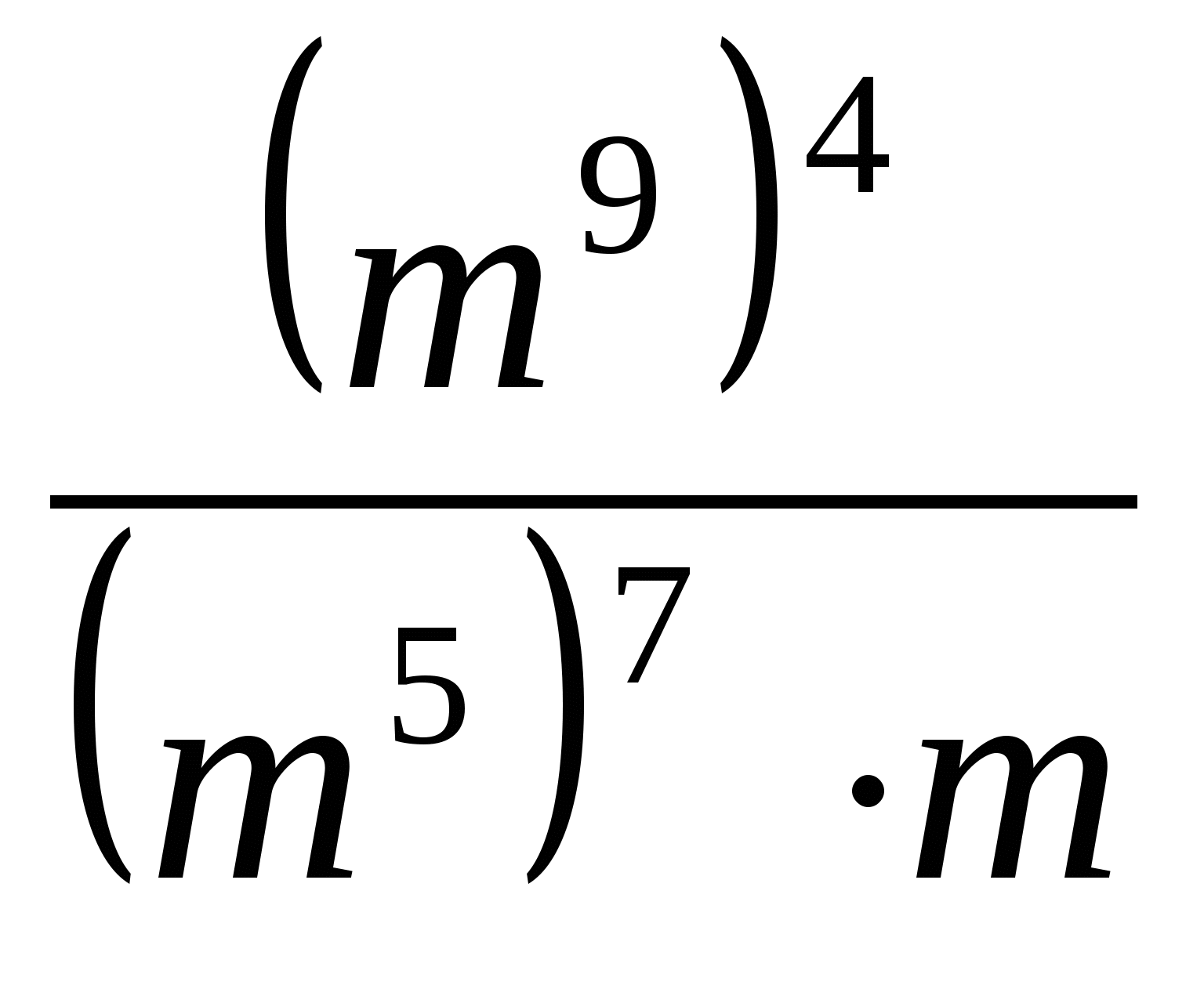2. Вычислите: .

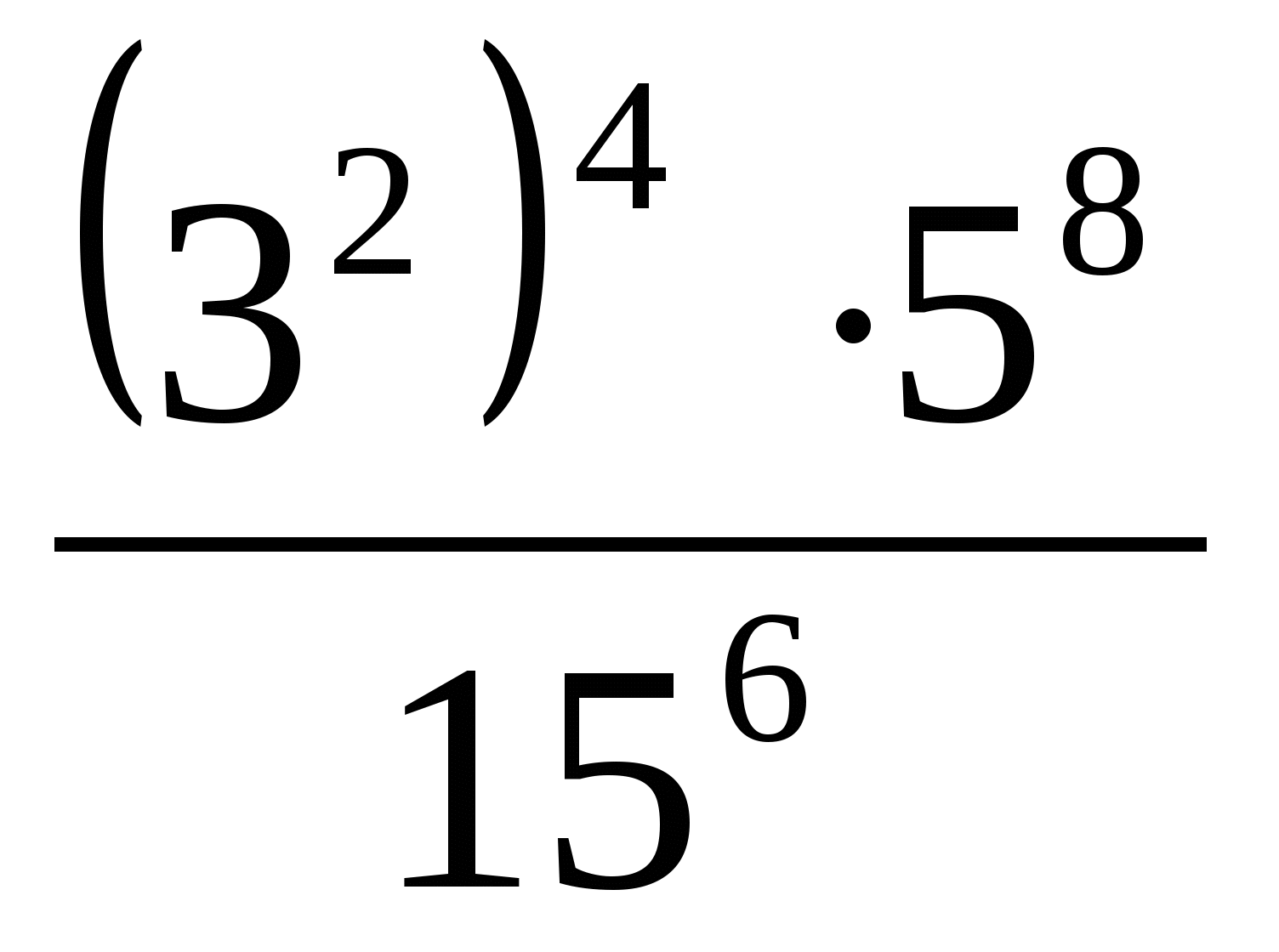3. Сравните значения выражений 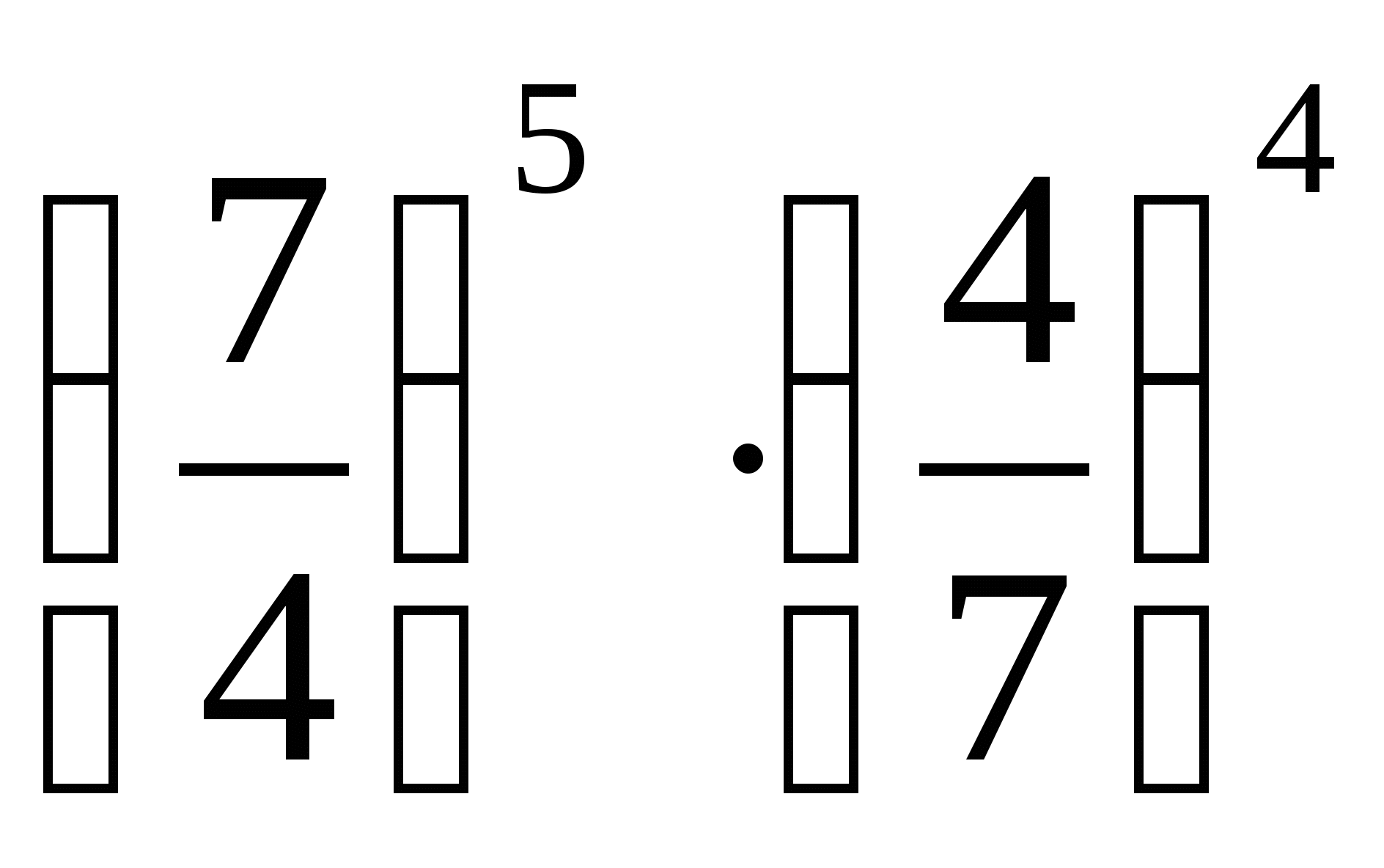и (-2)^о.

4. Площадь поверхности куба равен 24 см². Найти длину ребра куба и объем куба.

5. Решите уравнение:2^х = 512

Контрольная работа № 5 «Одночлены. Арифметические операции над одночленами»

Вариант 1

1. Приведите одночлен к стандартному виду и напишите, чему равен его коэффициент k: .

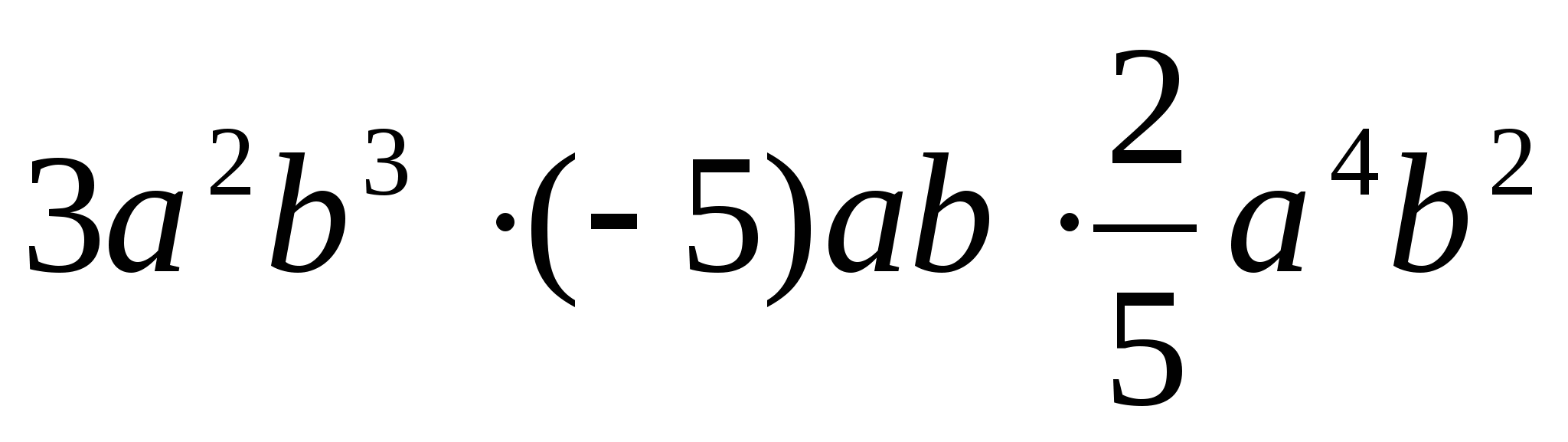2. Упростить выражение: а) 5х²у - 8х²у + х²у; б) ;

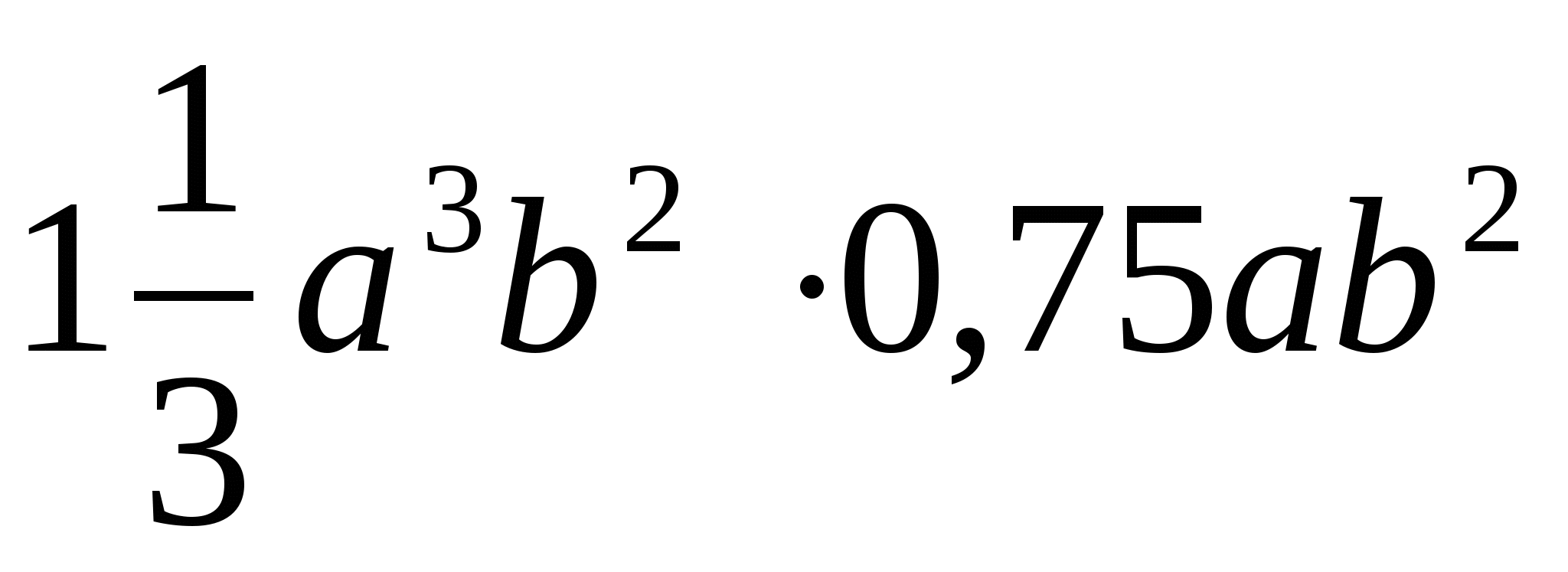в) ; г)

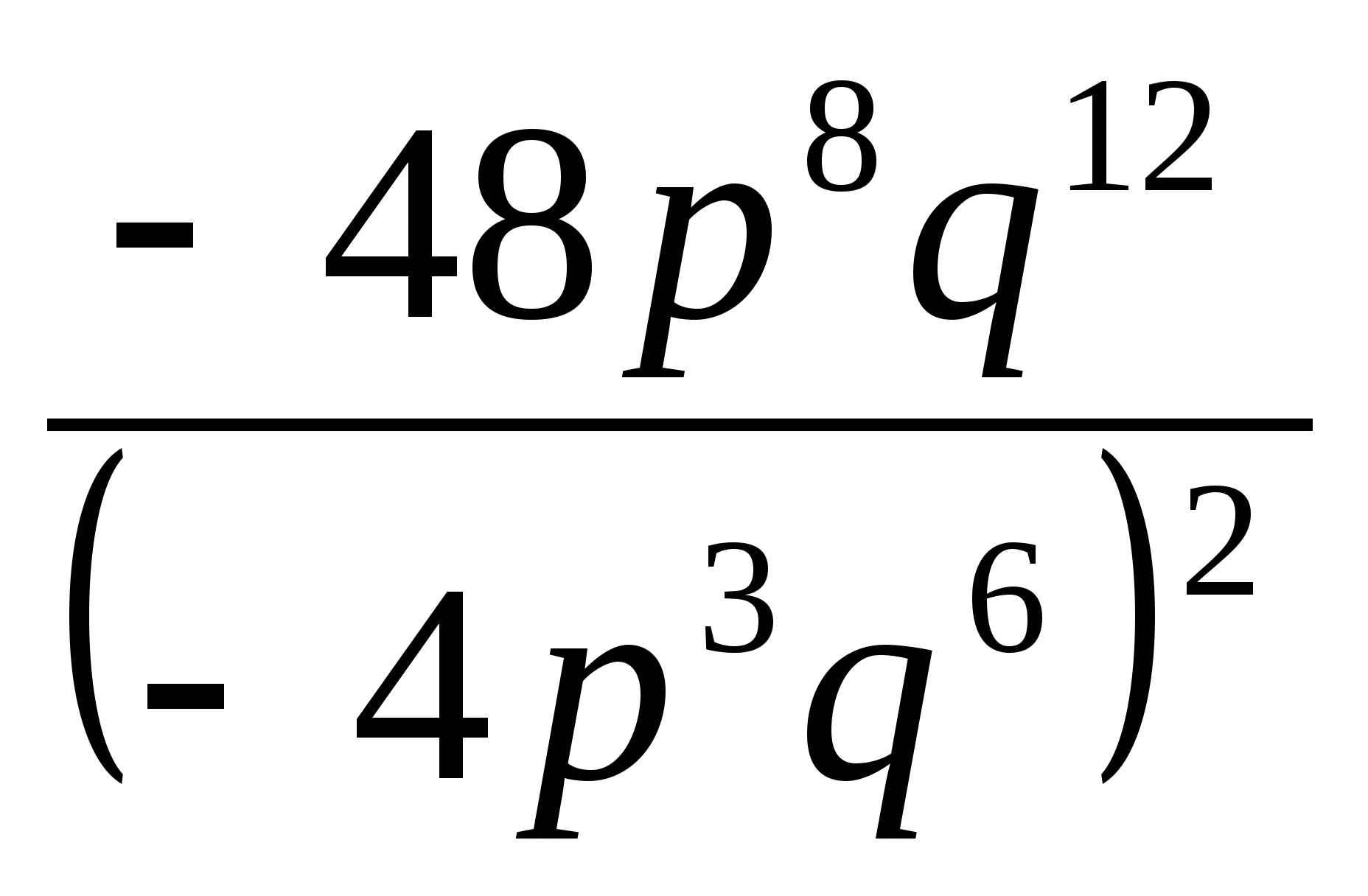
3. Незнайка, отправляясь на Луну на воздушном шаре, взял для балласта несколько мешков с песком. Когда воздушный шар первый раз пошел на снижение, незнайка выбросил 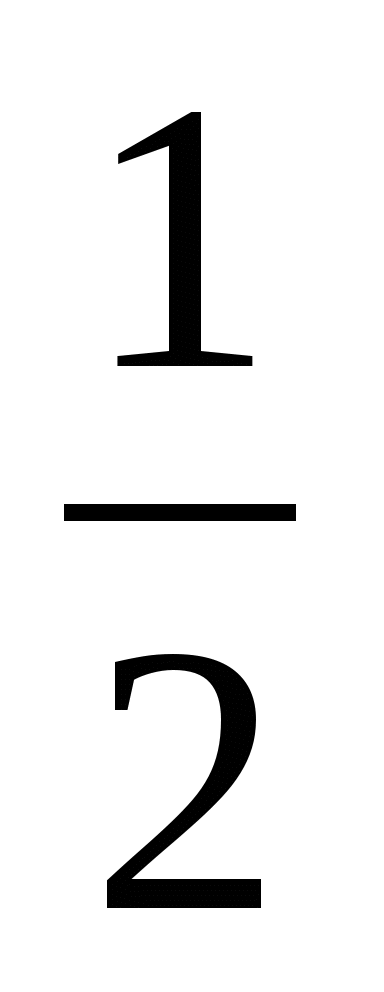всех мешков, во второй раз он выбросил еще 60% от оставшихся мешков, а в третий раз - последние 4 мешка. Сколько всего мешков с песком брал с собой Незнайка?

4. Найдите значение выражения: -2ху⁴х² + 3х³у²2у² - х²у(-ху³) при х = 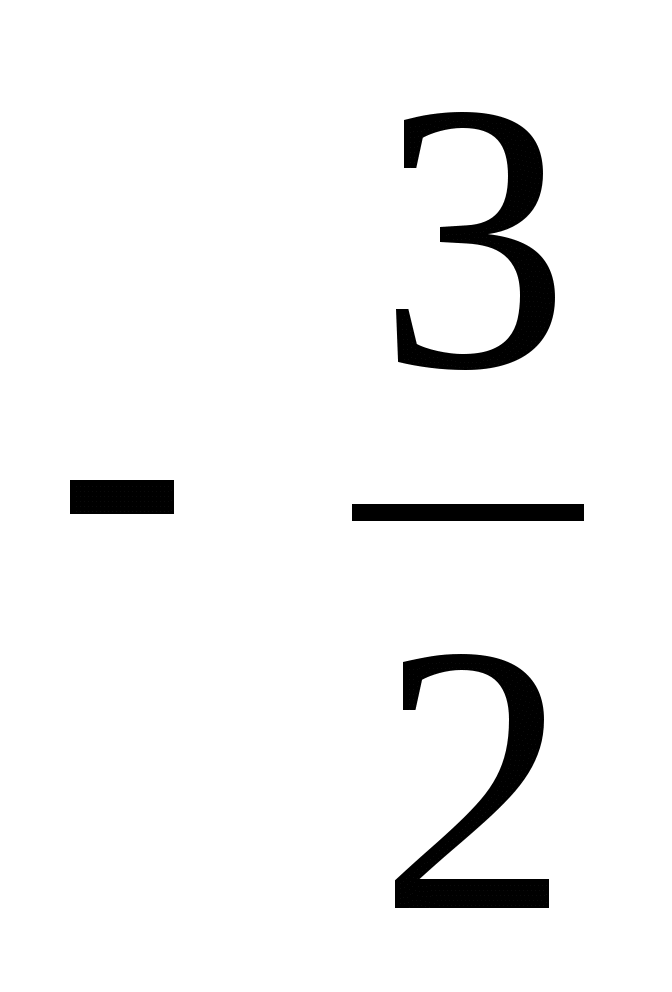; у = 2.

5. Решите уравнение .

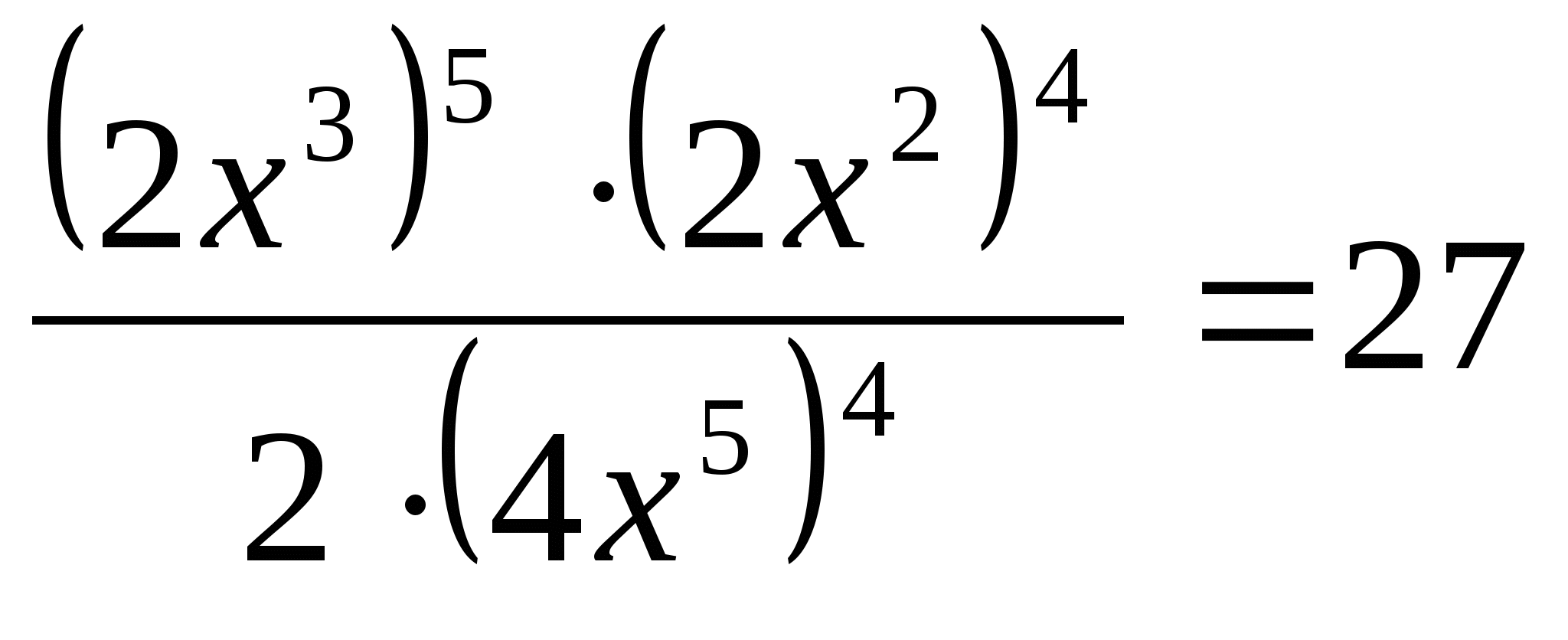Вариант 2

1. Приведите одночлен к стандартному виду и напишите, чему равен его коэффициент k: .

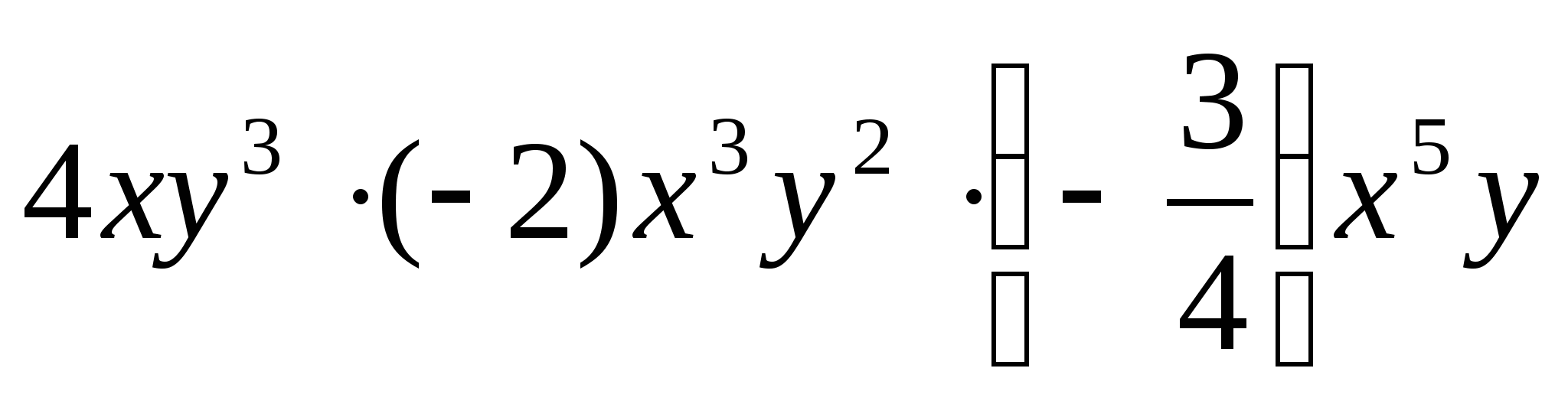2. Упростить выражение: а) ху² - 13ху² + 5ху²; б) ;

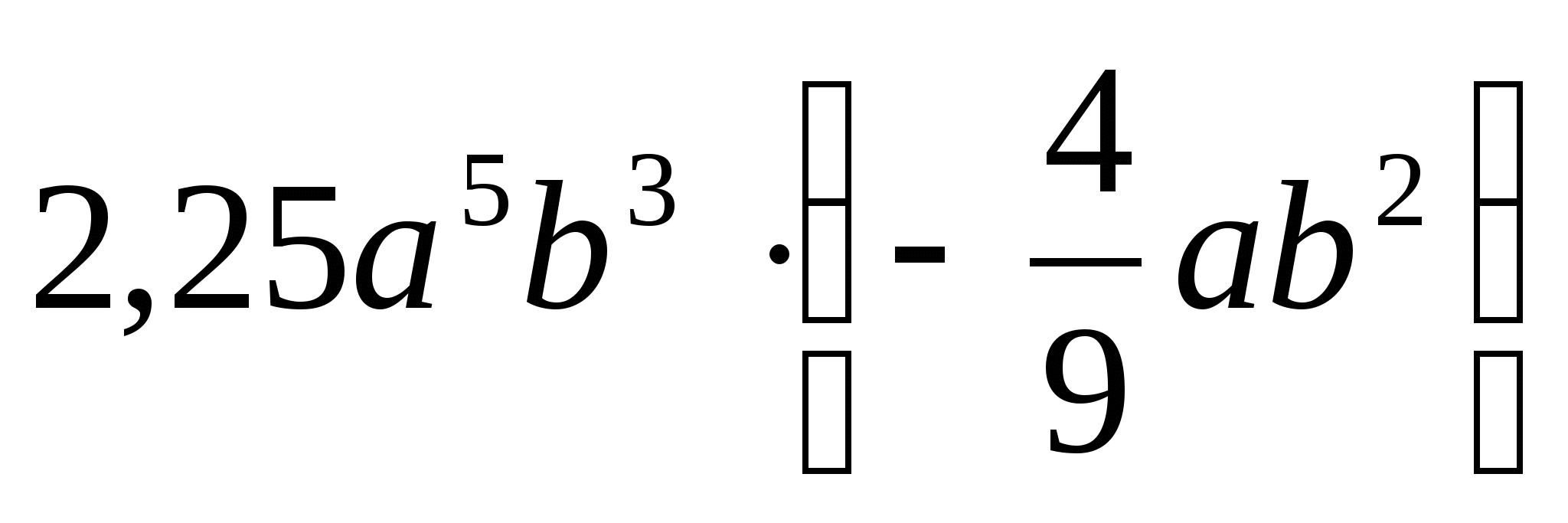в) ; г) .

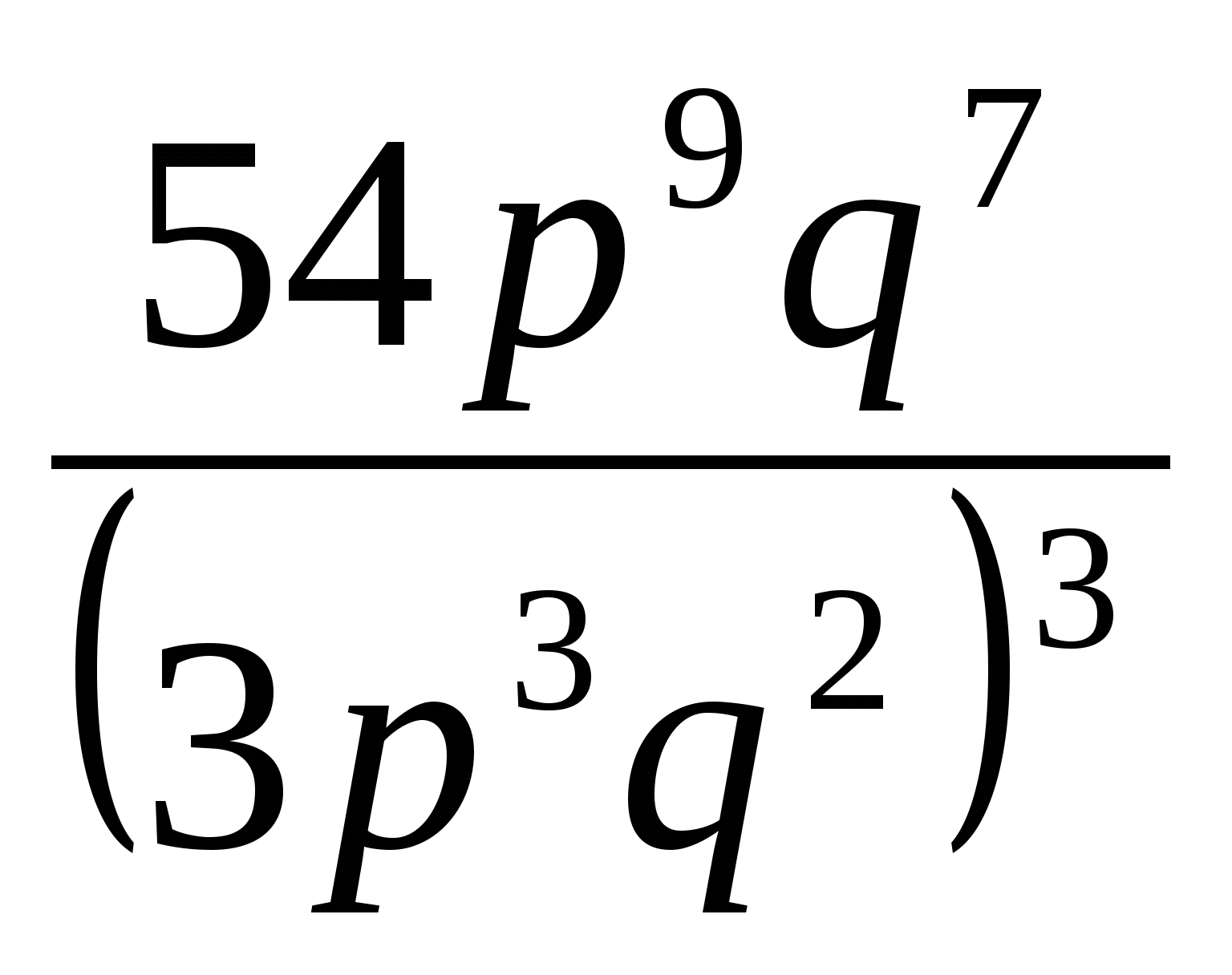3. Малыш подарил Карлсону банку клубничного варенья. Карлсон в первый день съел 25% всего варенья, во второй он съел 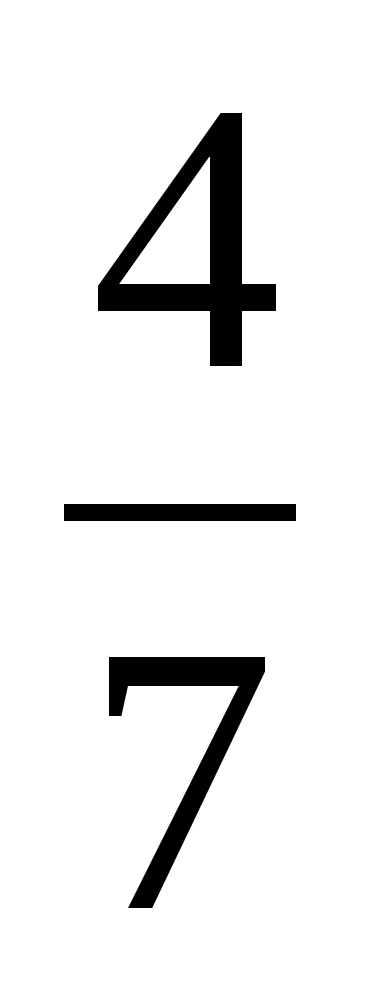от оставшегося варенья, а в третий - доел последние 270г. Сколько всего граммов варенья было в банке?

4. Найдите значение выражения: 2a²b³(-1,5a³b) + 5a⁴b⁴a + a²(-b)⁴a³ при b = 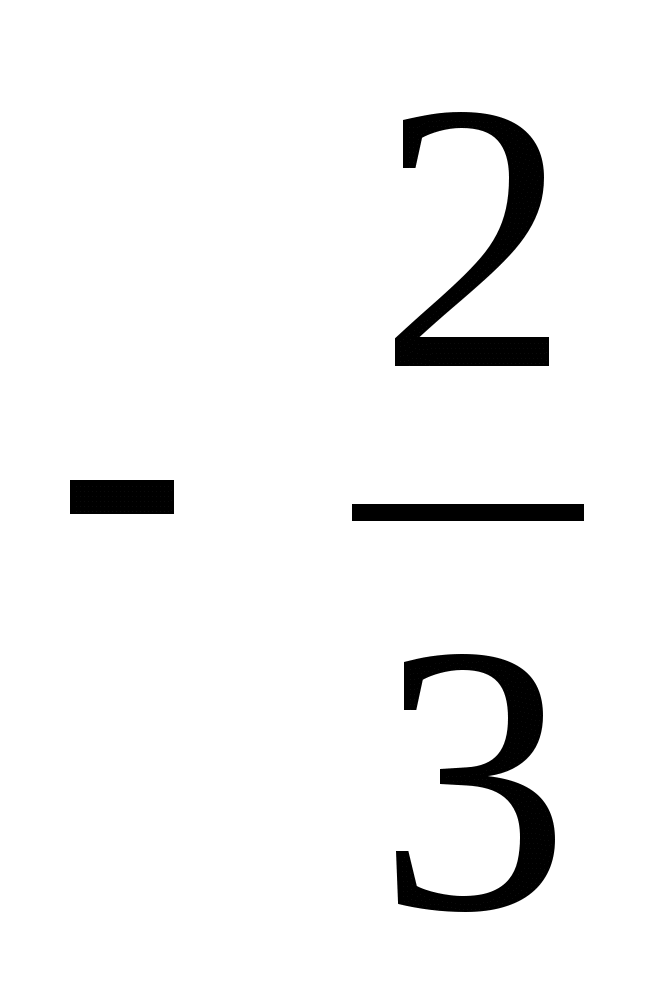; a = -3.

5. Решите уравнение .

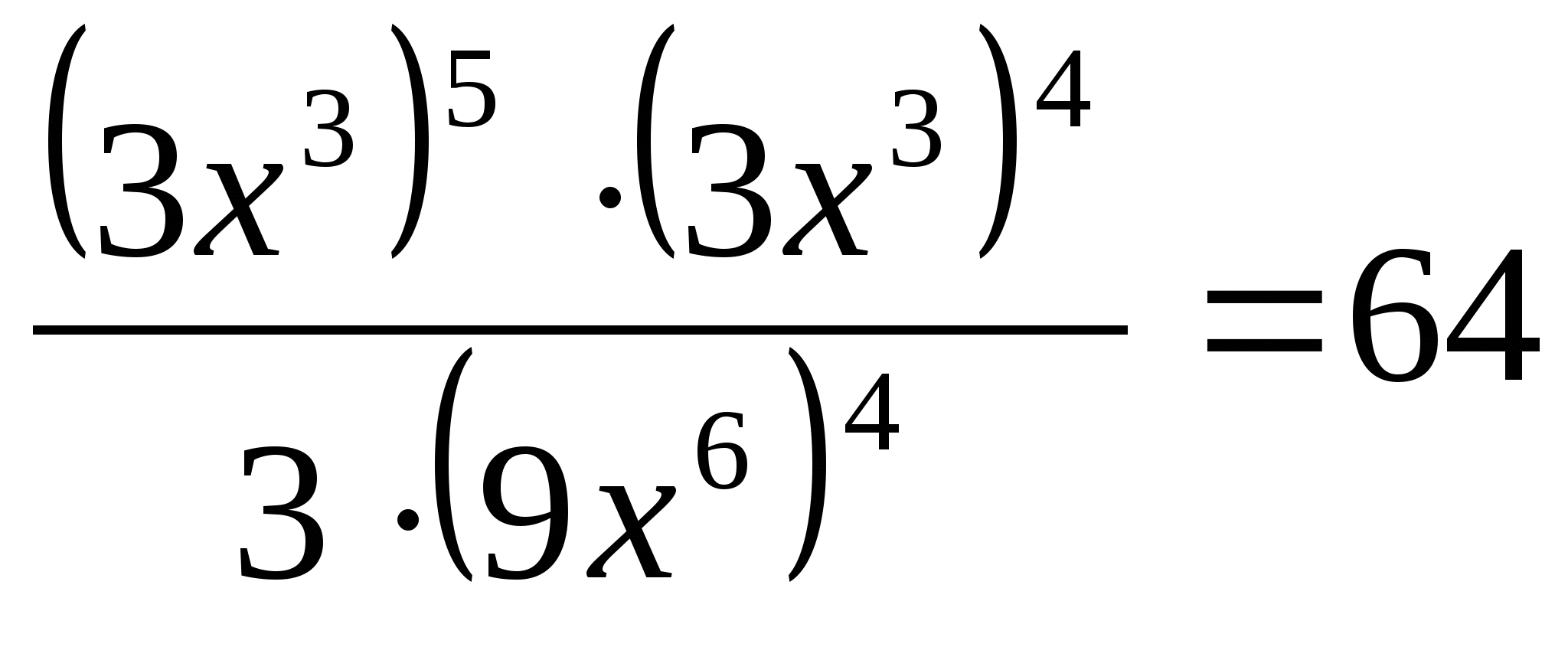Контрольная работа № 6 «Многочлены. Арифметические операции над многочленами»

Вариант 1

1. Найти многочлен р(х) и записать его в стандартном виде, если: р(х) = р₁(х) + р₂(х) - р₃(х) и р₁(х) = -2х² + 3х; р₂(х) = 4х² - 3; р₃(х) = 2х - 4.

2. Выполните действия:

а) 4ху(2х + 0,5у - ху); б) (х - 3)(х + 2); в) (24х²у + 18х³) : (-6х²).

3. Упростите выражение, используя ФСУ: (2р - 3)(2р + 3) - (р - 2)².

4. Найти три последовательных натуральных числа, если известно, что квадрат большего из них на 34 больше произведения двух других.

5. Докажите, что значение выражения не зависит от значения переменной:

5х³ - 5(х + 2)(х² - 2х + 4).

Вариант 2

1. Найти многочлен р(х) и записать его в стандартном виде, если: р(х) = р₁(х) + р₂(х) - р₃(х) и р₁(х) = 2х² - 5х; р₂(х) = 3х² + 1; р₃(х) = х - 2.

2. Выполните действия:

а) -5ху(3х² - 0,2у² + ху); б) (х - 5)(х + 4); в) (35х³у - 28х⁴) : 7х³.

3. Упростите выражение, используя ФСУ: (р + 3)² - (3р - 1)(3р + 1).

4. Найти три последовательных натуральных числа, если известно, что квадрат меньшего из них на 47 меньше произведения двух других.

5. Докажите, что значение выражения не зависит от значения переменной:

2х³ - 2(х - 3)(х² + 3х + 9).

Контрольная работа № 7 «Разложение многочленов на множители»

Вариант 1

1. Разложить на множители: а) 3х² - 12х; б) 2а + 4b - ab - 2b²

в) 4х² - 9; г) х³ - 8х² + 16х.

2. Сократите дробь: а) 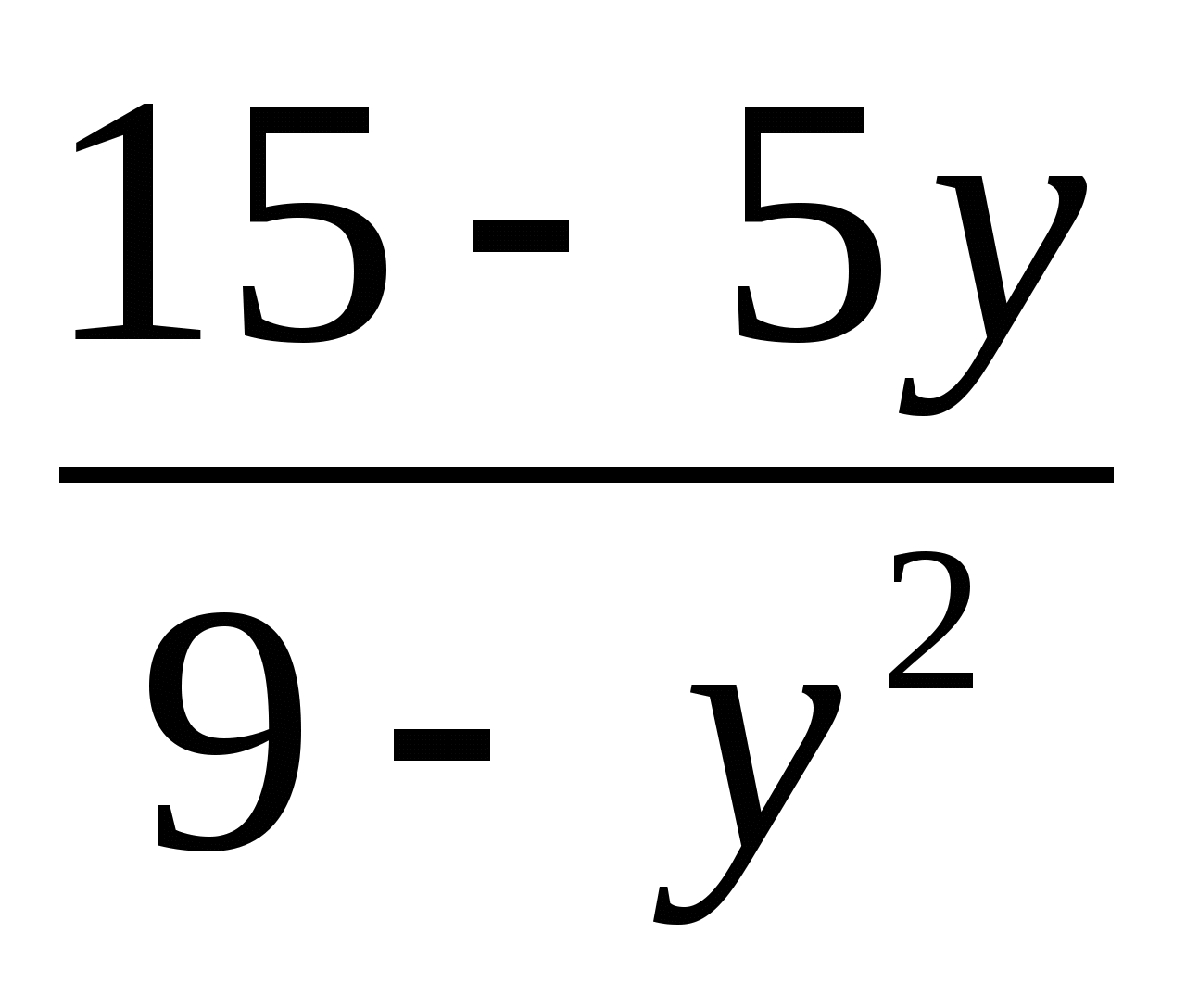; б) .

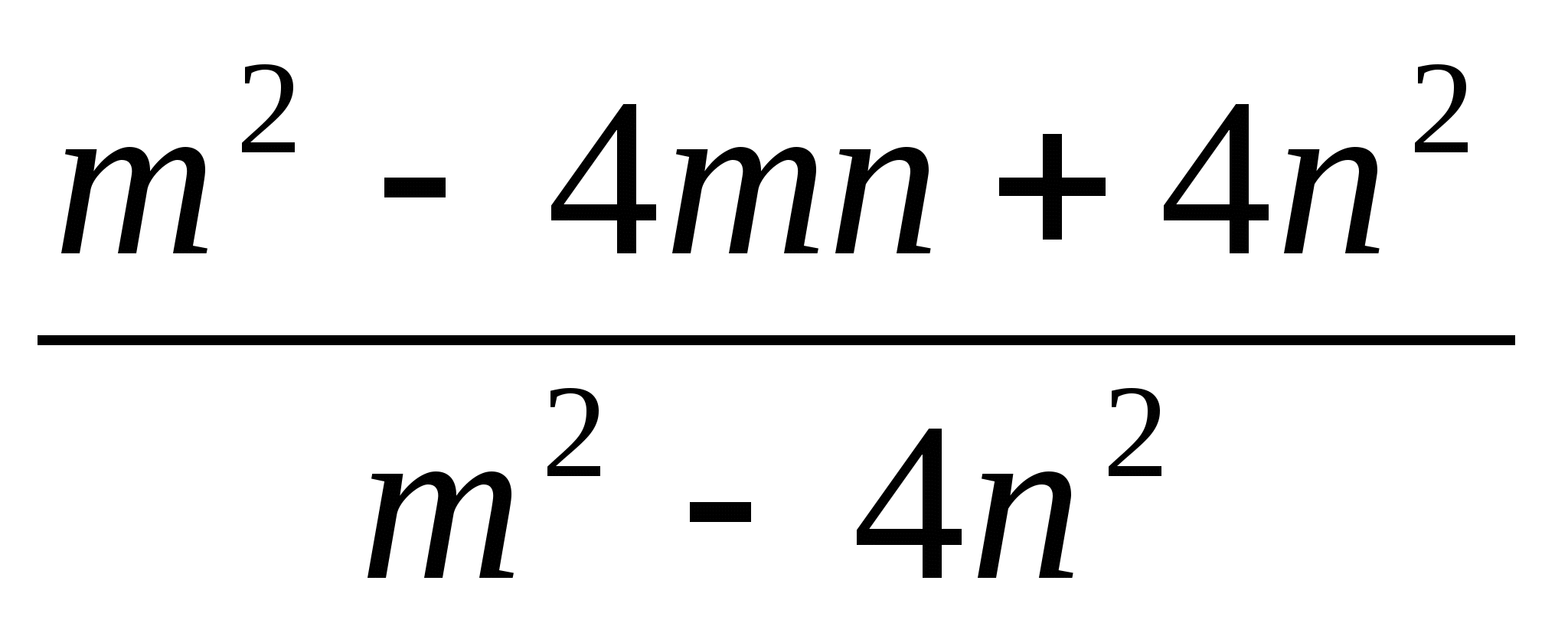3. Решите уравнение (х - 4)² - 25 = 0

4. Вычислите рациональным способом

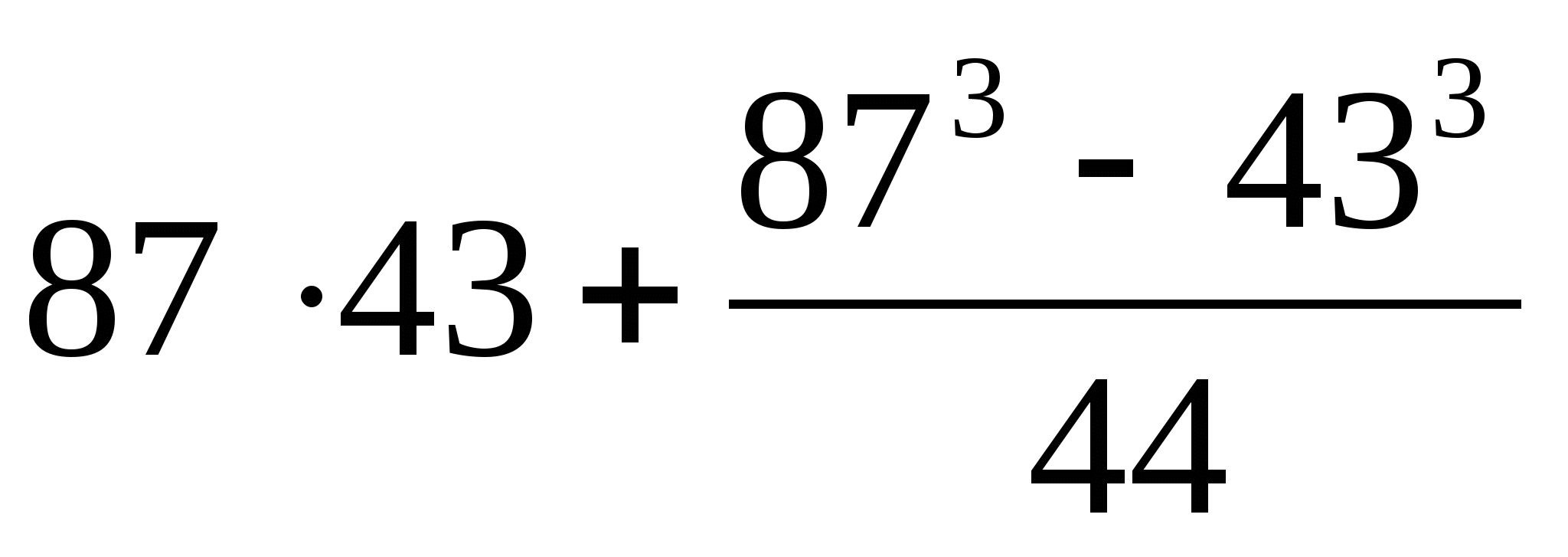
5. Докажите тождество: a³ + 3a²b + 3ab² + b³ = (a + b)³.

Вариант 2

1. Разложить на множители: а) 4х² + 8х; б) 3а - 6b + ab - 2b²;

в) 9х² - 16; г) х³ + 18х² + 81х.

2. Сократите дробь: а) 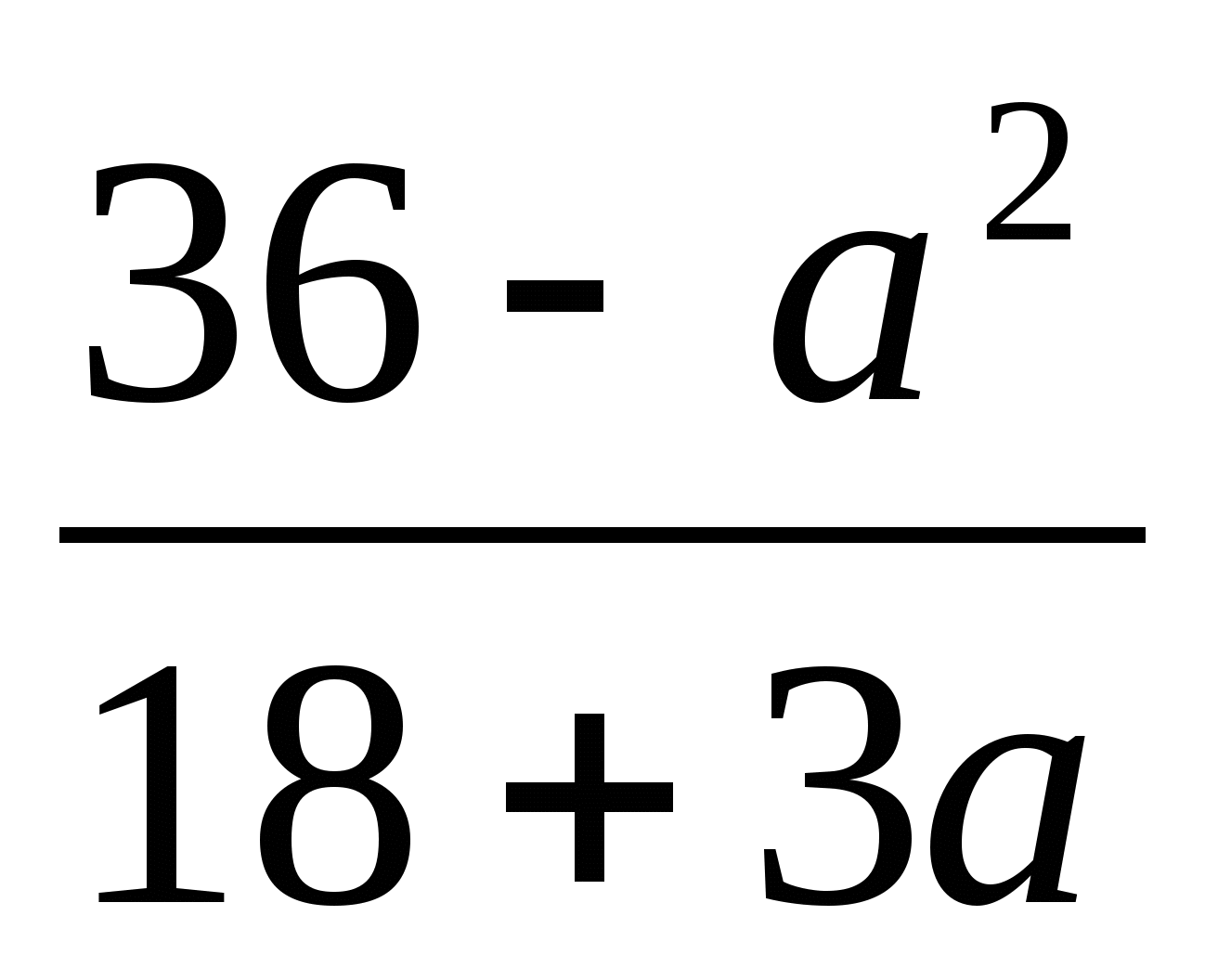; б) .

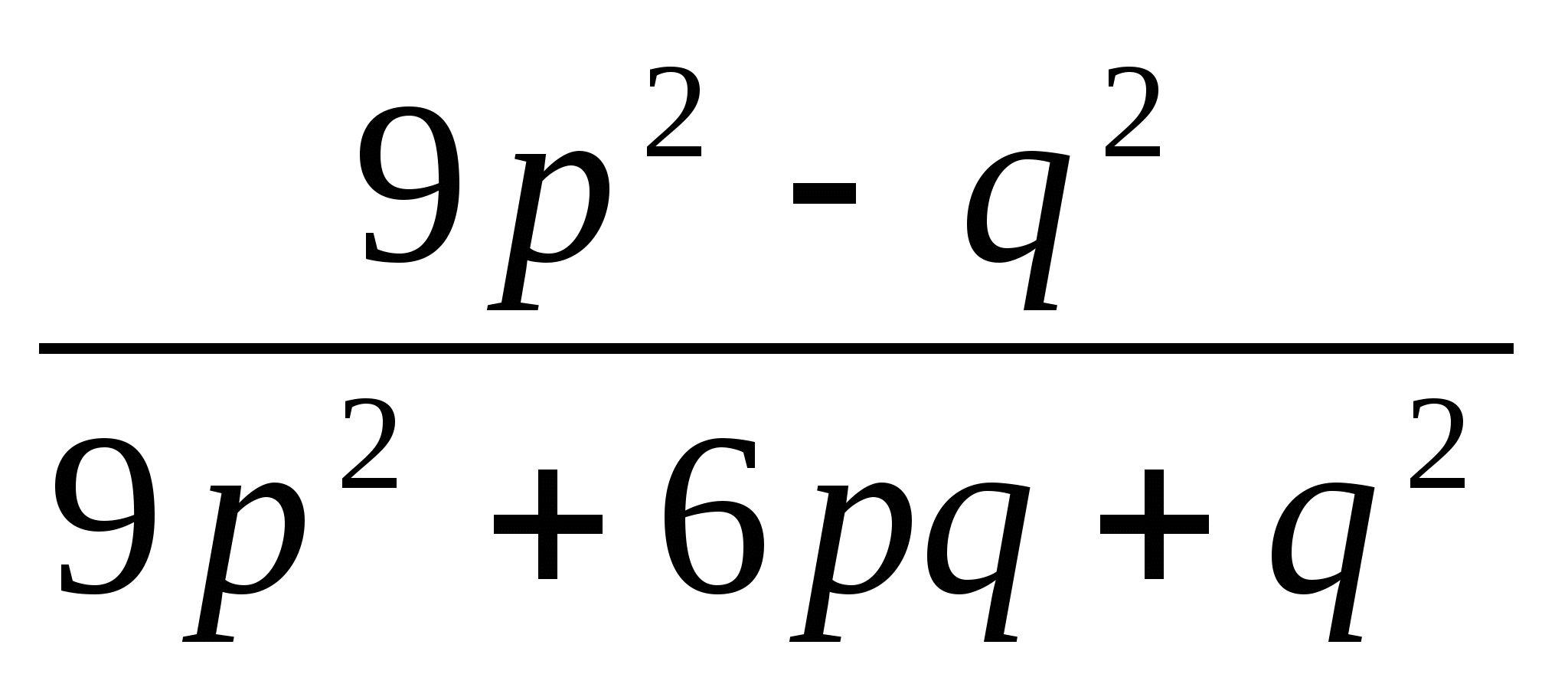3. Решите уравнение (х + 2)² - 49 = 0

4. Вычислите рациональным способом

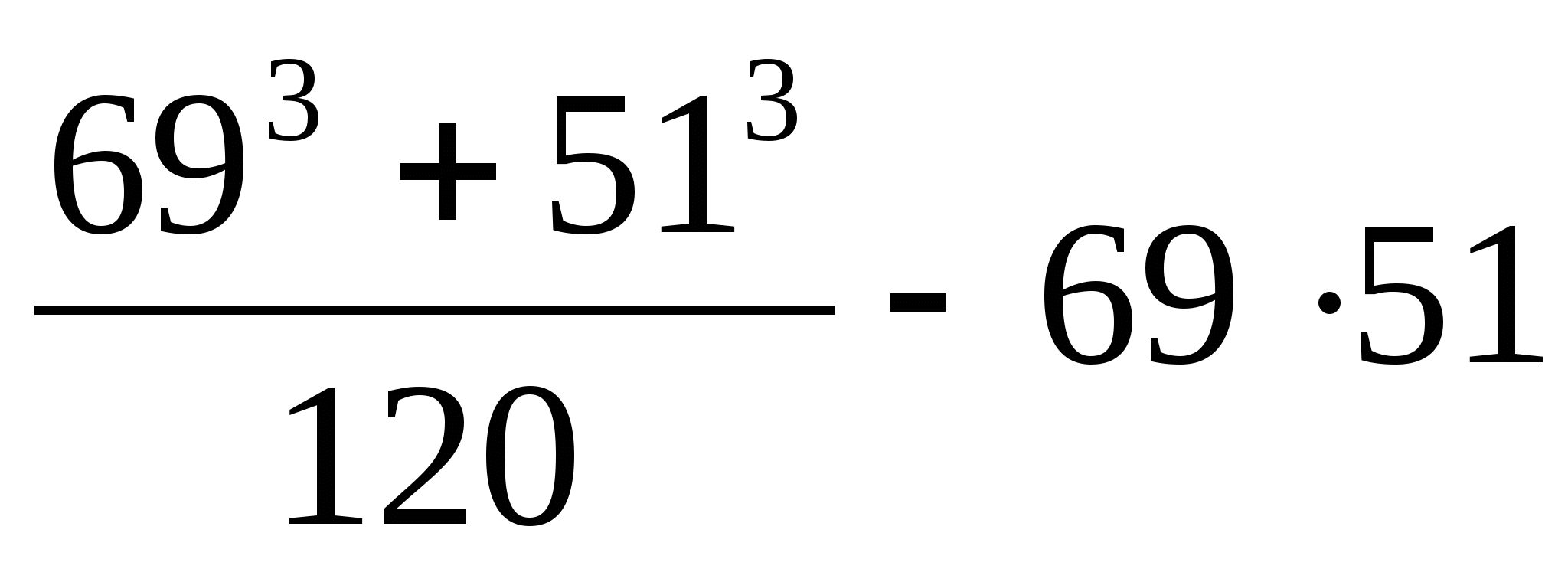
5. Докажите тождество: a³ - 3a²b + 3ab² - b³ = (a - b)³.

Контрольная работа № 8 «Функция y=x² и ее график»

Вариант 1

1. Постройте график функции у = х². С помощью графика найдите:

а) значение функции при значении аргумента, равном -2; 1; 3;

б) значение аргумента, если значение функции равно 4;

в) наибольшее и наименьшее значения функции на отрезке [-1;2].

2. Решите графически уравнение х² = 2х + 3.

3. Дана функция y = f(x), где f(x) = x². При каких значениях х верно равенство f(x-4) = f(x+3)?

4. Дана функция y = f(x), где .

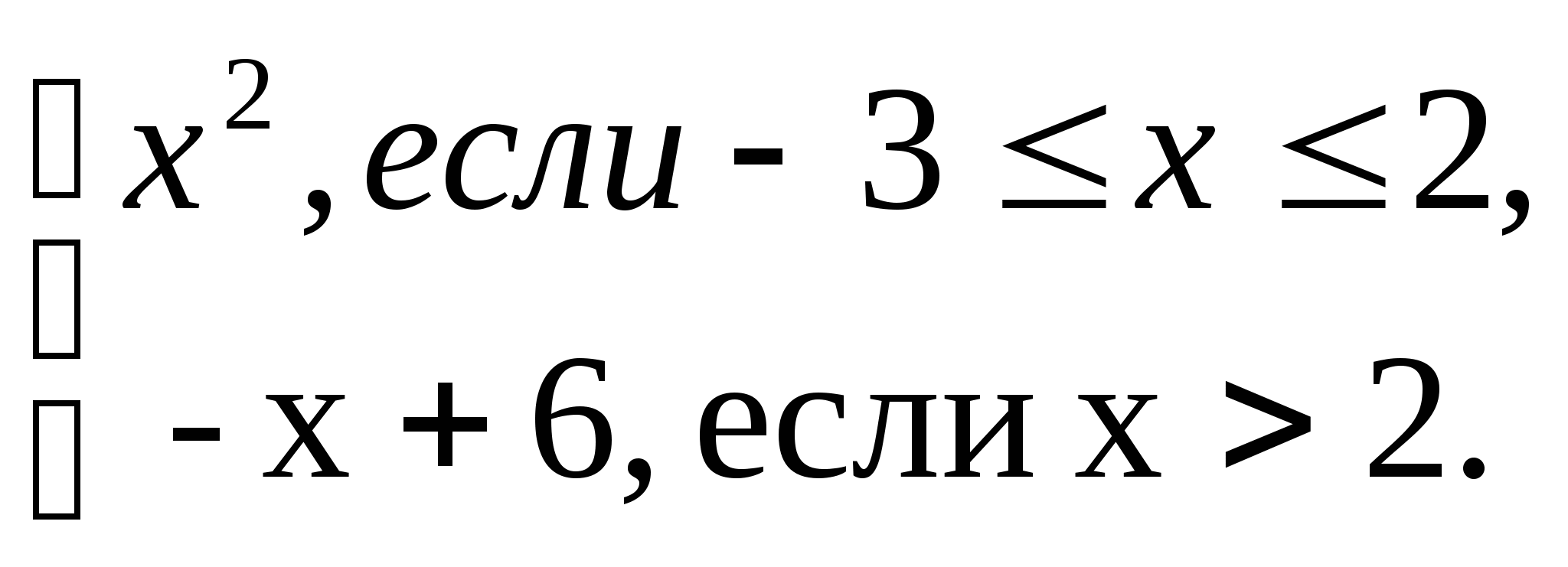Используя график функции, установите:

а) область определения функции;

б) наибольшее и наименьшее значения функции

в) является ли функция непрерывной: если нет, то в каких точках терпит разрыв;

г) промежутки возрастания и убывания функции;

д) при каких значениях аргумента у = 0, у < 0, y > 0.

5. Постройте график функции .

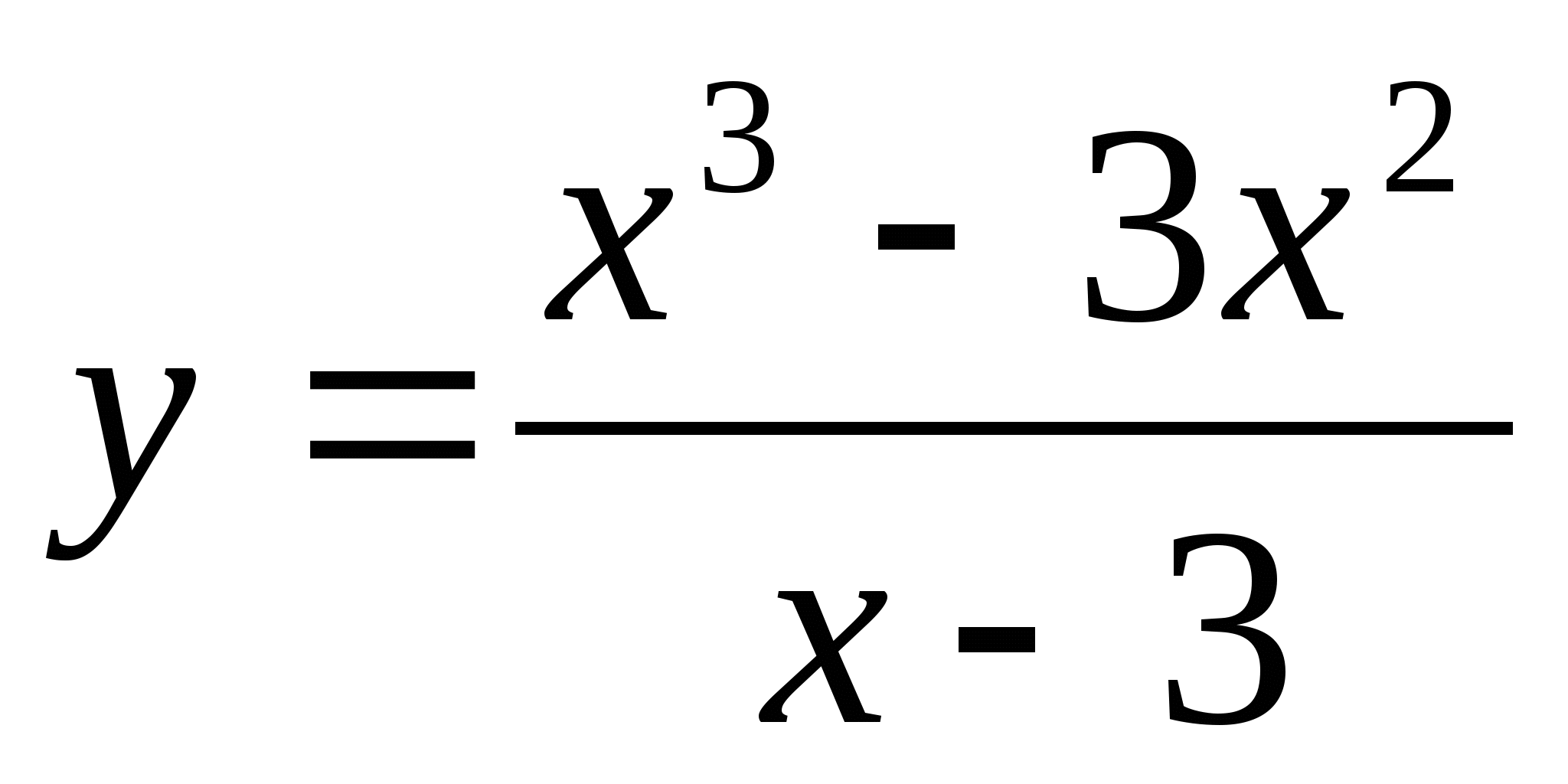Вариант 2

1. Постройте график функции у = х². С помощью графика найдите

а) значение функции при значении аргумента, равном -3; -1; 2;

б) значение аргумента, если значение функции равно 9;

в) наибольшее и наименьшее значения функции на отрезке [-3;2];

2. Решите графически уравнение х² = 4х - 3

3. Дана функция y = f(x), где f(x) = x². При каких значениях х верно равенство

f(x - 2) = f(x + 5)?

4. Дана функция y = f(x), где

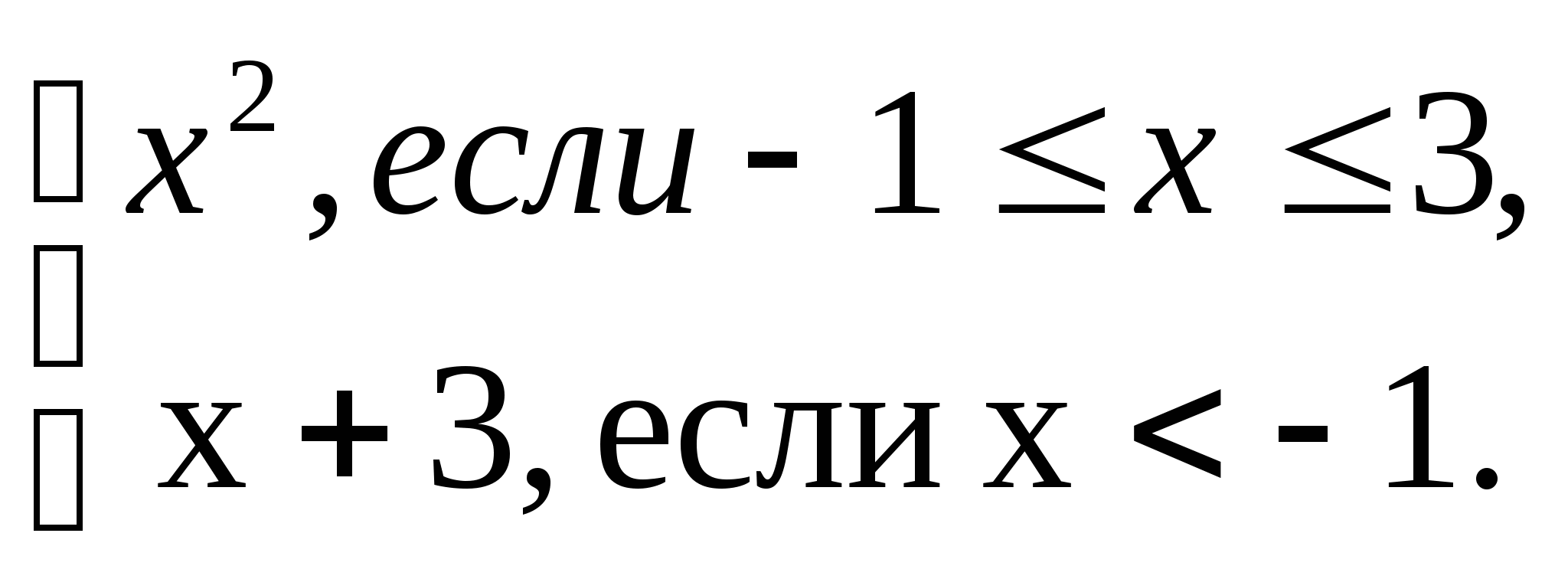
Используя график функции, установите:

а) область определения функции;

б) наибольшее и наименьшее значения функции

в) является ли функция непрерывной: если нет, то в каких точках терпит разрыв;

г) промежутки возрастания и убывания функции;

д) при каких значениях аргумента у = 0, у < 0, y > 0.

5.Постройте график функции .

Итоговая контрольная работа

Вариант 1

1. Постройте график функции y = - 3x + 6.

Используя график функции, установите:

a) наибольшее и наименьшее значения функции на отрезке [1;2];

б) значения аргумента, при которых у = 0, у < 0.

2. Решите уравнение (х - 3)(х + 2) - (х - 1)(х + 1) = 3х + 7.

3. Сократите дробь: а) 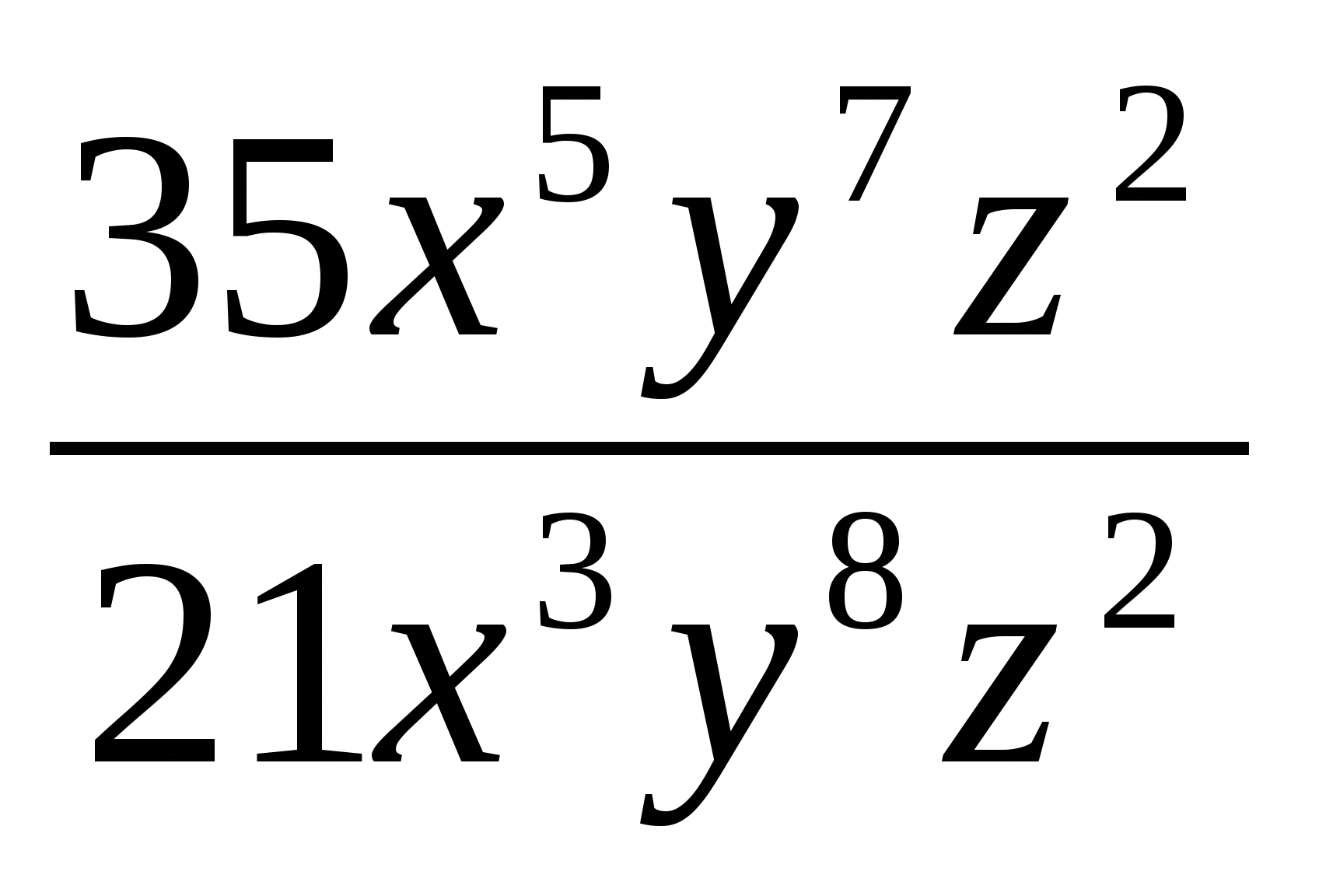; б) .

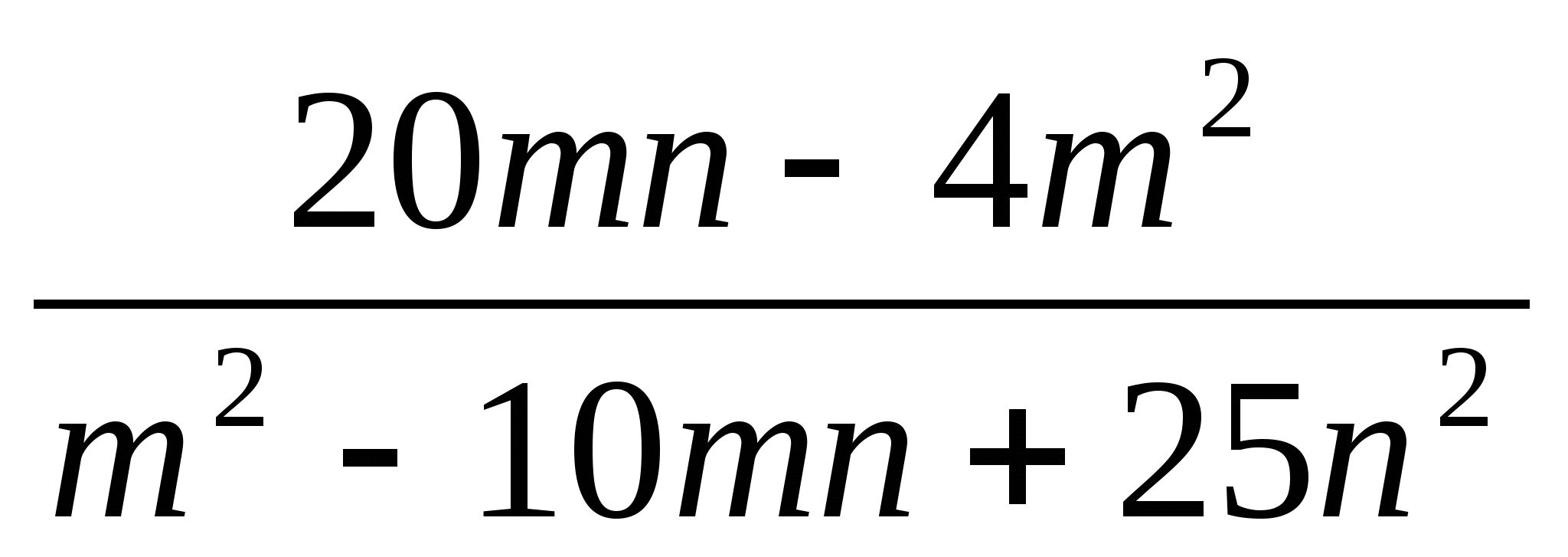4. Расстояние между двумя пристанями по реке равно 27км. Катер проплывает его по течению реки за 1,5 ч, а против течения за 2ч 15м. Найти собственную скорость катера и скорость течения реки.

5. Постройте график функции y = f(x), где

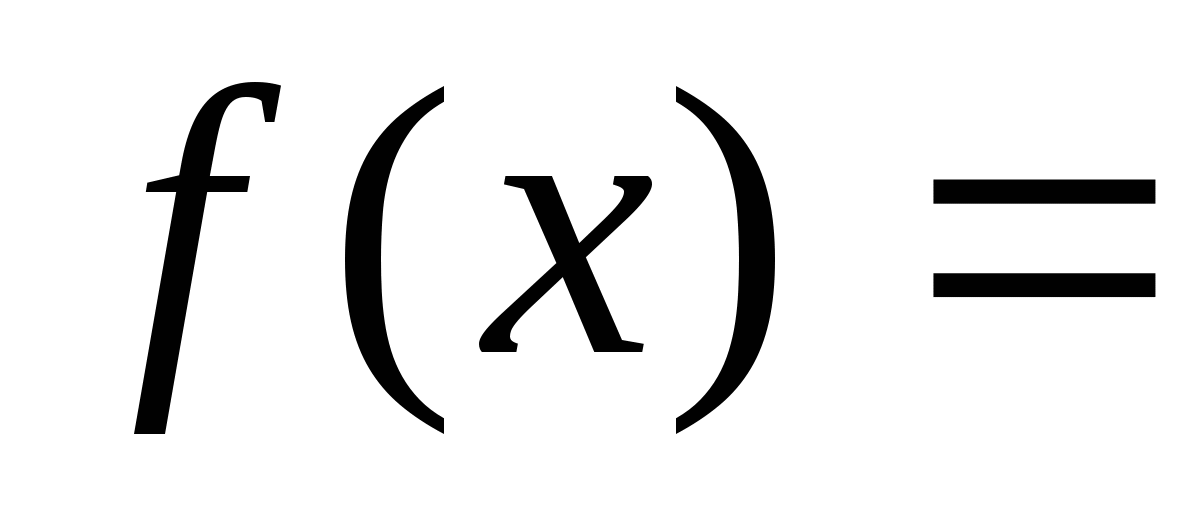
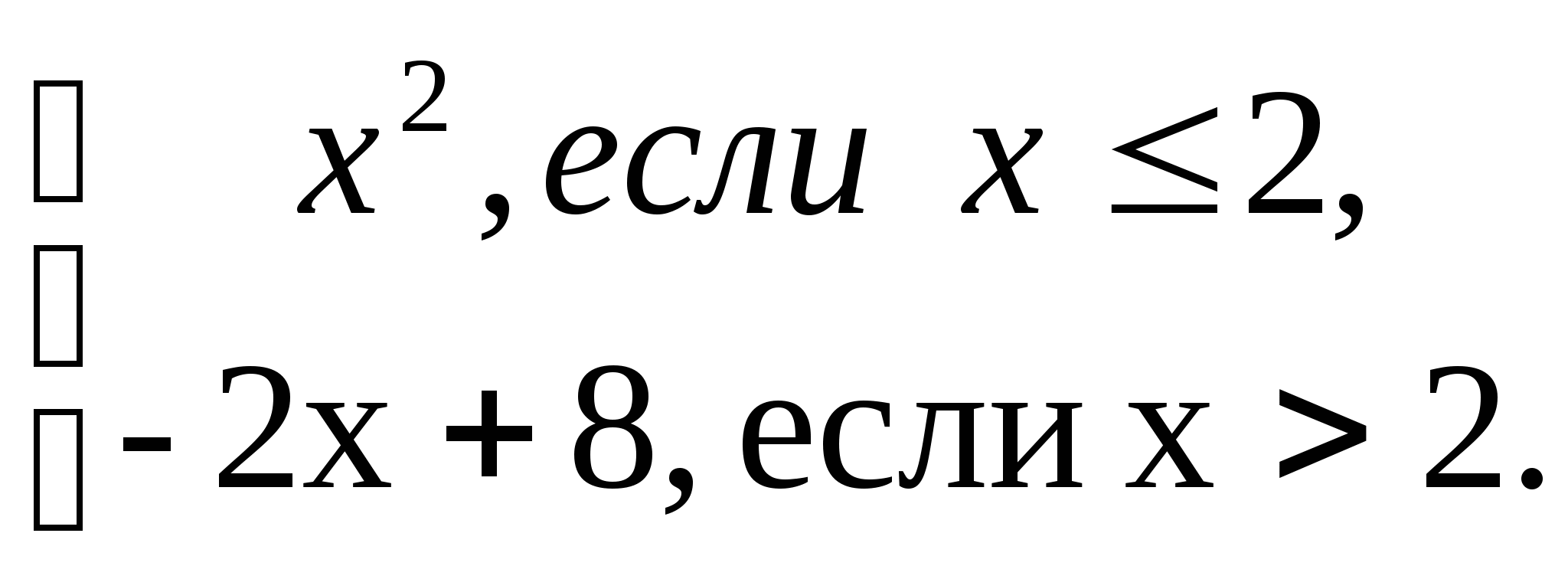
Вариант 2

1. Постройте график функции y = 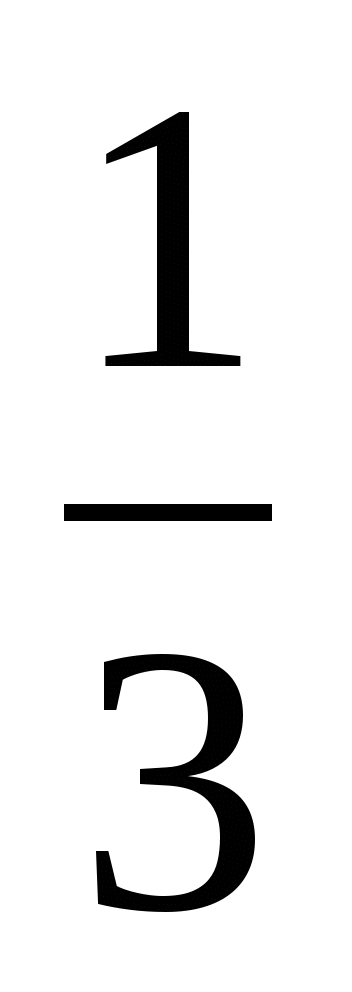x + 1.

Используя график функции, установите:

a) наибольшее и наименьшее значения функции на отрезке [0;3];

б) значения аргумента, при которых у = 0, у > 0.

2. Решите уравнение (х + 4)² - (х + 1)(х - 2) = 2х - 3.

3. Сократите дробь: а) 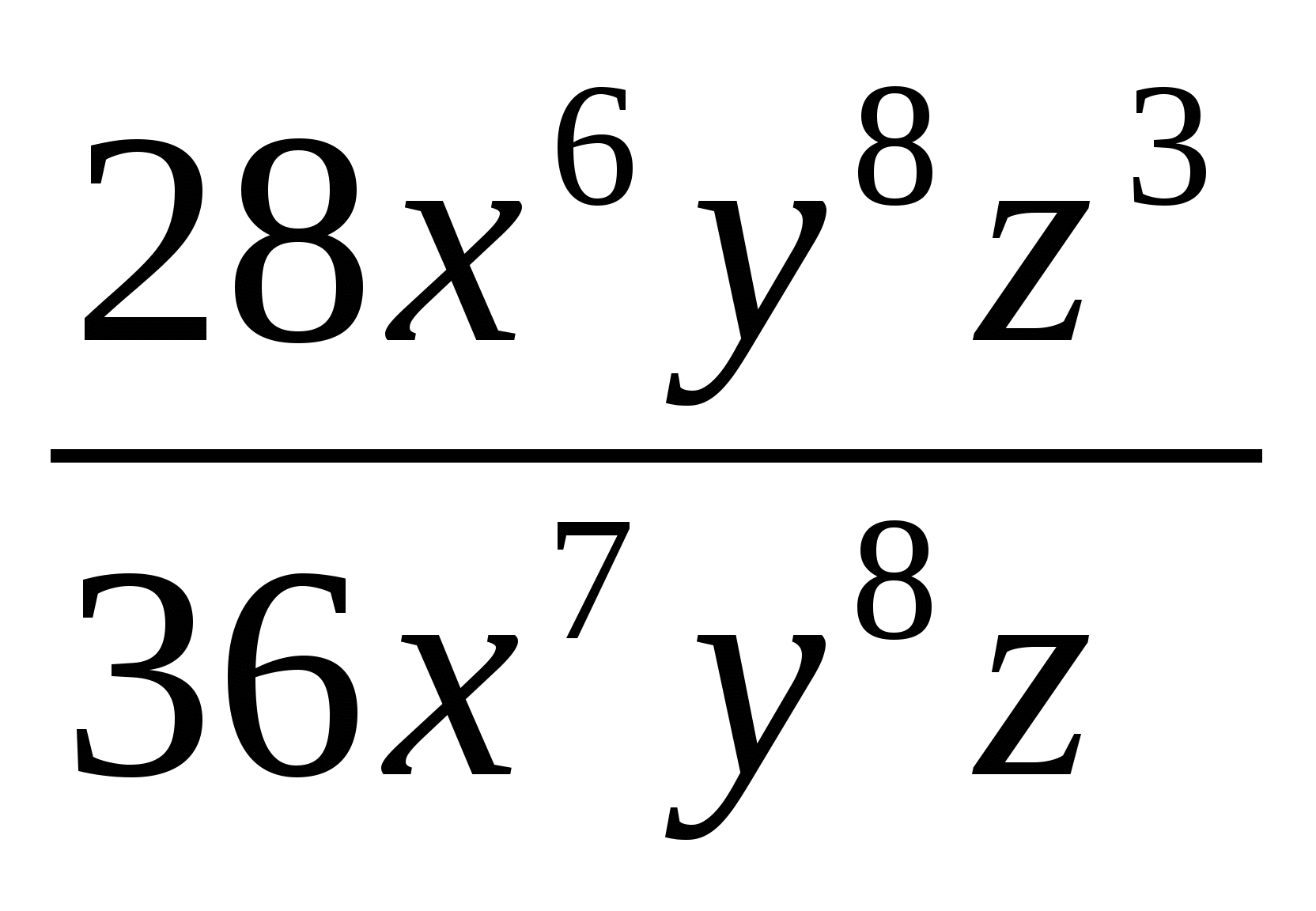; б) .

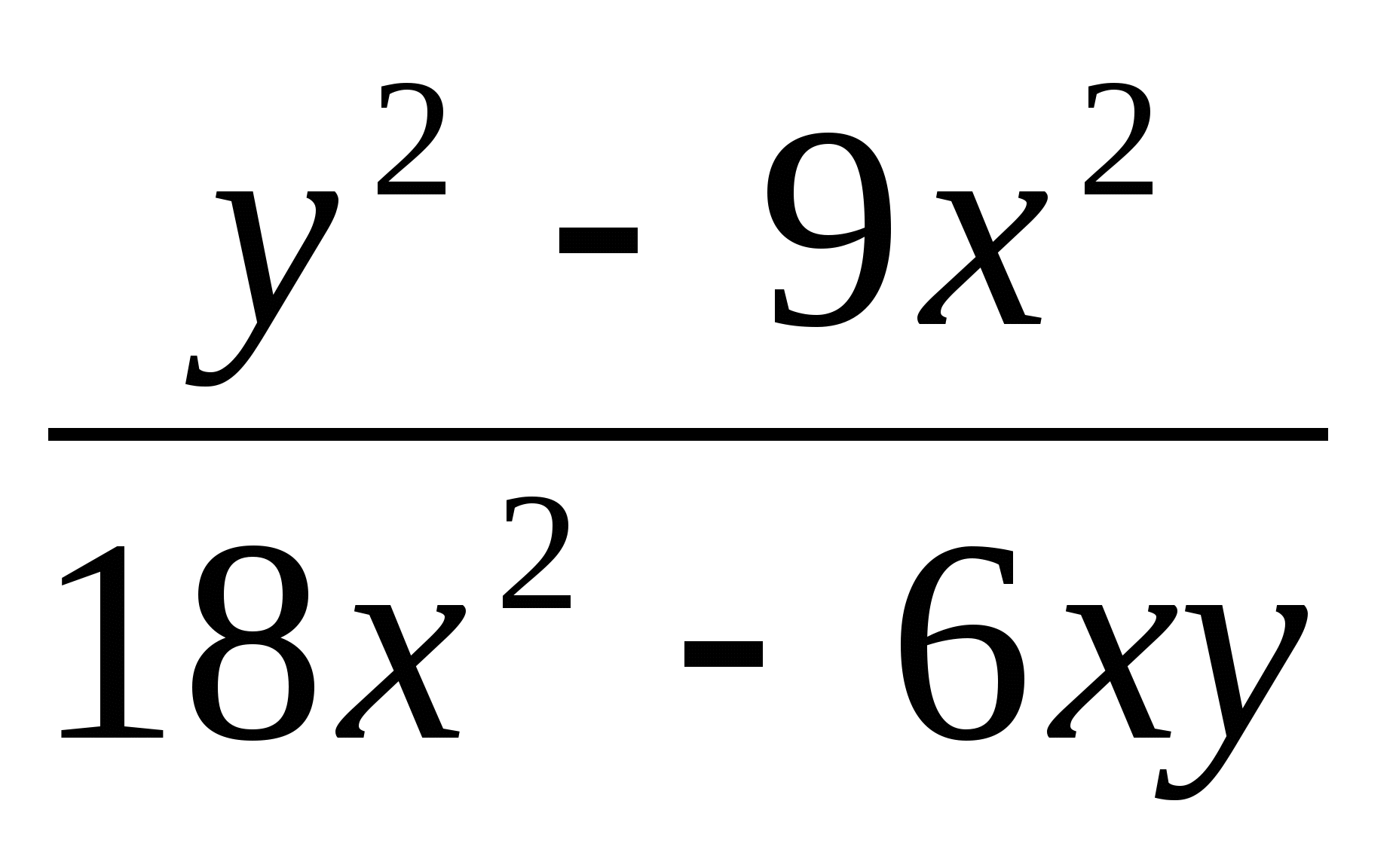4. Катер за 1ч 20м проплывает по течению реки 24км, а против течения за 1,5ч на 3км меньше. Найти собственную скорость катера и скорость течения реки.

5. Постройте график функции y = f(x), где