- Учителю
- Урок по математике на тему: 'Преобразование суммы тригонометрических выражений в произведение' (10 класс)
Урок по математике на тему: 'Преобразование суммы тригонометрических выражений в произведение' (10 класс)
Урок 139
Тема урока: «Преобразование суммы тригонометрических
выражений в произведение».
Цели урока:
Обучающая: Ввести формулы:
- суммы косинусов
cos![]() + cos
+ cos![]() = 2 cos
= 2 cos![]() ×cos
×cos![]() ;
;
-разности синусов
cos ![]() - cos
- cos![]() = -2 Sin
= -2 Sin![]() × Sin
× Sin ![]() .
.
Научить применять формулы суммы и разности
косинусов при выполнении упражнений.
Развивающая:
- активизировать мыслительную деятельность
учащихся;
- развивать навыки самостоятельной и поисковой
деятельности, аналитика - синтетического
мышления, познавательный интерес учащихся;
- способствовать развитию логического
мышления.
Воспитывающая:
- формировать навыки культуры поведения, речевого
и профессионального этикета.
Тип урока: комбинированный урок
Вид урока: Урок выполнения упражнений на преобразование
суммы и разности косинусов в произведение.
Методы обучения: Объяснительно-иллюстративный,
репродуктивный, самоконтроль.
Материально-техническое оснащение:
- Стенд «Таблица значений тригонометрических функций»
- Стенд «Основные формулы тригонометрии»
-Математика Учебник Общеобразовательные дисциплины
Начальное и среднее профессиональное образование
Автор М.И. Башмаков.
Москва Издательский центр «Академия» 201
-Математика Учебник Общеобразовательные дисциплины
для профессий и специальностей социально-экономического
профиля. Авторы В.А. Гусев, С.Г.Григорьев, С.В.Иволгина
Москва Издательский центр «Академия» 2011
- Математика Задачник Общеобразовательные дисциплины
Начальное и среднее профессиональное образование
Автор М.И. Башмаков.
Москва Издательский центр «Академия» 2012
- дидактический раздаточный материал (карточки для
индивидуальной работы)
Ход урока
1. Организационный момент урока
- сдача рапорта
2. Целевая ориентация
( Преподаватель формулирует тему, цели и задачи урока. Мотивирует учащихся к учебной деятельности. Разъясняет последовательность этапов урока, приводящих к достижению цели)
3. Проверка домашнего задания
4. Актуализация опорных знаний
Устно:
Назовите формулы:
а) суммы синусов
Ответ: Sin![]() + Sin
+ Sin![]() = 2 Sin
= 2 Sin![]() ×cos
×cos![]() ;
;
б) разности синусов
Ответ: Sin![]() - Sin
- Sin![]() = 2 Sin
= 2 Sin![]() ×cos
×cos![]() .
.
Формирование новых понятий и способов действий
1. Вывод формул:
- суммы косинусов
cos![]() + cos
+ cos![]() = 2 cos
= 2 cos![]() ×cos
×cos![]() ;
;
-разности синусов
cos ![]() - cos
- cos![]() = -2 Sin
= -2 Sin![]() × Sin
× Sin ![]() .
.
2. Примеры для объяснения нового материала (преподаватель)
Пример 1.
Вычислить:
cos 1050 + cos750 = 2 cos ![]() ×cos
×cos![]() = 2 cos900 × cos150 = 2 ×0 cos15=0.
= 2 cos900 × cos150 = 2 ×0 cos15=0.
Пример 2.
Вычислить:
cos![]() - cos
- cos![]() = - 2 Sin
= - 2 Sin Sin
Sin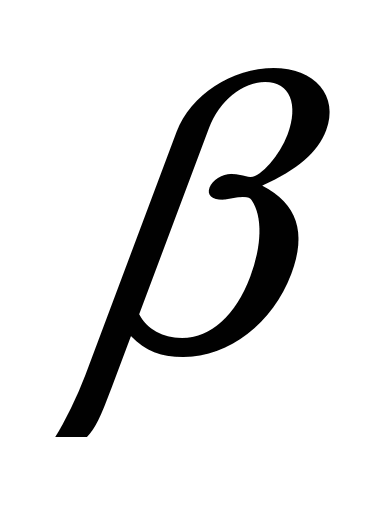 = - 2 Sin
= - 2 Sin ![]() Sin
Sin![]() =
=
= - 2 Sin![]() Sin
Sin ![]() = - 2
= - 2![]()
![]() = -
= -![]() .
.
3. Выполнение упражнений у доски (обучающиеся)
Пример 1.
Вычислить:
cos (![]() -
- ![]() ) - cos (
) - cos (![]() +
+ ![]() ) = -2 Sin
) = -2 Sin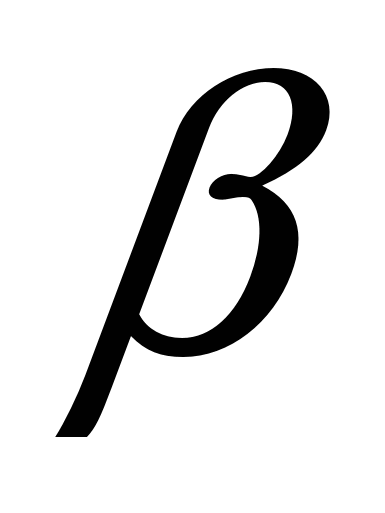 × Sin
× Sin 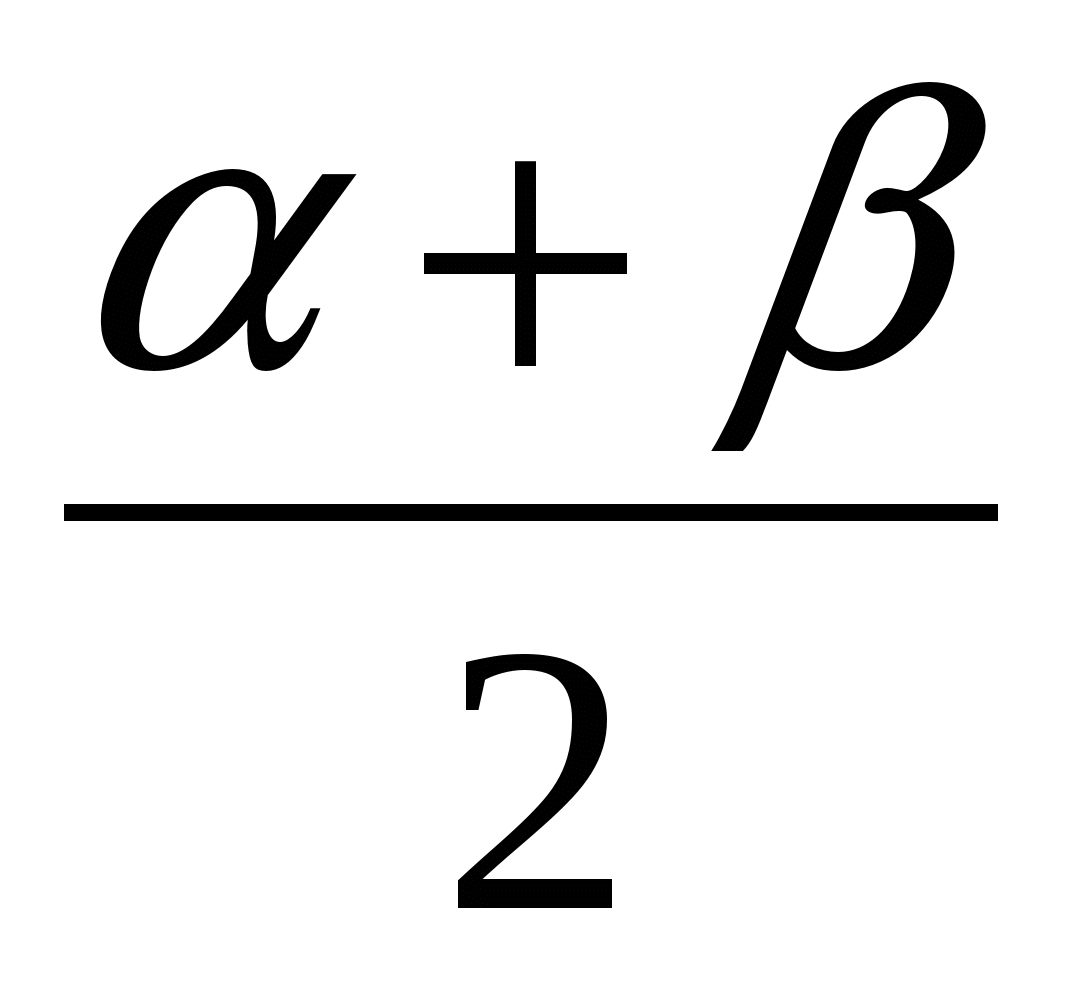 =
=
= 2 Sin ![]() × Sin (-
× Sin (-![]() ) = -2×
) = -2×![]() × Sin
× Sin ![]() =
=![]() Sin
Sin ![]() .
.
Пример 2.
Преобразовать в произведение:
2 cos a + ![]() = 2(cos a +
= 2(cos a + ![]() ) = 2(cos a + cos
) = 2(cos a + cos![]() ) =
) =
= 2×2 cos ![]() × cos
× cos ![]() = 4× cos (
= 4× cos (![]() ) × cos(
) × cos(![]() ).
).
Пример 3.
Упростить выражение:
cos2 (a -![]() ) - cos2 (a +
) - cos2 (a +![]() ) =( cos (a -
) =( cos (a -![]() ) - cos (a +
) - cos (a +![]() ))( cos (a -
))( cos (a -![]() ) +cos (a +
) +cos (a +![]() )) =
)) =
= - 2Sin 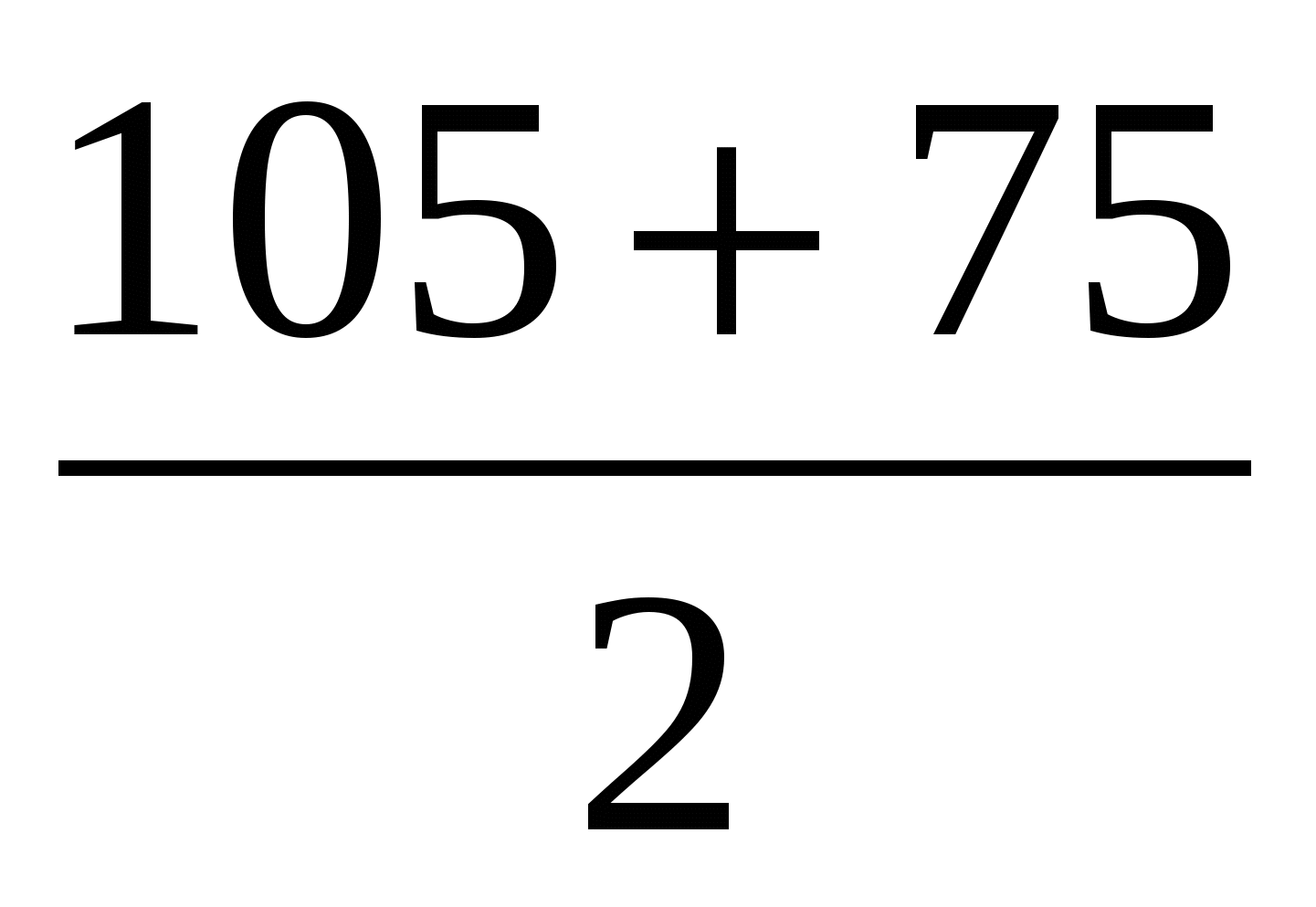 × Sin
× Sin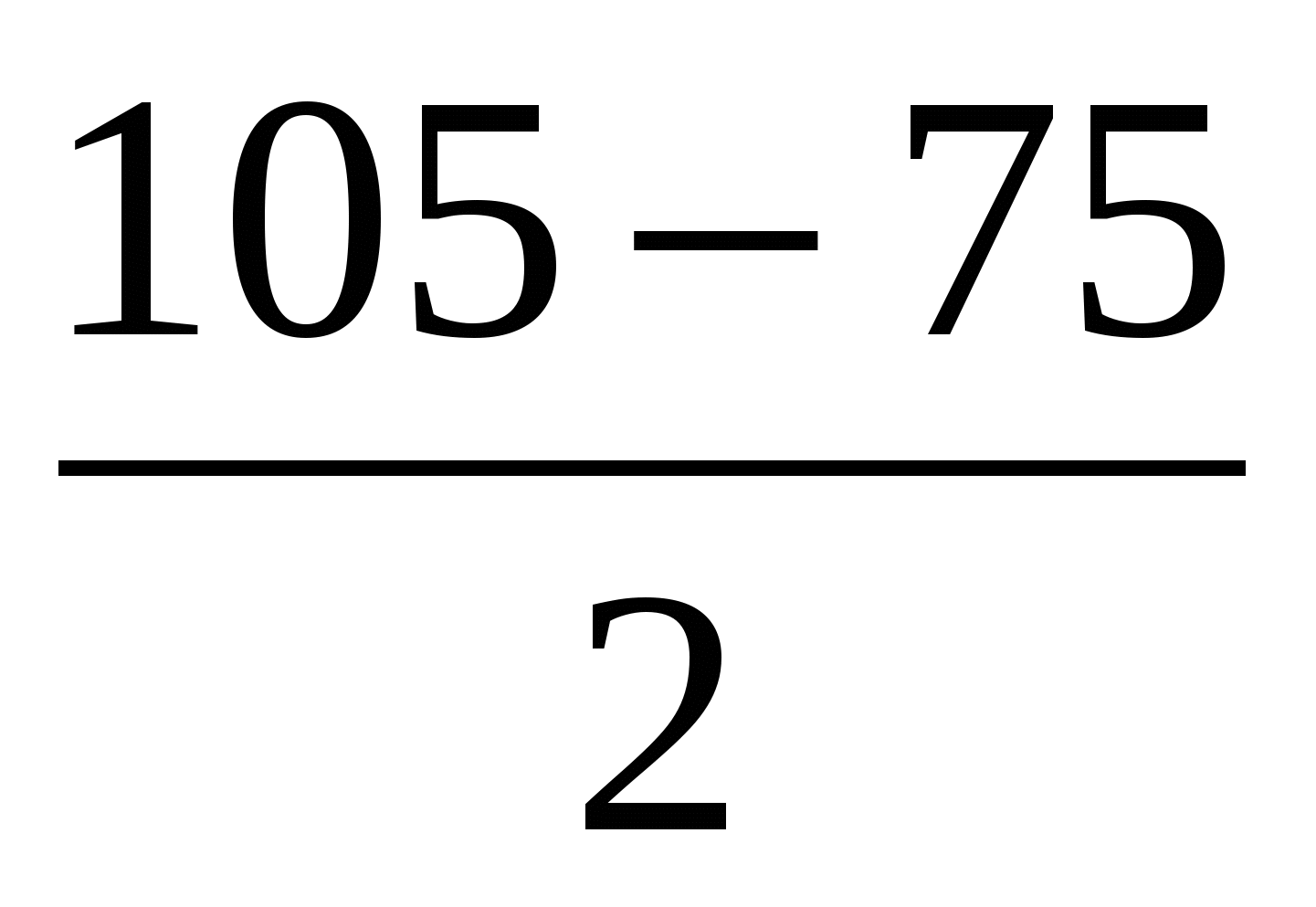 2 cos
2 cos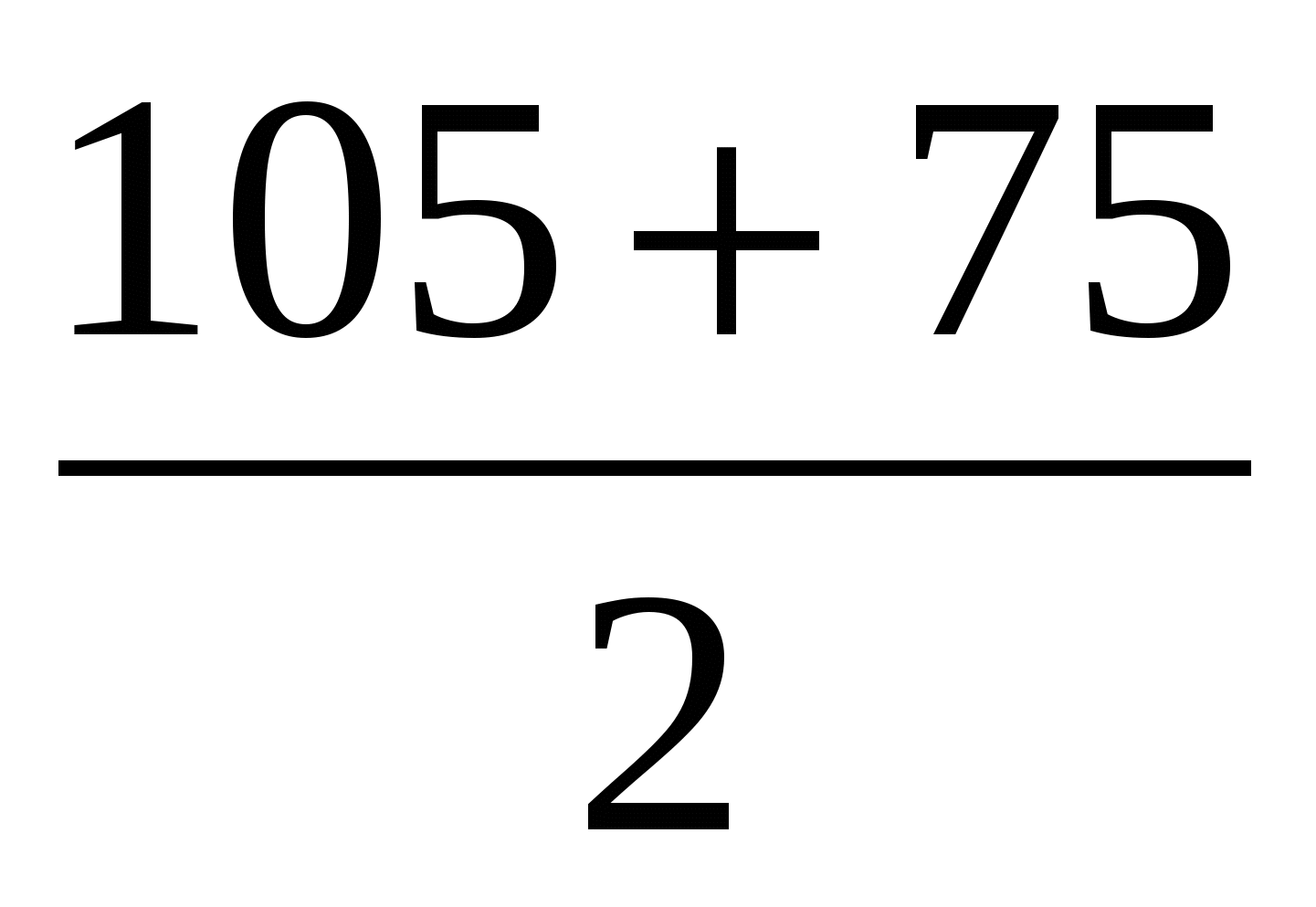 cos
cos 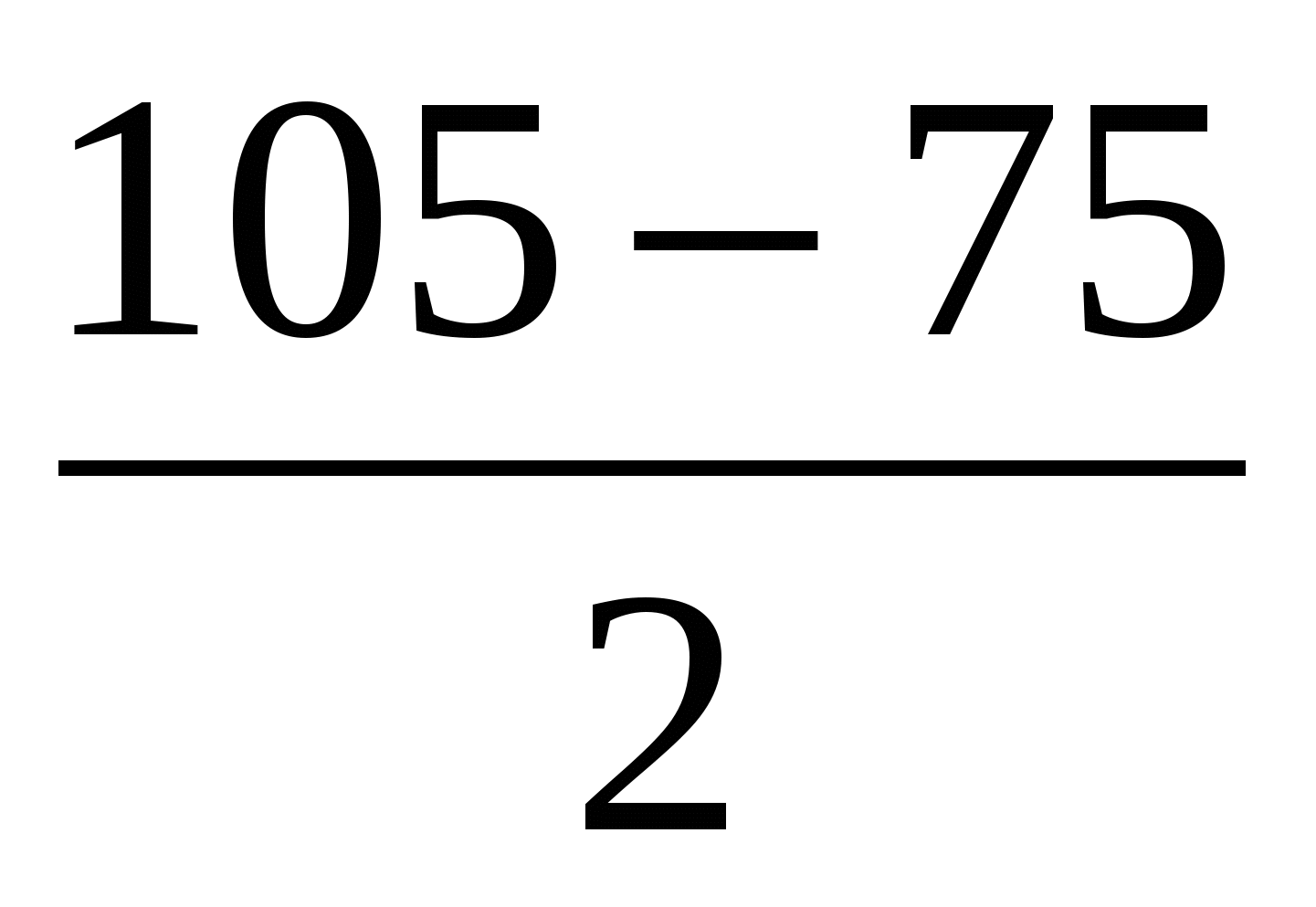 =
=
= -2 Sina Sin (-![]() ) 2 cosa cos(-
) 2 cosa cos(-![]() )= 4 Sina
)= 4 Sina![]() cosa
cosa![]() =2 Sina cosa= Sin2a.
=2 Sina cosa= Sin2a.
6. Формирование навыков умственного труда
Самостоятельная работа
Вариант №1
Вариант №2
1). Вычислить:
cos 1050 - cos 750;
1).Вычислить:
cos 750 - cos 150;
2). Вычислить:
cos![]() - cos
- cos ![]() ;
;
2). Вычислить:
cos ![]() - cos
- cos ![]() ;
;
3). Упростить выражение:
cos (![]() +
+![]() ) + cos (
) + cos (![]() -
- ![]() );
);
3). Упростить выражение:
cos (![]() +
+![]() ) + cos (
) + cos (![]() -
- ![]() );
);
4). Преобразовать в произведение:
2 cos a + 1;
4). Преобразовать в произведение:
2 cos a + ![]() ;
;
5). Упростить выражение:
cos2 (a -![]() ) - cos2 (a +
) - cos2 (a +![]() );
);
5). Упростить выражение:
cos2 (a -![]() ) - cos2 (a +
) - cos2 (a +![]() );
);
Критерии оценки:
Оценка «5» - правильные полные решения 5-ти заданий.
Оценка «4» - правильные полные решения 4-х заданий.
Оценка «3» - правильные полные решения 3-х заданий.
Решение
Вариант 1
1). Вычислить:
cos 1050 - cos 750;
Решение
cos 1050 - cos 750 = -2 Sin![]() Sin
Sin![]() =
=
= - 2 Sin 900 Sin 150= - 2 Sin 150.
2). Вычислить:
cos![]() - cos
- cos ![]() ;
;
Решение
cos![]() - cos
- cos ![]() = - 2× Sin
= - 2× Sin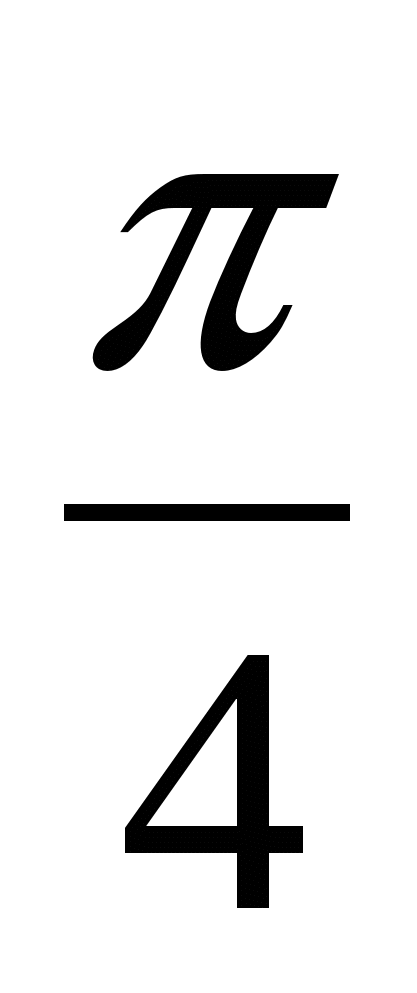 × Sin
× Sin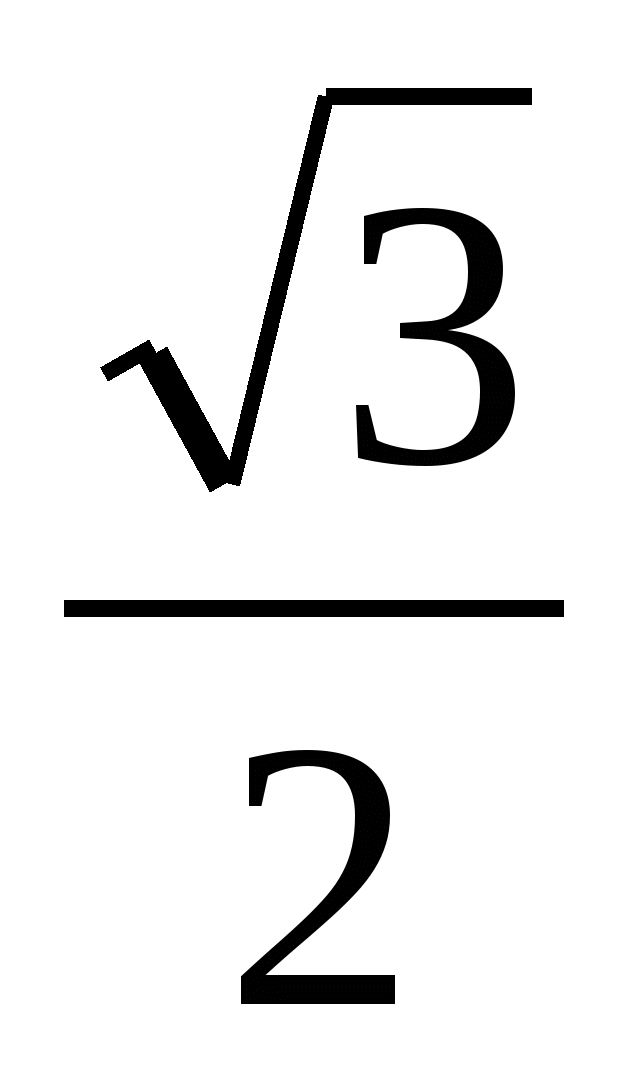 = - 2× Sin
= - 2× Sin ![]() × Sin
× Sin![]() =
=
= - 2× Sin![]() × Sin
× Sin ![]() = - 2×
= - 2×![]() ×
×![]() = -
= -![]() .
.
3). Упростить выражение:
cos (![]() +
+![]() ) + cos (
) + cos (![]() -
- ![]() );
);
Решение
cos (![]() -
- ![]() ) + cos (
) + cos (![]() +
+ ![]() ) = 2 cos
) = 2 cos 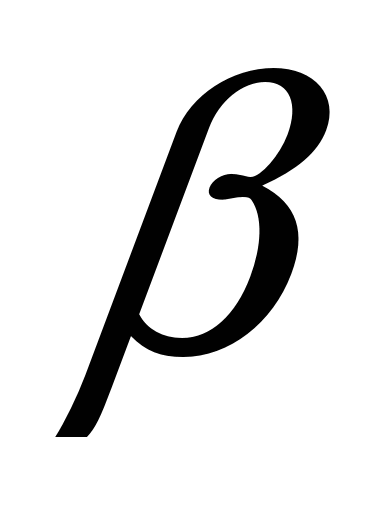 × cos
× cos 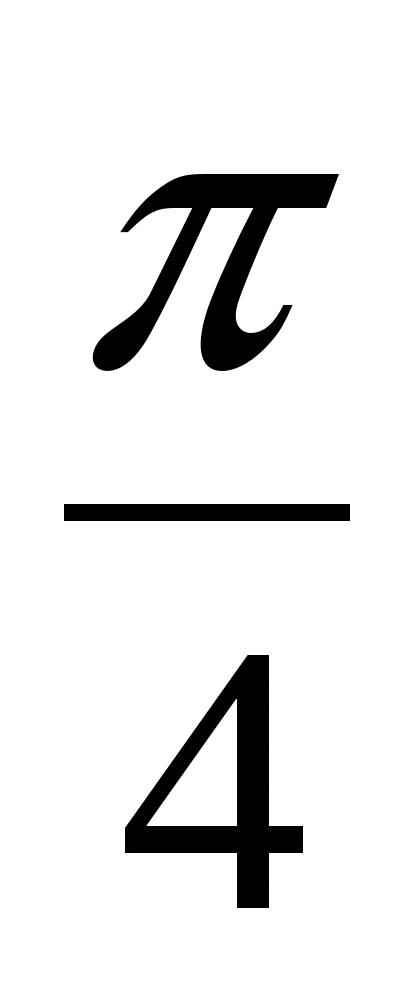 =
=
= 2 cos ![]() × cos (-
× cos (-![]() ) = 2×(-
) = 2×(-![]() )× cos
)× cos ![]() = - cos
= - cos ![]() .
.
4). Преобразовать в произведение:
2 cos a + 1;
Решение
Преобразовать в произведение:
2 cos a + 1 = 2(cos a + ![]() ) = 2(cos a + cos
) = 2(cos a + cos![]() ) =
) =
= 2×2 cos ![]() × cos
× cos ![]() = 4× cos (
= 4× cos (![]() ) × cos(
) × cos(![]() ).
).
5). Упростить выражение:
cos2 (a -![]() ) - cos2 (a +
) - cos2 (a +![]() );
);
Решение
cos2 (a -![]() ) - cos2 (a +
) - cos2 (a +![]() ) =( cos (a -
) =( cos (a -![]() ) - cos (a +
) - cos (a +![]() ))×( cos (a -
))×( cos (a -![]() ) +cos (a +
) +cos (a +![]() )) =
)) =
= - 2Sin 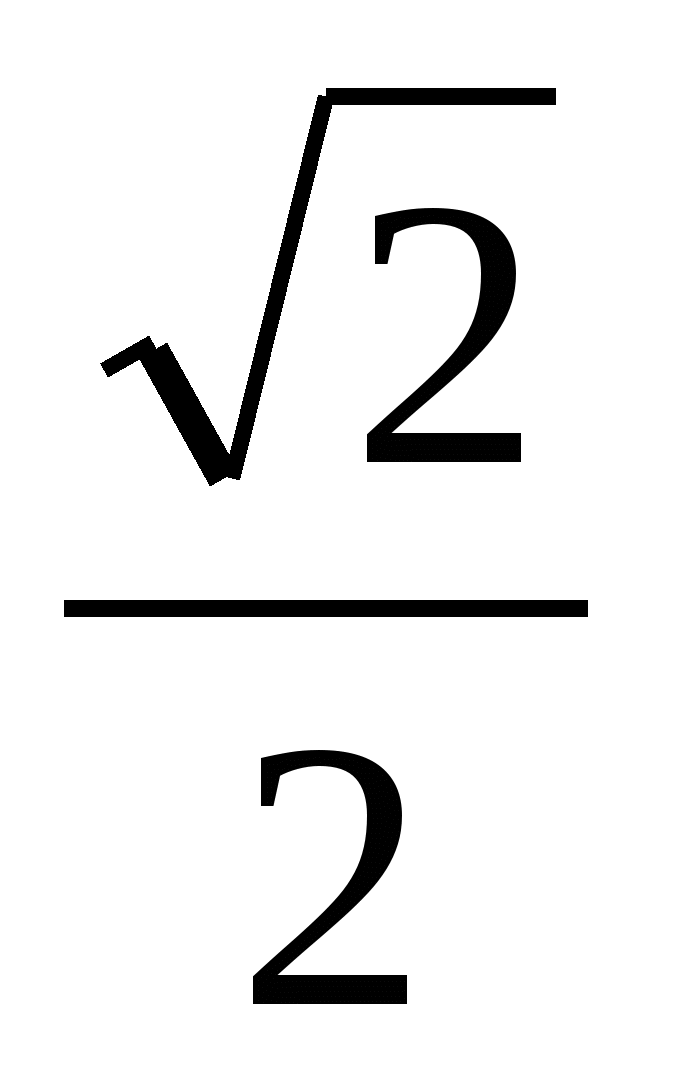 × Sin
× Sin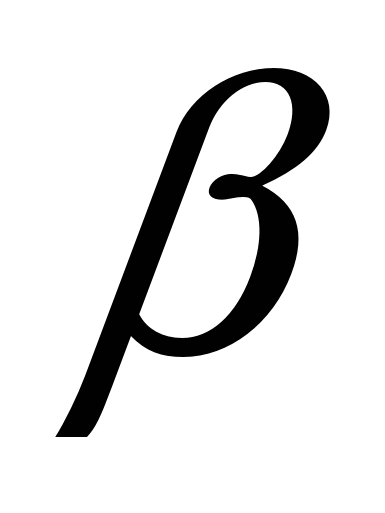 ×2 cos
×2 cos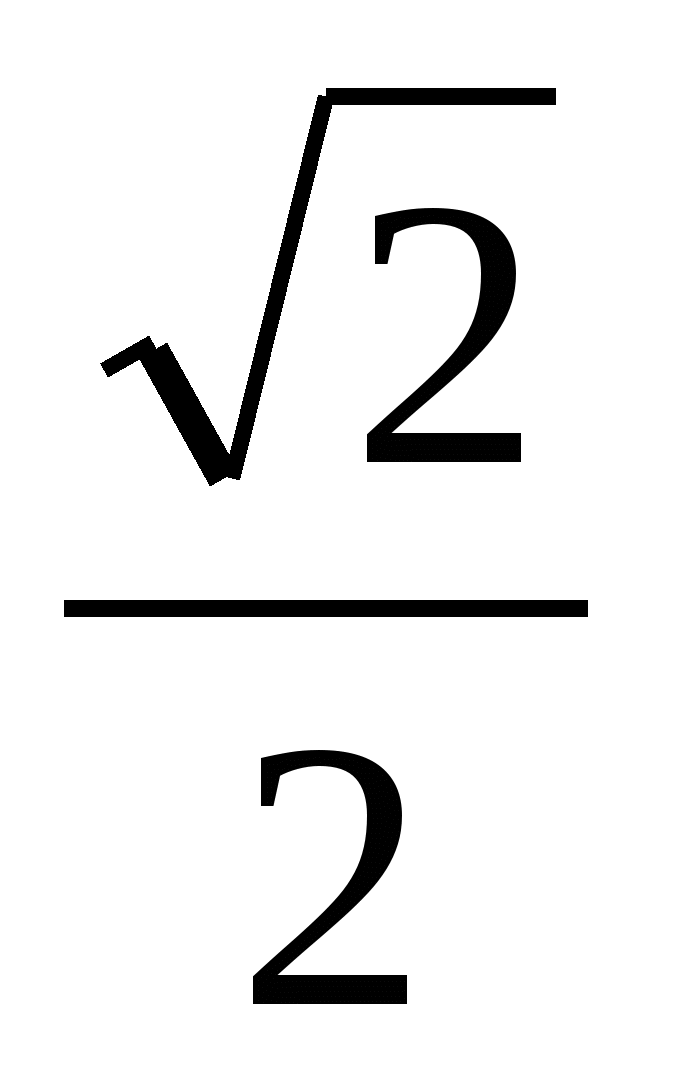 × cos
× cos 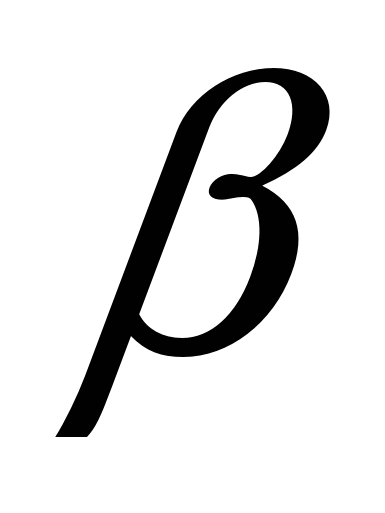 =
=
= -2 Sina× Sin (-![]() ) ×2 cosa × cos(-
) ×2 cosa × cos(-![]() )= 4 Sina×
)= 4 Sina×![]() × cosa×
× cosa×![]() =
=![]() Sina cosa.
Sina cosa.
Решение
Вариант 2
1).Вычислить:
cos 750 - cos 150;
Решение
cos 750 - cos 150 = -2 Sin![]() Sin
Sin![]() =
=
= - 2 Sin 450 Sin 300= - 2 ×![]() ×
×![]() = -
= - ![]() .
.
2). Вычислить:
cos ![]() - cos
- cos ![]() ;
;
Решение
cos ![]() - cos
- cos ![]() = - 2× Sin
= - 2× Sin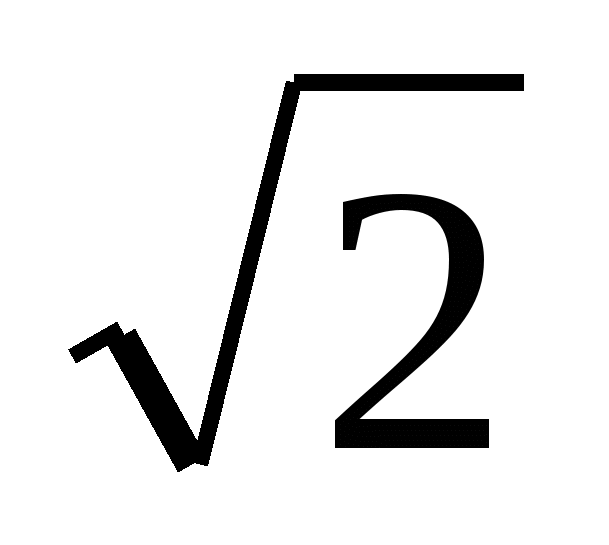 × Sin
× Sin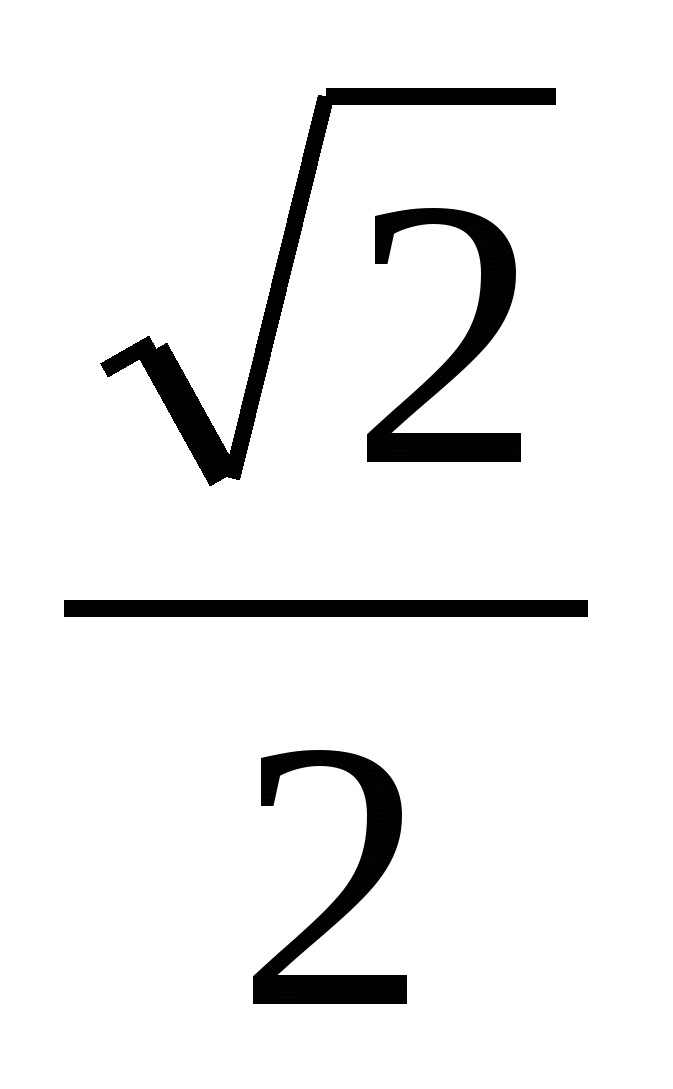 = - 2× Sin
= - 2× Sin ![]() × Sin
× Sin![]() =
=
= - 2× Sin![]() × Sin
× Sin![]() = - 2×
= - 2×![]() ×
×![]() = -
= -![]() .
.
3). Упростить выражение:
cos (![]() +
+![]() ) + cos (
) + cos (![]() -
- ![]() );
);
Решение
cos (![]() +
+![]() ) + cos (
) + cos (![]() -
- ![]() ) = 2 cos
) = 2 cos 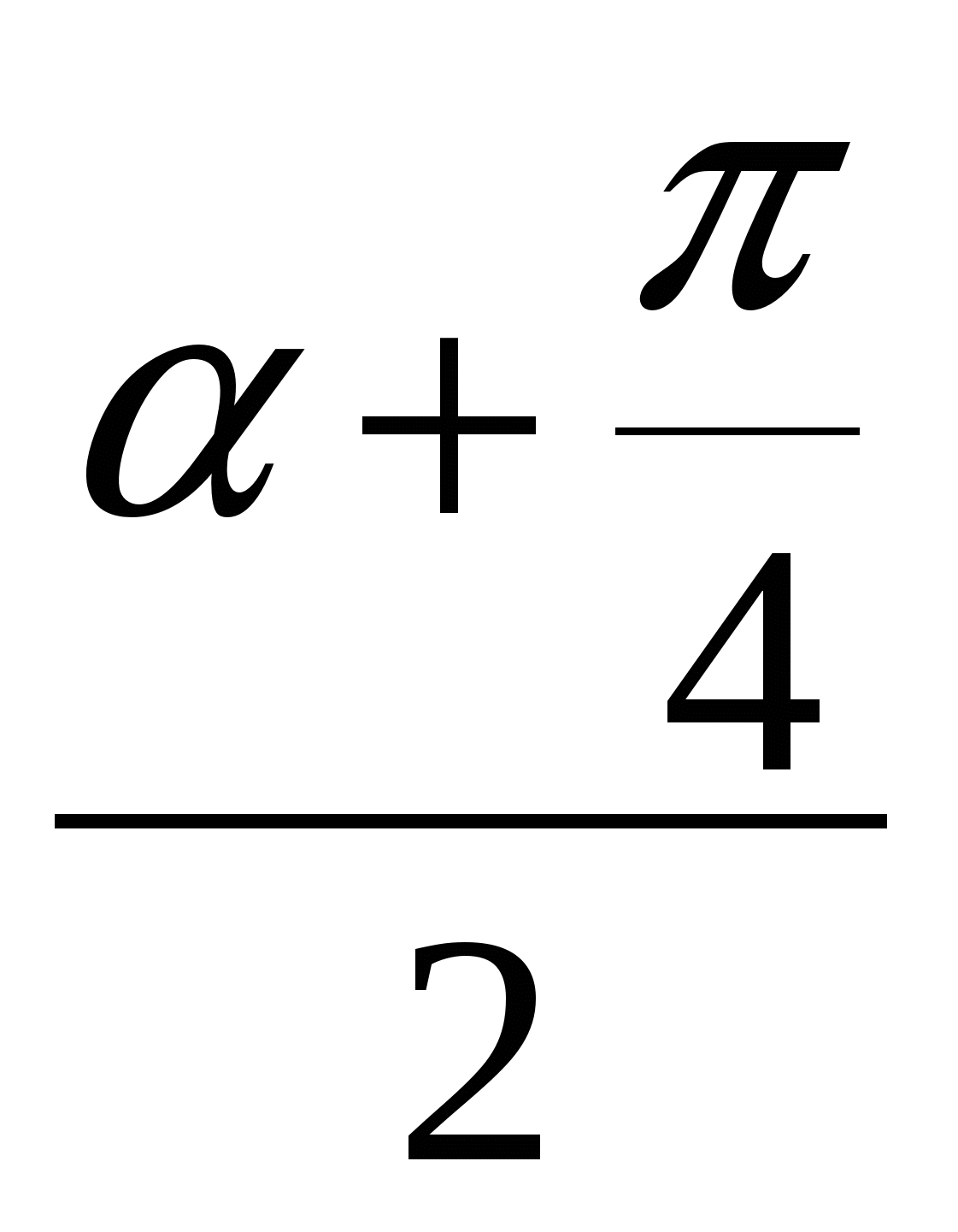 × cos
× cos 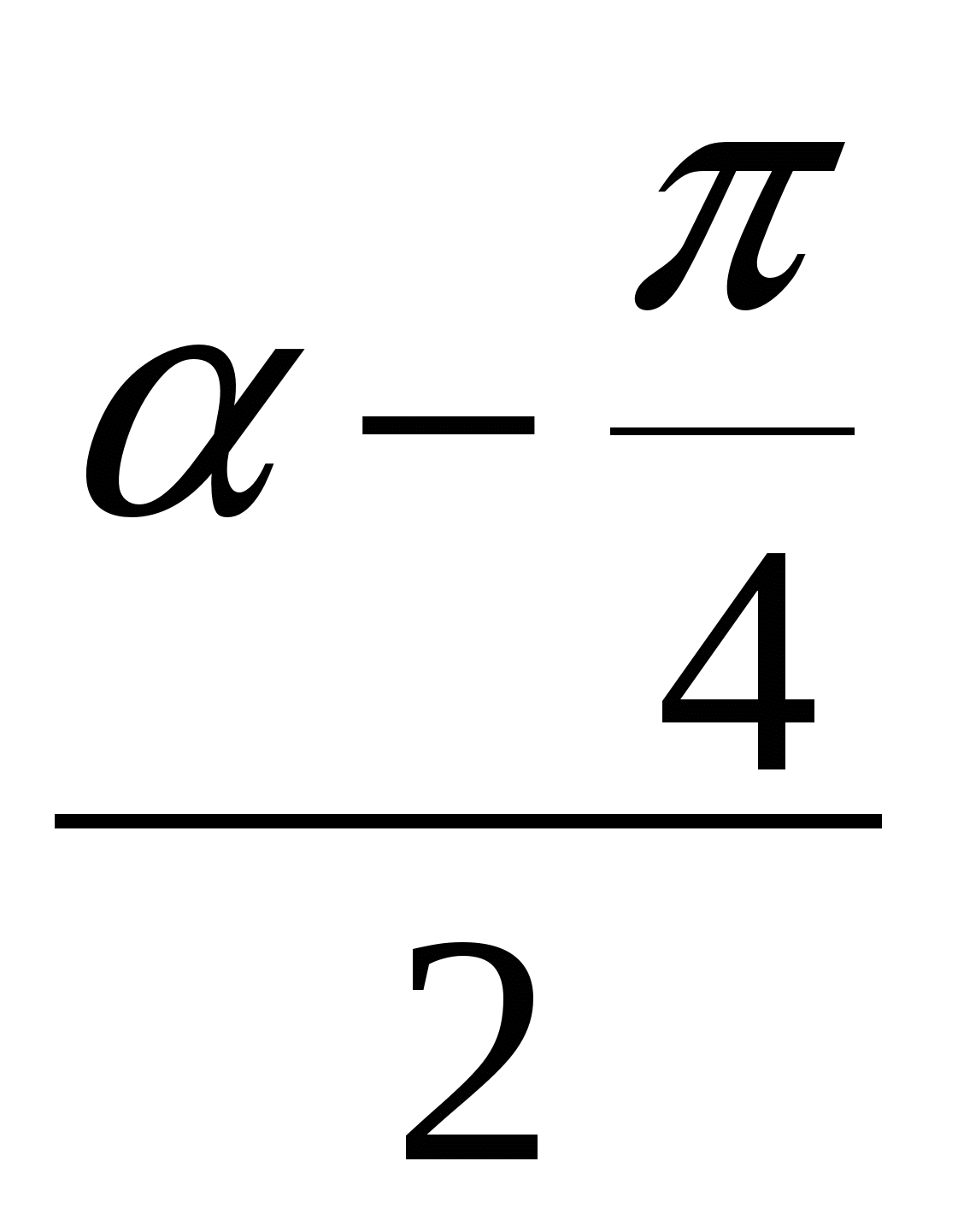 =
=
= 2 cos ![]() × cos
× cos ![]() = 2×(
= 2×(![]() )× cos
)× cos ![]() = cos
= cos ![]() .
.
4). Преобразовать в произведение:
2 cos a + ![]() ;
;
Решение
2 cos a + ![]() = 2(cos a +
= 2(cos a + ![]() ) = 2(cos a + cos
) = 2(cos a + cos![]() ) =
) =
= 2×2 cos ![]() × cos
× cos ![]() = 4× cos (
= 4× cos (![]() ) × cos(
) × cos(![]() ).
).
5). Упростить выражение:
cos2 (a -![]() ) - cos2 (a +
) - cos2 (a +![]() );
);
Решение
cos2 (a -![]() ) - cos2 (a +
) - cos2 (a +![]() ) =( cos (a -
) =( cos (a -![]() ) - cos (a +
) - cos (a +![]() ))×( cos (a -
))×( cos (a -![]() ) +cos (a +
) +cos (a +![]() )) =
)) =
= - 2Sin 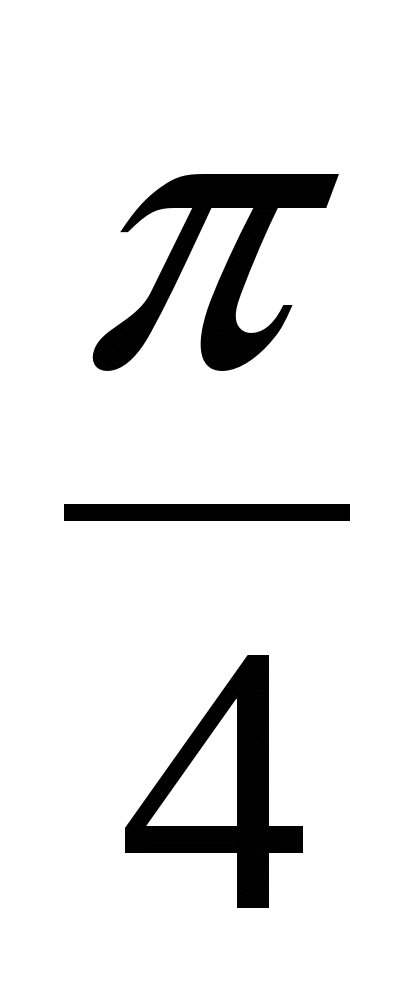 × Sin
× Sin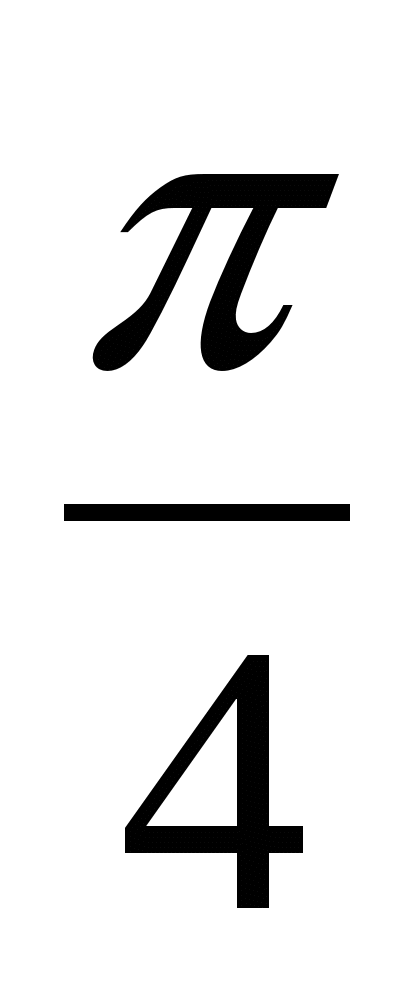 ×2 cos
×2 cos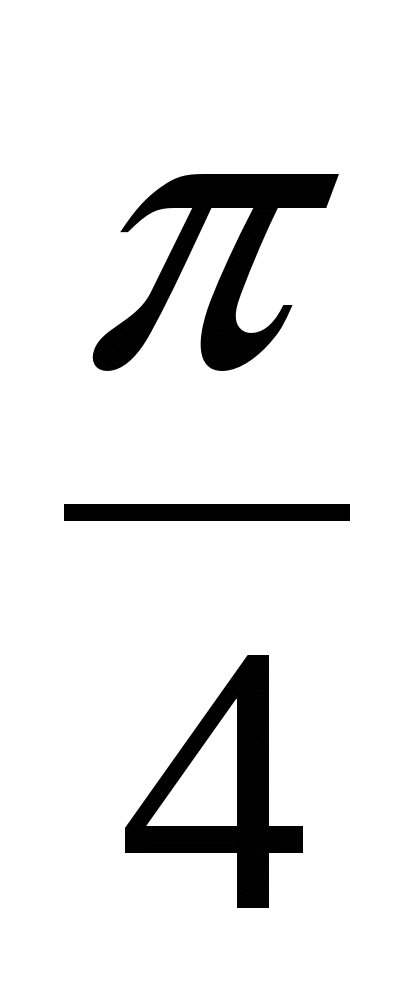 × cos
× cos 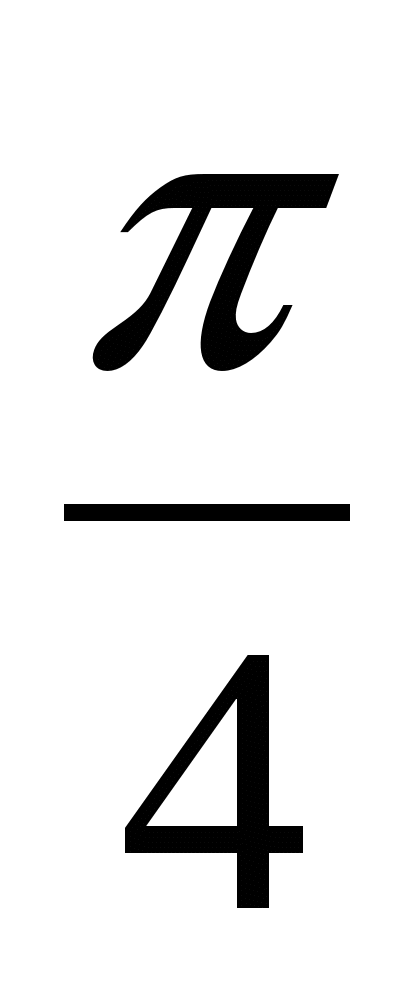 =
=
= -2 Sina× Sin (-![]() ) ×2 cosa × cos(-
) ×2 cosa × cos(-![]() )= 4 Sina×
)= 4 Sina×![]() × cosa
× cosa![]() =
=![]() Sina cosa.
Sina cosa.
-
Самоконтроль самостоятельной работы. Выставление отметок.
Ответы
№
задания
Вариант 1
Вариант 2
1
- 2 Sin 150.
- ![]()
2
-![]()
-![]()
3
- cos ![]() .
.
cos ![]() .
.
4
4× cos (![]() ) × cos(
) × cos(![]() )
)
4× cos (![]() ) × cos(
) × cos(![]() )
)
5
![]() Sina cosa
Sina cosa
![]() Sina cosa.
Sina cosa.
Итог урока. Домашнее задание.
Преобразовать в произведение:
1) 1 - 2 cos a ;
2) ![]() -2 cos a.
-2 cos a.
3) Вычислить:
cos (![]() -
- ![]() ) - cos (
) - cos (![]() +
+ ![]() );
);