Разработка урока:Введение декартовых координат в пространстве. Расстояние между точками. Координаты середины отрезка.

Введение декартовых координат в пространстве. Расстояние между точками. Координаты середины отрезка.

Цели урока:

Образовательные: Рассмотреть понятие системы координат и координаты точки в пространстве; вывести формулу расстояния в координатах; вывести формулу координат середины отрезка.

Развивающие: Способствовать развитию пространственного воображения учащихся; способствовать выработке решения задач и развития логического мышления учащихся.

Воспитательные: Воспитание познавательной активности, чувства ответственности, культуры общения, культуры диалога.

Оборудование: Чертежные принадлежности, презентация, ЦОР

Тип урока: Урок изучения нового материала

Структура урока:

1. Организационный момент.

2. Актуализация опорных знаний.

3. Изучение нового материала.

4. Актуализация новых знаний

5. Итог урока.

Ход урока

1. Сообщение из истории «Декартовая система координат» (Обучающийся)

Решая геометрическую, физическую, химическую задачу можно использовать различные координатные системы: прямоугольную, полярную, цилиндрическую, сферическую.

В общеобразовательном курсе изучается прямоугольная система координат на плоскости и в пространстве. Иначе её называют Декартовой системой координат по имени французского ученого философа Рене Декарта (1596 - 1650) впервые введшего координаты в геометрию.

(Рассказ ученика об Рене Декарте.)

Рене Декарт родился в 1596 г. в городе Лаэ на юге Франции, в дворянской семье. Отец хотел сделать из Рене офицера. Для этого в 1613 г. он отправил Рене в Париж. Много лет пришлось Декарту пробыть в армии, участвовать в военных походах в Голландии, Германии, Венгрии, Чехии, Италии, в осаде крепости гугенотов Ла-Рошали. Но Рене интересовала философия, физика и математика. Вскоре по приезде в Париж он познакомился с учеником Виета, видным математиком того времени - Мерсеном, а затем и с другими математиками Франции. Будучи в армии, Декарт все свое свободное время отдавал занятиям математикой. Он изучил алгебру немецких, математику французских и греческих ученых.

После взятия Ла-Рошали в 1628 г. Декарт уходит из армии. Он ведет уединенный образ жизни с тем, чтобы реализовать намеченные обширные планы научных работ.

Декарт был крупнейшим философом и математиком своего времени. Самым известным трудом Декарта является его "Геометрия". Декарт ввел систему координат, которой пользуются все и в настоящее время. Он установил соответствие между числами и отрезками прямой и таким образом ввел алгебраический метод в геометрию. Эти открытия Декарта дали огромный толчок развитию как геометрии, так и другим разделам математики, оптики. Появилась возможность изображать зависимость величин графически на координатной плоскости, числа - отрезками и выполнять арифметические действия над отрезками и другими геометрическими величинами, а также различными функциями. Это был совершенно новый метод, отличавшийся красотой, изяществом и простотой.

2. Повторение. Прямоугольная система координат на плоскости.

Вопросы:

1. Что называют системой координат на плоскости?

2. Как вводится, декартова система координат? Из чего она состоит?

3. Как определяются координаты точки на плоскости?

4. Назовите координаты начала координат?

5. Чему равно расстояние от начала координат до заданной точки?

6. Назовите формулу координат середины отрезка и расстояния между точками на плоскости?

3. Изучение нового материала:

Прямоугольной системой координат в пространстве называется тройка взаимно перпендикулярных координатных прямых с общим началом координат. Общее начало координат обозначается буквой O.

Ох - ось абсцисс,

Оу - ось ординат,

Оz - ось аппликат

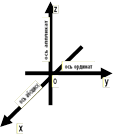
Три плоскости, проходящие через оси координат Ох и Оу, Оу и Оz, Оz и Ох, называются координатными плоскостями: Оху, Оуz, Оzх.

В прямоугольной системе координат каждой точке М пространства сопоставляется тройка чисел - её координаты.

М (х,у,z), где х - абсцисса, у - ордината, z - аппликата.

Система координат в пространстве

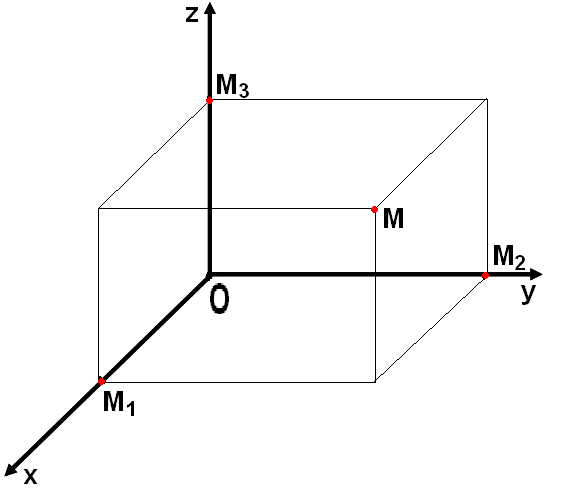
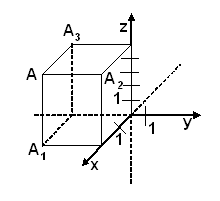
Коордиаты точки

Расстояние между точками

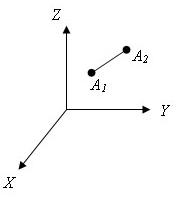
Есть две произвольные точки A₁(x₁;y₁;z₁) и A₂(x₂;y₂;z₂)

Тогда расстояние между точками A₁ и A₂ вычисляется так:

Координаты середины отрезка в пространстве

Есть две произвольные точки A₁(x₁;y₁;z₁) и A₂(x₂;y₂;z₂). Тогда серединой отрезка A₁A₂ будет точка С с координатами x, y, z, где

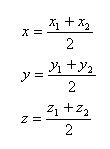
4. Получение навыков решения:

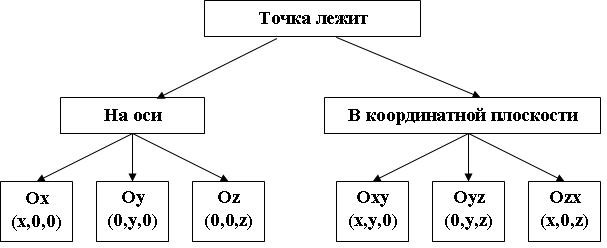
1) Найдите координаты ортогональных проекций точек A(1, 3, 4) и

B(5, -6, 2) на:

а) плоскость Oxy; б) плоскость Oyz; в) ось Ox; г) ось Oz.

Ответ: а) (1, 3, 0), (5, -6, 0); б) (0, 3, 4), (0, -6, 2); в) (1, 0, 0), (5, 0, 0);

г) (0, 0, 4), (0, 0, 2).

2) На каком расстоянии находится точка A(1, -2, 3) от координатной плоскости:

а) Oxy; б) Oxz; в) Oyz?

Ответ: а) 3; б) 2; в) 1

3)Найдите координаты середины отрезка:

а) AB, если A(1, 2, 3) и B(-1, 0, 1); б) CD, если C(3, 3, 0) и D(3, -1, 2).

Ответ: а) (1, 1, 2); б) (3, 1, 1).

5. Домашнее задание: учебник А.В.Погорелова «Геометрия 10-11» п. 23 - 25, стр.53 ответить на вопросы № 1 - 3; №7, №10(1)

6.Итог урока.

ТаблицаНа плоскости

В пространстве

Определение. Системой координат называется совокупность двух пересекающихся координатных осей, точки, в которой эти оси пересекаются, - начала координат - и единичных отрезков на каждой из осей

Определение. Системой координат называется совокупность трех координатных осей, точки, в которой эти оси пересекаются, - начала координат - и единичных отрезков на каждой из осей

2 оси,

ОУ- ось ординат,

ОХ- ось абсцисс

3 оси,

ОХ - ось абсцисс,

ОУ - ось ординат,

ОZ - ось аппликат.

ОХ перпендикулярна ОУ

ОХ перпендикулярна ОУ,

ОХ перпендикулярна ОZ ,

ОУ перпендикулярна ОZ

(О;О)

(О;О;О)

Направление, единичный отрезок

Направление, единичный отрезок

Расстояние между точками.

Расстояние между точками

Координаты середины отрезка.

Координаты середины отрезка

Вопросы:

1. Как вводится, декартова система координат? Из чего она состоит?

2. Как определяются координаты точки в пространстве?

3. Чему равна координата точки пересечения координатных осей?

4. Чему равно расстояние от начала координат до заданной точки?

5. Назовите формулу координат середины отрезка и расстояния между точками в пространстве?

Оценивание обучающихся

7.Рефлексия

На уроке

Я узнал …

Я научился…

Мне понравилось…

Я затруднялся…

Моё настроение…

Литература.

1. А.В. Погорелов. Учебник 10-11. М. "Просвещение", 2010г.

2. И.С. Петраков. Математические кружки в 8-10 классах. М, "Просвещение", 1987 г.