Ростовская область Багаевский район п.Ясный

муниципальное бюджетное общеобразовательное учреждение

Ясненская средняя общеобразовательная школа

«Утверждаю»

Директор МБОУ Ясненской СОШ

Приказ от г.№

__________________ Л.П.Бинько.

Рабочая программа

по предмету «Алгебра»

9 класс.

Количество часов: 99 часов

Учитель: Давыденко Валентина Ивановна

Программа разработана на основе программы общеобразовательных учреждений. Алгебра. 7-9 классы. Составитель: Бурмистрова Т.А. - М.: Просвещение, 2011 г.

Пояснительная записка

Рабочая программа учебного курса по алгебре для 9 класса разработана на основе федерального компонента государственного образовательного стандарта основного общего образования по математике: «Обязательного минимума содержания основного общего образования по математике» и авторской программы по алгебре Ю. Н. Макарычева входящей в сборник рабочих программ «Программы общеобразовательных учреждений: Алгебра, 7-9 классы», составитель: Т.А. Бурмистрова «Программы общеобразовательных учреждений: Алгебра , 7-9 классы».- М. Просвещение, 2011. Планирование ориентировано на учебник «Алгебра 9 класс» под редакцией С.А.Теляковского, авторы: Ю.Н.Макарычев, Н.Г.Миндюк, К.И.Нешков, С.Б.Суворова, Издательство: М., «Просвещение», 2008-2011 годы.

Рабочая программа выполняет две основные функции:

• Информационно-методическая функция позволяет всем участникам образовательного процесса получить представление о целях, содержании, общей стратегии обучения, воспитания и развития учащихся средствами данного учебного предмета.

• Организационно-планирующая функция предусматривает выделение этапов обучения, структурирование учебного материала, определение его количественных и качественных характеристик на каждом из этапов, в том числе для содержательного наполнения промежуточной аттестации учащихся.

Изучение математики на ступени основного общего образования направлено на достижение следующих целей:

• овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;

• формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, пространственных представлений, способность к преодолению трудностей;

• формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;

• воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса.

Задачи учебного предмета

Математическое образование в основной школе складывается из следующих содержательных компонентов (точные названия блоков): арифметика; алгебра; геометрия; элементы комбинаторики, теории вероятностей, статистики и логики. В своей совокупности они отражают богатый опыт обучения математике в нашей стране, учитывают современные тенденции отечественной и зарубежной школы и позволяют реализовать поставленные перед школьным образованием цели на информационно емком и практически значимом материале. Эти содержательные компоненты, развиваясь на протяжении всех лет обучения, естественным образом переплетаются и взаимодействуют в учебных курсах.

В рамках указанных содержательных линий решаются следующие задачи:

• систематизация сведений о числах; изучение новых видов числовых выражений и формул;

• совершенствование практических навыков и вычислительной культуры; приобретение практических навыков, необходимых для повседневной жизни;

• формирование математического аппарата для решения задач из математики, смежных предметов, окружающей реальности;

• развитие алгоритмического мышления, необходимого, в частности, для освоения курса информатики; овладение навыками дедуктивных рассуждений;

• развитие воображения, способностей к математическому творчеству;

• важной задачей изучения алгебры является получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов (равномерных, равноускоренных, экспоненциальных, периодических и др.), для формирования у учащихся представлений о роли математики в развитии цивилизации и культуры;

• формирование функциональной грамотности - умений воспринимать и анализировать информацию, представленную в различных формах, понимать вероятностный характер многих реальных зависимостей, производить простейшие вероятностные расчеты в простейших прикладных задачах.

Нормативное обеспечение программы:

1.Закон об образовании РФ.

2.Федеральный компонент государственного стандарта общего образования. Стандарт основного общего образования по математике. //Вестник образования России.2004. №12 с.107-119.

3.Обязательный минимум содержания основного общего образования по предмету. (Приказ МО от 19.05.1998 №1276)

4.) Программы общеобразовательных учреждений. Алгебра. 7-9 классы. Составитель Бурмистрова Т. А. - М.: Просвещение, 2011.

Место предмета в базисном учебном плане

Согласно Федеральному базисному учебному плану для образовательных учреждений Российской Федерации на изучение алгебры в 9 классе отводится 102 часа из расчёта 3 часа в неделю. На изучение курса в соответствии с авторской программой Бурмистровой Т. А. «Программы общеобразовательных учреждений. Алгебра. 7-9 классы. Составитель Бурмистрова Т. А.,М.: Просвещение, 2011

В связи с тем, что 9 класс заканчивает учебный год 24.05, программа должна быть выполнена за 99 часов за счёт уплотнения изучения материала

Содержание учебного предмета

Рабочая программа конкретизирует содержание предметных тем образовательного стандарта и показывает распределение учебных часов по разделам курса.

Содержание курса алгебры 9 класса включает следующие тематические блоки:

Характеристика основных содержательных линий

1.Квадратичная функция, 25 ч

Функция. Возрастание и убывание функции. Квадратный трехчлен. Разложение квадратного трехчлена на множители. Решение задач путем выделения квадрата двучлена из квадратного трехчлена. Функция у=ах²+вх+с, ее свойства и график. Простейшие преобразования графиков функций. Функция у=хⁿ. Определение корня n-й степени. Вычисление корней n-й степени.

2.Уравнения и неравенства с одной переменной, 13 ч

Целое уравнение и его корни. Биквадратные уравнения. Дробные рациональные уравнения. Решение неравенств второй степени с одной переменной. Решение неравенств методом интервалов.

3.Уравнения и неравенства с двумя переменными и их системы, 19 ч.

Уравнение с двумя переменными и его график. Графический способ решения систем уравнений. Решение систем содержащих одно уравнение первой, а другое второй степени. Решение текстовых задач методом составления систем. Неравенства с двумя переменными. Системы неравенств с двумя переменными.

4.Прогрессии, 15ч

Последовательности. Арифметическая и геометрическая прогрессии. Формулы n-го члена и суммы n первых членов прогрессии.

5.Элементы комбинаторики и теории вероятностей, 13 ч.

Примеры комбинаторных задач. Перестановки, размещения, сочетания. Относительная частота случайного события. Равновозможные события и их вероятность.

6.Повторение. Решение задач по курсу алгебры 7-9кл , 14 ч

Тождественные преобразования алгебраических выражений. Решение уравнений. Решение систем уравнений. Решение текстовых задач. Решение неравенств и их систем. Прогрессии. Функции и их свойства.

Планируемые результаты изучения курса алгебры

В ходе преподавания алгебры в 9 классе следует обращать внимание на то, чтобы учащиеся овладевали умениями общеучебного характера, разнообразными способами деятельности, приобретали опыт:

• планирования и осуществления алгоритмической деятельности, выполнения заданных и конструирования новых алгоритмов;

• решения разнообразных классов задач из различных разделов курса, в том числе задач, требующих поиска пути и способов решения;

• исследовательской деятельности, развития идей, проведения экспериментов, обобщения, постановки и формулирования новых задач;

• ясного, точного, грамотного изложения своих мыслей в устной и письменной речи, использования различных языков математики (словесного, символического, графического), свободного перехода с одного языка на другой для иллюстрации, интерпретации, аргументации и доказательства;

• проведения доказательных рассуждений, аргументации, выдвижения гипотез и их обоснования;

• поиска, систематизации, анализа и классификации информации, использования разнообразных информационных источников, включая учебную и справочную литературу, современные информационные технологии.

Требования к уровню подготовки обучающихся в 9 классе.

В результате изучения курса алгебры 9 класса обучающиеся должны:

знать/понимать

• существо понятия математического доказательства; примеры доказательств;

• существо понятия алгоритма; примеры алгоритмов;

• как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;

• как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;

• как потребности практики привели математическую науку к необходимости расширения понятия числа;

• вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов;

• каким образом геометрия возникла из практических задач землемерия; примеры геометрических объектов и утверждений о них, важных для практики;

• смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации.

Арифметика

уметь

• выполнять устно арифметические действия: сложение и вычитание двузначных чисел и десятичных дробей с двумя знаками, умножение однозначных чисел, арифметические операции с обыкновенными дробями с однозначным знаменателем и числителем;

• переходить от одной формы записи чисел к другой, представлять десятичную дробь в виде обыкновенной и в простейших случаях обыкновенную в виде десятичной, проценты - в виде дроби и дробь - в виде процентов; записывать большие и малые числа с использованием целых степеней десятки;

• выполнять арифметические действия с рациональными числами, сравнивать рациональные и действительные числа; находить в несложных случаях значения степеней с целыми показателями и корней; находить значения числовых выражений;

• округлять целые числа и десятичные дроби, находить приближения чисел с недостатком и с избытком, выполнять оценку числовых выражений;

• пользоваться основными единицами длины, массы, времени, скорости, площади, объема; выражать более крупные единицы через более мелкие и наоборот;

• решать текстовые задачи, включая задачи, связанные с отношением и с пропорциональностью величин, дробями и процентами;

использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

• решения несложных практических расчетных задач, в том числе c использованием при необходимости справочных материалов, калькулятора, компьютера;

• устной прикидки и оценки результата вычислений; проверки результата вычисления с использованием различных приемов;

• интерпретации результатов решения задач с учетом ограничений, связанных с реальными свойствами рассматриваемых процессов и явлений;

Алгебра

уметь

• составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные;

• выполнять основные действия со степенями с целыми показателями, с многочленами и с алгебраическими дробями; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражений;

• применять свойства арифметических квадратных корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни;

• решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним, системы двух линейных уравнений и несложные нелинейные системы;

• решать линейные и квадратные неравенства с одной переменной и их системы;

• решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;

• изображать числа точками на координатной прямой;

• определять координаты точки плоскости, строить точки с заданными координатами; изображать множество решений линейного неравенства;

• распознавать арифметические и геометрические прогрессии; решать задачи с применением формулы общего члена и суммы нескольких первых членов;

• находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;

• определять свойства функции по ее графику; применять графические представления при решении уравнений, систем, неравенств;

• описывать свойства изученных функций (у=кх, где к0, у=кх+b, у=х², у=х³, у =, у=, у=ах²+bх+с, у= ах²+n у= а(х - m) ² ), строить их графики;

использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

• выполнения расчетов по формулам, составления формул, выражающих зависимости между реальными величинами; нахождения нужной формулы в справочных материалах;

• моделирования практических ситуаций и исследований построенных моделей с использованием аппарата алгебры;

• описания зависимостей между физическими величинами соответствующими формулами при исследовании несложных практических ситуаций;

• интерпретации графиков реальных зависимостей между величинами;

Элементы логики, комбинаторики,

статистики и теории вероятностей

уметь

• проводить несложные доказательства, получать простейшие следствия из известных или ранее полученных утверждений, оценивать логическую правильность рассуждений, использовать примеры для иллюстрации и контрпримеры для опровержения утверждений;

• извлекать информацию, представленную в таблицах, на диаграммах, графиках; составлять таблицы, строить диаграммы и графики;

• решать комбинаторные задачи путем систематического перебора возможных вариантов, а также с использованием правила умножения;

• вычислять средние значения результатов измерений;

• находить частоту события, используя собственные наблюдения и готовые статистические данные;

• находить вероятности случайных событий в простейших случаях;

использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

• выстраивания аргументации при доказательстве (в форме монолога и диалога);

• распознавания логически некорректных рассуждений;

• записи математических утверждений, доказательств;

• анализа реальных числовых данных, представленных в виде диаграмм, графиков, таблиц;

• решения практических задач в повседневной и профессиональной деятельности с использованием действий с числами, процентов, длин, площадей, объемов, времени, скорости;

• решения учебных и практических задач, требующих систематического перебора вариантов;

• сравнения шансов наступления случайных событий, оценки вероятности случайного события в практических ситуациях, сопоставления модели с реальной ситуацией;

• понимания статистических утверждений.

Контрольно-измерительный материал.

Контрольные работы составляются с учетом обязательных результатов обучения.

Тексты контрольных работ взяты из

1) Программы общеобразовательных учреждений. Алгебра. 7-9 классы. Составитель Бурмистрова Т. А. - М.: Просвещение, 2008;

2) Алгебра. Дидактические материалы. 9 класс / Ю.Н.Макарычев, Н.Г.Миндюк, Л.Б.Крайнева.. - М.: Просвещение, 2011.

Критерии и нормы оценки знаний, умений и навыков

обучающихся по алгебре.

1. Оценка письменных контрольных работ обучающихся по алгебре.

Ответ оценивается отметкой «5», если:

• работа выполнена полностью;

• в логических рассуждениях и обосновании решения нет пробелов и ошибок;

• в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).

Отметка «4» ставится в следующих случаях:

• работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);

• допущены одна ошибка или есть два - три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).

Отметка «3» ставится, если:

• допущено более одной ошибки или более двух - трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.

Отметка «2» ставится, если:

• допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.

Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.

2. Оценка устных ответов обучающихся по алгебре.

Ответ оценивается отметкой «5», если ученик:

• полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;

• изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;

• правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;

• показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;

• продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и устойчивость используемых при ответе умений и навыков;

• отвечал самостоятельно, без наводящих вопросов учителя;

• возможны одна - две неточности при освещение второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.

Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:

• в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;

• допущены один - два недочета при освещении основного содержания ответа, исправленные после замечания учителя;

• допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.

Отметка «3» ставится в следующих случаях:

• неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала;

• имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;

• ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;

• при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.

Отметка «2» ставится в следующих случаях:

• не раскрыто основное содержание учебного материала;

• обнаружено незнание учеником большей или наиболее важной части учебного материала;

• допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.

Формы промежуточной и итоговой аттестации:

Освоение образовательных программ основного общего образования завершается обязательной итоговой аттестацией выпускников.

Государственная итоговая аттестация выпускников школы осуществляется в соответствии с Положением о государственной (итоговой) аттестации выпускников общеобразовательных учреждений, утвержденным Министерством образования и науки Российской Федерации.

Промежуточная аттестация проводится в форме тестов, контрольных, самостоятельных работа.

На основании результатов промежуточной аттестации выставляются итоговые оценки.

График проведения контрольных работ

Календарно-тематическое планирование по алгебре 9 класс 3 часа

урока

дата

Тема урока

Оборудова

ние

Виды уч. деятельности,формы

занятий

Требования к уровню подготовки

обучающихся

Формы

контроля

Квадратичная функция - 25 часа

1

01.09

Вводный контроль

тест

практика

Знать: материал 7, 8 класса.

Уметь: выполнять упражнения за курс 7, 8 класса

тест

2

04. 09

Функция. Область определения и область значений функции

Таблица «Функции и их свойства»

Работа с учебником Теория,

практика

Знать: область определения и область значений функции.

Уметь: находить область определения и область значений функции, читать график функции

Твор. раб. «Мое настрое-

ние на уроке»

3

07. 09

Свойства функций

«Функция и их свойства»

Таблицы.

Учебная практическая работа в парах Теория, практика

Знать: основные свойства функций.

Уметь: находить промежутки знакопостоянства, возрастания, убывания функций

Сам. работа

4

08. 09

Свойства функций

«Монотонность функций» »

Учебная практическая работа в парах Практика

Тест

5

11. 09

Квадратный трехчлен и его корни

Таблица «Квадрат-ный трехчлен»

Работа с учебником Теория, практика

Знать: общий вид квадратного трехчлена, формулу корней квадратного уравнения.

Уметь: решать квадратные уравнения, определять знаки корней

Самост. раб

6

14. 09

Квадратный трехчлен и его корни

«Квадратный трехчлен»

Практика

Тест

7

15. 09

Разложение квадрат-ного трехчлена на множители

Составление опорного конспекта Теория, практика

Знать: формулу разложения квадратного трехчлена на множители

Уметь: выполнять разложение квадратного трехчлена на множители

Индиви-дуальные карточки

8

18. 09

Разложение квадрат-ного трехчлена на множители

Практика

Сам. раб.

9

21. 09

Функция у=ах², ее свойства и график

«Графики функций. Па-рабола у=ах²», 12

Работа с учебником Теория, практика

Знать: свойства функции у=ах^2.

Уметь: строить график функции у=ах^2, выполнять простейшие преобразования графиков функций

Устный опрос

10

22.09

Функция у=ах², ее свойства и график

Учебная практическая работа в парах Практика

Знать: свойства функции у=ах^2.

Уметь: применять свойства функции при выполнении различных заданий, по заданной точке графика находить а.

Сам. работа

11

25. 09

График функции

у=ах² +n и у=а(х-m)²

Таблица «Преобразование графика квадратичной функции»

Учебная практическая работа в парах Теория, практика

Уметь: строить график квадратичной функции, выполнять простейшие преобразования графиков функций

Устные

контрольные вопросы

12

28. 09

График функции

у=ах² +n и у=а(х-m)²

Учебная практическая работа в парах Практика

Уметь: строить график квадратичной функции, находить по графику нули функции, промежутки, где функция принимает положительные и отрицательные значения

Сам. работа

13

29.09

Построение графика квадратичной функ-ции

Таблица «График квадратичной функции»

Индивидуальная работа с самооценкой Теория, практика

Знать: формулу для вычисления координат вершины параболы.

Уметь: строить график квадратичной функции

Фронт. работа

14

02.10

Построение графика квадратичной функ-ции

«График и свойства квадратичной функции» таблицы

Индивидуальная работа с самооценкой Практика

Тест

15

05.10

Построение графика квадратичной функ-ции

«График и свойства квадратичной фун-кции» (

Индивидуальная работа Теория, практика

Уметь строить график квадратичной функции у=ах² +n, у=а(х-m)^2., у= ах² + bх +с и отвечать на вопросы

Сам. работа

16

06.10

Обобщение, систе-матизация и коррек-ция знаний

«Преобразование графиков функций», 21

Индивидуальная работа Практика

Коррек-ционная СР

17

09.10

Контрольная работа по теме «Квадратичная функция»

Проверка знаний и умений

Уметь: строить графики функций вида у=ах², у=ах² +n, у=а(х-m)^2., у= ах² + вх +с; читать графики

Контр. работа

18

12.10

Анализ контрольной работы.

Функция у=хⁿ

«Степенная функция», 15

Работа с учебником Теория, практика

Знать: свойства степенной функции с натуральным показателем.

Уметь: строить график функции у=хⁿ , решать уравнения хⁿ=а при n

а) четных и б)нечетных значениях

Фронт. работа

19

13.10

Корень n-й степени.

Работа с учебником Теория, практика

Знать: определение корня n- й степени, арифм. корня n- й степени; знать, при каких значениях а имеет смысл выражение .

Уметь: решать уравнения хⁿ=а при четных и нечетных n

Матем. диктант

20

16.10

Корень n-й степени

Учебная практическая работа в парах Практика

Уметь: выражать корень n-й степени из отрицательного числа через арифметический корень той же степени, вычислять корень n-й степени с помощью калькулятора

Сам. работа

21

19.10

Степень с рациональным показателем

Составление опорного конспекта Теория, практика

Знать: свойства степеней с рациональным показателем.

Умет: выполнять простейшие преобразования выражений, содержащих степени с дробным показателем

Индиви-дуальные

карточки

22

20.10

Преобразования вы-ражений, содержащих степени с рациональным показателем

Учебная практическая работа в парах

Уметь: выполнять преобразования выражений, содержащих степени с дробным показателем

СР с взаимопроверкой

23

23.10

Обобщение, систе-матизация и коррек-ция знаний

Индивидуальная работа с самооценкой Практика

Обобщить и систематизировать изученный материал

СР

24

26.10

Обобщение, систе-матизация и коррек-ция знаний

Проверка умений и навыков учащихся

Уметь: решать задачи по теме «Степенная функция. Корень n-й степени»

КР

25

27.10

Контрольная работа за 1 четверть «Степенная функция. Корень n-й степени»

Круговая СР

Уравнения и неравенства с одной переменной - 13 часов

26

30.10

Целое уравнение и его корни

Составление опорного конспекта Теория, Практика

Знать: методы решения уравнений:

а) разложение на множители;

Уметь: решать уравнения разложением на множители Уметь: решать уравнения введением новой переменной

ФР

27

02.11

Целое уравнение и его корни

Учебная практическая работа в парах Практика

Умет: решать биквадратные уравнения

СР

28

2 четв

10.11

Дробные рациональ-ные уравнения

Решение примеров с комментированием Теория, практика

Знать: метод решения уравнений введением новой переменной.

Уметь: решать целые уравнения методом введения новой переменной

Индивид.

карточки

29

13.11

Дробные рациональ-ные уравнения

Индивидуальная работа с самооценкой Практика

Индивид.

карточки

30

16.11

Дробные рациональ-ные уравнения

Индивидуальная работа Практика

СР

31

17.11

Решение неравенств второй степени с одной переменной

Таблица «Неравенство 2 степени с одной переменной»

Решение примеров с комментированием Теория, практика

Знать: алгоритм решения неравенств графическим способом.

Уметь решать неравенство

ах² +вх+с.≥0 на основе свойств квадратичной функции

ФР

32

20.11

Решение неравенств второй степени с одной переменной

Индивидуальная работа Практика

Индиви-дуальные

карточки

33

23.11

Решение неравенств второй степени с одной переменной

Индивидуальная работа Практика

Уметь: применять алгоритм решения нера-венств второй степени при нахождении области определения выражений, при решении текстовых задач

СР

34

24.11

Решение неравенств методом интервалов

Т Индивидуальная работа еория, практика

Знать: метод интервалов.

Уметь решать неравенства методом интервалов

ФР

35

27.11

Решение неравенств методом интервалов

Практик

Знать: метод интервалов.

Уметь: решать неравенства методом интервалов

СР

36

30.11

Решение неравенств методом интервалов

Практика

Знать: метод интервалов.

Уметь: решать неравенства методом интервалов

Тест

37

01.12

Обобщение, систе-матизация и коррек-ция знаний

Практика

Зачет

38

04.12

Контрольная работа по теме «Уравнения и неравенства с одной переменной»

Проверка знаний и умений

Уметь решать неравенство

ах² +вх+с.≥0 на основе свойств квадратичной функции; решать неравенства методом интервалов

КР

Уравнения и неравенства с двумя переменными и их системы - 19 часов

39

07.12

Анализ контрольной работы. Уравнение с двумя переменными и его график

Теория, практика

Знать: понятие равносильных уравнений.

Уметь: строить график уравнения с двумя переменными

ФР

Работа в парах

40

08.12

Уравнение с двумя переменными и его график

Составление опорного конспекта Практика

Уметь: строить график уравнения с двумя переменными

СР

41

11.12

Графический способ решения систем уравнений

«Графики функций»

Теория, практика

Знать: понятие решения системы уравнений; графический способ решения систем уравнений.

Уметь: решать системы 2 уравнений с 2 переменными графическим способом

ФР

42

14.12

Графический способ решения систем уравнений

Практика

Уметь: решать системы 2 уравнений с 2 переменными графическим способом

Работа в группах

43

15.12

Решение систем уравнений второй степени

Таблица «Системы уравнений с 2 переменными»

Теория, практика

Знать: способ подстановки и способ сложения решения систем.

Уметь: решать уравнения с 2 переменными способом подстановки

ФР

Индиви-дуальные

карточки

44

18.12

Решение систем уравнений второй степени

практика

Уметь: решать уравнения с 2 переменными

КР

45

21.12

Решение систем уравнений второй степени

«Решение систем рациональных уравнений» таблицы

Практика

Уметь: решать системы уравнений второй степени способами сложения и подстановки, графически

Тест

46

22.12

Контрольная работа за 2 четверть

Практика

СР

47

25.12

Решение задач с по-мощью систем урав-нений

Теория, практика

Уметь: решать задачи составлением систем уравнений

ФР

48

28.12

Решение задач с помощью систем уравнений

Практика

Уметь: решать задачи на «движение» составлением систем уравнений

Индиви-дуальные

карточки

49

3 четв

11.01

Решение задач с помощью систем уравнений

Практика

Уметь: решать задачи «на работу» составлением систем уравнений

Индиви-дуальные

карточки

50

12.01

Решение задач с помощью систем уравнений второй степени

Практика

Уметь: решать задачи на «проценты» составлением систем уравнений

Индиви-дуальные

карточки

51

15.01

Решение задач с помощью систем уравнений второй степени

Проверка знаний и умений

Уметь: решать задачи «на работу», «на движение», «на проценты» и другие состав. систем уравнений

КР

52

18.01

Неравенства с двумя переменными

Составление опорного конспекта Теория, практика

Знать: что представляет собой множество точек координатной плоскости, удовлетворяющих неравенствам ах+ву≤с и ах+ву≥с.

Уметь: изображать на координатной плоскости множество решений данного неравенства

ФР

53

19.01

Неравенства с двумя переменными

Практика

Уметь: изображать на координатной плоскости множество решений данного неравенства

Индиви-дуальные

карточки

54

22.01

Системы неравенств с двумя переменными

Теория, практика

Уметь: изображать на координатной плоскости множество точек, представляющих собой общую часть множеств, задаваемых неравенствами.

ФР

55

25.01

Системы неравенств с двумя переменными

Практика

Уметь: изображать на координатной плоскости множество точек, представляющих собой общую часть множеств, задаваемых неравенствами.

Работа в парах

56

26.01

Обобщение, систе-матизация и коррекция знаний

Практика

Уметь: решать системы графически, способами подстановки и сложения, решать текстовые задачи, изображать решения систем неравенств.

Работа в группах

57

29.01

Контрольная работа по теме «Уравнения и неравенства с двумя переменны-ми и их системы»

Проверка знаний и умений

Уметь: решать системы 2 уравнений с 2 переменными графическим способом; решать задачи составлением систем уравнений; изображать на координатной плоскости множество точек, представляющих собой общую часть множеств, задаваемых неравенствами.

КР

Прогрессии - 15 часов

58

01.02

Анализ контрольной работы. Последовательности.

Теория, практика

Знать и понимать: термины «член последовательности», «номер члена последовательности»

Уметь: по заданной формуле находить любой член последовательности.

МД

59

02.02

Определение арифметической прогрессии. Формула n-го члена арифметической прогрессии

Таблица «Арифме-тическая прогрессия»

Составление опорного конспекта Теория, практика

Знать: определение арифметической прогрессии, понятие формулы n -го члена арифметической прогрессии, способы задания.

Инд. зад.

разных уровней

60

05.02

Определение арифметической прогрессии. Формула n-го члена.

«Арифметическая прогрессия» таблица

Теория, практика

Знать: формулу n -го члена арифметической прогрессии, свойства членов арифметической прогрессии, способы задания арифметической прогрессии.

Уметь: определять номера отрицательных (положительных) членов арифметической прогрессии

ПР на компьют.

61

08.02

Определение арифметической прогрессии. Формула n-го члена арифметической прогрессии

Практика

Инд. зад.

разных уровней

62

09.02

Формула суммы n первых членов арифметической прогрессии

«Арифметическая прогрессия» таблица

Составление опорного конспекта Теория, практика

Знать: формулы I и II суммы n-членов арифметической прогрессии.

Уметь: применять формулу суммы n -первых членов арифметической прогрессии при решении задач

ФР

ПР на компьют.

63

12.02

Формула суммы n первых членов арифметической прогрессии

Арифметическая прогрессия» таблица

Практика

Знать: формулы I и II суммы n-членов арифметической прогрессии.

Уметь: находить сумму n отрицательных или положительных член.

Тест

64

15.02

Формула суммы n первых членов арифметической прогресс.

Арифметическая прогрессия» таблица

Практика

Знать: формулы I и II суммы n-членов арифметической прогресс.

Уметь: применять формулы к решению задач.

Зачет

65

16.02

Контрольная работа по теме «Арифметическая прогрессия»

Проверка знаний и умений

Уметь: находить n -ый член, сумму n-членов арифметической прогрессии

КР

66

19.02

Анализ контрольной работы. Определение геометрической прогрессии

Таблица «Гео-метрическая прогрессия»

Теория, практика

Знать: какая последовательность является геометрической.

Уметь: выявлять, является ли последовательность геометрической, если да, то находить q

Инд. зад.

разных уровней

67

22.02

Формула n - го члена геометрической прогрессии

«Геом. прогрессия» таблица

Теория, практика

Знать: формулу n - го члена геометрической прогрессии

Уметь: вычислять любой член геометрической прогрессии по формуле, знать свойства членов геометрической прогрессии

ФР

68

26.02

Формула n - го члена геометрической прогрессии

«Геометрическая прогрессия» (таблица)

Практика

1.Инд. зад.

раз. уров.

2.Тест

69

29.02

Формула суммы n членов геометри-ческой прогрессии

«Геометрическая прогрессия»

Практика

Знать: формулу суммы n членов геометрической прогрессии.

Уметь: применять формулу при решении стандартных задач

Инд. зад.

разных уровней

70

01.03

Формула суммы n членов геометри-ческой прогрессии

Практика

Инд. зад.

разных уровней

71

04.03

Бесконечая геомет-рическая прогрессия

«Сумма бесконечно убывающей геомет- прогрессии»

Теория, практика

Знать: формулу S=.

Уметь: применять формулу при решении практических задач

Зачет

72

07.03

Бесконечая геомет-рическая прогрессия

Проверка знаний и умений

Уметь: выполнять задания по теме «Геометрическая прогрессия»

КР

Элементы комбинаторики и теории вероятностей - 13 часов

73

11.03

Примеры комбинаторных задач

Теория, практика

Уметь: решать простейшие комбинаторные задачи перебором возможных вариантов, ознакомить деревом возможных вариантов

ФР

74

14.03

Решение комбина-торных задач

Практика

Знать: комбинаторное правило умножения.

Уметь: решать комбинаторные задачи с использованием комбинат. правила умножения.

ФР

Работа в группах

75

15.03

Перестановки

Теория, практика

Знать: формулу числа перестановок и уметь пользоваться при выполнении упражнений

ФР

76

18.03

Контрольная работа за 3 четверть «Геометрическая прогрессия»

Практика

Уметь: пользоваться при решении задач формулой размещений

СР

77

4 четв.

01.04

Перестановки

Практика

Уметь: пользоваться при решении задач формулой перестановок

СР с взаи-мопровер

78

04.04

Размещения

Теория, практика

Знать: формулы числа размещений

Уметь: пользоваться ими при выполнении упражнений

Индиви-

дуальные карточки

79

05.04

Размещения Сочетания

Теория, практика

Знать: формулы числа сочетаний и уметь пользоваться ими при решении задач

Индивид.

карточки

80

08.04

Сочетания

Практика

СР.

81

11.04

Относительная час-

тота случайного со-бытия

Теория,

практика

Знать: понятие случайного события, частоты события, относительной частоты события.

Уметь: находить относительную частоту случайного события

ФР

82

12.04

Относительная час-

тота случайного события

Практика

СР

83

15.04

Вероятность равно-

возможных событий

Теория,

практика

Знать: понятие благоприятные исходы, определение вероятности.

Уметь: пользоваться формулой комбинаторики при вычислении вероятностей

ФР

84

18.04

Вероятность равно-

возможных событий

Практика

Уметь: пользоваться формулой комбинаторики при вычислении вероятностей

СР

85

19.04

Контрольная работа по теме «Элементы комбинаторики и теории вероятностей»

Проверка знаний и умений

Уметь: решать простейшие комбинаторные задачи; пользоваться формулой комбинаторики при вычислении вероятностей

КР

Повторение. 14 ч Решение задач по курсу алгебры 7-9 - 19 часов

86

22.04

Анализ контрольной работы.

Числовые выражения

Практика

Уметь: выполнять действия с рациональными числами, свободно владеть навыками решения прим.

Выполне-ние тестов

87

25.04

Выражения с переменными

Практика

Уметь: находить значения выражений с переменными; находить область определения

Выполне-ние тестов

88-89

26.04

29.04

Линейные уравнения и их системы

Практика

Уметь решать линейные уравнения и их системы

Выполн. тестов

90

02.05

Преобразование целых выражений

Практика

Уметь: упрощения выражения

Выполн. тестов

91

03.05

Преобразование дробных выражений

Практика

Уметь: выполнять преобразования дробных выражений

Выполн. тестов

92

06.05

Степень и её свойства

Практика

Знать: все свойства степеней с целым показателем

Выполн. тестов

93

10.05

Квадратные уравне-ния и их корни

Практика

Уметь: решать квадр. уравнения

Выполн. тестов

94

13.05

Целые уравнения

Практика

Уметь: решать целые уравнения

Выполн. тестов

95

16.05

Решение линейных и квадратных нера-венств

Практика

Уметь: решать линейные и квадратные уравнения

Выполн. тестов

96

17.05

Функции и их гра-фики

Практика

Знать: свойства изученных функций.

Уметь: строить их графики, «читать графики».

Выполнение тестов

97

20.05

Решение текстовых задач

Практика

Уметь: составлять уравнения по условию задачи

Выполн. тестов

98

23.05

Контрольная работа итоговая (тестирование)

Проверка знаний и умений

Уметь: выполнять тесты по повторенным темам.

Тестирование

99

24.05

Анализ к/р. Решение текстовых задач

Практика

Уметь: составлять уравнения по условию задачи

Выполн. тестов

Перечень учебно - методического и материально-технического обеспечения образовательного процесса.

Печатные пособия:

1. Алгебра. 9 класс: учебник для общеобразоват.учреждений / Ю.Н.Макарычев, Н.Г.Миндюк, К.Н.Нешков, С.Б.Суворова; под редакцией С.А.Теляковского. - М.: Просвещение, 2007 - 2011гг.

2. Алгебра: дидактические материалы для 9 кл. / Ю.Н.Макарычев, Н.Г.Миндюк, Л.Б.Крайнева. - М.: Просвещение, 2007 - 2011гг.

3. Уроки математики в 9-м классе. Поурочные планы по учебнику Ю.Н. Макарычева и др. Ковалева С.П. «Учитель», 2009.

4. Уроки алгебры в 9 классе: кн. для учителя / В. И. Жохов, Л. Б. Крайнева. - М.: Просвещение, 2009.

5. Алгебра, 9 класс. Итоговая аттестация . Предпрофильная подготовка.под редакцией Д.А. Мальцева. Ростов-на -Дону, 20010,2011.

6. Ф.Ф.Лысенко. Подготовка к итоговой аттестации.Издательство «Легион», Ростов-на -Дону,2010,2011.

7. Карташёва Г.Д. Сборник тестовый заданий для тематического и итогового контроля . Геометрия 9 кл. (к уч. Л.С. Атанасяна и др.) - М.: , изд. Интеллект-Центр, 2007г.

.

Информационно-коммуникативные средства:

1. Тематические презентации

2. Компакт-диск Алгебра, 9 класс: поурочные планы по учебнику Ю.Н. Макарычева «Учитель», 2010.

3. Технические средства обучения

4. Компьютер

5. Оборудование класса

6. Ученические столы 2-местные с комплектом стульев

7. Стол учительский

8. Шкафы для хранения учебников, дидактических материалов, пособий и т.д.

9. Стол демонстрационный

10. Печатные пособия

11. Учебные таблицы по алгебре и геометрии

12. Таблица квадратов

13. Экранно- звуковые пособия

14. Компакт-диски

15. «Живая геометрия»

16. «Алгебра 7-9»

17. «Уроки алгебры Кирилла и Мефодия 9 класс»

18. Открытая математика.Планиметрия

19. Интерактивные уроки электронное пособие С.Н.Поздняков и др.

20. .Электронный учебник-справочник. Алгебра 7-11 классы

21. Большая детская энциклопедия. Математика.

22. Учебно-практическое и учебно-лабораторное оборудование

23. Набор геометрических тел «Стереометрия»

24. Набор по геометрии по теме «Площадь»

25. Набор линеек и треугольников для работы у доски

Интернет- ресурсы:

www.prosv.ru - сайт издательства «Просвещение» (рубрика «Математика»)

http:/www.drofa.ru - сайт издательства Дрофа (рубрика «Математика»)

www.center.fio.ru/som - методические рекомендации учителю-предметнику (представлены все школьные предметы). Материалы для самостоятельной разработки профильных проб и активизации процесса обучения в старшей школе.

www.edu.ru - Центральный образовательный портал, содержит нормативные документы Министерства, стандарты, информацию о проведение эксперимента, сервер информационной поддержки Единого государственного экзамена.

www.internet-scool.ru - сайт Интернет - школы издательства Просвещение. Учебный план разработан на основе федерального базисного учебного плана для общеобразовательных учреждений РФ и представляет область знаний «Математика». На сайте представлены Интернет-уроки по алгебре и началам анализа и геометрии, включают подготовку сдачи ЕГЭ, ГИА.

www.legion.ru - сайт издательства «Легион»

www.intellectcentre.ru - сайт издательства «Интеллект-Центр», где можно найти учебно-тренировочные материалы, демонстрационные версии, банк тренировочных заданий с ответами, методические рекомендации и образцы решений

www.fipi.ru</<font face="Times New Roman, serif"> - портал информационной поддержки мониторинга качества образования, здесь можно найти Федеральный банк тестовых заданий.

Приложения к рабочей программе алгебра 9 класс:

Контрольные работы

Диагностическая контрольная работа по тексту администрации.

Вариант - 1 Вариант - 2

1.Решите неравенство:

5(у - 1,2) - 4,6 3у+1. 6(у - 1,5) - 3,4 4у-2,4.

2.Решить систему неравенств:

2х-3 > 0 , 4х - 10 10,

7х + 4 18. 3х - 5 > 0.

3. Упростите выражение:

а) 10 - 4 - ; а) 6 - - 3;

б) ( 5 - ); б) ( - 2);

в) (3 - )² . в) (2 - )² .

4. Решите уравнение:

а) 14х² - 9х = 0; а) 6х ² - 3х = 0;

б) 16х² = 49; б) 25х² = 81;

в) 2х² - 11х + 12 = 0. в) 3х² - 7х - 6 = 0.

5.Упростите выражение:

( - ) . ( - ).

Контрольная работа №1 по алгебре в 9 классе по теме

«Функции и их свойства, квадратный трехчлен»

Вариант 1

• 1. Дана функция f (х) = 17х - 51. При каких значениях аргумента f (х) =0, f (х) < 0, f (х) > 0? Является ли эта функция возрастающей или убывающей?

• 2. Разложите на множители квадратный трехчлен: а) х² -14х +45; б) 3у² +7у-6.

• 3. Сократите дробь .

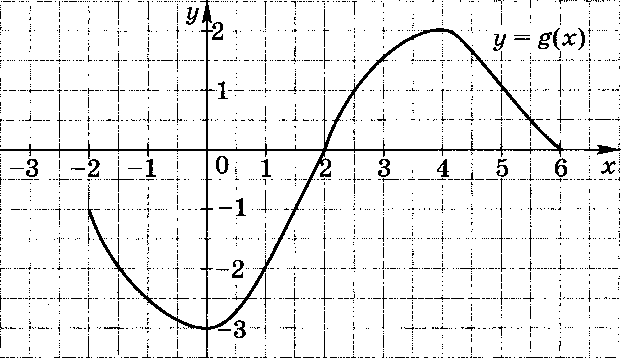
4. Область определения функции g (рис. 1) отрезок [-2; 6]. Найдите нули функции, промежутки возрастания и убывания, область значений функции.

5. Сумма положительных чисел а и b равна 50. При каких значениях а и b их произведение будет наибольшим?

Вариант 2

• 1. Дана функция g(х) = -13х + 65. При каких значениях аргумента g(х) = 0, g (х) < 0, g (х) > 0? Является ли эта функция возрастающей или убывающей?

• 2. Разложите на множители квадратный трехчлен: а) х²-10х+21; б) 5у²+9у-2.

• 3. Сократите дробь .

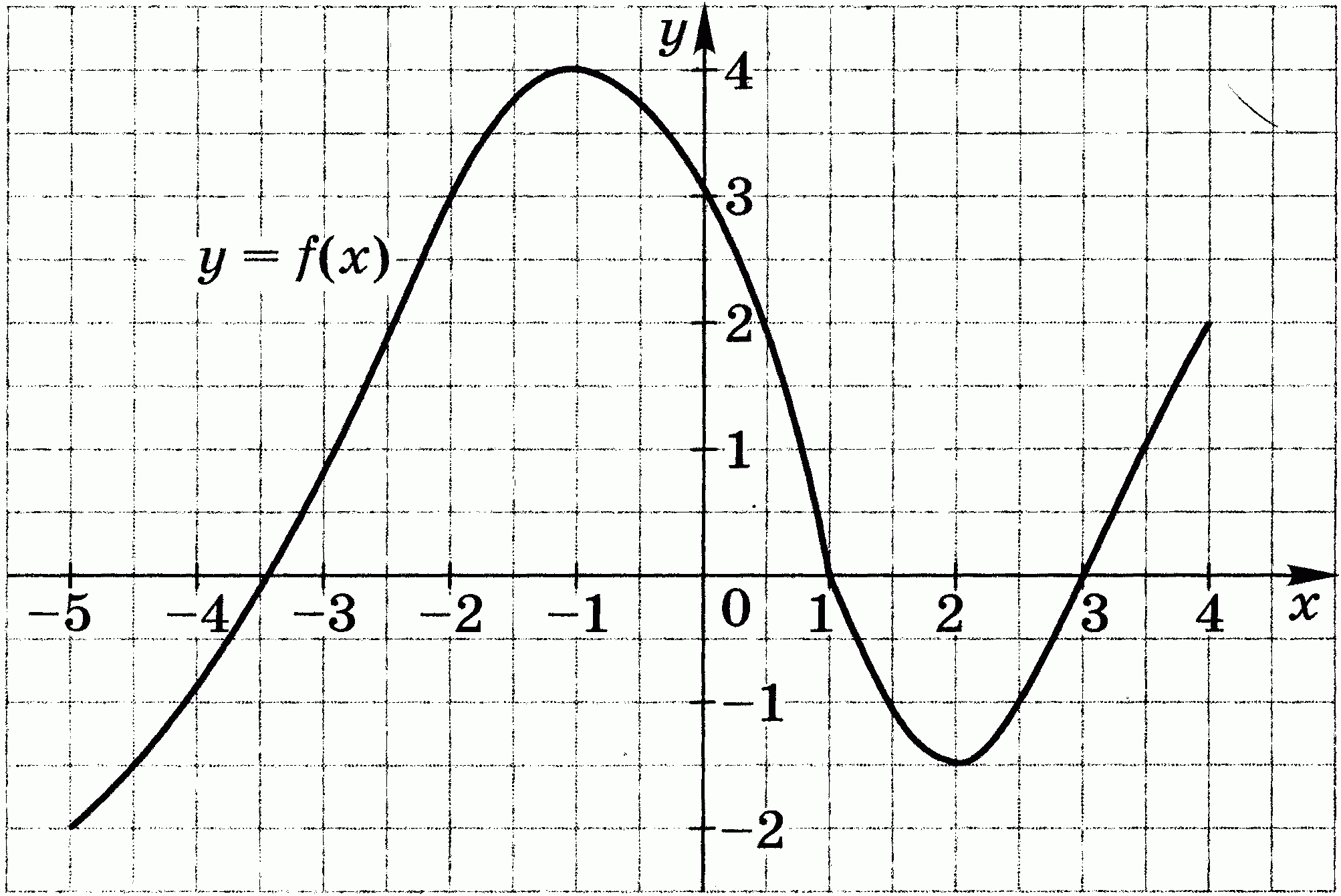
4. Область определения функции f (рис. 2) отрезок [-5; 4]. Найдите нули функции, промежутки возрастания и убывания, класть значений функции.

5. Сумма положительных чисел с и d равна 70. При каких значениях с и d их произведение будет наибольшим?

Контрольная работа №2 по алгебре в 9 классе

по теме «квадратичная функция и ее график»

Вариант 1

• 1. Постройте график функции у = х² - 6х + 5. Найдите с помощью графика:

а) значение у при х = 0,5; б) значения х, при которых у = -1;

в) нули функции; промежутки, в которых у > 0 и в которых у < 0;

г) промежуток, на котором функция возрастает.

• 2. Найдите наименьшее значение функции у = х² - 8х + 7.

• 3. Найдите область значений функции у = х² - 6х - 13, где x [-2; 7].

4. Не выполняя построения, определите, пересекаются ли парабола у = х² и прямая у = 5х -16. Если точки пересечения существуют, то найдите их координаты.

5. Найдите значение выражения .

Вариант 2

• 1. Постройте график функции у = х² - 8х + 13. Найдите с помощью графика:

а) значение у при х = 1,5; б) значения х, при которых у = 2;

в) нули функции; промежутки, в которых у > 0 и в которых y < 0;

г) промежуток, в котором функция убывает.

• 2. Найдите наибольшее значение функции у = -х² + 6х - 4.

3. Найдите область значений функции у = x² - 4х - 7, где х [-1; 5].

4. Не выполняя построения, определите, пересекаются ли парабола у =х² и прямая у =20-3х. Если точки пересечения существуют, то найдите их координаты.

5. Найдите значение выражения .

Контрольная работа №3 по алгебре в 9 классе

по теме «Уравнения и неравенства с одной переменной»

Вариант 1

• 1. Решите уравнение: а) х³ - 81х = 0; б) .

•2. Решите неравенство: а) 2х² - 13х + 6 < 0; б) х² > 9.

• 3. Решите неравенство методом интервалов:

а) (х + 8) (х - 4) (х - 7) > 0; б) < 0.

• 4. Решите биквадратное уравнение х⁴ - 19х² + 48 = 0.

5. При каких значениях т уравнение 3х² + тх + 3 = 0 имеет два корня?

6. Найдите область определения функции .

7. Найдите координаты точек пересечения графиков функций

у = и y = x² - 3x+1.

Вариант 2

• 1. Решите уравнение: а) x³ - 25x = 0; б) .

• 2. Решите неравенство: а) 2х² - х - 15 > 0; б) х² < 16.

•3. Решите неравенство методом интервалов:

а) (х + 11) (х + 2) (х - 9) < 0; б) > 0.

• 4. Решите биквадратное уравнение х⁴ - 4х² - 45 = 0.

5. При каких значениях п уравнение 2х² + пх + 8 = 0 не имеет корней?

6. Найдите область определения функции

7. Найдите координаты точек пересечения графиков функций y = и y = .

Контрольная работа по тексту администрации за 1 полугодие.

Контрольная работа №4 по алгебре в 9 классе

по теме «Уравнения и неравенства с двумя переменными»

Вариант 1

1. Решите систему уравнений:

2x + y = 7,

х² - у = 1.

• 2. Периметр прямоугольника равен 28 м,

а его площадь равна 40 м². Найдите стороны

прямоугольника.

•3. Изобразите на координатной плоскости множество решений системы неравенств:

х² + у² 9,

y x + 1.

26. Не выполняя построения, найдите

координаты точек пересечения параболы

у = х² + 4 и прямой х + у = 6.

5. Решите систему уравнений:

2y - х = 7,

х² - ху - у²= 20.

Вариант 2

1. Решите систему уравнений

x - 3y = 2,

xy + y = 6.

• 2. Одна из сторон прямоугольника на 2 см

больше другой стороны. Найдите стороны

прямоугольника, если его площадь равна 120 см².

•3. Изобразите на координатной плоскости множество решений системы неравенств:

x² +у² 16,

х + у -2.

27. Не выполняя построения, найдите

координаты точек пересечения окружности

х² + у² = 10 и прямой х + 2у = 5.

5. Решите систему уравнений:

y - 3x = l,

х² - 2ху + у² = 9.

Контрольная работа №5 по алгебре в 9 классе

по теме «Арифметическая прогрессия»

Вариант 1

• 1. Найдите двадцать третий член арифметической прогрессии (а_n), если а₁ = -15 и d = 3.

• 2. Найдите сумму шестнадцати первых членов арифметической прогрессии: 8; 4; 0; ....

3. Найдите сумму шестидесяти первых членов последовательности (b_n), заданной формулой b_n = 3п - 1.

4. Является ли число 54,5 членом арифметической прогрессии (а_n), в которой а₁ = 25,5 и а₉ = 5,5?

5. Найдите сумму всех натуральных чисел, кратных 3 и не превосходящих 100.

Вариант 2

• 1. Найдите восемнадцатый член арифметической прогрессии (а_n),, если а₁ = 70 и d = -3.

• 2. Найдите сумму двадцати первых членов арифметической прогрессии: -21; -18; -15; ....

3. Найдите сумму сорока первых членов последовательности (b_n), заданной формулой b_n = 4п - 2.

4. Является ли число 30,4 членом арифметической прогрессии (а_n), в которой а₁ = 11,6 и а₁₅ = 17,2?

5. Найдите сумму всех натуральных чисел, кратных 7 и не превосходящих 150.

Контрольная работа №6 по алгебре в 9 классе

по теме «Геометрическая прогрессия»

Вариант 1

• 1. Найдите седьмой член геометрической прогрессии (b_n), если b₁ = -32 и q =.

• 2. Первый член геометрической прогрессии (b_n), равен 2, а знаменатель равен 3. Найдите сумму шести первых членов это прогрессии.

3. Найдите сумму бесконечной геометрической прогрессии: 24; -12; 6; ....

4. Найдите сумму девяти первых членов геометрической прогрессии (b_n), с положительными членами, зная, что b₂ = 0,04 и b₄ = 0,16.

5. Представьте в виде обыкновенной дроби бесконечную десятичную дробь: а) 0,(27); б) 0,5(6).

Вариант 2

• 1. Найдите шестой член геометрической прогрессии (b_n), если b₁ = 0,81 и q = - .

• 2. Первый член геометрической прогрессии (b_n), равен 6, а знаменатель равен 2. Найдите сумму семи первых членов это прогрессии.

3. Найдите сумму бесконечной геометрической прогрессии: -40; 20; -10; ... .

4. Найдите сумму восьми первых членов геометрической прогрессии (b_n), с положительными членами, зная, что b₂ = 1,2 и b₄ = 4,8.

5. Представьте в виде обыкновенной дроби бесконечную десятичную дробь: а) 0,(153); б) 0,3(2).

Контрольная работа №7 по алгебре в 9 классе

по теме «Элементы комбинаторики и теории вероятности»

Вариант 1

• 1. Сколькими способами могут разместиться 5 человек в салоне автобуса на пяти свободных местах.

• 2. Сколько трехзначных чисел, в которых нет одинаковых цифр, можно составить из цифр 1, 2, 5, 7, 9?

• 3. Победителю конкурса книголюбов разрешается выбрать две книги из 10 различных книг. Сколькими способами он может осуществить этот выбор?

• 4. В доме 90 квартир, которые распределяются по жребию. Какова вероятность того, что жильцу не достанется квартира на первом этаже, если таких квартир 6?

5. Из 8 мальчиков и 5 девочек надо выделить для работы на пришкольном участке 3 мальчиков и 2 девочек. Сколькими способами это можно сделать?

6. На четырех карточках записаны цифры 1, 3, 5, 7. Карточки перевернули и перемешали. Затем наугад последовательно положили эти карточки в ряд одну за другой и открыли. Какова вероятность того, что в результате получится число 3157?

Вариант 2

• 1. Сколько шестизначных чисел можно составить из цифр 1, 2, 3, 5, 7, 9 без повторений цифр?

• 2. Из 8 учащихся класса, успешно выступивших на школьной олимпиаде, надо выбрать двух для участия в городской олимпиаде. Сколькими способами можно сделать этот выбор?

• 3. Из 15 туристов надо выбрать дежурного и его помощника. Какими способами это можно сделать?

• 4. Из 30 книг, стоящих на полке, 5 учебников, а остальные художественные произведения. Наугад берут с полки одну книгу. Какова вероятность того, что она не окажется учебником?

5. Из 9 книг и 6 журналов надо выбрать 2 книги и 3 журнала. Сколькими способами можно сделать этот выбор?

6. На пяти карточках написаны буквы а, в, и, л, с. Карточки перевернули и перемешали. Затем наугад последовательно эти карточки положили в ряд и открыли. Какова вероятность того, что в результате получится слово "слива"

Итоговая контрольная работа

Вариант 1

• 1. Упростите выражение: .

2. Решите систему уравнений:

x - у = 6,

ху = 16.

• 3. Решите неравенство:

5х - 1,5 (2х + 3) < 4х + 1,5.

•4. Представьте выражение в виде степени с основанием а.

5. Постройте график функции у = х² - 4. Укажите, при каких значениях х функция принимает положительные значения.

6. В фермерском хозяйстве под гречиху было отведено два участка. С первого участка собрали 105 ц гречихи, а со второго, площадь которого на 3 га больше, собрали 152 ц. Найдите площадь каждого участка, если известно, что урожайность гречихи на первом участке была на 2 ц с 1 га больше, чем на втором.

Вариант 2

• 1. Упростите выражение: .

2. Решите систему уравнений:

x - у = 2,

ху = 15.

• 3. Решите неравенство:

2х - 4,5 > 6х - 0,5 (4х - 3).

•4. Представьте выражение в виде степени с основанием у.

5. Постройте график функции у = -х² + 1. Укажите, при каких значениях х функция принимает отрицательные значения.

6. Из пункта А в пункт В, расстояние между которыми 45 км, выехал велосипедист. Через 30 мин вслед за ним выехал второй велосипедист, который прибыл в пункт B на 15 мин раньше первого. Какова скорость первого велосипедиста, если она на 3 км/ч меньше скорости второго?

Тест за первую четверть (9 кл)

Вариант 1

Часть А.

К каждому заданию этой части даны 4 варианта ответа, из которых только один верный. Запишите цифру, которая обозначает номер выбранного Вами ответа.

A1. Какое из чисел является корнем уравнения х³+3х²+3х+1=0?

1) 1; 2) 0; 3)-1; 4) 2.

A2. Решением системы уравнений является пара чисел

1) (1;2); 2) (2;1) 3(-1;2); 4) (-1;-2).

A3. Сколько корней имеет уравнение х(х-1)(х-2)(х-3)(х+4) = 0?

1) 5: 2) 2; 3) 4; 4)6.

А 4. Найдите произведение корней уравнения х(х+1)(х-2,5)(х-0,45)(х+4)(х+5) = 0.

1) 45; 2) 0; 3) -22,5; 4)-225.

А5. Выполните деление многочленов: (6х³+19х²+19х+6): (3х+2).

1) 2х²-5х+3; 2) 2х²+5х+3; 3) х²-5х+3+2; 4) 2х²+5х-3.

Часть В.

К каждому заданию этой части записать краткий ответ.

B1. Сколько решений имеет система ?

B2. Сократите дробь .

Часть С.

Решения заданий этой части напишите аккуратно и разборчиво на листе

С1. Решите уравнение х³ - 3х² - 4х + 12=0.

С2. Разность двух положительных чисел равна 20, а их произведение равно 96. Найдите эти числа.

Критерии оценивания работы:

5 заданий базового уровня - «3»,

6-7 заданий - «4»,

8-9 заданий - «5».

Тест за первую четверть (9 кл)

Вариант 2

Часть А.

К каждому заданию этой части даны 4 варианта ответа, из которых только один верный. Запишите цифру, которая обозначает номер выбранного Вами ответа.

A1. . Какое из чисел является корнем уравнения х³-3х²+3х -1=0?

1) 1; 2) 0; 3)-1; 4) 2.

A2. Решением системы уравнений является пара чисел

1) (1;2); 2) (2;-1) 3(-1;2); 4) (-1;-2).

A3. Сколько корней имеет уравнение х(х+1)(х-2)(х-3)(х+4)(х+5) = 0?

1) 5: 2) 2; 3) 4; 4)6.

А 4. Найдите произведение корней уравнения х(х+2)(х-0,5)(х- 4,5)(х+5) = 0.

1) 4,5; 2) 0; 3) 22,5; 4)-22,5.

А5. Выполните деление многочленов: (6х³-х²-20х+12): (2х- 3).

1) 3х²+4х - 4; 2) 3х²+2х - 4; 3) 3х²+х - 4; 4) 3х²- 4х - 4;

Часть В.

К каждому заданию этой части записать краткий ответ.

B1. Сколько решений имеет система ?

B2. Сократите дробь .

Часть С.

Решения заданий этой части напишите аккуратно и разборчиво на листе.

С 1. Решите уравнение х³ - 2х² - 3х + 6=0.

С 2. Сумма двух чисел равна 20, а их произведение равно 96. Найдите эти числа.

Критерии оценивания работы:

5 заданий базового уровня - «3»,

6-7 заданий - «4»,

8-9 заданий - «5».

Тест за вторую четверть(9 кл)

Вариант 1

Часть А.

К каждому заданию этой части даны 4 варианта ответа, из которых только один верный. Запишите цифру, которая обозначает номер выбранного Вами ответа.

А1. Представьте в виде степени с рациональным показателем а³

1) а^3,25 2) а^3,4 3) а^2,6 4) а^3,5

А2. Запись числа 0,000024 в стандартном виде:

1) 24* 10^-6; 2)2,4*10^-5; 3) )2,4*10⁵; 4)0,24*10^-4.

А3. Вычислите .

1) 6; 2) 4; 3) -5; 4) -4.

А4.Упростите выражение .

1) а; 2) а²; 3) а^0,5; 4) а^-1.

А5. Найдите область определения функции у =.

1) х - любое число; 2)х-5; 3) х>-5; 4) х<-5.

А6.Укажите чётную функцию

1) у=х²+х; 2) у=х⁶+х⁴; 3) у= х²+х-6; 4) у=.

А7.Найти наименьшее значение функции, изображённой на рисунке.

1) 1; 2) -2; 3) 4; 4) -1.

Часть В.

К каждому заданию этой части записать краткий ответ.

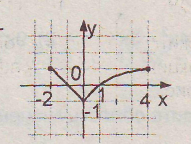
В1. Укажите промежуток возрастания функции, заданной графически на рисунке.

В2. При каких значениях х функция принимает отрицательные значения? (см. рисунок)

В3.Найдите значение выражения 4^1,5 - .

Часть С.

Решения заданий этой части напишите аккуратно и разборчиво на листе.

С1.Постройте график функции у = и опишите её свойства.

С2.Упростите выражение .

Тест за вторую четверть(9 кл)

Вариант 2

Часть А.

К каждому заданию этой части даны 4 варианта ответа, из которых только один верный. Запишите цифру, которая обозначает номер выбранного Вами ответа.

А1. Представьте в виде степени с рациональным показателем а³

1) а^3,75 2) а^3,4 3) а^2,25 4) а^3,3

А2. Запись числа 0,0000524 в стандартном виде:

1)524*10^-7; 2) 5,24*10^-5 ; 3) 5,24*10⁵ ; 4) 0,524*10^-4.

А3. Вычислите

1)-10; 2) -9; 3)-10,5; 4) -9,5.

А4.Упростите выражение .

1) а; 2) а²; 3) а^0,5; 4) а^-1.

А5. Найдите область определения функции у =.

1) х - любое число; 2)х-5; 3) х-5; 4) х=-5.

А6.Укажите нечётную функцию

1) у=х³+х; 2) у=х⁵+х⁴; 3) у= х²+х-6; 4) у=.

А7. Найти наибольшее значение функции, изображённой на рисунке.

1) -3; 2) 2; 3) 3; 4) -1.

Часть В.

К каждому заданию этой части записать краткий ответ.

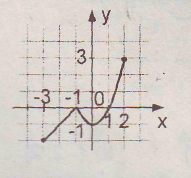
В1. Укажите промежуток убывания функции, заданной графически на рисунке.

В2. При каких значениях х функция принимает положительные значения? (см. рисунок)

В3. Найдите значение выражения - .

Часть С.

Решения заданий этой части напишите аккуратно и разборчиво на листе.

С1.Постройте график функции у = и опишите её свойства.

С2.Упростите выражение .

9 класс

Тест за третью четверть

Вариант 1

Часть А.

К каждому заданию этой части даны 4 варианта ответа, из которых только один верный. Запишите цифру, которая обозначает номер выбранного Вами ответа.

А1.Найдите градусную меру угла .

1) 100 2) 200 3) 50 4) 185

А2. Вычислите (2 sin + tg): cos .

1) 1; 2) 2; 3) 3; 4) 4.

А3. Определите четверть, в которой расположена точка, полученная поворотом точки

Р(1; 0) на заданный угол .

1)1 четв.; 2) 2 четв.; 3) 3 четв.; 4) 4 четв.

А4. Укажите пять первых членов последовательности, заданной формулой ее п-го члена

а_п = п ² (п - 3).

1) -2, -4, 0, 16, 50; 2) 1, 2, 3. 4, 5; 3) 0, -2, -4, -16, -50; 4) -4, -2, 0, 16, 50;

А5. Четвёртый член арифметической прогрессии 13; 9: … равен

1) 1; 2) 6; 3) -1; 4) 0.

А6. В геометрической прогрессии в₁=2, q =3. Найдите в₅.

1)162; 2) 180; 3)324; 4) 81.

А7. Число -22 является членом арифметической прогрессии 44, 38,32, …. Найдите его номер.

1) 13; 2) 12; 3) 11; 4)10.

Часть В.

К каждому заданию этой части записать краткий ответ.

В1. Определите знаки sin, cos , tg , если = .

В2. Найдите сумму первых десяти членов арифметической прогрессии 5; 2; -1;…

В3. В геометрической прогрессии в₁=72, в₂=8. Найдите q.

Часть С.

Решения заданий этой части напишите аккуратно и разборчиво на листе.

С1.Сумма первого и третьего членов геометрической прогрессии равна 10, а сумма второго и четвёртого её членов равна -20. Найти сумму шести первых членов прогрессии.

С2.Чему равно число членов арифметической прогрессии -2; 2; …, меньших 55.

9 класс

Тест за третью четверть

Вариант 2

Часть А.

К каждому заданию этой части даны 4 варианта ответа, из которых только один верный. Запишите цифру, которая обозначает номер выбранного Вами ответа.

А1. Найдите радианную меру угла 140.

1) ; 2) ; 3) ; 4) .

А2. Вычислите (2 cos - tg) : sin

1) 1; 2) 2; 3) 3; 4) 0.

А3. Определите четверть, в которой расположена точка, полученная поворотом точки

Р(1; 0) на заданный угол .

1)1 четв.; 2) 2 четв.; 3) 3 четв.; 4) 4 четв.

А4. Укажите пять первых членов последовательности, заданной формулой ее п-го члена

а_п= п³(п - 4).

1)-3, -16, -27, 0, 125; 2) 0, -3, -16, -27, -125; 3) 1, 2, 3, 4, 5; 4) -27, -16, -3, 0, 125.

А5. Первый член арифметической прогрессии а_1; а₂; 4; 8; … равен

1) 1; 2) 12; 3) -4; 4)-1.

А6. В геометрической прогрессии в₁=3, q =2. Найдите в₆.

1) 96; 2) 48; 3) 36; 4)192.

А7. Число -61 является членом арифметической прогрессии 1; -5; …. Найдите его номер.

1) 12; 2) 11; 3) 10; 4) 9.

Часть В.

К каждому заданию этой части записать краткий ответ.

В1. Определите знаки sin, cos, tg , если = 200.

В2. Найдите сумму первых десяти членов арифметической прогрессии 7; 1;…

В3. В геометрической прогрессии в₁=36, в₂=9. Найдите q.

Часть С.

Решения заданий этой части напишите аккуратно и разборчиво на листе.

С1.Разность между вторым и первым членами геометрической прогрессии равна -3, а разность между третьим и вторым её членами равна -6. Найдите сумму пяти её первых членов.

С2. Чему равно число членов арифметической прогрессии -12;-8; …, меньших 48.