- Учителю
- Міні-збірник. Квадратні рівняння. 8Клас
Міні-збірник. Квадратні рівняння. 8Клас
Т.Г. Балюк
Міні - збірник
Квадратні рівняння 






8
Балюк Тетяна Григорівна, вчитель математики, Криворізька загальноосвітня школа І- ІІІ ступенів № 99
Міні-збірник. Квадратні рівняння (13 стор)
Збірник містить завдання, які дають змогу ефективно здійснювати повний контроль за засвоєнням учнями теми «Квадратні рівняння». Крім того, збірник може використовуватися школярами для самостійної роботи.
Розраховано на учнів загальноосвітніх навчальних закладів та вчителів математики.
Рівняння виду а +bх +с = 0, де х - змінна, а, b, с - числа, причому а
+bх +с = 0, де х - змінна, а, b, с - числа, причому а 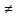 0, називається квадратним.
0, називається квадратним.
Число а називають першим (старшим) коефіцієнтом, b - другим коефіцієнтом, с - вільним членом.
Квадратне рівняння, в якому хоча б один із коефіцієнтів ( b або с ) дорівнює нулю, називають неповним квадратним рівнянням.
Неповні квадратні
рівняння
а = 0,
= 0,
х = 0
а +bх = 0,
+bх = 0,
х(ах + b) = 0,
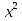 = 0,
= 0, 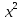 = -
= -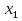
а = 0,
= 0,
х = 0
а +вх = 0,
+вх = 0,
х(ах + в) = 0,
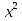 = 0,
= 0, 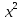 = -
= -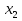
а + с = 0,
+ с = 0,
 = -
= -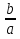
при ас 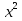 0 при ас
0 при ас 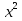 0
0
х = 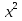 коренів немає
коренів немає
1.Доберіть до кожного квадратного рівняння його розв'язок.
А
Б
В
Г
Д
Е
А) 5 = 0 ; 1) 0; 1
= 0 ; 1) 0; 1
Б)  - х = 0 ; 2) 7 ; - 7;
- х = 0 ; 2) 7 ; - 7;
В) 25 = 121; 3) 0 ;
= 121; 3) 0 ;
Г)  - 49 = 0 ; 4) 0 ; 2,5 ;
- 49 = 0 ; 4) 0 ; 2,5 ;
Д) 2 - 5х = 0; 5) -2 ; 0 ;
- 5х = 0; 5) -2 ; 0 ;
Е)  + 2х = 0 ; 6)
+ 2х = 0 ; 6) 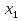 2,2 ;
2,2 ;
2. Розв'яжіть рівняння:
1) 7 = 0 ; 2) 33
= 0 ; 2) 33 = 0 ; 3)4
= 0 ; 3)4 + 7х = 0 ;
+ 7х = 0 ;
4) 11 =0,5х ; 5) 0,04
=0,5х ; 5) 0,04 + 5х = 0 ; 6) 13х = 0,26
+ 5х = 0 ; 6) 13х = 0,26  ;
;
7) 7,5х = 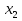 ; 8)
; 8)  - 144 = 0 ; 9) 64
- 144 = 0 ; 9) 64 = 169 ;
= 169 ;
10) 7 = 1575 ; 11) 11
= 1575 ; 11) 11 =704 ; 12) 0,09
=704 ; 12) 0,09 - 100 = 0 ;
- 100 = 0 ;
13) 625 - 0,0324 = 0 ; 14)
- 0,0324 = 0 ; 14) 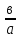 - 441 = 0 ;
- 441 = 0 ;
15) 9 +
+ 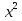 =
= 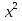 ; 16) 225
; 16) 225 +
+ 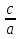 =
= 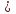 ;
;
17) 4 + 6х = 9
+ 6х = 9 - 15х ; 18) 13х +7
- 15х ; 18) 13х +7 = 5
= 5 + 8х;
+ 8х;
19) 12 - 5х = 9
- 5х = 9 +7х ; 20) 8,5х - 3
+7х ; 20) 8,5х - 3 = 3,5х + 2
= 3,5х + 2 ;
;
21) х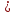 = 3
= 3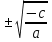 ; 22) 47 - х
; 22) 47 - х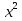 = 2
= 2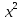 - 62;
- 62;
23)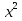 +
+ 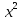 = 102 ;
= 102 ;
24) 10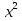 + 19 =
+ 19 = 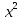 ;
;
25) 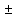 +
+ 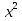 -
- 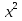 = 2
= 2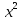 ;
;
26)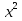 -
- 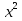 =3; 27)
=3; 27)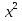 +
+ 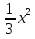 =10;
=10;
28)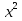 +
+ 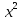 =2; 29)
=2; 29)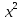 -
- 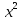 =3
=3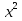 ;
;
Повні квадратні
рівняння
а +bх +с = 0
+bх +с = 0
якщо b = 2к, тобто
b - парне число, то
х = 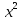 ,
,
де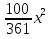 =
= 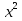 - ас,
- ас,
к = 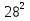
універсальна формула
х = 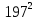 ,
,
де Д = 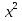 - 4ас
- 4ас
Дослідження кількості коренів квадратного рівняння
Д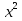 0 2 різні корені:
0 2 різні корені: 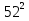 =
= 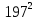 ;
;
Д = 0 2 рівні корені: 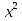 =
= 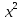 =
= 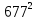 ;
;
Д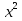 0 коренів немає
0 коренів немає
А
Б
В
Г
Д
3.Доберіть до кожного квадратного рівняння його числові коефіцієнти.
А)  - 2х - 2 = 0; 1) а = 2, в = -5, с =2;
- 2х - 2 = 0; 1) а = 2, в = -5, с =2;
Б) 6  - 7х + 2 = 0; 2) а = 1, в = -2, с = -2;
- 7х + 2 = 0; 2) а = 1, в = -2, с = -2;
В) 8  + 10х - 3 = 0; 3) а = 6, в = -7, с =2;
+ 10х - 3 = 0; 3) а = 6, в = -7, с =2;
Г) -  - 6х +5 = 0; 4) а = 8, в = 10, с = -3;
- 6х +5 = 0; 4) а = 8, в = 10, с = -3;
Д) 2  - 5х+ 2 = 0; 5) а = -1, в = -6, с =5.
- 5х+ 2 = 0; 5) а = -1, в = -6, с =5.
А
Б
В
Г
Д
4.Ідентифікуйте парами рівняння і його дискримінант.
А) 25  - 10х +1 = 0; 1)Д = 121;
- 10х +1 = 0; 1)Д = 121;
Б) 2  - х - 6 = 0; 2)Д = 0;
- х - 6 = 0; 2)Д = 0;
В) 10  - 7х - 3 = 0; 3)Д = 169;
- 7х - 3 = 0; 3)Д = 169;
Г) -3  +7х +6 = 0; 4)Д = 16;
+7х +6 = 0; 4)Д = 16;
Д)  + 2х - 3 = 0; 5) Д = 49.
+ 2х - 3 = 0; 5) Д = 49.
Д = 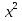 - 4ас
- 4ас
5.Знайдіть корені рівняння:
1) 2 + 3х + 1 = 0; 2) 2
+ 3х + 1 = 0; 2) 2 - 3х + 1 = 0;
- 3х + 1 = 0;
3) 2 + 5х +2 = 0; 4) 2
+ 5х +2 = 0; 4) 2 - 7х + 3= 0;
- 7х + 3= 0;
5) 3 + 11х + 6 = 0; 6) 4
+ 11х + 6 = 0; 6) 4 - 11х + 6 = 0;
- 11х + 6 = 0;
7) 9 - 6х + 1 = 0; 8) 16
- 6х + 1 = 0; 8) 16 - 8х + 1 = 0;
- 8х + 1 = 0;
9) 49 + 28х + 4 = 0; 10)36
+ 28х + 4 = 0; 10)36 + 12х + 1 = 0;
+ 12х + 1 = 0;
11) 2 + х + 1 = 0; 12) 3
+ х + 1 = 0; 12) 3 - х + 2 = 0;
- х + 2 = 0;
13) 5 + 2х + 3 = 0; 14)
+ 2х + 3 = 0; 14)  - 2х + 10 = 0;
- 2х + 10 = 0;
15) 7 - 6х + 2 = 0; 16) 3
- 6х + 2 = 0; 16) 3 - 5х + 4= 0;
- 5х + 4= 0;
17) 9 + 12х + 4 = 0; 18) 4
+ 12х + 4 = 0; 18) 4 - 20х + 25 = 0;
- 20х + 25 = 0;
19) 4 + 12х + 9 = 0; 20)
+ 12х + 9 = 0; 20)  - 3х -4 = 0;
- 3х -4 = 0;
21) 6 = 5х + 1 ; 22) 5
= 5х + 1 ; 22) 5 +1 = 6х;
+1 = 6х;
23) х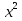 = 72; 24) х
= 72; 24) х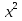 = 56;
= 56;
25) 2х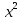 = 8х - 3; 26) 3х
= 8х - 3; 26) 3х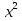 - 1 = х - 0,5
- 1 = х - 0,5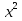 ;
;
27)  - 3
- 3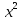 х + 4 = 0; 28)
х + 4 = 0; 28)  + 2
+ 2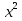 х + 8
х + 8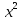 = 0;
= 0;
29)  - 3х - 5 -
- 3х - 5 -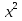 = 0;
= 0;
30) 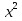 + х = 11; 31)
+ х = 11; 31) 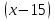 =
= 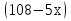 ;
;
32) 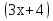 -
- 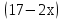 =
= 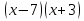 ; 33)
; 33) 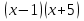 -
- 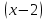 = 0,3 ;
= 0,3 ;
34) 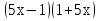 =
= 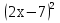 ;
;
35) 3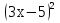 = 8
= 8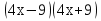 ;
;
36)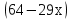 -
- 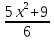 = 1 ;
= 1 ;
37) 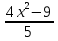 +
+ 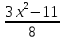 = 12;
= 12;
38) 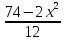 =
= 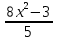 - 14х - 2;
- 14х - 2;
39) 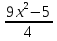 -
- 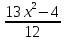 + 18 = 0;
+ 18 = 0;
40) 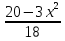 -
- 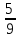 + 16 = 0;
+ 16 = 0;
41) 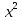 - 2
- 2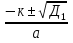 -
- 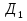 = 0;
= 0;
42) 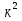 -
- 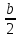 -
- 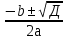 = 0;
= 0;
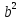 43)
43) 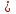 =
= 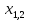 ;
;
44) 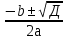 +
+ 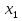 = 1 +
= 1 + 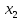 ;
;
45) 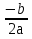 + 1 -
+ 1 - 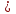 =
= 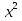 ;
;
46) 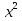 -
- 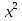 = 6 -
= 6 - 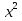 ;
;
47) 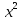 -
- 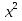 +
+ 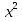 =
= 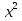 + 5 ;
+ 5 ;
48) 6х + 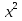 =
= 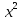 -
-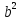 ;
;
49) х - 7 + 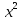 =
= 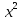 -
- 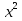 ;
;
Д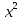 6. Знайдіть при якому значенні b рівняння має один корінь.
6. Знайдіть при якому значенні b рівняння має один корінь.
1) 5 - bх + 5 = 0; 2) 3
- bх + 5 = 0; 2) 3 - bх + 3 = 0;
- bх + 3 = 0;
3)2 + 4х - b = 0; 4)6
+ 4х - b = 0; 4)6 - 18х + b = 0;
- 18х + b = 0;
5) 3 - bх + 12 = 0; 6) 8
- bх + 12 = 0; 6) 8 + bх + 2 = 0;
+ bх + 2 = 0;
7) 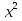 -
- 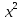 х + 3 = 0;
х + 3 = 0;
8)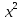 +
+ 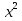 х + 15 = 0;
х + 15 = 0;
7.Розв'яжіть рівняння враховуючи парність другого коефіцієнта:
1) 8  - 30х +27 = 0; 2)
- 30х +27 = 0; 2)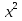 + 4х +1 = 0; 3)
+ 4х +1 = 0; 3)  + 8х - 33 = 0;
+ 8х - 33 = 0;
4)  + 12х +35 = 0; 5)
+ 12х +35 = 0; 5) - 4х -45 = 0; 6)
- 4х -45 = 0; 6)  - 2х + 1 = 0;
- 2х + 1 = 0;
7)  + 14х +24 = 0; 8)
+ 14х +24 = 0; 8)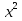 - 14х +16 = 0; 9)7
- 14х +16 = 0; 9)7 - 20х + 14 = 0;
- 20х + 14 = 0;
10)  + 12х - 64 = 0; 11)
+ 12х - 64 = 0; 11) - 10х - 25 = 0; 12)5
- 10х - 25 = 0; 12)5 + 26х -24 = 0;
+ 26х -24 = 0;
13)  + 6х -19 = 0; 14)
+ 6х -19 = 0; 14)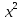 - 12х +1 = 0; 15)8
- 12х +1 = 0; 15)8 - 14х + 5 = 0;
- 14х + 5 = 0;
Увага! Параметр!8.При якому значенні а рівняння 3  - 2х - а = 0
- 2х - а = 0
1) має два різні корені;
2) не має жодного кореня;
3) має два рівні корені.
9. Розв'яжіть рівняння відносно х:
1) 8  - 13ах +36
- 13ах +36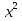 = 0; 2)
= 0; 2) - 3ах - 40
- 3ах - 40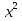 = 0;
= 0;
3)  + 2bх +
+ 2bх +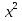 -1 = 0; 4)
-1 = 0; 4)  -
- 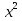 х -8а = 0;
х -8а = 0;
5)  +
+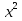 х - 6а = 0; 6)
х - 6а = 0; 6)  + 5ах +4
+ 5ах +4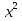 = 0;
= 0;
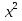 -
- 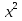 х +10а - 6 = 0;
х +10а - 6 = 0;

ТеоремаВієта
а + bх + с = 0
+ bх + с = 0
Якщо 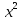 - корені рівняння, то
- корені рівняння, то
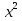
Зведені квадратні рівняння - це рівняння виду  + рх + q = 0.
+ рх + q = 0.
Якщо 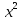 - корені зведеного квадратного рівняння
- корені зведеного квадратного рівняння
 + рх + q = 0 , то
+ рх + q = 0 , то 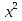
10.Знайдіть « підбором» корені рівняння:
1)  + 3х +2 = 0; 2)
+ 3х +2 = 0; 2) - 6х +5 = 0; 3)
- 6х +5 = 0; 3)  - 2х + 1 = 0;
- 2х + 1 = 0;
4)  + 2х - 35 = 0; 5)
+ 2х - 35 = 0; 5) - 3х + 2= 0; 6)
- 3х + 2= 0; 6)  + 6х + 8 = 0;
+ 6х + 8 = 0;
7)  - 3х - 4 = 0; 8)
- 3х - 4 = 0; 8) + 6х -16 = 0; 9)
+ 6х -16 = 0; 9)  - 6х + 9 = 0;
- 6х + 9 = 0;
10) 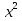 + 8у +7 = 0; 11)
+ 8у +7 = 0; 11) - 5х +4 = 0; 12)
- 5х +4 = 0; 12) 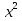 -7у + 12 = 0;
-7у + 12 = 0;
13)  + 2х -3 = 0; 14)
+ 2х -3 = 0; 14)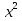 -2у- 3 = 0; 15)
-2у- 3 = 0; 15)  - 4х - 12 = 0;
- 4х - 12 = 0;
16)  + 4х - 5 = 0; 17)
+ 4х - 5 = 0; 17) - х - 2 = 0; 18)
- х - 2 = 0; 18)  +7х - 18 = 0;
+7х - 18 = 0;
19) 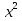 -5у- 6 = 0; 20)
-5у- 6 = 0; 20) +5х + 6 = 0; 21)
+5х + 6 = 0; 21) 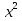 -7у + 10 = 0;
-7у + 10 = 0;
22)  -8х +12 = 0; 23)
-8х +12 = 0; 23) - х -12 = 0; 24)
- х -12 = 0; 24)  + х -6 = 0;
+ х -6 = 0;
25)  + 5х -14 = 0; 26)
+ 5х -14 = 0; 26) - 11х +18 = 0; 27)
- 11х +18 = 0; 27)  +7х + 6 = 0;
+7х + 6 = 0;
28)  + 3х -18 = 0; 29)
+ 3х -18 = 0; 29) + 4х + 4 = 0; 30)
+ 4х + 4 = 0; 30)  +5х + 4 = 0;
+5х + 4 = 0;
31)  + 2х +1 = 0; 32)
+ 2х +1 = 0; 32) +4х +3 = 0; 33)
+4х +3 = 0; 33)  - 4х + 3 = 0;
- 4х + 3 = 0;
34)  + 3х +2 = 0; 35)
+ 3х +2 = 0; 35) - 6х +5 = 0; 36)
- 6х +5 = 0; 36)  + х -2 = 0;
+ х -2 = 0;
37)  - 8х +16 = 0; 38)
- 8х +16 = 0; 38)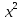 = 0; 39)
= 0; 39)  - х - 72 = 0;
- х - 72 = 0;
40)  + 18х +81 = 0; 41)
+ 18х +81 = 0; 41)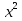 = 0; 42)
= 0; 42)  - х - 42 = 0;
- х - 42 = 0;
43)2 х - - 1 = 0; 44)
- 1 = 0; 44) - 2
- 2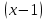 х -1= 0; 45)
х -1= 0; 45)  - 2
- 2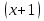 х + 1 = 0;
х + 1 = 0;
46)  +
+ 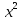 х - 4 = 0;
х - 4 = 0;
11.Складіть квадратне рівняння, корені якого дорівнюють:
1) 2 і 9; 2) 4 і - 3; 3) 6 і 2;
4)- 2 і 6; 5) 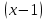 і 2; 6) 2
і 2; 6) 2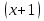 і
і 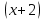 ;
;

Рівняння,що зводяться до квадратних
Дробово-раціональні
Рівняння,що розв'язуються способом введення нової змінної
Рівняння,що зводяться до добутку, який дорівнює 0
Біквадратні
а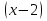 +b
+b +с = 0
+с = 0
12.Розв'яжіть біквадратне рівняння:
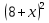 - 5
- 5 + 4 = 0;
+ 4 = 0; 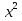 -3
-3 - 4 = 0;
- 4 = 0; 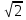 -10
-10 + 9 = 0;
+ 9 = 0;
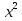 +3
+3 -12 = 0;
-12 = 0; 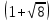 +7
+7 + 5 = 0;
+ 5 = 0; 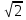 -13
-13 +36 = 0;
+36 = 0;
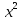 -10
-10 + 1 = 0;
+ 1 = 0; 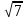 -20
-20 + 10 = 0;
+ 10 = 0; 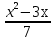 -4
-4 -45 = 0;
-45 = 0;
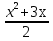 +6
+6 -35 = 0;
-35 = 0; 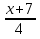 - 5
- 5 + 2 = 0;
+ 2 = 0; 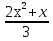 -10
-10 + 3 = 0;
+ 3 = 0;
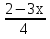 +23
+23 + 3 = 0;
+ 3 = 0; 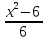 +41
+41 + 5 = 0;
+ 5 = 0; 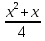 -24
-24 + 9 = 0;
+ 9 = 0;
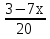 -20
-20 + 4 = 0;
+ 4 = 0; 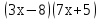 -8
-8 -9 = 0;
-9 = 0; 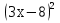 +23
+23 -12 = 0;
-12 = 0;
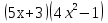 -409
-409 + 225 = 0;
+ 225 = 0; 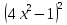 - 5
- 5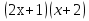 + 49 = 0;
+ 49 = 0; 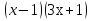 -3
-3 -4 = 0;
-4 = 0;
13.Розв'яжіть рівняння, використовуючи метод заміни змінної:
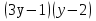 - 3
- 3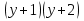 -4 = 0;
-4 = 0; 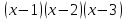 + 2
+ 2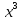 -8 = 0;
-8 = 0;
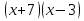 -28
-28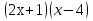 + 171 = 0;
+ 171 = 0; 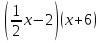 )
) 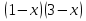 +4
+4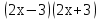 +3 = 0;
+3 = 0;
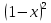 = 15
= 15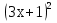 -50; 6)
-50; 6) 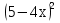 = 14
= 14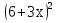 -45;
-45;
7)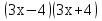 = - 40; 8)
= - 40; 8)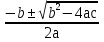 = - 24;
= - 24;
9)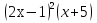 = 2; 10)
= 2; 10)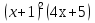 = 12;
= 12;
11) х +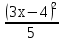 = 6; 12) х -
= 6; 12) х - 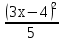 = 12; 13) х -3
= 12; 13) х -3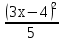 +2 = 0;
+2 = 0;
14) 2х - 3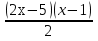 = 0; 15)8х -10
= 0; 15)8х -10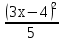 +3= 0; 16) х +
+3= 0; 16) х +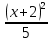 = 7;
= 7;
18) у -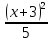 = 5; 19) у +
= 5; 19) у +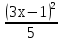 = 96;
= 96;
14.Розв'яжіть рівняння:
1) 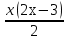 +
+ 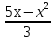 = 2
= 2 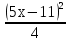 ; 2)
; 2) 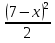 +
+ 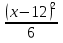 = 5
= 5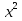 ;
;
3) 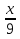 +
+ 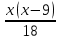 = 3
= 3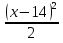 ; 4)
; 4) 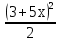 -
- 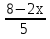 = 8
= 8 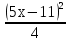 ;
;
5) 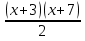 - 15 = 8х; 6) 1 -
- 15 = 8х; 6) 1 - 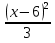 =
= 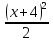 ; 7) х - 25 =
; 7) х - 25 = 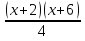 ;
;
8) 1 - 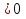 =
= 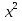 ; 9) х -
; 9) х - 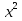 = 1; 10) 7 - 2х =
= 1; 10) 7 - 2х = 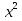 ;
;
15)Розв'яжіть рівняння, розклавши ліву частину на множники:
1) 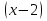 +
+ 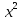 - 5
- 5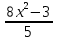 - 5
- 5 +4х + 4 = 0; 2)
+4х + 4 = 0; 2) 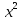 -
- 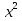 - 4
- 4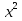 = 0;
= 0;
3) 2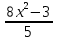 + 2
+ 2 =
= 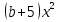 ; 4) 6
; 4) 6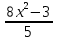 - 31
- 31 - 31х + 6 = 0;
- 31х + 6 = 0;
5) 5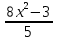 - 19
- 19 - 38х + 40 = 0.
- 38х + 40 = 0.

16) Завдання для самостійної роботи
1
х² = 16
х² - х = 0
8х² + 5х = 0
х² - 2х -2 = 0
4у² = 4у - 15
2
у² = 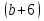
у² + 100у = 0
-2х² + 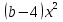 = 0
= 0
х² + 3х+ 4= 0
2х² = 5х + 3
3
х² = 1
х² - 8х = 0
2у² -26у = 0
у² +6у = 5
-х²= 5х - 14
4
z² = 8
5у² + у = 0
у² + 6у = 0
х² - 2х + 2= 0
5х²- 9х - 2 = 0
5
х² = - 4
у - 4у² = 0
- 3х² + 21х = 0
х² -4х + 4 = 0
3х²- 2х + 1 = 0
6
- х² = - 0,2
2х² - 6х = 0
-х² + 10 = 1
х² + х - 2 = 0
-х²+ 5х -1 = 0
7
- х² = 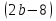
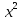
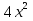 х² - 3х = 0
х² - 3х = 0
у² + 2у = 0
х²- 4х + 3 = 0
-у²- у + 12 = 0
8
- 2 t² = - 4
5z² + 2z = 0
3у² = 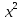
х² -2х - 1 = 0
х²+ 5х -1 = 0
9
1,2 х² = 1
3х² = 4х
2х² - 8х = 0
у² + 2у -1= 0
у²+8у +16 = 0
10
16у² - 1 = 3
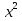 х² = - 3х
х² = - 3х
х² - 5х = 0
у² +4у + 2= 0
х²- х - 6 = 0
11
4х² - 5 = 0
1,2х² - 6х = 0
0,1х² = -0,3х
х² + 4х +3= 0
у²+ 11у+30= 0
12
3х² - 12 = 0
0,7х - 7х² = 0
6у² + 3у = 0
-у² +6у- 5= 0
х²- х - 2 = 0
13
- 3х² - 48 = 0
2у² - 0,6 у = 0
-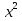 х² = 394
х² = 394
х²+3х - 4 = 0
4х²+ 3х -1 = 0
14
z² - 8 = 8
0,5х² = 4х
1,25 = у² - 5
х²+ х + 2 = 0
16у² +8у+1= 0
15
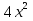 х² - 4 = 28
х² - 4 = 28
-0,8у² +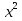 у = 0
у = 0
0,4х²- 2х = 0
-х²+ 6х+5 = 0
х²-12х +32 = 0
16
0,4у² + 1,6 = 8
0,2х² - 6х = 0
- 8х² + 0,5х = 0
х²- 4х -3 = 0
у²- 8у - 8 = 0
17
0,5х² +14 = 16
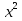 х² - 0,2х = 0
х² - 0,2х = 0
1,3 х²- 16,9 = 0
у²+6у - 9 = 0
7х²-11х- 6 = 0
18
- 0,4х² +2 = 0
-0,3х² - 12х = 0
3х² = 4х
х²- х + 90 = 0
3у²-10у +3 = 0
19
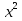 х² = -
х² = -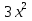
4у² - 26у = 0
х² - 121 = 0
6у² -7у+2 = 0
х²+х + 4 = 0
20
у² = 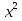
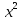
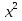 х² - 27х = 0
х² - 27х = 0
х² + 13х = 0
8х²+10х-3 =0
-х²+6х - 25 =0