Обучение учащихся решению текстовых задач в 5-6 классах

Обучение учащихся решению текстовых задач в 5-6 классах

Раздел 1

Задачи трех типов

1 Задачи на нахождение двух чисел по сумме

и кратному отношению.

Основные понятия в задачах на нахождение двух чисел по сумме и кратному отношению.

В задачах данного типа дается отношение величин, которое является отвлеченным данным и поэтому более трудно детьми воспринимается. Но, кроме этого, при их решении величины выражаются частями - условными единицами измерения.

Поэтому, чтобы решить задачу на нахождение чисел по сумме и кратному отношению, учащиеся должны:

1. понимать части - условные единицы измерения;

2. понимать отношение величин, уметь заменять части отношением величин и наоборот, а также уметь практически делить величину на части в нужном отношении.

Примеры решения задач.

Схема задачи:

100, 4, , .

 - обозначены искомые числа.

Условие задачи:

В магазине было черного сукна в 4 раза больше, чем серого. Всего в магазине было 100 м сукна.

Сколько было черного и серого сукна в отдельности?

Решение.

Пусть серого сукна было х метров, тогда черного х*4 = 4х (метров).

Всего было 100 м. Поэтому х + 4 х = 100.

Мы составили уравнение. Решим его.

5 х = 100;

х = 20

Ответ: 20 м серого сукна и 20*4 = 80 (м) черного сукна.

2. Задачи на нахождение чисел по разностному

и кратному отношению.

Пример решения задачи.

Схема задачи:

60, 4, , .

Условие задачи:

В магазине было черного сукна в 4 раза или на 60 м больше чем серого.

Сколько было черного и серого сукна в отдельности?

Решение.

Пусть серого сукна было у метров, тогда черного у*4 = 4у (метров).

Поэтому 4у - у = 60 или 3у = 60;

у = 20

Ответ: 20 м серого сукна и 20*4 = 80 (м) черного сукна.

Задачи на нахождение чисел по сумме и разности.

Примеры решения задачи.

Схема задачи:

, , 100 м, 60 м,

Условие задачи:

В магазине было серое и черное сукно всего 100 м. Черного сукна было на 60 м больше чем серого.

Сколько было черного и серого сукна в отдельности?

Решение (1-й способ).

Пусть серого сукна было к метров, тогда черного (к+60) м так как черного было на 60 м больше чем серого.

Всего сукна было 100 м.

Составим уравнение:

к + 60 + к = 100

60 + 2к = 100

2к = 40

к = 20

Ответ: на складе было 20 м серого сукна, а черного -

20 + 60 = 80 м.

Решение (2-й способ).

Пусть черного сукна было у метров, тогда серого (у - 60) м так как серого было на 60 м меньше чем черного.

Всего сукна было 100 м.

Составим уравнение:

у - 60 + у = 100

2у = 160

у = 80

Ответ: на складе было 80 м черного сукна, а серого -

80 - 60 = 20 м.

Составление задач данных трех типов: сумма чисел, разностное отношение, кратное отношение.

При составлении задач приходится заранее сравнивать (связывать) числа, которые в условии задачи будут неизвестными.

Пусть мы хотим составить задачу с такими данными: 20 м серого сукна и 80 м черного сукна.

Существует три способа " связывания" данных:

1.Сложением (найдем сумму чисел):

20+80=100(м) было всего сукна.

2.Вычитанием (найдем разностное отношение):

80-20=60(м)

На 60 м было больше черного сукна, чем серого.

3.Делением (найдем кратное отношение):

80:20=4(раза)

В 4 раза было больше черного сукна, чем серого.

Для составления задач нам надо выбрать два числа из трех полученных нами результатов сравнения: 100, 60, 4.

Получаем следующую таблицу задач:

Задачи для работы в классе.

1.а) Школа-интернат заготовила всего 4500 кг капусты и картофеля, причем картофеля было заготовлено в 8 раз больше, чем капусты. Сколько заготовили капусты и картофеля в отдельности?

б) Школа-интернат заготовила картофеля на 3500 кг больше, чем капусты. Всего было заготовлено картофеля и капусты 4500 кг. Сколько заготовили капусты и картофеля в отдельности?

в) Школа-интернат заготовила картофеля на 3500 кг больше, чем капусты, причем картофеля было заготовлено в 8 раз больше, чем капусты. Сколько заготовили капусты и картофеля в отдельности?

2. В двух ящиках лежат помидоры. Во втором ящике в 3 раза больше помидоров, чем в первом. Сколько помидоров в обоих ящиках, если в первом ящике 12 кг?

3. У мальчика было 16 почтовых марок. Он купил еще несколько марок, после этого подарил младшему брату 23 марки, и у него осталось 19 марок. Сколько марок купил мальчик?

4. В пакете было 350 г сахара. Когда в него добавили еще сахару, в нем стало 900 г. Сколько граммов сахару добавили в пакет?

5. В двух карманах было 28 орехов, причем в левом кармане в 3 раза больше, чем в правом. Сколько орехов было в каждом кармане?

Задачи для самостоятельного решения

1. Проволоку длиной 135 м разрезали на две части так, что одна из них короче другой в 2 раза. Найти длину каждой части.

2. В первую смену на фабрике работает на 50 рабочих больше, чем во вторую. Всего в двух сменах работает 650 рабочих. Сколько рабочих работает в каждую смену в отдельности?

3.По данных предыдущей задачи составить задачу на нахождение двух чисел по сумме и кратному отношению. Решить составленную задачу.

4. При первой космической скорости космический корабль может вращаться вокруг земли, не падая на нее. При третьей космической скорости космический корабль может покинуть пределы солнечной системы и навсегда улететь во Вселенную. Третья космическая скорость в 4 раза, или на 24 км/с больше первой космической скорости. Найти первую и третью космические скорости.

5. Площадь двух комнат квартиры равна 49,5 м². Одна комната имеет площадь в 1,25 раза большую, чем другая комната. Какова площадь каждой комнаты?

6. На основе предыдущей задачи составить и решить задачу по схеме: 22 м²;  ; 49,5 м².

7. Составить и решить задачи на нахождение двух чисел:

а) по сумме и разности ; ; ; .

б) по сумме и кратному отношению: ; в раза; ;.

в) по разности и кратному отношению ; в раза ;.

8. В первый день скосили 40 га посевов; во второй день в 2 раза , чем в первый день. В третий день скосили на 15 га , чем во второй день.

Сколько гектаров скосили в третий день?

9. Дед старше отца на 35 лет. Отец старше сына в 7 раз. Всем троим 110 лет.

Сколько лет каждому из них?

Тест-задания.

1

А1.На одной ферме 847 коров, а на другой - на 309 коров больше. Сколько коров на двух фермах?

а)847-309=538(к.) б)847+309=1156(к.) в)847+309=1156(к.)

847+538=1385(к.) 847+1156=2003(к.)

А2.Масса яблока 140 г, а масса груши на 60 г больше. Какова масса трех таких яблок и груши?

а)140+60=200(г) б)140+60=200(г) в)140-60=80(г)

б)140*3=420(г) 140+200=340(г) 140*3=420(г)

140+420=560(г) 80+420=500(г)

В1.Расстояние от дома до школы 370 м, а расстояние от дома до стадиона 1240 м. На сколько метров расстояние от дома до школы меньше расстояния от дома до стадиона?

а)1610 б)870 в)1510

В2.В двух корзинах 16,8 кг помидоров. В одной корзине в 2 раза больше помидоров, чем в другой. Сколько килограммов помидоров в каждой корзине?

а)5,6 и 11,2 б)8,4 и 8,4 в)4,2 и 12,6

С. Сумма двух чисел 549, Одно из них в 8 раз больше другого. Найдите эти числа?

2

А1. Я задумал число. Если его увеличить в 11 раз и результат уменьшить на 2,75, то получится 85,25. Какое число я задумал?

а)85,25-2,75=82,5 б)85,25+2,75=88 в)85,25+2,75=88

82,5:11=7,5 88:11=8 88*11=968

А2. Два комбайнера убрали пшеницу с 64,2 га. Сколько гектаров убрал каждый комбайнер, если первый убрал на 2,8 га меньше чем второй?

а)х+х-2,8=64,2 б) х+х+2,8=64,2 в)х+х-2,8=64,2

2х=64,2+2,8 2х=64,2-2,8 х-2,8=64,2

2х=67 2х=61,4 х=67

х=33,5 х=30,7

33,5-2,8=30,7 67-2,8=64,2

В1. Два тракториста вспахали 12,32 га земли, причем один из них вспахал в 1,2 раза меньше другого. Сколько гектаров земли вспахал каждый тракторист?

а)5,6 га,6,72 га б)61,6 га,73,92 га в)6,3 га,6,02 га

В2. В трех ящиках было 76 кг вишни. Во втором ящике было в 2 раза больше, чем в первом, а в третьем - на 8 кг больше вишни, чем в первом. Сколько килограммов вишни было в каждом ящике?

а)15кг;35кг;26кг б)10кг;36кг;20кг в)17кг;34кг;25кг

С. Сумма двух чисел равна 12⁴/₇. Одно из них в 1²/₇ раза больше другого. Найдите эти числа.

Раздел 2

Задачи на нахождение дроби от числа и числа от дроби.

I. Основные понятия в задачах на нахождение дроби от числа и числа от дроби.

Если каждый тип задач на нахождение дроби от числа и числа от дроби учащиеся решают по отдельности, то они как правило особых затруднений при этом не испытывают. Все трудности начинаются, когда ученикам приходится самим относить ту или иную задачу к определенному типу.

Ученики должны понять и заучить, что дробь от числа находят умножением на дробь, а число по его дроби - делением на дробь. Мотивировать необходимость запоминания можно тем, что в таком случае сокращается и облегчается процесс решения задач данных типов.

II. Основные этапы решения задач.

Рассмотренные типы задач сводятся воедино с помощью выделения основных компонентов каждой задачи на дроби. Эти компоненты могут быть представлены в следующем виде:

Далее учитель рассматривает вместе с учениками любую из уже решенных в классе задач.

Задача 1

В хоре 80 учащихся, 1/4 из них - мальчики.

Сколько мальчиков в хоре?

Заполняем таблицу с помощью ответов на вопросы:

Что есть все число в задаче? Известно ли оно? О какой дроби от всего числа говорится в задаче? Известно ли значение этой дроби?

Далее анализируем заполненную таблицу и выделяем все имеющиеся зависимости между рассматриваемыми величинами с помощью следующих вопросов:

Как найти значение дроби, если известно все число - 80 учеников и дробь от него - 1/4?

Как найти все число, если известна дробь от него - 1/4 и значение дроби - 20 человек?

Как найти дробь зная все число - 80 учеников и значение дроби 20 учеников?

Что показывает дробь 1/4?

Ответы на поставленные вопросы можно записать схематично следующим образом:

(значение дроби) = (все число) * (дробь от числа),

(все число) = (значение дроби) : (дробь от числа),

(дробь от числа) = значение дроби) : (все число)

Эту схему ученики должны записать в своих тетрадях вместе с исходной таблицей. Желательно также оформить ее на плакате с тем, чтобы она присутствовала на нескольких уроках, пока учащиеся ее запомнят.

Далее решаются элементарные задачи, но таким образом, чтобы учащиеся сами осуществляли выбор типа задачи и соответствующего правила и действия.

После того как с помощью таблицы решено необходимое количество элементарных задач, осуществляется переход к решению более сложных задач.

Итак, при решении сложных задач рассматриваемых типов можно выделить следующие шаги:

1. Выделить отдельные ситуации в задаче - отдельные подзадачи;

2. отнести каждую ситуацию к определенному типу с помощью ответов на вопросы таблицы (что есть все число, известно ли оно и т.д.?);

3. решить каждую элементарную подзадачу, опираясь на соответствующее правило;

4. свести все ситуации воедино.

III. Примеры решения задач.

Задача

Туристы за три дня прошли 48 км. В первый день они прошли 1/4 всего расстояния, а во второй день - 5/9 остатка.

Сколько км они прошли в третий день?

Решение задачи разбиваем на ряд элементарных подзадач с помощью традиционных вопросов:

«Сколько ситуаций рассматривается в задаче, какие это ситуации, что известно про каждую ситуацию?».

При ответе на последний вопрос ученики должны указать, что в первой ситуации (движение туристов в первый день) известно:

1. все число - это путь;

2. дробь от всего числа;

3. неизвестно значение дроби, которое можно найти.

Не делая вычислений, продолжаем анализ ситуации (движение во второй день) школьники должны заметить, что всем числом теперь является путь, оставшийся после того, что было пройдено в первый день.

Итак, при анализе задачи оказывается заполненной таблица:

После составления таблицы план решения задачи следует детально обсудить с учениками и проследить за его реализацией.

Решение.

1) 48 * 1/4 = 12 км - путь, пройденный в 1-й день.

2) 48 - 12 = 36 км - остаток после первого дня пути.

3) 26 * 5/9 = 20 км путь, пройденный во 2-й день.

4) 48 - 12 - 20 = 16 км путь, пройденный в 3-й день.

Ответ: 16 км.

4.Задачи для работы в классе.

1. Начертите отрезок длиной 8 см. Отметьте цветным карандашом 5/8 отрезка. Какая часть отрезка осталась не отмеченной?

2. Купили кусок ткани длиной 2м 50 см и из 1/5 куска сшили платье для куклы. Сколько сантиметров ткани ушло на это платье?

3. От дыни массой 2кг 400 г Ване отрезали 1/5 дыни, а Маше 1/6 дыни. Чему равна масса каждого отрезанного куска? Сколько граммов дыни осталось?

4. Велосипедист проехал 2/9 дороги. Какова длина дороги, если он проехал 40 км?

5. До обеда выгрузили 7/10 зерна, находившегося в товарном вагоне. Сколько тонн зерна было в вагоне, если выгрузили 42 т?

6. В книге 140 страниц. Володя прочитал 4/5 этой книги. Сколько страниц прочитал Володя?

7. Свая возвышается над водой на 1,5 м, что составляет 3/16 длины всей сваи. Какова длина всей сваи?

8. У брата и сестры 90 марок. Сколько марок у сестры, если у брата 0,3 всех марок?

9. В первый день туристы прошли 5/24 намеченного пути, а во второй день 0,8 того, что прошли в первый день. Как велик намеченный путь, если во второй день туристы прошли 24 км?

10. В первый день тракторная бригада вспахала 3/8 участка, во второй день 2/5 остатка, а в третий день - остальные 216 га. Определите площадь участка.

5.Тест-задания.

1.

А1. Начертите квадрат со стороной 6 клеток. Разделите его на 3 доли и закрасьте 2/3 квадрата. Какая часть квадрата осталась не закрашенной?

а) Осталась 1/3.

б) Осталось 1/3

в) Осталось 2/3

А2. Человек прошел 2/3 дороги. Какова длина всей дороги, если он прошел 4 км?

а)4:2=2(км) б)4*3=12(км) в)4*3=12(км)

2*3=6(км) 12:2=6(км)

В1. Миша исписал 10 страниц тетради, что составляет 5/6 всей тетради. Сколько страниц в тетради?

а) 20 б) 8 в) 12

В2. Длина дороги 20 км. Заасфальтировали 2/5 дороги. Сколько километров дороги заасфальтировали?

а) 50 км б) 8 км в) 2 км

С. Купили 5 кг 600 г сахара и израсходовали на варенье 7/8 всего сахара. Сколько сахара пошло на варенье? Сколько сахара осталось?

2.

А1. В книге 140 страниц. Алеша прочитал 0,8 этой книги. Сколько страниц прочитал Алеша?

а)140*0,8=112(стр.) б)140:0,8=145(стр.) в)140*0,8=114(стр.)

А2. Девочка прошла на лыжах 300 м, что составляло 3/8 всей дистанции. Какова длина дистанции?

а)300:³ /₈=800(м) б)300:³/₈ =700(м) в)300*³/₈=112(м)

В1. Площадь одной комнаты 21 м², а площадь второй комнаты составляет 3/7 площади первой комнаты. Найдите площадь двух комнат.

а)32 м² б)12 м² в)30 м²

В2. Продано 3/8 полученных магазином лыж, после чего осталось 120 пар лыж. Сколько пар лыж было получено магазином?

а)192 б)72 в)292

С. До обеда путник прошел 0,75 намеченного пути, а после обеда он прошел 1/3 пути, пройденного до обеда. Прошел ли путник за день весь намеченный путь?

Раздел 3

Задачи на пропорции.

1. Основные понятия в задачах на пропорции.

Проведение подготовительной работы при обучении решению задач на прямую и обратную пропорциональность и построение цепочки задач от простого к сложному повысят доступность задач этого типа. Разумеется, нельзя требовать, чтобы все учащиеся умели решать такие задачи, но участие в поиске решения, тренировка в различении прямой и обратной пропорциональности, ознакомление с практикой решения задач будут полезны каждому из них.

С чего же начинать?

1. Научить школьников решать пропорции сознательно используя основное свойство пропорций.

2. Научить выделять в условиях задач две величины, устанавливать вид зависимости между ними.

3. Научить по условию задачи составлять пропорцию.

II. Основные этапы решения задач на прямую и обратную пропорциональность.

Первые задачи нацелены на подготовку к введению понятий прямой и обратной пропорциональности, они предполагают получение ответа с опорой на опытные представления учащихся.

Здесь полезно напомнить, что стоимость покупки определяется по формуле:

Стоимость = цена х количество;

И на примерах проследить, как при увеличении (уменьшении) одной величины в несколько раз изменяется вторая величина при неизменной третьей. Аналогичная работа проводится по формуле:

Путь = скорость х время

Работа = производительность х время

1. За несколько одинаковых карандашей девочка заплатила 80 руб. Сколько нужно заплатить за такие же карандаши мальчику, который купил карандашей:

а) в 3 раза больше?

б) в 3 раза меньше?

2. Расстояние от села до города велосипедист проехал за 3 часа.

а) За сколько часов это расстояние пройдет пешеход, скорость которого в 3 раза меньше скорости велосипедиста?

б) За сколько часов это расстояние проедет мотоциклист, скорость которого в 5 раз больше скорости велосипедиста?

Опыт, полученный учащимися при решении задач 1 и 2 нужно использовать при формировании понятий прямой и обратной пропорциональности.

Далее, опираясь на полученный опыт т определения прямой и обратной пропорциональности, учащиеся должны ответить на вопросы заданий 3 и 4. Здесь следует постоянно обращать их внимание на то, какие величины изменяются, а какие - нет. В случае затруднений, нужно обращаться к конкретным числовым данным.

3. Какова зависимость между:

а) ценой одного карандаша и стоимостью нескольких карандашей при постоянном количестве?

б) количеством карандашей и их стоимостью при постоянной их цене?

В) количеством карандашей и их ценой при постоянной стоимости покупки?

4. а)Покупают одинаковые тетради. Какова зависимость между количеством тетрадей и стоимостью всей покупки?

б) Расстояние между городами можно проехать на велосипеде или мотоцикле. Какова зависимость между временем и скоростью движения?

Работу над задачами 1-4 надо обобщить, заметив, что если три величины связаны равенством а = b * c, то при постоянном произведении множители обратно пропорциональны, а при постоянном множителе другой множитель и произведение прямо пропорциональны.

III. Примеры решения задач.

1. За 6 ч поезд прошел 480 км. Сколько километров поезд прошел за первые 2 часа, если его скорость была постоянна?

Краткая запись условия задачи:

В процессе устного обсуждения выясняем, что время и путь уменьшились в одно и то же число раз, так как при постоянной скорости эти величины прямо пропорциональны (уменьшение величины показываем стрелкой вниз, а увеличение - стрелкой вверх).

Во сколько раз уменьшилось время? (В 6/2 раза), а путь (в 480/х). Приравняем полученные отношения и решим пропорцию:

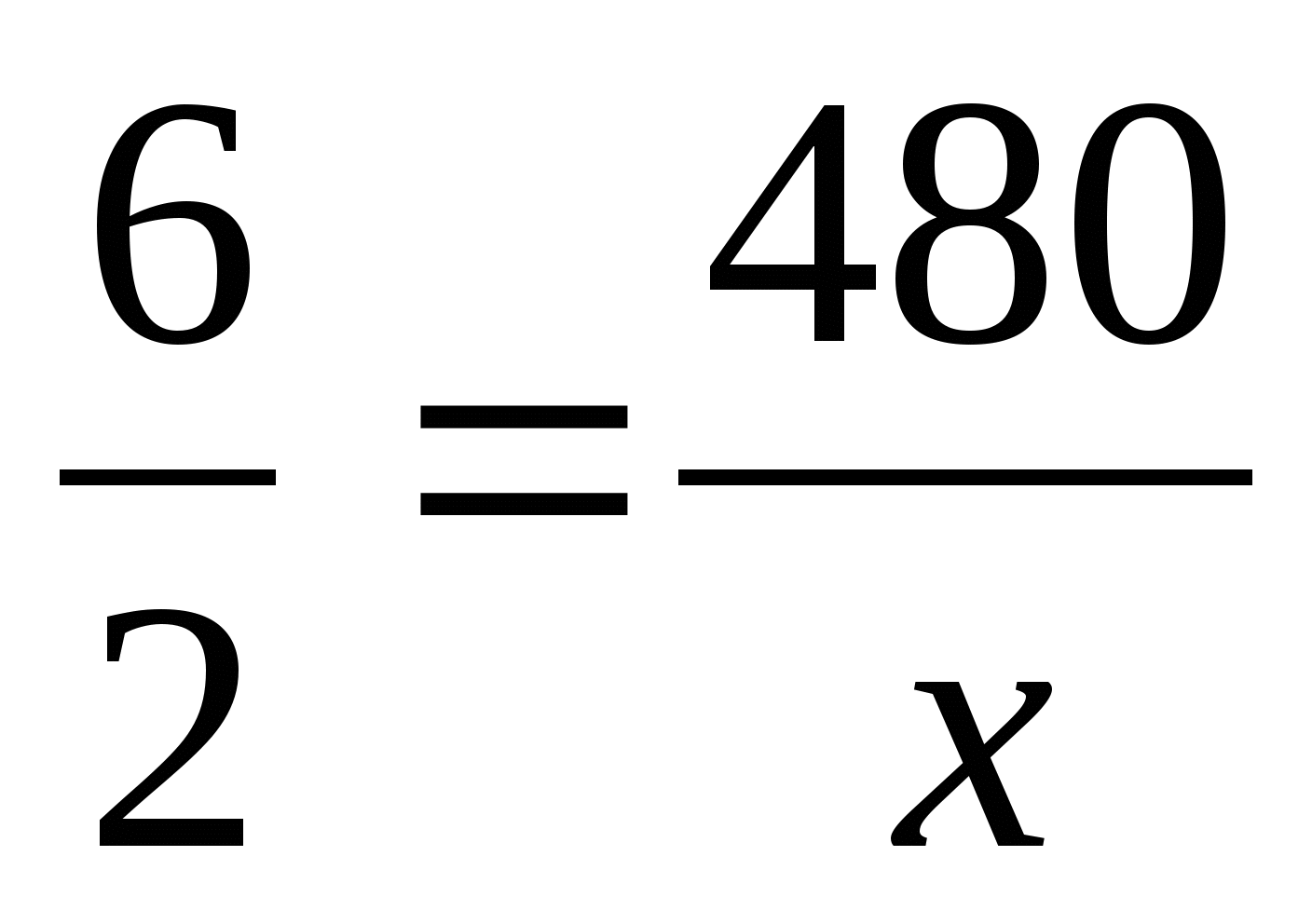; x = 160 км

Задачи для работы в классе.

1. Найти четыре числа, образующих пропорцию, если известно, что сумма крайних членов равна 14, сумма средних членов равна 11, а сумма квадратов таких четырех чисел равна 221. (Ответ: 12, 8, 3, 2)

2. За одно и то же время токарь делает 6 деталей, а его ученик 4 детали.

Сколько деталей сделает ученик за то же время, за которое токарь сделает 27 деталей?

3. Старинная задача.

Взяли 560 человек солдат, корма на 7 месяцев, а приказано им на службе быть 10 месяцев; и захотели людей от себя убавить, чтобы корма хватило на 10 месяцев. Спрашивается сколько человек надо убавить.

4. Из «арифметики» А.П. Киселева.

Для освещения 18 комнат в 48 дней издержано 120 фунтов керосина, причем в каждой комнате горело по 4 лампы.

На сколько дней достанет 125 фунтов керосина, если освещать 20 комнат и в каждой комнате будет гореть по 3 лампы?

5. Сумма первых трех членов пропорции равна 58. Третий член составляет 2/3, а второй 3/4 первого члена. Найти четвертый член пропорции и записать его.

Задачи для самостоятельного решения.

1. Для варки варенья из вишни на 6 кг ягод берут 4 кг сахарного песку.

Сколько килограммов сахарного песку надо взять на 12 кг ягод?

2. 5 маляров могли бы покрасить забор за 8 дней. За сколько дней 10 маляров покрасят тот же забор?

3. Расстояние между двумя городами пассажирский поезд прошел со скоростью 80 км/ч за 3 ч. За сколько часов товарный поезд пройдет то же расстояние со скоростью 60 км/ч?

4. Из «арифметики» А.П. Киселева.8 аршин сукна стоят 30 руб.

Сколько стоят 15 аршин этого сукна?

5. Старинная задача.

Одна артель плотников, состоящая из 28 человек, может построить дом в 54 дня, а другая из 30 человек - в 45 дней. Какая артель работает лучше?

6. 3 курицы за 3 дня снесли 3 яйца. Сколько яиц снесут 12 кур за 12 дней?

7. 100 синиц за 100 дней съедают 100 кг зерна. Сколько кг зерна съедят 10 синиц за 10 дней?

8. Из «арифметики» Л.Ф. Магницкого.

Некто имел 100 рублей в купечестве 1 год и приобрел ими только 7 рублей. А когда отдал в купечество 1000 рублей на 5 лет, сколько ими приобретет?

9. Старинная задача.

Переписчик в течение четырех дней может переписать 40 листов, работая по 9 ч в день.

Во сколько дней он перепишет 60 листов, работая по 12 ч в день?

10. Из «Всеобщей арифметики» И. Ньютона.

Если писец может за 8 дней написать 15 листов, сколько понадобится писцов, чтобы написать 405 листов за 9 дней?

Задачи, в которых слагаемые пропорциональны

некоторым числам.

Особенностью этого типа задач является то, что данные задачи пропорциональны некоторым числам. В связи с этим при решении вводится число: коэффициент пропорциональности, обозначающее количество, приходящегося на одну часть.

Пример решения задач.

Задача.

На производство костюма было израсходовано 2,8 м² ткани. Площади ткани, израсходованной на пиджак, брюки и жилетку, относятся как 7:5:2.

Сколько ткани пошло на брюки?

Решение.

1. Через r обозначим площадь ткани, приходящуюся на одну часть.

2. Количество ткани, которое пошло на пиджак, брюки и жилетку можно записать: 7r, 5r, 2r.

3. Общее количество ткани: 7r+5r+2r=2,8

4. Следовательно, r = 0,2

На брюки израсходовано 5*0,2=1 м² ткани.

Ответ: 1 м².

Задачи для работы в классе.

1. Числители трех дробей пропорциональны числам 1,2,5 а знаменатели соответственно пропорциональны числам 1,3,7. Среднее арифметическое этих дробей равно 200/441.

Найти эти дроби.

(Ответ: 4/7, 8/21, 120/49)

2. Площади трех участков земли находятся в отношении 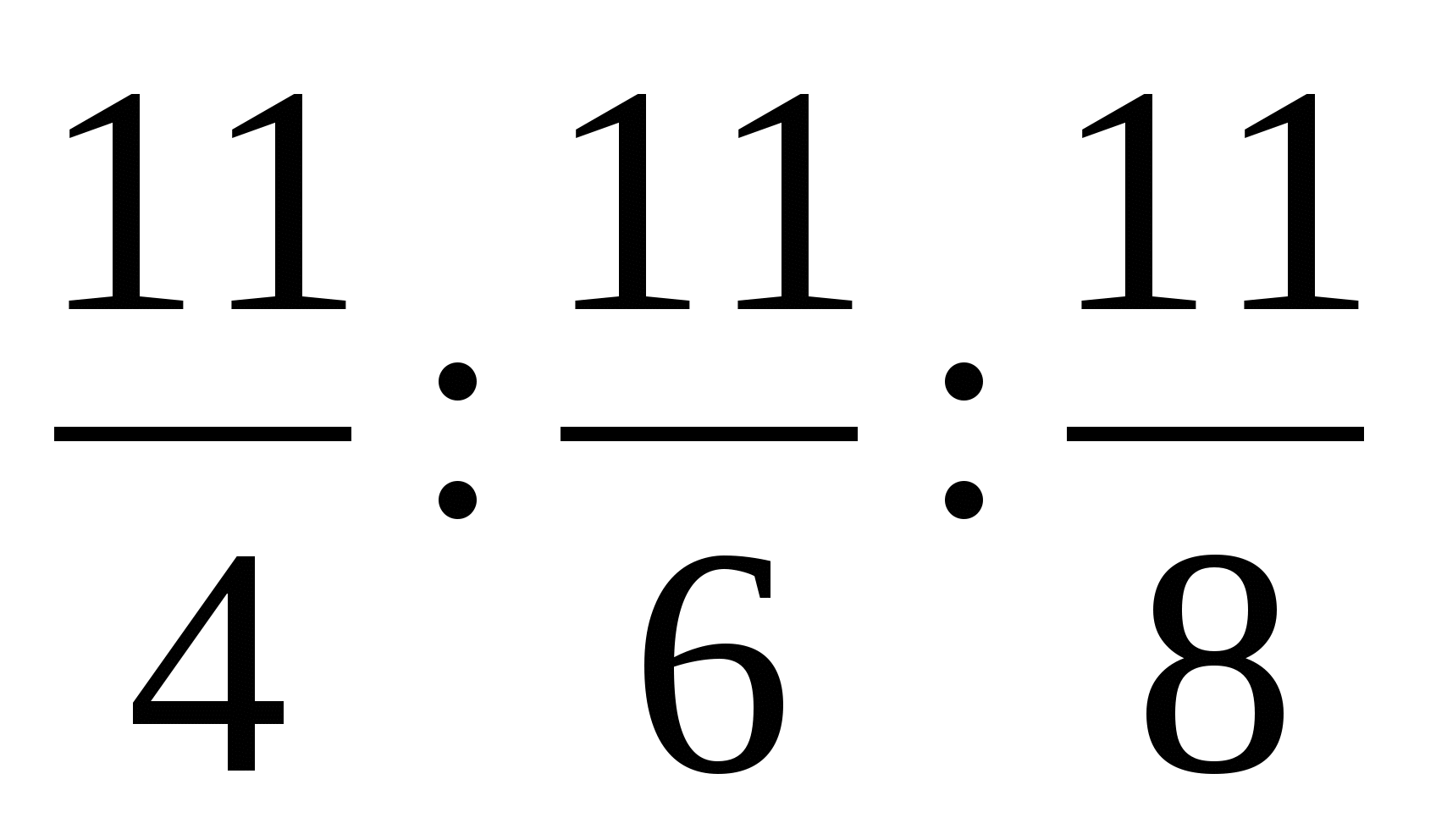. Известно, что с первого участка собрано зерна на 72 ц больше, чем со второго.

Найдите площадь всех трех участков, если средняя урожайность составляет 18 ц с 1 га.

(Ответ: 26 га)

3. Длина Дуная относится к длине Днепра как 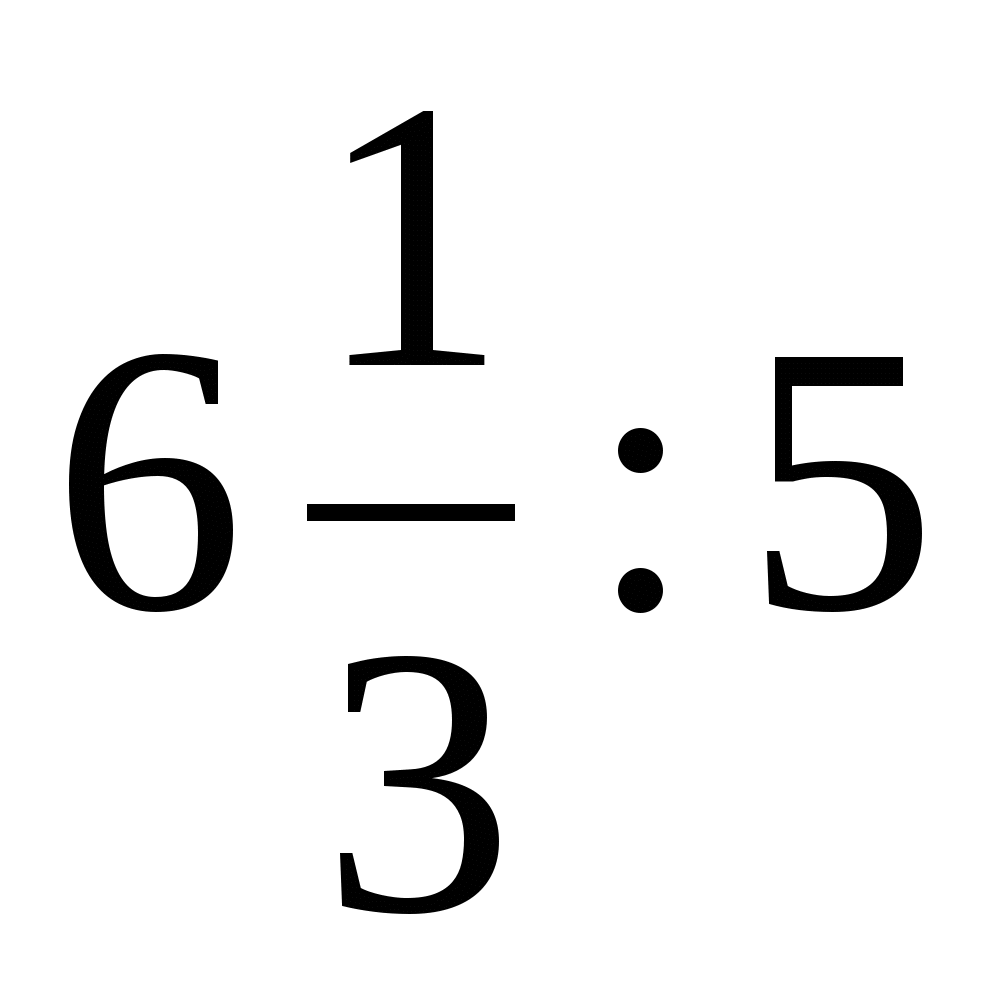, а длина Дона относится к длине Дуная как 6,5 : 9,5.

Найдите протяженность каждой из рек, если Днепр длиннее Дона на 300 км.

(Ответ: 2850 км, 2250 км, 1950 км)

Задачи для самостоятельного решения.

1. Из четырех чисел первые три относятся между собой как

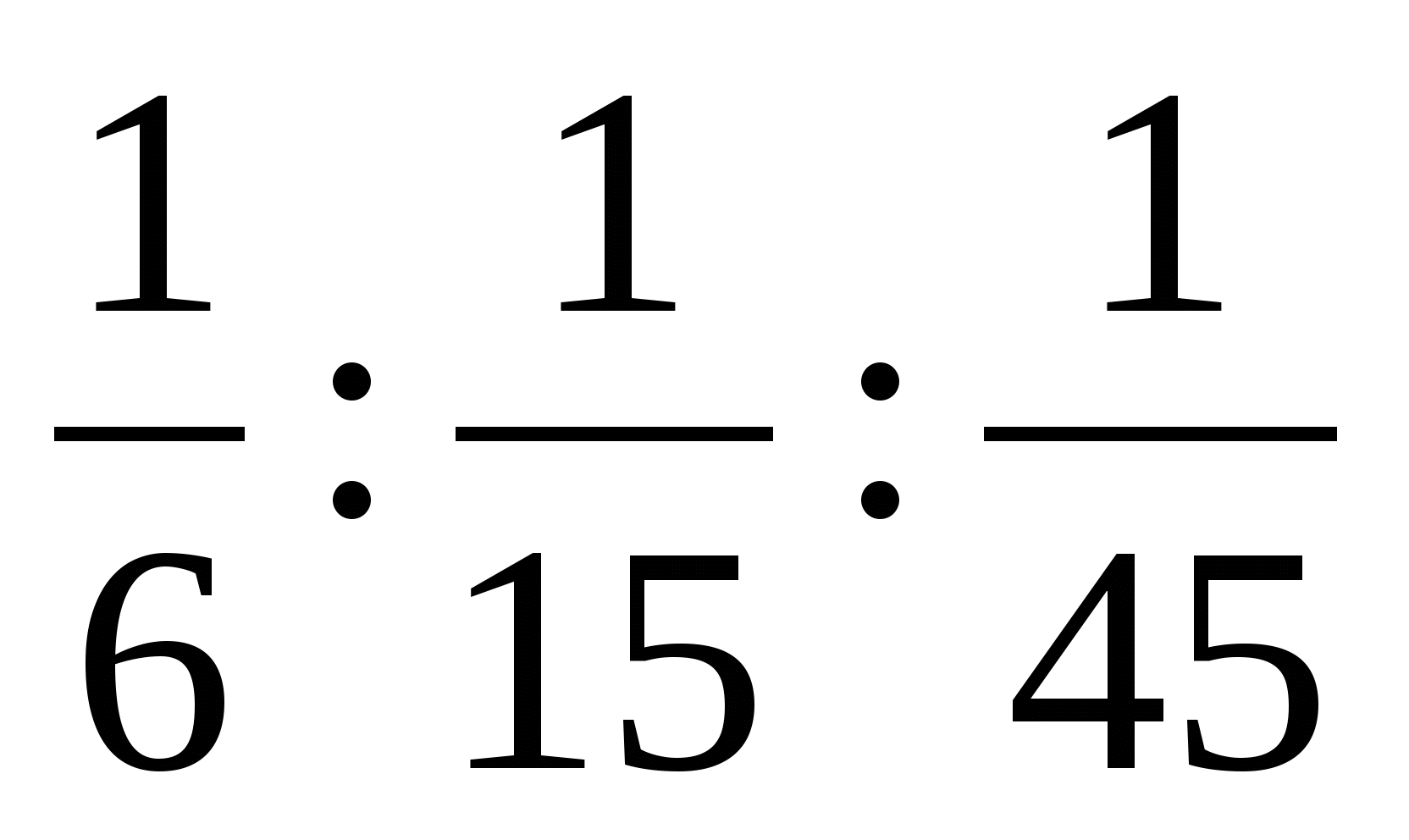, а четвертое составляет 20% первого числа.

Найдите сумму всех четырех чисел, если известно, что первое число больше суммы остальных на 40.

2. Три бригады рабочих, в которых было вместе 225 человек, вырыли каждая по одному пруду. Время, затраченное бригадами на работу, оказалось пропорционально числам: .

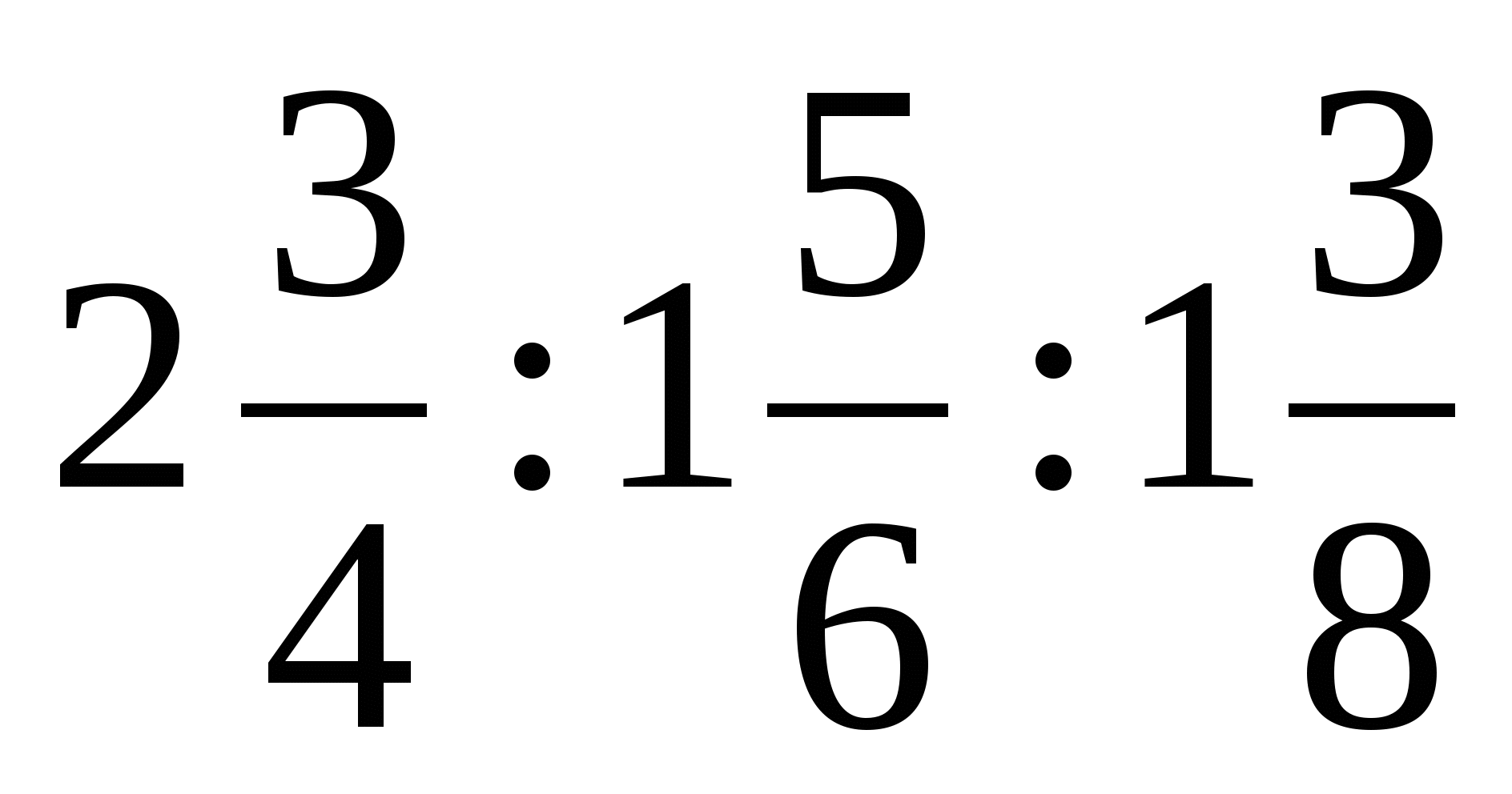Зная, что все рабочие работали с одинаковой производительностью труда и что пруды были одинакового размера, определите число рабочих в каждой бригаде.

3. Четыре числа находятся в отношении .

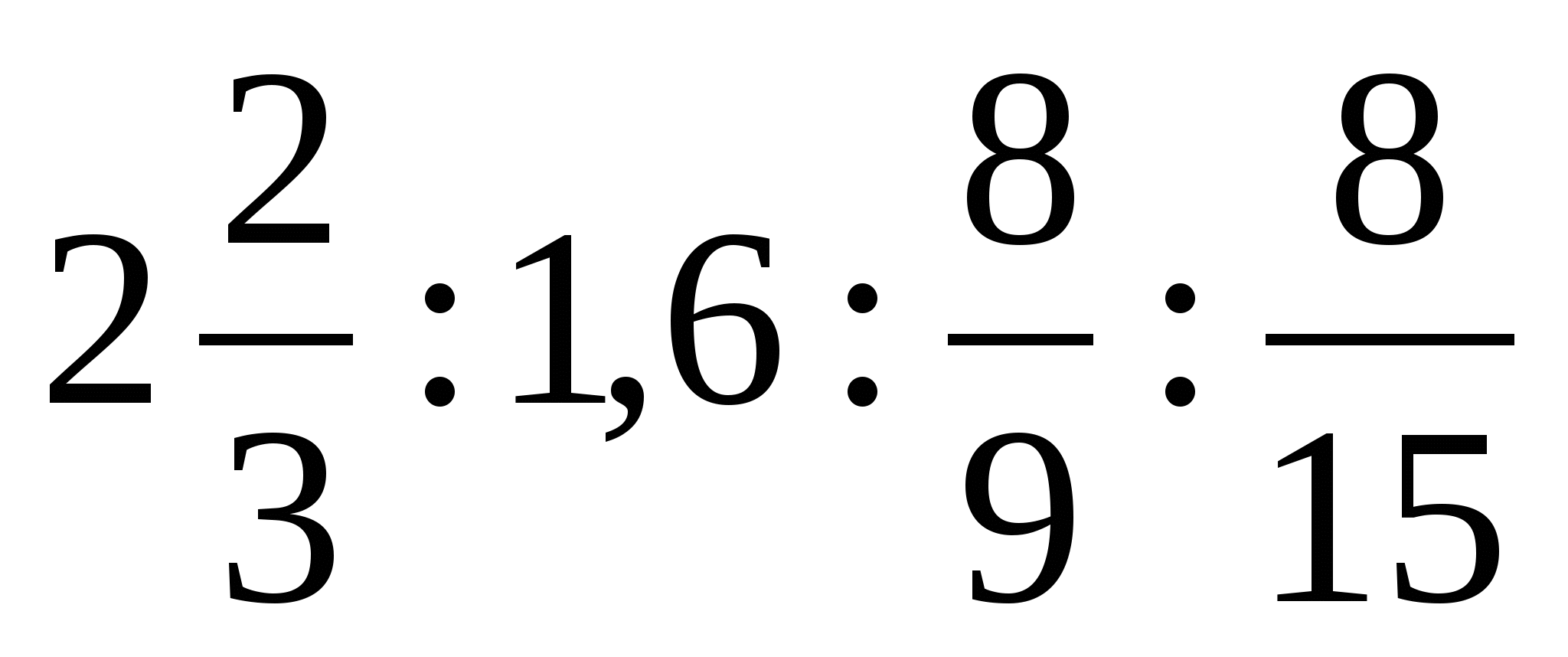Найдите эти числа, если известно, что сумма первых двух на 240 больше суммы двух последних.

4. Заработная плата рабочего за октябрь и ноябрь относились как 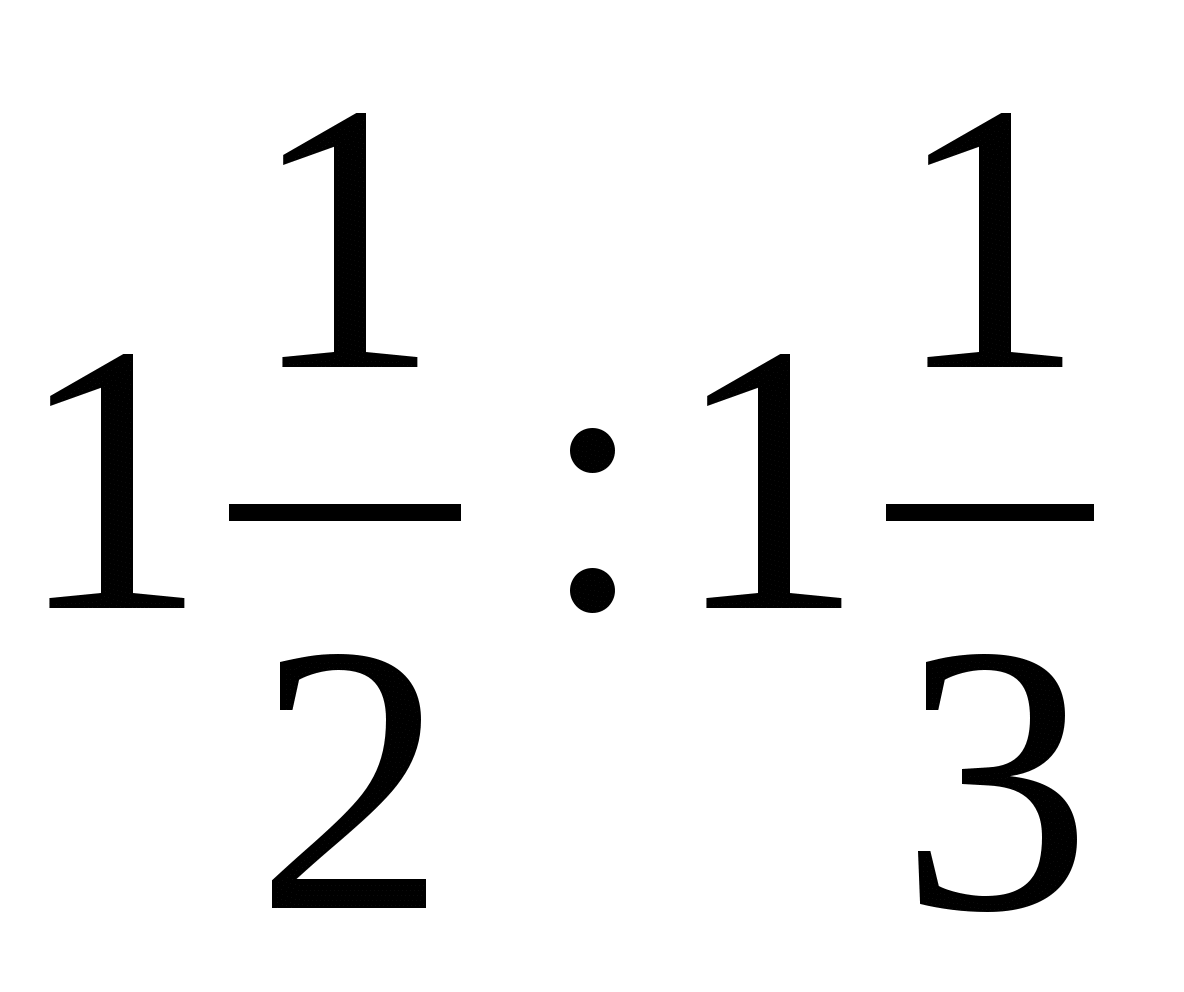, а за ноябрь и декабрь как 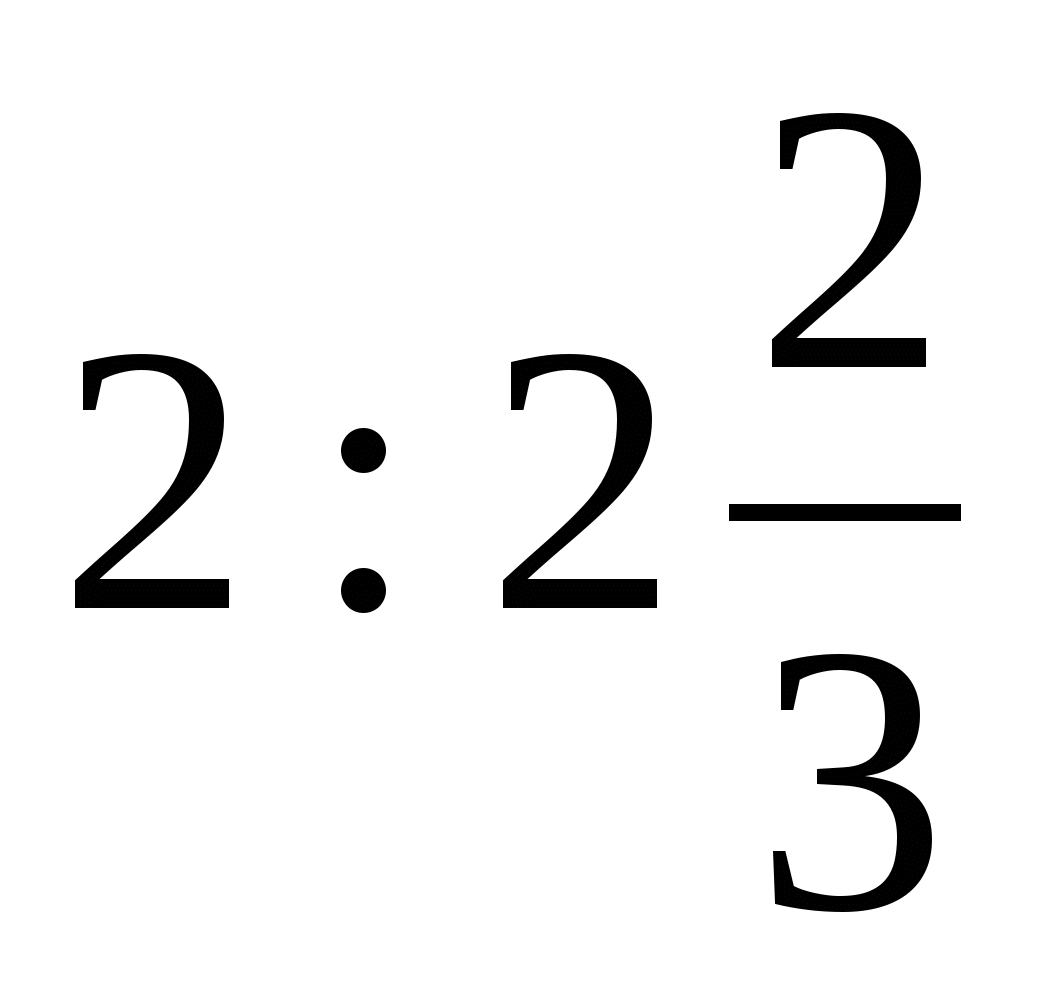. За декабрь он получил на 15 руб. больше, чем за октябрь, и за перевыполнение квартального плана рабочему начислили премию в размере 20% его 3-х месячного заработка.

Найти размер премии.

5. Числители трех данных дробей пропорциональны числам 1,2 и 3, а обратные величины соответствующих знаменателей пропорциональны числам 1,1/3 и 0,2.

Найти эти дроби, если их среднее арифметическое равно 136/315.

6. Найти сумму трех чисел, зная, что третье относится к первому, как 1,5:15/4 и составляет 40% второго, а сумма первого и второго равна 400.

7. Некоторый сплав состоит из двух металлов входящих в отношении 1:2, а другой содержит те же металлы в отношении 2:3.

Сколько частей каждого сплава нужно взять, чтобы получить третий сплав, содержащий те же металлы в отношении 17:27?

8. Некоторый сплав содержит металлы А и В в отношении m:n, другой - те же металлы в отношении p:g.

Какие количества первого и второго сплавов нужно взять, чтобы получить 1 кг третьего сплава с равным содержанием металлов А и В?

9. Имеются два слитка сплавов золота и меди. В первом слитке отношение золота к меди равно 1:2, а во втором 2:3. Если сплавить 1/3 первого слитка с 5/6 второго, то в получившемся слитке окажется столько золота, сколько было в первом меди, а если 2/3 первого слитка сплавить с половиной второго, то в получившемся слитке окажется меди на 1 кг больше, чем было золота во втором слитке.

Сколько золота в каждом слитке?