- Учителю
- «Лінійні рівняння з однією змінною» (алгебра 7 клас)
«Лінійні рівняння з однією змінною» (алгебра 7 клас)
Методичні рекомендації щодо вивчення теми
« Лінійні рівняння з однією змінною» (алгебра 7 клас)
Одним з важливих завдань шкільного курсу математики є формування навичок розв'язання лінійних рівнянь з однією змінною. Значення даної теми полягає в тому,що лінійні рівняння з однією змінною утворюють важливий тип математичних моделей реальних процесів. Цей чинник має значною мірою визначити види і методи розв'язування лінійних рівнянь. На вивчення теми відводиться обмежена кількість годин - сім, що обумовлює необхідність вивчення теми як з допомогою вчителя , так і самостійно. Державні вимоги до рівня загальноосвітньої підготовки учнів
-
Розпізнає лінійне рівняння серед даних рівнянь.
-
Наводить приклади лінійних рівнянь.
-
Характеризує етапи розв'язування задачі за допомогою рівняння.
-
Розв'язує: лінійні рівняння з однією змінною і рівняння, що
зводяться до них; текстові задачі за допомогою лінійних рівнянь з
однією змінною.
Після вивчення теми учні повинні:
мати уявлення про:
-
рівняння;
-
корінь рівняння;
-
рівносильні рівняння;
знати:
-
означення лінійного рівняння з однією змінною, рівняння першого степеня;
-
зміст вимоги «розв'язати рівняння»;
уміти:
-
розпізнавати та розв'язувати лінійні рівняння з однією змінною;
-
перевіряти, чи є дане число коренем рівняння;
-
розв'язувати нескладні текстові задачі на складання лінійних рівнянь з однією змінною.
У ході вивчення теми відстежуються між предметні зв'язки з історією,літературою, образотворчим мистецтвом. Важливу роль у вивченні теми відіграє систематичне використання історичного матеріалу , який підвищує інтерес до вивчення математики, стимулює потяг до наукової творчості, пробуджує критичне ставлення до фактів, дає учням уявлення про математику як невід'ємну складову загальнолюдської культури. На дохідливих змістовних прикладах слід показувати учням, як розвивалися математичні поняття і відношення, теорії й методи. Ознайомлювати учнів з іменами та біографіями видатних учених, які створювали математику, зокрема видатних українських математиків, що сприятиме національному і патріотичному вихованню.
Урок 1
Тема. Рівняння. Рівносильні рівняння.
Мета :
освітня : активізувати загальні відомості учнів про рівняння, корені рівняння, вміння розв'язувати нескладні рівняння на основі залежності між компонентами арифметичних дій; ввести поняття рівносильних рівнянь, сформулювати основні властивості рівнянь.
розвиваюча: розвивати вміння лаконічно и математично грамотно висловлювати свою думку;
виховна: виховувати працьовитість, спостережливість, кмітливість.
Тип уроку: засвоєння нових знань.
Обладнання: таблиця-ключ, правила проведення інтерактивних вправ«Мікрофон».
Очікуванні результати: Після уроку учні зможуть:знаходити невідомий компонент рівняння, складати рівняння за його коренем, засвоять поняття як «рівняння», «розв'язки рівняння»,набудуть навичок й умінь застосовувати основні властивості рівнянь.
Компетенції :полікультурна,інформаційна, соціальна
Епіграф уроку:
Є в математиці щось таке, що викликає людське захоплення.
Ф. Хаусдорф
ХІД УРОКУ
-
Організація класу.
Китайська мудрість говорить: «У своєму житті чоловік обов'язково повинен зробити три речі: посадити дерево, побудувати будинок і виростити сина». У цьому році ми з вами будемо вирощувати дерево знань .Щоб виростити наше дерево, необхідно посадити зернятко знань. Це те, що ви вже знаєте. І уявіть собі, це лише маленька частинка всіх знань. Але саме від неї залежить, яким великим і сильним зросте наше дерево і якими будуть ваші знання. Чим глибше і міцніше знання, тим вище і потужніше дерево знань.
Цього року у вас з'являються два нові предмети. Це алгебра і геометрія. Про геометрію ми поговоримо пізніше. А сьогодні - алгебра. Алгебра - це частина математики, що вивчає загальні властивості дій над різними величинами і рішення рівнянь, пов'язаних з цими діями
II. Мотивація пізнавальної діяльності
-
Історична довідка про рівняння

Скульптурний портрет аль-Хорезмі Хіва: Музей просто неба
У IX ст. видатний арабський математик Мухаммед бен Муса аль-Хорезмі у своєму трактаті «Кітай аль-джебр валь-мукабала» («Книга про відновлення та протиставлення») зібрав і систематизував методи розв'язування рівнянь. Слово «аль-джебр» з часом перетворилось в добре відоме всім слово «алгебра», а сама праця вченого стала поштовхом для розвитку науки про розв'язування рівнянь.
Перші рівняння люди вміли розв'язувати дуже давно. Єгипетські вчені
майже 4 тис. років тому невідоме число в рівнянні називали «хау»
(у перекладі - «купа») і позначали спеціальним знаком. У папірусі, що
дійшов до нас, є така задача: :
Купа і її сьома частина становлять 19.
Знайдіть купу. Сьогодні ця задача виглядала б так: «Сума невідомого числа і його сьомої частини дорівнює 19. Знайдіть невідоме число». Щоб розв'язати цю задачу, необхідно скласти рівняння: х+ 1/7х=19 .
2. Повідомлення теми і мети уроку.
Вчення про рівняння є одне з основних тем всієї алгебри. З рівнянням ми будемо зустрічатись при вирішенні багатьох питань фізики, механіки, астрономії і хімії. Отже , сьогодні на уроці мова піде про рівняння, і ми з вами спробуємо систематизувати свої знання про рівняння.
III. Актуалізація опорних знань
Отже, ви зрозуміли, як важливо уміти розв'язувати рівняння. Давайте пригадаємо прості правила, які ви вивчили ще в молодших класах і за якими ми можемо знайти невідомий компонент рівняння.
Технологія «Мікрофон»
Учитель ставить запитання до учнів.
-
Як знайти невідомий доданок?
-
Як знайти невідоме зменшуване?
-
Як знайти невідомий від'ємник?
-
Як знайти невідомий множник?
-
Як знайти невідоме ділене?
-
Як знайти невідомий дільник?
-
Знайдіть невідомий член рівняння: 6х = 60, х- 23=42,18+х = 75, 17:х=85.
IV. Вивчення нового матеріалу. Сприймання й усвідомлення загальних відомостей про рівняння
Пояснення вчителя. Ви всі любите розв'язувати кросворди. Рівняння
можна теж уявити як кросворд, де в порожню клітинку потрібно постави
ти деяке число. Наприклад, 9*-36=9, але ніхто не малює порожню клітинку,
а на її місце ставить букву, що називається змінною. Змінні найчастіше позначаються буквами х та у, але можна позначити змінну
будь-якою буквою.
!!! Рівняння - це рівність, що містить змінну
Якщо в рівнянні 9х-36=9 замість змінної х написати число 5, то дістанемо правильну числову рівність 9*5-36=9. Кажуть, що число 5 задовольняє дане рівняння.
!!! Число, яке задовольняє рівняння, називається коренем рівняння або розв'язком рівняння
Дане рівняння має тільки один корінь - число 5. Але є рівняння, що можуть мати два, три і більше коренів або взагалі не мають коренів.
Кожне рівняння має ліву і праву частини. Так, у рівнянні 9х-36=9 різниця 9х-36 - це ліва частина, а число 9 - права. 9х, -36,9 - називаються членами цього рівняння.
!!! Розв'язати рівняння - означає знайти всі його корені або показати, що їх немає
З даних рівнянь виберіть ті, для яких число 75 є корнем :
а) х - 3 = 72;б) 3х + 2 = 2х + 70;в) (х - 75) (х + 8 ) = 0; г) 9х = 0;д) 2х + 2 = -75 Відповідь: а) и в)
!!! Два рівняння називають рівносильними (рівносильні рівняння - equivalent equations), якщо вони мають однакові розв'язки.
Рівносильними вважають і такі рівняння, які не мають розв'язків. Щоб розв'язувати складніші рівняння, слід вміти замінювати їх простішими і рівносильними даним.
Основні властивості рівнянь.
1. У будь-якій частині рівняння можна звести подібні доданки або розкрити дужки. 2x+8x+5=3( x-2) 10x+5=3x-6
2. Будь-який член рівняння можна перенести з однієї частини рівняння в іншу, змінивши його знак на протилежний. 4x+9=x-3 4x-x=-3-9
3. Обидві частини рівняння можна помножити або поділити на одне й те саме число, відмінне від нуля. 10x=5 x=0,5
V. Узагальнення і систематизація вивченого матеріалу Усне розв'язування тренувальних вправ
-
Які з чисел - 2,5; 5; 7,5 - є коренями рівняння (х-6,5)(х4-1,5)=9?
-
Складіть будь-яке рівняння, коренем якого є число -15.
-
Яке з наведених рівнянь рівносильне рівнянню 2x=8?
А) 4x+16=0 ; Б) 3x=4 ; В) 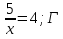 ) 2x-8=0.
) 2x-8=0.
Робота з підручником
-
Розв'язати усно № 48,49,50
-
Робота біля дошки № 52,54
VI. Підбиття підсумків уроку
Рефлексія. Чи вдалося вам заповнити прогалини в знаннях? Чи продуктивною була ваша робота на уроці? Що нового дізналися?
VII Домашнє завдання:
Обов'язково : №53, 55,56 По - можливості : № 76