- Учителю
- Урок по математике 'Пропорции в нашей жизни'
Урок по математике 'Пропорции в нашей жизни'
Тема: Пропорции в нашей жизни
Урок ведут: учитель математики и учитель трудового обучения.
Цели урока: ввести понятие пропорции, вывести ее основное свойство; закрепить новые понятия; научить применять основное свойство пропорции при решении задач; рассчитать количество крупы, необходимое для приготовления каши (на следующем уроке труда).
Оборудование: интерактивная доска, презентация с примерами пропорций, где указаны крайние и средние члены пропорции; слайды с заданием; слайды с ответами математического диктанта;
сигнальные карточки (красные, зеленые) для игры «Молчанка».
Ход урока
Учитель математики:
- Что объединяет движение транспорта и кулинарию, изготовление сплавов и малярные работы, картографию и биологию.
Оказывается, что нередко возникают ситуации, когда пропорции помогают решать казалось бы разные задачи.
Сегодня на уроке вы «ознакомитесь» с пропорцией, узнаете несколько новых математических терминов, вместе с вами мы выведем основное свойство пропорции, которое часто применяется при решении задач. Рассмотрим задачи не только из учебника математики, но и из учебника по технологии.
(Учащиеся записывают в тетради дату и тему урока.)
Прежде, чем перейти к новой теме, повторим, что вы знаете об отношениях.
В виде отношений определяется скорость, производительность труда, урожайность, цена.
Например, скорость - это отношение длины пройденного пути ко времени, за которое этот путь пройден. Приведите свои примеры отношений.
(Ученики приводят примеры.)
Учитель технологии:
- Для того, чтобы пользоваться кулинарными рецептами, производить по ним перерасчет продуктов, требуется знать, что такое отношение, пропорциональность. Рассмотрим конкретный рецепт.
Овощная икра. Репчатый лук, соленые огурцы и морковь берутся в весовом отношении 3:4:4. Вымытые, очищенные и порезанные овощи перемешиваются с небольшим количеством томатной пасты и 15 минут тушатся на огне. Подают к столу в холодном виде.
В зависимости от того, на какое количество людей или на какой срок хранения вы будете готовить овощную икру, нужно взять разное количество продуктов.
Пример. Для одной семьи достаточно взять по 1 кг огурцов и моркови. Сколько нужно добавить лука?
Огурцы и морковь входят в блюдо в объеме 4 весовых частей. Значит, одна единица массы составит 1000 : 4 = 250 (г). А лук по рецепту составляет три весовые части, т. е. 250∙3 = 750 (г).
Итак, для приготовления овощной икры можно взять 750 г репчатого лука, 1 кг соленых огурцов и 1 кг моркови (массы находятся в отношениях 3:4:4).
Подсчитайте количество продуктов, необходимое для приготовления икры, если за основу хотите взять 1,5 кг лука.
(Ученики производят расчеты.)
Ответ: для приготовления икры на семью потребуется 1,5 кг лука, 2 кг соленых огурцов, 2 кг моркови.
Учитель математики:
- У каждого на парте, лежат две цветные карточки - красная и зеленая.
Мы будем играть в игру «Молчанка». Если вы согласны с ответом ученика, которому я задаю вопрос, то молча поднимаете зеленую карточку, если нет - красную.
Задача. Мама заплатила 10 руб. за 2 кг сахара, а бабушка 15 руб. за 3 кг Захара. Выясните, по одинаковой ли цене был куплен сахар.
Решение. Стоимость 1 кг сахара, купленного мамой, 10:2 = 5 (руб.); бабушка купила сахар по цене 15 : 3 = 5 (руб.). Имеем
10:2=150:3 или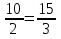 
.
Такие равенства называют пропорциями. Например равенства 5 : 2=50:20,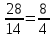 
являются пропорциями.
Запишем a:b=c:d (читается: а делённое на 
, равно с, делённому на d) или
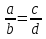
(читается: отношение а к ,равно отношению с к d).
Числа а, , с, d называют членами пропорции; а, d - крайние члены, , с - средние члены пропорции.
Историческая справка
Пропорцией называют равенство отношений двух или нескольких пар чисел или величин. Слово «пропорция» означает «соразмерный», имеющий правильное соотношение частей». Например, размеры модели машины или сооружения отличаются от размеров оригинала одним и тем же множителем, задающим масштаб модели. Справедлива и другая пропорция, которая показывает, что отношения точек оригинала такие же, как и отношения расстояний соответствующих точек модели. Пропорции начали изучать в Древней Греции. Сначала рассматривали только пропорции, составленные из натуральных чисел.
В IV в. до н. э. древнегреческий математики Евдокс дал определение пропорции, составленной из величин любой природы.
Древнегреческие математики с помощью пропорций решали задачи, которые в настоящее время решают с помощью уравнений, выполняли алгебраические преобразования, переходя от одной пропорции к другой.
Роль теории пропорций заметно уменьшилась после того, как было осознано, что отношение величин является числом (может быть, иррациональным), а поэтому пропорция - это равенство чисел. Это позволило вместо пропорции использовать уравнения, а вместо преобразований пропорций - алгебраические преобразования.
Учитель математики:
- Из пропорции можно вывести равенство произведений ее членов. Так, для пропорции
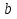произведения 5∙20 и 20∙5
Чтобы не перепутать, какие члены пропорции надо перемножить, посмотрите, как они расположены в пропорции. Они лежат «крест накрест». Их так и называют: накрест лежащие члены. В любой пропорции произведения накрест лежащих членов равны. Произведение крайних членов пропорции равно произведению средних членов (основное свойство пропорции).
Задание 1 (задание клоуна на интерактивной доске).
Клоун составил следующие пропорции:
1)3 :
6
= 2 :
4
2)4 :
6
= 2 :
3
3)3 :
6
= 4 :
2
4) 6 :
3
= 2 :
4
5) 6 :
2
= 4 :
6
6) 6 :
4
= 3 :
2
7) 6 :
3
= 4 :
2
8) 8 :
4
= 2 :
3.
Все ли пропорции составлены правильно?
Учитель читает равенство по одному, а учащиеся с помощью сигнальных карточек показывают, является это равенство пропорцией или нет.
Задание 2. Решите задачу.
Из 18 т железной руды выплавляют 10 т железа. Сколько железа можно выплавить из 36 т руды?
Задание 3. Математический диктант.
Вариант 1.
Равенство двух отношений называют ... .
Вариант 1.
Равенство двух отношений называют ... .
Вариант 1.
1) Закончите предложение:
Равенство двух отношений называют ... .
2) Запишите пропорцию
7 : 21 = 1 : 3, подчеркните ее средние члены.
3) Закончите предложение
Если пропорция верна, то произведение ее средних членов равно произведению
4) Решите уравнение:
8 : у = 20 : 5
7:14=16:аВариант 2.
1)Если пропорция верна, то произведение ее крайних членов равно произведению
2)3 : 4 = 9 : 12, подчеркните ее крайние члены.
3)Равенство двух отношений называют ... .
х : 3 = 8 : 6
17:51=:8
Форма проверки математического диктанта - взаимоконтроль по образцу. Учащиеся меняются листочками с соседом по парте и проверяют работу друг друга, плакат с ответами высвечивается на доске.
Учитель технологии:
- На следующем уроке мы с бригадой девочек будем варить гречневую рассыпчатую кашу. А сегодня произведем расчет продуктов.
Задача. Из 1 кг крупы получается 2,1 кг гречневой рассыпчатой каши. Мы хотим получить 1600 г каши. Сколько нужно взять крупы?
(Ученики решают задачу методом пропорции. Ответ: 760 г.)
Задание на дом. Сосчитайте, сколько понадобится крупы, чтобы сварить такую кашу для вашей семьи. Предполагается, что человек в среднем съедает 200 г каши.
В конце урока учителя математики и технологии подводят итог урока, объявляют оценки.