Урок по геометрии на тему Конус (11 класс)

Муниципальное общеобразовательное учреждение

«Гимназия № 7 города Буденновска

Буденновского района»

Урок по геометрии

«Конус»

11б класс

19 октября 2015 года

Подготовила

учитель математики

Бородина Нина Петровна

2015 год

Цель: формирование навыков решения практических задач по теме

Задачи:

Образовательная: сформировать понятия: конической поверхности, сечений конуса и его элементов; формировать навыки решения задач на нахождение элементов конуса, навыки использования формул вычисления боковой и полной поверхности конуса, навыки решения прикладных задач; показать связь теории с практикой

Развивающая: способствовать развитию логического мышления учащихся и расширению кругозора; развивать пространственное воображение учащихся, умение применять формулы планиметрии при решении стереометрических задач; развивать и совершенствовать умения применять накопленные знания в измененной ситуации; развивать грамотную математическую речь, навыки самоконтроля.

Воспитательная: воспитывать аккуратность при оформлении работ в тетрадях, ответственность за результат своего труда; формировать навыки и умения коммуникативного общения.

Средства обучения: компьютер, мультимедийный проектор, экран, аудиоколонки, классная доска, учебник «Геометрия 10-11» Л.С. Атанасян, рабочая тетрадь, чертёжные инструменты, ресурсы Интерната, USB-модем

Формы организации учебной деятельности: фронтальная, индивидуальная, диалог, работа с материалами слайда, учебника; самостоятельная и исследовательская работа.

Методы: наглядный, словесный, условно-символический, исследовательский.

Приложение: слайдовая презентация в программе PowerPoint

Девиз урока: «Дорогу осилит идущий, а математику - мыслящий».

Цитаты урока: «Изучение геометрии без должной связи с жизнью,

без наглядности мешает развитию логического

мышления; снижает уровень математической

подготовки учащихся».

А.И.Маркушевич

Ожидаемые результаты:

должны знать:

• основные понятия: конической поверхности, сечений конуса и его элементов,

• формулы и методы для нахождения основных компонентов конуса,

• формулы площади боковой и полной поверхности конуса;

должны уметь:

• строить чертежи по условию задачи,

• решать практические задачи на нахождение элементов конуса,

• видеть фигуры вращения.

1 этап: Организационный.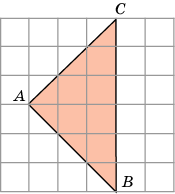

2 этап: Повторение. Подготовка учащихся к экзамену по математике в форме ЕГЭ. Устное решение задач В3 из материалов типовых тестовых заданий.

(Закрепление навыков нахождения площадей геометрических фигур.

С целью организации самопроверки на слайдах приводятся решения заданий)

1. Найдите площадь ΔABC, считая стороны квадратных клеток равными 1.(Ответ: 9)(см. слайд 2)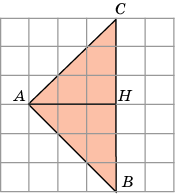

Решение: Проведем высоту AH. Тогда BC = 6, AH = 3 и, следовательно

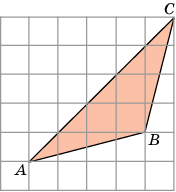
2. Найдите площадь ΔABC, считая стороны квадратных клеток равными 1.(Ответ: 7,5)(см. слайд 3)

Решение: Разобьем данный ΔABC на два треугольника ABDи BDC. Их общая сторона BD = 3, а высоты, к ней проведенные, равны соответственно 1 и 4. Площадь ΔABD равна 1,5, а площадь ΔBDC равна 6. Площадь ΔABC равна сумме площадей этих треугольников и, следовательно, равна 7,5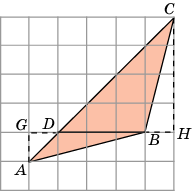

3. Найдите площадь треугольника, вершины которого имеют координаты (1, 1), (4, 4), (5, 1). (Ответ: 6) (см. слайд 4)

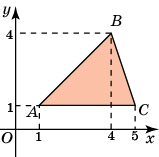
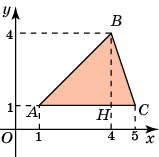
Решение: из вершины B ΔABC опустим высоту BH= 3. Сторона AC= 4. Следовательно, площадь треугольника равна 6

3 этап: Определение темы урока. Постановка задач

Учитель: Назовите тему урока, разгадав ребус.

(см. слайды 5-6)

4 этап: Теоретический опрос.

По материалам учебника «Понятие конуса» и «Площадь поверхности конуса»

(с целью проверки усвоения теоретических понятий)

Учитель: Ребята, а вы знаете, что латинское слово «conus» заимствовано из греческого языка (konos - втулка, сосновая шишка)… С конусом люди знакомы с глубокой древности. В книге Архимеда (287 - 212гг. до н.э. «О методе» приводятся решения практических задач, связанных с конусом.

А исследование свойств конуса принадлежит школе Платона (428 - 348 гг. до н.э.), над входом которой было написано: «Пусть сюда не входит никто, не знающий геометрии». (см. слайд 7)

Подробнее о конусе из видеоролика (лекция «Конус»: что называется конусом; что такое коническая поверхность; пример конической поверхности, и что называется круговым конусом). (Просмотр видеоролика- 2минуты 26 секунд)

Учитель:

Ребята, ответьте, пожалуйста, на вопросы из слайда :

1. Что называется конусом?

2. Что такое образующая?

3. Что называется радиусом конуса?

4. Какая фигура получается в сечении цилиндра плоскостью, проходящей через ось цилиндра?

5. Какая фигура получается в сечении цилиндра плоскостью, проходящей перпендикулярно оси цилиндра?

6. Равны ли друг другу углы между образующими конуса и плоскостью основания?

7. Что является развёрткой конуса?

8. Чему равна площадь боковой поверхности конуса? (см. слайд 8-9)

(На слайдах приводится наглядная интерпретация, с целью развития навыков самоконтроля и формирования пространственных представлений учащихся)

9. Почему цилиндр и конус называют телами вращения? (см. слайд 10)

Учитель:

Познакомится с алгоритмом построения, рассмотреть трехмерное изображение конуса можно на страницах Интернета

www.youtube.com/watch?v=DGn6fXsHQx0 (просмотр 1 минута 16 сек)

Или пройдя по ссылке www.youtube.com/watch?v=aY1uVp4EoRI

www.youtube.com/watch?v=o1LGLUcU5O0 (см. слайд 11)

5 этап: Знакомство с практическим применением.

Учитель:

Конус можно рассмотреть в различных предметах, начиная с обычного мороженого и заканчивая техникой.

В детстве многие ваши игрушки, или их составляющие имели форму конуса… А как часто его можно встретить в природе. (см. слайды 12-19)

«Природа говорит языком математики:

буквы этого языка - круги,

треугольники и иные геометрические фигуры»

Г. Гильберт

Учитель:

Это формы деревьев, рельеф земной поверхности: горы и холмы. Их можно найти и на дне океана. «Конусами» называется семейство морских моллюсков. Конусов свыше 500 видов. Живут в тропиках и субтропиках, являются хищниками, имеют ядовитую железу. Укус конусов очень болезнен. Известны смертельные случаи. Раковины используются как украшения, сувениры.

Формы конуса могут принимать и природные явления, и космические объекты. (см. слайды 20-24)

А без конусов архитектурные сооружения не были бы так привлекательны и великолепны! (см лайды 25-30)

6 этап: Выполнение среза (самостоятельной) работы.

(с целью проверки усвоения теоретических понятий)

Учитель: Проверим ваши знания. Ответьте, пожалуйста, письменно в тетрадях на вопросы: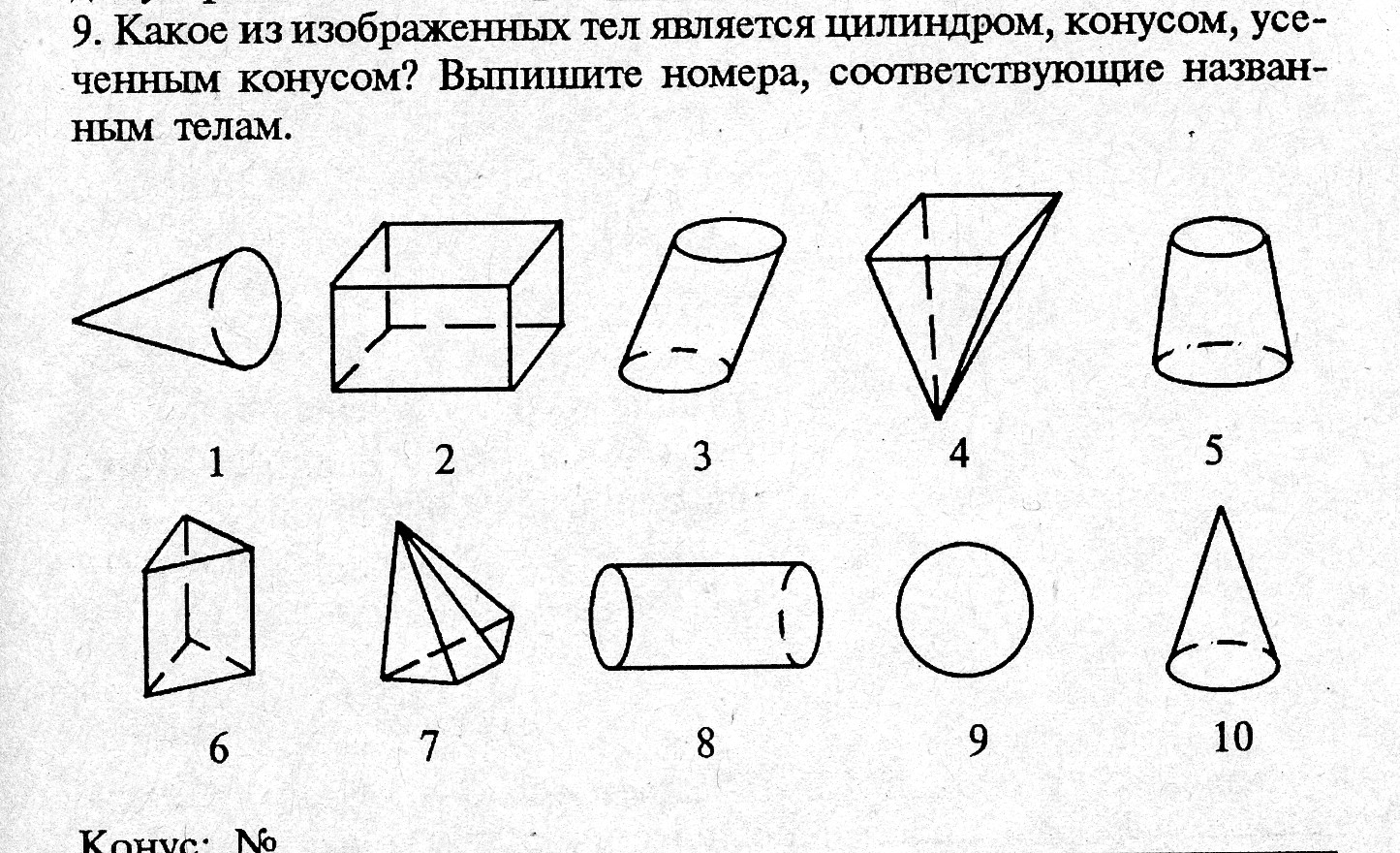

1. Какое из изображённых тел является конусом?

2.Ответы запишите в столбик. Из первых букв составьте слово:

• Фигура, полученная при поперечном сечении конуса?

• Отрезок, соединяющий вершину с окружностью основания?

• Имеет ли конус центр симметрии?

• Тело, полученное при пересечении конуса плоскостью, параллельной основанию?

• Фигура, являющаяся боковой поверхностью конуса?(см слайды31-32)

Учитель: Теперь попрошу вас обменяться тетрадями и проверить работу друга по слайду. Каковы результаты? (см.слайд 33)

7 этап: Решение задач по готовым чертежам.

(с целью формирования навыков решения задач на нахождение элементов конуса, используя знания и навыки решения прямоугольных и равнобедренных треугольников)

Задача №1.Найти радиус и высоту конуса, если его образующая равна а, а угол при вершине составляет 90°.

Решение: По свойству равнобедренного треугольника высота является медианой и биссектрисой. Зная, что диагональ квадрата , а также гипотенуза равнобедренного прямоугольного треугольника равна находим катеты. Ответ:R=3, h=3. (см. слайд 34)

Задача №2.Найти высоту и диаметр основания конуса, если его образующая равна 6, а угол при вершине составляет 120°.

Решение: Находим величины острых углов прямоугольного треугольника. По второму свойству прямоугольного треугольника и по Теореме Пифагора находим катеты. Определяем диаметр основания конуса.

Ответ:h=3, d= (см.слайд 35)

8 этап: Решение практических задач.

Учитель: Понятие «Освещённость» как физическая величина, численно равная световому потоку, падающему на единицу поверхности, известна вам из курса физики. Освещённость прямо пропорциональна силе света источника света. А мы сегодня будем вычислять площадь освещаемой поверхности.

Задача № 3. Фонарь установлен на высоте 8 м. Угол рассеивания фонаря 120°. Определите, какую поверхность освещает фонарь.

Решение:

Освещаемая поверхность - круг, основание конуса. Лампа фонаря - вершина конуса. Лучи направленные на окружность основания - образующие конуса. Рассмотрим осевое сечение конуса. Это равнобедренный треугольник. Опустим высоту. Она поделит данный треугольник на два равных прямоугольных треугольника с острыми углами в 30° и 60°.

Из FOC по второму свойству прямоугольного треугольника находим FC=16 м. По определению тангенса (или по теореме Пифагора) вычисляем ОС=.

Площадь освещаемой поверхности равна площади основания (круга).

S = πR² = 192π ≈ 603(м²). Ответ: S= 603 м². (см. слайд 36)

Задача № 4. Вычислите, сколько метров гирлянды понадобится для украшения ёлки? Гирлянды будут висеть под углом 30⁰ при вершине, высота елки - 12 м, а длина еловой ветви при основании - 5 м.

Решение: Форму елки примем за конус с высотой 12м и радиусом основания - 5 м.

Нити гирлянд закреплены на макушке елки и распределены по боковой поверхности конуса через 30°.

Сколько нитей гирлянд на елке? 360°:30° = 12 (нитей). Как найти длину одной нити?

Она равна образующей конуса.

Рассмотрим осевое сечение конуса - равнобедренный треугольник. Из прямоугольного НВС находим ВС= 13 см.

Чтобы найти длину всей гирлянды, длину нити умножаем на количество нитей. Длина гирлянды 12·13 =156 (м) Ответ: 156 м. (см. слайд 37)

Учитель:

А сейчас представьте туристические палатки. Они могут быть разнообразных форм. Мы сегодня будем решать задачу о палатке-конусе. Решаем её с комментированием.(см. слайд 38)

Задача № 5. Сколько квадратных метров брезента потребуется для сооружения палатки конической формы высотой 4 метра и диаметром основания 6 метров?

На подгиб и швы необходимо добавить 5%.(см. слайд 39)

Дано: конус, h=4 м, d_осн=6 м

Найти: S_бок=?

Решение: Палатка имеет форму конуса, следовательно, нам необходимо вычислить площадь поверхности конуса. Мы знаем, что S_пол = S_осн + S_бок ,гдеS_бок = πRℓ и S_осн = πR²

R=d:2 = 6:2 = 3(м)

Рассмотрим осевое сечение конуса - равнобедренный треугольник. Опустим высоту (медиану) ВН. Она разобьет АВС на два равных прямоугольных треугольника. Из ВНС по теореме Пифагора найдем образующую, ВС = 5м.

S_бок=πRℓ= π· 3·5 = 15 π ≈ 47,1 (м²), (см.слайд 40)

S_осн = πR²= 9π ≈ 28,26(м²),

S_пол = S_осн + S_бок = 75,36 ≈ 75,4(м²) брезента

Найдем 5% от S_пол,что составит 3,8 м². Значит S= S_пол+ 3,8 =79,2(м²)

Ответ: 79,2м² брезента потребуется для палатки.

Учитель:

Молнии, атмосферные разряды - постоянный и практически повсеместный источник угрозы для человека и его имущества. Это одно из самых разрушительных и устрашающих природных явлений, с которыми повсеместно сталкивается человек. Последствия, в тех случаях, когда в доме нет надежной системы молниезащиты (грозозащиты) - унесенные жизни, разрушенные здания, пожары, выход из строя электропроводки, оборудования и приборов. По статистике на Земле ежегодно гибнет от разрядов молний 6 человек на 1000000 жителей.

Молниеотвод («громоотвод») - устройство, устанавливаемое на зданиях и сооружениях и служащее для защиты от удара молнии. (см слайд 41)

Первый молниеотвод был изобретён Бенджамином Франклином</<font color="#000000"> в 1752 году.

Я предлагаю вам самостоятельно решить следующую задачу. Решите! Сверим ответы.(см.слайды 42-43)

Задача № 5.Вычислите высоту молниеотвода, если радиус "защищенного" круга 15 м, а угол между молниеотводом и образующей конуса безопасности 60 º

Решение: Поток света от фонаря можно сравнить с конусом. Тогда наша задача сведется к нахождению высоты конуса.

Рассмотрим осевое сечение конуса - равнобедренный треугольник. Опустим высоту ВН. Она разобьет АВС на два равных прямоугольных треугольника. Из ВНС по определения тангенса имеем tg60°= .

Значит ВН = = =≈ 8,5 (м).

Ответ: высота молниеотвода должна быть не менее 8,5 метров

8 этап: Подведение итогов.

Учитель: Все вы хорошо поработали. Я попрошу каждого закончить предложение: «Сегодня на уроке МЫ……»

(Выставление оценок, запись домашнего задания

Д/З п.55-57 № 562,565. )(см.слайд 44)

А урок хочется закончить словами Татьяничевой Л:

Да, путь познания не гладок,

Но знаем мы со школьных лет:

Загадок больше чем разгадок

И поискам предела нет.