Таблица по геометрии к теме 'Четырехугольники' 8 класс

Основные определения и свойства

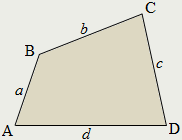
Четырёхугольником называется фигура, которая состоит из четырёх точек (вершин) и четырёх отрезков (сторон), которые последовательно соединяют вершины. При этом никакие три из данных точек не должны лежать на одной прямой, а соединяющие их отрезки не должны пересекаться.

Четырёхугольник называется выпуклым, если он расположен в одной полуплоскости относительно прямой, которая содержит любую из его сторон.

Сумма углов выпуклого четырёхугольника равна 360°:

∠A+∠B+∠C+∠D=360°.

Не существует четырёхугольников, у которых все углы острые или все углы тупые.

Каждый угол четырёхугольника всегда меньше суммы трёх остальных углов:

∠A < ∠B+∠C+∠D, ∠B < ∠A+∠C+∠D,

∠C <����������������������������������������������������������

��������������������������������������������������

�������b < a+c+d,

c <�������������������

������������������������������������������������������������

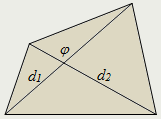
����али выпуклого четырёхугольника пересекаются, а невыпуклого - нет.

Параллелограмм

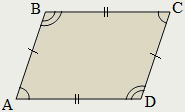
Параллелограммом называется четырёхугольник, противолежащие стороны которого попарно параллельны:

AB||CD, BC||AD.

У параллелограмма противолежащие стороны равны и противолежащие углы равны:

AB=CD, BC=AD;

∠A=∠C, ∠B=∠D.

Сумма любых двух соседних углов параллелограмма равна 180°:

∠A+∠B=∠B+∠C=∠C+∠D=∠A+∠D=180°.

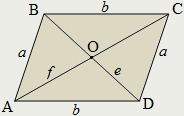
Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам:

AO=OC; BO=OD.

Каждая диагональ делит параллелограмм на два равных треугольника:

∠ABC=∠CDA; ∠ABD=∠CDB.

Признаки параллелограмма:

• Если у четырёхугольника противолежащие стороны попарно равны, то этот четырёхугольник - параллелограмм.

• Если у четырёхугольника две противолежащие стороны равны и параллельны, то этот четырёхугольник - параллелограмм.

• Четырёхугольник, диагонали которого в точке пересечения делятся пополам - параллелограмм.

• Если у четырёхугольника противолежащие углы попарно равны, то этот четырёхугольник - параллелограмм.

Ромб

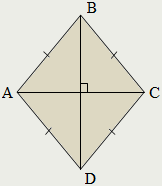
Ромбом называется параллелограмм, у которого все стороны равны:

AB=BC=CD=AD.

Диагонали ромба пересекаются под прямым углом и являются биссектрисами его углов:

AC⊥BD;

∠ABD=∠CBD=∠ADB=∠CDB; ∠BAC=∠DAC=∠BCA=∠DCA.

Признаки ромба:

• Если у четырёхугольника все стороны равны, то это ромб.

• Если у четырёхугольника диагонали перпендикулярны и точкой пересечения делятся пополам, то это ромб.

• Если в параллелограмме диагональ лежит на биссектрисе его угла, то это ромб.

• Если в параллелограмме высоты равны, то это ромб.

Прямоугольник

Прямоугольником называется параллелограмм, у которого все углы прямые:

∠A=∠B=∠C=∠D=90°.

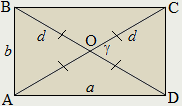
Диагонали прямоугольника равны и точкой пересечения делятся на четыре равных отрезка:

AC=BD;

AO=BO=CO=DO.

Признаки прямоугольника:

• Если у четырёхугольника три угла прямые, то это прямоугольник.

• Если у четырёхугольника диагонали равны и точкой пересечения делятся пополам, то это прямоугольник.

• Если в параллелограмме один угол прямой, то это прямоугольник.

• Если в параллелограмме диагонали равны, то это прямоугольник.

Квадрат

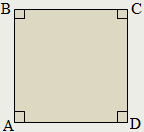
Квадрат - это прямоугольник, у которого все стороны равны:

∠A=∠B=∠C=∠D=90°,

AB=BC=CD=AD.

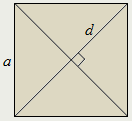
Диагонали квадрата равны и перпендикулярны.

Признаки квадрата:

• Если в ромбе один угол прямой, то это квадрат.

• Если в ромбе диагонали равны, то это квадрат.

• Если в ромбе соседние углы равны, то это квадрат.

• Если в прямоугольнике соседние стороны равны, то это квадрат.

• Если в прямоугольнике диагонали перпендикулярны, то это квадрат.

• Если в прямоугольнике диагонали являются биссектрисами его углов, то это квадрат.

Трапеция

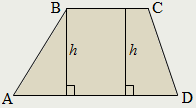
Трапецией называется четырёхугольник у которого только две противолежащие стороны параллельны:

AD||BC.

Параллельные стороны называются основаниями трапеции, непараллельные - боковыми сторонами.

Высота трапеции - перпендикуляр, проведённый из произвольной точки одного основания трапеции к прямой, содержащей другое основание трапеции.

Сумма углов, прилегающих к боковой стороне, равна 180°:

∠A+∠B=∠C+∠D=180°.

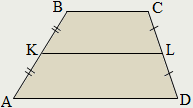
Средней линией трапеции называется отрезок, который соединяет середины боковых сторон данной трапеции:

AK=KB; CL=LD.

Средняя линия трапеции параллельна её основаниям и равна их полусумме:

KL||AD; KL||BC;

KL = ½(AD+BC).

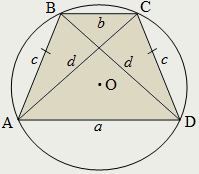
Равнобокой называется трапеция, у которой боковые стороны равны:

AB=CD.

У равнобокой трапеции:

• диагонали равны:

AC=BD;

• углы при основании равны:

∠A=∠D, ∠B=∠C;

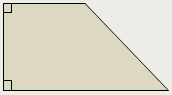
Трапеция называется прямоугольной, если одна из её боковых сторон перпендикулярна основаниям.