Решение уравнений, содержащих модуль

МЕТОДЫ РЕШЕНИЯ УРАВНЕНИЙ, СОДЕРЖАЩИХ ПЕРЕМЕННУЮ ПОД ЗНАКОМ МОДУЛЯ

Цели урока:

- вспомнить определение понятия «модуль»

- рассмотреть все виды уравнений, содержащих модули и способы решения этих уравнений;

- раскрытие модуля по определению, возведение обеих частей уравнения в квадрат и метод разбиения на промежутки;

-развивать умение анализировать и правильно выбирать способ решения уравнений

Но для начала вспомним определение модуля. Итак, модулем числа a называется само это число, если a неотрицательно и -a, если число a меньше нуля. Записать это можно так:

|a| = a, если a ≥ 0 и |a| = -a, если a < 0

Говоря о геометрическом смысле модуля, следует помнить, что каждому действительному числу соответствует определенная точка на числовой оси - ее к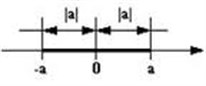оордината. Так вот, модулем или абсолютной величиной числа называется расстояние от этой точки до начала отсчета числовой оси. Расстояние всегда задается положительным числом. Таким образом, модуль любого отрицательного числа есть число положительное. Кстати, даже на этом этапе многие ученики начинают путаться. В модуле может стоять какое угодно число, а вот результат применения модуля всегда число положительное.

Теперь перейдем непосредственно к решению уравнений.

1. Рассмотрим уравнение вида |x| = с, где с - действительное число. Это уравнение можно решить с помощью определения модуля.

Все действительные числа разобьем на три группы: те, что больше нуля, те, что меньше нуля, и третья группа - это число 0. Запишем решение в виде схемы:

{±c, если с > 0

Если |x| = c, то x = {0, если с = 0

{нет корней, если с < 0

Примеры:

1) |x| = 5, т.к. 5 > 0, то x = ±5;

2) |x| = -5, т.к. -5 < 0, то уравнение не имеет корней;

3) |x| = 0, то x = 0.

2. Уравнение вида |f(x)| = b, где b > 0. Для решения данного уравнения необходимо избавиться от модуля. Делаем это так: f(x) = b или f(x) = -b. Теперь необходимо решить отдельно каждое из полученных уравнений. Если в исходном уравнении b< 0, решений не будет.

Примеры:

1) |x + 2| = 4, т.к. 4 > 0, то

x + 2 = 4 или x + 2 = -4

x = 2 x = -6

2) |x² - 5| = 11, т.к. 11 > 0, то

x² - 5 = 11 или x² - 5 = -11

x² = 16 x² = -6

x = ± 4 нет корней

3) |x² - 5x| = -8 , т.к. -8 < 0, то уравнение не имеет корней.

3. Уравнение вида |f(x)| = g(x). По смыслу модуля такое уравнение будет иметь решения, если его правая часть больше или равна нулю, т.е. g(x) ≥ 0. Тогда будем иметь:

f(x) = g(x) или f(x) = -g(x).

Примеры:

1) |2x - 1| = 5x - 10. Данное уравнение будет иметь корни, если 5x - 10 ≥ 0. Именно с этого и начинают решение таких уравнений.

1. О.Д.З. 5x - 10 ≥ 0

5x ≥ 10

x ≥ 2.

2. Решение:

2x - 1 = 5x - 10 или 2x - 1 = -(5x - 10)

3x = 9 7x = 11

x = 3 x = 11/7

3. Объединяем О.Д.З. и решение, получаем:

Корень x = 11/7 не подходит по О.Д.З., он меньше 2, а x = 3 этому условию удовлетворяет.

Ответ: x = 3

2) |x - 1| = 1 - x².

1. О.Д.З. 1 - x² ≥ 0. Решим методом интервалов данное неравенство:

(1 - x)(1 + x) ≥ 0

-1 ≤ x ≤ 1

2. Решение:

x - 1 = 1 - x² или x - 1 = -(1 - x²)

x² + x - 2 = 0 x² - x = 0

x = -2 или x = 1 x = 0 или x = 1

3. Объединяем решение и О.Д.З.:

Подходят только корни x = 1 и x = 0.

Ответ: x = 0, x = 1.

4. Уравнение вида |f(x)| = |g(x)|. Такое уравнение равносильно двум следующим уравнениям f(x) = g(x) или f(x) = -g(x).

Пример:

1) |x² - 5x + 7| = |2x - 5|. Данное уравнение равносильно двум следующим:

x² - 5x + 7 = 2x - 5 или x² - 5x +7 = -2x + 5

x² - 7x + 12 = 0 x² - 3x + 2 = 0

x = 3 или x = 4 x = 2 или x = 1

Ответ: x = 1, x = 2, x = 3, x = 4.

5. Уравнения, решаемые методом подстановки (замены переменной). Данный метод решения проще всего объяснить на конкретном примере. Так, пусть дано квадратное уравнение с модулем:

x² - 6|x| + 5 = 0. По свойству модуля x² = |x|², поэтому уравнение можно переписать так:

|x|² - 6|x| + 5 = 0. Сделаем замену |x| = t ≥ 0, тогда будем иметь:

t² - 6t + 5 = 0. Решая данное уравнение, получаем, что t = 1 или t = 5. Вернемся к замене:

|x| = 1 или |x| = 5

x = ±1 x = ± 5

Ответ: x = -5, x = -1, x = 1, x = 5.

Рассмотрим еще один пример:

x² + |x| - 2 = 0. По свойству модуля x² = |x|², поэтому

|x|² + |x| - 2 = 0. Сделаем замену |x| = t ≥ 0, тогда:

t² + t - 2 = 0. Решая данное уравнение, получаем, t = -2 или t = 1. Вернемся к замене:

|x| = -2 или |x| = 1

Нет корней x = ± 1

Ответ: x = -1, x = 1.

6. Еще один вид уравнений - уравнения со «сложным» модулем. К таким уравнениям относятся уравнения, в которых есть «модули в модуле». Уравнения данного вида можно решать, применяя свойства модуля.

Примеры:

1) |3 - |x|| = 4. Будем действовать так же, как и в уравнениях второго типа. Т.к. 4 > 0, то получим два уравнения:

3 - |x| = 4 или 3 - |x| = -4.

Теперь выразим в каждом уравнении модуль х, тогда |x| = -1 или |x| = 7.

Решаем каждое из полученных уравнений. В первом уравнении нет корней, т.к. -1 < 0, а во втором x = ±7.

Ответ x = -7, x = 7.

2) |3 + |x + 1|| = 5. Решаем это уравнение аналогичным образом:

3 + |x + 1| = 5 или 3 + |x + 1| = -5

|x + 1| = 2 |x + 1| = -8

x + 1 = 2 или x + 1 = -2. Нет корней.

x = 1 x = -3

Ответ: x = -3, x = 1.

Существует еще и универсальный метод решения уравнений с модулем. Это метод интервалов. Но мы его рассмотрим в дальнейшем