- Учителю
- Рабочая программа по алгебре и началам анализа в 11 классе по учебнику Алимова
Рабочая программа по алгебре и началам анализа в 11 классе по учебнику Алимова
Раздел I. Пояснительная записка
Рабочая программа по алгебре и начала анализа для 11 класса составлена в соответствии с требованиями федерального компонента государственного стандарта общего образования, Основной образовательной программы МКОУ «Лицей №7 имени Шуры Козуб с. Новоивановского», на основании программы для общеобразовательных школ, гимназий, лицеев: Сборник "Программы общеобразовательных учреждений: Алгебра и начала математического анализа."/ Сост. Т. А. Бурмистрова, изд.: Просвещение, 2011 г..
Рабочая программа выполняет две основные функции:
1. Информационно-методическая функция позволяет всем участникам образовательного процесса получить представление о целях, содержании, общей стратегии обучения, воспитания и развития обучающихся средствами данного учебного предмета.
2. Организационно-планирующая функция предусматривает выделение этапов обучения, структурирование учебного материала, определение его количественных и качественных характеристик на каждом из этапов, в том числе для содержательного наполнения промежуточной аттестации учащихся.
Рабочая программа рассчитана на 68 часов - 2 часа в неделю. Контроль осуществляется в виде самостоятельных работ, зачётов, письменных тестов, числовых и математических диктантов по теме урока, контрольных работ по разделам учебника. Всего 7 контрольных работ.
Реализация рабочей программы осуществляется с использованием учебно-методического комплекта:
1. Алгебра и начала анализа: Учеб. для 10-11 кл. общеобразоват. учреждений / Алимов Ш.Ф., Колягин Ю.М., Сидоров Ю.В. и др- М.: Просвещение, 2015г./
2. Дидактические материалы по алгебре и началам анализа для 10 класса /Б.М. Ивлев, С.М. Саакян, С.И. Шварцбурд. - М.: Просвещение, 2015.
Цели программы обучения:
-
Формирование представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, об идеях и методах математики.
-
Развитие логического мышления, пространственного воображения, алгоритмической культуры, критичности мышления на уровне, необходимом для будущей профессиональной деятельности, а также последующего обучения в высшей школе.
-
Овладение математическими знаниями и умениями, необходимыми в повседневной жизни, для изучения школьных естественнонаучных дисциплин на базовом уровне, для получения образования в областях, не требующих углубленной математической подготовки.
-
Воспитание средствами математики культуры личности, понимания значимости математики для научно-технического прогресса, отношения к математике как к части общечеловеческой культуры через знакомство с историей развития математики, эволюцией математических идей.
При изучении курса математики на базовом уровне продолжаются и получают развитие содержательные линии: «Алгебра», «Функции», «Уравнения и неравенства», «Элементы комбинаторики, теории вероятностей, статистики и логики», вводится линия «Начала математического анализа».
В рамках указанных содержательных линий решаются следующие задачи:
1. Систематизация сведений о числах; изучение новых видов числовых выражений и формул; совершенствование практических навыков и вычислительной культуры, расширение и совершенствование алгебраического аппарата, сформированного в основной школе, и его применение к решению математических и нематематических задач;
2. Расширение и систематизация общих сведений о функциях, пополнение класса изучаемых функций, иллюстрация широты применения функций для описания и изучения реальных зависимостей;
3. Развитие представлений о вероятностно-статистических закономерностях в окружающем мире, совершенствование интеллектуальных и речевых умений путем обогащения математического языка, развития логического мышления;
4. Знакомство с основными идеями и методами математического анализа.
Формы организации и проведения уроков алгебры и начала анализа в 11 классе, используемые педагогические технологии:
При реализации рабочей программы, с учетом психо-физического развития обучающихся данного возраста, планируется использовать следующие виды и типы уроков:
- комбинированный урок;
- урок-игра;
- урок-практикум;
- урок-эврика;
- урок-исследование;
-уроки контроля знаний: тестирования, контрольная работа, самостоятельная работа, математический диктант.
При реализации Программы применяются педагогические технологии:
- технология дифференциального обучения;
- модульная технология;
- ИКТ;
- технология эффективной речевой деятельности;
- технология проблемного обучения.
Основные развивающие и воспитательные цели
Развитие:
-
ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей;
-
математической речи;
-
сенсорной сферы;
-
внимания;
-
памяти;
-
навыков само и взаимопроверки.
Формированиепредставлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов.
Воспитание:
-
культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса;
-
волевых качеств;
-
коммуникабельности;
-
ответственности.
</ Раздел II. Требования к уровню базовой подготовки выпускников
В результате изучения математики на базовом уровне обучающийся должен
знать/понимать:
-
значение математической науки для решения задач, возникающих в теории и практике; широту и в то же время ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;
-
значение практики и вопросов, возникающих в самой математике для формирования и развития математической науки; историю развития понятия числа, создания математического анализа;
-
универсальный характер законов логики математических рассуждений, их применимость во всех областях человеческой деятельности;
-
вероятностный характер различных процессов окружающего мира.
Алгебра
уметь:
-
выполнять арифметические действия, сочетая устные и письменные приемы, применение вычислительных устройств; находить значения корня натуральной степени, степени с рациональным показателем, используя при необходимости вычислительные устройства;
-
пользоваться оценкой и прикидкой при практических расчетах;
-
проводить по известным формулам и правилам преобразования буквенных выражений, включающих степени, радикалы, тригонометрические функции;
-
вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
-
практических расчетов по формулам, включая формулы, содержащие степени, радикалы, тригонометрические функции, используя при необходимости справочные материалы и простейшие вычислительные устройства;
Функции и графики
уметь:
-
определять значение функции по значению аргумента при различных способах задания функции;
-
строить графики изученных функций;
-
описывать по графику и в простейших случаях по формуле поведение и свойства функций, находить по графику функции наибольшие и наименьшие значения;
-
решать уравнения, простейшие системы уравнений, используя свойства функций и их графиков;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
-
описания с помощью функций различных зависимостей, представления их графически, интерпретации графиков.
Начала математического анализа
уметь:
-
вычислять производные элементарных функций, используя справочные материалы;
-
исследовать в простейших случаях функции на монотонность, находить наибольшие и наименьшие значения функций, строить графики многочленов и простейших рациональных функций с использованием аппарата математического анализа
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
-
решения прикладных задач, в том числе социально-экономических и физических, на наибольшие и наименьшие значения, на нахождение скорости и ускорения.
Уравнения и неравенства
уметь:
-
решать рациональные, простейшие тригонометрические уравнения, их системы;
-
составлять уравнения и неравенства по условию задачи;
-
использовать для приближенного решения уравнений и неравенств графический метод;
-
изображать на координатной плоскости множества решений простейших уравнений и их систем;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
-
построения и исследования простейших математических моделей.
Раздел III. Содержание программы
3.1. Учебно-тематический план
п /п
Наименование разделов
Всего часов
Из них
Контрольные работы
Тесты,
самостоятель-ные работы
Примечание
1
Повторение
2
1
2
Производная и её геометрический смысл
11
2
2
3
Применение производной к исследованию функций
14
1
2
4
Первообразная и интеграл
15
2
2
5
Комбинаторика
5
1
6
Элементы теории вероятностей
5
1
7
Статистика
4
1
1
8
Обобщающее повторение курса алгебры и начал анализа за 10- 11 классы
12
1
3
Итого
68
7
13
3.2. Содержание тем учебного курса
1. Повторение курса 10 класса (2 часа)
Основные цели:
-
формирование представлений о целостности и непрерывности курса алгебры;
-
овладение умением обобщения и систематизации знаний по основным темам курса алгебры 10 класса;
-
развитие логического, математического мышления и интуиции, творческих способностей в области математики.
2. Производная и её геометрический смысл (11 часов). Производная. Производная степенной функции. Правила дифференцирования. Производные некоторых элементарных функций. Геометрический смысл производной.
Основные цели:
-
формирование понятий о мгновенной скорости, о касательной к плоской кривой, о касательной к графику функции, о производной функции, о физическом смысле производной, о геометрическом смысле производной, о скорости изменения функции, о пределе функции в точке, о дифференцировании, о производных элементарных функций;
-
формирование умения использовать алгоритм нахождения производной элементарных функций простого и сложного аргумента;
-
овладение умением находить производную любой комбинации элементарных функций;
-
овладение навыками составления уравнения касательной к графику функции при дополнительных условиях, нахождения углового коэффициента касательной, точки касания.
В результате изучения темы обучающиеся должны:
знать:
-
понятие производной функции, физического и геометрического смысла производной;
-
понятие производной степени, корня;
-
правила дифференцирования;
-
формулы производных элементарных функций;
-
уравнение касательной к графику функции;
-
алгоритм составления уравнения касательной;
уметь:
-
вычислять производную степенной функции и корня;
-
находить производные суммы, разности, произведения, частного;
-
производные основных элементарных функций;
-
находить производные элементарных функций сложного аргумента;
-
составлять уравнение касательной к графику функции по алгоритму.
3. Применение производной к исследованию функций (11 часов). Возрастание и убывание функций. Экстремумы функции. Применение производной к построению графиков функций. Наибольшее и наименьшее значения функции. Выпуклость графика. Точки перегиба.
Основные цели:
-
формирование представлений о промежутках возрастания и убывания функции, о достаточном условии возрастания функции, о промежутках монотонности функции, об окрестности точки, о точках максимума и минимума функции, о точках экстремума, о критических точках;
-
формирование умения строить эскиз графика функции, если задан отрезок, значения функции на концах этого отрезка и знак производной в некоторых точках функции;
-
овладение умением применять производную к исследованию функций и построению графиков;
-
овладение навыками исследовать в простейших случаях функции на монотонность, находить наибольшее и наименьшее значения функций, точки перегиба и интервалы выпуклости.
В результате изучения темы обучающиеся должны:
знать:
-
понятие стационарных, критических точек, точек экстремума;
-
как применять производную к исследованию функций и построению графиков;
-
как исследовать в простейших случаях функции на монотонность, находить наибольшее и наименьшее значения функции.
уметь:
-
находить интервалы возрастания и убывания функций;
-
строить эскиз графика непрерывной функции, определённой на отрезке;
-
находить стационарные точки функции, критические точки и точки экстремума;
-
применять производную к исследованию функций и построению графиков;
-
находить наибольшее и наименьшее значение функции;
-
работать с учебником, отбирать и структурировать материал.
4. Первообразная и интеграл (15 часов). Первообразная. Правила нахождения первообразных. Площадь криволинейной трапеции и интеграл. Вычисление интегралов. Вычисление площадей с помощью интегралов.
Основные цели:
-
формирование представлений о первообразной функции, о семействе первообразных, о дифференцировании и интегрировании, о таблице первообразных, о правилах отыскания первообразных;
-
формирование умений находить для функции первообразную, график которой проходит через точку, заданную координатами;
-
овладение умением находить площадь криволинейной трапеции, ограниченной графиками функций y = f(x) и y = g(x), ограниченной прямыми x = a. х = b, осью Ох и графиком y = h(x).
В результате изучения темы обучающиеся должны:
знать:
-
понятие первообразной, интеграла;
-
правила нахождения первообразных;
-
таблицу первообразных;
-
формулу Ньютона Лейбница;
-
правила интегрирования;
уметь:
-
проводить информационно-смысловой анализ прочитанного текста в учебнике, участвовать в диалоге, приводить примеры; аргументировано отвечать на поставленные вопросы, осмысливать ошибки и их устранять;
-
доказывать, что данная функция является первообразной для другой данной функции;
-
находить одну из первообразных для суммы функций и произведения функции на число, используя справочные материалы;
-
выводить правила отыскания первообразных;
-
изображать криволинейную трапецию, ограниченную графиками элементарных функций;
-
вычислять интеграл от элементарной функции простого аргумента по формуле Ньютона Лейбница с помощью таблицы первообразных и правил интегрирования;
-
вычислять площадь криволинейной трапеции, ограниченной прямыми x = a, х = b, осью Ох и графиком квадратичной функции;
-
находить площадь криволинейной трапеции, ограниченной параболами;
-
вычислять путь, пройденный телом от начала движения до остановки, если известна его скорость;
-
предвидеть возможные последствия своих действий;
-
владеть навыками контроля и оценки своей деятельности.
5. Комбинаторика (5 часов)
Табличное и графическое представление данных. Числовые
характеристики рядов данных. Поочерёдный и одновременны выбор
нескольких элементов из конечного множества. Формулы числа
перестановок, сочетаний, размещений. Решение комбинаторных задач.
Формула бинома Ньютона. Свойства биноминальных коэффициентов.
Треугольник Паскаля.
Основные цели:
-
формирование представлений о научных, логических, комбинаторных методах решения математических задач;
-
формирование умения анализировать, находить различные способы решения одной и той же задачи, делать выводы;
-
развитие комбинаторно-логического мышления.
В результате изучения темы обучающиеся должны:
знать:
-
понятие комбинаторной задачи и основных методов её решения (перестановки, размещения, сочетания без повторения и с повторением);
-
понятие логической задачи;
-
приёмы решения комбинаторных, логических задач;
-
элементы графового моделирования;
уметь: -
использовать основные методы решения комбинаторных, логических задач;
-
разрабатывать модели методов решения задач, в том числе и при помощи графового моделирования;
-
переходить от идеи задачи к аналогичной, более простой задаче, т.е. от основной постановки вопроса к схеме;
-
ясно выражать разработанную идею задачи.
6. Элементы теории вероятностей (5часов).
Элементарные и сложные события. Рассмотрение случаев: вероятность
суммы несовместных событий, вероятность противоположного события.
Понятие о независимости событий. Вероятность и статистическая
частота наступления события, случайные величины, центральные
тенденции и меры разброса. Решение практических задач с применение
вероятностных методов.
Основные цели:
-
формирование представления о теории вероятности, о понятиях: вероятность, испытание, событие (невозможное и достоверное), вероятность событий, объединение и пересечение событий, следствие события, независимость событий;
-
формирование умения вычислять вероятность событий, определять несовместные и противоположные события;
-
овладение умением выполнять основные операции над событиями;
-
овладение навыками решения практических задач с применением вероятностных методов.
В результате изучения темы обучающиеся должны:
знать:
-
понятие вероятности событий;
-
понятие невозможного и достоверного события;
-
понятие независимых событий;
-
понятие условной вероятности событий;
-
понятие статистической частоты наступления событий;
уметь: -
вычислять вероятность событий;
-
определять равновероятные события;
-
выполнять основные операции над событиями;
-
доказывать независимость событий;
-
находить условную вероятность;
-
решать практические задачи, применяя методы теории вероятности.
6. Статистика (4 часа). Случайные величины. Центральные тенденции. Меры разброса.
Основные цели:
-
формирование представления о статистике, о понятиях: размах, мода, среднее арифметическое.
знать:
-
понятие случайных величин,
-
понятие статистических характеристик ряда.
уметь:
-
вычислять размах, моду среднее арифметическое ряда.
7. Итоговое повторение курса алгебры и начал
анализа (12 часов).
Основные цели:
-
обобщение и систематизация курса алгебры и начал анализа;
-
создание условий для плодотворного участия в групповой работе, для формирования умения самостоятельно и мотивированно организовывать свою деятельность;
-
формирование представлений об идеях и методах математики, о математике как средстве моделирования явлений и процессов
-
развитие логического и математического мышления, интуиции, творческих способностей;
-
воспитание понимания значимости математики для общественного прогресса.
Раздел IV. Календарно-тематическое планирование
п/п
Содержание материала
Дата
по плану
Дата фактическая
Примечание
Повторение (2 часа)
1
Степенная функция, показательная, логарифмическая.
02.09
2
Тригонометрические функции.
04.09
Производная и ее геометрический смысл (11 часов)
3
Производная
07.09
4
Производная
09.09
5
Производная степенной функции
14.09
6
Производная степенной функции
15.09
7
Административная контрольная работа
16.09
8
Правила дифференцирования
17.09
9
Производная некоторых элементарных функций
23.09
10
Геометрический смысл производной
30.09
11
Геометрический смысл производной
05.10
12
Геометрический смысл производной
07.10
13
Контрольная работа
№1 по теме «Производная и ее геометрический смысл».
12.10
Применение производной к исследованию функций (14 часов)
14
Возрастание и убывание функций
14.10
15
Возрастание и убывание функций
19.10
16
Экстремумы функции
21.10
17
Экстремумы функции
26.10
18
Экстремумы функции
28.10
19
Применение производной к построению графиков функций
09.11
20
Применение производной к построению графиков функций
11.11
21
Применение производной к построению графиков функций
16.11
22
Наибольшее и наименьшее значения функций
18.11
23
Наибольшее и наименьшее значения функций
23.11
24
Наибольшее и наименьшее значения функций
25.11
25
Наибольшее и наименьшее значения функций
30.11
26
Наибольшее и наименьшее значения функций
02.12
27
Контрольная работа №2 по теме «Применение производной к исследованию функций».
07.12
Первообразная и интеграл (15 часов)
28
Первообразная
09.12
29
Правила нахождения первообразных
14.12
30
Правила нахождения первообразных
16.12
31
Административная контрольная работа
21.12
32
Площадь криволинейной трапеции и интеграл
23.12
33
Площадь криволинейной трапеции и интеграл
25.12
34
Вычисление интегралов
11.01
35
Вычисление интегралов
13.01
36
Вычисление площадей с помощью интегралов
18.01
37
Вычисление площадей с помощью интегралов
20.01
38
Вычисление площадей с помощью интегралов
25.01
39
Применение производной и интеграла к решению практических задач
27.01
40
Применение производной и интеграла к решению практических задач
01.02
41
Применение производной и интеграла к решению
03.02
42
Контрольная работа №3 по теме «Интеграл»
08.02
Комбинаторика (5 часов)
43
Правило произведения
10.02
44
Перестановки
15.02
45
Размещения.
16.02
46
Сочетания и их свойства.
18.02
47
Бином Ньютона.
24.02
Элементы теории вероятностей (5 часов)
48
Элементы теории вероятностей. События.
29.02
49
Вероятность события. Сложение вероятностей.
02.03
50
Независимые события. Умножение вероятностей.
05.03
51
Статистическая вероятность.
09.03
52
Статистическая вероятность.
14.03
Статистика (4 часа)
53
Статистика. Случайные величины.
14.03
54
Центральные тенденции. Меры разброса
16.03
55
Центральные тенденции. Меры разброса
04.04
56
Контрольная работа №4 по теме «Комбинаторика. Элементы теории вероятностей. Статистика»
06.04
Обобщающее повторение курса алгебры и начал анализа за 10- 11 классы (12 часов)
57
Вычисления и преобразования
11.04
58
Текстовые задачи
13.04
59
Уравнения, системы уравнений
18.04
60
Неравенства
20.04
61
Геометрический смысл производной
25.04
62
Наибольшее и наименьшее значения функций
27.04
63
Вычисление площадей с помощью интегралов
04.05
64
Размеры и единицы измерения
11.05
65
Административная (итоговая) контрольная работа
16.05
66
Анализ графиков и диаграмм
18.05
67
Анализ утверждений
23.05
68
Числа и их свойства. Задачи на смекалку
25.05
Раздел V. Формы и средства контроля знаний
Организация текущего и промежуточного контроля знаний. Организация текущего и промежуточного контроля знаний проводится в каждой теме, в каждом разделе (указано в учебно-тематическом планировании).
Виды и формы контроля знаний, умений, навыков обучающихся класса: контрольная работа, самостоятельная работа, тест, математический диктант, он-лайн тестирование.
Раздел VI. Перечень учебно-методического обеспечения
1. Учебник: Алгебра и начала математического анализа, 10 11 классы: учеб. Для общеобразоват. учреждений /Ш.А. Алимов [и др.], - М.: Просвещение, 2015г.
2. Алгебра и начала анализа 10-11, тематические тесты: учеб.пособие./В.К.Шарапова. - Ростов н/Д.: Феникс, 2014.
3. Контрольно-измерительные материалы. Алгебра и начала анализа: 10 класс / сост. А.Н. Рурукин. - М.: ВАКО, 2014
4. Контрольно-измерительные материалы. Алгебра и начала анализа: 11 класс / сост. А.Н. Рурукин. - М.: ВАКО, 2014
Дополнительная литература:
1.Примерные программы по математике. Сборник нормативных документов. Математика / сост. Э.Д. Днепров, А.Г. Аркадьев. М.: Дрофа, 2012.
2.Алгебра и начала математического анализа. 7 -11 классы: развёрнутое тематическое планирование. Линия Ш.А. Алимова / авт.-сост. Н.А.Ким. Волгоград: Учитель,2015.
3. Дидактические материалы по алгебре и началам анализа для 10 и 11 класса /Б.И. Ивлев, С.И.Саакян,С.И.Шварцбург. М.: Просвещение,2015.
4. Устные упражнения по алгебре и началам анализа / Р.Д.Лукин, Т.К. Лукина, И.С. Якунина. М.: Просвещение, 2013.
5. Контрольные и проверочные работы по алгебре. 10 -11 кл.: Методическое пособие / Звавич Л.И., Шляпочник Л.Я. М.: Дрофа, 2012.
6. Алгебра и начала анализа. Тесты. 10 - 11 классы: учебно-метод. Пособие. М.: Дрофа, 2011.
7. Математика. 10- 11 классы. Развитие комбинаторно-логического мышления. Задачи, алгоритмы решений / авт.-сост. Т.Г. Попова. Волгоград: Учитель, 2014.
8. Алгебра и начала анализа: сборник задач для подготовки и проведения итоговой аттестации за курс средней школы / И.Р. Высоцкий, Л.И. Звавич, Б.П. Пигарев и др.; под ред. С.А. Шестакова. М.: Внешсигма-М, 2008
9. Математика. 10- 11 классы: технология подготовки учащихся к ЕГЭ / авт.-сост. Н.А. Ким. Волгоград: Учитель, 2010.
10. Математика. ЕГЭ. Практикум. 2015 г. ( авт. Л.Д. Лаппо, М.А. Попов).
11. Математика. Подготовка к ЕГЭ - 2012: учебно - методическое пособие /под редакцией Ф.Ф. Лысенко, С.Ю. Кулабухова. - Ростов - на - Дону: Легион - М, 2012.
12. Решение сложных задач ЕГЭ по математике: 9 - 11 классы. - М.: ВАКО, 2011 (авт. С.И. Колесникова).
ПРИЛОЖЕНИЕ
ОЦЕНКА УСТНЫХ ОТВЕТОВ ОБУЧАЮЩИХСЯ
Ответ оценивается отметкой "5", если ученик:
1. полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;
-
изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;
-
правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
-
показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;
-
продемонстрировал усвоение ранее изученных сопутствующих вопросов, сформированность и устойчивость используемых при ответе умений и навыков;
-
отвечал самостоятельно, без наводящих вопросов учителя.
Возможны одна-две неточности при освещении второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.
Ответ оценивается отметкой "4", если удовлетворяет в основном требованиям на оценку "5", но при этом имеет один из недостатков:
1. в изложении допущены небольшие пробелы, не исказившие математическое содержание ответа;
2. допущены один-два недочета при освещении основного содержания ответа, исправленные после замечания учителя;
3. допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.
Отметка "3" ставится в следующих случаях:
1. неполно раскрыто содержание материала (содержание изложено фрагментально, не всегда последовательно), не показано общее понимание вопроса и продемонстрированы умения, достаточные для дальнейшего усвоения программного материала (определенные "требования к математической подготовке учащихся") в настоящей программе по математике;
2. имелись затруднения или допущены ошибки в определении понятий, использовании математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
3. ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
4. при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.
Отметка "2" ставится в следующих случаях:
1. не раскрыто основное содержание учебного материала;
2. обнаружено незнание или непонимание учеником большей или наиболее важной части учебного материала;
3. допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.
ОЦЕНКА ПИСЬМЕННЫХ КОНТРОЛЬНЫХ РАБОТ ОБУЧАЮЩИХСЯ
Отметка "5" ставится, если:
1. работа выполнена полностью;
2. в логических рассуждениях и обосновании решения нет пробелов и ошибок;
3. в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).
Отметка "4" ставится в следующих случаях:
1. работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не явилось специальным объектом проверки);
2. допущена одна ошибка или есть два-три недочета в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).
Отметка "3" ставится, если:
3. допущено более одной ошибки или более двух-трех недочетов в выкладках, чертежах или графиках, но учащийся обладает обязательными умениями по проверяемой теме.
Отметка "2" ставится, если:
1. допущены существенные ошибки, показавшие, что учащийся не обладает обязательными умениями по данной теме в полной мере.
Контрольная работа №1 «Производная и ее геометрический смысл».
Вариант 1
-
Найдите производную функции:
а)f(x) = x3 - x2 - 7x; б)y(x) = + 7;
в) g(x) = 2tg(x) и вычислите g´(- ); г) h(x) = и вычислите h´(-2).
-
Решите уравнение f´(x)·g´(x) = 0, если f(x) = x3- 6x2, g(x) = .
-
Точка движется прямолинейно по закону x(t) = 3t3 + 2t + 1. Найдите ее ускорение в момент времени t = 2 (координата x(t) изменяется в сантиметрах, время t - в секундах).
-
Найдите угол наклона касательной к графику функции f(x) =1 -
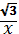
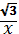 в
точке с абсциссой x0 = -1.
в
точке с абсциссой x0 = -1.
-
Напишите уравнение касательной к графику функции f(x) = x2- 2xв точке его с абсциссой x0=2. Выполните рисунок.
-
Найдите значения х, при которых значения производной функции положительны.
Вариант 2
-
Найдите производную функции:
а)f(x) = -x3+ 4x2+2x; б)y(x) = -10;
в) g(x) = 4сtg(x) и вычислите g´(- ); г) h(x) = и вычислите h´(4).
-
Решите уравнение f´(x)·g´(x) = 0, если f(x) = x3- 3x2, g(x) = .
-
Точка движется прямолинейно по закону x(t) = 2t3 + 3t + 1. Найдите ее ускорение в момент времени t = 3(координата x(t) изменяется в сантиметрах, время t - в секундах).
-
Найдите угол наклона касательной к графику функции f(x) =2-
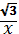
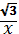 в
точке с абсциссой x0 = 1.
в
точке с абсциссой x0 = 1.
-
Напишите уравнение касательной к графику функции f(x) = x2+ 2xв точке его с абсциссой x0=-2. Выполните рисунок.
-
Найдите значения х, при которых значения производной функции
 отрицательны.
отрицательны.
А - 11 Контрольная работа №2
Применение производной к исследованию функций
Вариант 1
1. Найдите экстремумы функции:
![]()
![]()
2. Найдите интервалы возрастания и убывания функции
![]() .
.
3. Постройте график функции ![]() на отрезке
на отрезке ![]() .
.
4. Найдите наибольшее и наименьшее значения функции
![]() на отрезке
на отрезке ![]() .
.
5. Среди прямоугольников, у которых сумма длин двух сторон равна 20, найдите прямоугольник с наибольшей площадью.
Контрольная работа №2
Применение производной к исследованию функций
Вариант 2
1. Найдите экстремумы функции:
![]()
![]()
2. Найдите интервалы возрастания и убывания функции
![]() .
.
3. Постройте график функции ![]() на отрезке
на отрезке ![]() .
.
4. Найдите наибольшее и наименьшее значения функции
![]() на отрезке
на отрезке ![]() .
.
5. Найдите ромб с наибольшей площадью, если известно, что сумма длин его диагоналей равна 10.
А - 11 Контрольная работа №3
Интеграл
Вариант1
1. Докажите, что функция ![]() является первообразной функции
является первообразной функции ![]() на всей числовой оси.
на всей числовой оси.
2. Найдите первообразную F функции ![]() график которой проходит через точку
график которой проходит через точку ![]() .
.
3. Вычислите площадь фигуры F, изображенной на рисунке.
Контрольная работа №3
Интеграл
Вариант2
1. Докажите, что функция ![]() является первообразной функции
является первообразной функции ![]() на всей числовой оси.
на всей числовой оси.
2. Найдите первообразную F функции ![]() , график которой проходит через точку
, график которой проходит через точку ![]() .
.
3. Вычислите площадь фигуры F, изображенной на рисунке.
А - 11 Кон
Контрольная работа № 4
Элементы комбинаторики
1. Вычислите: ![]()
![]()
2. Сколько существует способов для обозначения вершин четырехугольника с помощью букв A, B, C, D, E, F?
3. Запишите разложение бинома ![]()
Контрольная работа №4
Знакомство с вероятностью
1.Из урны, содержащей 15 белых, 10 красных и 5 синих шаров, наугад выбирают один шар. Какова вероятность того, что шар окажется: а) красного цвета; б) зеленого цвета?
2.Бросаются монета и игральная кость. Какова вероятность того, что появится решка и 5 очков?
3. Вероятность попадания по мишени равна 0.7. Какова вероятность того, что, не попав по мишени при первом выстреле, стрелок попадет при втором?
ибо других заданий.
21