Урок з геометрії для 9 класу Многогранники. Пряма призма. Площа поверхні та обєм призми

РОЗРОБКА УРОКУ ГЕОМЕТРІЇ 9 КЛАСУ З ТЕМИ

</ «ПОЧАТКОВІ ВІДОМОСТІ ЗІ СТЕРІОМЕТРІЇ»

УРОК №1

Тема. Многогранники. Пряма призма. Площа поверхні та об'єм призми

Мета:

• повторити властивості основних геометричних фігур;

• розширити відомості про многогранники, пряму призму, площу поверхні та об'єм призми;

• навчитися знаходити площу поверхні та об'єми призми;

• розвивати проторове мислення, вміння будувати геометричні тіла, позначати відповідні елементи;

• виховувати культуру поведінки в колективі.

Тип уроку: вивчення нового матеріалу

Наочність і обладнання: моделі паралелепіпеда, піраміди, призми,розгортки геометричних тіл, презентацією до уроку, мультимедійне оснащення

Хід уроку

І. Перевірка домашнього завдання

1. Перевірити правильність виконання домашнього завдання за записами, зробленими на дошці до початку уроку. [10]

№ 798. ° З точки А проведение перпендикуляр АВ до площини а, точка С належить площині а. Знайдіть: 1) АВ, якщо АС = 13 см, ВС = 5 см;

Дано: площина а, С , АВ , АС = 13см, ВС = 5 см

Знайдіть: АВ

Розв'язання

Оскільки АВ перпендикуляр до площнини , то АВ перендикулярно ВС. Таким чино АВС прямокутний трикутник (кутВ = 90⁰). За теоремою Піфагора :

АВ = = = 12 (см).

Відповідь: АВ = 12 см.

№ 812. Точка К лежить поза площиною трикутника АЕС. Встановити взаємне розміщення прямих АК та ЕС

К Е

А

С

Розвязання

Оскільки точка К лежить поза площиною трикутника АЕС, то пряма АК перетинає площину трикутника. Тоді ЕС та АК мимобіжні за означенням мимобіжних прямих

2. Графічний диктант (5 хвилин, кожна відповідь 1 б, на окремих аркушах, виконується взаємоперевірка, і на початок уроку кожен учень вже має певну кількість балів, протягом уроку він зможе підвищити свій бал )

1. Побудуйте дві паралельні прямі а і с

2. Побудуйте зображення куба АВСЕА₁ В₁ С₁ Е₁

3. Побудуйте площину а та пряму с, яка їй паралельна

4. За допомогою малюнка назвіть три випадка існування площини

5. Побудуйте дві площини, які перетинаються

Відповіді Слайд 3

ІІ. Актуалізація знань

Запитання класу: наведіть приклади обємних фігур зі світу який нас оточує?

(Слайд 4)

III. Поетапне сприймання й усвідомлення нового матеріалу

Многогранник та його елементи

Фігури, які вивчає стереометрія, називають тілами. Наочно тіло уявляють як частину простору, зайняту фізичним тілом і обмежену поверхнею. (Демонструємо моделі многогранників.)

Многогранником називається тіло (частина простору), обмежене скінченною кількістю плоских многокутників (Слайд 5) Многокутники, які обмежують многогранник, називають його гранями, їх сторони - ребрами, а вершини - вершинами многогранника.

На малюнку 1 гранями є многокутники: ABC, А₁В₁С₁, АВВ₁A₁, ВВ₁C₁С, АА₁C₁С; ребрами - сторони АС, ВС, АВ, АА₁, ВВ₁, CC₁, A₁B₁, A₁C₁, B₁C₁, вершинами - точки А, В, С, A₁, В₁, С₁.

Завдання класу (за кожну правильну відповідь 1б , таким чином кожен учень працює на свій рівень знань і в кінці отримує відповідну оцінку)

1. Наведіть приклади предметів побуту, які мають форму многогранників.

2. Скільки вершин, ребер, граней має: а) паралелепіпед; б) куб? (12)

3. Яке найменше число ребер може мати многогранник? (6)

Призма та її елементи

Многогранник, дві грані якого - рівні n-кутники з відповідно паралельними сторонами, а всі інші п граней - паралелограми, називається n-кутною призмою мал. 2 (Слайд ). (Демонструємо моделі призм.)

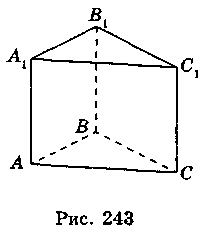
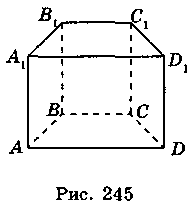
Мал. 1 Мал. 2

Рівні n-кутники призми називаються основами, а паралелограми - бічними гранями, сторони основи - ребрами основи, інші ребра - бічними ребрами.

З означення призми випливає, що основи призми рівні, а також лежать у паралельних площинах. Бічні ребра паралельні й рівні.

Поверхня призми складається з основ і бічної поверхні. Площею поверхні призми називається сума площ усіх її граней. Оскільки основи рівні, то S_np = S_6ічн + 2S_осн, де S_np - площа поверхні призми; S_6ічн - площа бічної поверхні призми; S_осн - площа основи.

Завдання класу (за кожну правильну відповідь 1б)

1. Скільки граней має n-кутна призма? Чи може призма мати 10 граней?

2. Скільки ребер має п-кутна призма? Чи може призма мати 10 ребер?

Призма називається прямою, якщо її бічні ребра перпендикулярні до основи. (Демонструються моделі прямих призм.) (Слайд 6 )

Пряма призма називається правильною, якщо в її основі лежить правильний многокутник. (Демонструються моделі правильних призм.) (Слайд 7)

Слід зазначити, що бічними гранями прямої призми є прямокутники.

Площа поверхні та об'єм прямої призми

Теорема. Площа бічної поверхні прямої призми дорівнює добутку периметра її основи на довжину ребра.

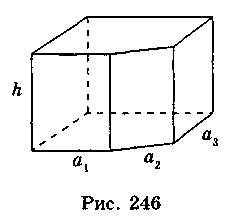
S_бічн = Ph.

Пряма призма, в основі якої лежить прямокутник, називається прямокутним паралелепіпедом. Прямокутний паралелепіпед, усі ребра якого рівні, називається кубом.(Слайд 8 )

У молодших класах ви вже обчислювали об'єм прямокутного паралелепіпеда за формулою

V = abc, (1)

де a, b, c - відповідно довжина, ширина і висота паралелепіпеда. Формулу (1) можна записати у вигляді

V = Sh, (2)

де S = ab - площа основи, h = c - висота паралелепіпеда.

Формула (2) справедлива для будь-якої прямої призми. Отже:

Об'єм прямої призми дорівнює добутку площі її основи на довжину бічного ребра (висоту):

V = Sh.

Завдання класу (за кожну правильну відповідь 1б )

1. Знайдіть площу поверхні куба, ребро якого дорівнює 5 см.

2. Знайдіть об'єм прямокутного паралелепіпеда, сторони основи якого дорівнюють 3 см і 4 см, а бічне ребро - 5 см.

IV. Закріплення й осмислення нового матеріалу

Розв'язування задач (один учень біля дошки виконує завдання решта на місцях за правильно розвязану задачу 3 б)

№ 829. ° Знайдіть площу бічної поверхні , площу поверхні та обєм прямої чотирикутної призми, в основі якох лежить квадрат зі стороною 7 см та бічним ребром 6 см. (Розвязання предствлене на слайді, учні можуть самостійно перевірити себе)

№ 841. Класна кімна має форму прямокутного паралелепіпеда, виміри якого 8,5 м, 6 м і 3,6 м. Чи можливо в цій кімнаті розташувати 30 учнів, якщо згідно санітарним ноомам кожному учневі необхідно 6м³ повітря? (Слайд 9,10)

V. Контроль засвоєння знань (Кожна задача 3б)

Варіант 1

Знайдіть площу поверхні та обєм куба з ребром 8 см (384 см², 512 см³)

Варіант 2

Знайдіть площу поверхні та обєм куба з ребром 6 см (216 см², 216 см³ )

Взаємоперевірка

VII. Підбиття підсумків уроку

Запитання до класу

1. Що таке n-кутна призма?

2. Яка призма називається прямою? правильною?

3. Чому дорівнює площа бічної поверхні прямої призми?

4. Чому дорівнює об'єм призми?

Кожен з учнів оголошує свої надбання за урок, учитель оцінює.

VI. Домашнє завдання

1. Вивчити формули площі поверхні та об'єму прямої призми , параграф 21

2. Розв'язати задачі № 827, №831 [10]