Рабочая программа по математике 7 класс

РАБОЧАЯ ПРОГРАММА

ПО ИЗУЧЕНИЮ КУРСА МАТЕМАТИКИ В 7 КЛАССЕ

ПОСНИТЕЛЬНАЯ ЗАПИСКА

Рабочая программа по математике составлена на основе федерального компонента государственного стандарта основного общего образования.

Данная рабочая программа ориентирована на учащихся 7 классов и реализуется на основе следующих документов:

1. Сборник нормативных документов, Математика. Примерные программы по математике. /сост. Э.Д. Днепров, А.Г. Аркадьев. - 2-е изд., стереотип. - М. :Дрофа, 2008 г.

2. Алгебра. Рабочие программы. Предметная линия учебников Ю.Н. Макарычева и других. 7 - 9 классы: пособие для учителей общеобразовательных учреждений/ Н.Г. Миндюк. - М.: Просвещение, 2011 г.

3. Программы общеобразовательных учреждений. Геометрия, 7 - 9 классы/ М. : Просвещение, 2008 г.

4. Государственный стандарт начального общего, основного общего и среднего (полного) общего образования. Приказ Министерства образования РФ от 05.03.2004 г № 1089.

5. Алгебра 7 класс. Учебник для общеобразовательных учреждений/ Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова., 20-е изд. - М. : Просвещение, 2011 г.

6. Геометрия, 7 - 9 : учебник для общеобразовательных учреждений/Л.С. Атанасян, В. Ф. Буткзов, С. Б. Кадомцев и др. - 18-е изд. - М. Просвещение, 2009 г

В ходе освоения содержания курса учащиеся получают возможность:

• сформировать практические навыки выполнения устных, письменных, инструментальных вычислений, развить вычислительную культуру;

• овладеть символическим языком алгебры, выработать формально-оперативные алгебраические умения и научиться применять их к решению математических и нематематических задач;

• изучить свойства и графики элементарных функций, научиться использовать функционально-графические представления для описания и анализа реальных зависимостей;

• развить логическое мышление и речь - умения логически обосновывать суждения, проводить несложные систематизации, приводить примеры и контрпримеры, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства;

• сформировать представления об изучаемых понятиях и методах как важнейших средствах математического моделирования реальных процессов и явлений.

Изучение математики на ступени основного общего образования направлено на достижение следующих целей:

• овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;

• интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, пространственных представлений, способность к преодолению трудностей;

• формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;

• воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса.

Арифметика

уметь

• выполнять устно арифметические действия: сложение и вычитание двузначных чисел и десятичных дробей с двумя знаками, умножение однозначных чисел, арифметические операции с обыкновенными дробями с однозначным знаменателем и числителем;

• переходить от одной формы записи чисел к другой, представлять десятичную дробь в виде обыкновенной и в простейших случаях обыкновенную в виде десятичной, проценты - в виде дроби и дробь - в виде процентов; записывать большие и малые числа с использованием целых степеней десятки;

• выполнять арифметические действия с рациональными числами, сравнивать рациональные и действительные числа; находить в несложных случаях значения степеней с целыми показателями и корней; находить значения числовых выражений;

• округлять целые числа и десятичные дроби, находить приближения чисел с недостатком и с избытком, выполнять оценку числовых выражений;

• пользоваться основными единицами длины, массы, времени, скорости, площади, объема; выражать более крупные единицы через более мелкие и наоборот;

• решать текстовые задачи, включая задачи, связанные с отношением и с пропорциональностью величин, дробями и процентами;

использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

• решения несложных практических расчетных задач, в том числе c использованием при необходимости справочных материалов, калькулятора, компьютера;

• устной прикидки и оценки результата вычислений; проверки результата вычисления с использованием различных приемов;

• интерпретации результатов решения задач с учетом ограничений, связанных с реальными свойствами рассматриваемых процессов и явлений;

Алгебра

уметь

• составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные;

• выполнять основные действия со степенями с натуральными показателями, с многочленами; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражений;

• решать линейные уравнения решать линейные решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;

• изображать числа точками на координатной прямой;

• определять координаты точки плоскости, строить точки с заданными координатами;

• находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;

• применять графические представления при решении уравнений, систем, неравенств;

• описывать свойства изученных функций (у=кх, где к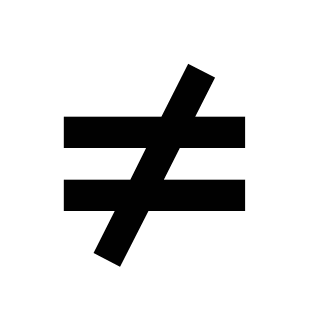0, у=кх+b, у=х², у=х³), строить их графики.

использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

• выполнения расчетов по формулам, составления формул, выражающих зависимости между реальными величинами; нахождения нужной формулы в справочных материалах;

• моделирования практических ситуаций и исследовании построенных моделей с использованием аппарата алгебры;

• описания зависимостей между физическими величинами соответствующими формулами при исследовании несложных практических ситуаций;

• интерпретации графиков реальных зависимостей между величинами.

Элементы логики и комбинаторики.

Уметь

• решать комбинированные задачи путем систематического перебора возможных вариантов и с использованием правил умножения;

• вычислять средние значения результатов измерений.

Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

• анализа реальных числовых данных, представленных в виде диаграмм.

Владеть компетенциями:

• познавательной;

• информационной;

• коммуникационной;

• рефлексивной.

Общеучебные умения и навыки:

• понимать учебную задачу, поставленную учителем, и действовать строго в соответствии с ней;

• работать в заданном темпе;

• учиться пооперационному контролю учебной работы (своей и товарища), оценивать учебные действия (свои и товарища) по образцу оценки учителя;

• уметь работать самостоятельно и вместе с товарищем, работать в группах;

• оказывать необходимую помощь учителю на уроке и вне его;

• самостоятельно обращаться к вопросам и заданиям учебника;

• работать с материалами приложения учебника;

• использовать образцы в процессе самостоятельной работы;

• отвечать на вопросы по тексту; учиться связно отвечать по плану. Самостоятельно приобретать и применять знания в различных ситуациях;

• аргументировать и отстаивать свою точку зрения, уметь слушать других;

• извлекать учебную информацию на основе сопоставительного анализа объектов;

самостоятельно действовать в ситуации неопределенности при решении актуальных для них проблем.

Требования к математической подготовке учащихся 7 класса

В результате изучения алгебры ученик должен

• знать/понимать

• существо понятия математического доказательства; примеры доказательств;

• существо понятия алгоритма; примеры алгоритмов;

• как используются математические формулы, уравнения; примеры их применения для решения математических и практических задач;

• как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;

• смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации;

• формулы сокращенного умножения;

• уметь

• составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные;

• выполнять основные действия со степенями с натуральными показателями, с одночленами и многочленами; выполнять разложение многочленов на множители; сокращать алгебраические дроби;

• решать линейные уравнения и уравнения, сводящиеся к ним, системы двух линейных уравнений с двумя переменными;

• решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;

• определять координаты точки плоскости, строить точки с заданными координатами; строить графики линейных функций и функции y=x²;

• находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;

• определять свойства функции по ее графику; применять графические представления при решении уравнений и систем;

• описывать свойства изученных функций, строить их графики;

использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

• выполнения расчетов по формулам, составления формул, выражающих зависимости между реальными величинами; нахождения нужной формулы в справочных материалах;

• моделирования практических ситуаций и исследования построенных моделей с использованием аппарата алгебры;

• описания зависимостей между физическими величинами соответствующими формулами при исследовании несложных практических ситуаций;

• интерпретации графиков реальных зависимостей между величинами.

Место предмета в федеральном базисном учебном плане

Согласно федеральному базисному учебному плану для образовательных учреждений Российской Федерации предмет математика состоит из двух модулей «Алгебра» и «Геометрия» на ступени основного общего образования отводится не менее 875 ч из расчета 5 ч в неделю с V по IX класс. Математика изучается в 7 классе 5 ч в неделю, всего 175 ч., на модуль «Алгебра» - 3 часа в неделю, модуль «Геометрия» - 2 часа в неделю.

Содержание тем учебного модуля «Алгебра»

1. Выражения. Тождества уравнения (18)

Числовые выражения с переменными. Простейшие преобразования выражений. Уравнение, корень уравнения. Линейное уравнение с одной переменной. Решение текстовых задач методом составления уравнений.

Основная цель - систематизировать и обобщить сведения о преобразованиях алгебраических выражений и решении уравнений с одной переменной.

Первая тема курса 7 класса является связующими звеном между курсом математики 5-6 классов и курсом алгебры. В ней закрепляются вычислительные навыки, систематизируются и обобщаются сведения о преобразованиях выражений и решении уравнений.

Нахождение значений числовых и буквенных выражений дает возможность повторить с учащимися правила действий с рациональными числами. Умения выполнять арифметические действия с рациональными числами являются опорными для всего курса алгебры. Следует выяснить, насколько прочно овладели ими учащиеся, и в случае необходимости организовать повторение с целью ликвидации выявленных пробелов. Развитию навыков вычислений должно уделяться серьезное внимание и в дальнейшем при изучении других тем курса алгебры.

В связи с рассмотрением вопроса о сравнении значений выражений расширяются сведения о неравенствах: вводятся знаки и , дается понятие о двойных неравенствах.

При рассмотрении преобразований выражений формально-оперативные умения остаются на том же уровне, учащиеся поднимаются на новую ступень в овладении теорией. Вводятся понятия «тождественно равные выражения», «тождество», «тождественное преобразование выражений», содержание которых будет постоянно раскрываться и углубляться при изучении преобразований различных алгебраических выражений. Подчеркивается, что основу тождественных преобразований составляют свойства действий над числами.

Усиливается роль теоретических сведений при рассмотрении уравнений. С целью обеспечения осознанного восприятия учащимися алгоритмов решения уравнений вводится вспомогательное понятие равносильности уравнений, формулируются и разъясняются на конкретных примерах свойства равносильности. Дается понятие линейного уравнения и исследуется вопрос о числе его корней. В системе упражнений особое внимание уделяется решению уравнений вида ах=b при различных значениях а и b. Продолжается работа по формированию у учащихся умения использовать аппарат уравнений как средство для решения текстовых задач. Уровень сложности задач здесь остается таким же, как в 6 классе.

2.Функции.(11)

Функция, область определения функции. Вычисление значений функции по формуле. График функции. Прямая пропорциональность и ее график. Линейная функция и ее график.

Основная цель - ознакомить учащихся с важнейшими функциональными понятиями и с графиками прямой пропорциональности и линейной функции общего вида.

Данная тема является начальным этапом в систематической функциональной подготовке учащихся. Здесь вводятся такие понятия, как функция, аргумент, область определения функции, график функции. Функция трактуется как зависимость одной переменной от другой. Учащиеся получают первое представление о способах задания функции. В данной теме начинается работа по формированию у учащихся умений находить по формуле значение функции по известному значению аргумента, выполнять ту же работу по графику и решать по графику обратную задачу.

Функциональные понятия получают свою конкретизацию при изучении линейной функции и ее частного вида - прямой пропорциональности. Умения строить и читать графики этих функций широко используются как в самом курсе алгебры, так и в курсах геометрии и физики. Учащиеся должны понимать, как влияет знак коэффициента на расположение в координатной плоскости графика функции у=kx, где k≠0, как зависит от значений k и b взаимное расположение графиков двух функций вида у=kx+b.

Формирование всех функциональных понятий и выработка соответствующих навыков, а также изучение конкретных функций сопровождаются рассмотрением примеров реальных зависимостей между величинами, что способствует усилению прикладной направленности курса алгебры.

3. Степень с натуральным показателем(11)

Степень с натуральным показателем и ее свойства. Одночлен. Функции у = х², у = х³ и их графики.

Основная цель: - выработать умение выполнять действия над основными степенями с натуральными показателями.

В данной теме дается определение степени с натуральным показателем. В курсе математики 6 класса учащиеся уже встречались с примерами возведения чисел в степень. В связи с вычислением значений степени в 7 классе дается представление о нахождении значений степени с помощью калькулятора. Рас­сматриваются свойства степени с натуральным показателем. На примере доказательства свойств а^т • а^п = а^{т + п}, а^т : а^п = а^т~ ^п, где т> л, (а^т)^п = а^тп, (ab)ⁿ = а^пb^п учащиеся впервые знакомятся с доказательствами, проводимыми на алгебраическом материа­ле. Указанные свойства степени с натуральным показателем на­ходят применение при умножении одночленов и возведении одночленов в степень. При нахождении значений выражений, со­держащих степени, особое внимание следует обратить на порядок действий.

Рассмотрение функций у = х², у = х³ позволяет продолжить работу по формированию умений строить и читать графики функ­ций. Важно обратить внимание учащихся на особенности графи­ка функции у = х²: график проходит через начало координат, ось Оу является его осью симметрии, график расположен в верхней полуплоскости.

Умение строить графики функций у = х² и у = х³ используется для ознакомления учащихся с графическим способом решения уравнений.

4. Многочлены (17)

Многочлен. Сложение, вычитание и умножение многочленов. Разложение многочленов на множители.

Основная цель - выработать умение выполнять сложе­ние, вычитание, умножение многочленов и разложение много­членов на множители.

Данная тема играет фундаментальную роль в формировании умения выполнять тождественные преобразования алгебраических выражений. Формируемые здесь формально-оперативные умения являются опорными при изучении действий с рациональными дробями, корнями, степенями с рациональными показателями.

Изучение темы начинается с введения понятий многочлена, стандартного вида многочлена, степени многочлена. Основное ме­сто в этой теме занимают алгоритмы действий с многочлена­ми - сложение, вычитание и умножение. Учащиеся должны по­нимать, что сумму, разность, произведение многочленов всегда можно представить в виде многочлена. Действия сложения, вы­читания и умножения многочленов выступают как составной компонент в заданиях на преобразования целых выражений. По­этому нецелесообразно переходить к комбинированным заданиям прежде, чем усвоены основные алгоритмы.

Серьезное внимание в этой теме уделяется разложению мно­гочленов на множители с помощью вынесения за скобки общего множителя и с помощью группировки. Соответствующие преоб­разования находят широкое применение как в курсе 7 класса, так и в последующих курсах, особенно в действиях с рациональ­ными дробями.

В данной теме учащиеся встречаются с примерами использо­вания рассматриваемых преобразований при решении разнооб­разных задач, в частности при решении уравнений. Это позволя­ет в ходе изучения темы продолжить работу по формированию умения решать уравнения, а также решать задачи методом составления уравнений. В число упражнений включаются неслож­ные задания на доказательство тождества.

5. Формулы сокращенного умножения (19)

Формулы (а ± b)² = а²± 2аb + b², (а ± b)³ = а³ ± 3а²b + 3ab² ± b³, (а ± b) (а²+ ab + b²) = а³ ± b³. Применение формул сокращенного умножения в преобразованиях выражений.

Основная цель - выработать умение применять формулы сокращенного умножения в преобразованиях целых выражений в многочлены и в разложении многочленов на множители.

В данной теме продолжается работа по формированию у уча­щихся умения выполнять тождественные преобразования целых выражений. Основное внимание в теме уделяется формулам (а - b) (а + b) = а² - b², (а ± b)² = а² ± 2аb + b². Учащиеся должны знать эти формулы и соответствующие словесные формулировки, уметь применять их как «слева направо», так и «справа налево».

Наряду с указанными рассматриваются также формулы (а ± b)³ = а³± 3а²b + Заb² ± b³, а³±b³ = (а± b) (а² + аb + b²). Одна­ко они находят меньшее применение в курсе, поэтому не следует излишне увлекаться выполнением упражнений на их использо­вание.

В заключительной части темы рассматривается применение различных приемов разложения многочленов на множители, а также использование преобразований целых выражений для ре­шения широкого круга задач.

6. Системы линейных уравнений(16)

Система уравнений. Решение системы двух линейных урав­нений с двумя переменными и его геометрическая интерпрета­ция. Решение текстовых задач методом составления систем урав­нений.

Основная цель - ознакомить учащихся со способом ре­шения систем линейных уравнений с двумя переменными, выра­ботать умение решать системы уравнений и применять их при ре­шении текстовых задач.

Изучение систем уравнений распределяется между курсами 7 и 9 классов. В 7 классе вводится понятие системы и рассматри­ваются системы линейных уравнений.

Изложение начинается с введения понятия «линейное уравне­ние с двумя переменными». В систему упражнений включаются несложные задания на решение линейных уравнений с двумя пе­ременными в целых числах.

Формируется умение строить график уравнения а + by = с, где а ≠ 0 или b≠0, при различных значениях а, b, с. Введение графических образов дает возможность наглядно исследовать вопрос о числе решений системы двух линейных уравнений с двумя переменными.

Основное место в данной теме занимает изучение алгоритмов решения систем двух линейных уравнений с двумя переменными способом подстановки и способом сложения. Введение систем позволяет значительно расширить круг текстовых задач, решаемых с помощью аппарата алгебры. Применение систем упрощает про­цесс перевода данных задачи с обычного языка на язык уравнений.

7. Элементы логики, комбинаторики, статистики (4)

Ознакомление учащихся с простейшими статистическими характеристиками: средним арифметическим, модой, медианой, размахом. Учащиеся должны уметь использовать эти характеристики для анализа ряда данных в несложных ситуациях

8.Повторение (9)

КОНТРОЛЬ УРОВНЯ ОБУЧЕННОСТИ

ПЕРЕЧЕНЬ КОНТРОЛЬНЫХ РАБОТ

№

п/п

Тема

Кол-во часов

Сроки проведения

1

Выражения. Тождества

1

2

Уравнение с одной переменной

1

3

Линейная функция

1

4

Степень с натуральным показателем

1

5

Сложение и вычитание многочленов

1

6

Умножение многочленов

1

7

Формулы сокращенного умножения

1

8

Преобразование целых выражений

1

9

Системы линейных уравнений

1

10

Итоговая контрольная работа

2

Итого: 6

Тип урока

Форма контроля

УОНМ

Урок ознакомления с новым материалом

УО

Устный опрос

УЗИ

Урок закрепления изученного

ФО

Фронтальный опрос

УПЗУ

Урок применения знаний и умений

СР

Самостоятельная работа

УОСЗ

Урок обобщения и систематизации знаний

ИЗ

Индивидуальное задание

УПКЗУ

Урок проверки и коррекции знаний и умений

МТ

Математический тест

КУ

Комбинированный урок

МД

Математический диктант

УКЗ

Урок коррекции знаний

ИК

Индивидуальный контроль

УИ

Урок -игра

ПР

Практическая работа

КР

Контрольная работа

.

.Календарно-тематическое планирование

по алгебре в 7 классе (3 часа в неделю, всего 105 часа)

№ урока

Тема урока

Тип урока

Кол-во часов

Элементы обучения

Требования к уровню подготовки обучающихся

Вид контроля

Элементы дополнительного содержания или компьютерное обеспечение урока

Дата проведения

Повторение (3)

1

Выполнить действия

УОСЗ

1

Систематизировать и обобщить сведения о преобразовании выражений и решений уравнений полученные учащимися в курсе математики 5 - 6 классов

Уметь выполнять действия над натуральными числами, обыкновенными дробями. Решать задачи на проценты. Решать уравнения

ИК

2

Решение задач.

УОСЗ

1

ИК

3

Контрольный срез

УКЗУ

1

ИК

ВЫРАЖЕНИЯ. ТОЖДЕСТВА УРАВНЕНИЯ (18ч )

§1. ВЫРАЖЕНИЯ (5)

4

Числовые

выражения, п.1.

УОНМ

2

Числовые

выражения

Знать какие числа являются целыми, дробными рациональными. Положительными,

отрицательными и др.; Свойства действий над числами;

знать и понимать термин «числовое выражение»

УО

5

КУ

ПР

6

Выражения с переменными, п.2.

УОНМ

2

Переменная. Выражения с переменными Допустимое значение переменной. Недопустимое значение переменной.

знать и понимать термин «выражение с переменными».

Уметь осуществлять в буквенных выражениях числовые подстановки и выполнять соответствующие вычисления.

7

УОНМ

СР

8

Сравнение

значений выражений п.3.

УОНМ

1

Сравнение

значений выражений, строгие и нестрогие неравенства

Знать и понимать термин «значение

выражении».

Уметь сравнивать значения буквенных выражений при заданных значениях входящих в них переменных.

СР

§2. ПРЕОБРАЗОВАНИЕ ВЫРАЖЕНИЙ (4)

9

Свойства действий над

числами,п.4.

УОНМ

2

Основные свойства сложения и умножения чисел

Уметь применять свойства действий над

числами при нахождении значений числовых выражений

МД

10

УОНМ

СР

11

Тождества. Тождественные преобразования. п.5.

УОНМ

2

Тождества

Знать и понимать термин «тождество»,

УО

12

УОСЗ

Тождественные преобразования выражений

знать и понимать термин «тождественные преобразования»

ПР

13

Контрольная работа №1 «Выражения. Тождества»

УКЗУ

1

Уметь применять изученную теорию при тождественных преобразованиях выражений

КР

§3. УРАВНЕНИЯ С ОДНОЙ ПЕРЕМЕННОЙ (7)

14

Уравнение и его корни, п.6.

УОНМ

1

Уравнение и его корни . Свойства уравнений

Знать, что значит решить уравнение, что такое корни уравнения.

Уметь правильно употреблять термины «уравнение»,«корень уравнения», понимать их в тексте и в речи учителя,

Текущий

15

Линейное уравнение с

одной переменной, п. 7

УОНМ

3

Линейные уравнения с одной переменной.

Знать что называется линейным уравнением с одной переменной,

Уметь решать линейные уравнения с одной переменной, а также сводящиеся к ним;

УО

16

УПЗУ

ФО

17

УПЗУ

СР

18

Решение задач с

помощью уравнений, п.8

УЗИ

3

Линейные уравнения как математические модели реальных ситуаций

Понимать формулировку задачи «решить

уравнение»;

Уметь решать текстовые задачи с помощью составления линейных уравнений с одной переменной

ФО

19

УПЗУ

ФО

20

УПЗУ

СР

21

Контрольная работа №2 «Уравнение с одной переменной»

УКЗУ

1

Уметь применять изученную теорию при решении уравнений с одной переменной, решать задачи с помощью уравнений.

КР

ФУНКЦИИ (11)

§4 ФУНКЦИИ И ИХ ГРАФИКИ (5)

22

Что такое функция, п. 12

УОНМ

1

Функциональная зависимость, аргумент,

Знать определения функции, области определения функции, области значений, что такое аргумент, какая переменная называется зависимой, какая независимой;

понимать, что функция - это математическая модель, позволяющая описывать и изучать разнообразные зависимости между реальными величинами, что конкретные типы функций (прямая и обратная пропорциональности,

линейная) описывают большое разнообразие реальных зависимостей

Уметь правильно употреблять функциональную терминологию (значение функции, аргумент, график функции, область определения, область значений), понимать ее в тексте, в речи учителя,

в формулировке задач;
находить значения функций, заданных формулой, таблицей, графиком;
решать обратную задачу;

Строить графики линейной функции, прямой и обратной пропорциональности;

Интерпретировать в несложных случаях графики реальной зависимостей между величинами, отвечая на поставленные вопросы

СР

23

Вычисление значений функции по формуле, п 13.

УОНМ

2

Значения функции по формуле.

СР

24

УПЗУ

Текущий

25

График функции, п.14.

УПЗУ

2

Определение графика функции

Текущий

26

УПЗУ

СР

§5. ЛИНЕЙНАЯ ФУНКЦИЯ (5)

27

Прямая

Пропорциональность и её график, п.15.

УОНМ

1

Линейная функция у = kx и ее график

УО

28

Линейная

функция и ее график, п.16.

УЗИ

1

Определение линейной функции и ее график

ФО

29

Взаимное расположение графиков линейных функций, п.15.

УОНМ

3

Графики линейных функций, угловой коэффициент.

Текущий

30

УОНМ

УО

31

УПЗУ

СР

32

Контрольная работа №3 «Линейная функция»

УКЗУ

1

Уметь применять изученную теорию при выполнении письменных заданий, строить графики

КР

СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ (11)

§6.СТЕПЕНЬ И ЕЕ СВОЙСТВА (5)

33

Определение степени с

натуральным показателем, п.18.

УОНМ

1

Степень. Основание степени. Показатель степени. Свойства степени с натуральным показателем.

Степень с нулевым показателем.

Знать определение степени;

свойства степени с натуральным показателем.

Уметь выполнять действия со степенями с натуральным показателем;

Преобразовывать выражения, содержащие

степени с натуральным показателем;

самоконтроль

34

Умножение и

деление степеней, п.19.

УОНМ

2

Умножение и деление степеней с одинаковыми показателями.

Взаимопроверка

35

УПКЗУ

СР

36

Возведение в

степень произведения и степени, п.20.

КУ

2

Возведение произведения в степень, степени в степень

МД

37

УЗИМ

СР

§7. ОДНОЧЛЕН (5)

38

Одночлен и его стандартный вид, п.21.

УОНМ

1

Одночлен. Коэффициент одночлена. Стандартный вид одночлена. Подобные одночлены. Сложение одночленов.

Знать определение одночлена, многочлена. Уметь приводить одночлен к стандартному виду.

Уметь выполнять сложение и вычитание одночленов

ФО

39

Умножение

одночленов.

Возведение одночлена в степень, п.22.

УОНМ

1

Умножение одночленов. Возведение одночлена в натуральную степень. Деление одночлена на одночлен.

Знать правила умножения одночленов и возведения одночлена в натуральную степень.
Уметь выполнять умножение одночленов и возведение одночлена в степень

Текущий

40

УПЗУ

1

СР

41

Функции ,

и их графики, п.23.

УОНМ

1

Функция у = х², ее свойства и график. Функция у = - х², ее свойства и график.

Графическое решение уравнений.

Функция у = х³, ее свойства и график.

Уметь находить значения функций, заданных формулой, таблицей, графиком;
решать обратную задачу;

Знать свойства функций ,.

Уметь строить графики функций,;

УО

42

УПКЗУ

1

СР

43

Контрольная работа №4 «Степень с натуральным показателем»

УКЗУ

1

Уметь применять изученную теорию при построении графиков ,, упрощать выражения, содержащие степени с натуральным показателем.

КР

МНОГОЧЛЕНЫ (17)

§9 СУММА И РАЗНОСТЬ МНОГОЧЛЕНОВ (3)

44

Многочлен и его стандартный вид,

п.25

УОНМ

1

Многочлен и его стандартный вид, степень многочлена

Знать определение многочлена, понимать формулировку заданий; «упростить выражение»,

«разложить на множители».

УО

45

Сложение и вычитание

многочленов, п.26.

УОНМ

2

Раскрытие скобок, перед которыми стоит знак + или -.
Приведение подобных слагаемых

МД

46

УПКЗУ

СР

§10 ПРОИЗВЕДЕНИЕ ОДНОЧЛЕНА И МНОГОЧЛЕНА (6)

47

Умножение

одночлена на многочлен, п. 27

КУ

3

Применение распределительного закона умножения. Правила умножения одночлена на многочлен

Уметь приводить многочлен к стандартному

виду, выполнять действия с одночленом и многочленом;
выполнять разложение многочлена вынесением общего множителя за скобки.

МД

48

УПЗУ

ФО

49

УПЗУ

CР

50

Вынесение

общего

множителя за скобки,п.28.

УОНМ

3

УО

51

УПЗУ

ФО

52

УОСЗ

СР

53

Контрольная работа №5 «Сложение и вычитание многочленов»

УКЗУ

1

Применение изученного материала при выполнении действий с многочленами; преобразование выражений.

КР

§11 ПРОИЗВЕДЕНИЕ МНОГОЧЛЕНОВ (6)

54

Умножение

многочлена на

многочлен, п.29.

УОНМ

3

Правила умножения многочлена на многочлен.

Уметь умножать многочлен на многочлен,

ФО

55

УЗИМ

тест

56

УПЗУ

СР

57

Разложение

многочлена на множители способом группировки, п.30.

УОНМ

3

Разложение

многочлена на множители способом группировки. Вынесение общего множителя за скобки.

Уметь раскладывать многочлен на множители способом

группировки,

ФО

58

УЗИМ

МД

59

УПЗУ

СР

60

Контрольная работа №6
«Умножение многочленов»

УКЗУ

1

Применение изученного материала при преобразовании выражений

ИК

ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ (19)

§12. КВАДРАТ СУММЫ И КВАДРАТ РАЗНОСТИ (5)

61

Возведение в

квадрат суммы и разности двух выражений, п.32.

УОНМ

2

Вывод формул сокращенного умножения: квадратов суммы и разности двух выражений

Знать формулы сокращенного умножения: квадратов суммы и квадрата разности двух выражений; куба суммы и куба разности двух выражений

Уметь читать формулы сокращенного умножения, выполнять преобразование выражений применением формул сокращенного

умножения: квадрата суммы и разности двух выражений, умножения разности двух выражений на их сумму;

выполнять разложение разности квадратов двух выражений на множители.

МД

62

УЗИМ

СР

63

Возведение в куб суммы и разности двух выражений

УОНМ

1

Вывод формул сокращенного умножения. Куб суммы и куб разности двух выражений

УО

64

Разложение на множители с помощью формул

квадрата суммы и квадрата разности, п.33.

УОНМ

2

Формулы квадрата суммы и квадрата разности

Представление трехчленав виде произведения

ФО

65

УЗИМ

СР

§13. РАЗНОСТЬ КВАДРАТОВ,СУММА И РАЗНОСТЬ КУБОВ (6)

66

Умножение разности двух

выражений на их сумму, п.34.

УОНМ

2

Представить

УО

67

УЗИМ

МД

68

Разложение

разности

квадратов на множители, п.35.

КУ

2

Вывести формулу

ФО

69

УПЗУ

СР

70

Разложение на множители

суммы и разности кубов, п.36.

УОНМ

2

Знакомство с формулой сокращенного умножения.

Разложение на множители суммы и разности кубов.

Знать формулы сокращенного умножения, суммы и разности кубов

Уметь выполнять разложение на множители

суммы и разности кубов

УО

71

УЗИМ

Самоконтроль, взаимоконтроль

72

Контрольная работа №7
«Формулы сокращенного умножения»

УКЗУ

1

Применение изученного материала

ИК

§14.ПРЕОБРАЗОВАНИЕ ЦЕЛЫХ ВЫРАЖЕНИЙ (6)

73

Преобразование целого выражения в многочлен, п.37.

УОНМ

2

Преобразование целого выражения в многочлен. Способы разложения на множители: формулы сокращенного умножения, умножение многочлена на многочлен, умножение одночлена на многочлен, вынесение общего множителя за скобки, способ группировки

Знать различные способы разложения многочленов на множители.

Уметь применять различные способы разложения многочленов на множители;
преобразовать целые выражения;

ФО

74

УПЗУ

Самоконтроль, взаимоконтроль

75

Применение

различных

способов для разложения на множители, п.38.

КУ

4

МД

76

УЗИМ

СР

77

УПЗУ

МТ

78

УПКЗУ

ИК

79

Контрольная работа №8
«Преобразование целых выражений»

УКЗУ

1

Уметь применять изученную теорию при выполнении письменных заданий по данной теме.

ИК

СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ(16 ч)

§15. ЛИНЕЙНЫЕ УРАВНЕНИЯ С ДВУМЯ ПЕРЕМЕННЫМИ И ИХ СИСТЕМЫ (5)

80

Линейное уравнение с двумя переменными, п.40.

УОНМ

1

Определение линейного уравнения с двумя переменными. Определение решения линейного уравнения с двумя переменными. Правила решения линейного уравнения с двумя переменными. Равносильные уравнения.

Знать, что такое линейное уравнение с двумя переменными, система уравнений, график линейного уравнения с двумя переменными

Знать различные способы решения систем уравнений с двумя переменными: способ подстановки, способ сложения;
понимать что уравнение - это математический аппарат решения разнообразных задач из математики, смежных областей знаний, практики.

Уметь правильно употреблять термины: «уравнение с двумя переменными», «система»;
понимать их в тексте, в речи учителя, понимать формулировку задачи «решить систему уравнений с двумя переменными»; строить некоторые уравнения с двумя переменными; решать системы уравнений с двумя переменными различными способами.

Текущий

81

График

линейного уравнения с двумя переменными, п.41.

УОНМ

2

Понятие графика линейного уравнения с двумя переменными. Виды графиков.

ПР

82

УЗИМ

СР

83

Системы линейных уравнений с двумя переменными, п.42.

УОНМ

2

Определение систем линейных уравнений с двумя переменными, решение системы линейных уравнений с двумя переменными, определение решений систем уравнений по угловым коэффициентам прямых, являющихся графиками данных линейных уравнений.

ФО

84

УЗИМ

§16. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ (10)

85

Способ

подстановки, п. 43.

КУ

3

Алгоритм решения систем уравнений способом подстановки, способом сложения

Знать алгоритм решения систем уравнений способом подстановки, способом сложения

Уметь решать системы уравнений способом подстановки, способом сложения

ФО

86

УЗИМ

Текущий

87

УЗИМ

СР

88

Способ

сложения, п.44.

УОНМ

3

Текущий

89

УЗИМ

МД

90

УЗИМ

СР

91

Решение задач с

помощью систем

уравнений, п.45.

КУ

4

Алгоритм решения задач с помощью систем уравнений

Знать алгоритм решения задач с помощью систем уравнений

Уметь решать задачи с помощью систем уравнений

ФО

92

КУ

СР

93

КУ

ИЗ

94

КУ

СР

95

Контрольная работа №9
«Системы линейных уравнений»

УКЗУ

1

Уметь применять приобретенные знания, умения и навыки при выполнении письменных заданий.

ИК

ЭЛЕМЕНТЫ ЛОГИКИ, КОМБИНАТОРИКИ, СТАТИСТИКИ

СТАТИСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ (4)

96

Среднее арифметическое, размах и мода, п. 9

УОНМ

2

Среднее арифметическое, размах, мода ряда

Знать определения среднего арифметического, размаха ряда и моды ряда.

Уметь находить Среднее арифметическое, размах ряда , моду ряда при решении задач.

ФО

97

УЗИМ

ПР

98

Медиана как статистическая характеристика, п. 10

УОНМ

2

Определение медианы ряда, нахождение медианы ряда.

Знать определение медианы ряда.

Уметь находить медиану ряда

УО

99

УЗИМ

ФО

Повторение (6)

100

Функции.

УОСЗ

1

Урок-практикум.

Закрепление знаний, умений и навыков, полученных на уроках по данным темам (курс алгебры 7 класса).

Взаимопроверка

101

Степень с натуральным показателем

УОСЗ

1

Урок-практикум

102

103

Формулы сокращенного умножения

УОСЗ

2

Урок-игра

Групповой

104

105

Контрольная работа №10
Итоговая работа.

УКЗУ

2

ИК

Содержание тем учебного модуля «Геометрия»

Геометрия - один из важнейших компонентов математического образования, необходимый для приобретения конкретных знаний о пространстве и практически значимых умений, фор­мирования языка описания объектов окружающего мира, для развития пространственного воображения и интуиции, математи­ческой культуры, для эстетического воспитания обучающихся. Изучение геометрии вносит вклад в развитие логического мышления, в формирование понятия доказательства.

Геометрия

Отличительных особенностей рабочей программы по сравнению с примерной программой нет.

В данном классе ведущими методами обучения предмету являются: объяснительно-иллюстративный и репродуктивный, хотя используется и частично-поисковый. На уроках используются элементы следующих технологий: личностно ориентированное обучение, обучение с применением опорных схем, ИКТ.

Начальные геометрические сведения (10 часов)

Простейшие геометрические фигуры: прямая, точка, отрезок, луч, угол. Понятие равенства геометрических фигур. Сравнение отрезков и углов. Измерение отрезков, длина отрезка. Измерение углов, градусная мера угла. Смежные и вертикальные углы, их свойства. Перпендикулярные прямые.

Цель: систематизировать знания обучающихся о простейших геометрических фигурах и их свойствах; ввести понятие равенства фигур.

В данной теме вводятся основные геометрические понятия и свойства простейших геометрических фигур на основе наглядных представлений обучающихся путем обобщения очевидных или известных из курса математики I- 6 классов геометрических фактов. Понятие аксиомы на начальном этапе обучения не вводится, и сами аксиомы не формулируются в явном виде. Необходимые исходные положения, на основе которых изучаются свойства геометрических фигур, приводятся в описательной форме. Принципиальным моментом данной темы является введение понятия равенства геометрических фигур на основе наглядного понятия наложения. Определенное внимание должно уделяться практическим приложениям геометрических понятий.

Треугольники (17 часов)

Треугольник. Признаки равенства треугольников. Перпендикуляр к прямой. Медианы, биссектрисы и высоты треугольника. Равнобедренный треугольник и его свойства. Задачи на построение с помощью циркуля и линейки.

Цель: ввести понятие теоремы; выработать умение доказывать равенство треугольников с помощью изучен­ных признаков; ввести новый класс задач - на построение с помощью циркуля и линейки.

Признаки равенства треугольников являются основным рабочим аппаратом всего курса геометрии. Доказательство большей части теорем курса и также решение многих задач проводится по следующей схеме: поиск равных треугольников - обоснование их равенства с помощью какого-то признака - следствия, вытекающие из равенства треугольников.

Применение признаков равенства треугольников при решении задач дает возможность постепенно накапливать опыт проведения доказательных рассуждений. На начальном этапе изучения и применения признаков равенства треугольников целесообразно использовать задачи с готовыми чертежами.

Параллельные прямые (13часов)

Признаки параллельности прямых. Аксиома параллельных прямых. Свойства параллельных прямых.

Цель: ввести одно из важнейших понятий - понятие параллельных прямых; дать первое представление об аксиомах и аксиоматическом методе в геометрии; ввести аксиому параллельных прямых.

Признаки и свойства параллельных прямых, связанные с углами, образованными при пересечении двух прямых секущей (накрест лежащими, односторонними, соответственными), широ­ко используются в дальнейшем при изучении четырехугольников, подобных треугольников, при решении задач, а также в курсе стереометрии.

Соотношения между сторонами и углами треугольника (18 часов)

Сумма углов треугольника. Соотношение между сторонами и углами треугольника. Неравенство треугольника. Прямоугольные треугольники, их свойства и признаки равенства. Расстояние от точки до прямой. Расстояние между параллельными прямыми. Построение треугольника по трем элементам.

Цель: рассмотреть новые интересные и важные свойства треугольников.

В данной теме доказывается одна из важнейших теорем геометрии - теорема о сумме углов треугольника. Она позволяет дать классификацию треугольников по углам (остроугольный, прямоугольный, тупоугольный), а также установить некоторые свойства и признаки равенства прямоугольных треугольников.

Понятие расстояния между параллельными прямыми вводится на основе доказанной предварительно теоремы о том, что все точки каждой из двух параллельных прямых равноудалены от другой прямой. Это понятие играет важную роль, и частности используется в задачах на построение.

При решении задач на построение в 7 классе следует ограничиться только выполнением и описанием построения искомой фигуры. В отдельных случаях можно провести устно анализ и доказательство, а элементы исследования должны присутствовать лишь тогда, когда это оговорено условием задачи.

Повторение (12 часов)

Цель: Повторение, обобщение и систематизация знаний, умений и навыков за курс геометрии 7 класса.

В результате изучения курса геометрии 7 класса обучающиеся должны:

знать/понимать

• существо понятия математического доказательства; примеры доказательств;

• существо понятия алгоритма; примеры алгоритмов;

• как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;

• как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;

• как потребности практики привели математическую науку к необходимости расширения понятия числа;

• вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов;

• каким образом геометрия возникла из практических задач землемерия; примеры геометрических объектов и утверждений о них, важных для практики;

• смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации;

уметь

• пользоваться языком геометрии для описания предметов окружающего мира;

• распознавать геометрические фигуры, различать их взаимное расположение;

• изображать геометрические фигуры; выполнять чертежи по условию задач; осуществлять преобразования фигур;

• вычислять значения геометрических величин (длин, углов, площадей, объемов), находить стороны, углы треугольников, длины ломаных, дуг окружности, площадей основных геометрических фигур и фигур, составленных из них;

• решать геометрические задачи, опираясь на изученные свойства фигур и отношений между ними, применяя дополнительные построения, алгебраический аппарат, идеи симметрии;

• проводить доказательные рассуждения при решении задач, используя известные теоремы, обнаруживая возможности для их использования;

использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

• описания реальных ситуаций на языке геометрии;

• расчетов, включающих простейшие формулы;

• решения практических задач, связанных с нахождением геометрических величин (используя при необходимости справочники и технические средства);

• построений геометрическими инструментами (линейка, угольник, циркуль, транспортир).

Тематическое планирование по геометрии 7 класс

№

п/п

Раздел, название урока в

поурочном планировании

Дидактические единицы образовательного процесса

Тип урока. Контроль

знаний

учащихся

Коли-

чество

часов

Дата

ГЛАВА I. НАЧАЛЬНЫЕ ГЕОМЕТРИЧЕСКИЕ СВЕДЕНИЯ

10

§1. ПРЯМАЯ И ОТРЕЗОК.

1

Точки, прямые, отрезки. Провешивание прямой на местности, п.1, 2.

Знать, сколько прямых можно провести через две точки, сколько общих точек могут иметь две прямые, какая фигура наз отрезком; уметь обозн точки и прямые на рисунке, изображать возможные случаи взаимного располож точек и прямых, двух прямых, объяснить, что такое отрезок, изобр и обозн отрезки на рисунке.

Комбинированный урок: изучение и первичное закрепление новых знаний (лекция); практическая работа на местности. Групповой контроль.

1

§2. ЛУЧ И УГОЛ.

2

Луч. Угол, п.3, 4.

Знать, какая геометрическая фигура называется углом, что такое стороны и вершина угла. Уметь обозначать неразвернутые и развернутые углы, показать на рисунке внутреннюю область угла, провод луч, разделяющий угол на два угла.

Комбинированный урок: изучение и первичное закрепление новых знаний (беседа); п/р (задание 8); ВК ИК

1

§3. СРАВНЕНИЕ ОТРЕЗКОВ И УГЛОВ.

3

Равенство геометрических фигур. Сравнение отрезков и углов, п.5,6.

Знать, какие геометрические фигуры наз равными, какая точка называется серединой отрезка, какой луч наз биссектрисой угла. Уметь сравнивать отрезки и углы и записывать результат сравнения, отмеч с помощью масштабной линейки середину отрезка, с пом транспортира проводить биссектрису угла.

Урок - практикум. Работа с моделями геом фигур (частично-поисковая деятельность: сравнение, анализ, обобщение, выводы). самоконтроль.

1

§4. ИЗМЕРЕНИЕ ОТРЕЗКОВ.

4

Длина отрезка, п.7.

Знать, что при выбранной единице измерения длина любого данного отрезка выражается положительным числом; уметь измерять данный отрезок с помощью линейки и выразить

Усвоение изученного материала в процессе решения задач. Самоконтроль, ИК

1

5

Единицы измерения. Измерительные инструменты, п.8.

его длину в сантиметрах, миллиметрах, метрах, находить длину отрезка в тех случаях, когда точка делит данный отрезок на два отрезка, длины которых известны, р/з 30 - 33, 35, 37.

Комбинированный урок: беседа о единицах измерения;п/р (№24, 25, 28, 36), с/р ИК.

1

6

§5. ИЗМЕРЕНИЕ УГЛОВ.

Градусная мера угла. Измерение углов на местности, п.9, 10.

Знать, что такое градусная мера угла, чему равны минута и секунда; уметь находить градусные меры данных углов, используя транспортир, Изображать прямой, острый, тупой, развернутый углы, р/ задачи типа 47 - 50.

Практическая работа (41, 42). Решение задач. С/Р обучающего характера. Индивидуальный контроль.

1

§6. ПЕРПЕНДИКУЛЯРНЫЕ ПРЯМЫЕ.

7

Смежные и вертикальные углы, п.11.

Знать, какие углы наз смежными и чему равна сумма смежных углов, какие углы называются вертикальными и каким свойством обладают вертикальные углы, какие прямые называются перпендикулярными. Уметь строить угол, смежный с данным углом, изображать вертикальные углы, объяснять, почему две прямые, перпендикулярные к третьей, не пересекаются, р/з 57, 58, 61, 64, 65, 69.

Урок усвоения новых знаний, умений и навыков.

1

8

Перпендикулярные прямые. Построение прямых углов на местности, п.12, 13.

Урок практических с/р (исследовательского типа). Тематический контроль.

1

9

Решение задач.

Закрепить в процессе решения задач, полученные ЗУН, подготовиться к контрольной работе.

Урок обобщения и систематизации знаний. Практикум по р/з. Зачет.

1

10

КОНТРОЛЬНАЯ РАБОТА №1 «Начальные геометрические сведения», п.1-13.

Уметь применять все изученные формулы и теоремы при решении задач

Урок контроля, оценки и коррекции знаний учащихся. Фронтальный тематический контроль.

1

ГЛАВА II. ТРЕУГОЛЬНИКИ

17

§1. ПЕРВЫЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ.

11

Треугольник, п.14.

Знать, что такое периметр треугольника, какие треугольники называются равными, формулировку и доказательство первого признака равенства треугольников. Уметь объяснить, какая фигура называется треугольником, и назвать его элементы, решать задачи типа 90, 92 - 95, 97.

Урок - практическая работа. взаимоконтроль.

1

12

Первый признак равенства треугольников, пю15.

Урок лекция с необходимым минимумом задач.

1

13

Решение задач.

Практикум по р/з Проверочная С/Р. ИК.

1

§2. МЕДИАНЫ, БИССЕКТРИСЫ И ВЫСОТЫ ТРЕУГОЛЬНИКА.

14

Перпендикуляр к прямой. Медианы, биссектрисы и высоты треугольника, п.16, 17.

Уметь объяснить, какой отрезок называется перпендикуляром, проведенным из данной точки к данной прямой, какие отрезки называются медианой, биссектрисой, высотой треугольника, какой треугольник называется равнобедренным, равносторонним; знать формулировку теоремы о перпендикуляре к прямой; знать и уметь доказывать теоремы о свойствах равнобедренного треугольника; уметь выполнять практические задания типа 100 - 104 и р/з 105, 107, 108, 112, 115, 117, 119.

Комбинированный урок: лекция, практическая работа.

1

15

Свойства равнобедренного треугольника, п.18.

Усвоение нового материала в процессе р/за С/Р обучающего хар-ра с проверна уроке.

1

16

Решение задач.

Усвоение изученного материала в процессе р/з. С/Р обучающего характера. СК.

1

§3. ВТОРОЙ И ТРЕТИЙ ПРИЗНАКИ РАВЕНСТВА ТРЕУГОЛЬНИКОВ.

17

Второй признак равенства треугольников, п.19.

Знать формулировку и доказательство второго признака равенства треугольников.

Усвоение нового материала в проц р/з. СК

1

18

Решение задач.

Знать формулировки и доказательства второго и третьего признаков равенства треугольников; уметь решать задачи типа 121 - 123, 125, 129, 132, 136, 137 - 139.

Усвоение изученного материала в процессе р/з. С/Р обучающего хар СК.

1

19

Третий признак равенства треугольников, п.20.

Усвоение нового материала в проц р/з.

1

20

Решение задач.

Усв-е изуч мат-ла в проц р/з.. Проверочная С/Р.

1

§4. ЗАДАЧИ НА ПОСТРОЕНИЕ.

21

Окружность, п.21.

Знать определение окружности. Уметь объяснить, что такое центр, радиус, диаметр, хорда, дуга окружности, выполнять с помощью циркуля и линейки простейшие построения: отрезка, равного данному; биссектрисы данного угла; прямой, проходящей через данную точку и перпендикулярной к данной прямой; середины данного отрезка; применять простейшие построения при р/а 148 - 151, 154, 155.

Изучение нового мат-ла. Беседа. П/работа.

1

22

Построение циркулем и линейкой. Примеры задач на построение, п.22, 23.

Урок с частично- поисковой работой.

ВК. ИК.

1

23

Решение задач.

Урок закрепления знаний. Практикум. Проверочная С/Р.

1

24

Решение задач.

Закрепить навыки в р/з на прим призн равенства треугольников, продолж выработку навыков р/з на построение с помощью циркуля и линейки.

Урок обобщения и систематизации знаний. Практикум по р/з.

3

25

26

27

КОНТРОЛЬНАЯ РАБОТА №2 «Треугольники», п.14-23.

Уметь применять весь изученный материал при решении задач.

Урок контроля, оценки и коррекции знаний. ФК

1

ГЛАВА III. ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ.

13

§1. ПРИЗНАКИ ПАРАЛЛЕЛЬНОСТИ ДВУХ ПРЯМЫХ.

28

Определение параллельных прямых, п.24.

Знать опр-е параллельных прямых, назв углов, образующихся при пересеч двух прямых секущей, формулировки призн параллельности прямых; понимать какие отрезки и лучи являются параллельными; уметь показать на рис пары накрест лежащих, соответственных, одност-х углов, доказ призн паралл-и двух прямых и исп-ть их при решении задач типа 186 - 189, 191, 194.; уметь стр-ть паралл-ые прямые при помощи чертежугольника и линейки.

Усвоение изученного материала в проц р/з

1

29

Признаки параллельности двух прямых, п.25.

Комбинированные уроки: лекция, практикум, проверочная С/Р.

2

30

31

Практические способы построения параллельных прямых, п.26.

Решение задач.

Уметь строить параллельные прямые при помощи чертежного угольника и линейки, исп-ть теоретический материал при решении задач.

Урок обобщения и систематизации знаний. Практикум по р/з.

1

§2. АКСИОМА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ.

32

Об аксиомах геометрии. Аксиома параллельных прямых, п.27,28.

Знать аксиому параллельных прямых и следствия из нее, знать и уметь док св-ва параллельных прямых и прим их при решении задач типа 196, 198, 199, 203 - 205, 209.

Урок усвоения новых знаний. Беседа.

1

33

Теорема об углах, образ-х двумя параллельными прямыми и секущей, п.29.

Усвоение изуч мат-ла в процессе р/з. ГК, ИК.

2

34

35

Решение задач.

Закрепить навыки в решении задач.

Практикум по решению задач. ГК и ИК.

2

36

37

Решение задач.

Уметь применять все изученные теоремы при решении задач.

Практикум по решению задач. ГК и ИК. Проверочная С/Р.

3

38

39

40

КОНТРОЛЬНАЯ РАБОТА №3 «Параллельные прямые», п.24-29.

Урок контроля, оценки и корр знаний. Фронт-ый письменный контроль.

1

ГЛАВА IV СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА.

18

§1. СУММА УГЛОВ ТРЕУГОЛЬНИКА.

41

Теорема о сумме углов треугольника. Остроугольный, прямоугольный и тупоугольный треугольники, п.30, 31.

Знать, какой угол наз внешним углом треугольника, какой треугольник наз остроугольным, тупоугольным, прямоугольным; уметь док-ть теорему о сумме углов треуг-ника и ее след р/з 223 - 226, 228, 229, 234.

Усвоение изученного материала в процессе выполнения практической работы, р/з Обучающая С/Р. СК.

2

42

§2. СООТНОШЕНИЯ МЕЖДУ УГЛАМИ И СТОРОНАМИ ТРЕУГОЛЬНИКА.

43

Теорема о соотношениях между сторонами и углами треугольника, п.32.

Уметь доказывать теорему о соотношениях между сторонами и углами треугольника и следствия из нее, теорему о неравенстве треугольника, применять их при решении задач типа 236 - 240, 243, 244, 248, 249, 250.

Усвоение нового материала в процессе решения задач. Самоконтроль.

2

44

45

Неравенство треугольника, п.33.

Усвоение изученного материала в процессе решения задач. С/Р обучающего характера.

1

46

КОНТРОЛЬНАЯ РАБОТА №4 «Сумма углов треугольника», п.30-33.

Уметь применять все изученные теоремы при решении задач.

Урок контроля, оценки и коррекции знаний. Фронтальный письменный контроль.

1

§3. ПРЯМОУГОЛЬНЫЕ ТРЕУГОЛЬНИКИ.

47

Некоторые свойства прямоугольных треугольников, п.34.

Уметь доказывать свойства 1⁰ - 3⁰ прямоугольных треугольников; знать формулировки признаков равенства прямоугольных треугольников уметь их доказывать; уметь применять свойства и признаки при р/з 254 - 256, 258, 260, 263, 265.

Изучение нового материала.

2

48

49

50

Признаки равенства

прямоугольных треугольников. Угловой отражатель, п.35, 36.

Урок с частично- поисковой деятельностью Проверочная С/Р.

2

§4. ПОСТРОЕНИЕ ТРЕУГОЛЬНИКА ПО ТРЕМ ЭЛЕМЕНТАМ.

51

Расстояние от точки до прямой. Расстояние между параллельными прямыми, п.37.

Знать, какой отрезок наз наклонной, пров-ой из данной точки к данной прямой, что наз расст-м от точки до прямой и расст-м между двумя параллельными прямыми; уметь док, что перпендикуляр, пров-й из точки к прямой, меньше любой наклонной, пров-ой из той же точки к этой прямой; теорему о том, что все точки каждой из двух паралл-ых прямых равноудалены от другой прямой; уметь строить треуг-к по двум стор и углу м/у ними, по стор и двум прилеж-м к ней углам, по трем стор; уметь р/з 271, 273, 277, 278(а), 283, 284, 288, 290, 291.

Урок изучения и закрепления новых знаний и умений.

2

52

53

Построение треугольника по трем элементам. Решение задач, п.38.

Урок с частично- поисковой деятельностью. Практикум.

Проверочная С/Р.

2

54

55

Решение задач.

Закрепить навыки в решении задач.

Урок обоб и систем зн. Практикум по р/з.

1

56

57

58

КОНТРОЛЬНАЯ РАБОТА №5 «Прямоугольный треугольник», п.34-38.

Уметь применять все изученные теоремы при решении задач.

Урок контроля, оценки и коррекции знаний. Фронтальный контроль.

1

ИТОГОВОЕ ПОВТОРЕНИЕ

10

59

Измерение отрезков и углов. Перпендикулярные прямые.

Закрепление знаний, умений и навыков, полученных на уроках по данным темам (курс геометрии 7класса).

Комбинированный урок

2

60

61

Треугольники.

Комбинированный урок

2

62

63

Параллельные прямые.

Комбинированный урок

3

64

65

66

Задачи на построение.

Урок учебный практикум

2

67

68

Итоговый тест

1

69

Итоговое занятие.

Урок «заним-ных задач»

2

70