Урок алгебры Задачи на проценты (8 класс)

Тема урока: Задачи на проценты (2 часа)

Цель урока: обобщение, систематизация, углублений знаний, умений, навыков учащихся.

Ход урока.

I. Повторение понятия процента и основных видов задач на проценты.

1. Процентом от любой величины называется ее одна сотая часть. Р% от S равно - эту формулу называют формулой процентов.

2. Рассмотрим три тира задач на проценты.

Рассмотрим Ι тип задач.

Задача №1.

Банк обещает своим клиентам годовой рост вклада 130%. Какую сумму может получить через год человек, вложивший в этот банк 320.000 рублей?

Решение:

Через год банк должен начислить на счет вкладчика 130% от суммы 320.000 рублей, то есть 1,3∙320.000  416.000 рублей, так что на счете будет находиться 320.000  416.000  736.000 рублей.

Ответ: 736.000 рублей.

А теперь решим задачу в общем виде.

Если в банк, дающий p% в год, вложена сумма S рублей, то рассуждая точно так же, как в рассмотренном примере, мы получим, что проценты составляют ()S рублей, а всего на счете вкладчика будет S  , или (1  )S рублей.

Поэтому, обозначив сумму, которая должна быть на счете вкладчика по истечении одного года, через S₁, мы получим, что S₁  (1  )S.

Рассмотрим 2-ой тип задач на проценты.

Если в основной формуле процентов обозначить p% от S через S₁, то формула примет вид S₁ = , или = .

Из последнего равенства можно видеть, что величина S₁, S, p и 100 составляют пропорцию.

Задача №2.

Сколько соли содержится в 145 г 80% раствора?

Решение:

Составим пропорцию:

100 г раствора - 80 г соли,

145 г раствора - Х г соли,

Х   116 г соли.

Ответ: 116 г.

Еще более удобным становиться применение пропорций при решении так называемых обратных задач на проценты.

Например, известна не исходная величина, а заданное число процентов от нее, и требуется найти саму исходную величину.

Задача №3.

Какое количество 10% раствора может получиться из 25 г соли?

Решение:

Составим пропорцию:

10 г соли - 100 г раствора,

25 г соли - Х г раствора,

Х  250 г раствора.

Ответ: 250 г.

Рассмотрим 3-ий тип задач на процентное отношение.

Задача №4.

В городе А с населением 100.000 жителей граждан в возрасте до 18 лет составляет 40.000, а в городе Б с населением 120.000 - 60.000. В каком городе население «моложе»?

Решение:

Составим пропорцию:

Город А: Город Б:

100.000 человек ­- 100% 120.000 - 100%

40.000 - Х% 60.000 - Х%

Х   40% Х  50%

Таким образом, население города Б относительно моложе.

Ответ: в городе Б.

Задача №5.

В 200 г воды растворили 50 г соли. Какова концентрация полученного раствора?

Решение:

1) 200  50  250(г) - масса полученного раствора.

2) Составим пропорцию:

250 г - 100%,

50 г - Х %,

Х   20%.

Ответ: 20%.

Итак, процентное отношение двух величин - это частное от деления первой величины на вторую, выраженное в процентах. Для его вычисления надо разделить первую величину на вторую и полученный результат умножить на 100.

А теперь полученный знания можно свести в следующий плакат.

Три типа задач на проценты

p% от числа а

есть 0.01 ра

p% от числа а есть число b такое, что

а = b/0.01p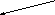

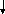
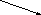
a от b составляет

100%

II. Рассмотрим процентные изменения.

1. Простой процентный рост.

Если некоторая величина увеличивается на постоянное число % за каждый фиксированный период времени, то можно использовать формулу простого процентного роста:

S_n  (1  )S.

Она показывает значение, которое принимает величина через n промежутков времени, если в каждый из промежутков она увеличивается на одно и то же число процентов p, считая от ее начального значения S.

Задача №6.

При покупке товара в рассрочку выплачивается сразу половина стоимости, а вторая половина выплачивается по 5% от нее ежемесячно. Какая часть стоимости товара будет выплачена через 8 месяцев?

Решение.

По формуле простого процентного роста имеем:

(1  )∙0,5  0,7 (полной стоимости товара)

Ответ: 0,7.

2. Сложный процентный рост.

Пусть банк начисляет p% годовых, внесенная сумма равно S рублей, а сумма, которая будет на счете через n лет, равна S_n рублей.

P% от S составляет рублей, и через год на счете окажется сумма

S₁  S   (1  )S, то есть начальная сумма увеличилась в

(1  ) раз. За следующий год сумма S₁ увеличивается во столько раз, поэтому через два года на счете будет сумма:

S₂  (1  ) ∙ S₁  (1 + ) (1  )S  (1  )²∙S.

Аналогично, S₃  (1  )³∙S и т.д.

S_n (1  )ⁿ∙S - формула сложного процента.

Задача №7.

Каким должен быть начальный вклад, чтобы через два года вклад в банке, начисляющем 30% годовых, возрос до 845.000 рублей?

Решение:

Пусть x - начальная величина вклада. Тогда, используя формула сложного процента, имеем:

(1 + )² ∙ x = 845.000;

() ² ∙ x = 845.000;

x = ;

x = 500.000.

Ответ: 500.000 рублей.

3. Итог урока.

Домашнее задание:

1) В магазине цены сначала были повышении на 10%, а потом снижены на 10%. Как изменились цены?

2) Банк начисляет 20% годовых и внесена сумма 500.000 рублей. Какая сумма будет на счете клиента через 5 лет:

а) при начислении банком простых процентов; б) при начислении сложных процентов.