«Решение систем линейных уравнений».

Разработка урока алгебры в 7 классе

Автор: учитель математики МБОУ "Уренская СОШ № 1" Коробейникова Мария Леонидовна

Тема: «Решение систем линейных уравнений»

Цели:

• Обобщение и систематизация знания по теме: «Системы линейных уравнений»;

Задачи:

• Повторить алгоритмы решения систем линейных уравнения

• Развивать навыки решения систем линейных уравнения различными способами

• Способствовать развитию общеучебных умений и навыков.

• Развивать креативное мышление, умение ясно и точно излагать свои мысли.

• Воспитывать умение слушать одноклассников;

Основные технологии и методы: элементы технологии критического мышления, работа в группе.

Тип урока: урок обобщения и систематизации знаний

Оборудование :

компьютер

проектор

интерактивная доска Smart Board

Ход урока:

Приветствие.

Время

Действия учителя

Действия ученика

Слайд Smart Notebook

I. Вызов. Прием «Верные и неверные утверждения»

5^/

- Ребята, тема нашего урока: «Решение систем линейных уравнений»

На столах перед каждым местом лежит лист на котором мы сегодня будем работать

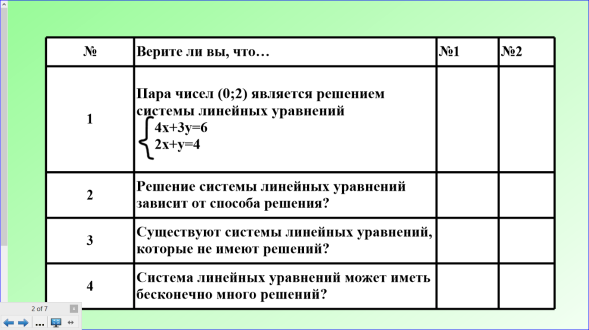
- Я предлагаю вспомнить все, что мы изучали, что вы уже знаете и ответить на вопросы, которые находятся в таблице

- Все вопросы начинаются со слов: «Верите ли вы, что…» Если вы верите, то в первом столбце (№1) ставите «+», если нет, то «-». Если сомневаетесь, то подумайте и ставьте знак, к которому более склонны.

И помните ребята

</ «Математику нельзя изучать,

наблюдая как это делает сосед»

А. Нивен.

- Как вы получили ответ на первый вопрос?

Т.е. вы руководствовались теоретическими знаниями о том, что решением системы двух неизвестных называют такую пару чисел х и у, которые при подстановке в эту систему обращают каждое её уравнение в верное равенство.

Молодцы. В первой строчке столбик № 2 ставим «-»

На доске появляется первый слайд с темой урока.

Переворачивают первый лист.

Отвечают на вопросы.

Ответ детей. (Подставили значения х и у в уравнения при этом одно из них является верным числовым равенством, а другое нет.)

II. Осмысление. Групповая форма работы.

10^/

- Ребята, чем вы руководствовались при ответе на следующие вопросы .

- Можно ли как - то подтвердить или опровергнуть ваши предположения.

- Как практически проверить зависит ли решение системы линейных уравнений от способа решения?

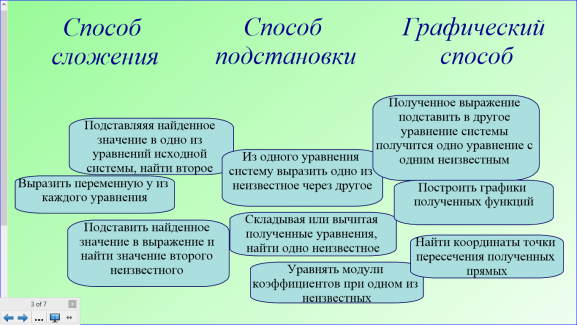
-Какие способы решения системы линейных уравнений вы знаете?

- Ребята я предлагаю поработать в группах. Каждой группе я раздаю разрезанные правила этих способов. Ваша задача составить три алгоритма решения системы линейных уравнения.

Давайте решим систему уравнений тремя различными способами, тем самым ответим на вопрос : «зависит ли решение системы линейных уравнений от способа решения?»

Работать будем по вариантам:

1 вариант решает систему способом сложения

2 вариант - эту же систему способом подстановки.

А графическим способом нам на доске решит эту систему………

Ответ детей. (Интуитивно)

Ответ детей. (Да, практически)

Ответ детей. (Решить одну и ту же систему различными способами).

Ответ детей. (Способ подстановки, способ сложения и графический).

Ребята работают в группах.

(Опрос 3 человек у доски)

Три ученика у доски объясняют свой способ решения.

Учащиеся решают систему уравнений указанным способом

12^/

- Ребята, какой можно сделать вывод , отвечая на второй вопрос

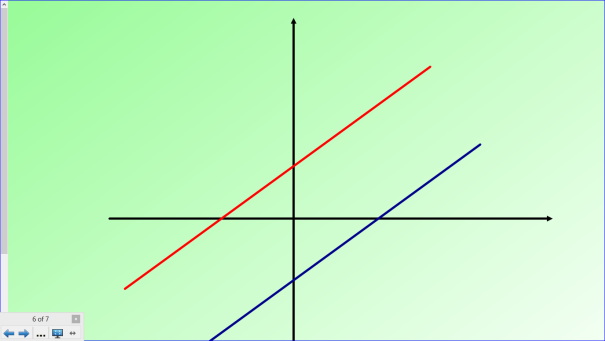
Графический способ решения систем уравнений очень ярко иллюстрирует ответ на вопрос о количестве решений системы. Сейчас мы в этом убедимся.

Скажите пожалуйста , что на графике показывает нам решение системы?

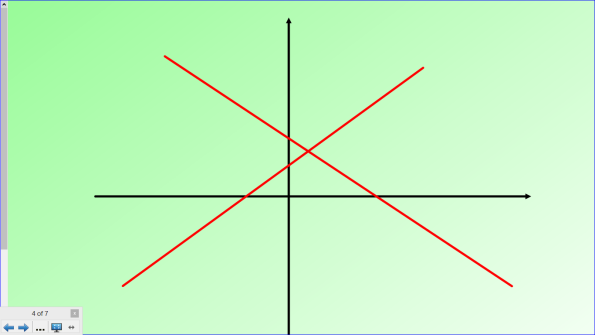
Ребята, обращаясь к следующему вопросу, как вы думаете, существуют ли системы линейных уравнений, которые не имеют решений?

А как это можно показать?

Если система не имеет решений то графики не пересекаются.

А когда прямые у нас не пересекаются?

Каково взаимное расположение этих прямых.

Придумайте функцию график которой параллелен данной

у = 2х + 1

Что бы придумать такую функцию о чем мы должны помнить?

Покажем аналитически что данная система не имеет решений.

Мы с вами ответили на третий вопрос, обращаясь к графическому способу, ответим на последний вопрос

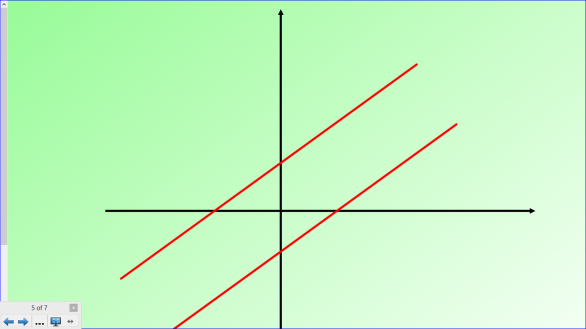
Может ли система линейных уравнений иметь бесконечно много решений?

Множество общих точек, когда прямые совпадают.

Решение системы не зависит от способа решения и можно решать любым выбирая наиболее удобный в конкретной ситуации.

Точка пересечения графиков уравнений системы.

(если угловые коэффициенты прямых, являющихся графиками функций, различны, то система имеет единственное решение. )

Ответы детей

(если угловые коэффициенты прямых, являющихся графиками функций, одинаковы, а b различны, то система не имеет решений.)

(если уравнения имеют одинаковый вид, то система имеет бесконечно много решений.)

III. Проверка. Прием «Самостоятельная работа»

8^/

Закрепим наши знания , решим самостоятельно две системы уравнений используя разные способы решения.

1 вариант

_{2 вариант}

Учащиеся решают системы уравнений, выбирая способы самостоятельно

IѴ Рефлексия. Прием «Возвращение к вопросам «Верите ли вы, что…»

3^/

- И так, подведем итоги. Какие выводы мы можем сделать?

Возможны варианты ответов:

- Решение системы не зависит от способа решения.

- Система линейных уравнений может иметь одно решение, бесконечно много решений или вообще не иметь решений.

2^/

- Ваш домашним задание будет из предложенных уравнений составит системы линейных уравнений которые:

Имеет одно решение

Не имеет решений

Имеет бесконечно много решений

Систему имеющую одно решение решить тремя различными способами.

- Всем большое спасибо.

«Математику нельзя изучать,

наблюдая как это делает сосед»

А. Нивен.