- Учителю
- Конспект урока по математике на тему Разложение положительной обыкновенной дроби в конечную десятичную дробь (6 класс)
Конспект урока по математике на тему Разложение положительной обыкновенной дроби в конечную десятичную дробь (6 класс)
Математика 6
УРОК № 136. Глава 5. Обыкновенные и десятичные дроби (25 часов)
Тема. Разложение положительной обыкновенной дроби в конечную
десятичную дробь.![]()
Цель. Проанализировать выполнение к/р. Провести коррекцию их знаний и умений. Научится раскладывать положительную обыкновенную дробь в конечную десятичную дробь.
Ход урока.
-
Организационный момент.
-
Анализ контрольной работы.
-
Объяснение нового материала.
Разложение положительной обыкновенной дроби в
конечную десятичную дробь.![]()
До сих пор мы рассматривали десятичные дроби, которые называют конечными, потому что после запятой у них стоит конечное число цифр.
В дальнейшем мы будем рассматривать и бесконечные десятичные дроби. У них после запятой бесконечно много цифр.
Конечные десятичные дроби всегда можно записать в виде обыкновенных дробей.
Пример 1. Представьте конечную десятичную дробь в виде несократимой обыкновенной дроби и разложить знаменатель на простые множители:
1) 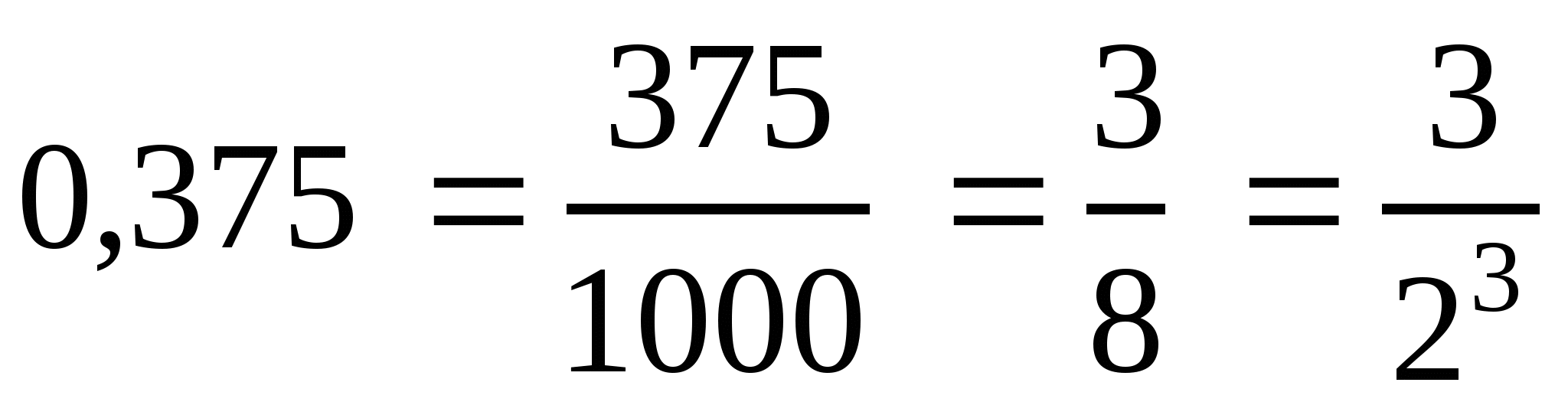 (сократили на 25);
(сократили на 25);
Признак делимости на 25. Если число оканчивается двумя нулями или две последние цифры выражают число, делящееся на 25, то оно делится на 25.
2) 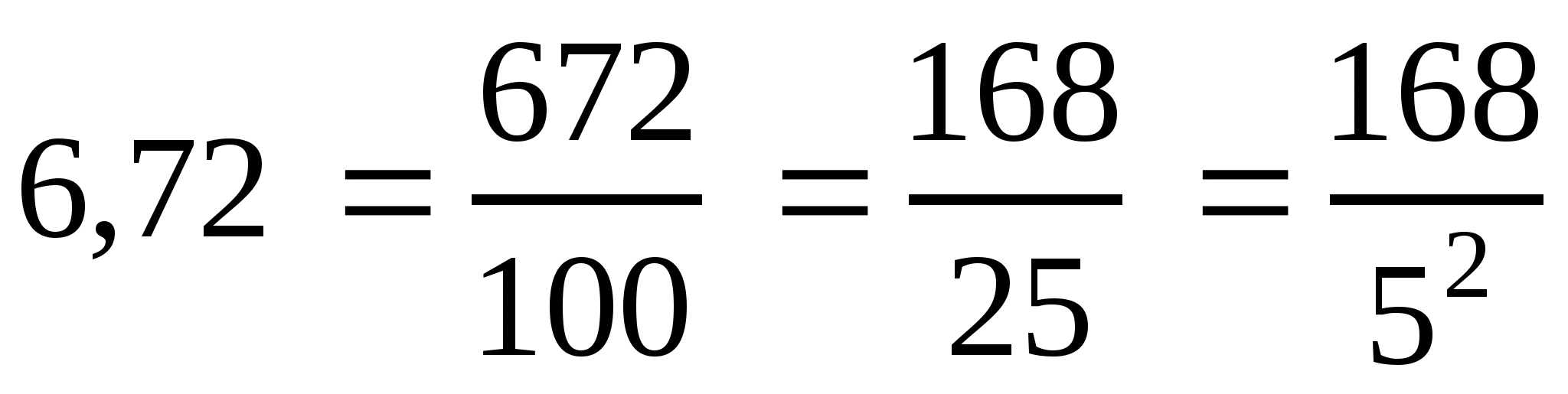 (сократили на 4);
(сократили на 4);
Признак делимости на 4. Если число оканчивается двумя нулями или две последние цифры выражают число, делящееся на 4, то оно делится на 4.
3) 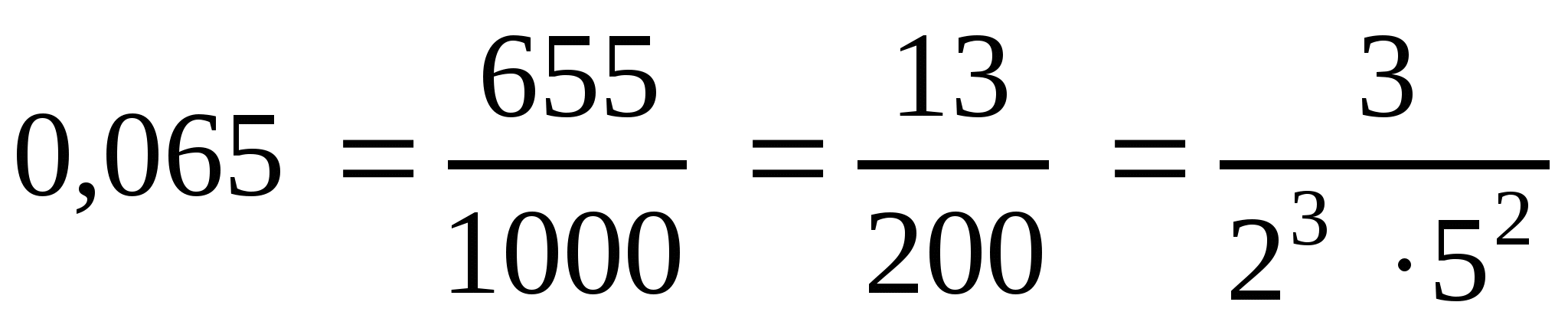 (сократили на 5).
(сократили на 5).
Признак делимости на 5. Если число оканчивается одной из цифр 0 или 5, то оно делится на 5.
Из этих примеров видно, что
Правило. Если конечную десятичную дробь записать в виде
обык-новенной несократимой дроби ![]() , то ее знаменатель q не имеет других простых делителей, кроме
2 и 5.
, то ее знаменатель q не имеет других простых делителей, кроме
2 и 5.
Верно и обратное утверждение.
Правило. Если знаменатель q несократимой дроби ![]() не имеет других простых делителей, кроме 2 и 5, то эта дробь
разлагается в конечную десятичную дробь.
не имеет других простых делителей, кроме 2 и 5, то эта дробь
разлагается в конечную десятичную дробь.
Для разложения обыкновенной несократимой дроби, знаменатель
которой не имеет других простых делителей, кроме 2 и 5 в конечную
десятичную дробь, существует два способа. Один из них сводится к
умножению числителя и знаменателя дроби ![]() на соответствующую степень числа 2 или числа 5. Другой способ
деление числителя на знаменатель уголком.
на соответствующую степень числа 2 или числа 5. Другой способ
деление числителя на знаменатель уголком.
Пример 2. Разложите обыкновенную дробь в конечную десятичную
дробь: 1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() .
.
1) ![]() . 1 способ. Числитель и знаменатель дроби умножим на 2, чтобы
получить в знаменателе 10:
. 1 способ. Числитель и знаменатель дроби умножим на 2, чтобы
получить в знаменателе 10:
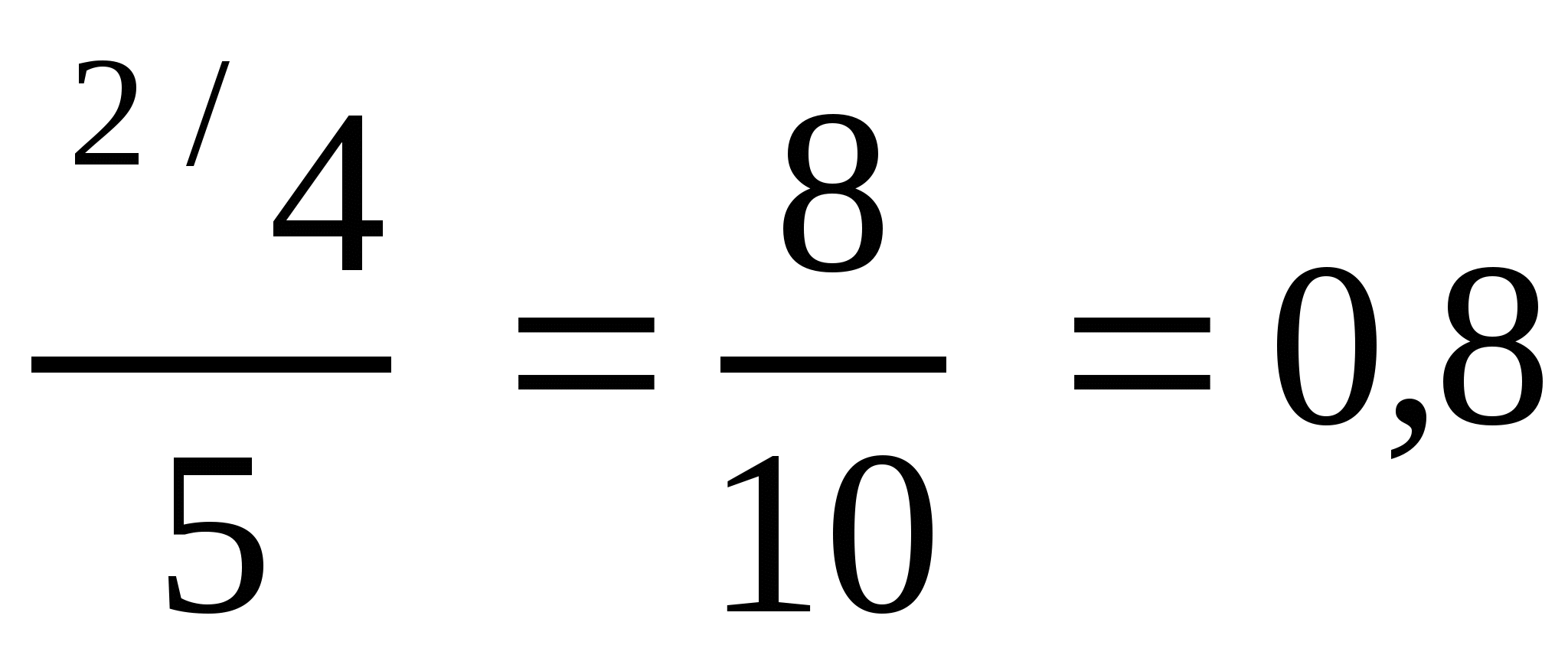 .
.
2 способ. Деление числителя на знаменатель уголком:
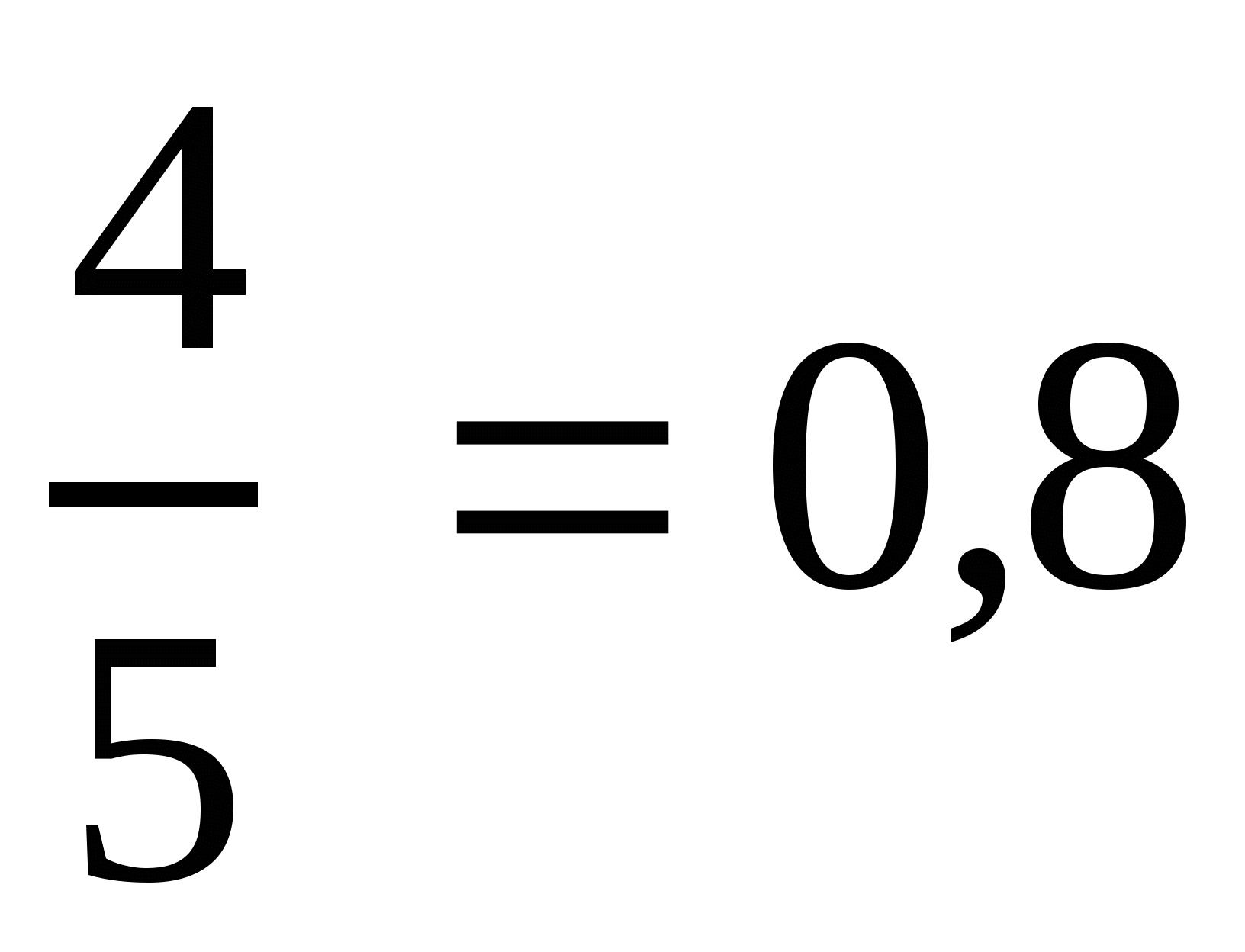
 .
.
2) ![]() . 1 способ. Числитель и знаменатель дроби умножим на 5, чтобы
получить в знаменателе 1000:
. 1 способ. Числитель и знаменатель дроби умножим на 5, чтобы
получить в знаменателе 1000:
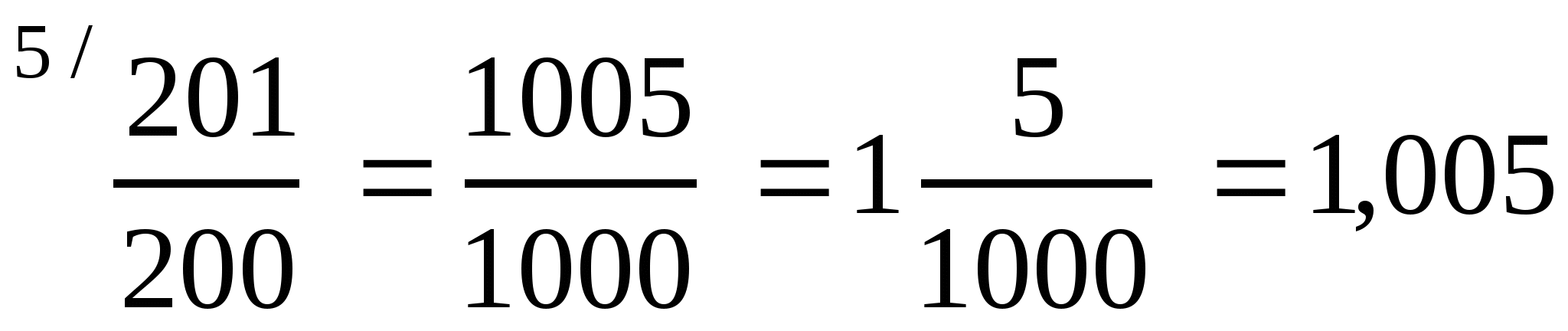 .
.
2 способ. Деление числителя на знаменатель уголком:
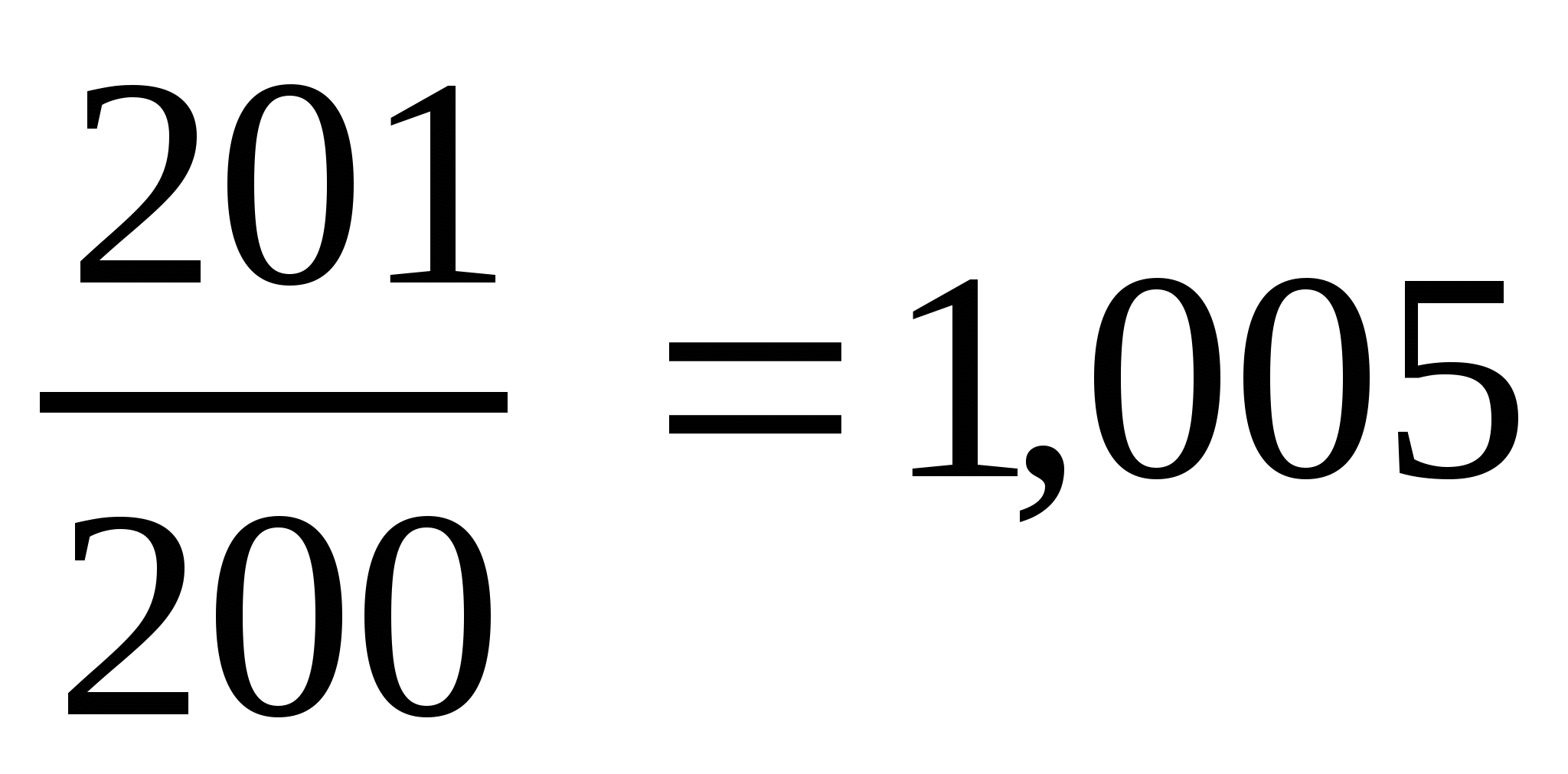
 .
.
3) ![]() . 1 способ. Числитель и знаменатель дроби умножим на 25, чтобы
получить в знаменателе 100:
. 1 способ. Числитель и знаменатель дроби умножим на 25, чтобы
получить в знаменателе 100:
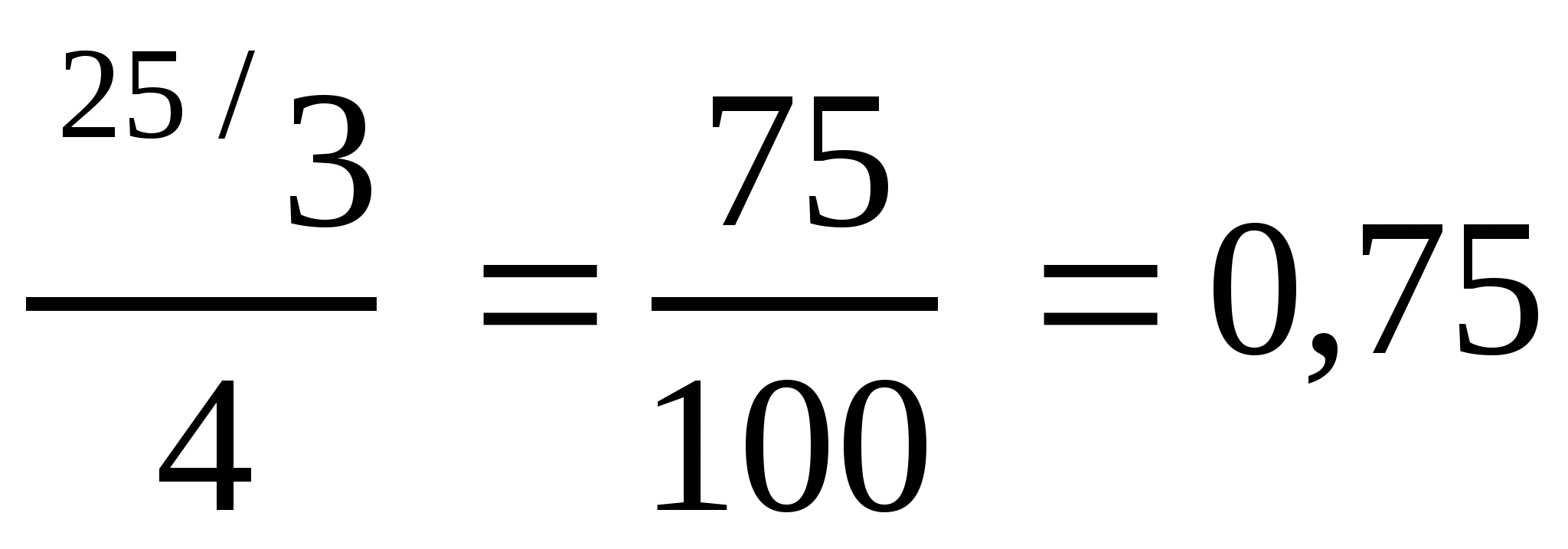 .
.
2 способ. Деление числителя на знаменатель уголком:
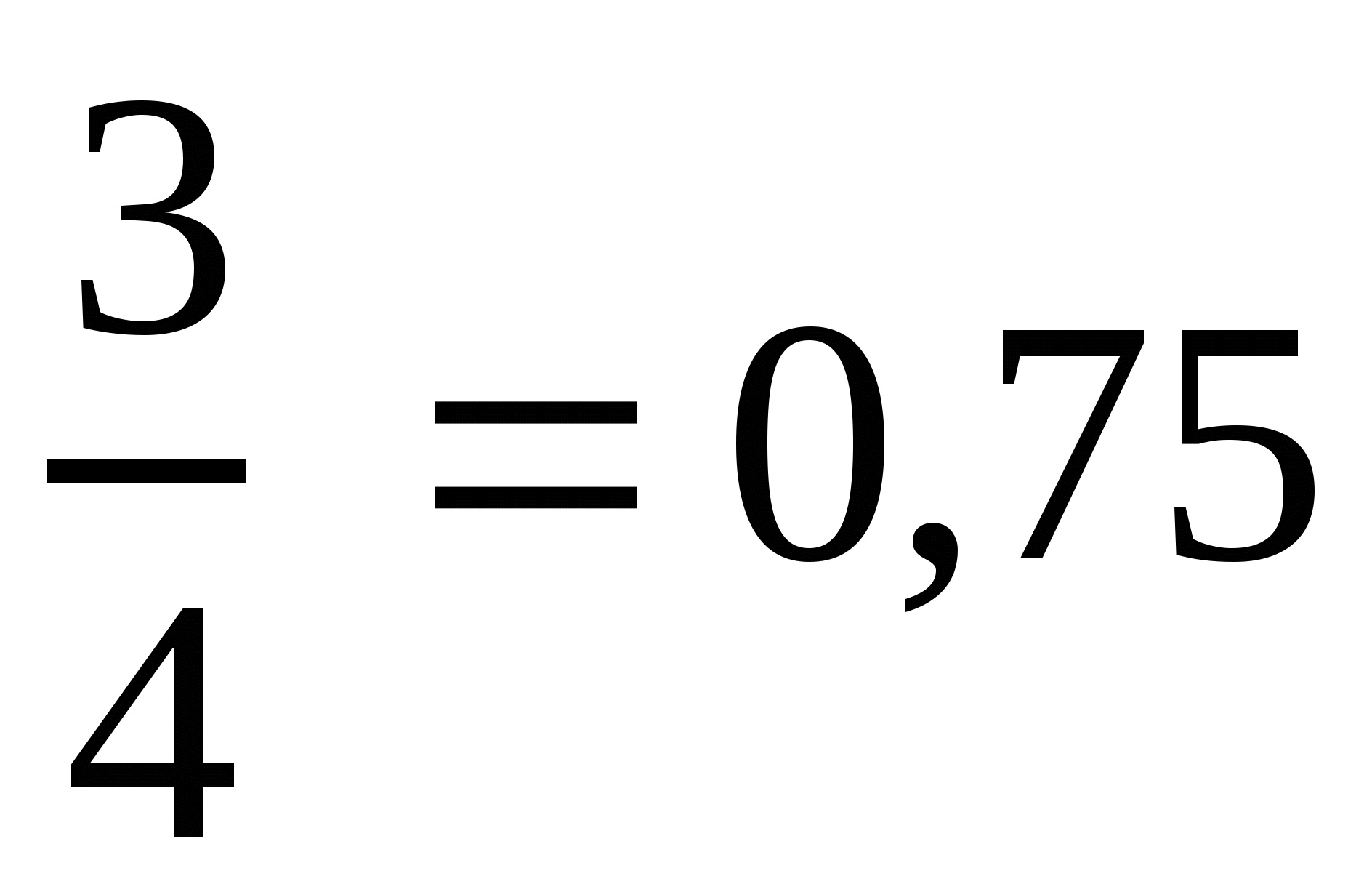
 .
.
-
Решение упражнений.
Уч.с.190 № 959(3 ст.). Какие простые множители содержит знаменатель дроби:
в) 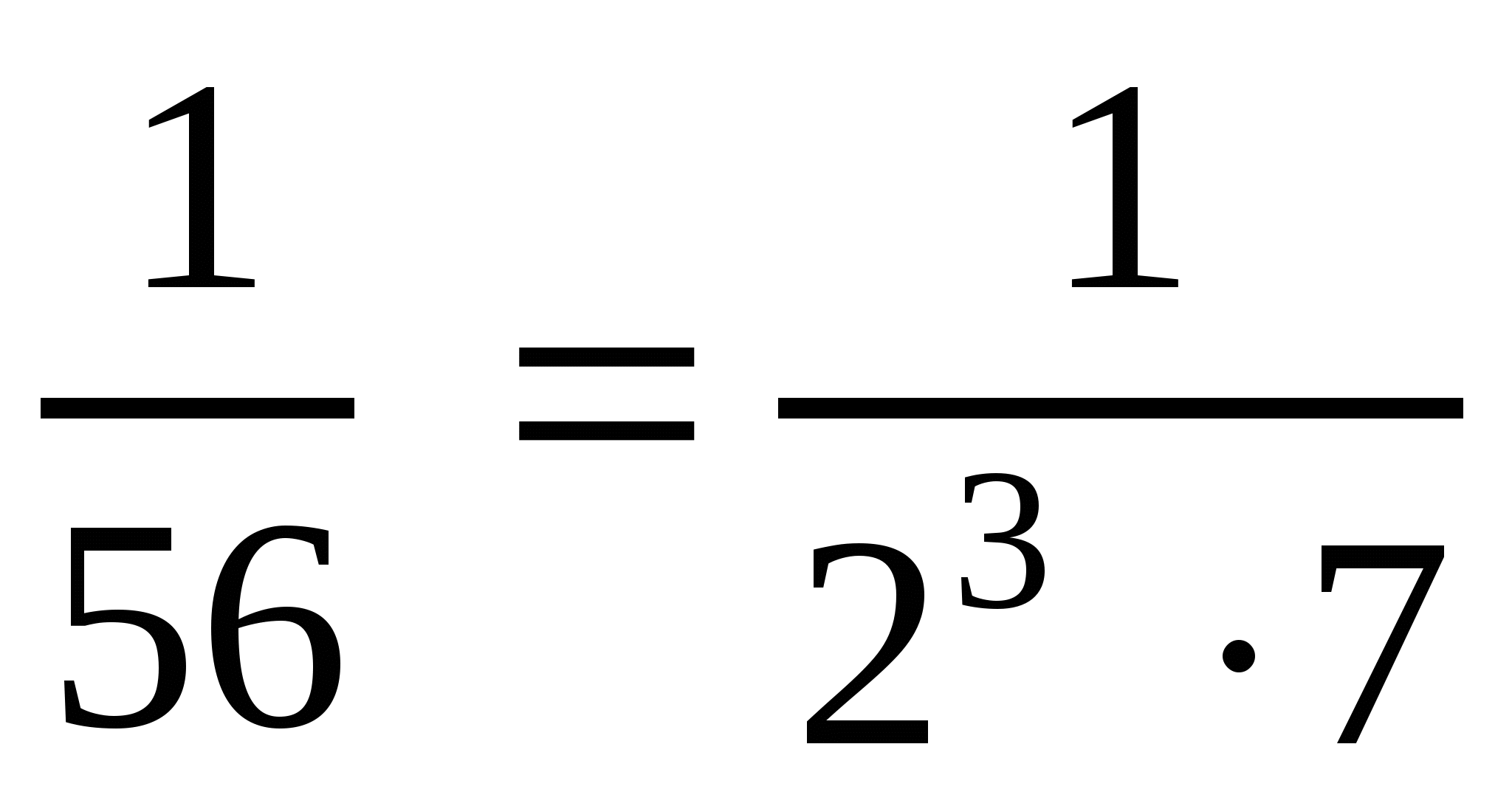 . Ответ: 2 и 7.
. Ответ: 2 и 7.
ж) 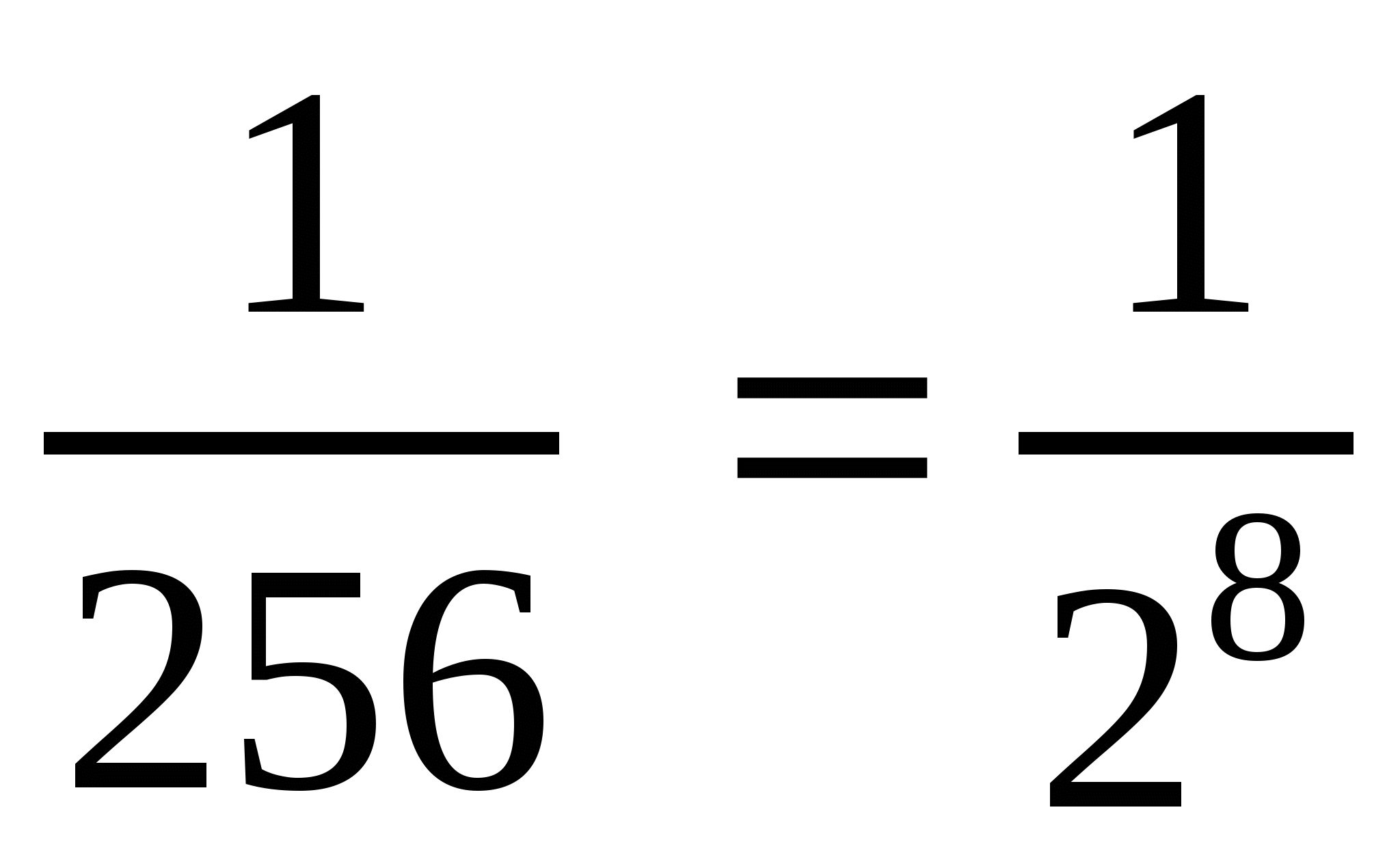 ; Ответ: 2.
; Ответ: 2.
л) 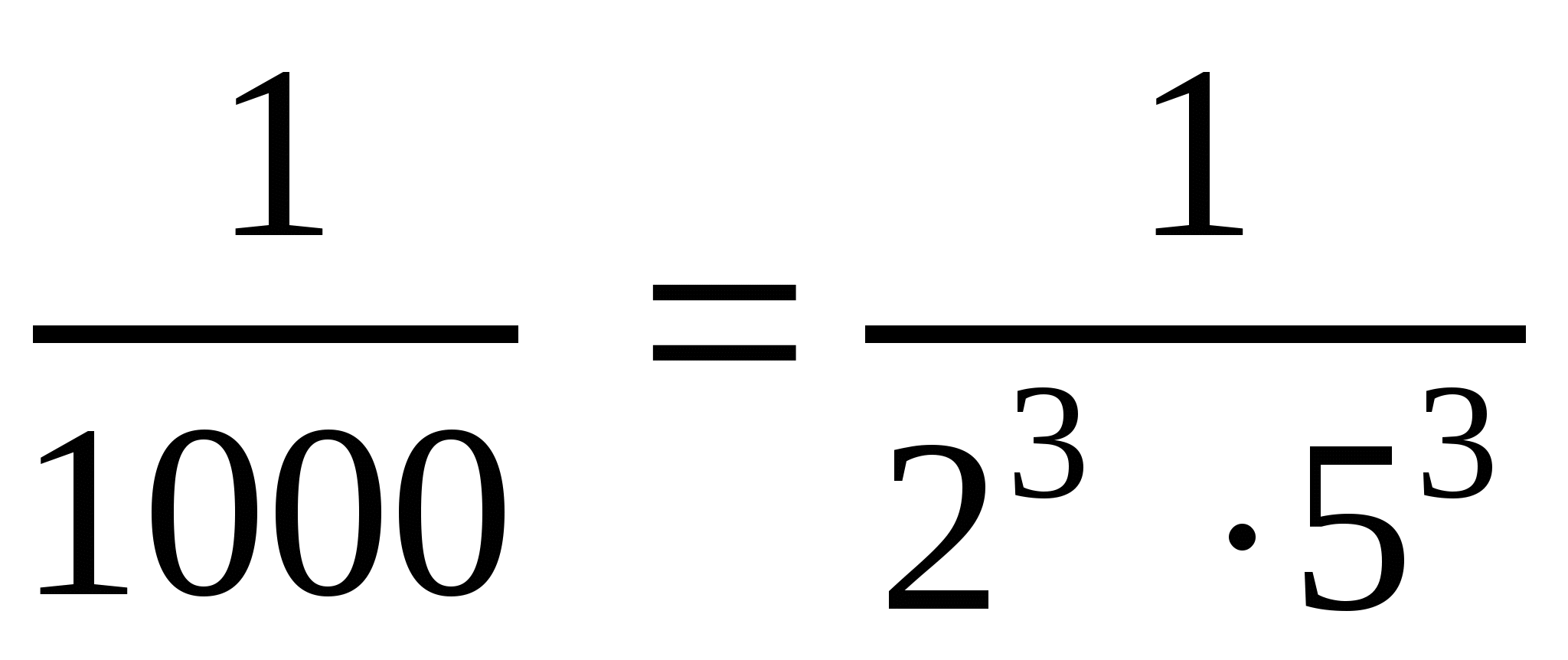 . Ответ: 2 и 5.
. Ответ: 2 и 5.
Уч.с.190 № 960(3 ст.). Сократите дробь:
в) 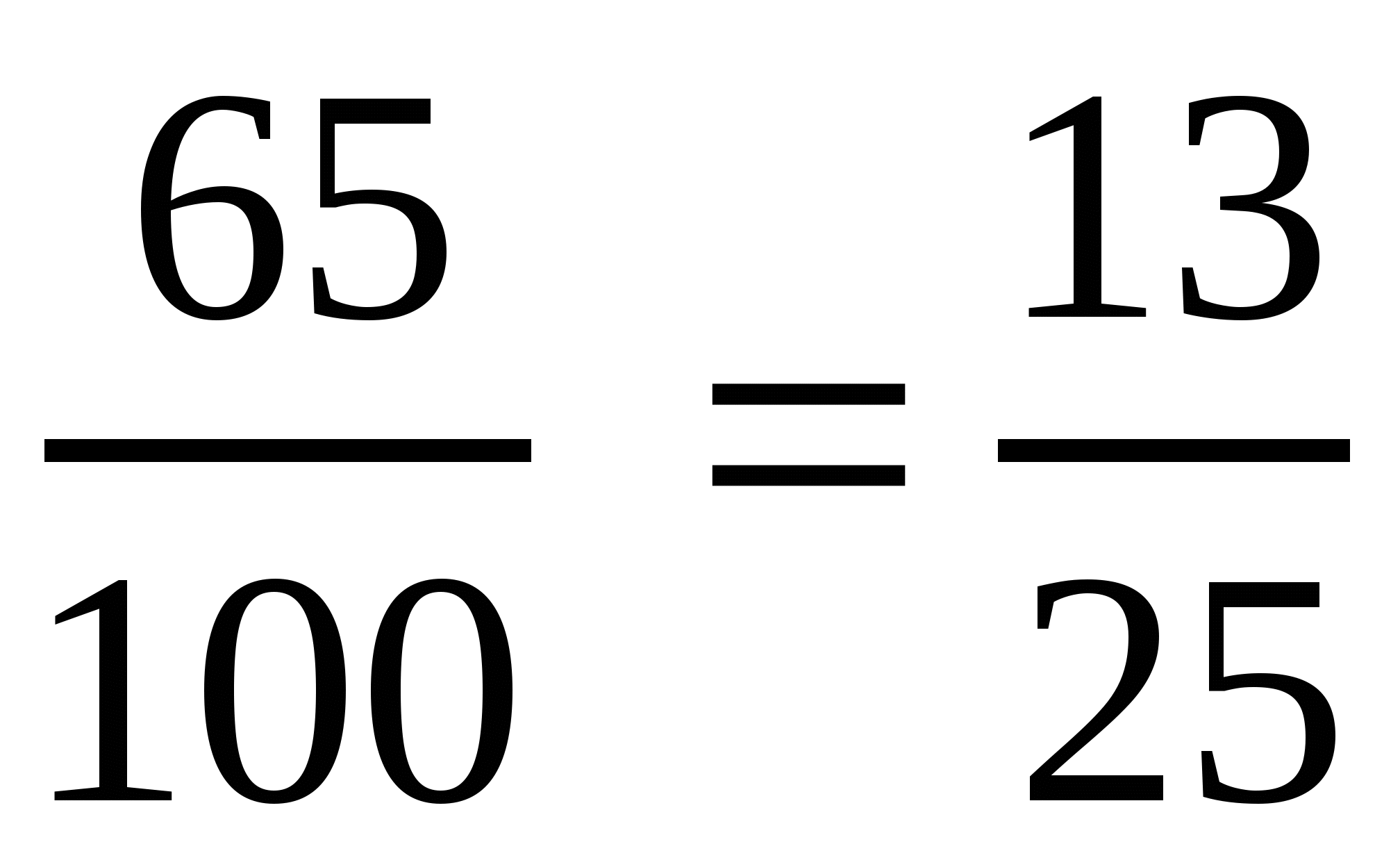 ; ж)
; ж) 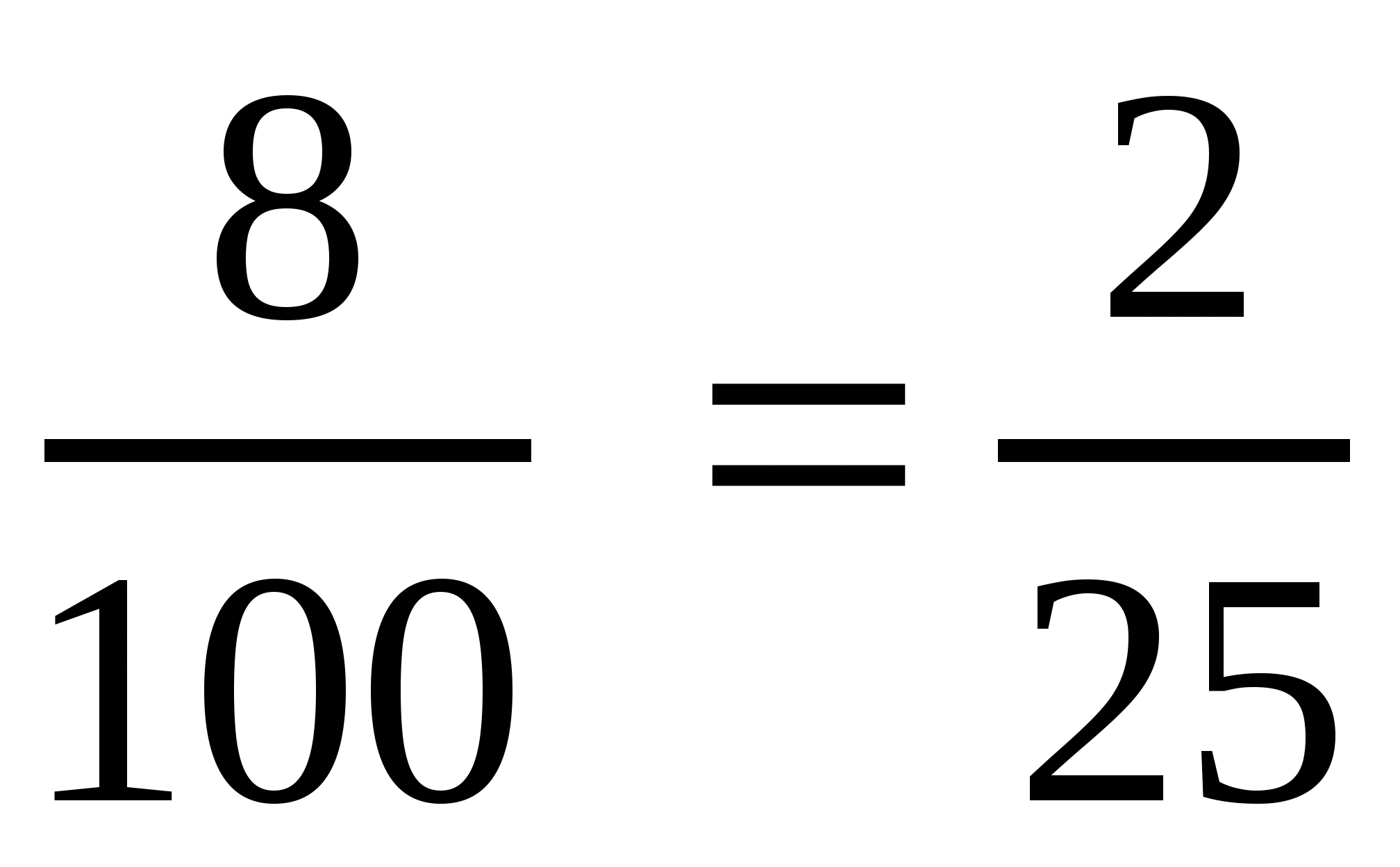 .
.
Уч.с.190 № 961(3 ст.). Запишите в виде обыкновенной несократимой дроби:
в) 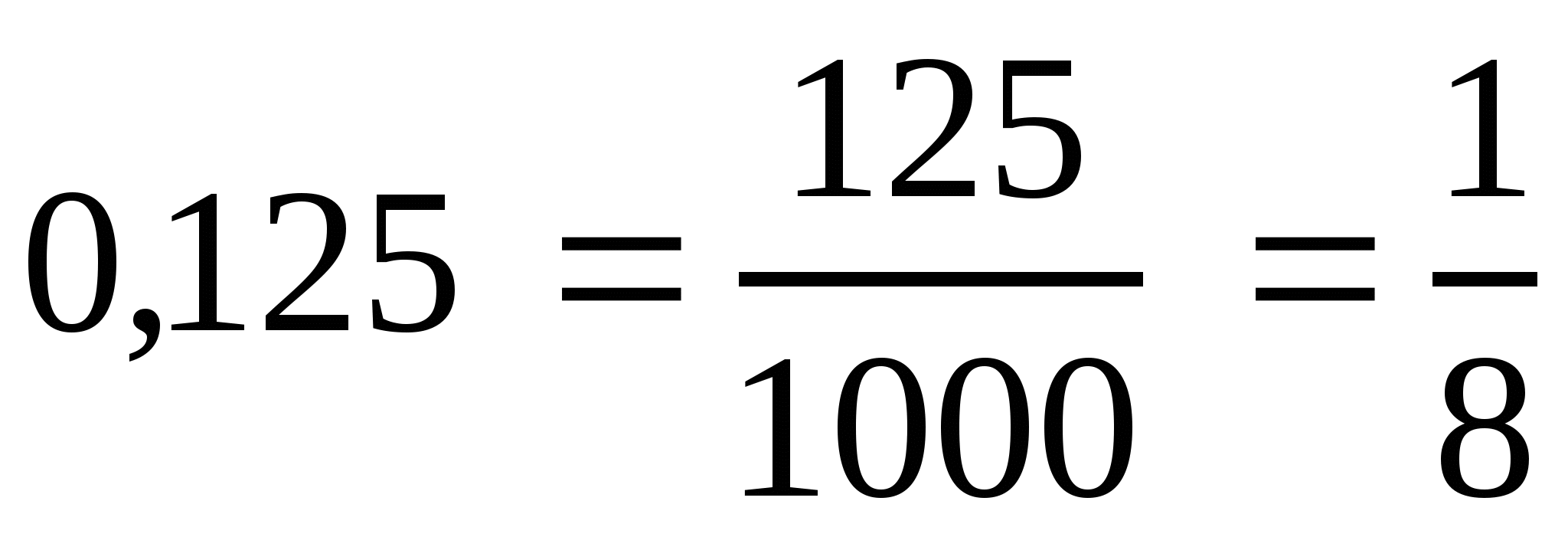 ; ж)
; ж) 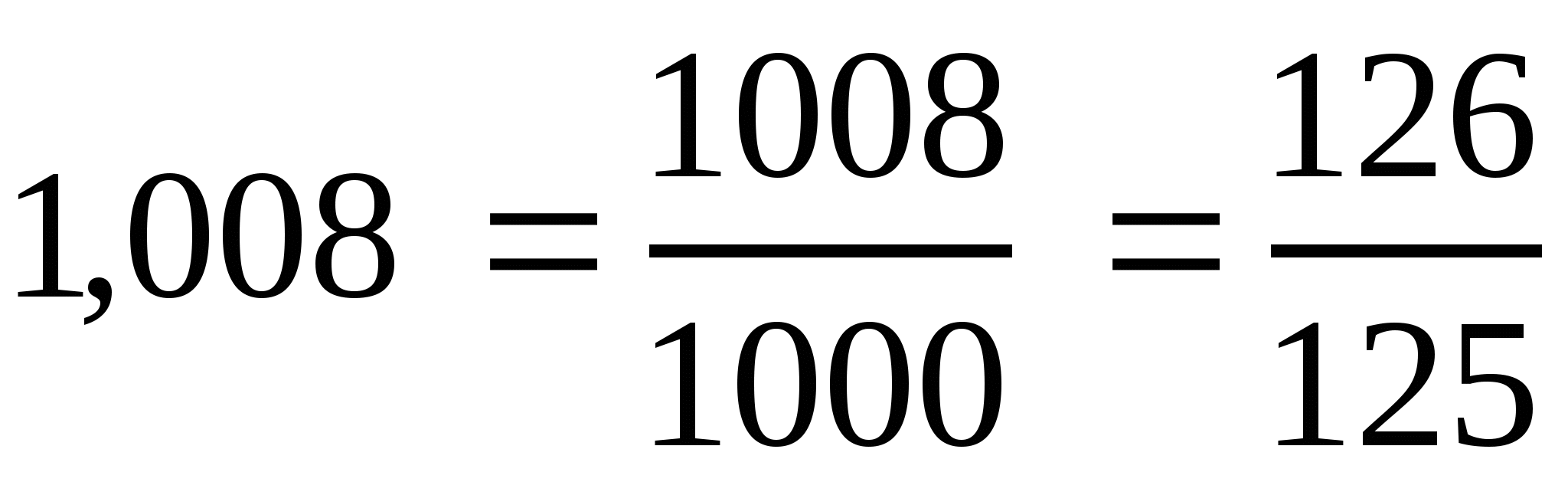 .
.
Уч.с.190 № 962(3 ст.). Приведите дробь к знаменателю 10, или 100, или 1000:
в) 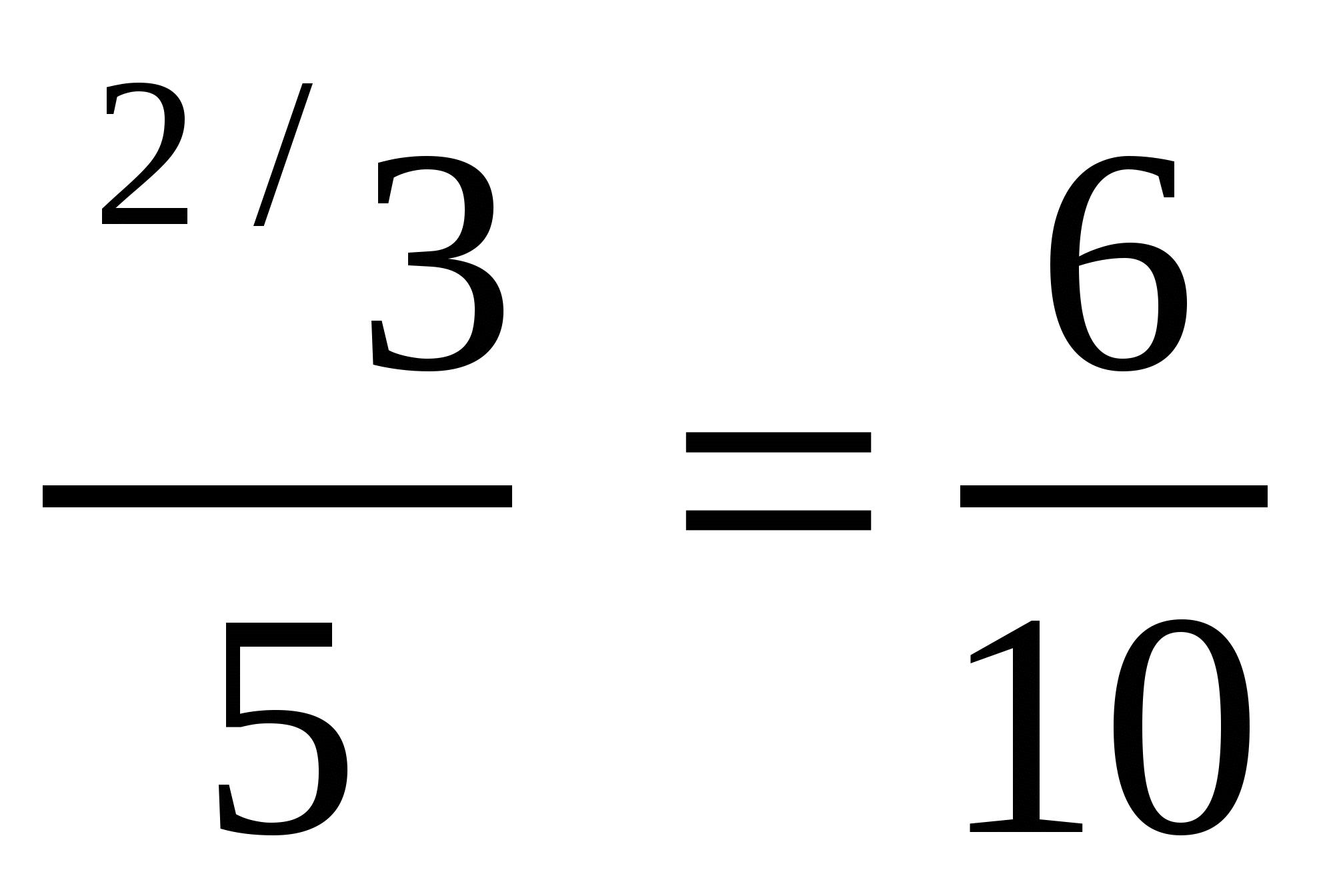 ; ж)
; ж) 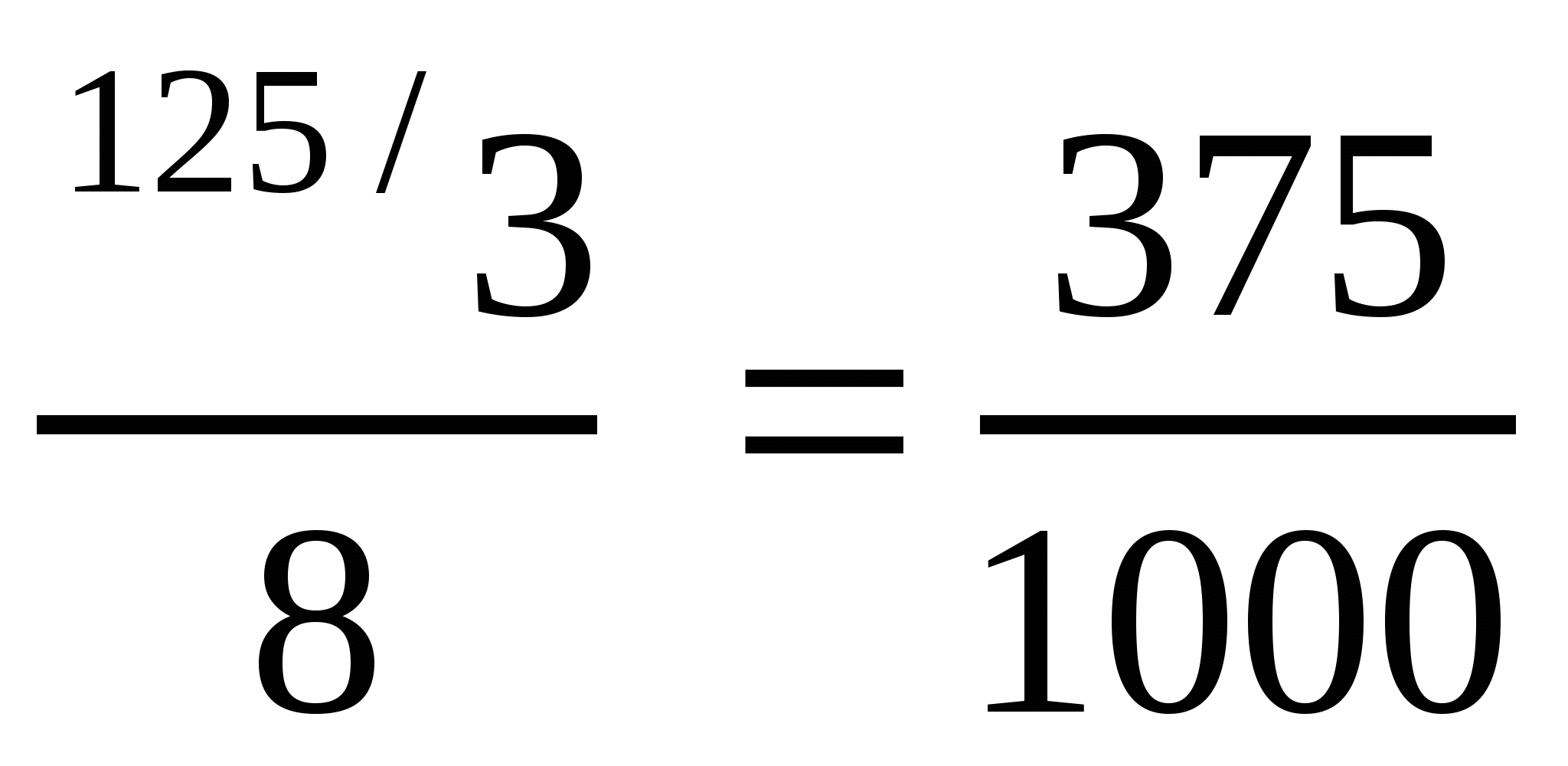 .
.
Уч.с.190 № 963(б). Разложите двумя способами в десятичную дробь:
б) ![]() .
.
1 способ. Числитель и знаменатель дроби умножим на 2, чтобы получить в знаменателе 10:
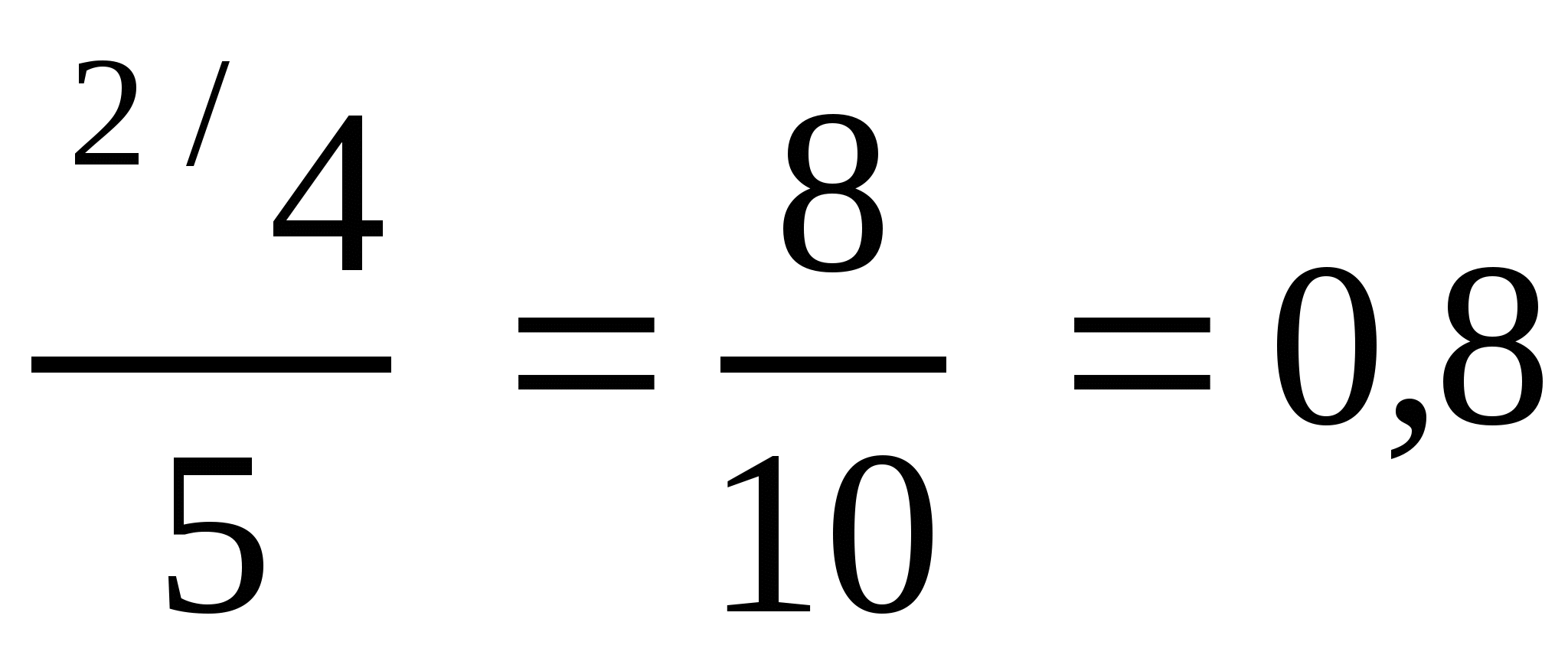 .
.
2 способ. Деление числителя на знаменатель уголком:
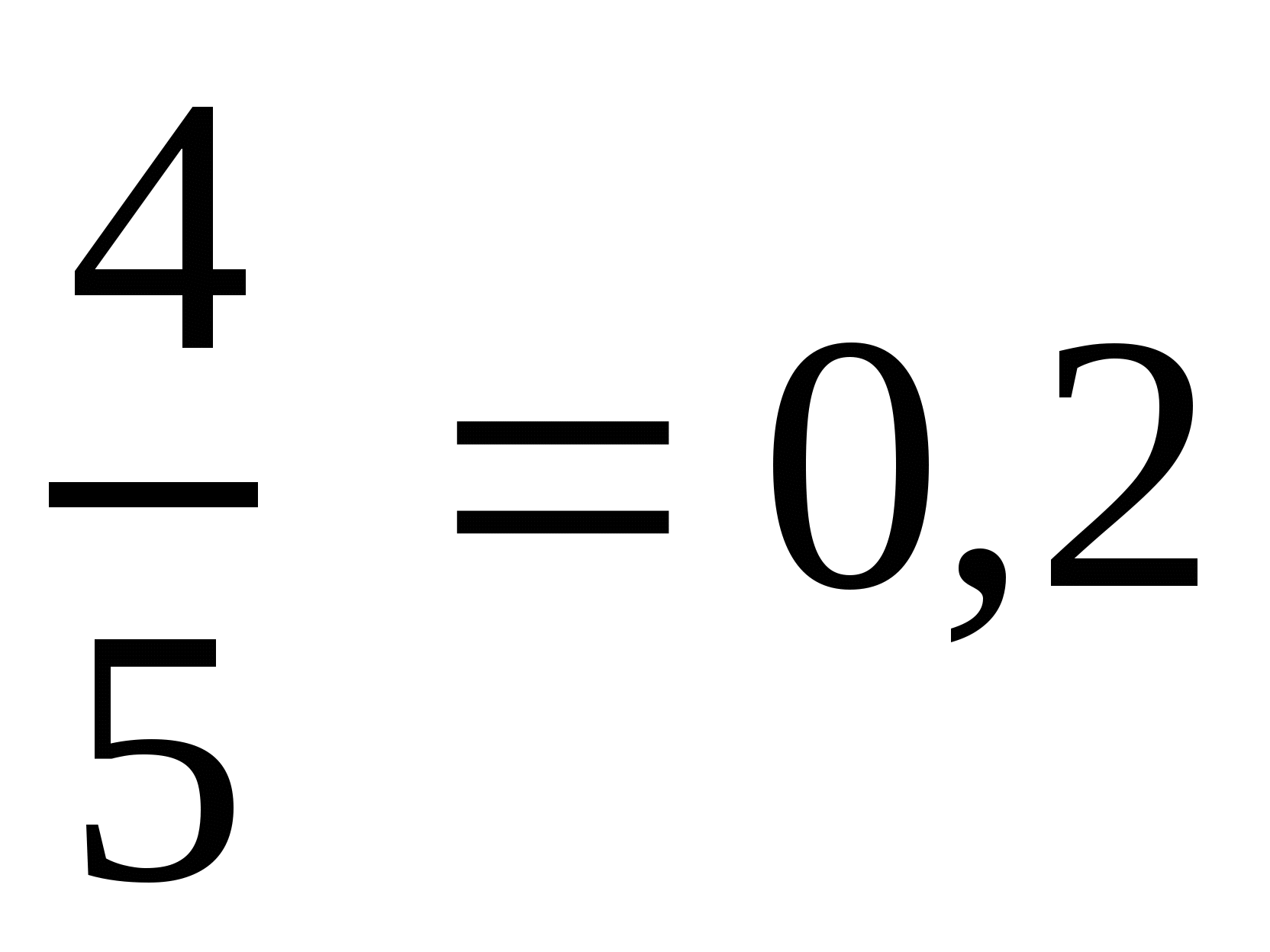 .
.
Уч.с.190 № 964(3-4ст). Разложите обыкновенную дробь в десятичную делением числителя на знаменатель уголком:
в) 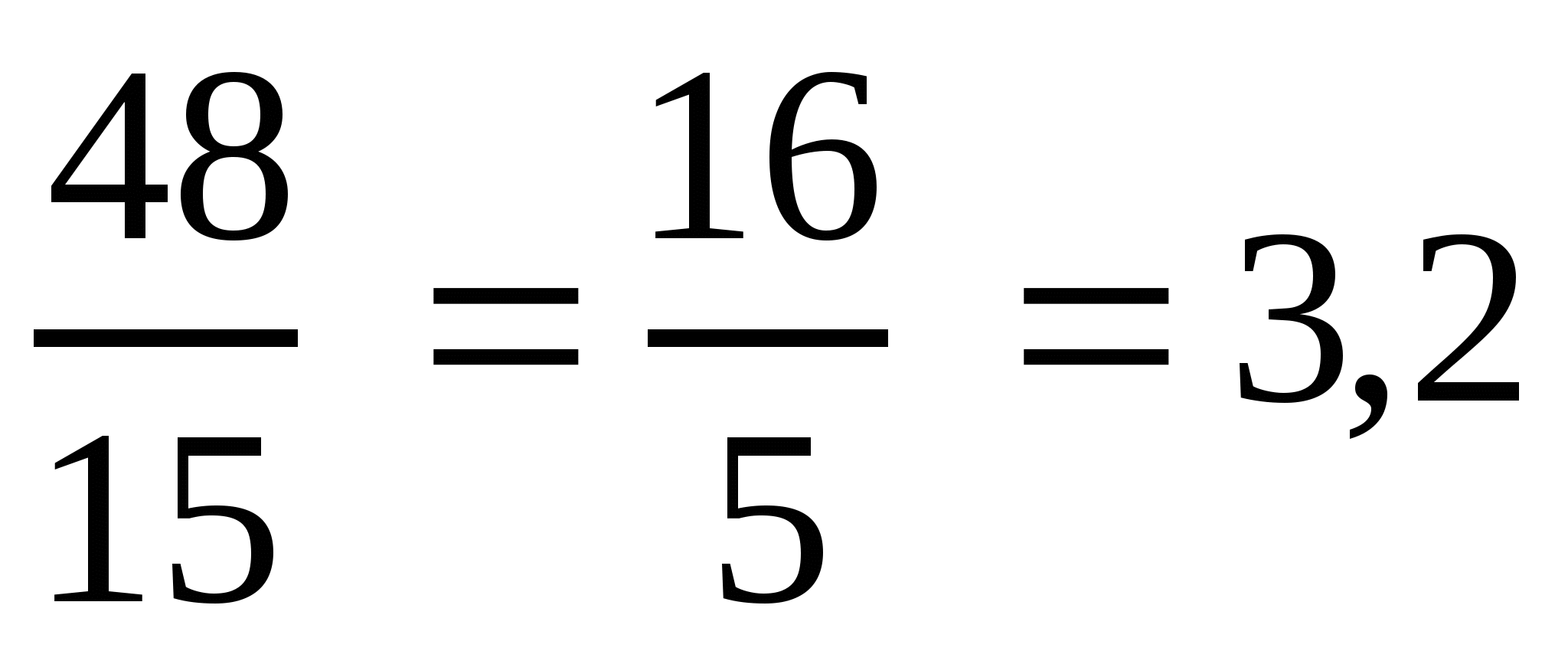 ; г)
; г) 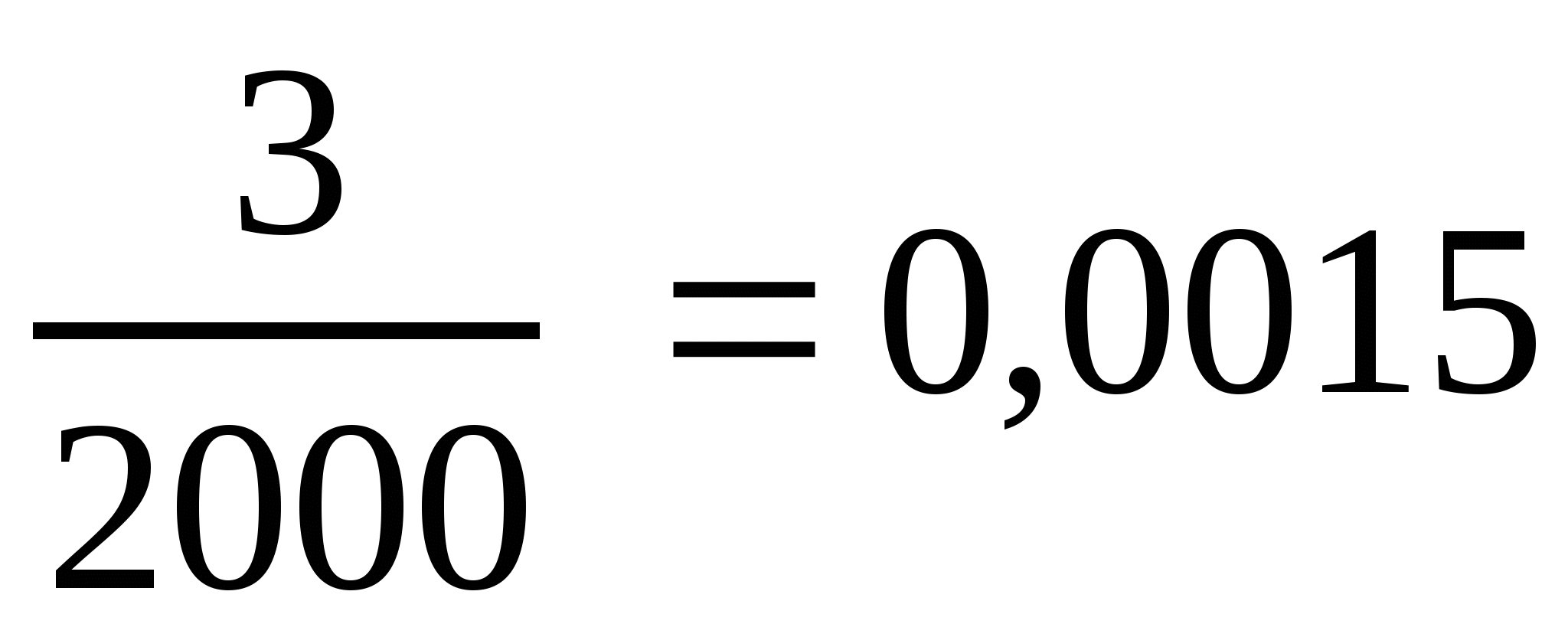 ;
;
ж) 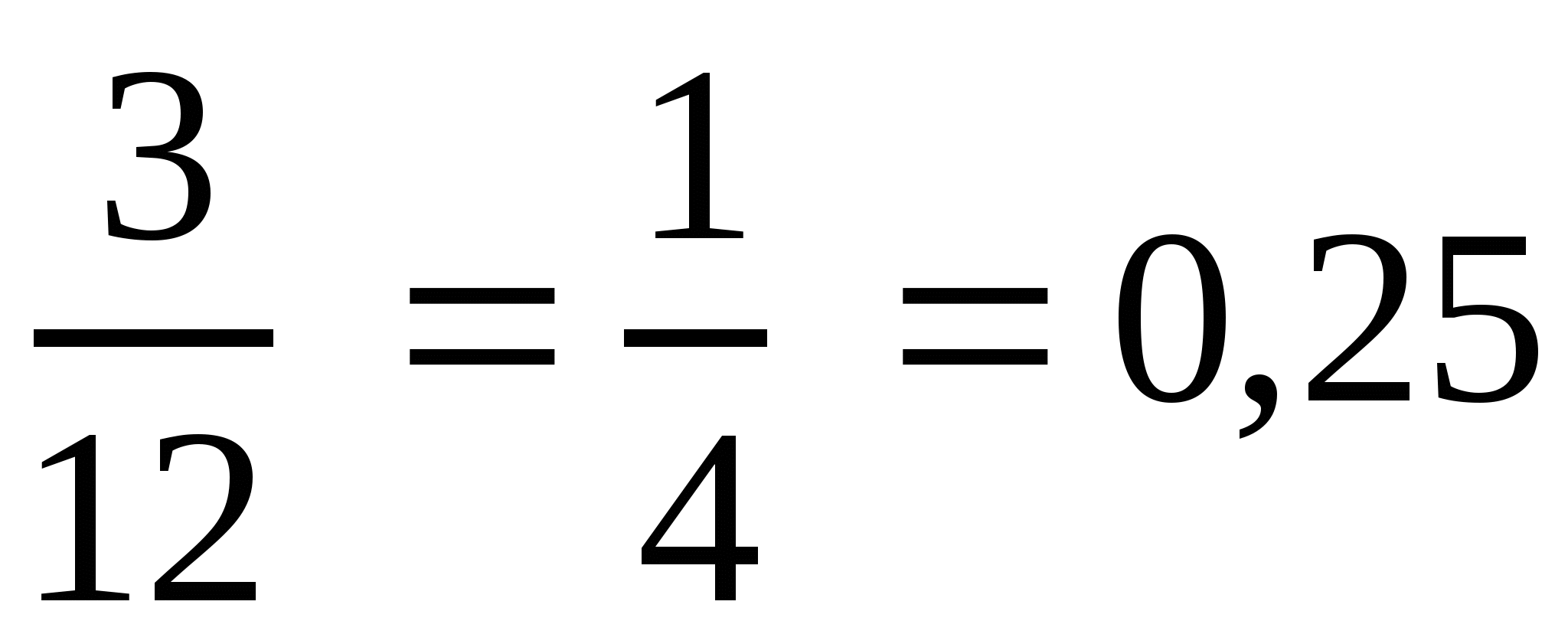 ; з)
; з) 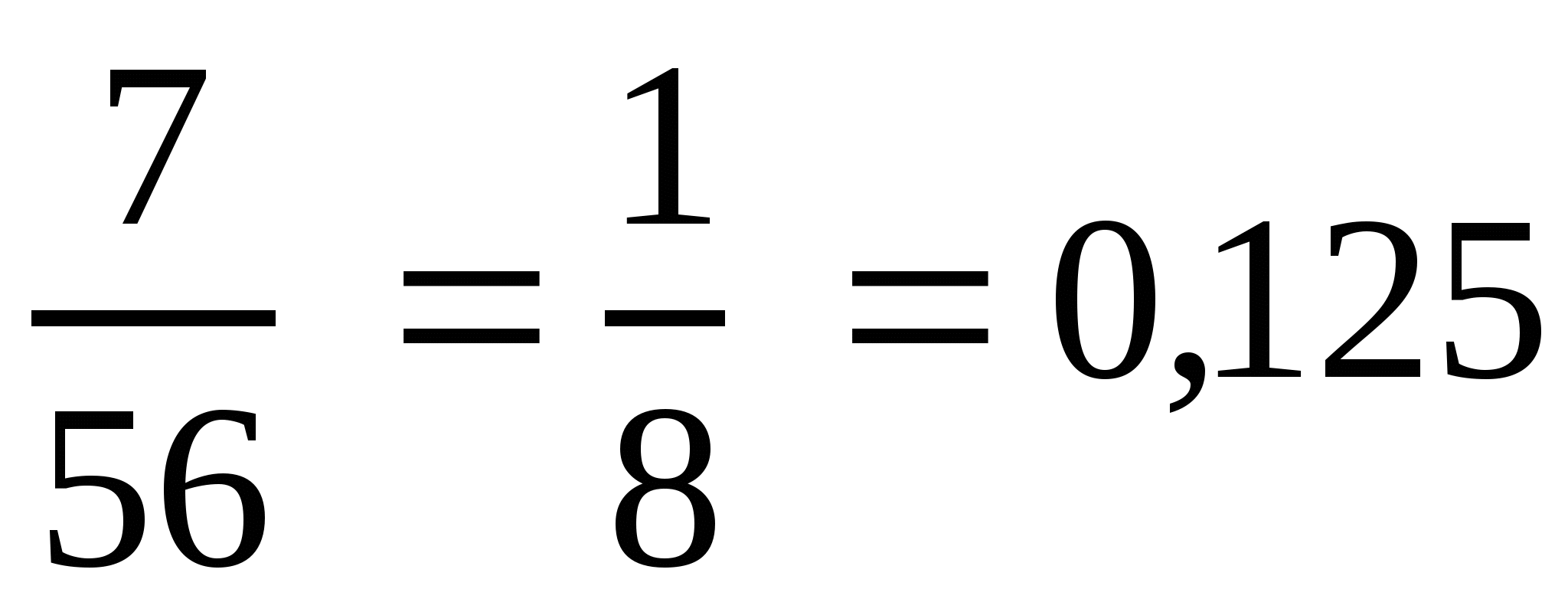 .
.
-
Подведение итогов урока.
-
Домашнее задание. п. 5.1 (выучить теорию). № 959(1ст.), 960(1ст.), 961(1ст.), 962(1ст.), 964(1-2ст.).